Next Article in Journal
Quantum Contextuality with Stabilizer States
Previous Article in Journal
An Entropy-Based Weighted Concept Lattice for Merging Multi-Source Geo-Ontologies
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Entropy
Volume 15
Issue 6
10.3390/e15062319
entropy-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Characterization of Ecological Exergy Based on Benthic Macroinvertebrates in Lotic Ecosystems

by
Mi-Jung Bae
1,
Fengqing Li
1,
Piet F.M. Verdonschot
2 and
Young-Seuk Park
1,3,4,*
1
Department of Biology, Kyung Hee University, Seoul 130-701, Korea
2
Alterra, Green World Research, Department of Freshwater Ecosystems, P.O. Box 47, 6700 AA Wageningen, The Netherlands
3
Research Institute for Basic Science, Kyung Hee University, Seoul 130-701, Korea
4
Department of Life and Nanopharmaceutical Sciences, Kyung Hee University, Seoul 130-701, Korea
*
Author to whom correspondence should be addressed.
Entropy 2013, 15(6), 2319-2339; https://doi.org/10.3390/e15062319
Submission received: 21 March 2013 / Revised: 30 May 2013 / Accepted: 1 June 2013 / Published: 7 June 2013
Browse Figures
Versions Notes

Abstract

:
The evaluation of ecosystem health is a fundamental process for conducting effective ecosystem management. Ecological exergy is used primarily to summarize the complex dynamics of lotic ecosystems. In this study, we characterized the functional aspects of lotic ecosystems based on the exergy and specific exergy from headwaters to downstream regions in the river’s dimensions (i.e., river width and depth) and in parallel with the nutrient gradient. Data were extracted from the Ecologische Karakterisering van Oppervlaktewateren in Overijssel (EKOO) database, consisting of 249 lotic study sites (including springs, upper, middle and lower courses) and 690 species. Exergy values were calculated based on trophic groups (carnivores, detritivores, detriti-herbivores, herbivores and omnivores) of benthic macroinvertebrate communities. A Self-Organizing Map (SOM) was applied to characterize the different benthic macroinvertebrate communities in the lotic ecosystem, and the Random Forest model was used to predict the exergy and specific exergy based on environmental variables. The SOM classified the sampling sites into four clusters representing differences in the longitudinal distribution along the river, as well as along nutrient gradients. Exergy tended to increase with stream size, and specific exergy was lowest at sites with a high nutrient load. The Random Forest model results indicated that river width was the most important predictor of exergy followed by dissolved oxygen, ammonium and river depth. Orthophosphate was the most significant predictor for estimating specific exergy followed by nitrate and total phosphate. Exergy and specific exergy exhibited different responses to various environmental conditions. This result suggests that the combination of exergy and specific exergy, as complementary indicators, can be used reliably to evaluate the health condition of a lotic ecosystem.

1. Introduction

The evaluation of ecosystem health is a fundamental process for conducting effective ecosystem management and developing proper environmental policies. In this context, various ecological indicators have been developed, including maximum power [1], diversity [2], biomass [3], emergy [4], exergy [5], ascendency [6] and entropy [7]. Of these indicators, exergy and specific exergy have been used most recently to assess ecosystem health in freshwater ecosystems [8,9,10,11,12].
Exergy, which was introduced into ecology at the end of the 1970s [13,14], represents the difference in the concentrations of specific components between the studied system and a reference state. However, we cannot precisely calculate the total exergy of an ecosystem because it is impossible to measure all of the possible contributions to exergy in a particular ecosystem [15]. Thus, exergy only provides a relative value in comparison with a predefined reference system [16,17]. However, changes in exergy (e.g., comparisons between two different structures) can be indicative of alterations in ecosystem function because exergy, as a holistic indicator, expresses the degree of development and complexity in the ecosystem of interest [17]. For this reason, exergy can be used to assess ecosystem health [18,19]. Exergy represents the total information carried by the biomass, and specific exergy is the relative exergy carried by the units of matter [20]. More developed organisms have more biological information content per unit, and they usually inhabit higher trophic levels and more complicated food webs than do less developed organisms. Therefore, a higher specific exergy is expected in a more complicated ecosystem with more efficient niche utilization [21,22,23]. If the total biomass is constant in a certain system, then variations in exergy largely depend on its structural complexity.
The effectiveness of exergy and specific exergy have been demonstrated in aquatic ecosystems [10,17,24] to assess natural disturbance [25], water quality (e.g., acidification, copper, oil, pesticide contamination [26] and eutrophication [15,20,27,28,29]), course type [16], the food webs of phytoplankton, zooplankton and fish [11] and the temporal changes of aquatic ecosystems from yearly [30] and long-term monitoring [31].
Among the various groups of freshwater organisms, benthic macroinvertebrate assemblages are highly diverse in most streams and play important roles in both bottom-up and top-down processes, such as detritus processing, animal-microbial interactions, herbivory and energy transfer to consumers at higher trophic levels [31,32]. Benthic macroinvertebrates employ a wide variety of structural and functional responses to various factors (e.g., longitudinal changes in energy sources, food webs, nutrient input and pollution gradients) [33] because macroinvertebrate species possess diverse life cycles and generation times and represent several trophic levels and different feeding behaviors. Exergy has typically been used in benthic studies [10] because it has been a useful functional indicator for the evaluation of the impacts of human disturbance on benthic communities [34].
Structural indicators based on community composition (e.g., species richness, Shannon diversity, Simpson diversity and evenness) have been used as surrogates for functional indicators (e.g., metabolism, productivity, emergy and exergy). The patterns (structure) determine the processes (function) and the processes in turn influence the patterns [35]. Structural indicators alone, however, cannot detect all types of impairment [36]. Thus, true functional studies should be developed and included to assess the health and integrity of running-water ecosystems. Previous studies of general system patterns, in terms of their functional and structural aspects, produced contradictory results due to differences in environmental conditions, such as forest composition [37,38,39], pH gradient [38], water abstraction [40,41], temperature [42], nutrient gradients [42] and land-use types [43,44,45]. Therefore, improving our understanding of the relationships between structural and functional indicators will support the monitoring and assessment of lotic ecosystems [46].
The aim of this study is to characterize changes in the functional aspects of lotic ecosystems in terms of exergy and specific exergy using benthic macroinvertebrate communities from the headwaters to downstream. Accordingly, we assume that exergy and specific exergy respond differently to the effects of various environmental characteristics and hypothesize that: (1) the patterns of exergy and specific exergy differ along an upstream to downstream hydrological gradient (i.e., river width and depth gradient), and (2) high nutrient loads can cause exergy to increase whereas specific exergy to decrease.

2. Materials and Methods

2.1. Ecological Data

Macroinvertebrate data were extracted from the “Ecologische Karakterisering van Oppervlaktewateren in Overijssel (Ecological characterization of surface waters in the province of Overijssel: EKOO)” database in The Netherlands [47]. The EKOO database was compiled from 1981 through 1985 to improve aquatic ecosystem management through the use of water typology to establish a baseline course, including a total of 650 sampling sites classified into 42 different water body types representing both lotic and lentic conditions (e.g., acid springs, springs, temporary streams, upper courses, stream pools, middle courses, lower courses, canals, ditches, lakes, ponds and moorland pools). From the 42 water-body types, we selected 249 sampling sites from four river types (springs: 52 sites, upper courses: 46 sites, middle courses: 76 sites and lower courses: 75 sites) to characterize the longitudinal gradient (Table 1). The details of the sampling protocols for the EKOO database were described in Verdonschot and Nijboer [47].
In total, 690 species were identified from 249 sampling sites. Community diversity indices (species richness, Shannon index, Simpson index and evenness) were calculated to compare the structural characteristics of the four different river course types.
Feeding strategies of macroinvertebrates reflect the adaptations of species to environmental conditions [48]. Accordingly, a functional feeding classification for macroinvertebrates would improve the knowledge of trophic dynamics in streams [49]. Changes in the distribution patterns of the functional feeding groups (FFGs: scrapers, shredders, gatherers, filterers, predators and piercers), as well as the trophic guilds (carnivores, detritivores, detriti-herbivores, herbivores and omnivores), would reflect the environmental gradient of a lotic ecosystem. Although trophic guilds differ from FFGs, FFGs have been used widely as an alternative to trophic guilds in macroinvertebrate studies [50]. Thus, FFGs have been used to characterize the spatial changes in FFG composition in response to environmental changes in lotic ecosystems, as reviewed in Mihuc [51].
Nineteen environmental variables were selected to reflect the different habitat conditions in the four river course types (Table 1). There were distinct longitudinal gradients in geological and hydrological variables; the slope tended to decrease, and the river width and depth tended to increase along rivers from the springs toward the lower courses. The substrates were classified into two categories (micro substrates: the sum of the relative proportions of peat, clay, silt and sand; and macro substrates: the sum of the relative proportions of gravel and stone). The relative proportion of macro substrate was the highest in the springs, and micro substrate proportions were highest in the middle courses. The sampling sites in springs showed the lowest relative proportion of all macrophyte growth forms, a category that comprises emergent, floating and submerged macrophytes. The relative proportion of floating macrophytes was the highest in the lower courses. The concentrations of ammonium (NH4+), orthophosphate (o-P), total phosphate (t-P), chloride (Cl−) and calcium (Ca2+) were relatively low in the springs and lower courses, and the concentration of nitrate (NO3−) was highest in the springs. All other water quality variables, except for dissolved oxygen (DO) and NO3−, were highest in the middle courses, indicating a high nutrient load or eutrophic conditions [52].

2.2. Exergy

Ecological exergy is defined as the amount of work a system can perform if it is brought to thermodynamic equilibrium with its environment or a reference state [13,21]. The exergy of an ecosystem cannot be measured exactly because of the high complexity of almost any ecosystem. However, exergy may be calculated for each system component [53] and thus provide an exergy index as a model of an ecosystem [16]. According to Jørgensen et al. [24], exergy (Ex) can be calculated as follows in Equation (1):
Entropy 15 02319 i001
where Ci is the concentration of component i (i.e., the biomass of species i) in the ecosystem and βi is the weight coefficient that expresses the “quantity of information” embedded in the biomass [54]. Detritus is used as a reference level (βi = 1), and exergy is calculated using this equation in detritus energy equivalents. We multiplied the exergy value by 18.7 to express exergy in units of kJ [55]. In this study, the weighting coefficients were based on trophic groups (carnivores, 47; detritivores, 30; detriti-herbivores, 32.5; herbivores, 35; and omnivores, 41) [56].
Specific exergy (SpEx) is defined as the exergy divided by the concentration of biological content and is calculated using Equation (2):
Entropy 15 02319 i002

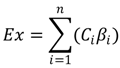
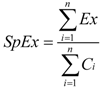
2.3. Self-Organizing Map

To characterize macroinvertebrate communities based on their abundance in the four river-course types, we applied Self-Organizing Maps (SOMs) [57,58]. SOM is an unsupervised learning algorithm based on artificial neural networks that approximates the probability density function of the input data [58]. A SOM consists of input and output layers connected with computational weights (connection intensities). The array of input neurons (computational units) operates as a flow-through layer for the input vectors, whereas the output layer consists of a two-dimensional network of neurons arranged in a hexagonal lattice.
In the learning process of a SOM, the input data (i.e., the abundances of 243 species) were initially subjected to the network. The number of output neurons was set to 77 (= 11 × 7) in a 2D hexagonal lattice derived from previous experience and a preliminary study. The weights of the network were trained for a given dataset. Each node of the output layer computes the summed distance between the weight and input vectors. The output nodes are considered to be virtual units that represent typical patterns of the input dataset assigned to their units after the learning process [59]. Among all of the virtual units, the best matching unit, which has the minimum distance between weight and input vectors, becomes the winner. For the best matching unit and its neighborhood units, new weight vectors are calculated by the SOM learning rule. This procedure trains the network to classify the input vectors according to the weight vectors that are closest to the inputs. For the training SOM, we used the functions provided in the SOM toolbox [60] in Matlab for Windows, version 6.1 [61].
We used two different methods to cluster the trained SOM units into several groups. First, the unified distance matrix algorithm (U-matrix) [62] was applied. The U-matrix calculates distances between neighboring map units, and these distances can be visualized to represent clusters using a grey scale display on the map. Second, a hierarchical cluster analysis with Ward's linkage method based on the Euclidean distance measure [63] was applied to the weights of the SOM output units [59,64]. After the clusters in the SOM analysis were defined, Multi-Response Permutation Procedures (MRPP) were conducted to test whether there was a significant difference among the clusters. The analyses were performed using PC-ORD for Windows version 5.0 [65].
Prior to the analysis of the SOM, we selected 243 species having an occurrence frequency of > 5% in the study sites. Significant correlation was identified between the selected species and all other species through a Spearman correlation analysis (species richness: R2 = 0.988, abundance: R2 = 0.992, exergy: R2 = 0.985 and specific exergy: R2 = 0.926). The abundance data were natural log-transformed, with a value of one added to the abundance data to avoid taking logarithms of zero.
Indicator species analysis (IndVal) [66] was used to determine the significant indicator species in the clusters based on SOM analysis. IndVal determines indicator species by combining information on the relative abundance of species with their degree of occurrence in a particular group. Indicator values range from 0 to a maximum value of 100. The maximum value indicates perfect indication for a particular group. Species having an IndVal greater than 25 were considered indicator species (i.e., individuals of a certain species were present in more than 50% of the samples in one cluster, and the relative abundance of the indicator species in the clusters was more than 50%) [67,68]. The significance of the indicator values for each species was tested with Monte Carlo permutation (9,999 random permutations) using PC-ORD for Windows version 5.0 [65].

2.4. Random Forest

The Random Forest method [69] was used to evaluate the relative explanations of environmental variables for exergy and specific exergy. The Random Forest is a non-parametric method for the prediction and assessment of the relationship between a group of potential predictor variables and a response variable [69]. To measure feature importance, we used the mean decrease Gini (MDG), which quantifies the importance of a variable by summing all decreases in Gini impurity due to a given variable when the values of the variable are randomly permuted. This approach is based on a comparison with the original observations. The values of the MDG for each environmental variable were rescaled for exergy and specific exergy within a range of 0 to 100 to represent the relative importance of each environmental variable. Random Forest analysis was repeated 10 times, and the extracted MDG values were averaged for the smallest generalized error. This analysis was performed using the ‘randomForest’ package in R (http://cran.r-project.org).

2.5. Statistical Analysis

An analysis of variance (ANOVA) [70] test was used to evaluate the differences in exergy, specific exergy, community indices and environmental variables among the four river course types and among different clusters defined by the SOM results. A Tukey’s multiple comparison test was applied to detect significant differences between factors in the ANOVA test (p < 0.05). A Spearman rank correlation was applied to determine the relationships between community diversity indices, exergy and specific exergy. All statistical analyses were performed with STATISTICA for Windows version 7 [71].

3. Results

3.1. Differences in Biological Indices

Exergy and the community indices tended to increase from springs to the lower courses (Table 1). However, specific exergy was lowest in the middle courses and highest in the lower courses. The relative abundance (%) of shredders decreased from the springs (16.7%) to the lower courses (5.5%), whereas collector-filterers increased from the springs (8.3%) to the lower courses (17.9%) (Figure 1). The proportion of collector-gatherers was relatively high in the springs (47.6%) and the middle courses (45.2%), whereas scrapers (springs: 4.2% and middle courses: 8.8%) and piercers (springs: 2.0% and middle courses: 7.1%) were lower in these two river types.
Table
Table 1. Differences (mean (standard deviation)) of environmental variables and community indices at four different river types. Different letters indicate significant differences among four different river types based on a Tukey’s multiple comparison test (p < 0.05).
Table 1. Differences (mean (standard deviation)) of environmental variables and community indices at four different river types. Different letters indicate significant differences among four different river types based on a Tukey’s multiple comparison test (p < 0.05).
CategoryVariable (unit)AbbreviationRiver Type (number of study sites)
Spring (52)Upper (46)Middle (76)Lower (75)
Environmental variableSlope (m/km) 52.0 (5.8)a0.7 (0.2)b0.7 (0.1)b0.1 (0.0)b
Current velocity (m/s) 0.16 (0.02)a0.03 (0.01)b0.18 (0.02)a0.00 (0.01)b
Width (m) 0.7 (0.1)c2.0 (0.2)bc8.7 (0.8)b25.1 (3.2)a
Depth (m) 0.1 (0.0)c0.3 (0.0)c0.9 (0.1)b2.1 (0.2)a
Emergent macrophytes (%)Emergent_v3.8 (1.5)b17.9 (3.3)a6.47 (1.63)b19.3 (2.6)a
Floating macrophytes (%)Floating_v0.0 (0.0)c9.0 (2.7)ab5.1 (1.5)bc16 (2.3)a
Submerged macrophytes (%)Submerged_v1.4 (10)c18.9 (2.9)a13.59 (2.76)ab9.1 (1.9)bc
Detritus (%) 40.0 (3.4)a3.5 (1.4)b6.46 (1.34)b2.1 (0.8)b
Micro substrate (%) 36.2 (2.9)ab30.8 (3.0)bc42.27 (2.77)a21.7 (1.9)c
Macro substrate (%) 10.0 (2.0)a0.50 (0.50)b2.29 (0.76)b0.90 (0.40)b
pH 6.77 (0.08)c6.77 (0.14)c7.21 (0.06)b7.60 (0.05)a
Electric conductivity (μS/cm)Conductivity258.9 (11.5)c425.0 (30.5)b581.4 (40.9)a536.7 (18.1)a
Dissolved oxygen (mg/L)DO8.68 (0.41)b9.88 (0.54)ab9.84 (0.24)ab10.94 (0.44)a
Ammonium (mgN/L)NH4+0.16 (0.02)c2.40 (0.36)a1.95 (0.30)a0.73 (0.09)b
Nitrate (mgN/L)NO3−11.76 (1.11)a5.85 (0.95)b8.25 (2.08)b2.07 (0.19)c
Orthophosphate (mgP/L)o-P0.24 (0.08)b0.35 (0.13)b0.64 (0.12)a0.16 (0.06)b
Total phosphate (mgP/L)t-P0.24 (0.03)b0.56 (0.21)b1.03 (0.16)a0.39 (0.08)b
Chloride (mg/L)Cl−31.74 (1.89)b49.59 (10.71)ab65.02 (10.39)a58.03 (3.83)ab
Calcium(mg/L)Ca2+39.32 (2.5)b59.33 (5.07)a63.21 (2.61)a66.16 (2.15)a
Biological indexSpecies richness 28 (9)d37 (14)c56 (14)b82 (21)a
Shannon diversity 3.06 (0.34)d3.30 (0.43)c3.79 (0.29)b4.19 (0.26)a
Simpson diversity 0.94 (0.02)d0.95 (0.03)c0.97 (0.01)b0.98 (0.01)a
Evenness 0.93 (0.02)c0.94 (0.02)c0.95 (0.01)b0.96 (0.01)a
Exergy 56196 (20198)c69313 (30180)c96662 (27596)b139611 (53349)a
Specific exergy 676 (24)bc688 (33)b675 (21)c700 (21)a
Entropy 15 02319 g001 1024
Figure 1. Relative abundances (%) of the functional feeding groups (FFGs) of macroinvertebrates at four different river types.
Figure 1. Relative abundances (%) of the functional feeding groups (FFGs) of macroinvertebrates at four different river types.
Entropy 15 02319 g001

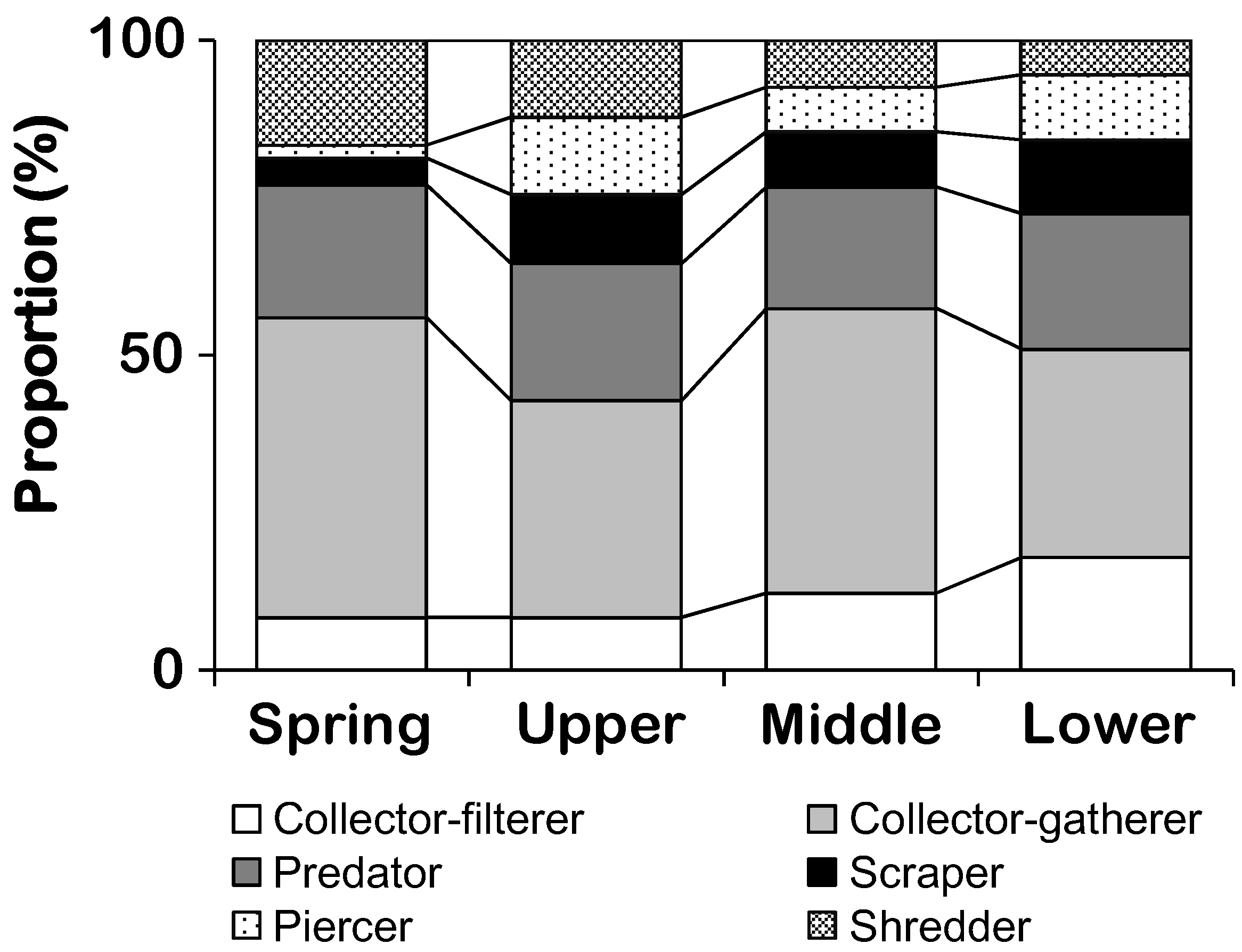
3.2. Patterning Benthic Macroinvertebrate Communities

The study sites were patterned based on the similarities of benthic macroinvertebrate communities in the SOM (final quantization error: 3.989 and final topographic error: 0.012) (Figure 2). The SOM output units were classified into four clusters based on the U-matrix and the dendrogram obtained with hierarchical cluster analysis (Figure 2). An MRPP showed significant differences between benthic macroinvertebrate communities among the four clusters (A = 0.12, p < 0.01). The size of the letters in the figure is proportional to the number of sampling sites in the SOM map and ranges from 1 to 17 sampling units (Figure 2). The classification of the study sites reflects the characteristics of different river types (e.g., topographical variation, spatial variation and nutrient gradients). The study sites in the springs were classified primarily in cluster 1, and all study sites in the upper courses were classified in cluster 2. Most sites in the middle courses were classified in cluster 3. The sampling sites in the lower courses were primarily classified in cluster 4.
Cluster 1 showed low values for community diversity indices, conductivity, NH4+, o-P, t-P, Cl− and Ca2+ (Table 2), whereas clusters 2 and 3 displayed intermediate ranges for community diversity indices and high values for the water quality variables. Cluster 4 displayed the highest community diversity indices and low values for the water quality variables, except for conductivity and Ca2+. The relative proportion of collector-filterers increased from cluster 1 to cluster 4, whereas the proportion of shredders decreased (Table 2). The proportion of piercers was lowest in cluster 1, and collector-gatherers were higher in clusters 1 and 3. The differences in exergy values among the four clusters were similar to the differences in the community diversity indices (Table 2). Exergy values tended to increase along with the stream size. In contrast, the changes in the specific exergy among the four clusters were different from the changes in the community diversity indices and exergy. Specific exergy was low in cluster 1, representing the study sites in springs, and cluster 3, representing the study sites with high nutrient loads. The highest specific exergy was observed in cluster 4, representing study sites in the lower courses with relatively low nutrient levels.
Entropy 15 02319 g002 1024
Figure 2. (a) Classification of sampling sites in SOM using macroinvertebrate abundance, (b) U-matrix and (c) dendrogram of a hierarchical cluster analysis of the SOM units using the Ward linkage method based on Euclidean distance. Acronyms in the SOM units refer to different river types (S: spring, U: upper course, M: middle course and L: lower course).
Figure 2. (a) Classification of sampling sites in SOM using macroinvertebrate abundance, (b) U-matrix and (c) dendrogram of a hierarchical cluster analysis of the SOM units using the Ward linkage method based on Euclidean distance. Acronyms in the SOM units refer to different river types (S: spring, U: upper course, M: middle course and L: lower course).
Entropy 15 02319 g002
Based on IndVal of the SOM clusters, 113 species were selected as indicator species (p < 0.05) (Appendix 1). The abundance and frequency of rheophilic species inhabiting oligosaprobic rivers were relatively high in cluster 1 and included Nemoura cinerea, Nemurella pictetii, Plectrocnemia conspersa, Hexatominae, Brillia modesta, Micropsectra sp. and Elodes minuta. The decomposition of fallen leaves in forest areas resulted in a relatively high level of detritus and a high abundance of Gammarus pulex (Table 2) in the sites of cluster 1. In cluster 2, the species usually inhabiting alpha to beta mesosaprobic rivers were dominant and included Hydrobius fuscipes, Hydroporus palustris, Anisus leucostoma and Psectrotanypus varius. Piercers were also common in cluster 2, including Haliplus lineatocollis, Hydroporus palustris and Agabus sp. The abundance and the occurrence frequency of detritivores were high in cluster 3, representing the middle courses. Cluster 3 was characterized with Limnodrilus hoffmeisteri, Tubificidae and Procladius sp., and cluster 4, representing the lower courses, was characterized with the species (primarily predators and piercers) inhabiting emergent macrophytes and typically swimming at the water surface. These species were represented by the Coleoptera, including Haliplus fluviatilis, Hygrotos versicolor, Noterus clavicornis, Laccophilus hyalinus and Haliplus sp. and the Hemiptera, including Sigara falleni, S. strigata, S. distincta/falleni/longipalis and Ilyocoris cimicoides.
Table
Table 2. Differences (mean (standard deviation)) in environmental variables, community indices and the relative ratio of FFGs at the four different clusters defined by SOM. Different letters indicate significant differences between four different clusters based on a Tukey’s multiple comparison test (p < 0.05).
Table 2. Differences (mean (standard deviation)) in environmental variables, community indices and the relative ratio of FFGs at the four different clusters defined by SOM. Different letters indicate significant differences between four different clusters based on a Tukey’s multiple comparison test (p < 0.05).
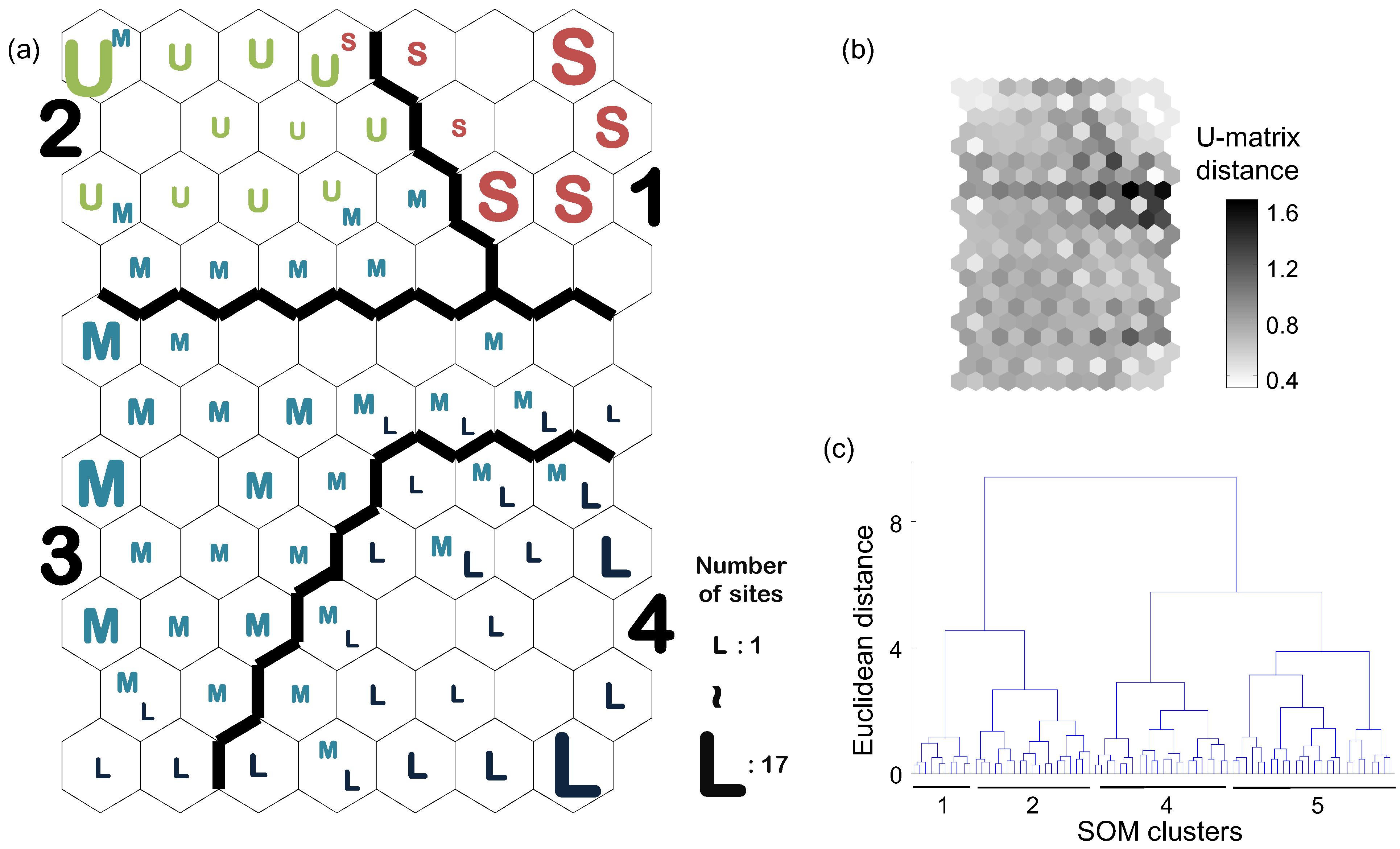
Category VariableSOM Cluster (number of study sites)
1 (51)2 (57)3 (69)4 (72)
Environmental VariableSlope (m/km)51.0 (41.7)a2.5 (13.2)b0.6 (0.8)b0.1 (0.2)b
Current velocity (m/s)0.16 (0.14)a0.06 (0.1)b0.19 (0.2)a0.02 (0.04)b
Width (m)0.7 (0.7)c2.4 (2.2)bc9.1 (8.5)b26 (27.3)a
Depth (m)0.1 (0.1)c0.3 (0.2)c0.9 (0.7)b2.2 (1.5)a
Emergent macrophytes (%)3.9 (11.1)c16.3 (22.1)ab8.5 (15.7)bc17.4 (22.0)a
Floating macrophytes (%)0.0 (0.0)c8.3 (17.3)b3.9 (11.9)bc17.5 (20.2)a
Submerged macrophytes (%)1.4 (7.5)b16.7 (19.1)a15.8 (25.4)a7.6 (15.2)b
Detritus (%)40.8 (23.7)a3.5 (9.4)b6.5 (11.6)b2.3 (7.6)b
Micro substrate (%)35.2 (20.5)a34.8 (22.5)a41.3 (25.3)a20.8 (14.2)b
Macro substrate (%)10.2 (14.1)a0.8 (3.9)b2.2 (6.7)b0.9 (3.2)b
pH6.77 (0.61)b6.8 (0.89)b7.28 (0.51)a7.54 (0.38)a
Conductivity (μS/cm)259.5 (83.8)b486.5 (415.9)a524.9 (192.7)a559.3 (155.4)a
DO (mg/L)8.67 (2.98)b9.92 (3.41)ab9.93 (2.08)ab10.86 (3.93)a
NH4+ (mgN/L)0.16 (0.14)c2.57 (3.09)a1.55 (1.78)b0.83 (1.1)bc
NO3− (mgN/L)11.86 (8.03)a5.59 (6.04)b8.55 (19.01)ab2.09 (1.62)c
o-P (mgP/L)0.24 (0.56)0.51 (1.2)0.50 (0.73)0.20 (0.51)
t-P (mgP/L)0.24 (0.25)b0.75 (1.68)ab0.87 (1.09)a0.42 (0.71)ab
Cl− (mg/L)31.67 (13.77)b65.14 (101.1)a52.37 (64.73)ab59.49 (33.42)ab
Ca2+ (mg/L)39.67 (18)c56.76 (33.4)b62.77 (20.07)ab68.75 (19.28)a
Biological IndexSpecies richness28 (9)c37 (13)c59 (14)b83 (19)a
Shannon index3.06 (0.35)d3.31 (0.41)c3.85 (0.23)b4.21 (0.23)a
Simpson index0.94 (0.02)b0.95 (0.03)b0.97 (0.01)a0.98 (0.00)a
Evenness0.93 (0.02)c0.94 (0.02)b0.95 (0.01)a0.96 (0.01)a
Exergy56206 (20399)c69393 (28168)c101275 (33297)b140525 (50483)a
Specific exergy676 (25)b684 (34)b678 (20)b699 (22)a
Functional feeding groupCollector-filterers8.3 (5.7)c9.1 (6.4)c13.1 (5.3)b17.3 (5.7)a
Collector-gatherers47.6 (11.4)a36.2 (12.9)b43.9 (8.9)a34 (8.0)b
Predators21.1 (8.4)20.9 (8.1)19.8 (5.6)21.5 (7)
Piercers2.0 (2.5)c11.5 (7.0)ab7.6 (4.4)b9.7 (3.7)a
Scrapers4.2 (3.3)c10.6 (7.6)a8.5 (5.4)b12.1 (3.9)a
Shredders16.8 (8.6)a11.8 (7.6)a7.1 (2.9)b5.4 (1.9)b

3.3. Prediction of Exergy

Exergy and specific exergy were predicted based on differences in environmental variables through the learning process in the Random Forest model, and the relative importance of environmental variables was evaluated (Figure 3). The values of predictive power for exergy and specific exergy were specified by coefficients of determination (R2) of 0.51 and 0.23, respectively. Exergy and specific exergy responded differently to environmental variables. For example, the longitudinal gradient of stream size (i.e., river width) was the most influential environmental factor for exergy prediction, followed by DO, ammonium and the river width. Orthophosphate was the most important predictor of specific exergy, followed by nitrate and total phosphate.
The Spearman rank correlation coefficients indicated that exergy, specific exergy and the community indices (species richness, Shannon diversity index and Simpson diversity index) were positively correlated, with correlations ranging from 0.267 to 0.998 (p < 0.01). The highest correlation was between the Simpson diversity and the Shannon diversity indices (0.998), while the lowest was between exergy and specific exergy (0.267). In addition, the exergy and community indices showed high correlation coefficients (0.589 to 0.919) when compared with the correlation coefficients between specific exergy and the community indices (0.267 to 0.320) (Table 3).
Entropy 15 02319 g003 1024
Figure 3. Relative importance of environmental variables for predicting (a) exergy and (b) specific exergy using a Random Forest models based on the mean decrease Gini (MDG). MDG values were rescaled to a range of 0–100. Abbreviations of environmental variables are given in Table 1.
Figure 3. Relative importance of environmental variables for predicting (a) exergy and (b) specific exergy using a Random Forest models based on the mean decrease Gini (MDG). MDG values were rescaled to a range of 0–100. Abbreviations of environmental variables are given in Table 1.
Entropy 15 02319 g003
Table
Table 3. Spearman rank correlation between community indices.
Table 3. Spearman rank correlation between community indices.
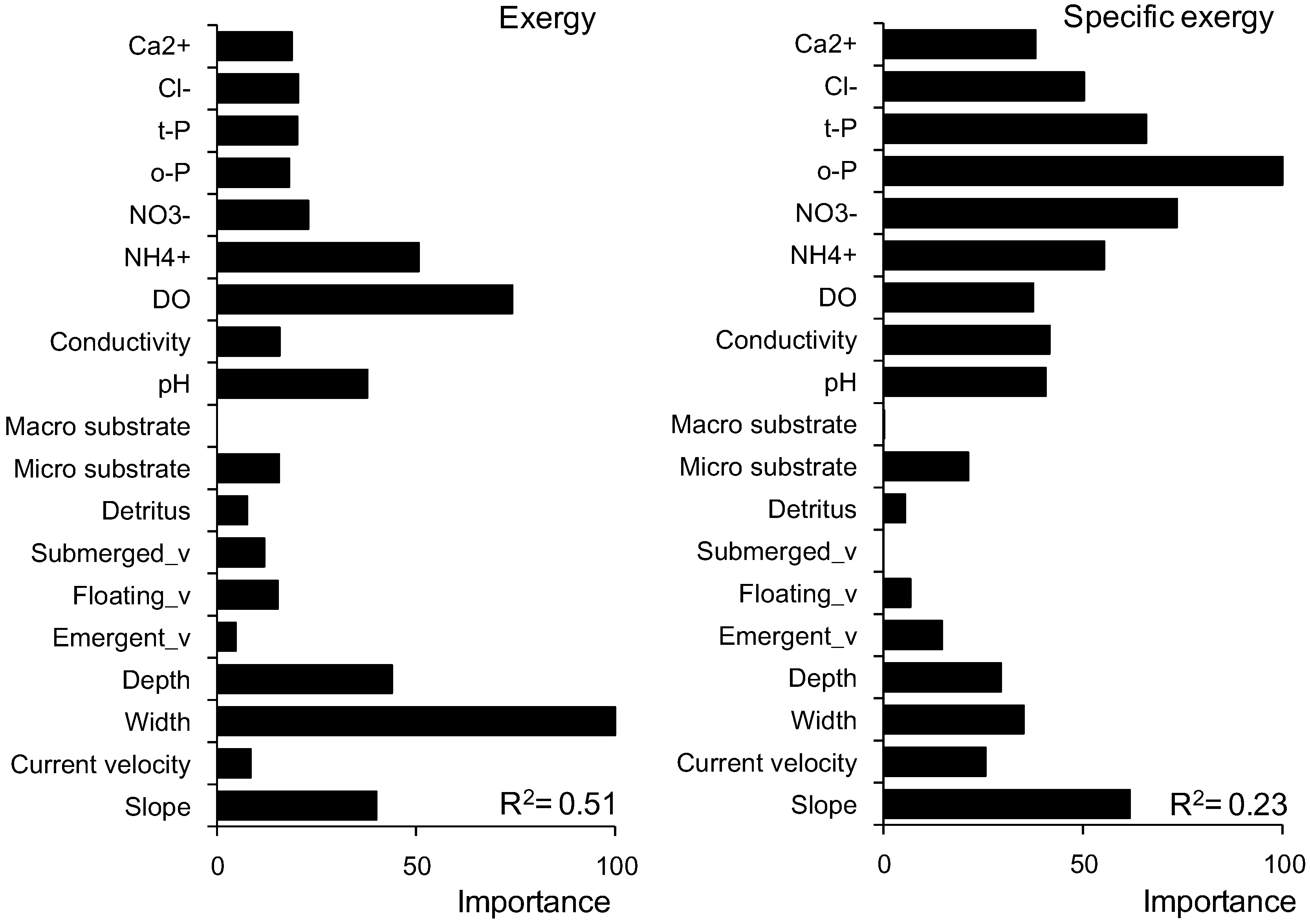
IndicesSpecies RichnessShannon IndexSimpson IndexEvennessExergy
Shannon index0.997**
Simpson index0.992**0.998**
Evenness0.702**0.745**0.773**
Exergy0.919**0.911**0.912**0.589**
Specific exergy0.299**0.316**0.320**0.316**0.267**
Note: **: p < 0.01.

4. Discussion

Lotic ecosystems are complicated and dynamic, and their physical, chemical and biological components interact and influence each other through non-equilibrium, dissipative processes [72]. Changes in environmental factors often cause alterations in ecosystem structure. These alterations include changes in species composition or biodiversity as well as ecosystem function. A high load of organic substances and nutrients (e.g., nitrogen or phosphorus) usually causes changes in species composition and trophic structure. Accordingly, from the water management point of view, there is a need to find indices that express the alteration of the physicochemical environment in the lotic ecosystem as well as the changes in energy flow between the various trophic levels in the food web [73].
In this study, four naturally separated groups are clearly classified by the SOM clusters. A comparison between natural separated groups (Table 1) and SOM clustered groups (Table 2) indicates the effectiveness of the SOM model. Such similar results suggest that SOM is a useful tool for identifying differences between naturally separated groups [59,74].
The exergy and biodiversity indices tended to increase from cluster 1 to cluster 4 in the SOM analysis. However, specific exergy was lowest in cluster 3 with a high proportion of detritivores (i.e., a low β value), whereas specific exergy was highest in cluster 4 with a high proportion of carnivores (i.e., a high β value). Similar results were observed in the lotic and lentic ecosystems. According to Marques et al. [28] and de Wit et al. [75], eutrophication (i.e., a high nutrient load) results in higher exergy and lower specific exergy because the biomass bulk has a low weighting factor. Unlike exergy, specific exergy is not dependent on biomass alone and expresses the ability of the ecosystem to accept and utilize external fluxes of energy while simultaneously serving as an indicator of ecosystem development, reflecting the complexity and level of evolutionary development of species in an ecosystem [10]. Accordingly, specific exergy reflects diversity (i.e., a more complex ecosystem), and a higher specific exergy represents more highly developed organisms (i.e., higher β values that represent more information) [34].
Middle river courses (cluster 3) were directly influenced by nutrients transported in runoff from the adjacent pastures and agricultural areas along the streams together with nutrient inputs from upstream. Furthermore, the relative ratio of micro substrate was higher than in the lower courses. The middle courses receive large amounts of sediment as well as organic matter, resulting in the accumulation of detritus on the stream bottom and thus producing a high abundance of detritivores. The lower courses (cluster 4) showed relatively stable habitat conditions, and such conditions typically support high species complexity and diversity. The nutrient sources for the lower courses originated primarily from upstream nutrient input and represented a dilution of the nutrients coming from the middle courses. Discharge and current velocity were low but stable over all seasons, as is also the case for lentic habitats [52,76].
Even though any environmental factor could potentially influence the exergy and specific exergy in our study, the Random Forest models demonstrated that exergy was more heavily influenced by long-term conditions such as the longitudinal gradient (e.g., river width); whereas short-term disturbances, such as those associated with the nutrient concentrations (e.g., o-P, t-P, NO3− and NH4+), were more important in determining the specific exergy. This was congruent with a study by Marques et al. [27], which suggested that exergy reflected slower changes, whereas specific exergy may shift drastically if the species composition of a particular body of water changed abruptly. Those findings indicated that the complementary use of exergy and specific exergy provides information on long-term gradients such as the longitudinal gradient (i.e., river continuum concept), as well as the ecosystem response, including the suppression of the food web and diversity due to environmental stress [77].
Most biodiversity indicators interpret the community composition from structural characteristics, while the exergy and specific exergy focus on the functional characteristics of an ecosystem. In recent ecological studies, exergy values have been used as ecosystem health indicators, reflecting such processes as human activities and eutrophication [10]. However, exergy and specific exergy are promising indicators for shifts in species composition and trophic structures along longitudinal and nutrient gradients. In this study, exergy and the community indices showed the same trends in the different river courses and increased from the springs to the lower courses. In contrast, specific exergy was the highest in the lower courses, with relatively low values in other river types. Such a relationship indicates that the complicated results from different bioassessment methods and that the combined use of structural and functional indicators could therefore provide comprehensive information on ecosystem development and complexity along both longitudinal and nutrient gradients in lotic ecosystems.

5. Conclusions

It is clearly crucial to obtain an integrative biological indicator to interpret the structure and function of lotic ecosystems. Exergy and specific exergy are potentially promising target functions for this purpose, indicating shifts in species composition, as well as trophic structure along longitudinal and nutrient gradients. Exergy increased from the springs to the lower watercourses, but specific exergy was highest in the lower watercourses. Specific exergy represented ecological complexity based on nutrient concentrations. In this sense, it is advisable to use both indicators to evaluate ecosystem health assessment because exergy and specific exergy relate different and complementary information regarding the functioning of a lotic ecosystem.

Acknowledgments

This work was supported by a National Research Foundation of Korea (NRF) grant funded by the Korean government (MEST) (No. 2011-0027628).

Conflict of Interest

The authors declare no conflict of interest.

Appendix

Table
Table A1. Indicator species analysis (IndVal) and significance (p) obtained from Monte Carlo permutations for macroinvertebrate taxa at four different clusters defined in the SOM. Only macroinvertebrate taxa with IndVal > 25 are shown.
Table A1. Indicator species analysis (IndVal) and significance (p) obtained from Monte Carlo permutations for macroinvertebrate taxa at four different clusters defined in the SOM. Only macroinvertebrate taxa with IndVal > 25 are shown.
TaxaIndicator speciesClusterIndValp
EphemeropteraCaenis horaria3420.0001
4430.0001
Cloeon dipterum3320.0001
4360.0001
Caenis robusta4320.0001
Cloeon simile4320.0001
ChironomidaeBrillia modesta1730.0001
Micropsectra sp.1600.0001
Polypedilum breviantennatum1290.0001
Parametriocnemus stylatus1270.0001
Macropelopia sp.1270.0001
Psectrotanypus varius2370.0001
Chironomus sp.2330.0002
Xenopelopia nigricans2260.0001
Natarsia sp.2250.0001
Procladius sp.3420.0001
4310.0001
Cryptochironomus sp.3370.0001
4350.0001
Polypedilum gr. nubeculosum3370.0001
3320.0001
Conchapelopia sp.3320.0001
Paratanytarsus sp.3290.0001
Endochironomus albipennis4850.0001
Polypedilum gr. Sordens4620.0001
Glyptotendipes sp.4620.0001
Cricotopus sp.4550.0001
Endochironomus tendens4490.0001
Dicrotendipes gr. nervosus4450.0001
Parachironomus gr. arcuatus4450.0001
Microtendipes sp.4330.0001
Ablabesmyia longistyla4320.0001
Cladotanytarsus sp.4300.0001
Tanytarsus sp.4290.0001
Clinotanypus sp rvosus4280.0001
Corynoneura sp.4260.0001
Plecoptera Nemoura cinerea 1290.0001
Nemurella pictetii1270.0001
TricopteraPlectrocnemia conspersa1740.0001
Stenophylax sp.1470.0001
Sericostoma personatum1410.0001
Beraea Maura1350.0001
Athripsodes aterrimus3310.0001
Mystacides sp.4470.0001
Cyrnus flavidus4450.0001
Triaenodes bicolor4330.0001
Ecnomus tenellus4290.0001
DipeteraHexatominae1630.0001
Ptychoptera sp.1510.0001
Pedicia sp.1450.0001
Dicranota bimaculata1450.0001
Dixa maculate1410.0001
Tipula sp.1340.0001
Ceratopogonidae3260.0088
ColeopteraElodes minuta1820.0001
Hydrobius fuscipes2420.0001
Hydroporus palustris2410.0001
Haliplus lineatocollis2280.0001
Agabus sp./Ilybius sp.2270.0002
Haliplus fluviatilis4300.0001
Hygrotus versicolor4300.0001
Noterus clavicornis4280.0001
Laccophilus hyalinus4280.0001
Haliplus sp.4270.0002
OdonataIschnura sp.4400.0001
HemipteraSigara fallen4530.0001
Sigara striata4390.0001
Sigara distincta/falleni/longipalis4340.0001
Ilyocoris cimicoides4300.0001
HirudineaErpobdella octoculata3420.0001
Glossiphonia complanata3280.0001
Helobdella stagnalis4510.0001
Glossiphonia heteroclite4440.0001
Hemiclepsis marginata4440.0001
Piscicola geometra4300.0001
AmphipodaGammarus pulex1580.0001
Asellus aquaticus4300.0001
Proasellus coxalis4290.0001
BivalvaSphaerium sp.3340.0001
ActinedidaSperchon squamosus1350.0001
Limnesia koenikei3330.0001
Hygrobates longipalpis3320.0001
Hygrobates nigromaculatus3230.0001
Limnesia maculate4700.0001
Piona alpicola/coccinea4600.0001
Arrenurus crassicaudatus4540.0001
Limnesia undulate4520.0001
Mideopsis orbicularis4400.0001
Acercinae4380.0001
Piona pusilla4330.0001
Unionicola crassipes4320.0001
Piona variabilis4310.0001
Limnesia sp4290.0001
Arrenurus globator4280.0001
Eylais extendens4270.0001
OligochaetaEiseniella tetraedra1320.0001
Enchytraeidae1260.0001
Lumbriculus variegatus2270.0151
Tubificidae sp.13340.0001
4330.0001
Tubificidae sp.23340.0001
Stylaria lacustris4440.0001
Ophidonais serpentine4350.0001
Potamothrix hammoniensis4290.0001
Limnodrilus hoffmeisteri3280.0004
4290.0004
Potamothrix moldaviensis4260.0001
GastropodaAnisus leucostoma/spirorbis2400.0001
Radix peregra2310.0001
Bithynia leachi4630.0001
Bithynia tentaculata4580.0001
Valvata piscinalis4540.0001
Anisus vortex4530.0001
Gyraulus albus4470.0001
Valvata cristata4390.0001
Physa fontinalis4340.0001
Acroloxus lacustris4320.0001

References

  1. Odum, E.P. Ecological potential and analogue circuits for the ecosystem. Am. Sci. 1960, 48, 1–8. [Google Scholar]
  2. Margalef, R. Communication of structure in plankton population. Limnol. Oceanogr. 1961, 6, 124–128. [Google Scholar] [CrossRef]
  3. Straskraba, M. Cybernetic categories of ecosystem dynamics. ISEM J. 1980, 2, 81–96. [Google Scholar]
  4. Odum, H.T. Pulsing, power and hierarchy. In Energetics and Systems; Mitsh, W.J., Ragade, R.K., Bosserman, R.W., Dillon, J.A., Jr., Eds.; Ann Arbor Science: Ann Arbor, MI, USA, 1982; pp. 33–59. [Google Scholar]
  5. Jørgensen, S.E. Exergy and Buffering Capacity in Ecological System. In Energetics and Systems; Mitsh, W.J., Ragade, R.K., Bosserman, R.W., Dillon, J.A., Jr., Eds.; Ann Arbor Science: Ann Arbor, MI, USA, 1982; pp. 61–72. [Google Scholar]
  6. Ulanowicz, R.E. Growth and Development: Ecosystem Phenomenology; Springer: New York, NY, USA, 1986. [Google Scholar]
  7. Schneider, E. Thermodynamics, ecological succession, and natural selection: A common thread. In Entropy, Information and Evolution; Weber, B.H., Depew, D.J., Smith, J.D., Eds.; MIT Press: Cambridge, MA, USA, 1988. [Google Scholar]
  8. Xu, F.L.; Jørgensen, S.E.; Tao, S.; Li, B.G. Modeling the effects of ecological engineering on ecosystem health of a shallow eutrophic Chinese lake (Lake Chao). Ecol. Model. 1999, 117, 239–260. [Google Scholar] [CrossRef]
  9. Silow, E.A.; Oh, I.H. Aquatic ecosystem assessment using exergy. Ecol. Indic. 2004, 4, 189–198. [Google Scholar] [CrossRef]
  10. Silow, E.A.; Mokry, A.V. Exergy as a tool for ecosystem health assessment. Entropy 2010, 12, 902–925. [Google Scholar] [CrossRef]
  11. Mandal, S.; Ray, S.; Jørgensen, S.E. Exergy as an indicator: Observations of an aquatic ecosystem model. Ecol. Inform. 2012, 12, 1–9. [Google Scholar] [CrossRef]
  12. Li, F.; Bae, M.J.; Kwon, Y.S.; Chung, N.; Hwang, S.J.; Park, S.J.; Park, H.K.; Kong, D.S.; Park, Y.S. Ecological exergy as an indicator of land-use impacts on functional guilds in river ecosystems. Ecol. Model. 2013, 252, 53–62. [Google Scholar] [CrossRef]
  13. Jørgensen, S.E.; Mejer, H. Ecological buffer capacity. Ecol. Model. 1977, 3, 39–61. [Google Scholar] [CrossRef]
  14. Jørgensen, S.E.; Mejer, H. A holistic approach to ecological modelling. Ecol. Model. 1979, 7, 169–189. [Google Scholar] [CrossRef]
  15. Xu, F.L.; Tao, S.; Dawson, R.W. System-level responses of lake ecosystems to chemical stresses using exergy and structural exergy as ecological indicators. Chemosphere 2002, 46, 173–185. [Google Scholar] [CrossRef]
  16. Park, Y.S.; Lek, S.; Scardi, M.; Verdonschot, P.F.M.; Jørgensen, S.E. Patterning exergy of benthic macroinvertebrate communities using self-organizing maps. Ecol. Model. 2006, 195, 105–113. [Google Scholar] [CrossRef] [Green Version]
  17. Jørgensen, S.E.; Nielsen, S.N. Application of exergy as thermodynamic indicator in ecology. Energy 2007, 32, 673–685. [Google Scholar] [CrossRef]
  18. Fonseca, J.C.; Pardal, M.A.; Azeiteiro, U.M.; Marques, J.C. Estimation of ecological exergy using weighing parameters determined from DNA contents of organisms—A case study. Hydrobiologia 2002, 475, 79–90. [Google Scholar] [CrossRef]
  19. Mandal, S.; Ray, S.; Roy, S.; Mandal, S. The Concept of Exergy and its Extension to Ecological System. In Handbook of Exergy, Hydrogen Energy and Hydropower Research; Pélissier, G., Calvet, A., Eds.; Nova Science: New York, NY, USA, 2009; Chapter 13. [Google Scholar]
  20. Ludovisi, A.; Poletti, A. Use of thermodynamic indices as ecological indicators of the development state of lake ecosystems: 2. Exergy and specific exergy indices. Ecol. Model. 2003, 159, 223–238. [Google Scholar] [CrossRef]
  21. Jørgensen, S.E. Integration of Ecosystem Theories: A Pattern; 3nd revised ed.; Kluwer Academic Publishers: Boston, MA, USA, 2002. [Google Scholar]
  22. Jørgensen, S.E. Review and comparison of goal functions in system ecology. Vie et Milieu 1994, 44, 11–20. [Google Scholar]
  23. Xu, F.L.; Jørgensen, S.E.; Tao, S. Ecological indicators for assessing freshwater ecosystem health. Ecol. Model. 1999, 116, 77–106. [Google Scholar] [CrossRef]
  24. Jørgensen, S.E. The application of ecological indicators to assess the ecological condition of a lake. Lakes Reserv.: Res. Manag. 1995, 1, 177–182. [Google Scholar] [CrossRef]
  25. Bae, M.J.; Park, Y.S. Characterizing ecological exergy as an ecosystem indicator in streams using a self-organizing map. Korean J. Environ. Biol. 2008, 26, 203–213. [Google Scholar]
  26. Xu, F.-L.; Wang, J.-J.; Chen, B.; Qin, N.; Wu, W.W.; He, W.; He, Q.S.; Wang, Y. The variations of exergies and structural exergies along eutrophication gradients in Chinese and Italian lakes. Ecol. Model. 2011, 222, 337–350. [Google Scholar] [CrossRef]
  27. Marques, J.C.; Pardal, M.Â.; Nielsen, S.N.; Jørgensen, S.E. Analysis of the properties of exergy and biodiversity along an estuarine gradient of eutrophication. Ecol. Model. 1997, 102, 155–167. [Google Scholar] [CrossRef]
  28. Marques, J.C.; Nielsen, S.N.; Pardal, M.A.; Jørgensen, S.E. Impact of eutrophication and river management within a framework of ecosystem theories. Ecol. Model. 2003, 166, 147–168. [Google Scholar] [CrossRef]
  29. Fabiano, M.; Vassalo, P.; Vezzulli, L.; Salvo, V.S.; Marques, J.C. Temporal and spatial change of exergy and ascendency in different benthic marine ecosystems. Energy 2004, 29, 1697–1712. [Google Scholar] [CrossRef]
  30. Pranovi, F.; Da Ponte, F.; Torricelli, P. Application of biotic indices and relationship with structural and functional features of macrobenthic community in the lagoon of Venice: An example over a long time series of data. Mar. Pollut. Bull. 2007, 54, 1607–1618. [Google Scholar] [CrossRef] [PubMed]
  31. Wallace, J.B.; Webster, J.R. The role of macroinvertebrates in stream ecosystem function. Annu. Rev. Entomol. 1996, 41, 115–139. [Google Scholar] [CrossRef] [PubMed]
  32. Covich, A.P.; Palmer, M.A.; Crowl, T.A. The role of benthic invertebrate species in freshwater ecosystems. BioScience 1999, 49, 119–127. [Google Scholar] [CrossRef]
  33. Rosenberg, D.M.; Resh, V.H. Freshwater Biomonitoring and Benthic Macroinvertebrates; Chapman & Hall: London, UK, 1993; p. 325. [Google Scholar]
  34. Libralato, S.; Torricelli, P.; Pranovi, F. Exergy as ecosystem indicator: An application to the recovery process of marine benthic communities. Ecol. model. 2006, 192, 571–585. [Google Scholar] [CrossRef]
  35. Gessner, M.O.; Chauvet, E. A case for using litter breakdown to assess functional stream integrity. Ecol. Appl. 2002, 12, 498–510. [Google Scholar] [CrossRef]
  36. Bunn, S.E.; Mosisch, T.D.; Davies, P.M. Ecosystem measures of river health and their response to riparian and catchment degradation. Freshwater Biol. 1999, 41, 333–345. [Google Scholar] [CrossRef]
  37. McKie, B.G.; Malmqvist, B. Assessing ecosystem functioning in streams affected by forest management: increased leaf decomposition occurs without changes to the composition of benthic assemblages. Freshwater Biol. 2009, 54, 2086–2100. [Google Scholar] [CrossRef]
  38. Riipinen, M.P.; Davy-Bowker, J.; Dobson, M. Comparison of structural and functional stream assessment methods to detect changes in riparian vegetation and water pH. Freshwater Biol. 2009, 54, 2127–2138. [Google Scholar] [CrossRef]
  39. Stephenson, J.M.; Morin, A. Covariation of stream community structure and biomass of algae, invertebrates and fish with forest cover at multiple spatial scales. Freshwater Biol. 2009, 54, 2139–2154. [Google Scholar] [CrossRef]
  40. Ferreira, V.; Graca, M.A.S.; de Lima, J.; Gomes, R. Role of physical fragmentation and invertebrate activity in the breakdown rate of leaves. Arch. Hydrobiol. 2006, 165, 493–513. [Google Scholar] [CrossRef]
  41. Death, R.G.; Dewson, Z.S.; James, A.B.W. Is structure or function a better measure of the effects of water abstraction on ecosystem integrity? Freshwater Biol. 2009, 54, 2037–2050. [Google Scholar] [CrossRef]
  42. Friberg, N.; Dybkjær, J.B.; Olafsson, J.S.; Gislason, G.M.; Larsen, S.E.; Lauridsen, T.L. Relationships between structure and function in streams contrasting in temperature. Freshwater Biol. 2009, 54, 2051–2068. [Google Scholar] [CrossRef]
  43. Bird, G.A.; Kaushik, N.K. Invertebrate colonization and processing of maple leaf litter in a forested and an agricultural reach of a stream. Hydrobiologia 1992, 234, 65–77. [Google Scholar] [CrossRef]
  44. Gücker, B.; Boüchat, I.G.; Giani, A. Impacts of agricultural land use on ecosystem structure and whole-stream metabolism of tropical Cerrado streams. Freshwater Biol. 2009, 54, 2069–2085. [Google Scholar] [CrossRef]
  45. Young, R.G.; Collier, K.J. Contrasting responses to catchment modification among a range of functional and structural indicators of river ecosystem health. Freshwater Biol. 2009, 54, 2155–2170. [Google Scholar] [CrossRef]
  46. Sandin, L.; Solimini, A.G. Freshwater ecosystem structure-function relationships: from theory to application. Freshwater Biol. 2009, 54, 2017–2024. [Google Scholar] [CrossRef]
  47. Verdonschot, P.F.M.; Nijboer, R.C. Typology of Macrofaunal assemblages applied to water and nature management: A Dutch approach. In Assessing the Biological Quality of Fresh Waters: RIVPACS and Other Techniques; Wright, J.F., Sutcliffe, D.W., Furse, M.T., Eds.; The Freshwater Biological Association: Ambleside, Cumbria, UK, 2000; pp. 241–262. [Google Scholar]
  48. Tomanova, S.; Goitia, E.; Helešic, J. Trophic levels and functional feeding groups of macroinvertebrates in Neotropical streams. Hydrobiologia 2006, 556, 251–264. [Google Scholar] [CrossRef]
  49. Cummins, K.W. Invertebrates. In The Rivers Handbook; Calow, P., Petts, G.E., Eds.; Blackwell Scientific: Oxford, UK, 1995; pp. 234–250. [Google Scholar]
  50. Mihuc, T.B. The functional trophic role of lotic primary consumers: generalist versus specialist strategies. Freshwater Biol. 1997, 37, 455–462. [Google Scholar] [CrossRef]
  51. Merritt, R.W.; Cummins, K.W.; Berg, M.B. An Introduction to the Aquatic Insects of North America, 4th revised ed; Hunt Publishing Company: Dubugue, IA, USA, 2006. [Google Scholar]
  52. Verdonschot, P.F.M. Typology of macrofaunal assemblages: A tool for the management of running waters in The Netherlands. Hydrobiologia 1995, 297, 99–122. [Google Scholar] [CrossRef]
  53. Austoni, M.; Giordani, G.; Viaroli, P.; Zaldívar, J.M. Application of specific exergy to macrophytes as an integrated index of environmental quality for coastal lagoons. Ecol Indic. 2007, 7, 229–238. [Google Scholar] [CrossRef]
  54. Jørgensen, S.E.; Nielsen, S.N. Thermodynamic orientors: Exergy as a Goal Function in Ecological Modeling and as an Ecological Indicator for the Description of Ecosystem Development. In Eco Targets, Goal Functions, and Orientors; Müller, F., Leupelt, M., Eds.; Springer: Berlin, Germany, 1998; pp. 63–86. [Google Scholar]
  55. Jørgensen, S.E.; Nielsen, S.N.; Mejer, H. Emergy, environ, exergy and ecological modelling. Ecol. Model. 1995, 77, 99–109. [Google Scholar] [CrossRef]
  56. Jørgensen, S.E.; Verdonschot, P.; Lek, S. Explanation of the observed structure of functional feeding groups of aquatic macro-invertebrates by an ecological model and the maximum exergy principle. Ecol. Model. 2002, 158, 223–231. [Google Scholar] [CrossRef]
  57. Kohonen, T. Self-organized formation of topologically correct feature maps. Biol. Cybern. 1982, 42, 59–69. [Google Scholar] [CrossRef]
  58. Kohonen, T. Self-Organizing Maps, 3rd ed.; Springer: Berlin, Germany, 2001. [Google Scholar]
  59. Park, Y.S.; Chang, J.; Lek, S.; Cao, W.; Brosse, S. Conservation strategies for endemic fish species threatened by the Three Gorges Dam. Conser. Biol. 2003, 17, 1748–1785. [Google Scholar] [CrossRef]
  60. Alhoniemi, E.; Himberg, J.; Parhankangas, J.; Vesanto, J. SOM Toolbox; Laboratory of Information and Computer Science, Helsinki University of Technology: Helsinki, Finland, 2000; Available online: http://www.cis.hut.fi/projects/somtoolbox/ (accessed on 31/03/2012).
  61. MATLAB; Version 6.1; software for technical computation; The Mathworks Inc.: Natick, MA, USA, 2001.
  62. Ultsch, A. Self-Organizing Neural Networks for Visualization and Classification. In Information and Classification; Opitz, O., Lausen, B., Klar, R., Eds.; Springer: Berlin, Germany, 1993; pp. 307–313. [Google Scholar]
  63. Ward, J.H. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
  64. Jain, A.K.; Dubes, R.C. Algorithms for Clustering Data; Prentice Hall: Englewood Cliffs, NJ, USA, 1988. [Google Scholar]
  65. McCune, B.; Mefford, M.J. PC-ORD; Multivariate Analysis of Ecological Data; MjM Software Design: Glenden Beach, OR, USA, 1999. [Google Scholar]
  66. Dufrene, M.; Legendre, P. Species assemblages and indicator species: The need for a flexible asymmetrical approach. Ecol. Mono. 1997, 67, 345–366. [Google Scholar] [CrossRef]
  67. Chaves, M.L.; Rieradevall, M.; Chainho, P.; Costa, J.L.; Costa, M.J.; Prat, N. Macroinvertebrate communities of non-glacial high altitude intermittent streams. Freshwater Biol. 2008, 53, 55–76. [Google Scholar] [CrossRef]
  68. García-Roger, E.; Sánchez-Montoya, M.M.; Gomez, R.; Suárez, M.L.; Vidal-Abarca, M.R.; Latron, J.; Rieradevall, M.; Prat, N. Do seasonal changes in habitat features influence aquatic macroinvertebrate assemblages in perennial versus temporary Mediterranean streams? Aquat. Sci. 2011, 73, 567–579. [Google Scholar] [CrossRef]
  69. Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
  70. Zar, J. Biostatistical Analysis, 4th ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
  71. STATISTICA; Version 7; data analysis software system; StatSoft Inc.: Tulsa, OK, USA, 2004; Available online: http://www.statsoft.com (accessed on 31/03/2012).
  72. Schneider, E.D.; Kay, J.J. Life as a manifestation of the second law of thermodynamics. Math. Comp. Model. 1994, 9, 25–48. [Google Scholar] [CrossRef]
  73. Spieles, D.J.; Mitsch, W.J. A model of macroinvertebrate trophic structure and oxygen demand in freshwater wetlands. Ecol. Model. 2003, 161, 183–194. [Google Scholar] [CrossRef]
  74. Park, Y.S.; Kwak, I.S.; Chon, T.S.; Kim, J.K.; Jørgensen, S.E. Implementation of artificial neural networks in patterning and prediction of exergy in response to temporal dynamics of benthic macroinvertebrate communities in streams. Ecol. Model. 2001, 146, 143–157. [Google Scholar] [CrossRef]
  75. de Wit, R.; Stal, L.J.; Lomstein, B.A.; Herbert, R.A.; van Gemerden, H.; Viaroli, P.; Ceccherelli, V.U.; Rodriguez-Valera, F.; Bartoli, M.; Giordani, G.; et al. Robust: The role of buffering capacities in stabilising coastal lagoon ecosystems. Cont. Shelf Res. 2001, 21, 2021–2041. [Google Scholar] [CrossRef]
  76. Verdonschot, P.F.M. Ecological Characterization of Surface Waters in the Province of Overijssel, The Netherlands. Ph.D. Thesis, Agriculture University of Wageningen, Wageningen, The Netherlands, 1990. [Google Scholar]
  77. Molozzi, J.; Salas, F.; Callisto, M.; Marques, J.C. Thermodynamic oriented ecological indicators: Application of Eco-Exergy and specific Eco-Exergy in capturing environmental changes between disturbed and non-disturbed tropical reservoirs. Ecol. Indi. 2013, 24, 543–551. [Google Scholar] [CrossRef]

Share and Cite

MDPI and ACS Style

Bae, M.-J.; Li, F.; Verdonschot, P.F.M.; Park, Y.-S. Characterization of Ecological Exergy Based on Benthic Macroinvertebrates in Lotic Ecosystems. Entropy 2013, 15, 2319-2339. https://doi.org/10.3390/e15062319

AMA Style

Bae M-J, Li F, Verdonschot PFM, Park Y-S. Characterization of Ecological Exergy Based on Benthic Macroinvertebrates in Lotic Ecosystems. Entropy. 2013; 15(6):2319-2339. https://doi.org/10.3390/e15062319

Chicago/Turabian Style

Bae, Mi-Jung, Fengqing Li, Piet F.M. Verdonschot, and Young-Seuk Park. 2013. "Characterization of Ecological Exergy Based on Benthic Macroinvertebrates in Lotic Ecosystems" Entropy 15, no. 6: 2319-2339. https://doi.org/10.3390/e15062319

Article Metrics

Back to TopTop