Phase-Space Position-Momentum Correlation and Potentials
Abstract
:1. Introduction
2. The Quantum Corral Model
3. Results and Discussion
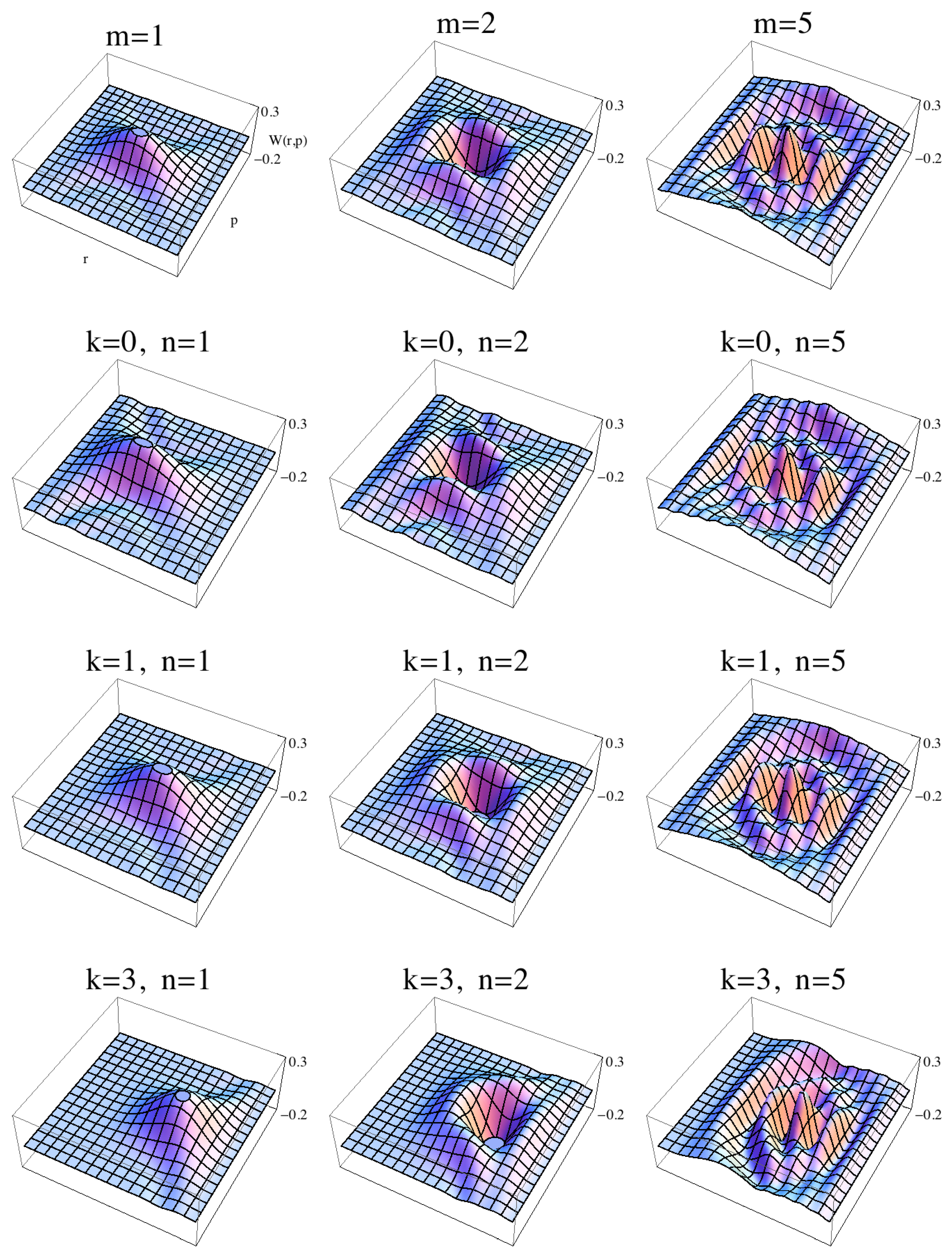
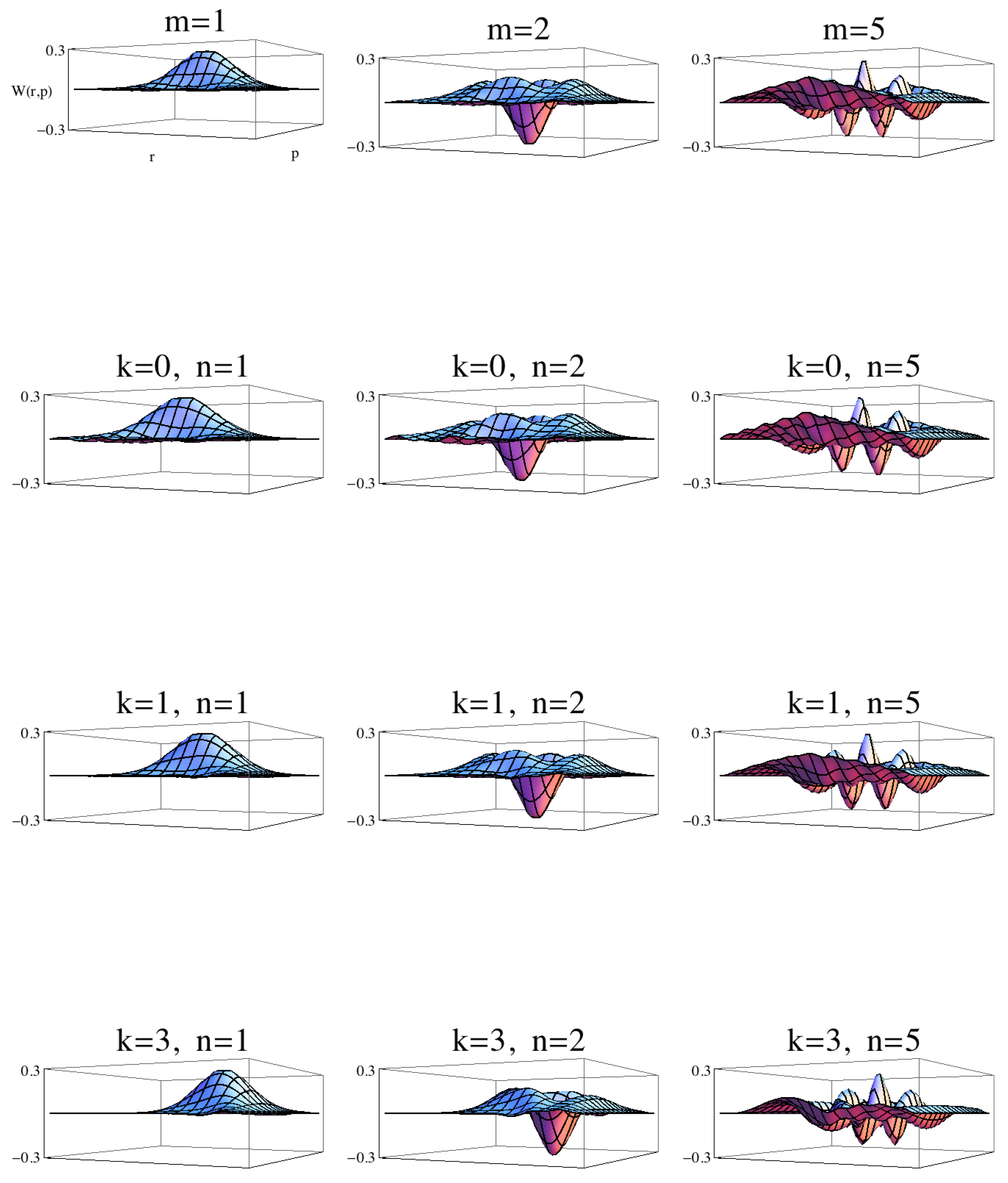
3.1. Wigner Functions
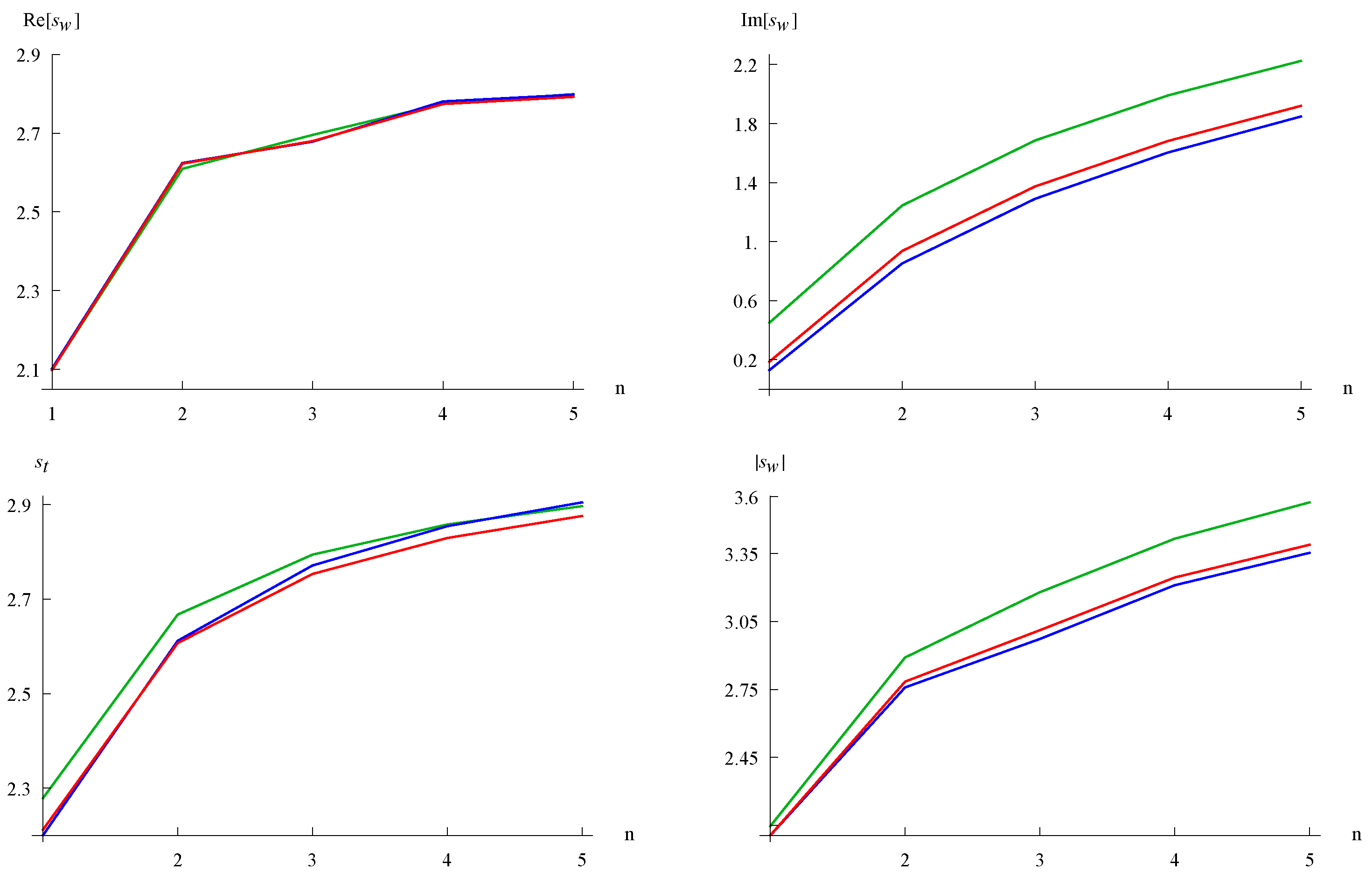
3.2. Shannon Entropy of the Wigner Function
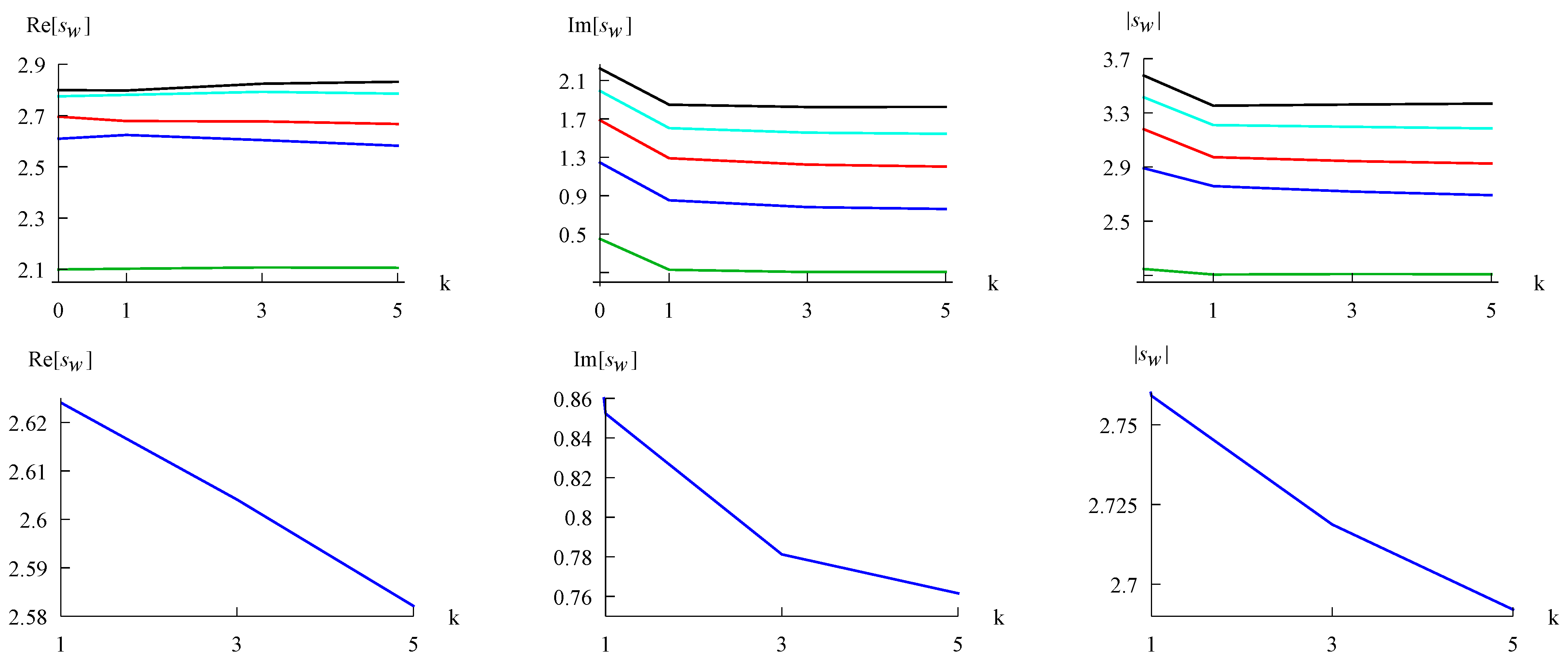
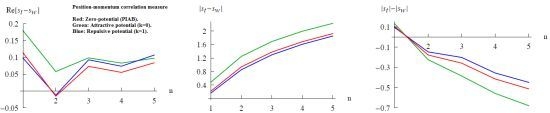
3.3. Mutual Information
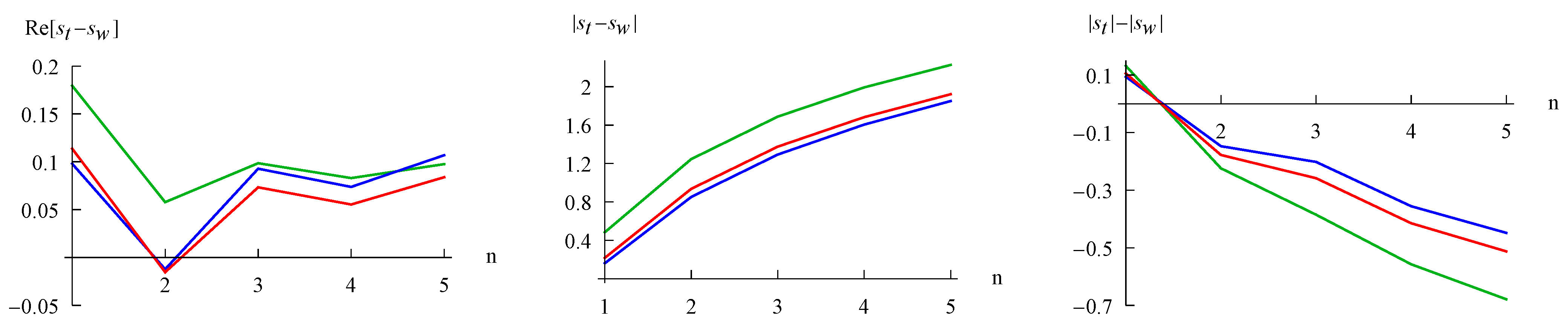
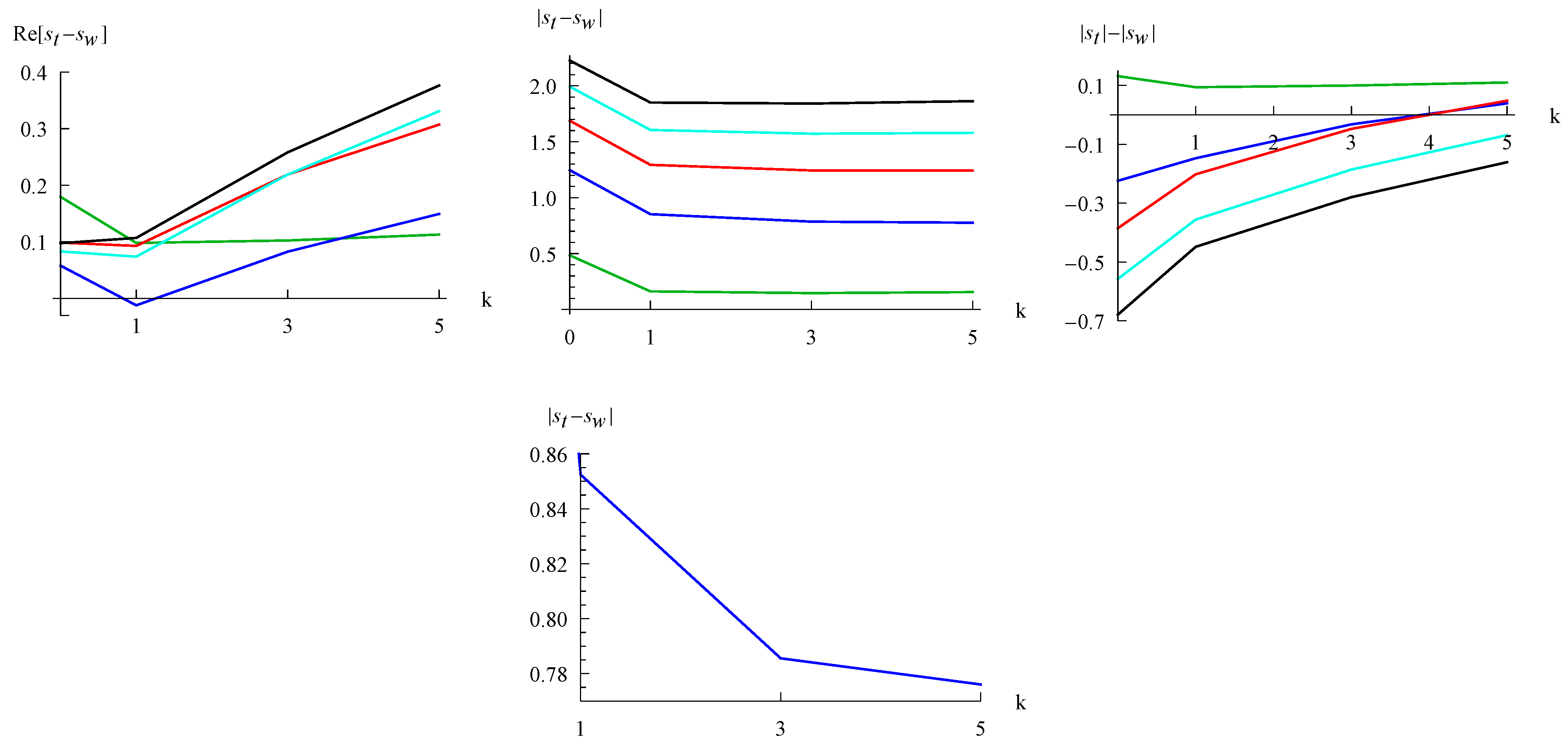
4. Conclusions
Acknowledgments
References
- Lévy-Leblond, J.-M. Correlation of quantum properties and the generalized Heisenberg inequality. Am. J. Phys. 1986, 54, 135–136. [Google Scholar] [CrossRef]
- De la Torre, A.C.; Iguain, J.L. Manifest and concealed correlations in quantum mechanics. Eur. J. Phys. 1998, 19, 563–568. [Google Scholar] [CrossRef]
- Campos, R.A. Correlation coefficient for incompatible observables of the quantum harmonic oscillator. Am. J. Phys. 1998, 66, 712–718. [Google Scholar] [CrossRef]
- Campos, R.A. Wigner quasiprobability distribution for quantum superpositions of coherent states, a Comment on “Correlation coefficient for incompatible observables of the quantum harmonic oscillator" [Am. J. Phys. 66 (8), 712-718 (1998)]. Am. J. Phys. 1999, 67, 641–642. [Google Scholar] [CrossRef]
- Campos, R.A. Quantum correlation coefficient for position and momentum. J. Mod. Opt. 1999, 46, 1277–1294. [Google Scholar] [CrossRef]
- Laguna, H.G.; Sagar, R.P. Shannon entropy of the Wigner function and position-momentum correlation in model systems. Int. J. Quantum Inf. 2010, 8, 1089–1100. [Google Scholar] [CrossRef]
- Laguna, H.G.; Sagar, R.P. Position-momentum correlations in the Moshinsky atom. J. Phys. A Math. Theor. 2012, 45, 025307. [Google Scholar] [CrossRef]
- Wigner, E.P. On the quantum correction for thermodynamic equilibrium. Phys. Rev. 1932, 40, 749–759. [Google Scholar] [CrossRef]
- Hillery, M.; O’Connell, R.F.; Scully, M.O.; Wigner, E.P. Distribution-functions in physics-fundamentals. Phys. Rep. 1984, 106, 121–167. [Google Scholar] [CrossRef]
- Tatarskii, V.I. The Wigner representation of quantum mechanics. Usp. Fiz. Nauk. 1983, 139, 587–619. [Google Scholar] [CrossRef]
- Halliwell, J.J. Correlations in the wave-function of the universe. Phys. Rev. D 1987, 36, 3626–3640. [Google Scholar] [CrossRef]
- Anderson, A. On predicting correlations from Wigner functions. Phys. Rev. D 1990, 42, 585–589. [Google Scholar] [CrossRef]
- Robinett, R.W.; Doncheski, M.A.; Bassett, L.C. Simple examples of position-momentum correlated Gaussian free-particle wave packets in one dimension with the general form of the time-dependent spread in position. Found. Phys. Lett. 2005, 18, 455–475. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley and Sons: New York, NY, USA, 1991; p. 251. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Wehrl, A. General properties of entropy. Rev. Mod. Phys. 1978, 50, 221–260. [Google Scholar] [CrossRef]
- Bialynicki-Birula, I.; Mycielski, J. Uncertainty relations for information entropy in wave mechanics. Commun. Math. Phys. 1975, 44, 129–132. [Google Scholar] [CrossRef]
- Dahl, J.P.; Mack, H.; Wolf, A.; Schleich, W.P. Entanglement versus negative domains of Wigner functions. Phys. Rev. A 2006, 74, 042323. [Google Scholar] [CrossRef]
- Kenfack, A.; Życzkowski, K. Negativity of the Wigner function as an indicator of non-classicality. J. Opt. B Quantum Semiclass. Opt. 2004, 6, 396–404. [Google Scholar] [CrossRef]
- Lütkenhaus, N.; Barnett, S.M. Nonclassical effects in phase-space. Phys. Rev. A 1995, 51, 3340–3342. [Google Scholar] [CrossRef] [PubMed]
- Sperling, J.; Vogel, W. Representation of entanglement by negative quasi-probabilities. Phys. Rev. A 2009, 79, 042337. [Google Scholar] [CrossRef]
- Mirbach, B.; Korsch, H.J. A generalized entropy measuring quantum localization. Ann. Phys. 1998, 265, 80–97. [Google Scholar] [CrossRef]
- Gnutzmann, S.; Życzkowski, K. Renyi-Wehrl entropies as measures of localization in phase space. J. Phys. A Math. Gen. 2001, 34, 10123–10139. [Google Scholar] [CrossRef]
- Pennini, F.; Plastino, A. Localization estimation and global vs. local information measures. Phys. Lett. A 2007, 365, 263–267. [Google Scholar] [CrossRef]
- Pennini, F.; Plastino, A.; Ferri, G.L.; Olivares, F. Semiclassical localization and uncertainty principle. Phys. Lett. A 2008, 372, 4870–4873. [Google Scholar] [CrossRef]
- Olivares, F.; Pennini, F.; Ferri, G.L.; Plastino, A. Note on semiclassical uncertainty relations. Braz. J. Phys. 2009, 39, 503–506. [Google Scholar] [CrossRef]
- Crommie, M.F.; Lutz, C.P.; Eigler, D.M. Confinement of electrons to quantum corrals on a metal-surface. Science 1993, 262, 218–220. [Google Scholar] [CrossRef] [PubMed]
- Crommie, M.F.; Lutz, C.P.; Eigler, D.M. Imaging standing waves in a 2-dimensional electron-gas. Nature 1993, 363, 524–527. [Google Scholar] [CrossRef]
- Dehesa, J.S.; Martínez-Finkelshtein, A.; Sorokin, V.N. Short-wave asymptotics of the information entropy of a circular membrane. Int. J. Bifurcation Chaos 2002, 12, 2387–2392. [Google Scholar] [CrossRef]
- Corzo, H.H.; Castaño, E.; Laguna, H.G.; Sagar, R.P. Measuring localization-delocalization phenomena in a quantum corral. J. Math. Chem. 2013, 51, 179–193. [Google Scholar] [CrossRef]
- Belloni, M.; Doncheski, M.A.; Robinett, R.W. Wigner quasi-probability distribution for the infinite square well: Energy eigenstates and time-dependent wave packets. Am. J. Phys. 2004, 72, 1183–1192. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Laguna, H.G.; Sagar, R.P. Phase-Space Position-Momentum Correlation and Potentials. Entropy 2013, 15, 1516-1527. https://doi.org/10.3390/e15051516
Laguna HG, Sagar RP. Phase-Space Position-Momentum Correlation and Potentials. Entropy. 2013; 15(5):1516-1527. https://doi.org/10.3390/e15051516
Chicago/Turabian StyleLaguna, Humberto G., and Robin P. Sagar. 2013. "Phase-Space Position-Momentum Correlation and Potentials" Entropy 15, no. 5: 1516-1527. https://doi.org/10.3390/e15051516