1. Introduction
The estimation of the state variables of a dynamic system through noisy measurements is one of the fundamental problems in control systems and signal processing. This problem has been an active topic over the past few decades, and some effective estimation approaches have been exploited in the literatures, such as Kalman filtering schemes,
filtering and robust filtering methods; see e.g., [
1,
2,
3,
4]. The celebrated Kalman filtering has been proven to be an optimal estimator for linear systems with disturbances described as white noise. The filtering scheme is based on the assumption of having an exact and accurate system model as well as perfect knowledge about the statistical properties of noise sources. Compared with the Kalman filtering, the advantage of
filtering is that the noise sources are arbitrary signals with bounded energy, and the exact statistic information about the external disturbance is not precisely known.
However, many well-established filtering techniques focus only on two quantities,
i.e., mean and variance or covariance, as key design targets. Since the output of a nonlinear stochastic system is usually non-Gaussian, mean and variance or covariance are not enough to characterize the output process. Thus, the existing classical stochastic filtering theory may be incomplete for non-Gaussian stochastic systems. Entropy is a scalar quantity that provides a measure for the average “uncertain” information contained in a given probability density function (PDF). When entropy is minimized, all moments of the error PDF are constrained [
5,
6]. Entropy has been widely used in information, thermodynamics and control fields. The minimum entropy filtering problem has recently received renewed research interests in dealing with the stochastic state estimation problem for non-Gaussian systems. This subject is one of the important topics of the research of stochastic distribution control (SDC). Differing from traditional stochastic control where only the output mean and variance are considered, stochastic distribution control aims to control the shape of the output probability density functions for non-Gaussian and dynamic stochastic systems; see [
7,
8], and the reference therein. Based on SDC, current studies mainly focus on the problems of the probability density function tracking control [
9,
10,
11,
12], fault detection and fault isolation of stochastic systems [
13,
14], parameter estimation [
15],
etc.
The entropy optimization filtering methodology has been studied for non-Gaussian systems in [
16], where the concepts of a hybrid PDF and a hybrid entropy are introduced, and an optimal filter gain design algorithm is proposed to minimize the hybrid entropy of the estimation error. Using the idea of the iterative learning control, in [
17], the filter gain is determined by the gradient ILC tuning law. The learning rate is studied to guarantee the convergence of the proposed algorithm. In [
18], based on the form of the hybrid characteristic function of the conditional estimation error, a new Kullback–Leibler-like performance function is constructed. An optimal PDF shaping tracking filter is designed such that the tracking error between the characteristic function of the estimation error and the target characteristic function is minimized.
It should be pointed out that, in the literatures mentioned above, only stochastic stability analysis is given after the recursive solution, direct and analytical stabilization design and other closed-loop performance design cannot be carried on along with the minimum entropy filtering. To the best of the author’s knowledge, analytical filtering algorithm that links the minimum entropy filtering and the stochastic stabilization together has not yet been addressed for non-Gaussian stochastic systems and still remains a challenging problem.
Inspired by the aforementioned situations, we aim at solving the resilient minimum entropy filtering problem for the stochastic systems subject to non-Gaussian noise. The main contributions of this paper are as follows: (1) A recursive solution of the filter gain updating is proposed such that the entropy of the estimation error decreases strictly, which means the shape of the distribution of the error is as narrow as possible; (2) Based on linear matrix inequality and the resilient control theory, a new suboptimal stochastic stability filter gain updating law is proposed to guarantee that the estimation error is stochastically exponentially ultimately bounded in the mean square. Compared with the previous works on filtering for non-Gaussian stochastic systems, the advantage of the results presented in this paper is that the relationship between the entropy performance and the stochastic stability, even other important closed-loop performance can be established directly. In the future work, we will further discuss other closed-loop performance of the non-Gaussian stochastic systems in detail.
The rest of this article is organized as follows. The problem formulations and preliminaries are given in
Section 2.
Section 3 is dedicated to derive the filter gain updating algorithm to guarantee that the entropy of the error reduces at every sampling time
k. The boundedness of the filter gain is analyzed in
Section 4. A sufficient condition for the existence of the recursive resilient filter is given to ensure the exponential ultimate boundedness of the error system in
Section 4. Numerical example is included in
Section 5, which is then followed by concluding remarks.
Notation. The notations in this paper are quite standard. means the Euclidean norm in . is the transpose of the matrix A. is the operator of matrix A, i.e., , where means the largest eigenvalue of A. Moreover, Ω is the sample space, F is a set of events. Let be a complete probability space, and stands for the mathematical expectation operator with respect to the given probability measure P. The expected value of a random variable x is denoted by . represent the variance of random variables. The star * represents a transpose quantity.
2. Problem Formulation
Consider the following stochastic system:
where
is the state,
is the output,
is the random disturbance. It should be pointed out that
can be non-Gaussian vector.
A,
C and
G are known system matrices.
It is assumed that
has known PDF
defined on a known closed interval
. There are some identification methods, such as the kernel estimation technique, experiment technique, direct physical measurement and other identification methods, that can be used to model the PDF. Therefore, the assumption can be satisfied in many practical systems. Without loss of generality, we assume
, and
. The nonlinear function
is assumed to be Lipschitz with respect to
, which means
for all
, and
.
For the system given by Equation (
1), the full-order filter is of the form
where
is the state estimate and
is the gain to be determined. Let the estimation error be
, then it follows from Equation (
1) and Equation (
3) that
where
is a nonlinear function. The PDF of the estimation error is defined as
where
is the probability of the estimation error
when the filter gain
is given. It can be seen from Equation (
4) that the shape of the PDF of the estimation error at time
k is governed by the filtering gain
.
Let the initial estimation of the state
be taken to be equal to the known mean of the initial state
. In order to study the stochastic behavior of the error system Equation (
4), the following definition is introduced.
Definition 1 ([
19,
20]) The dynamics of the estimation error
is exponentially ultimately bounded in the mean square if there exist constants
,
,
such that for any initial condition
,
where
,
and
. In this case, the filter in Equation (
3) is said to be exponential.
Remark 1 When the error dynamic is exponentially ultimately bounded in the mean square, the estimation error will initially decrease exponentially in the mean square, and remain within a certain region in the steady state, again in the mean square sense. The stability bound is defined in terms of the norm of the Hilbert space of random vectors, and is specified by the coefficient c.
The main purpose of the proposed filter design scheme can be stated as follows:
(1). To design the filter gain such that the dynamics of the estimation error is guaranteed to be stochastically exponentially ultimately bounded in the mean square.
(2). The filter should be designed such that the shape of the PDF of the estimation error is made as narrow as possible.
A narrow distribution generally indicates that the uncertainty of the related random variable is small,
i.e., the entropy is small. Considering the requirement of energy, we will design
such that the following performance function is minimized at every sampling time
k,
where
and
are weighting matrices,
is the entropy of the estimation errors.
3. The Minimum Entropy Filter Gain Updating Algorithm
In order to minimize the performance function in Equation (
7), the PDF of
is required. Applying probability theory [
21], the PDF of
can be formulated as
where
is the inverse function of
with respect to the noise term
. In this case,
is continuous and first order differentiable with all its variables.
Then, using Equation (
8), the filtering design algorithm can be developed by minimizing the performance function Equation (
7). Given
the optimal filtering strategy can be obtained via the following equality,
To formulate the recursive design procedure, we introduce
where
.
The function
can be approximated via
where
Then the following result can be obtained.
Theorem 1 The recursive filtering gain design algorithm to minimize the performance function subject to the estimation model Equation (4) is given bywhere the weight matrix satisfies Proof. From Equation (
11), it can be seen that
Substituting Equation (
16) into Equation (
10) yields
Then, we can obtain the recursive algorithm (Equation (
14)) for
.
Equation (
14) is derived from a necessary condition for optimization. To guarantee its sufficiency, the second-order derivative should be satisfied
which will hold when Equation (
15) holds.□
4. The Bound of the Filter Gain
In this section, we will study the bound of the filtering gain by introducing the kernel density estimation technique for estimating the probability density function. For estimating the density function
, [
22,
23] studied a general class of consistent and asymptotically normal estimators as a kernel weighted average over the empirical distribution
where the kernel
is a Gaussian kernel function.
From Equation (
10), we have
Then the filtering gain of model (1) is bounded as
Using Equation (
19), the partial differential term in Equation (
21) can be written as follows
From the dynamic equation of the estimation error in Equation (
4), we have
Noting that
, we get the following bound of
if
Furthermore, since
is a bounded function and
ξ is defined on
,
is bounded. We denote
, by Equation (
21) and Equation (
24), we get
Thus,
Remark 2. It should be noted that the function is a Gaussian kernel function, and the error is bounded in the interval . This guarantees that the upper bound of is easy to obtain.
5. Resilient Filter Gain Design
In the section, we will show how the resilient filter gain is obtained to guarantee the stochastic stability of the error system in Equation (
4). Generally, it is difficult to analyze the closed-loop stability for the stochastic distribution systems. In order to overcome the difficulty, using the results of
Section 4, we will design a gain-variation filter to assure Equation (
4) to be stochastically exponentially ultimately bounded in the mean square. We define the variable gain
as follows
where
is given by Equation (
14) of Theorem 1 to guarantee the decreasing of the performance function Equation (
7). In this case, Equation (
27) is a suboptimal recursive strategy to make sure that the distribution of the estimation error is made as narrow as possible.
Substituting Equation (
27) into Equation (
4), the estimation error can be written as
For the resilient gain design, we introduce the following Lemma.
Lemma 1 ([
24]) Given matrices
Y,
M and
N. Then
for all Δ satisfying
if and only if there exists a constant
such that
Based on Lemma 1 and the resilient control theory [
25], we present the following results to establish the relationship between the entropy performance and the stochastic stability for stochastic distribution control systems.
Theorem 2 Consider the error system in Equation (4), the filter gain variation is given by Equation (26), for given constants , and , there exist a positive scalar β, and matrices and Y such that the following inequalities holdthen system in Equation (28) is exponentially bounded in the mean square, and the filter gain is given bywhere is defined by Equation (14). Proof. Define a Lyapunov functional candidate for Equation (
28) as
where
. Since
,
, we have
Note that
and
, then
then, if
holds, we have
From Equation (
37), we have that there exists a sufficiently small scalar
θ satisfying
and
On the other hand,
Then, it follows from Equation (
35) and Equation (
38) that
and subsequently,
where
By using inequality of Equation (
40) again, we get
Then, it follows directly from Definition 1 that if Equation (
38) holds, the dynamics of the error system is exponentially bounded in the mean square.
Next, we will show the equivalence of Equation (
32) and Equation (
37).
By the Schur complement, Equation (
37) is equivalent to the following inequality
Then from Lemma 1 and
, we have
It follows that the above inequality is equivalent to Equation (
37). This completes the proof.□
Remark 3 In Theorem 2, the filter gain updating law is a suboptimal recursive strategy that guarantees the strictly decreasing nature of the entropy of the estimation errors. Meanwhile, is a control law to ensure the mean square exponential stability. Hence, based on the resilient control theory, Theorem 2 establishes the relationship between the entropy performance and the stochastic stability for stochastic distribution control systems.
6. Numerical Example
The proposed resilient filter gain algorithm is demonstrated via a numerical example in this section. Consider the stochastic system given as follows,
The Lipschitz constant of the nonlinear part of the system is
. The random disturbance
is defined by
According to Equation (
3), the designed filter is
where
L is the solution of Equation (
32),
is given by Equation (
14).
By solving Equation (
32), we have
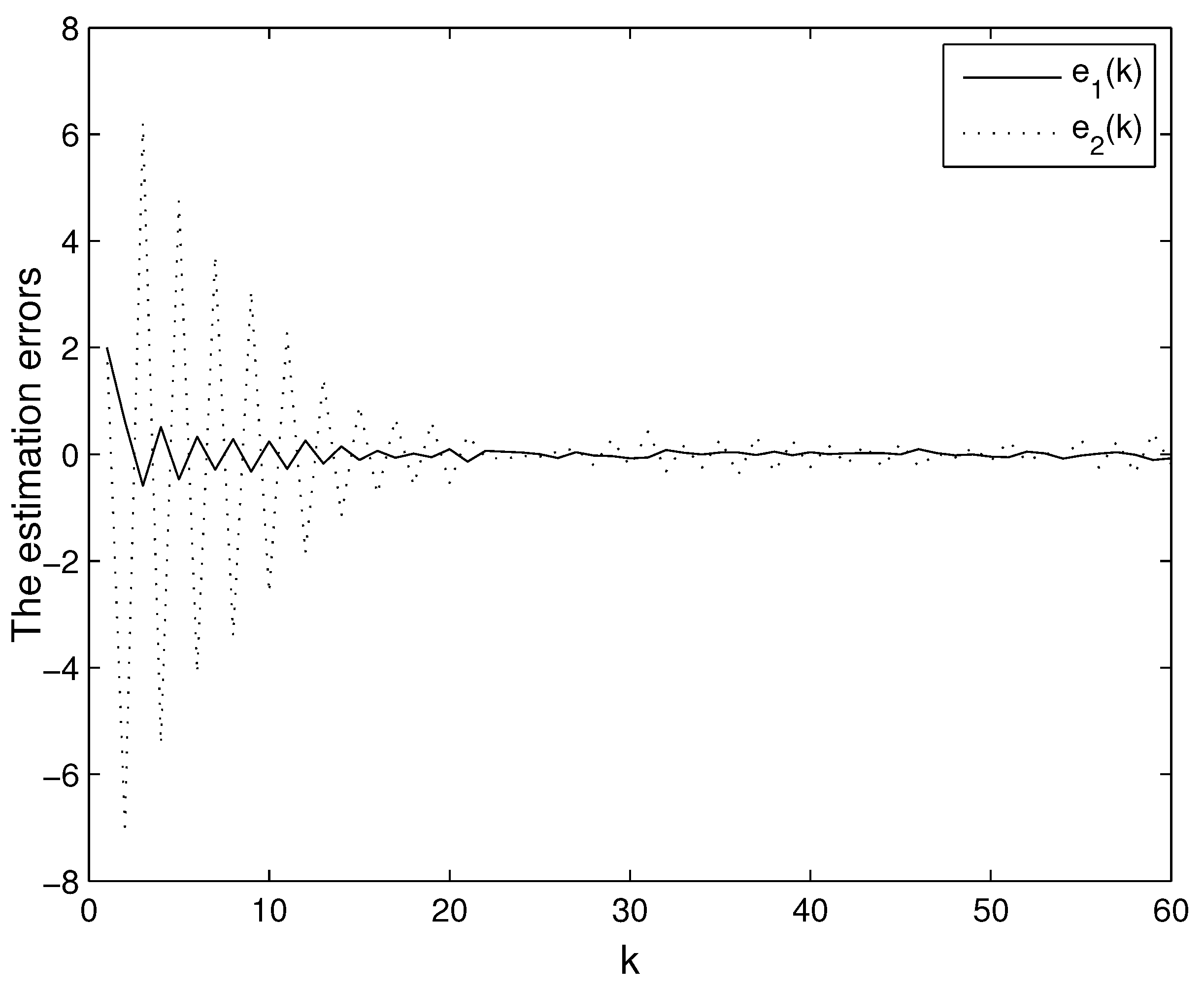
The response of the error dynamics is shown in
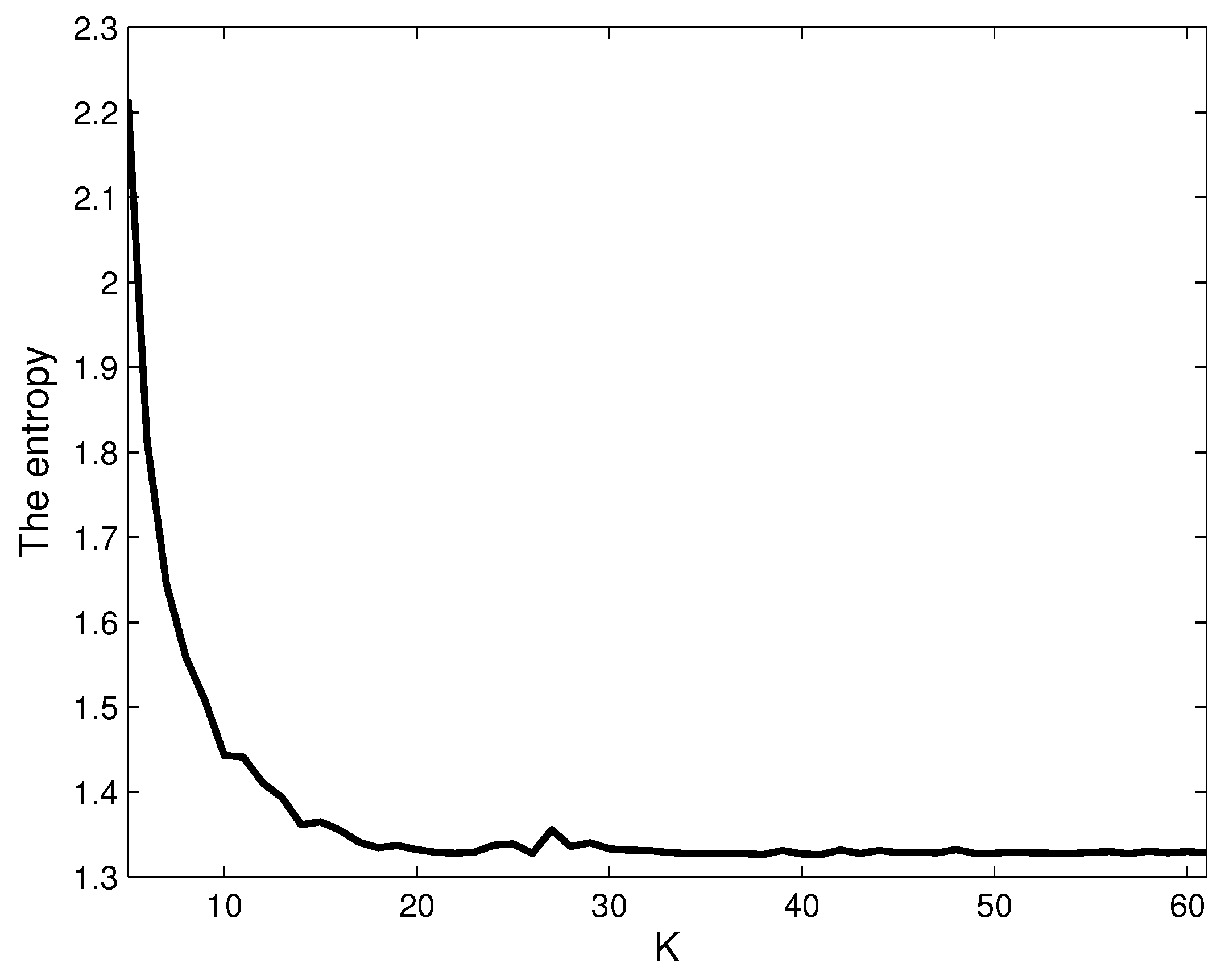
Figure 1. It can be shown that the steady-state estimation error variance is bounded. The response of the entropy is displayed in
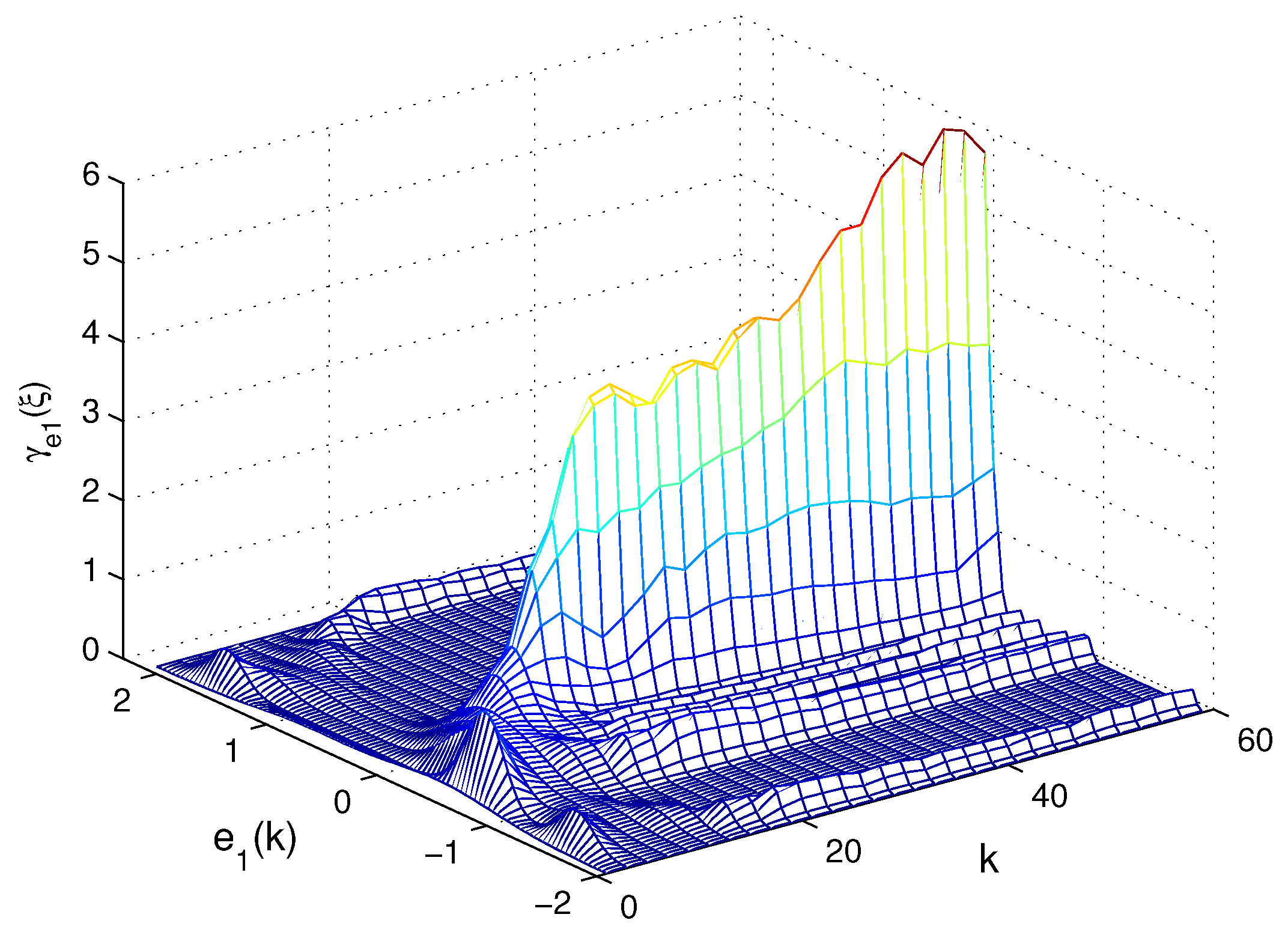
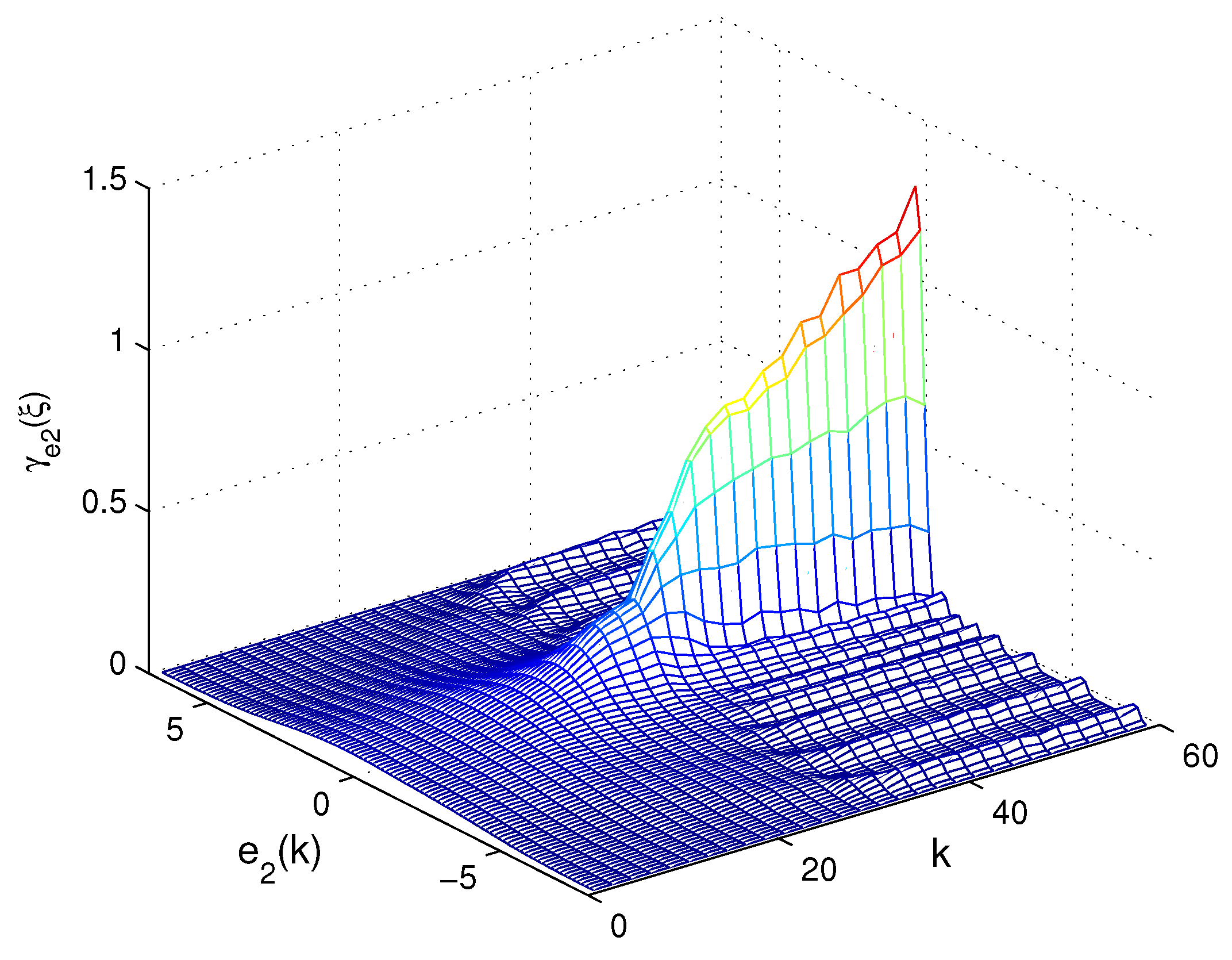
Figure 2. The 3D-mesh plots of the PDF of
and
are given in
Figure 3 and
Figure 4. These figures demonstrate that the error system is exponentially bounded in mean square, the entropy of the estimation errors decreases monotonically, and the PDF of the estimation error is close to a narrow Gaussian shape.
Figure 1.
Trajectories of the estimation errors.
Figure 1.
Trajectories of the estimation errors.
Figure 2.
The entropy of the estimation errors.
Figure 2.
The entropy of the estimation errors.
Figure 3.
The 3D-mesh plot of PDF of the estimation error .
Figure 3.
The 3D-mesh plot of PDF of the estimation error .
Figure 4.
The 3D-mesh plot of PDF of the estimation error .
Figure 4.
The 3D-mesh plot of PDF of the estimation error .