Minimum Mutual Information and Non-Gaussianity through the Maximum Entropy Method: Estimation from Finite Samples
Abstract
:1. Introduction
1.1. The State of the Art
1.2. The Rationale of the Paper
2. Minimum Mutual Information and Its Estimators
2.1. Imposing Marginal PDFs
2.2. Imposing Marginals through ME Constraints
2.2.1. The Formalism
2.2.2. A Theorem about the MinMI Covariance Matrix
2.3. Gaussian and Non-Gaussian MI
2.4. Estimators of the Minimum MI from Data and Their Errors
3. Errors of the Expectation’s Estimators
3.1. Generic Properties
3.2. The Effects of Morphisms and Bivariate Sampling
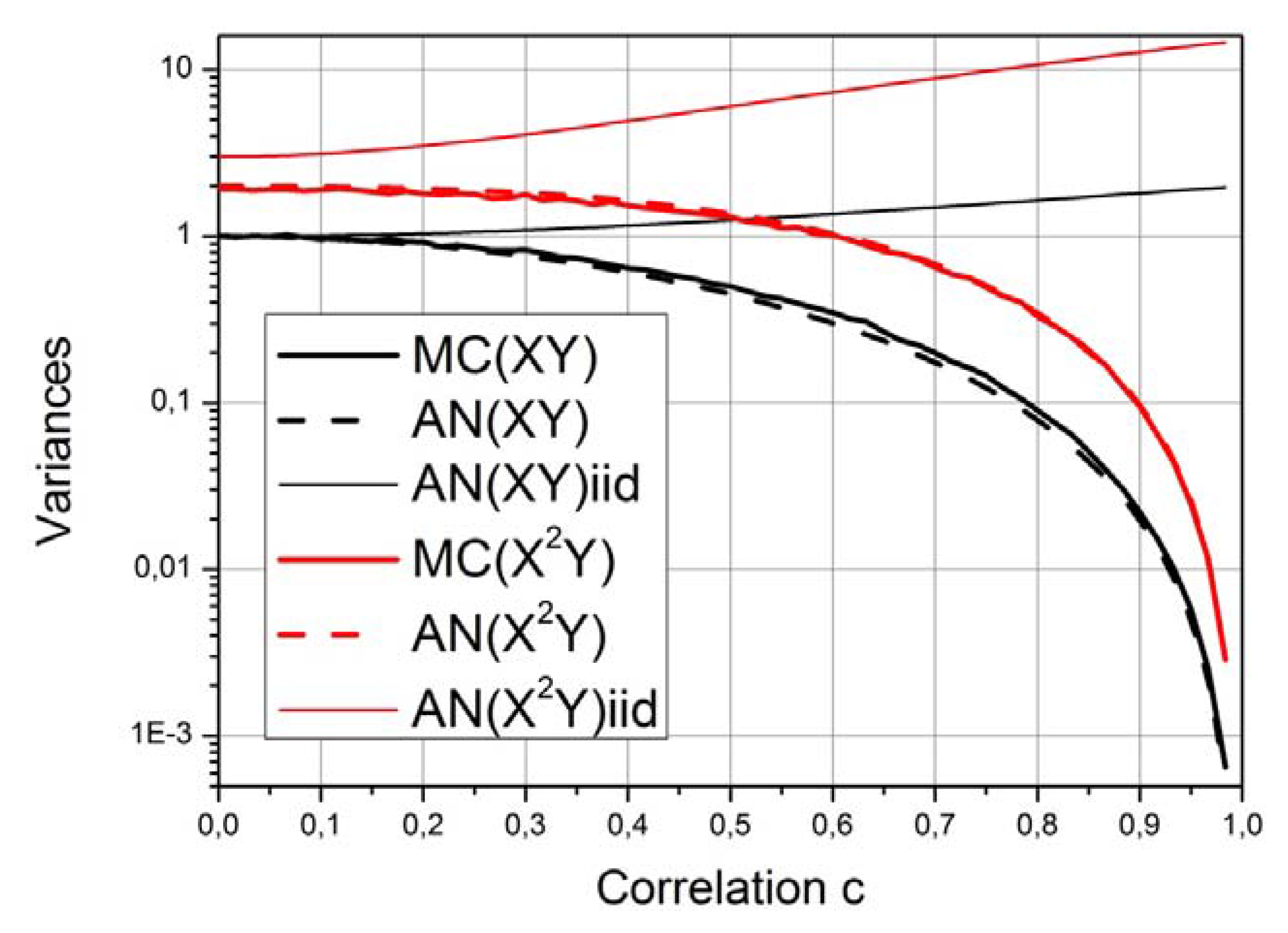
3.3. Errors of the Estimators of Polynomial Moments under Gaussian Distributions
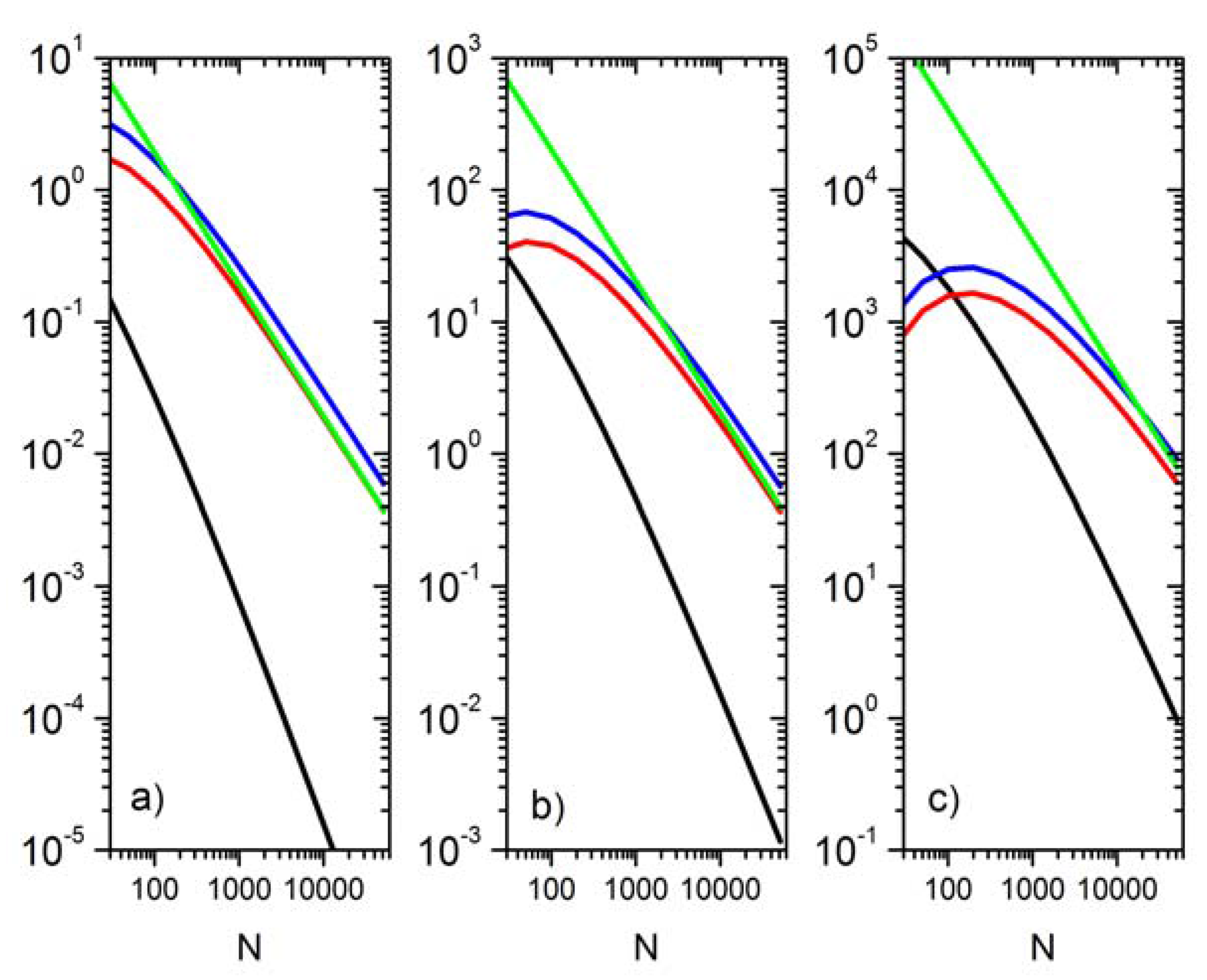
3.4. Statistical Modeling of Moment Estimation Errors
4. Modeling of MinMI Estimation Errors, Their Bias, Variance and Distribution
- The estimation of bias, variance, quantiles and distribution of estimators of the incremental MinMI issued from finite samples of N (iid) realizations of bivariate original variables and then transformed into RVs
- The distribution of estimators of under the null hypothesis H0 that follows the ME distribution constrained by a weaker constraint set (j>p). These estimators work as a significance test for determining whether there is statistically significant MI beyond that explained by cross moments in .
4.1. Bias, Variance, Quantiles and Distribution of MI Estimation Error
4.2. Significance Tests of MinMI Thresholds
4.3. Significance Tests of the Gaussian and Non-Gaussian MI
4.3.1. Error and Significance Tests of the Gaussian MI
4.3.2. Error and Significance Tests of the Non-Gaussian MI
4.4. Validation of Significance Tests by Monte-Carlo Experiments
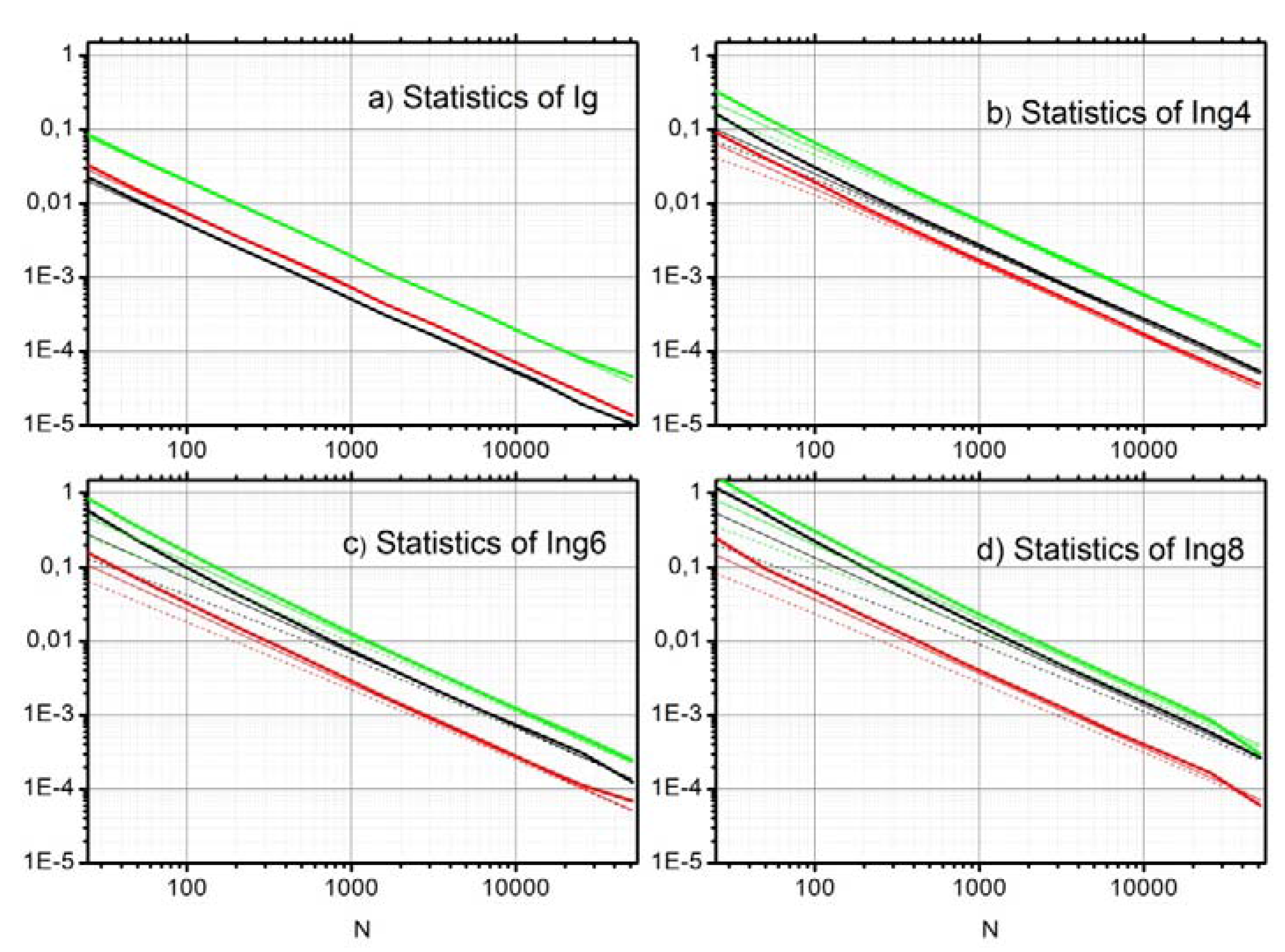
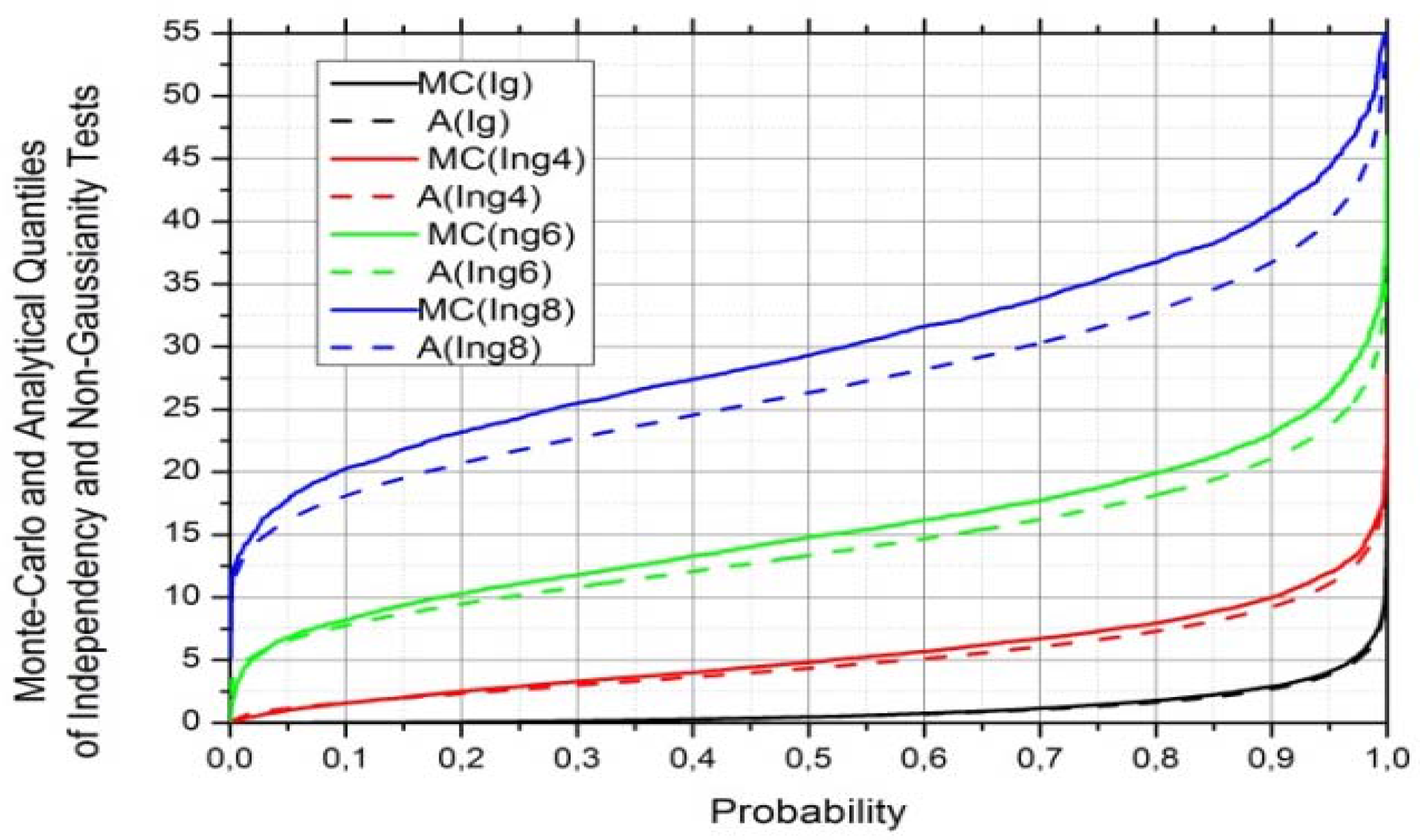
5. MI Estimation from Under-Sampled Data
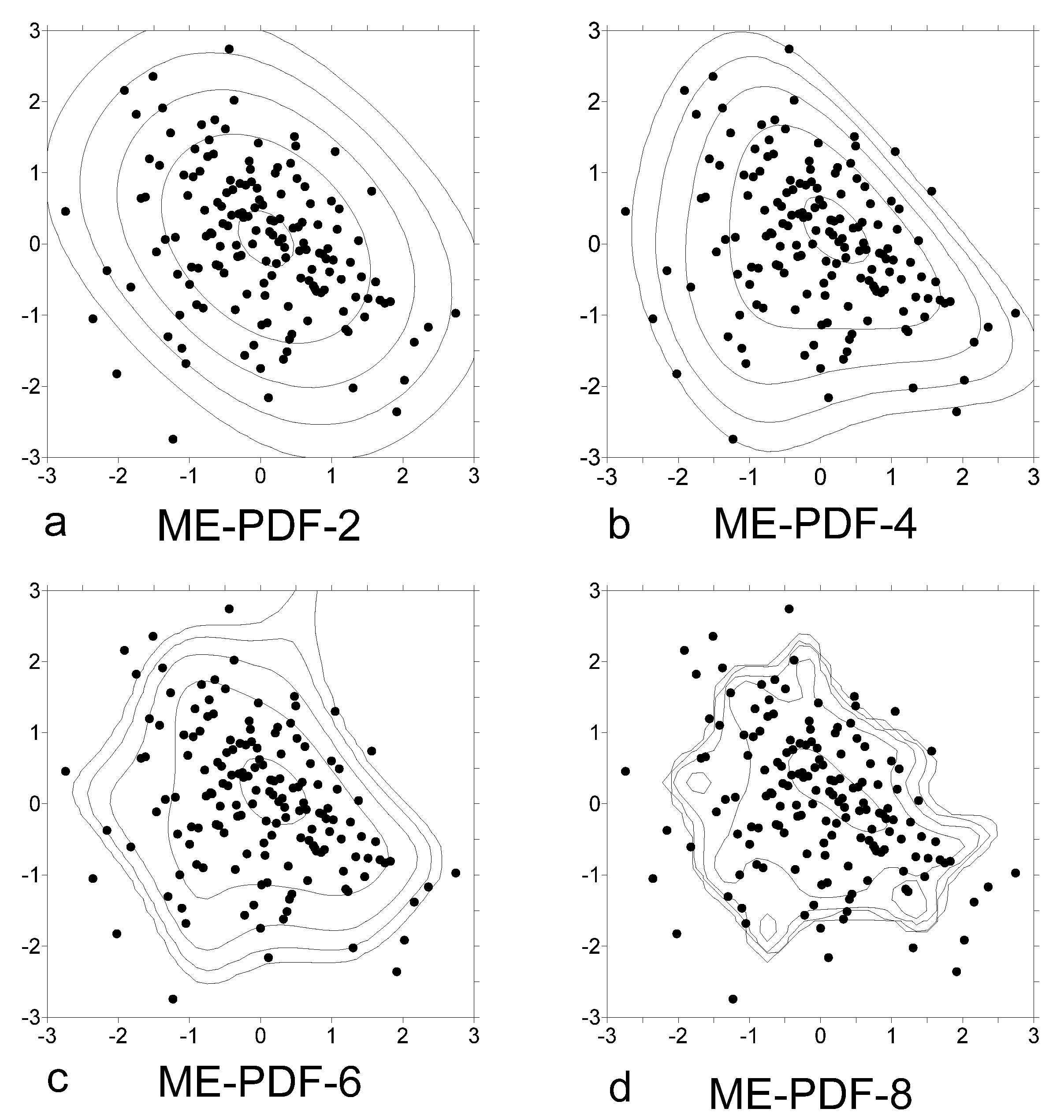
6. Discussion and Conclusions
Acknowledgments
References
- Shannon, C.E. The mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons, Inc.: New York, NY, USA, 1991. [Google Scholar]
- Averbeck, B.B.; Latham, P.E.; Pouget, A. Neural correlations, population coding and computation. Nat. Rev. Neurosci. 2006, 7, 358–366. [Google Scholar] [CrossRef] [PubMed]
- Goldie, C.M.; Pinch, R.G.E. Communication Theory. In London Mathematical Society Student Texts (No. 20); Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Sims, C.A. Rational Inattention: Beyond the Linear-Quadratic Case. Am. Econ. Rev. 2006, 96, 158–163. [Google Scholar] [CrossRef]
- Sherwin, W.E. Entropy and Information Approaches to Genetic Diversity and its Expression: Genomic Geography. Entropy 2010, 12, 1765–1798. [Google Scholar] [CrossRef]
- Pothos, E.M.; Juola, P. Characterizing linguistic structure with mutual information. Br. J. Psychol. 2007, 98, 291–304. [Google Scholar] [CrossRef] [PubMed]
- Pires, C.A.; Perdigão, R.A.P. Non-Gaussianity and asymmetry of the winter monthly precipitation estimation from the NAO. Mon. Wea. Rev. 2007, 135, 430–448. [Google Scholar] [CrossRef]
- Globerson, A.; Tishby, N. The minimum information principle for discriminative learning. In Proceedings of the 20th conference on Uncertainty in artificial intelligence, Banff, Canada, 7–11 July 2004; pp. 193–200.
- Globerson, A.; Stark, E.; Vaadia, E.; Tishby, N. The minimum information principle and its application to neural code analysis. Proc. Natl. Accd. Sci. USA 2009, 106, 3490–3495. [Google Scholar] [CrossRef] [PubMed]
- Foster, D.V. Grassberger, P. Lower bounds on mutual information. Phys. Rev. E 2011, 83, 010101(R):1–010101(R):4. [Google Scholar] [CrossRef]
- Pires, C.A.; Perdigão, R.A.P. Minimum Mutual Information and Non-Gaussianity Through the Maximum Entropy Method: Theory and Properties. Entropy 2012, 14, 1103–1126. [Google Scholar] [CrossRef]
- Walters-Williams, J.; Li, Y. Estimation of mutual information: A survey. Lect. Notes Comput. Sci. 2009, 5589, 389–396. [Google Scholar]
- Khan, S.; Bandyopadhyay, S.; Ganguly, A.R.; Saigal, S.; Erickson, D.J.; Protopopescu, V.; Ostrouchov, G. Relative performance of mutual information estimation methods for quantifying the dependence among short and noisy data. Phys. Rev. E 2007, 76, 026209:1–026209:15. [Google Scholar] [CrossRef]
- Paninski, L. Estimation of entropy and mutual information. Neural Comput. 2003, 15, 1191–1254. [Google Scholar] [CrossRef]
- Panzeri, S.; Treves, A. Analytical estimates of limited sampling biases in different information measures. Comp. Neur. Syst. 1996, 7, 87–107. [Google Scholar] [CrossRef]
- Victor, J.D. Asymptotic Bias in Information Estimates and the Exponential (Bell) Polynomials. Neur. Comput. 2000, 12, 2797–2804. [Google Scholar] [CrossRef]
- Panzeri, S.; Senatore, R.; Montemurro, M.A.; Petersen, R.S. Train Information Measures Correcting for the Sampling Bias Problem in Spike Information Measures. J. Neurophysiol. 2007, 98, 1064–1072. [Google Scholar] [CrossRef] [PubMed]
- Strong, S.P.; Koberle, R.; de Ruyter van Steveninck, R.; Bialek, W. Entropy and information in neural spike trains. Phys. Rev. Lett. 1998, 86, 197–200. [Google Scholar] [CrossRef]
- Miller, G. Note on the bias of information estimates. In Information Theory in Psycholog; Quastler, H., Ed.; II-B Free Press: Glencoe, IL, USA, 1955; pp. 95–100. [Google Scholar]
- Grassberger, P. Entropy Estimates from Insufficient Samplings. 2008; arXiv:physics/0307138v2.pdf. [Google Scholar]
- Bonachela, J.A.; Hinrichsen, H.; Muñoz, M.A. Entropy estimates of small data sets. J. Phys. A 2008, 41, 202001. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 1999; ISBN 0-387-98623-5. [Google Scholar]
- Calsaverini, R.S.; Vicente, R. An information-theoretic approach to statistical dependence: Copula information. Europhys. Lett. 2009, 88, 68003. [Google Scholar] [CrossRef]
- Ma, J.; Sun, Z. Mutual information is copula entropy. 2008; arXiv:0808.0845v1. [Google Scholar]
- Macke, J.H.; Murray, I.; Latham, P.E. How biased are maximum entropy models? Adv. Neur. Inf. Proc. Syst. 2011, 24, 2034–2042. [Google Scholar]
- Hutter, M.; Zaffalon, M. Distribution of mutual information from complete and incomplete data. Comput. Stat. Data An. 2005, 48, 633–657. [Google Scholar] [CrossRef]
- Jaynes, E.T. On the Rationale of Maximum-entropy methods. P. IEEE 1982, 70, 939–952. [Google Scholar] [CrossRef]
- Shore, J.E.; Johnson, R.W. Axiomatic derivation of the principle of maximum entropy and the principle of the minimum cross-entropy. IEEE Trans. Inform. Theor. 1980, 26, 26–37. [Google Scholar] [CrossRef]
- Ebrahimi, N.; Soofi, E.S.; Soyer, R. Information Measures in Perspective. Int. Stat. Rev. 2010, 78, 383–412. [Google Scholar] [CrossRef]
- Wackernagel, H. Multivariate Geostatistics—An Introduction with Applications; Springer Verlag: Berlin, Germany, 1995. [Google Scholar]
- Charpentier, A.; Fermanian, J.D. Copulas: From Theory to Application in Finance; Rank, J., Ed.; Risk Publications: London, UK, 2007; Section 2. [Google Scholar]
- Tam, S.M. On Covariance in Finite Population Sampling. J. Roy. Stat. Soc. D-Sta. 1985, 34, 429–433. [Google Scholar] [CrossRef]
- Van det Vaart, A.W. Asymptotic statistics. Cambridge University Press: New York, NY, USA, 1998; ISBN ISBN 978–0-521–49603–2, LCCN. V22 1998 QA276. V22. [Google Scholar]
- Rockinger, M.; Jondeau, E. Entropy densities with an application to autoregressive conditional skewness and kurtosis. J. Econometrics 2002, 106, 119–142. [Google Scholar] [CrossRef]
- Bates, D. Quadratic Forms of Random Variables. STAT 849 lectures. Available online: http://www.stat.wisc.edu/~st849–1/lectures/Ch02.pdf (accessed on 22 February 2013).
- Goebel, B.; Dawy, Z.; Hagenauer, J.; Mueller, J.C. An approximation to the distribution of finite sample size mutual information estimates. 2005. In Proceedings of IEEE International Conference on Communications (ICC’ 05), Seoul, Korea, 16–20 May 2005; pp. 1102–1106.
- Fisher, R.A. On the “probable error” of a coefficient of correlation deduced from a small sample. Metron 1921, 1, 3–32. [Google Scholar]
- Zientek, L.R.; Thompson, B. Applying the bootstrap to the multivariate case: bootstrap component/factor analysis. Behav. Res. Methods 2007, 39, 318–325. [Google Scholar] [CrossRef] [PubMed]
- Mardia, K.V. Algorithm AS 84: Measures of multivariate skewness and kurtosis. Appl. Stat. 1975, 24, 262–265. [Google Scholar] [CrossRef]
- Hurrell, J.W.; Kushnir, Y.; Visbeck, M. The North Atlantic Oscillation. Science 2001, 26, 291. [Google Scholar]
- The NCEP/NCAR Reanalysis Project. Available online: http://www.esrl.noaa.gov/psd/data/reanalysis/reanalysis.shtml/ (accessed on 22 February 2013).
Appendix 1
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Pires, C.A.L.; Perdigão, R.A.P. Minimum Mutual Information and Non-Gaussianity through the Maximum Entropy Method: Estimation from Finite Samples. Entropy 2013, 15, 721-752. https://doi.org/10.3390/e15030721
Pires CAL, Perdigão RAP. Minimum Mutual Information and Non-Gaussianity through the Maximum Entropy Method: Estimation from Finite Samples. Entropy. 2013; 15(3):721-752. https://doi.org/10.3390/e15030721
Chicago/Turabian StylePires, Carlos A. L., and Rui A. P. Perdigão. 2013. "Minimum Mutual Information and Non-Gaussianity through the Maximum Entropy Method: Estimation from Finite Samples" Entropy 15, no. 3: 721-752. https://doi.org/10.3390/e15030721





