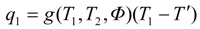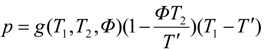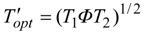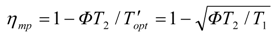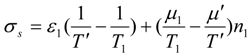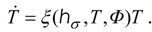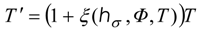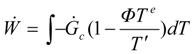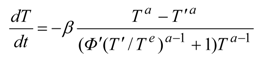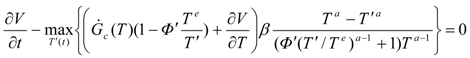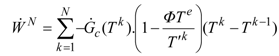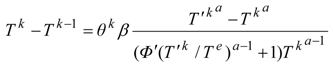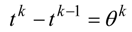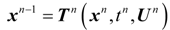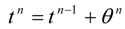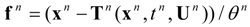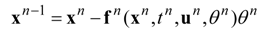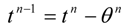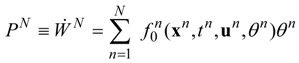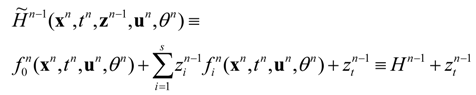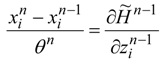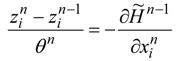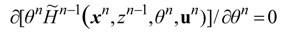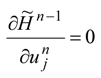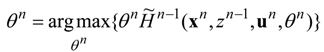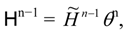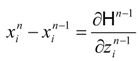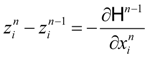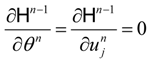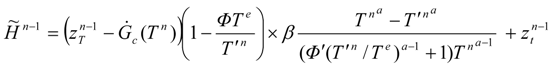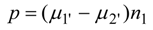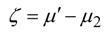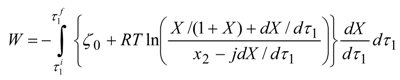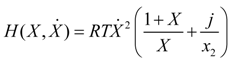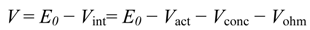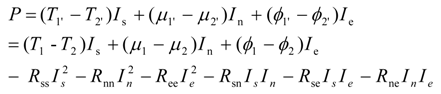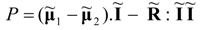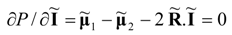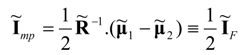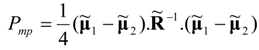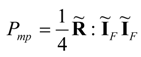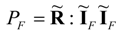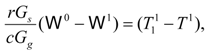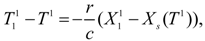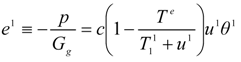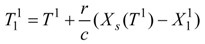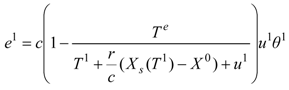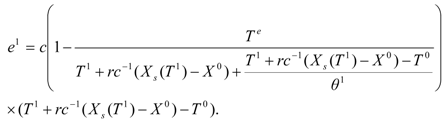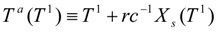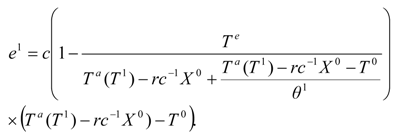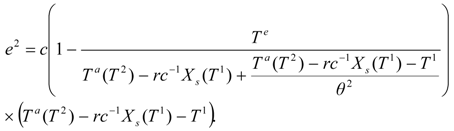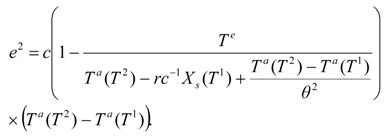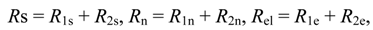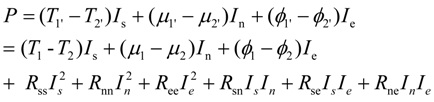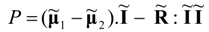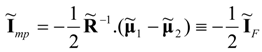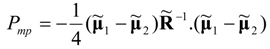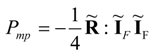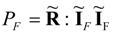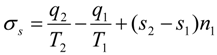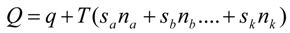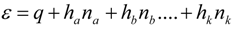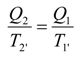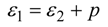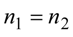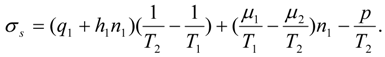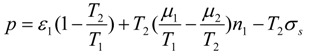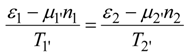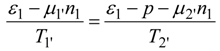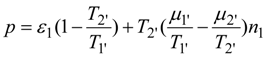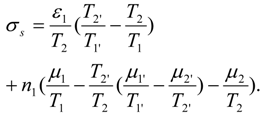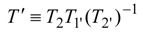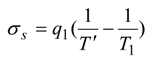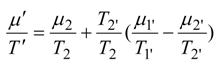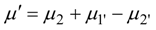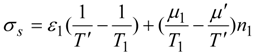2. Steady Thermal Systems with Internal Dissipation
A great deal of research on power limits published to date considers stationary systems, in which case both reservoirs are infinite. Consider, for instance, steady-state analyses of the Chambadal-Novikov-Curzon-Ahlborn engine (CNCA engine [
1,
13,
14]), in which the energy exchange is described by Newtonian law of cooling, or the Stefan-Boltzmann engine: a system with two radiation fluids and the energy exchange governed by the Stefan-Boltzmann law [
15]. Because of their stationarity (caused by the infiniteness of each reservoir), the power maximizing controls are lumped to a fixed point in the state space. For a CNCA engine, the maximum power point may be related to the optimum value of a free (unconstrained) control variable, which can be efficiency
η or Carnot temperature
T'. The text below summarizes basic results in this field obtained for systems with internal dissipation (irreversibility factor
Φ).
For a stationary heat operation of CNCA type [
1,
13,
14], with bulk temperatures
T1 and
T2 and internal irreversibility factor
Φ, the propelling heat in terms of Carnot temperature is [
1,
13]:
where
g is an effective overall conductance which may be the function of bulk state and
Φ. Hence the power output is:
Setting to zero the partial derivative of
p with respect to
T' one finds at the maximum power point:
Since the effective environment temperature equals
ΦT2 and the Carnot structure holds for thermal efficiency
η in terms of Carnot
T', the power-maximizing efficiency follows as:
This equation represents a generalization of the classical CNCA formula whenever internal imperfections (coefficient Φ) are essential in the heat power system.
For the Stefan-Boltzmann engine an exact expression at the optimal power point cannot be determined analytically, yet, the temperature can be found graphically from the chart
p = f(
T'). A pseudo-Newtonian model [
4,
15,
16], which treats state dependent energy exchange with coefficient
α(
T3), omits to a considerable extent analytical difficulties of the Stefan-Boltzmann equation. Moreover, we can extend the present approach to dynamical systems, as outlined in the next section.
As shown in
Appendix Equation (A19), total entropy production of the endoreversible power generation by the simple reaction A
1 − A
2 = 0 (isomerisation or phase change of A
1 into A
2), takes the following form:
where
is total energy flux in state 1 (driving the process). Decrease of efficiency in endoreversible engines, heat pumps and drying separators is the consequence of external irreversibilities quantified by the above expression.
When internal irreversibilities are essential, the imperfection factor
Φ should be included in the considered expression according to the substitution rules:
as shown in [
1], Equation (4.20) therein.
3. Some Results for Dynamical Thermal Systems
In the considered case, power maximization problem requires the use of variational metods (to handle extrema of functionals) in place of static optimization methods (which handle extrema of functions). The obtained non-exponential shape of the relaxation curve is the consequence of nonlinear properties of a driving fluid (e.g., radiation fluid). Non-exponential are also other curves describing the radiation relaxation, e.g., those based on the Stefan-Boltzmann equation [
4,
15,
16,
17]. A discrete model, involving difference equations, is usually used for calculation of a dynamical engine.
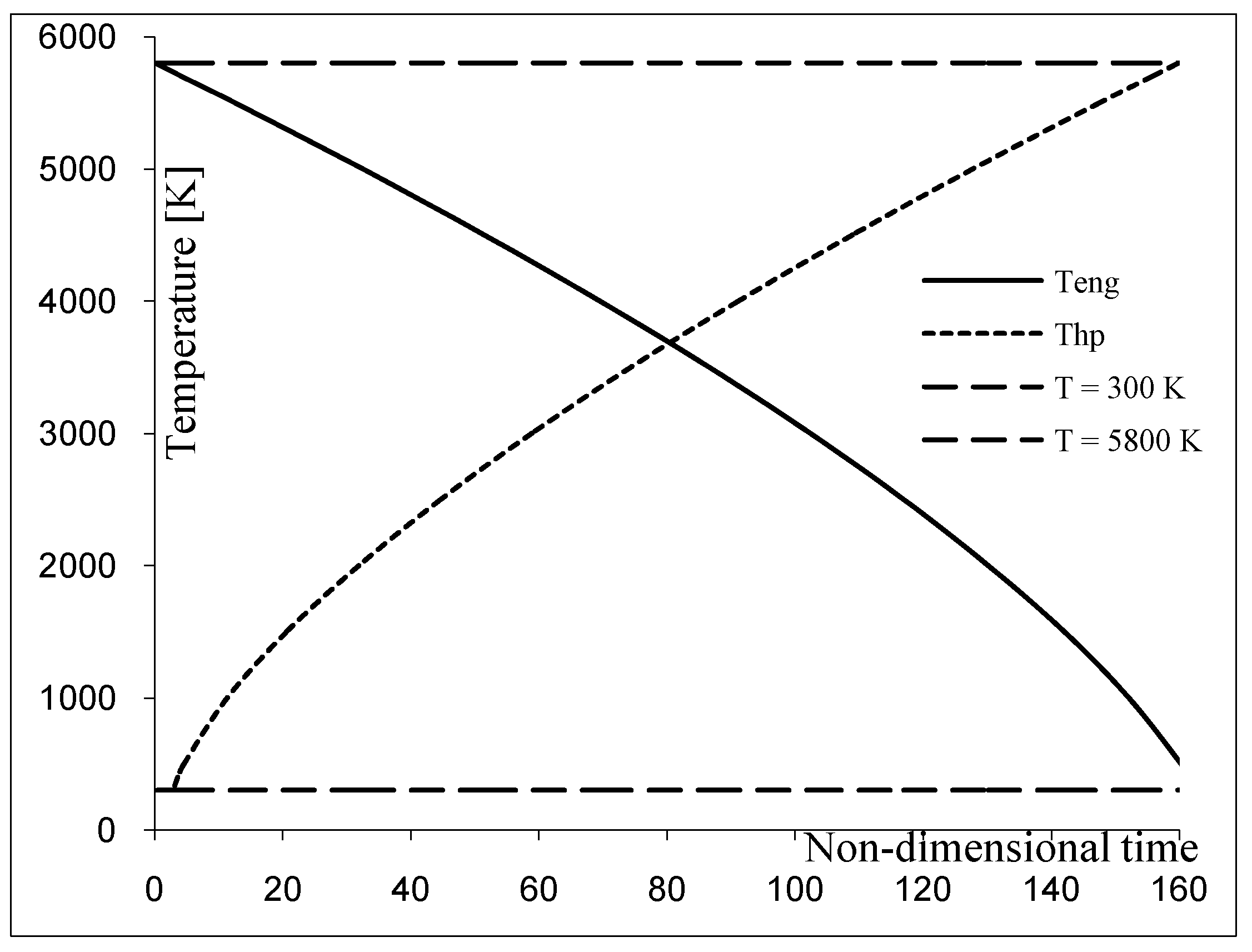
The dynamical energy yield,
Figure 1 and
Figure 2, is connected with a limited amount of the resource fluid. The operation may be viewed as the sequence of small elementary engines of CNCA type,
i.e., the sequence of small units shown in
Figure 1. In a thermal engine this mode of power yield involves the continual decrease of the resource temperature
T1 =
T(
t) (approximated here by the sequence
Tn). The optimization procedure searches for an extremal curve rather than an extremum point.
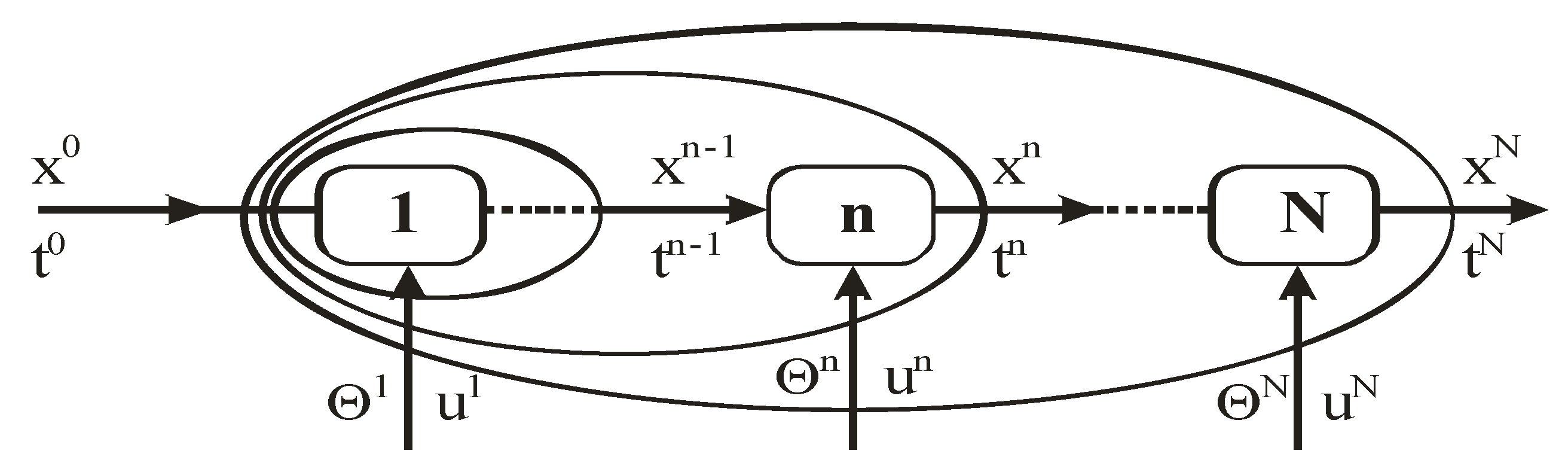
Figure 1.
A scheme of a multistage control with distinguished time interval, Θn. When the method of the dynamic programming is applied, in the forward algorithm, elipse-shaped balance areas pertain to sequential subprocesses which grow by inclusion of following units in the way described by Bellman’s recurrence equation. When algorithms of Pontryagin’s type are applied, the optimal evolution is characterized by the difference canonical equations and extremum conditions of the Hamiltonian Hn with respect to controls.
Figure 1.
A scheme of a multistage control with distinguished time interval, Θn. When the method of the dynamic programming is applied, in the forward algorithm, elipse-shaped balance areas pertain to sequential subprocesses which grow by inclusion of following units in the way described by Bellman’s recurrence equation. When algorithms of Pontryagin’s type are applied, the optimal evolution is characterized by the difference canonical equations and extremum conditions of the Hamiltonian Hn with respect to controls.
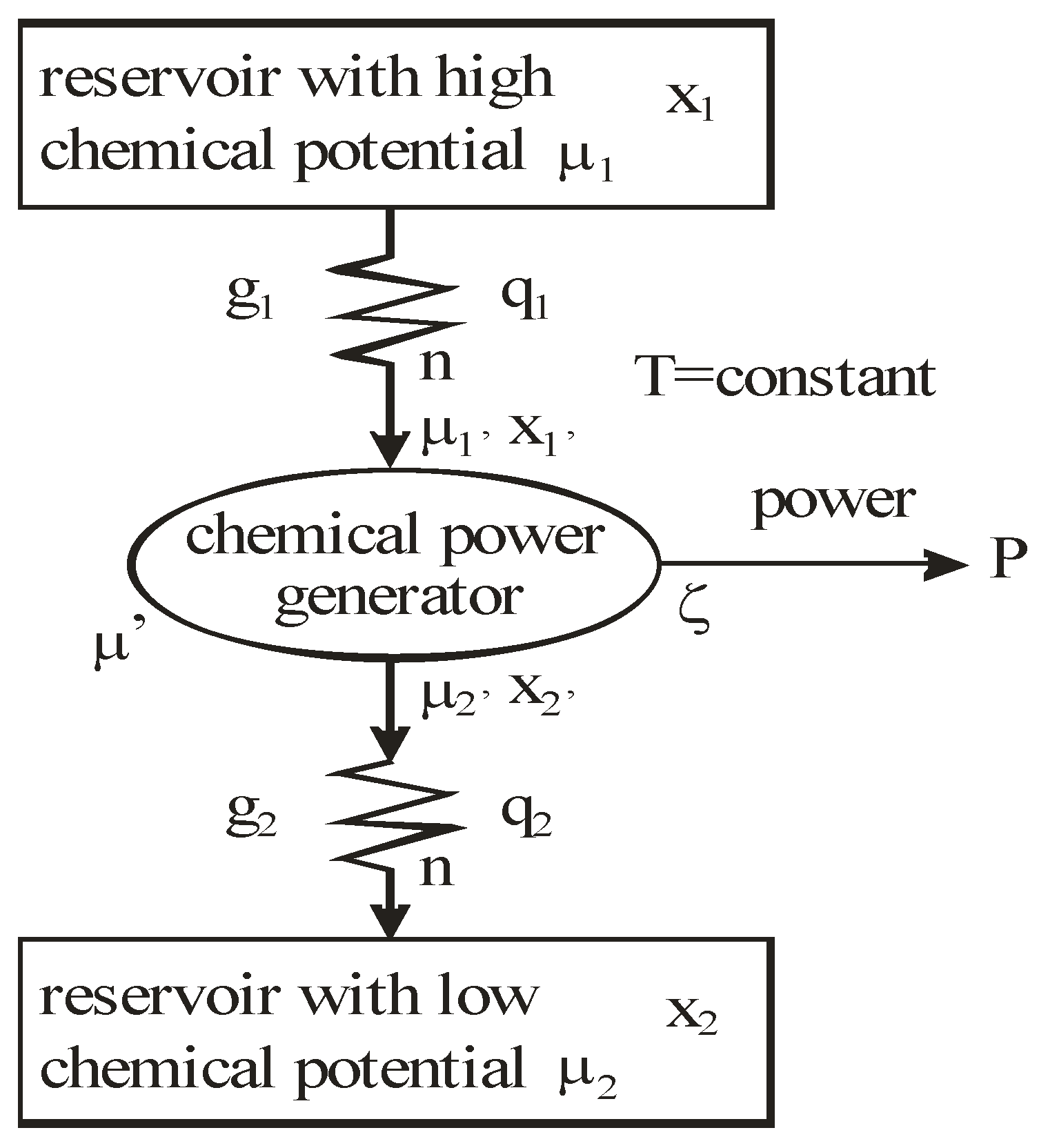
Figure 2.
Principle of a steady thermo-chemical engine driven by heat and mass transfer.
Figure 2.
Principle of a steady thermo-chemical engine driven by heat and mass transfer.
Power maximizing T(t) is accompanied by optimal control T'(t); they are both components of the dynamical solution which satisfies a Hamilton-Jacobi-Bellman equation (HJB equation) for the optimal control. Expressions extremized in HJB equations of dynamical power problems are Hamiltonians, H. With a feedback control, the optimal temperature T' is obtained as the quantity maximizing H with respect to Carnot temperature at each point of the path.
For example, by applying the pseudo-Newtonian model, we obtain an optimal dynamics of relaxing radiation in the form:
Equation (6) describes the optimal trajectory in terms of state
T and constant
hσ which is a constant numerical value of
H along an optimal path. The related optimal Carnot control has the structure:
Compared with linear systems, the pseudo-Newtonian relaxation curve is not exponential. When standard boundary conditions for exergy are used, optimal work functions become generalized (rate dependent) exergies [
1,
13]. A more exact approach to radiation engines, described below, abandons the pseudo-Newtonian approximation and uses the exact Stefan-Boltzmann equations from the beginning.
5. Hamiltonian-Based Approaches
The dynamic changes for the discrete state of a multistage system can be described by a set of ordinary difference equations called state transformations which describe the discrete state from the stage n−1 in terms of the state from the stage n and some control variables Un.
The set of discrete state transformations can be written in the following general form:
where:
and,
is an enlarged vector of control variables which includes the discrete interval of time
, and the time variable
tn is identified with any state variable growing monotonically. After defining the function:
the above state transformations can be given the form of discrete state equations [
17,
18]:
and:
Since they involve the discrete rates (fn, 1), we call this form the “standard form”.
A performance index describing a generalized profit (total power in our case) is defined by the following equation:
where
f0 is a generation rate for the generalized profit (power in the case of energy yield problems).
To solve the optimization problem of extremum
W, an enlarged (time-constraint absorbing) Hamiltonian is defined in the following form:
where
zi are adjoint (Pontryagin’s) variables.
In an optimal process the enlarged Hamiltonian
satisfies in the enlarged phase space
x = (
x,
t) and
z = (
z, z
t) the following equations:
(state equations) and:
(adjoint equations), and the equations which describe the necessary optimality conditions for decision variables
un. For example, if the optimal control lies within an interior of admissible control set:
and:
Equation (24) implies the vanishing of the enlarged Hamiltonian
along a discrete optimal path whenever discrete rates
fi are independent of
θn. In addition, the energy-like Hamiltonian (without
zt term) is constant for the process whose rates are independent of time
tn. Under convexity properties for rate functions and constraining sets the optimal controls are defined by the equations:
and:
(
n = 1,...
N; i = 1,...s+1 and
j = 1,...r.)
Optimization theory for generalized (
θn -dependent) costs and rates provides a bridge between constant-
H algorithms [
5,
19,
20] and more conventional ones such as those by Katz [
21], Halkin [
6], Canon
et al. [
7], Boltyanskii [
8], and many others [
9,
18]. Since, as shown by Equation (24), control
θn can be included in the Hamiltonian definition,
i.e., an effective Hamiltonian can be used:
extremum conditions (22)–(27) can be written in terms of H
n−1. The related canonical set is that of Halkin [
6,
7]:
Qualitative difference between the role of controls u
n and
θn in the optimization algorithm is then lost since they both follow from the same stationarity condition for Hamiltonian H
n−1 in an optimal process. For example, in the weak maximum principle:
in agreement with Equations (24) and (25) above. Moreover, for the enlarged Hamiltonian
, Equations (24), (28) and (31) imply the condition
if
is independent of time interval
θ.
Until recently, Hamiltonian algorithms were used in power systems for models with
θ- independent discrete rates [
10]. Poświata and Szwast have shown many their applications in exergy optimization of thermal and separation systems, in particular fluidized dryers [
11,
12,
17]. Sieniutycz has shown some other applications for energy and separation systems and for a minimum time problem [
18]. Taking into account the diversity of discrete rates, which may contain explicit intervals
as the consequence of various ways of discretizing, applications of algorithm (17)–(25) in power or separation systems are both appropriate and useful.
In particular, the algorithm is applicable in numerical studies of the optimal solutions for the discrete equations of the radiation engine, Equations (11)–(13), for which the enlarged Hamiltonian has the form:
Optimal dynamics corresponding to this function are shown in
Figure 3.
Figure 3.
Decreasing temperatures of radiation relaxing in engine mode and increasing temperature of radiation utilized in heat pump mode in terms of time, for a constant value of Hamiltonian
H = 1 × 10
−8 [J K
−1m
−3] [
4].
Figure 3.
Decreasing temperatures of radiation relaxing in engine mode and increasing temperature of radiation utilized in heat pump mode in terms of time, for a constant value of Hamiltonian
H = 1 × 10
−8 [J K
−1m
−3] [
4].
6. Simple Chemical Systems
Thermodynamic approaches can also be applied to chemical [
2,
14] and electro-chemical [
22,
23] engines. In chemical engines mass transports drive transformation of chemical energy into mechanical power. In chemical machines, as opposed to thermal machines, generalized streams or reservoirs are present, capable of providing both heat and substance. Large streams or infinite reservoirs assure constancy of chemical potentials. Problems of maximum of power produced or minimum of power consumed are then the static problems. For a finite “upper stream”, however, the amount and chemical potential of an active reactant decrease in time, and problems considered are those of dynamic optimization and variational calculus. Because of the diversity of chemical systems the area of power producing chemistries is quite broad.
Power expression and efficiency formula for a chemical system follow from the entropy conservation and energy balance in the power-producing zone of the system (‘active part’). The simplest model of power producing chemical engine is that with an isothermal isomerization reaction, A
1 − A
2=0 [
2,
14]. In an ‘endoreversible engine’ total entropy flux is continuous through the active zone. When a formula describing this continuity is combined with an isothermal energy balance we find:
where the feed flux
n1 equals to
n, an invariant molar flux of reagents. Process efficiency
ζ is defined as power yield per molar flux,
n. This efficiency is identical with the chemical affinity of reaction in the chemically active part of the system. While
ζ is not dimensionless, it describes correctly the system. In terms of Carnot variable,
μ', which satisfies Equation (19) in the
Appendix:
For a steady engine the following function describes chemical Carnot control
μ' in terms of fuel flux
n1 and its mole fraction
x:
As Equation (34) is valid, Equation (35) also characterizes the efficiency control in terms of n and fuel fraction x. Equation (35) shows that an effective concentration of the reactant in upper reservoir x1eff = x1 − n is decreased, whereas an effective concentration of the product in lower reservoir x2eff = x2 + n is increased due to the finite mass flux. Therefore efficiency ζ decreases nonlinearly with n. When the effect of resistances is negligible or flux n is very small, reversible Carnot-like chemical efficiency, ζC, is attained. The power function, described by the product ζ(n)n, exhibits a maximum for a finite value of the fuel flux, n.
A related dynamical problem may also be considered [
3]. Application of Equation (35) to the Lagrangian relaxation path leads to a work functional:
whose maximum describes the dynamical limit of the system. Here X = x/(1 − x) and
j equals the ratio of upper to lower mass conductance,
g1/
g2. The path optimality condition may be expressed in terms of the constancy of the following Hamiltonian:
For low rates and large concentrations X (mole fractions x1 close to the unity) optimal relaxation rate of the fuel resource is approximately constant. Yet, in an arbitrary situation optimal rates are state dependent so as to preserve constancy of H in Equation (37).
7. Power Limits in Fuel Cells
Fuel cells have attracted great attention by virtue of their inherently clean and reliable performance. Their main advantage as compared to heat engines is that their efficiency is not a major function of device size. A fuel cell is an electrochemical energy converter which directly and continuously transforms a part of chemical energy into electrical energy by consuming fuel and oxidant. Power maximization approaches can be applied to many electrochemical systems, in particular to fuel cells [
22,
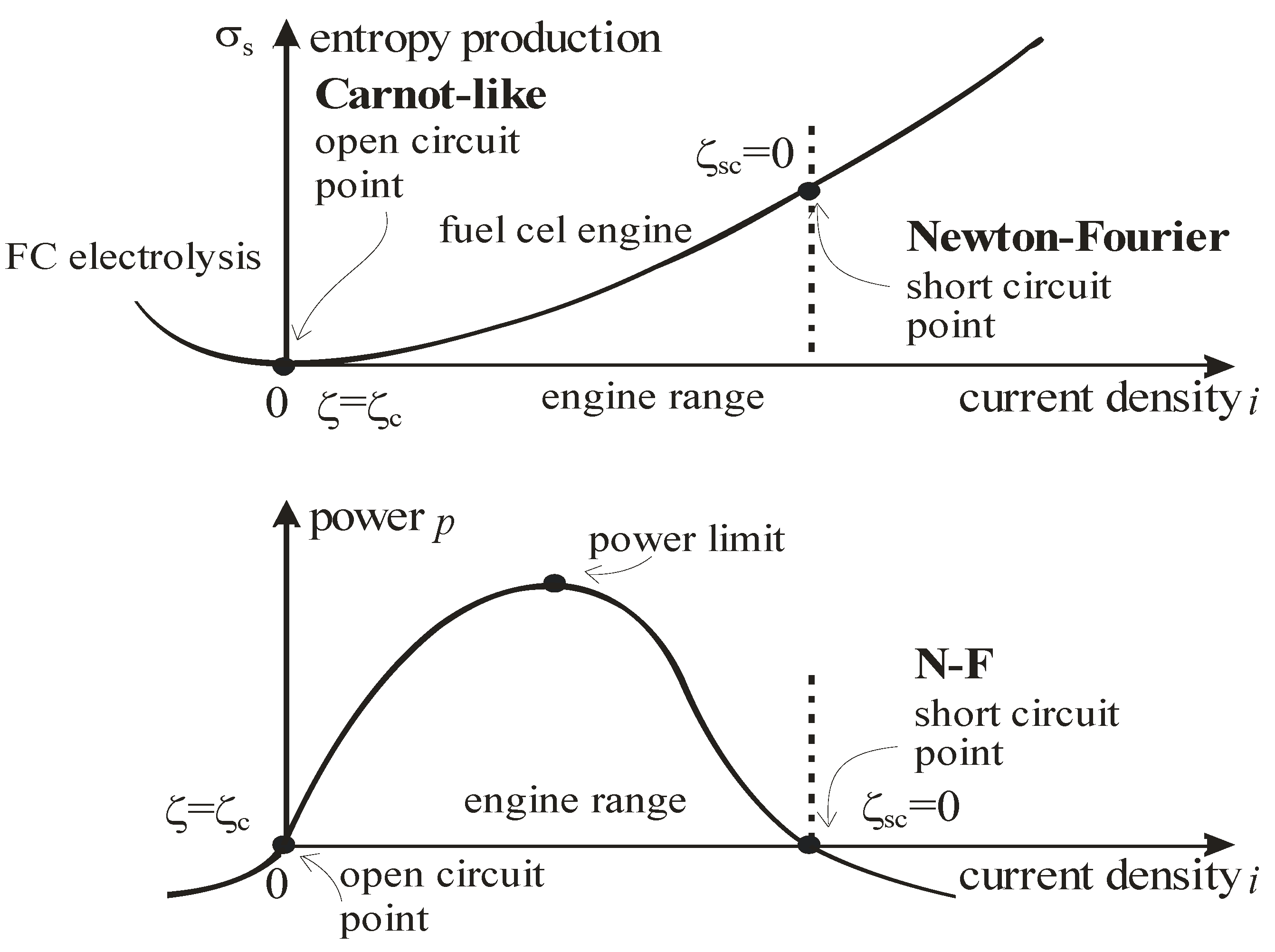
23]. Power decrease below ideal (Nernst) value and power maxima in engines are associated with entropy production,
Figure 4.
Figure 4.
Entropy production and power yield in an electrochemical engine or fuel cell in terms of density of electric current.
Figure 4.
Entropy production and power yield in an electrochemical engine or fuel cell in terms of density of electric current.
Voltage lowering in fuel cells below the reversible value is a reasonable measure of their imperfection. Reversible cell voltage
E0 is often a reference basis calculated from the Nernst equation. Yet, in more general cases, actual voltage without load must take into account losses of the idle run, which are the effect of flaws in electrode constructions and other imperfections. In [
23] and many other works the operating voltage of a cell is evaluated as the departure from the idle run voltage
E0:
Losses, which are called polarization, include three main sources: activation polarization (
Vact), ohmic polarization (
Vohm), and concentration polarization (
Vconc). Power density is the product of voltage
V and current density
i. A large number of approaches for calculating polarization losses has been presented in literature, as reviewed in [
22]. Experiments show power maxima in fuel cells [
22,
23]. Activation and concentration polarization occur at both anode and cathode locations. The resistive polarization represents ohmic losses throughout the cell. As the voltage losses increase with current, the initially increasing power begins finally to decrease for sufficiently large currents, so that maxima of power are observed [
22,
23]. The data include the losses of the idle run, attributed to flaws in electrode constructions and other imperfections.
Validation of the thermodynamic model of fuel cell is based on the application of the Aspen Plus
TM software for simulation purposes and organization of FC power experiments, as described in Wierzbicki’s M.Sc thesis [
23]. A complete review of the theory and experiments is presented in the report [
24].
To quantify the power yield and power limits let us focus on fuel cells described by the formalism of inert components [
25,
26] rather than the ionic description [
27]. Assume, for simplicity, that the active (power producing) driving forces involve only: one temperature difference
, single chemical affinity
and the operating voltage
ϕ1' −
ϕ2'. Total power production is the sum of thermal, substantial and electric components,
i.e.,:
Equation (38) represents linear thermo-electro-chemical systems. Linear systems are those with constant (current independent or flux independent) resistances or conductances. They satisfy Ohm type or Onsager type laws linking thermodynamic fluxes and thermodynamic forces (dissipative driving forces which are represented by products R
ikI
k in Equation (39)). While many fuel cell systems are nonlinear,
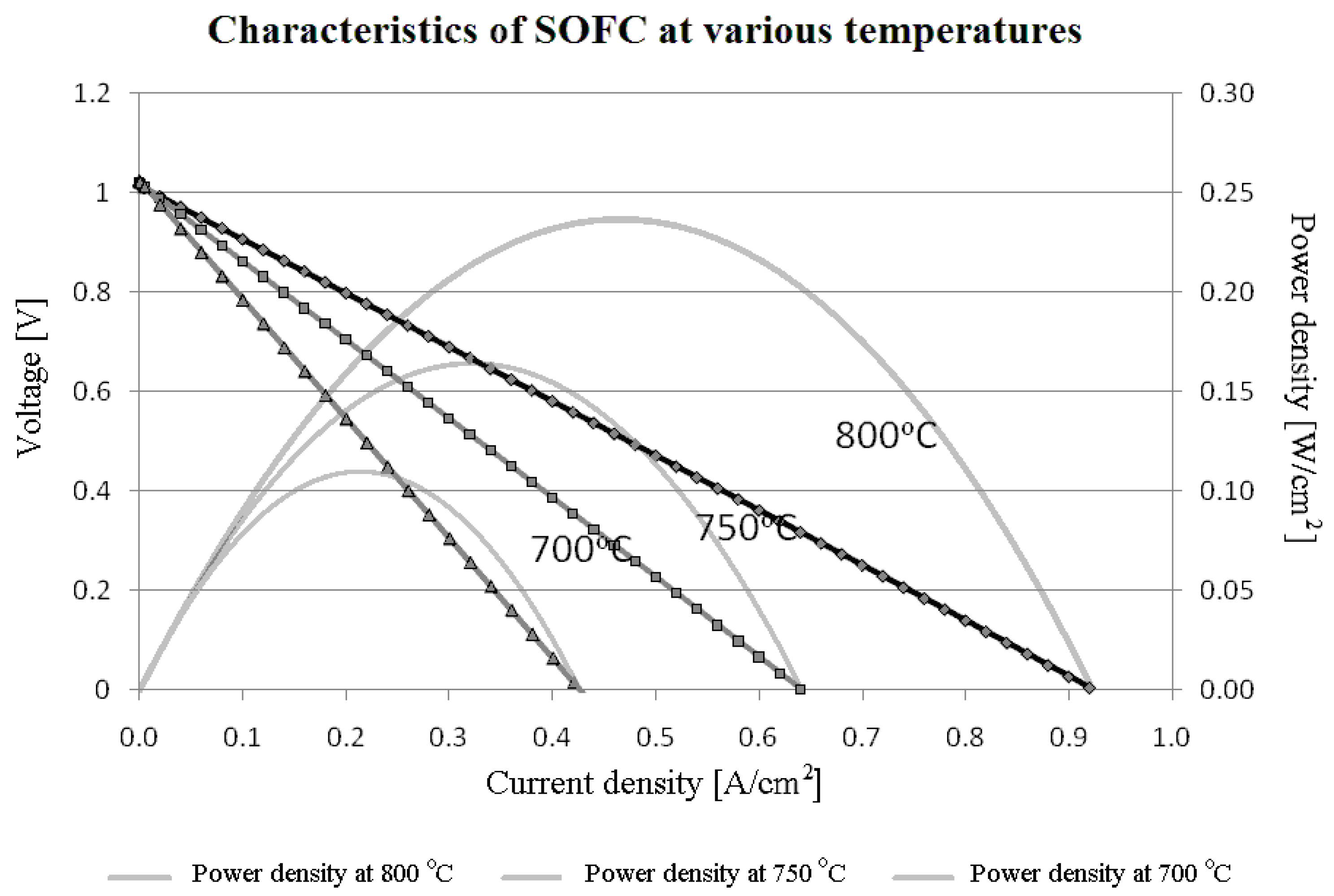
i.e., possess current dependent resistances, the dependence is often weak, so the linear model can be a good approximation. Below we develop a simple theory of power limits for these systems. Based on experiments, these power limits are exemplified in
Figure 5.
After introducing the enlarged vector of all driving potentials
= (
T,
μ,
ϕ), the flux vector
of all currents and the overall resistance tensor
, Equation (39) can be written in a simple matrix-vector form:
Maximum power corresponds with the vanishing of the partial derivative vector:
Consequently, the optimal (power-maximizing) vector of currents at the maximum point of the system can be written in the form:
This result means that the power-maximizing current vector
in strictly linear systems equals one half of the purely dissipative current at the Fourier-Onsager point,
at which no power production occurs. Moreover, we note that Equations (40) and (42) yield the following result for the maximum power limit of the system:
Figure 5.
Experimental voltage-current density and power-current density characteristics of the SOFC for various temperatures. Continuous lines represent the Aspen Plus
TM calculations testing the model versus the experiments. The lines were obtained in Wierzbicki’s M.Sc thesis supervised by S. Sieniutycz and J. Jewulski [
8]. Points refer to experiments of Wierzbicki and Jewulski in Warsaw Institute of Energetics (Wierzbicki [
8], and his ref. [
9]).
Figure 5.
Experimental voltage-current density and power-current density characteristics of the SOFC for various temperatures. Continuous lines represent the Aspen Plus
TM calculations testing the model versus the experiments. The lines were obtained in Wierzbicki’s M.Sc thesis supervised by S. Sieniutycz and J. Jewulski [
8]. Points refer to experiments of Wierzbicki and Jewulski in Warsaw Institute of Energetics (Wierzbicki [
8], and his ref. [
9]).
In terms of the purely dissipative flux vector at the Fourier-Onsager point,
the above limit of maximum power is represented by an equation:
Of course, the power dissipated at the Fourier-Onsager point equals:
Equations (44) and (45) prove that only at most 25% of power (45), which is dissipated in the natural transfer process, can be transformed into the noble form of the mechanical power. This result holds for linear systems, and, probably, cannot be easily generalized to the nonlinear transfer systems where significant deviations from Equation (44) are expected depending on the nature of diverse nonlinearities. Despite of the limitation of the result (44) to linear transfer systems its value is significant because it shows explicitly the order of magnitude of thermodynamic limitations in power production systems.
The above analysis also proves that a link exists between the mathematics of the thermal engines and fuel cells, and also that the theory of fuel cells can be unified with the theory of thermal and chemical engines.
A word of explanation of related physical effects is in order. While power ratios involving Equations (44) and (45) can be regarded as efficiency measures, they should not be mixed with commonly used, popular efficiencies, especially with first law efficiencies. In fact, the considered power ratios represent some specific, second-law efficiencies of the overall thermo-electro-chemical process. There is a number of definitions of FC efficiencies, based on first or second laws, proposed for measuring and comparing the performance of electrochemical processes. Only second-law efficiencies are correct measures, which show how closely the process approaches a reversible process. Efficiencies based on the first law (often found in the literature) can generate efficiency values greater than 100% for certain systems depending on whether the change in entropy for the overall chemical reaction involved in the process is positive or negative. See, for example, paper [
28] on various definitions of FC efficiencies.
The popular fuel cell efficiencies, ηFC = ΔG/ΔH or ηFC = −W/ΔH, which are commonly applied to many fuel cell systems, can easily achieve numerical values much higher than ¼ [power ratio of Equations (44) and (45)]. They are, however, first-law efficiencies defined in a different way than the power ratios Pmp/PF satisfying Equations (44) and (45).
8. Power Consumption Limits in Thermochemical Systems
Heat pumps and HP-supported dryers are typical representatives of systems driven by the consumed power. Since the use of power and efficiency formulae derived from analyses of power generators can be extended to units which consume power, it is interesting to develop analyses for units such as thermal and solar heat pumps, drying separators and electrolyzers. A meaningful reduction of drying exergy could be achieved by the optimal control of many dryers; on average, the potential for exergy reduction is more than 20%. Some industrial data are, however, still reported in terms of energy (enthalpy) rather than exergy efficiency, and suffer from a lack of a strong link with well established kinetic models.
Awareness of limited energy supplies prompts a significant effort in developing recovery processes. Possible operations and design modifications involve waste heat recovery from solids, energy recuperation from gases, application of heat pumps for waste energy upgrading, recycling of exhausted drying agent, combinations of mechanical and thermal drying, and use of solar energy.
Application of optimal control principles to processes with consumption of mechanical energy gives a certain extra potential for improving their economy. Some of these processes use thermal separators and heat pumps. The heat pump is in principle the only device which would allow exploitation of low-exergy sources commonly available in nature and industry. Heat pumps increase driving energy by adding low-quality energy taken from a low-exergy source to obtain energy of high quality economically. Mathematical analyses of power-assisted processes lead to optimization-determined bounds on power input and exergy dissipation.
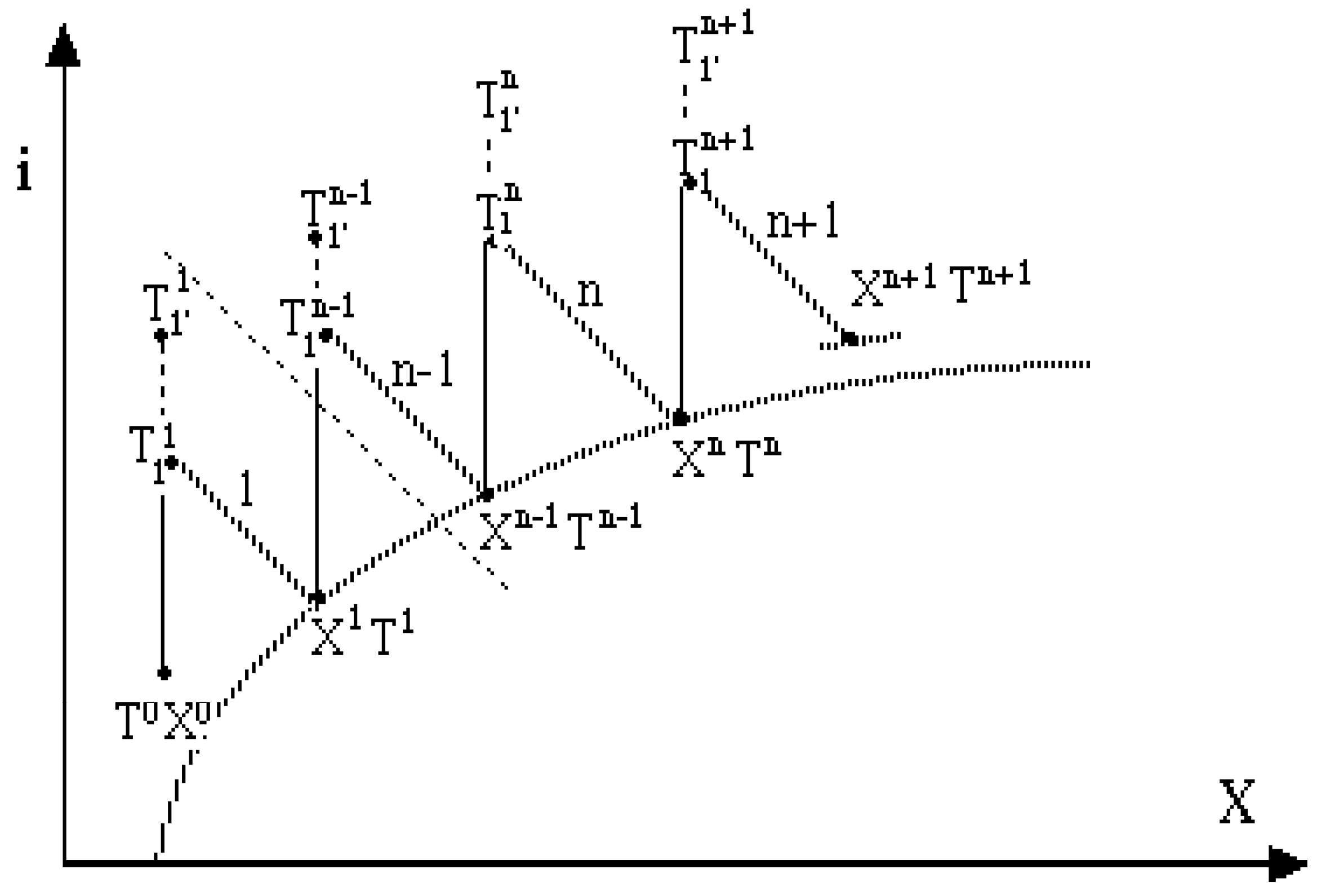
We consider an optimal operation with HP-supported drying. Our optimization example refers to a non-ideal fluidized drying in which one stage can be modeled in two ways (pseudo-homogeneous and non-homogeneous), as shown in
Figure 6 below. Symbols X and Y in
Figure 6,
Figure 7 and
Figure 8 refer to absolute moisture content and absolute humidity in solid and gas phase, respectively.
Figure 6.
Two ways of modeling of fluidized drying (Szwast [
29] and Sieniutycz [
20], case A, and Poświata [
22,
30,
31], case B). The scheme allows a simultaneous treatment of the batch fluidization and the fluidization in a horizontal exchanger as the continuous limit of the cascade.
Figure 6.
Two ways of modeling of fluidized drying (Szwast [
29] and Sieniutycz [
20], case A, and Poświata [
22,
30,
31], case B). The scheme allows a simultaneous treatment of the batch fluidization and the fluidization in a horizontal exchanger as the continuous limit of the cascade.
Figure 7.
A scheme of one-stage drying operation with a heat pump 1 and a continuous co-current dryer D1 with falling particles. The multistage idea means, of course, the repetition of this single-stage set in the next stages.
Figure 7.
A scheme of one-stage drying operation with a heat pump 1 and a continuous co-current dryer D1 with falling particles. The multistage idea means, of course, the repetition of this single-stage set in the next stages.
Figure 8.
Changes of gas states in a multistage work-assisted drying operation on the gas enthalpy - gas humidity diagram, i-X. Primed states refer to temperatures of fluids circulating in the heat pumps which heat gases supplied to dryers 1, 2...n.
Figure 8.
Changes of gas states in a multistage work-assisted drying operation on the gas enthalpy - gas humidity diagram, i-X. Primed states refer to temperatures of fluids circulating in the heat pumps which heat gases supplied to dryers 1, 2...n.
The multistage process is composed of several HP supported fluidized dryers, each drying process governed by the hydrodynamic model presented in
Figure 6 and each stage characterized by
Figure 7. The multistage idea involves, of course, the repetition of a single-stage operation in next stages. As a global effect, we achieve the operation shown in
Figure 8 in which drying agents enter the dryer with suitably adjusted inlet states (with sufficiently high temperatures). Explicit input fluxes of mechanical power may be considered in these problems as possible controls.
In the considered power-assisted, multistage operation each drying agent is heated before each dryer by a heat pump, in order to achieve a sufficiently high temperature. This example involves a non-ideal fluidized drying in which one stage can be modeled in two ways (pseudo-homogeneous and non-homogeneous),
Figure 6. In the multistage process the gas leaving the previous stage enters the heat pump and dryer of the next stage,
Figure 7. For relatively efficient stages, we may assume that the outlet solid and gas are in the thermal equilibrium due to a large specific solid area. The properties of the heat pump as the heating device are important in this analysis; the better COP results in more efficient heating. The final effect is a complex process—in fact, a work-assisted drying operation—in which gas states vary as shown in
Figure 8.
As shown in
Figure 7 a stage of this complex multi-step operation comprises not a single dryer but rather an appropriate group of various units which is repeated when the process procedes from one step to another. This is a multi-stage drying operation, in which gas at each stage is first heated with a heat pump and then is directed to a dryer (note that only one stage of that operation is shown in
Figure 7). In the considered case a continuous drying process occurs in a co-current dryer; yet the countercurrent contacting can alternatively be applied. The purpose is to minimize work consumption in, say, a two-stage operation by a suitable choice of the intermediate moisture content between the first and the second stage.
One may ask: how many heat pumps (and stages) are there in the optimal system? The answer is possible by making an economical analysis, and terminating the cascade calculations when the sum of operational and investment cost stops to decrease. As the investment cost grows steeply with the number of stages, the optimal number of stages is usually limited to a few stages.
The balances of mass and heat yield:
where
r is evaporation heat of moisture and
c is specific heat of gas. The power consumed at a single stage per unit flow of gas,
e1, is described by an expression [compare with Equation (8)]:
where
u1 is the energy supply to the drying gas in the condenser of the heat pump, and
u1 = −
q1/
g>0 is a measure of this energy supply in the temperature units. We may include the effect of internal irreversibilities within the heat pump in which case the performance coefficient of the support heat pump contains imperfection factor
Φ as the multiplicative factor of the bath temperature
Te.
Substituting into Equation (48) the temperature
following from transformed Equation (47):
and taking into account that
=
X0 [also
=
Xn−1 =
Xs(Tn−1), for
n = 2,..
N] we find the mechanical energy consumption at the stage:
Equation (50) is transformed further in view of the link between
u1 and
θ1 (consider difference constraint describing Δ
Tn =
unθn for
n = 1):
In terms of the 'adiabatic temperature function':
The work expression takes the final form:
An analogous function, but with the shifted superscripts, is valid for the second stage:
The constraint
X1 =
Xs(
T1) resulting from the outlet phases equilibrium in the first dryer is incorporated in the second work expression. In terms of the adiabatic temperature at the second stage:
The sum of both works yields the total work consumed. This total work is the thermodynamic cost that should be minimized. For a fixed holdup time τ2 = θ1 + θ2 there are two free controls: θ1 and T1. Thus we can accomplish the power minimization procedure.
The procedure searches for an optimal interstage temperature T1and an optimal heat transfer area of the first heat pump a1 present in the control variable θ1. The requirement of sufficiently low final moisture content in a solid defines the amount of the evaporated moisture per unit time. The optimization can be generalized to the N-stage cascade system.
The example presented above shows how to optimize a drying operation with gas heated by a sequence of heat pumps. The optimization criterion is the power consumption, the optimal solution should assure the minimum of consumed power. The optimal transfer areas are close in value, the optimal temperatures constitute an increasing sequence. The optimal work supplied to the two-stage system decreases distinctly with the total transfer area.
A general thermokinetic theory of minimum power supply to power consumers can be developed, based on systems' thermodynamic and kinetic properties, as outlined below. Note a symmetry of this approach in relation to maximum power yield in power generators (fuel cells in
Section 7).
Consider power consumption in a linear thermochemical system with possible electric fluxes (in case of electrolysers). Assume that a two reservoir arrangement is sufficient to accomplish a separation process or heat pump heating. Both these operations need for their running some instantaneous power supplied to the system. In terms of total resistances of upper and lower parts of two-reservoir system:
and after considering coupled transfer of heat, mass, and electricity, the power supply reads:
where non-primed quantities refer to bulk states and primed ones to the active, power-consuming part of the system. As shown by this equation, the general thermodynamic framework allows for at least rough assessment of power consumption limits in thermo-electro-chemical systems of the simplest, standardized topology (with no counter-flows). This topology corresponds to a power consumption unit (e.g., heat pump) immersed between two reservoirs, one with high potentials and one with low ones, as described in a number of publications. The reason why this power assessment can only be rough is explicit in Equation (57) which has ignored information about the topological structure of many various flows in the system. Let us also add that possible electrolyzers are also described by the formalism of inert components rather than by the ionic description.
For simplicity, Equation (57) assumes that active (power consuming, primed) driving forces involve only: one temperature difference, trivial chemical affinity and the operating voltage as the difference of the electric potentials. Total power consumption (57) is the sum of thermal, substantial and electric components.
Equation (57) constitutes the simplest account of thermo-electro-chemical separators and heat pumps; indeed it does not contain any "topology parameter". Complex configurations of flows contacting, such as countercurrent contacts, that may exist in fuel cell electrolysers, are not taken into account in Equation (57). Linear systems described by this equation are those with constant (current independent or flux independent) resistances or conductances. They satisfy Ohm type or Onsager type laws linking thermodynamic fluxes and thermodynamic forces (dissipative driving forces which are represented by products ΣRikIk in Equation (57). While many thermal separation systems and fuel cell electrolyzers are nonlinear, i.e., possess current dependent resistances, the dependence is often weak, so a linear model can be a good approximation. Below, by applying Equation (57) we shall attempt to develop a simple evaluation of power limits for heat pumps and separation systems under the specified assumptions.
After introducing the enlarged flux vector
I = (
Is,
In,
Ie), the enlarged vector of potentials
= (
Τ,
μ,
ϕ), and the related resistance tensor R, Equation (57) can be written in a simple form:
The bulk driving forces μ1 − μ2 are given constants. Therefore, in systems with constant resistances, we are confronted with a simple minimization problem for a quadratic power consumption function p. While the dimensionality of the potential vector will often be quite large in real systems, the structure of Equation (58) will be preserved whenever the power expression will be considered in the above matrix-vector notation.
Minimum power corresponds with vanishing partial derivatives of function
P. The optimal (power-minimizing) vector of currents at the minimum power point of the system can be written in the form:
This result means that the power-minimizing current vector in separators and heat pumps is equal to the negative of one half of the purely dissipative current at the Fourier-Onsager point. The latter point refers to the system’s state at which no power production occurs.
Equations (58) and (59) yield the following result for the minimum power input to heat pump or thermal separation system:
(negative power supply follows because the engine convention is always used, in which power released is positive). In terms of the purely dissipative flux vector at the Fourier-Onsager point, where neither power production nor power consumption occurs, the above limit of minimum power is represented by an equation:
The minus sign corresponds again with the engine convention which requires that power supplied to the system is negative.
On the other hand, the power dissipated at the Fourier-Onsager point is:
Comparison of Equations (61) and (62) proves that, in linear thermo-electro-chemical separators with power support, at least 25% of power dissipated in the natural transfer process must be supplied as power surplus in order to run a power-consuming system. Yet, this result may not be exact for systems of complex topology and for those with strong nonlinearities, where significant deviations may be expected.
In fact, the present result describes the largest (most disadvantageous) power surplus that can be approximately applied to real heat pumps, dryers, electrolysers, and other separation systems. For these systems significant deviations from Equations (59)–(61) are nonetheless expected depending on nature of nonlinearities and topology variations, and also on topology improvements to include countercurrent contacting. Despite of the limitation of the result (61) to linear cases, its value is significant because it shows the order of magnitude of thermodynamic limitations in power consumption systems.
The analysis presented here proves that a link exists between the mathematics of heat pumps, separators and electrolysers, and also that, possibly, the theory of electrolysers can be unified with the theory of thermal and chemical separators and heat pumps. All these systems are power consumers. However, serious topological differences between these systems may occasionally render them quite dissimilar.
While the power ratios involving Equations (61) and (62) can be regarded as efficiency measures, they should not be confused with reciprocals of commonly used, popular performance coefficients, especially first law-based coefficients of heat pumps and some separation systems. There are several definitions of performance coefficients, based on first or second laws, proposed for measuring and comparing performance of separation processes. The reciprocals of considered power ratios are the second-law-based performance coefficients which show how closely a concrete process approaches a reversible process.