Abstract
We study the unitary time evolution of a simple quantum Hamiltonian describing two harmonic oscillators coupled via a three-level system. The latter acts as an engine transferring energy from one oscillator to the other and is driven in a cyclic manner by time-dependent external fields. The S-matrix (scattering matrix) of the cycle is obtained in analytic form. The total number of quanta contained in the system is a conserved quantity. As a consequence, the spectrum of the S-matrix is purely discrete, and the evolution of the system is quasi-periodic. The explicit knowledge of the S-matrix makes it possible to do accurate numerical evaluations of the time-dependent wave function. They confirm the quasi-periodic behavior. In particular, the energy flows back and forth between the two oscillators in a quasi-periodic manner.
1. Introduction
The use of a three-level system as an engine to transfer energy between two quantum systems was proposed half a century ago by Scovil and Schulz-Dubois [1,2]. The population of the levels can be manipulated using light pulses. In particular, the Stimulated Raman Adiabatic Passage (STIRAP) technique [3,4,5] has become a very efficient experimental tool [6]. The three-level system is brought in contact alternatingly with the system of interest and with an energy reservoir, called the heat bath. In this way, energy can be removed from the system under study.
The three-level system is one of the simplest realizations of a quantum heat engine. Quantum heat engines produce work or pump energy by repeated execution of a thermodynamic cycle, much in analogy with the original Carnot engine or the Otto engine [1,2,7,8,9,10,11,12,13,14,15,16,17,18,19]. The theoretical modeling of these engines usually relies on the following ingredients. The state of the engine is described by a density matrix. During phases 1 and 3 of the cycle, the engine is in contact with one of the heat baths. The time evolution of the density matrix is then described by a master equation of the Lindblad form [20,21]. During phases 2 and 4, the state of the engine is modified by external forces working upon it. The adiabatic theorem is invoked to modify the energy levels without changing their occupational probability.
Interest in quantum heat engines arose because experimental realizations seem feasible in the near future [22]. In addition, such engines can teach us how quantum thermodynamics [23] deviates from classical thermodynamics.
Quantum entanglement between the system and the heat bath is usually neglected. It is assumed to be suppressed by decoherence phenomena active in the heat bath (see, for instance, the dispersed discussions of decoherence in [23]). We believe that a better understanding of the role of entanglement can be obtained from a rigorous quantum mechanical treatment of some simple models, either analytically or by a fully quantum mechanical simulation, or by a combination of both. In this direction, not much has been done so far.
In the present model, both the system and the reservoir consist of single harmonic oscillators. These are too simple to cause decoherence. This is confirmed by our numerical work, which shows that the three components together behave coherently as a single quantum system. It is therefore no surprise that quantum entanglement is dominantly present. The importance of the entanglement of system and reservoir has been stressed in [23]. It has recently been proposed as a mechanism of entropy production [24]. It is our aim to study this entanglement by a combination of a rigorous analysis and numerically exact calculations.
The thermal state of the system is usually described by a density matrix. Here, we deviate from this tradition by assuming that the state of our three-component system is described by a time-dependent wave function, ψ, which is a solution of the Schrödinger equation. It is a closed system in the sense that the time evolution is unitary and deterministic. This corresponds experimentally with an operation on a short time scale compared to the time scale of thermal equilibration.
In closed devices, quantum pumping (see, for instance, [25] and the references therein) is a form of quantum stirring. This is a relatively new area of research [26,27,28,29,30,31,32]. It touches on some fundamental aspects of quantum physics, such as non-steady state behavior, the occurrence of quantum chaos and the emergence of classical (i.e., non-quantum) behavior as the system size increases.
Our interest focuses on the thermodynamical aspects of driven quantum systems. It is expected that, even for a small quantum system, such as the one under study here, only a small part of the state space is explored by the time-dependent wave function. This is known as the typicality of states and holds for the reduced density matrix of any subsystem. See, for instance, [23], Chapters 6 and following. We investigate whether typicality holds also for driven systems.
The knowledge of the S-matrix (scattering matrix) for a single cycle of operation of the engine enables an efficient numerical evaluation, which, unlike full quantum simulations involving the numerical solution of the time-dependent Schrödinger equation, can cover hundreds of successive cycles with high accuracy. We have tried out this opportunity. It appears that the behavior of our toy model is more complex than expected. A systematic investigation of the parameter space is postponed to a future paper [33]. Some preliminary results are reported in Section 5.
The model is introduced in the next section. The S-matrix approach is explained in Section 3. The analytic expression for the S-matrix corresponding with one cycle of the engine is obtained. In Section 4, we analyze our results. Section 5 studies repeated cycles using numerical evaluation. Final conclusions follow in Section 6. The details of the analytical calculations are explained in the Appendices.
2. The Model
The model Hamiltonian, H, consists of an unperturbed part, , describing two harmonic oscillators (HO) and an engine, to which are added time-dependent external fields operating the engine and time-dependent interactions between the oscillators and the engine. For convenience, one of the oscillators is called the cold HO, the other the hot HO. The engine is operated in such a way that an energy transfer from cold to hot is expected.
All together, the unperturbed Hamiltonian reads (we use units in which ):
The operators a and c are the annihilation operators of the cold HO and of the hot HO, respectively. The Hamiltonian of the three-level system is given by:
The three levels are labeled g, e and f and have energies , μ and , respectively.
The engine is operated by means of a rather primitive sequence of two square pulses. More realistic pulses can be treated analytically, as well [34], but would complicate our analysis of the coupled system as a whole. Their contribution is:
where and are the Gell-Mann matrices (see Appendix A).
The interaction between the three-level system and each of the harmonic oscillators is inspired by the Jaynes–Cummings model. It describes an exchange of one quantum of energy between an HO and a two-level system. Important for the present work is that its eigenvalues and eigenvectors can be calculated analytically.
The coupling at the cold side is given by:
with:
It couples the g and e levels of the three-level system. Note that in the Jaynes–Cummings model, is multiplied with instead of . The change made here is needed, because the ground state of our three-level system corresponds with the excited state in the Jaynes–Cummings model.
At the hot side, the interaction Hamiltonian is given by:
with:
It couples the e and f levels of the three-level system with the hot HO. The total time-dependent Hamiltonian is now:
3. Cycles
The external field strengths, and , and the coupling parameters, and , all depend on time t. They are pulsed one after another in such a way that a (not necessarily closed) cycle is traversed. See Figure 1.
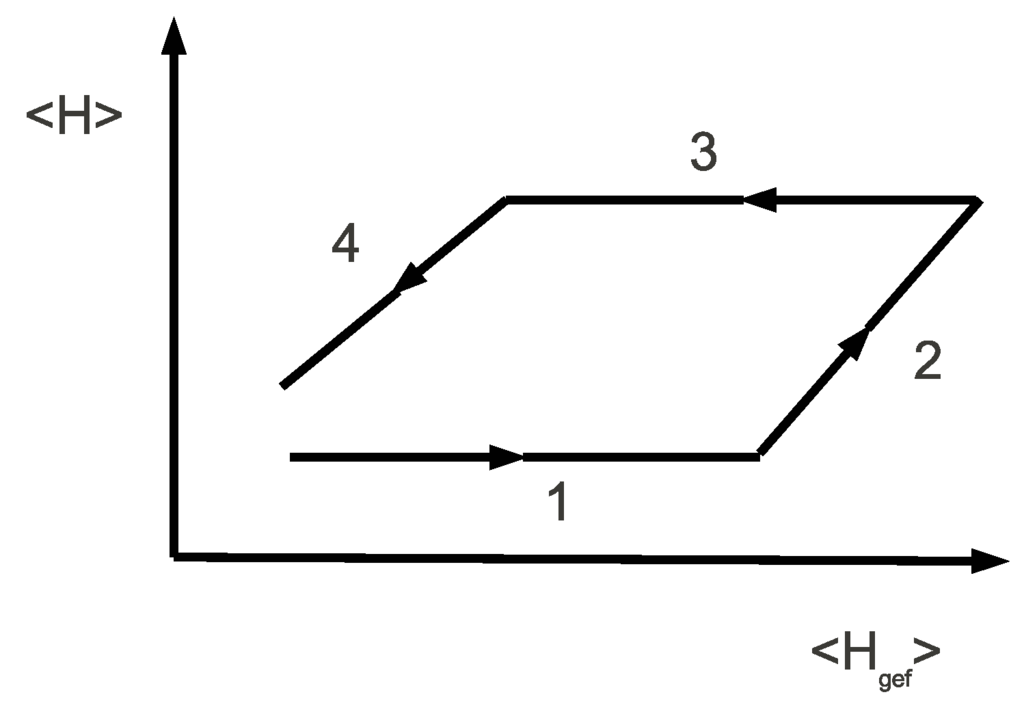
Figure 1.
The four phases of the cycle. The horizontal axis shows the energy of the engine. The vertical axis shows the total energy of the system.
The cycle starts by coupling the engine to the cold HO. The switching on and off changes the total energy of the system (this contribution is omitted in the figure). However, during the first phase of the cycle, the total energy is constant. In the second phase, the energy of the engine is pumped up by applying a sequence of two pulses. Work is performed by doing so. In phase 3, the engine releases energy to the hot oscillator. In phase 4, the engine delivers work to the environment. By the latter, we mean the experimental apparatus controlling the external fields. Switching on and off the external fields changes the total energy of the system. Hence, it requires work or delivers work depending on the sign of the energy change. Phase 4 is again modeled by two externally applied pulses, which pump down the internal energy of the engine.
Note that the cycle does not necessarily close. It is obvious that in the energy transfer mode, the engine will consume more work (during phase 2) than it can deliver (during phase 4). Because the system is finite, this would imply that the total energy goes up after every cycle of the process. See Figure 2.
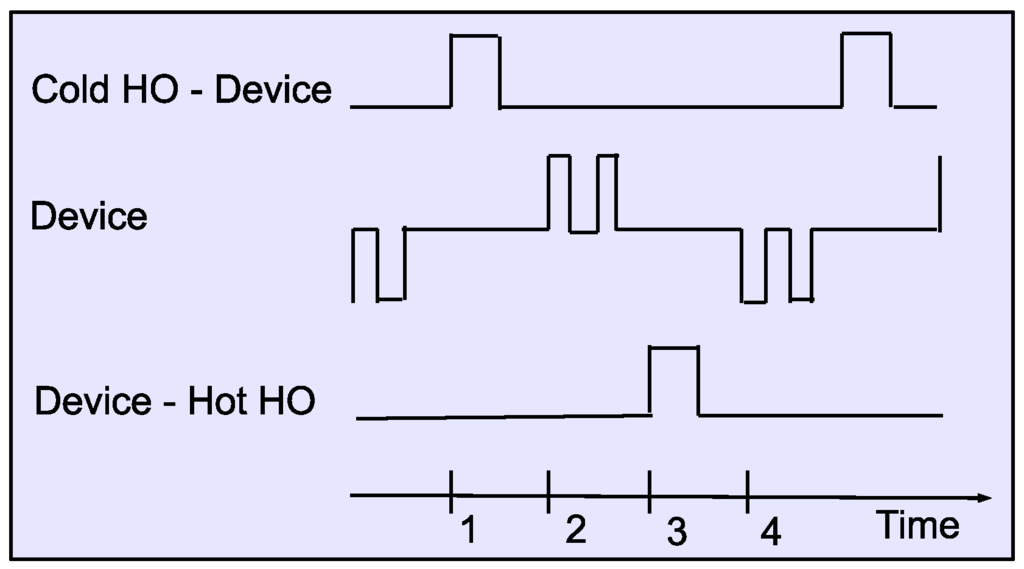
Figure 2.
Overview of the activation of the time-dependent terms in the Hamiltonian. Each cycle contains four phases. In phase 1, the cold harmonic oscillator (HO) is coupled to the engine during some time . In phase 2, the engine is pulsed twice to swap the population of the energy levels. See Figure 3. In phase 3, the engine is coupled to the hot HO during some time . In phase 4, the energy levels of the engine are swapped in reverse order.
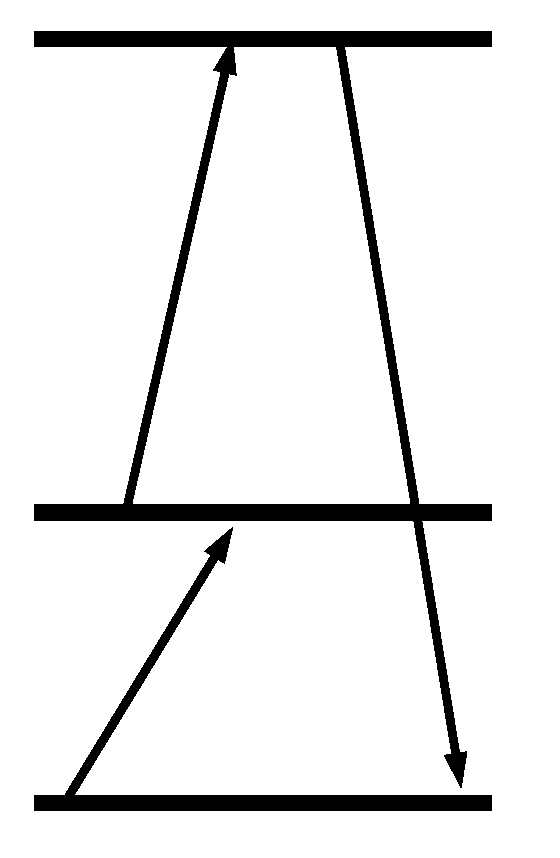
Figure 3.
Swap of the energy levels of the engine during phase 2 of the cycle according to the expression in Equation (23).
The S-Matrix Approach
The time evolution of the system with the Hamiltonian in Equation (8) is studied without making approximations. The calculation is simplified by the use of the interaction picture. Then, the wave function of the total system—the engine plus oscillators—is time-independent in the periods when none of the time-dependent terms is active. The effect of activating one of the interaction terms or one of the external fields is then to transform the wave function ψ by means of an S-matrix into a new wavefunction, .
We now calculate the four contributions to S. The S-matrices of the four phases of one cycle combine to the S-matrix of the full cycle via:
Step 1: Absorbing Energy from the Cold HO
In the first phase of the cycle, the three-level system is connected to the cold HO during a time . The corresponding S-matrix is denoted . It is not very difficult to calculate it exactly. See Appendix B. The result is of the form:
with:
and:
The coefficients, , and the angles, , are given by:
The operator is the orthogonal projection , onto the ground state of the cold HO.
Step 2: Pumping up
We apply a sequence of two pulses of the on/off type. The first pulse is realized by giving a constant non-zero value during a time . It tries to invert the population of the levels e and f. The change of the population as a consequence of this pulse is given by the S-matrix , which is now calculated.
Note that we switched notations, using two-dimensional Pauli matrices instead of the Gell-Mann matrices, omitting one dimension for a moment. Introduce the constant .There follows:
Let us now make an appropriate choice of the pulse duration . The goal is to minimize the population of the e-level after the pulse. Since one can expect that before the pulse, the e-level is more populated than the f-level, the best one can do is to require that the e matrix element of is as small as possible in modulus. Let, therefore, . Then, the S-matrix becomes:
When the third dimension is restored, this becomes:
In the limit of a strong short pulse, this becomes:
The first pulse of the second phase of the cycle is followed by a pulse of duration , intended to invert the population of levels e and g. The corresponding S-matrix reads, using the notation :
With similar arguments as before, let us choose . Then, the S-matrix becomes:
In the limit of a strong short pulse, this becomes:
All together, the S-matrix for the second phase of the cycle equals:
In the limit of strong short pulses, it becomes:
See Figure 3.
Step 3: Exchanging Energy with the Hot Oscillator
In the third phase of the cycle, the three-level system is connected to the hot HO during a time . The corresponding S-matrix is denoted . The calculation is similar to that in Step 1. The result is of the form:
with:
The coefficients and the angles are given by:
The operator is the orthogonal projection, , onto the ground state of the hot HO.
Step 4: Pumping down
The operation in the fourth phase is the inverse of that in the second phase. We thus have .
4. Analysis
In the previous section, the contribution to the S-matrix has been obtained for each of the four phases of the cycle. The composite matrix is now calculated. The result is rather complicated. Therefore, a tensor notation is appropriate. Remember that the Hilbert space of wave functions of the total system is the tensor product:
The first and the last factor are the Hilbert space of the cold and of the hot HO, respectively. The middle factor is the space of vectors with three complex components.
4.1. The Composed S-Matrix
The full S-matrix reads:
For simplicity, we use the value in Equation (23) of in the limit of strong short pulses. In this limit, one has: , , , , . Hence, the above expression for S simplifies to:
Note that the operators A, B, C, Y, Z and V, commute with the counting operators of the two harmonic oscillators. Hence, the two terms, which directly transfer energy between the two oscillators, are those proportional to and , respectively. They act in opposite directions. Other terms do not transfer energy or they exchange energy between the engine and one of the oscillators. See Table 1.
4.2. Eigenvectors of the S-Matrix
The above S-matrix describes the effect in the interaction picture of performing one cycle. It is immediately clear that the ground state, , of the system is an eigenstate of this S-matrix with an eigenvalue of one. This is an immediate consequence of the fact that the ground state of the Jaynes-Cummings model is not affected by the interactions of the model. An important question is whether the S-matrix has other eigenvectors. Indeed, such eigenvectors describe situations in which the action of the engine has no effect at all. Of course, the engine can have an effect on a superposition of eigenvectors. However, the result is an almost periodic function, which always returns arbitrarily close to its starting point. On the other hand, if part of the spectrum of S is continuous, then a genuine energy transfer is possible, by which the system approaches a stationary regime.

Table 1.
Interpretation of the terms appearing in Equation (29). The arrows indicate the direction of the energy flow, between the cold HO and the engine, and between the engine and the hot HO, respectively.
| — | — | |
| ← | — | |
| → | → | |
| — | → | |
| — | ← | |
| ← | ← | |
| → | — | |
| — | — |
An easy argument shows that the spectrum of the S-matrix is purely discrete. The Jaynes–Cummings interaction term describes the exchange of a single quantum of energy between an HO and a two-level system. The external action onto the three-level engine changes the total energy of the system, but not the number of quanta it contains. More precisely, if, initially, the total wave function is a superposition of product states, all containing the same number of quanta, then this remains so after execution of one cycle of the engine. As a consequence, the Hilbert space of wave functions decomposes into finite dimensional subspaces containing an exact number, n, of quanta. Indeed, the subspace, , is generated by the 2n + 1 basis vectors:
Using the explicit expression in Equation (29), one verifies that is invariant under S. In these finite-dimensional subspaces, S can be diagonalized. The eigenvectors all together span the total Hilbert space.
4.3. Energy Transfer
The result in Equation (29) seems hopelessly complicated, but can nevertheless be used to derive some unexpected properties of the engine. The change in the energy of the cold HO before and after one cycle is defined by:
One finds (see Appendix C):
The eigenvectors of D are of the form:
(we are neglecting the Hilbert space of the hot HO for a moment). The condition then yields:
This set of equations has a non-trivial solution when:
Corresponding eigenvectors are then given by:
Note that . Hence, the spectrum of D is completely known. For each strictly positive eigenvalue ρ > 0, also –ρ is an eigenvalue. ρ > 0 corresponds with raising the energy of the cold HO, ρ < 0 with cooling.
One concludes that raising or lowering the energy of the cold HO after one cycle of the engine depends completely on the choice of the initial wave function. The important question is, of course: what happens after one cycle with a wave function originally chosen as an eigenvector ψ of D with a negative eigenvalue? Will Sψ be a superposition of eigenvectors all with negative eigenvalues, or will part of them have a positive eigenvalue? Preliminary numerical evaluations show that the latter is the case. The resulting behavior of the engine is rather complicated.
A similar calculation for the hot HO is possible. However, note that an easy result only follows when the cycle starts by coupling the engine to the hot HO instead of the cold HO, as was done in the above calculations.
4.4. Performing Work
The previous subsections give a partial answer to the question of whether the engine is capable of transferring energy between the two oscillators. Now follows a discussion of the work needed to operate the engine.
In phases 1 and 3 of the cycle, some work is needed to operate the valves connecting the engine with the cold HO, respectively, the hot HO. Indeed, switching on and off the interaction terms in Equations (4) and (6) changes the total energy of the system. Since the wave function of the system evolves in time between the switching on and switching off, the involved energy changes do not necessarily cancel. Hence, we expect that a tiny amount of work is needed to operate these valves.
It is now indicated to consider a cycle starting with phase 2 instead of phase 1. Then, the energy changes during the respective phases are given by:
Using the simplified expression in Equation (18) for S2, one obtains:
and:
and:
and:
where [a, b, c] denotes the diagonal matrix with eigenvalues a, b, c. See Appendix D.
Several features can be observed. The contributions ΔE3 and ΔE1 represent the energy needed to switch on and off the interactions with the harmonic oscillators. They vanish when the coupling between the engine and the oscillators is at resonance.
The work performed by the engine equals the quantum expectation of the operator − ΔE2 − ΔE4. When μ = δ, then the operation of the engine is meaningless, no net energy is used and no net work is performed during phases 2 and 4. In the general case, the eigenvalues of ΔE2 + ΔE4 can be calculated analytically. One obtains:
The corresponding eigenvectors are linear combinations of (neglecting the state of the cold HO). Hence, also the spectrum of this operator is symmetric under a change of sign. This means that the initial conditions determine whether operating the engine consumes energy or whether it performs work.
4.5. Effective S-Matrix
Introduce the unitary operator:
To verify that use that:
and:
One calculates:
This shows that in the definition of D, one can use Seff instead of S.
5. Repeated Cycles
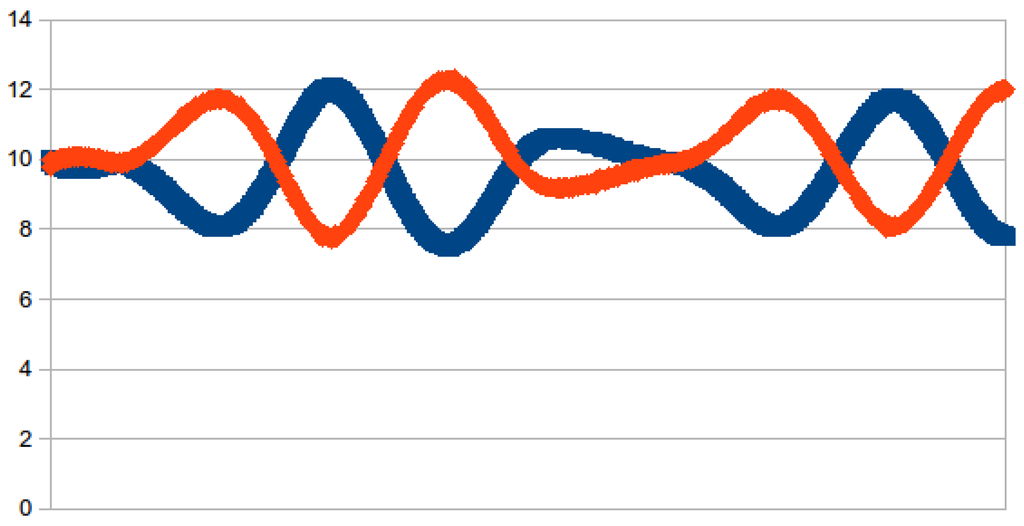
Figure 4.
Expectation value of the number operator of the cold (blue line) and of the hot (red line) oscillator. The initial state is . The total number of cycles is 1,000.
The analysis made so far has been complemented with numerical work. The S-matrix, S, is available in explicit form. Its action on a wave function of the three-component system can be easily programmed. This allows for a numerical evaluation of the behavior of the system under repeated cycles of the engine.
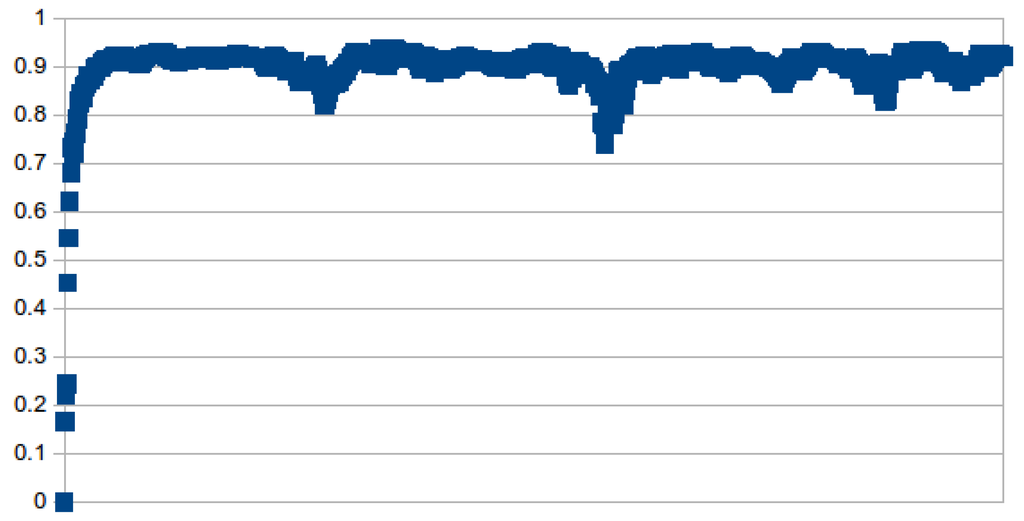
Figure 5.
Linear entropy of the reduced density operator as a function of the number of cycles. The initial state is . The total number of cycles is 1,000.
The parameters occurring in the Hamiltonian have been chosen as follows. The levels of the engine are determined by and . The frequencies of the oscillators are taken to be and . The coupling strengths between the engine and the oscillators are and . The duration of the couplings is and . Units are used in which .
Can the engine transfer energy from the cold to the hot oscillator? The answer depends on the number of cycles of the engine. See Figure 4. The initial state is a product state with an equal population of the levels of the two oscillators. The engine succeeds in transferring energy. However, quite soon, the energy flows back. This is a consequence of the dynamics of the system as a whole, which is very similar to the behavior of two weakly-coupled classical oscillators. In the latter case, it is well-known that the energy flows back and forth in a regular manner. The behavior of the quantum system is similar, but seems to be more complex. This additional complexity has two obvious explanations. The system is driven. In addition, the quantum state space has a much larger dimension than the classical one. Further investigation is needed at this point.
A main constant of the numerical work [33] is that the three components of the system get quickly entangled and that the entanglement stays at a fairly high level throughout the simulation. As a measure for the entanglement, the linear entropy [35] of the reduced density operator of the cold oscillatoris used:
See Figure 5. The statement found in [23], that product states are atypical, is confirmed. The entanglement of the three components of the system is maintained at a very high level.
6. Conclusions
It is feasible to obtain analytic results for a closed quantum system consisting of an engine operating between two small quantum systems, in casu two harmonic oscillators. The engine is operated by switching external fields on and off. The state of the system is at any moment determined by its wave function. The time evolution follows by solving the Schrödinger equation using a time-dependent Hamiltonian. No approximations have been made.
In the traditional approach, one considers a heat engine operating between the system of interest and a heat bath. The heat bath belongs to the environment and is taken into account in a phenomenological way. The present paper considers a closed system. Its state is described by a time-dependent wave function. The time evolution is unitary, and the quantum entanglement between the engine and the two harmonic oscillators is treated rigorously.
From our toy model, we have learned a number of points.
- The use of the interaction picture improves the transparency of the calculations;
- We do not make use of the adiabatic theorem. The change in the population of the energy levels of the engine results from the time evolution. As a consequence, all results depend only on intra-level distances and not on the positioning of oscillator levels with respect to the levels of the engine;
- At each of the two interfaces, the energy flows in both directions. Energy leaks away in the direction opposite to the intended one. Eight different energy contributions have been distinguished in Table 1. In the usual approach, these are replaced by two phenomenological terms;
- The S-matrix of a single cycle of the engine has a purely discrete spectrum. This follows immediately from the observation that the number of energy quanta in the system is conserved. The total energy is not conserved. The engine changes the energy content of a quantum before passing it on to one of the harmonic oscillators;
- The operator , which measures the change in energy of the cold harmonic oscillator during one cycle of the engine, has a fully discrete spectrum with explicitly known eigenvectors and eigenvalues. This is a benefit of the use of the Jaynes-Cummings mechanism for the interactions between the engine and the harmonic oscillators;
- The spectrum of this operator, D, is symmetric under the change of sign. This could be a more general feature, being a consequence of time inversion symmetry;
- The change of energy of the system as a whole during one cycle can be obtained analytically, as well. The operation of the valves connecting the engine with the oscillators costs energy, except when the interaction is at resonance. The pumping up and down of the occupational probabilities of the engine levels can cost energy or can perform work, depending on the initial state of the system; that is, depending on its wave function. This shows that the engine can be used either to transfer energy from the cold to the hot oscillator or to perform work produced by the energy flow from hot to cold.
Because the S-matrix for a single cycle is known in an analytic form, it is possible to do easy and accurate numerical evaluations of many consecutive cycles. Preliminary results show that energy transfer is feasible. However, what comes out is not what is expected. In the absence of any form of damping or decoherence, the energy starts to oscillate between the two harmonic oscillators, much like in the case of weakly-coupled classical oscillators. The numerical evaluations also show that an initial product state gets rapidly entangled to a high and fairly constant level. A full report of the numerical work will be published elsewhere [33].
A. The Gell-Mann Matrices
Conventionally, the Gell-Mann matrices are defined as follows.
B. The S-Matrix of Phase 1 of the Cycle
Here, we calculate the S-matrix of a Jaynes–Cummings Hamiltonian with a time-dependent interaction. The coupling is constant with strength during a time interval of a length of . It vanishes outside this interval. The relevant Hamiltonian is:
Let:
The eigenstates of the HO are denoted , with .
The ground state of H is:
It satisfies . The pairs of excited states are denoted , with . They are of the form:
From:
follows:
The requirement that yields the set of equations:
The solution is:
with:
A short calculation now gives:
These expressions can be written as in Equation (10).
C. Change in the State of the Cold Oscillator
Here, we derive Equation (32).
D. Work Performed during Phases 1, 3 and 4
We first calculate . Note that one can write . Therefore, we begin with:
Now, multiplying from the left with yields Equation (38).
Next, calculate using:
One calculates using :
This gives, using :
It is then straightforward to obtain:
This yields .
Conflicts of Interest
The authors declare no conflict of interest.
References
- Scovil, H.E.D.; Schulz-DuBois, E.O. Three-level masers as heat engines. Phys. Rev. Lett. 1959, 2, 262–263. [Google Scholar] [CrossRef]
- Geusic, J.E.; Schulz-DuBois, E.O.; Scovil, H.E.D. Quantum equivalent of the Carnot cycle. Phys. Rev. 1967, 156, 343–351. [Google Scholar] [CrossRef]
- Bergmann, K.; Theuer, H.; Shore, B.W. Coherent population transfer among quantum states of atoms and molecules. Rev. Mod. Phys. 1998, 70, 1003–1025. [Google Scholar] [CrossRef]
- Vitanov, V.N. Analytic model of a three-state system driven by two laser pulses on two-photon resonance. J. Phys. B 1998, 31, 709–725. [Google Scholar] [CrossRef]
- Na, K.; Reichl, L. Nonlinear dynamics of ladder and lambda STIRAP. Chaos Solitons Fractals 2005, 25, 185–196. [Google Scholar] [CrossRef]
- Kuznetsova, E.; Gacesa, M.; Pellegrini, P.; Yelin, S.F.; Côté, R. Efficient formation of ground-state ultracold molecules via STIRAP from the continuum at a Feshbach resonance. New J. Phys. 2009, 11, e055028. [Google Scholar] [CrossRef]
- Bender, C.; Brody, D.; Meister, B. Quantum mechanical Carnot engine. J. Phys. A 2000, 33, 4427–4436. [Google Scholar] [CrossRef]
- Scully, M.O.; Zubairy, M.S.; Agarwal, G.; Walther, H. Extracting work from a single heat bath via vanishing quantum coherence. Science 2003, 299, 862–864. [Google Scholar] [CrossRef] [PubMed]
- Kieu, T.D. The second law, Maxwell’s demon, and work derivable from quantum heat engines. Phys. Rev. Lett. 2004, 93, e140403. [Google Scholar] [CrossRef] [PubMed]
- Kieu, T.D. Quantum heat engines, the second law and Maxwell’s demon. Eur. Phys. J. D 2006, 39, 115–128. [Google Scholar] [CrossRef]
- Rezek, Y.; Kosloff, R. Irreversible performance of a quantum harmonic heat engine. New J. Phys. 2006, 8, e83. [Google Scholar] [CrossRef]
- Quan, H.T.; Liu, Y.; Sun, C.P.; Nori, F. Quantum thermodynamic cycles and quantum heat engines. Phys. Rev. E 2007, 76, e031105. [Google Scholar] [CrossRef] [PubMed]
- Quan, H.T. Quantum thermodynamic cycles and quantum heat engines. II. Phys. Rev. E 2009, 79, e041129. [Google Scholar] [CrossRef] [PubMed]
- Salamon, P.; Hoffmann, K.H.; Rezek, Y.; Kosloff, R. Maximum work in minimum time from a conservative quantum system. Phys. Chem. Chem. Phys. 2009, 11, 1027–1032. [Google Scholar] [CrossRef] [PubMed]
- Esposito, M.; Kawai, R.; Lindenberg, K.; van den Broeck, C. Efficiency at maximum power of low-dissipation Carnot engines. Phys. Rev. Lett. 2010, 105, e150603. [Google Scholar] [CrossRef] [PubMed]
- Esposito, M.; Kawai, R.; Lindenberg, K.; van den Broeck, C. Quantum-dot Carnot engine at maximum power. Phys. Rev. E 2010, 81, e041106. [Google Scholar] [CrossRef] [PubMed]
- Naudts, J.; O’Kelly de Galway, W. On the BCH formula of Rezek and Kosloff. Physica A 2011, 390, 3317–3319. [Google Scholar] [CrossRef]
- Scully, M.; Chapin, K.; Dorfman, K.; Kimb, M.; Svidzinsky, A. Quantum heat engine power can be increased by noise-induced coherence. Proc. Natl. Acad. Sci. USA 2011, 108, e15097. [Google Scholar] [CrossRef] [PubMed]
- Dorfman, K.; Voronine, D.; Mukamel, S.; Scully, M. Photosynthetic reaction center as a quantum heat engine. Proc. Natl. Acad. Sci. USA 2013, 110, e2746. [Google Scholar] [CrossRef] [PubMed]
- Kossakowski, A. On quantum statistical mechanics of non-Hamiltonian systems. Rep. Math. Phys. 1972, 3, 247–274. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119–130. [Google Scholar] [CrossRef]
- Abah, O.; Rossnagel, J.; Jacob, G.; Deffner, S.; Schmidt-Kaler, F.; Singer, K.; Lutz, E. Single-ion heat engine at maximum power. Phys. Rev. Lett. 2012, 109, e203006. [Google Scholar] [CrossRef] [PubMed]
- Gemmer, J.; Michel, M.; Mahler, G. Quantum Thermodynamics; Springer: Berlin, Germany, 2009. [Google Scholar]
- Esposito, M.; Lindenberg, K.; van den Broeck, C. Entropy production as correlation between system and reservoir. New J. Phys. 2010, 12, e013013. [Google Scholar] [CrossRef]
- Avron, J.E.; Elgart, A.; Graf, G.M.; Sadun, L. Geometry, statistics, and asymptotics of quantum pumps. Phys. Rev. B 2000, 62, R10618–R10621. [Google Scholar] [CrossRef]
- Cohen, D. Quantum pumping in closed systems, adiabatic transport, and the Kubo formula. Phys. Rev. B 2003, 68, e155303. [Google Scholar] [CrossRef]
- Cohen, D. Quantum pumping and dissipation in closed systems. Physica E 2005, 29, 308–319. [Google Scholar] [CrossRef]
- Rosenberg, G.; Cohen, D. Quantum stirring of particles in closed devices. J. Phys. A 2006, 39, e2287. [Google Scholar] [CrossRef]
- Hiller, M.; Kottos, T.; Cohen, D. Control of atomic currents using a quantum stirring device. Europhys. Lett. 2008, 82, e40006. [Google Scholar] [CrossRef]
- Bartsch, C.; Steinigeweg, R.; Gemmer, J. Occurrence of exponential relaxation in closed quantum systems. Phys. Rev. E 2008, 77, e011119. [Google Scholar] [CrossRef] [PubMed]
- Citro, R.; Minguzzi, A.; Hekking, F.W.J. Quantum stirring in a one-dimensional Bose gas. J. Phys. 2009, 150, e032015. [Google Scholar] [CrossRef]
- Waldherr, G.; Mahler, G. Lasing process in a closed bipartite quantum system: A thermodynamical analysis. Phys. Rev. E 2010, 81, e061122. [Google Scholar] [CrossRef] [PubMed]
- Naudts, J. Numerical study of a driven quantum system composed of a three-level system transferring energy between two harmonic oscillators. 2013; unpublished work. [Google Scholar]
- Naudts, J.; O’Kelly de Galway, W. Analytic solutions for a three-level system in a time-dependent field. Physica D 2011, 240, 542–545. [Google Scholar] [CrossRef]
- Buscemi, F.; Bordone, P.; Bertoni, A. Linear entropy as an entanglement measure in two-fermion systems. Phys. Rev. A 2007, 75, e032301. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).