Fractional Heat Conduction in an Infinite Medium with a Spherical Inclusion
1. Introduction
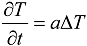
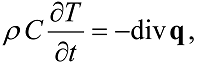
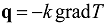
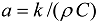 is the heat diffusivity coefficient.
is the heat diffusivity coefficient.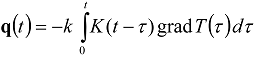
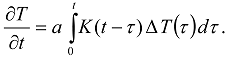
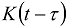 were analyzed in [9,10,11,12]. The time-nonlocal dependence between the heat flux vector q and the temperature gradient with the long-tail power kernel [9,10,11,12]
were analyzed in [9,10,11,12]. The time-nonlocal dependence between the heat flux vector q and the temperature gradient with the long-tail power kernel [9,10,11,12]
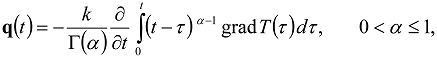
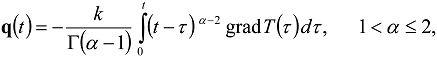
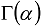 is the gamma function, can be interpreted in terms of fractional calculus:
is the gamma function, can be interpreted in terms of fractional calculus:
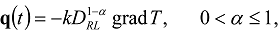
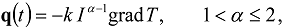
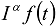 and
and 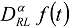 are the Riemann–Liouville fractional integral and derivative of the order respectively [13,14,15,16]:
are the Riemann–Liouville fractional integral and derivative of the order respectively [13,14,15,16]:
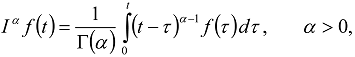
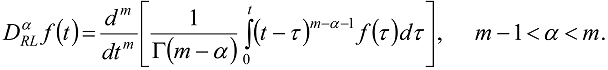
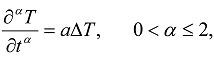
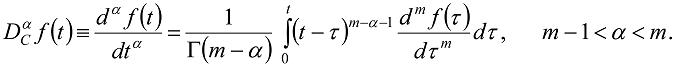

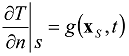
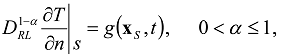
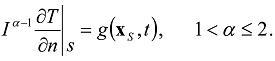
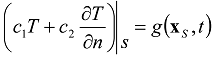
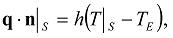
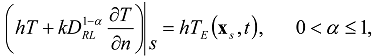
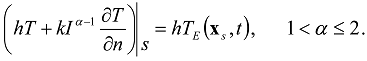
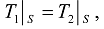
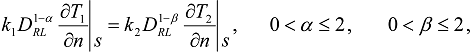
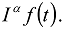 The fractional integral of the order
The fractional integral of the order  is denoted as
is denoted as 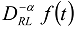 . In the equation of perfect thermal contact (23)
. In the equation of perfect thermal contact (23) 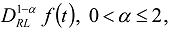 and
and 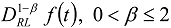 , are understood in this sense.
, are understood in this sense. and a matrix
and a matrix 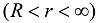 being in perfect thermal contact at
being in perfect thermal contact at 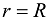 is considered. The heat conduction in each region is described by the time-fractional heat conduction equation with the Caputo derivative of fractional order
is considered. The heat conduction in each region is described by the time-fractional heat conduction equation with the Caputo derivative of fractional order 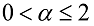 and
and 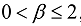 , respectively.
, respectively.2. Statement of the Problem
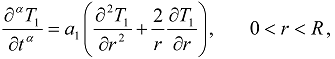
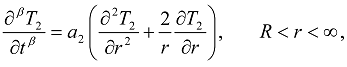
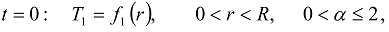
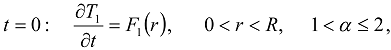
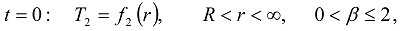
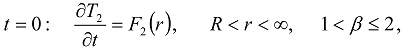
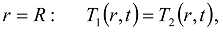
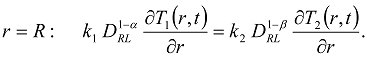

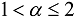 or
or 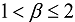 , then the additional condition on the first time derivative should be also imposed.
, then the additional condition on the first time derivative should be also imposed.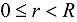 is at initial uniform temperature T0 and the matrix
is at initial uniform temperature T0 and the matrix 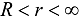 is at initial zero temperature
is at initial zero temperature
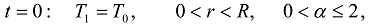
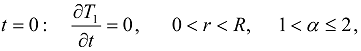
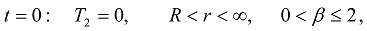
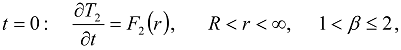
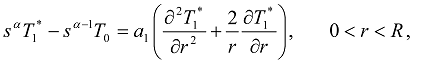
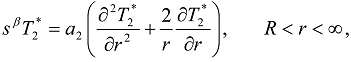
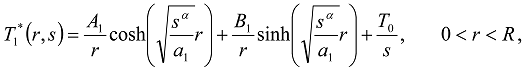
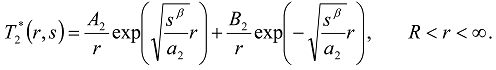

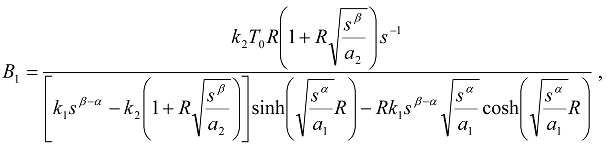
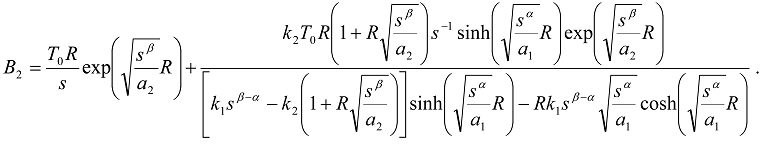
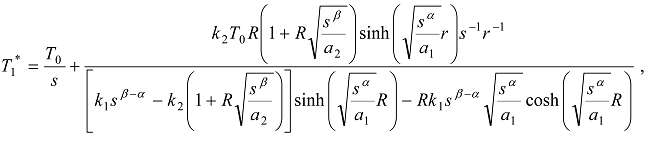
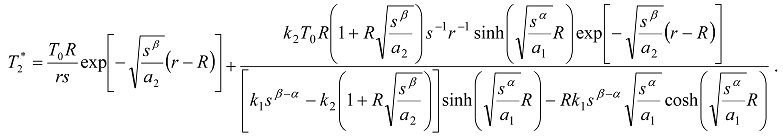
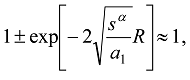
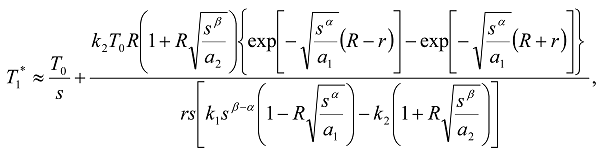
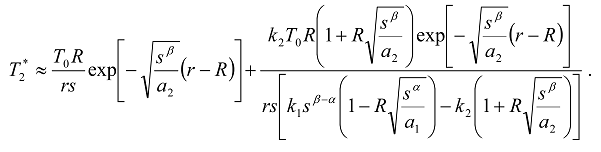
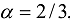 ,
, 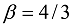 ;
; 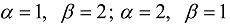 the denominator in Equations (47) and (48) can be treated as a cubic equation and the decomposition into the sum of partial fractions can be obtained similar to that used in [58].
the denominator in Equations (47) and (48) can be treated as a cubic equation and the decomposition into the sum of partial fractions can be obtained similar to that used in [58].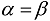
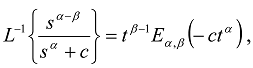
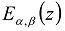 is the generalized Mittag-Leffler function in two parameters
is the generalized Mittag-Leffler function in two parameters
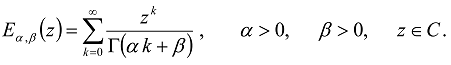
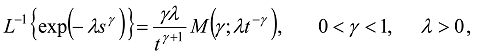
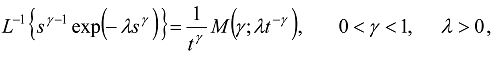
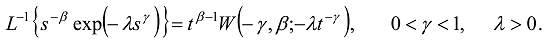
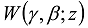 is the Wright function [1,51,52,62]
is the Wright function [1,51,52,62]
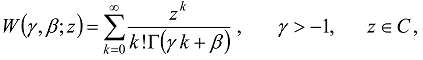
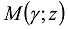 is the Mainardi function [15,51,52]
is the Mainardi function [15,51,52]
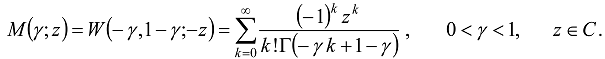
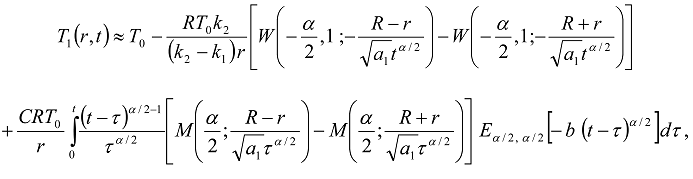
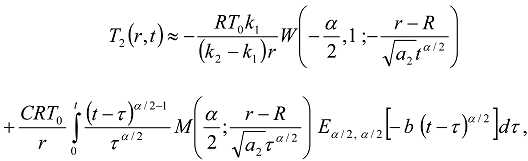
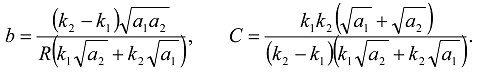
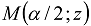 and the Wright function
and the Wright function 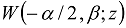 . The limitation
. The limitation 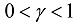 in Equations (51–53) means that
in Equations (51–53) means that 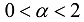 in Equations (56) and (57).
in Equations (56) and (57).4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Petrov, N.; Vulchanov, N. A note on the non-classical heat condition. Bulg. Acad. Sci. Theor. Appl. Mech. 1982, 13, 35–39. [Google Scholar]
- Chandrasekharaiah, D.S. Thermoelasticity with second sound: a review. Appl. Mech. Rev. 1986, 39, 355–376. [Google Scholar] [CrossRef]
- Joseph, D.D.; Preziosi, L. Heat waves. Rev. Mod. Phys. 1989, 61, 41–73. [Google Scholar] [CrossRef]
- Tamma, K.; Zhou, X. Macroscale and microscale thermal transport and thermo-mechanical inter-actions: some noteworthy perspectives. J. Thermal Stresses 1998, 21, 405–449. [Google Scholar] [CrossRef]
- Chandrasekharaiah, D.S. Hyperbolic thermoelasticity: a review of recent literature. Appl. Mech. Rev. 1998, 51, 705–729. [Google Scholar] [CrossRef]
- Ignaczak, J.; Ostoja-Starzewski, M. Thermoelasticity with Finite Wave Speeds; Oxford University Press: London, UK, 2009. [Google Scholar]
- Nigmatullin, R.R. To the theoretical explanation of the “universal response”. Phys. Stat. Sol. (b) 1984, 123, 739–745. [Google Scholar] [CrossRef]
- Nigmatullin, R.R. On the theory of relaxation for systems with “remnant” memory. Phys. Stat. Sol. (b) 1984, 124, 389–393. [Google Scholar] [CrossRef]
- Povstenko, Y.Z. Fractional heat conduction equation and associated thermal stresses. J. Thermal Stresses 2005, 28, 83–102. [Google Scholar] [CrossRef]
- Povstenko, Y.Z. Thermoelasticity which uses fractional heat conduction equation. J. Math. Sci. 2009, 162, 296–305. [Google Scholar] [CrossRef]
- Povstenko, Y.Z. Theory of thermoelasticity based on the space-time-fractional heat conduction equation. Phys. Scr. 2009. [Google Scholar] [CrossRef]
- Povstenko, Y.Z. Fractional Cattaneo-type equations and generalized thermoelasticity. J. Thermal Stresses 2011, 34, 97–114. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publisher: New York, NY, USA, 1993. [Google Scholar]
- Gorenflo, R.; Mainardi, F. Fractional calculus: integral and differential equations of fractional order. In Fractals and Fractional Calculus in Continuum Mechanics; Carpinteri, A., Mainardi, F., Eds.; Springer-Verlag: New York, NY, USA, 1997; pp. 223–276. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Povstenko, Y. Non-axisymmetric solutions to time-fractional diffusion-wave equation in an infinite cylinder. Fract. Calc. Appl. Anal. 2011, 14, 418–435. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk's guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The restaurant at the end of the random walk: Recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A: Math. Gen. 2004, 37, R161–R208. [Google Scholar] [CrossRef]
- Zaslavsky, G.M. Chaos, fractional kinetics, and anomalous transport. Phys. Rep. 2002, 371, 461–580. [Google Scholar] [CrossRef]
- Rabotnov, Yu.N. Creep Problems in Structural Members; North-Holland Publishing Company: Amsterdam, The Netherlands, 1969. [Google Scholar]
- Mainardi, F. Applications of fractional calculus in mechanics. In Transform Methods and Special Functions; Rusev, P., Dimovski, I., Kiryakova, V., Eds.; Bulgarian Academy of Sciences: Sofia, Bulgaria, 1998; pp. 309–334. [Google Scholar]
- Rossikhin, Yu.A.; Shitikova, M.V. Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids. Appl. Mech. Rev. 1997, 50, 15–67. [Google Scholar] [CrossRef]
- West, B.J.; Bologna, M.; Grigolini, P. Physics of Fractals Operators; Springer-Verlag: New York, NY, USA, 2003. [Google Scholar]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House Publishers, Inc.: Redding, CA, USA, 2006. [Google Scholar]
- Sabatier, J.; Agrawal, O.P.; Tenreiro Machado, J.A. (Eds.) Advances in Fractional Calculus: Theoretical Developments and Applications in Physics and Engineering; Springer-Verlag: Dordrecht, The Netherlands, 2007.
- Gafiychuk, V.; Datsko, B. Mathematical modeling of different types of instabilities in time fractional reaction-diffusion systems. Comput. Math. Appl. 2010, 59, 1101–1107. [Google Scholar] [CrossRef]
- Baleanu, D.; Güvenç, Z.B.; Tenreiro Machado, J.A. (Eds.) New Trends in Nanotechnology and Fractional Calculus Applications; Springer-Verlag: New York, NY, USA, 2010.
- Rossikhin, Y.A.; Shitikova, M.V. Application of fractional calculus for dynamic problems of solid mechanics: novel trends and recent results. Appl. Mech. Rev. 2010, 63, 010801. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; Imperial College Press: London, UK, 2010. [Google Scholar]
- Datsko, B.; Gafiychuk, V. Complex nonlinear dynamics in subdiffusive activator–inhibitor systems. Commun. Nonlinear Sci. Numer. Simulat. 2012, 17, 1673–1680. [Google Scholar] [CrossRef]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers; Springer-Verlag: Berlin, Germany, 2013. [Google Scholar]
- Zunino, L.; Pérez, D.G.; Martín, M.T.; Garavaglia, M.; Plastino, A.; Rosso, O.A. Permutation entropy of fractional Brownian motion and fractional Gaussian noise. Phys. Lett. A 2008, 372, 4768–4774. [Google Scholar] [CrossRef]
- Ubriaco, M.R. Entropies based on fractional calculus. Phys. Lett. A 2009, 373, 2516–2519. [Google Scholar] [CrossRef]
- Tenreiro Machado, J.A. Entropy analysis of integer and fractional dynamical systems. Nonlinear Dyn. 2010, 62, 371–378. [Google Scholar] [CrossRef]
- Tenreiro Machado, J.A. Fractional dynamics of a system with particles subjected to impacts. Commun. Nonlinear Sci. Numer. Simulat. 2011, 16, 4596–4601. [Google Scholar] [CrossRef]
- Jumarie, G. Path probability of random fractional systems defined by white noises in coarse-grained time applications of fractional entropy. Fract. Diff. Calc. 2011, 1, 45–87. [Google Scholar] [CrossRef]
- Tenreiro Machado, J.A. Shannon information and power law analysis of the chromosome code. Abstr. Appl. Anal. 2012. [Google Scholar] [CrossRef]
- Essex, C.; Schulzky, C.; Franz, A.; Hoffmann, K.H. Tsallis and Rényi entropies in fractional diffusion and entropy production. Physica A 2000, 284, 299–308. [Google Scholar] [CrossRef]
- Cifani, S.; Jakobsen, E.R. Entropy solution theory for fractional degenerate convection–diffusion equations. Ann. Inst. Henri Poincare (C) Nonlinear Anal. 2011, 28, 413–441. [Google Scholar] [CrossRef] [Green Version]
- Magin, R.; Ingo, C. Entropy and information in a fractional order model of anomalous diffusion. In Proceedings of the 16th IFAC Symposium on System Identification, Brussels, Belgium, 11–13 July 2011; Kinnaert, M., Ed.; International Federation of Automatic Control: Brussels, Belgium, 2012; pp. 428–433. [Google Scholar]
- Magin, R.; Ingo, C. Spectral entropy in a fractional order model of anomalous diffusion. In Proceedings of the 13th International Carpathian Control Conference, High Tatras, Slovakia, 28–31 May 2012; Petraš, I., Podlubny, I., Kostúr, J., Kačur, J., Mojžišová, A, Eds.; Institute of Electrical and Electronics Engineers: Košice, Slovakia, 2012; pp. 458–463. [Google Scholar]
- Prehl, J.; Essex, C.; Hoffmann, K.H. Tsallis relative entropy and anomalous diffusion. Entropy 2012, 14, 701–706. [Google Scholar] [CrossRef]
- Prehl, J.; Boldt, F.; Essex, C.; Hoffmann, K.H. Time evolution of relative entropies for anomalous diffusion. Entropy 2013, 15, 2989–3006. [Google Scholar] [CrossRef]
- Magin, R.L.; Ingo, C.; Colon-Perez, L.; Triplett, W.; Mareci, T.H. Characterization of anomalous diffusion in porous biological tissues using fractional order derivatives and entropy. Microporous Mesoporous Mater. 2013, 178, 39–43. [Google Scholar] [CrossRef] [PubMed]
- Povstenko, Y. Different kinds of boundary conditions for time-fractional heat conduction equation. In Proceedings of the 13th International Carpathian Control Conference, High Tatras, Slovakia, 28–31 May 2012; Petraš, I., Podlubny, I., Kostúr, J., Kačur, J., Mojžišová, A, Eds.; Institute of Electrical and Electronics Engineers: Košice, Slovakia, 2012; pp. 588–591. [Google Scholar]
- Povstenko, Y.Z. Fractional heat conduction in infinite one-dimensional composite medium. J. Thermal Stresses 2013, 36, 351–363. [Google Scholar] [CrossRef]
- Wyss, W. The fractional diffusion equation. J. Math. Phys. 1986, 27, 2782–2785. [Google Scholar] [CrossRef]
- Schneider, W.R.; Wyss, W. Fractional diffusion and wave equations. J. Math. Phys. 1989, 30, 134–144. [Google Scholar] [CrossRef]
- Fujita, Y. Integrodifferential equation which interpolates the heat equation and the wave equation. Osaka J. Math. 1990, 27, 309–321. [Google Scholar]
- Mainardi, F. The fundamental solutions for the fractional diffusion-wave equation. Appl. Math. Lett. 1996, 9, 23–28. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional relaxation-oscillation and fractional diffusion-wave phenomena. Chaos, Solitons Fractals 1996, 7, 1461–1477. [Google Scholar] [CrossRef]
- Chen, S.; Jiang, X. Analytical solutions to time-fractional partial differential equations in a two-dimensional multilayer annulus. Physica A 2012, 392, 3865–3874. [Google Scholar] [CrossRef]
- Povstenko, Y. Fundamental solutions to time-fractional heat conduction equations in two joint half-lines. Cent. Eur. J. Phys. 2013. [Google Scholar] [CrossRef]
- Luikov, A.V. Analytical Heat Diffusion Theory; Academic Press: New York, NY, USA, 1968. [Google Scholar]
- Özişik, M.N. Heat Conduction; John Wiley: New York, NY, USA, 1980. [Google Scholar]
- Debnath, L.; Bhatta, D. Integral Transforms and Their Applications; Chapman & Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
- Povstenko, Y. Time-fractional heat conduction in an infinite medium with a spherical hole under Robin boundary condition. Fract. Calc. Appl. Anal. 2013, 16, 354–369. [Google Scholar] [CrossRef]
- Mikusiński, J. On the function whose Laplace transform is
. Stud. Math. 1959, 18, 191–198. [Google Scholar]
- Stanković, B. On the function of E.M. Wright. Publ. Inst. Math. 1970, 10, 113–124. [Google Scholar]
- Gajić, Lj.; Stanković, B. Some properties of Wright’s function. Publ. Inst. Math. 1976, 20, 91–98. [Google Scholar]
- Erdélyi, A.; Magnus, W.; Oberhettinger, F.; Tricomi, F.G. Higher Transcendental Functions; Volume 3, McGraw-Hill: New York, NY, USA, 1955. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Povstenko, Y. Fractional Heat Conduction in an Infinite Medium with a Spherical Inclusion. Entropy 2013, 15, 4122-4133. https://doi.org/10.3390/e15104122
Povstenko Y. Fractional Heat Conduction in an Infinite Medium with a Spherical Inclusion. Entropy. 2013; 15(10):4122-4133. https://doi.org/10.3390/e15104122
Chicago/Turabian StylePovstenko, Yuriy. 2013. "Fractional Heat Conduction in an Infinite Medium with a Spherical Inclusion" Entropy 15, no. 10: 4122-4133. https://doi.org/10.3390/e15104122





