Abstract
Multivariate hydrologic frequency analysis has been widely studied using: (1) commonly known joint distributions or copula functions with the assumption of univariate variables being independently identically distributed (I.I.D.) random variables; or (2) directly applying the entropy theory-based framework. However, for the I.I.D. univariate random variable assumption, the univariate variable may be considered as independently distributed, but it may not be identically distributed; and secondly, the commonly applied Pearson’s coefficient of correlation (γ) is not able to capture the nonlinear dependence structure that usually exists. Thus, this study attempts to combine the copula theory with the entropy theory for bivariate rainfall and runoff analysis. The entropy theory is applied to derive the univariate rainfall and runoff distributions. It permits the incorporation of given or known information, codified in the form of constraints and results in a universal solution of univariate probability distributions. The copula theory is applied to determine the joint rainfall-runoff distribution. Application of the copula theory results in: (i) the detection of the nonlinear dependence between the correlated random variables-rainfall and runoff, and (ii) capturing the tail dependence for risk analysis through joint return period and conditional return period of rainfall and runoff. The methodology is validated using annual daily maximum rainfall and the corresponding daily runoff (discharge) data collected from watersheds near Riesel, Texas (small agricultural experimental watersheds) and Cuyahoga River watershed, Ohio.
Keywords:
Shannon entropy; principle of maximum entropy; rainfall; runoff; univariate probability distribution; copulas Classification MSC:
28D20; 47N30; 62G32
1. Introduction
In multivariate hydrological frequency analysis, studies have been extensively carried out along three lines: (I) application of the covariance structure (i.e., Pearson’s linear covariance/correlation matrix) with known multivariate and univariate probability distributions [1,2,3,4,5]; (II) application of copula theory to the pseudo-observations (i.e., empirical probability distribution function) first and then study the risk with fitted univariate distributions [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]; and (III) application of linear covariance with the maximum entropy framework [25,26,27,28,29].
In the above three types of applications, use of the copula theory separates approach II from approaches I and III with the capability of capturing the nonlinear dependence structure of studied variables, whereas the application of Pearson’s linear covariance in approaches I and III is not sensitive to the nonlinear dependence structure. The advantage of approach III is that by applying the maximum entropy theory, one may reach the universal solution and better capture the shape of probability density function (PDF) [30,31,32,33,34,35,36]. Considering approaches I and II, there exists one common assumption, i.e., the univariate hydrological variables are considered as independently identically distributed (I.I.D.) random variables. Although depending on how the data is collected, it may be valid to assume it as independently distributed random variables, the assumption of the variable being identically distributed may not be valid for the unviariate data with a mixed structure. The misidentification of univariate probability distribution may result in underestimation/overestimation of the joint and conditional return period in case of risk analysis. In addition, even if the I.I.D. random variable assumption is valid, the univariate distribution determined is usually not universal for the same datasets. Thus, it is important to re-evaluate the determination of univariate distributions.
With the limitations of each approach discussed above, this study attempts to utilize the advantages held by approaches II and III and aims to provide a framework to link the maximum entropy and copula theories for the study of multivariate hydrological frequency analysis to avoid misusing the assumptions. Comparing to the existing frameworks, the proposed framework has the following advantages: (i) the universal probability distribution can be obtained from appropriately defined constraints; (ii) the multi-mode can be captured using the maximum entropy theory if the data show the multi-mode structure which may result in better estimation of multivariate/conditional return periods of given events; and (iii) the nonlinear dependence can be captured among the correlated random variables by applying the copula theory rather than applying the known or entropy-based multivariate probability distribution with the dependence captured by linear covariance. For illustration, the paper applies rainfall and runoff (discharge) data from: (1) watersheds near Riesel, Texas (the agricultural experimental watersheds maintained by the USA Department of Agriculture, Agricultural Research Service), and (2) the Cuyahoga River watershed in Ohio, collected by USGS and NOAA. The paper is organized as follows: after introducing the subject in this section, univariate rainfall and runoff frequency distributions are derived using the entropy theory in Section 2. Section 3 discusses the joint probability distribution estimation using copula theory, tail dependence for extreme events and corresponding joint and conditional return period analysis. Section 4 discusses the goodness of fit statistics, and application of the methodology is presented in Section 5. The paper is concluded in Section 6.
2. Determination of Maximum Entropy-Based Univariate Distributions
Derivation of univariate distributions of rainfall and runoff using the entropy theory entails: (1) defining entropy and specifying the known information about the random variables in terms of constraints, and (2), maximizing entropy to obtain the probability density function using the method of Lagrange multipliers and determining these multipliers.
2.1. Entropy and Specification of Constraints
For a univariate random variable X with a continuous probability density function fX(x), the Shannon entropy [37], H(X) can be expressed as:
In accordance with the principle of maximum entropy (POME) [38,39], one can obtain the most probable probability density function (PDF) for random variable X with the available information (i.e., constraints) by maximizing Equation (1). In this study, the sample statistical moments are used as constraints with two main advantages. First, it avoids assuming certain types of distributions from data based on a nonparametric approach (frequency histogram or kernel density function), and hence one may reach the universal PDF for the dataset analyzed. Second, the PDF so derived may capture the possible multi-modes embedded in the data.
It is well known that annual maximum daily rainfall amount and corresponding daily discharge are skewed to the right. Thus, at least the first three non-central sample statistical moments need to be considered as constraints. According to the probability theory, it is also known that if the excess kurtosis is significantly different from 0, the probability density function of the random variable is heavily tailed and results in the necessity to include the fourth non-central statistical moment as a constraint. This necessity is determined based on the excess kurtosis as follows:
In Equations (2), stands for the excess kurtosis and G2 stands for the sample excess kurtosis. Then, whether G2 is significantly different from zero can be determined by statistic (T) as:
where SEK stands for the standard error of kurtosis as:
In Equations (2,3), n is the sample size. For statistics T: if |T| > 2, the excess kurtosis is significantly different from zero and the fourth non-central moment needs to be applied as a constraint, otherwise, the fourth non-central moments does not need to be applied. In addition, considering the rainfall and runoff data structure, the first moment in the logarithm domain may also contribute to the PDF. Hence, the constraints for the maximum entropy-based distributions are:
if excess kurtosis is not significantly different from zero:
otherwise:
2.2. Entropy and Specification of Constraints
With the constraints defined in Equations (4–6), the entropy function [Equation (1)] is maximized using the method of Lagrange multipliers with the resulting maximum entropy-based PDF expressed as:
where ’s are the Lagrange multipliers.
The PDF defined by Equation (7) will be able to preserve the most important statistical moments that dominate its shape. Following [40,41], the Lagrange multipliers can be estimated. In what follows, the estimation concept and procedure are described in detail.
Substituting Equation (7) into Equation (4) one can obtain the partition function as:
or:
It is proved that λ0 is a strictly convex function of λ1, λ2, λ3, λN+1 [41]. Thus, one can write the objective function as:
where ai stands for the sample statistical moment of the constraint.
It should be noted that the objective function Z so defined is a convex function of , and minimizing the objective function Z will result in the maximum entropy. Now, the Lagrange parameters can be determined using Newton’s method as follows:
Let:
Then the objective function [(Equation (9)] can be approximated with the second-order Taylor series around parameter vector λ = [λ1,λ2,…,λN+1] as:
where the elements () of gradient vector G and the element () of Hessian matrix H can be written as:
The Lagrange parameters can then be estimated using Newton’s method with the initial parameter set and and the corresponding constraints of gradient vector as G = 0. It is necessary to state that needs to be greater than 0 [42].
3. Bivariate Rainfall and Runoff Distribution Using Copula Theory
Using the copula theory, one may successfully capture the nonlinear dependence between rainfall and runoff (discharge) variables. The copula concept was first introduced by Sklar [43]. For a bivariate case, let observations (x1, y1), (x2, y2),…, (xn, yn), be drawn from the bivariate population of (X,Y) with the marginal distributions as and . Then, the joint distribution, i.e., H(X,Y) or simply H can be expressed using the copula as:
where C is the copula. C is a unique mapping when and are continuous, and captures the dependence between random variable X and Y.
In what follows, the topics essential to apply the copula theory for rainfall and runoff analysis are discussed, i.e., dependence measure, choice of copulas, parameter estimation, tail dependence, and joint/conditional return period determination.
3.1. Dependence Measure for Bivariate Random Variables and Choice of Copulas
To apply the copula theory to investigate the bivariate random variables X and Y, the dependence structure can be examined using the rank-based coefficient of correlation, e.g., Kendall’s τ, Spearman’s ρ, and Geni’s γ [44]. The rank-based coefficient of correlation is distribution free and sensitive to the nonlinear dependence structure which makes it more robust than the commonly applied Pearson’s coefficient of correlation (only sensitive to linear dependence structure). In this study, the rank-based coefficients of correlation (i.e., Kendall’s τ, Spearman’s ρ) were applied to detect the dependence structure of rainfall and runoff variables.
It is known that the dependence between rainfall and runoff are usually positive by nature. Thus, the copula models dealing with positive dependence are selected as the candidates to model the joint rainfall and runoff distribution. Appendix I lists the copula functions examined, including one- and two-parameter Archimedean copulas, extreme-value copulas, and Plackett copula.
3.2. Estimation of Copula Parameters
Parameters of a copula model can be estimated using nonparametric estimation through rank-based coefficient of correlation, i.e., Kendall’s τ, Spearman’s ρ, and Geni’s γ. The parameters can also be estimated using the maximum likelihood estimation (MLE). In this study, MLE was applied for parameter estimation.
Let the empirical probability distributions of rainfall (X) and runoff (discharge) (Y) random variables be and , then for a given copula model candidate the maximum log-likelihood function may be written as:
where θ represents the copula parameter vector, n is the sample size, and represents the copula density function as:
then, the copula parameter was optimized by maximizing the log-likelihood function or minimizing the negative log-likelihood function.
3.3. Tail Dependence of Copula
In rainfall and runoff analysis, one is usually interested in the extreme behavior of the rainfall and runoff (discharge) variables for risk analysis, i.e., , and the conditional probability, i.e., and (or) . However, the best-fitted copula may not be guaranteed to appropriately model the extreme behavior [45]. Thus, it is important to study the tail dependence of the bivariate rainfall and runoff data. The tail dependence may be studied either graphically using the Chi-plot [46] or numerically from an empirical copula, a given group of multivariate distributions, and a given group of copula functions [47]. In this study, the tail dependence was numerically investigated by nonparametric estimation.
Nonparametric estimation was based on the empirical copula with no assumption imposed on either copula or marginal distributions [47]. Let (Rx, Ry) be the paired rank of the bivariate random sample , the empirical copula Cm is written as:
then, the nonparametric upper-tail dependence coefficient may be estimated in three different forms as:
where is the sample size; is the chosen threshold for Equations (14a,b); and in Equation (14b) denotes the relationship to the scant of the copula’s diagonal.
Equation (14a) was first proposed in [48], whereas Equation (14b) first appeared in [49] and it is sensitive when the extreme values are not along the diagonal as SEC stands for. The threshold in Equations (14a,b) can be estimated following the heuristic plateau-finding algorithm discussed in [47]. Equation (14c) was first proposed in [50] and may be appropriately applied only under the assumption that the empirical copula function approximates an extreme value (EV) copula.
3.4. Return Period of Bivariate Variables Using the Copula Theory
In rainfall and runoff analysis, the purpose of deriving the joint distribution and study of the tail dependence is to estimate the joint/conditional return period of extreme events. With the upper tail dependence appropriately assessed, the joint and conditional return period of extreme events may be studied.
3.4.1. Joint Return Period “AND” Case Using Copula Theory
Following [51], the joint return period can be determined with the appropriately selected copula function as follows. Considering the 2-dimensional continuous bivariate random variables , , the “AND” case may be determined using Kendall distribution, component-wise and most-likely excess design realizations [51]. In this study, the most-likely design realization approach was adopted. For rainfall and runoff variables X and Y, the joint return period is written as:
where stands for the critical layer and t stands for the joint return period:
is the joint probability density function derived from copula function as:
where stands for the copula density function as Equation (13a); and and stand for the fitted univariate PDF.
Then, the design event (x, y) can be estimated by finding the maximum of the joint density function in the logarithm domain over the critical layer with the corresponding (x*, y*) as the design event with T-year return period. The critical layer can be obtained using the Kendall distribution.
3.4.2. Conditional Return Period of Runoff Events Given Rainfall Events
Again, using X as rainfall random variable and Y as runoff random variable, the conditional return period of runoff events of given rainfall events can be written in two cases:
Case I: Return period of runoff events conditioned on rainfall events greater than the given rainfall values:
Applying the copula theory, the exceedance conditional distribution is written as:
The corresponding conditional return period is written as:
Case II: Return period of runoff events conditioned on rainfall events equal to the given rainfall values:
similarly, the exceedance conditional probability is written as:
Equation (16) can be also rewritten as:
The corresponding conditional return period is written as:
In Equations (16,17), x* represents the rainfall events; T represents the conditional return period of runoff events; and y* represents the runoff events that need to be estimated based on T and x*. In addition, Equation (16) is right tail increasing (RTI) if it is a nondecreasing function of x for all y, and Equation (17) or (17a) is stochastic increasing (SI) if it is a nondecreasing function of x for all y.
It should also be addressed that 1 in Equations (16a) and (17b) stands for the annual event. If one considers the partial duration time series (i.e., the events over a given threshold), 1 should be replaced with μ (the expected number of event/year).
4. Goodness-of-Fit Statistics
Before applying the copula-entropy framework to study the bivariate rainfall and runoff frequency and risk analysis, the goodness-of-fit statistic test need to be performed for both fitted univariate distribution and copula functions.
4.1. Goodness-of-Fit Statistics for Univariate Distribution
With the parametric univariate probability distribution fitted to the random variable X, the goodness-of-fit statistical tests need to be performed to assess whether the fitted probability distribution is valid. In the study, three goodness-of-fit statistics were considered.
The goodness-of-fit statistics using the root mean square error (RMSE) may be expressed respectively as:
where RMSE is root mean square error; is the estimated value from the fitted univariate probability distribution; is the corresponding observed value; and n is the sample size.
The Kolmogorov-Smirnov (K-S) goodness-of-fit test is a nonparametric probability distribution free test. For continuous random variables, it quantifies the distance between the empirical distribution (F) and the specified distribution function (). The null hypothesis (H0) is: X follows the specified distribution function . The alternative hypothesis (Ha) is: X does not follow the specified distribution function. The K-S goodness-of-fit statistics is defined as:
where : sample data sorted in increasing order.
In Equation (19), the null hypothesis (H0) is rejected if , and can be estimated using Miller’s approximation [52].
The Anderson-Darling (A-D) goodness-of-fit test is the test to examine whether the sample data is drawn from a specific probability distribution. Comparing with the K-S goodness-of-fit test, the A-D goodness-of-fit test is not distribution free and gives more weight to tails than the K-S goodness-of-fit test [53]. The null hypothesis (H0) is: X follows the specified distribution. The alternative (Ha) is: X does not follow the specified distribution. The A-D goodness-of-fit test can be expressed as follows:
where is sample size; θ is parameter vector of fitted probability distribution; and is sample data sorted in increasing order.
In Equation (20), the null hypothesis (H0) is rejected if . The value is approximated using parametric bootstrap simulation for maximum entropy-based univariate distribution.
4.2. Goodness-of-Fit statistics for Copula
The formal goodness-of-fit statistics for multivariate distributions have been extensively discussed based on the copula theory [54,55]. Following their discussion, the goodness-of-fit test based on the probability integral transformation (i.e., Kendall’s univariate probability transformation) was employed in the study.
For a given bivariate probability distribution function using a copula function [Equation (12)], the corresponding Kendall’s nonparametric univariate probability transformation can be written as:
where n is sample size and:
The null hypothesis is H0: the bivariate random variable can be modeled by a given copula function through the measure of the distance between Kn and parametric estimation using:
Now the test statistic of rank-based Cramér-von Mises statistics () can be written as:
The corresponding P-value of the statistic is then determined using the parametric bootstrap procedure proposed in [14] outlined as follows:
- (1)
- Estimate parameter vector for the copula function using MLE with pseudo-observations.
- (2)
- Calculate from Equation (21).
- (3)
- Determine and . The Archimedean copula family has the analytical formulation of , and thus the statistics defined in Equation (22) may be calculated directly. Otherwise the Monte Carlo simulation can be applied to approximate with the following steps:
- Generate a random sample from the fitted copula function with the sample size at least as the same length of the observed data.
- Calculate the approximated using an approach similar to Equation (21) as:
- Calculate the approximated as
- (4)
- Use parametric bootstrap procedure with a large number N to determine the associated P-value as follows:
- Generate N bivariate random samples from the fitted copula function of the observed data.
- Estimate the parameters for the fitted copula functions using the generated bivariate random samples.
- Calculate for each bivariate samples using Equation (21).
- Repeat step (3) to determine for each sample.
- Approximate the associated P-Value for the Cramér-von Mises statistic:
5. Results and Discussion
5.1. Data
In this study, four watersheds were selected for analysis (two agricultural experimental watersheds in Riesel, Texas, and two watersheds from th Cuyahoga River Watershed, Ohio). Two experimental watersheds are located near Riesel (Waco), Texas, and are maintained by Agricultural Research Service (ARS) of the U.S. department of Agriculture (USDA). In what follows, the procedure for selecting rainfall-runoff events from these watersheds is outlined:
- (1)
- Agricultural experimental watershed near Riesel (Waco), Texas:The experimental watersheds near Riesel (Waco) are, W1 and Y2 watersheds [Figure 1(a)] and these were selected based on the watershed area and the length of records maintained. There are multiple raingages in both watersheds, so the Thiessen polygon method was applied to determine daily areal rainfall depth. The Thiessen polygon weights and daily rainfall and corresponding runoff were obtained from the USDA-ARS data warehouse. Furthermore, annual maximum daily rainfall amounts and the resulting daily discharges were applied for rainfall and runoff analysis.
- (2)
- Cuyahoga River Watershed, Ohio:The discharge gages at Old Portage (USGS 04206000) and Independence (USGS 04208000) were selected for analysis. The digital terrain model (DTM) flow lines were obtained from USGS. The watersheds contributing to Old Portage and Independence are delineated in the Geographical Information System (GIS), as shown in Figure 1(b). The raingages within the watersheds were identified from the raingage information maintained by National Oceanic and Atmospheric Administration (NOAA). Again, the Thiessen polygon method was applied to determine the daily areal rainfall. The annual maximum daily rainfall amount and the resulting daily discharge were applied for rainfall and runoff analysis.
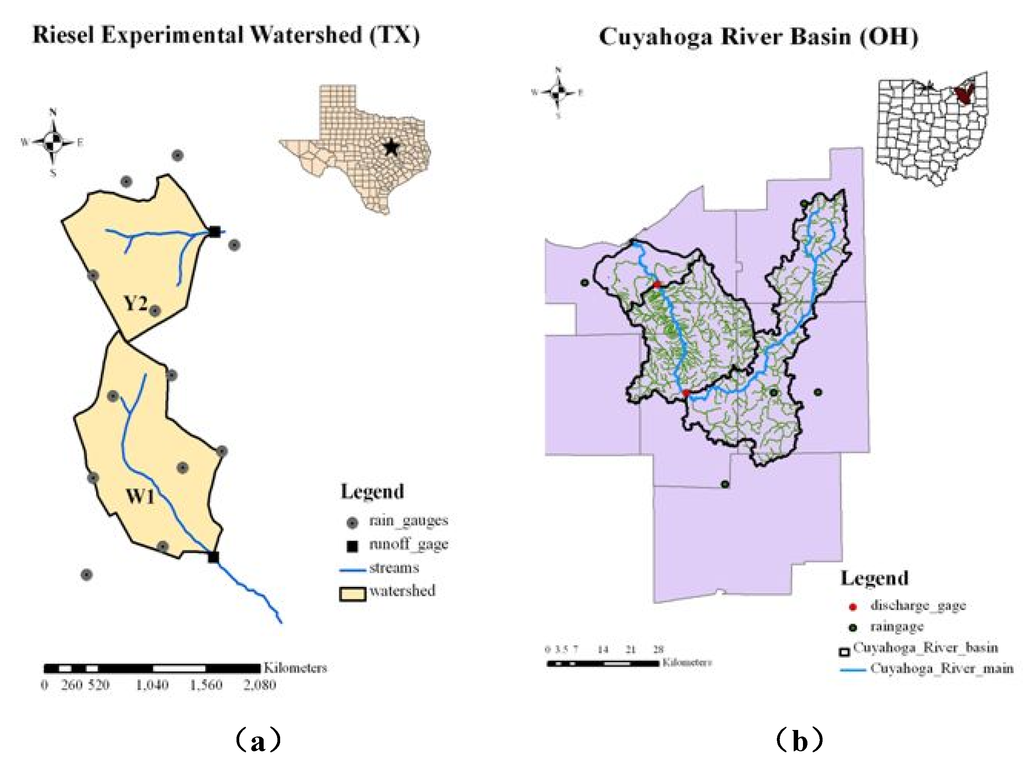
Figure 1.
Riesel experimental watershed and Cuyahoga river watershed maps.
Table 1 lists the pertinent information of the selected watersheds (i.e., drainage area, raingages and length of the record for each watershed). Table 2 lists the Thiessen polygon weight for Old Portage and Independence determined in GIS. This information is further applied to determine the areal rainfall amount at Old Portage and Independence.

Table 1.
Watershed Information.
| Watersheds | Area (km2) | Rain gauge | Duration | |
|---|---|---|---|---|
| Riesel TX | W1 | 0.72 | Rgs: 75a, 89, w1b, w2, w2a, w3, w4, w5a | 1940–2011 |
| Y2 | 0.53 | Rgs: 69, 69b, 70, 75a, 84a | 1940–2011 | |
| Cuyahoga OH | Old Portage (04206000) | 1,046 | Rgs: 330058, 336949, 333780, 331458 | 1953–2011 |
| Independence (04208000) | 1,831 | Rgs: 331657, 330058, 336949, 333780, 331458 | 1953–2011 | |

Table 2.
Thiessen polygon weight for Old Portage and Independence.
| Raingages | Thiessen Polygon Weight | |
|---|---|---|
| Old Portage | Independence | |
| 330058 | 12.18% | 9.82% |
| 336949 | 48.99% | 52.00% |
| 333780 | 4.61% | 2.58% |
| 331458 | 34.22% | 19.16% |
| 331657 | N/A | 16.44% |
5.2. Entropy-Based Univariate Rainfall and Runoff Distributions
As discussed in Section 2, the first moment in the logarithm domain and at least first three non-central moments (Table 3) are needed as constraints to derive the maximum entropy-based univariate distribution for rainfall and runoff random variables with the necessity of fourth non-central moment based on the study of excess kurtosis [Equations (2,3)]. The study of excess kurtosis for rainfall and runoff variables indicates that the fourth non-central moment needs to be considered, except for daily rainfall of Old Portage watershed and daily runoff (discharge) of Independence watershed.

Table 3.
Sample statistics for each watershed.
| Variables | Watershed | E[ln(X)] | E[X] | E[X2] | E[X3] | E[X4] | γ1 | γ2 |
|---|---|---|---|---|---|---|---|---|
| Rainfall (mm) | W1 | 4.40 | 86.02 | 8217.74 | 8.73E+05 | 1.03E+08 | 1.09 | 4.51 |
| Y2 | 4.41 | 86.96 | 8557.03 | 9.58E+05 | 1.21E+08 | 1.30 | 4.83 | |
| Old Portage | 3.77 | 45.71 | 2294.86 | 1.26E+05 | 7.46E+06 | 0.72 | 3.30 | |
| Independence | 3.73 | 43.71 | 2107.30 | 1.12E+05 | 6.55E+06 | 0.98 | 4.24 | |
| Runoff (m3/s) | W1 | −1.51 | 0.34 | 0.18 | 0.13 | 0.11 | 1.15 | 4.58 |
| Y2 | −2.14 | 0.23 | 0.10 | 0.06 | 0.04 | 1.43 | 5.64 | |
| Old Portage | 3.52 | 44.08 | 3146.42 | 3.17E+05 | 3.93E+07 | 1.74 | 5.99 | |
| Independence | 4.58 | 134.27 | 2.88E+04 | 8.02E+06 | 2.61E+09 | 1.16 | 3.76 |
Note: γ1: skewness, γ2: kurtosis.
With the number of the non-central moments identified, the Lagrange multipliers of the PDF defined in Equation (7) were estimated by finding the minimum of the objective function defined in Equation (9) with the constraints and Hessian matrix given by Equations (11a,b). Table 4 lists the parameters estimated for each watershed. Table 5 lists the relative differences between sample moments and those calculated from entropy-based distributions. Table 5 indicates that the sample moments were well preserved.

Table 4.
Lagrange multipliers for univariate rainfall and discharge distribution.
| Variables | Watershed | λ0 | λ1 | λ2 | λ3 | λ4 | λ5 |
|---|---|---|---|---|---|---|---|
| Rainfall (mm) | W1 | 18.36 | 0.46 | −0.58 | 0.007 | −3.77E-05 | 7.09E-08 |
| Y2 | 18.08 | 0.89 | −0.64 | 0.008 | −4.15E-05 | 7.71E-08 | |
| Old portage | 8.60 | 0 | −0.22 | 0.002 | 1.38E-07 | N/A | |
| Independence | 19.28 | −0.57 | −1.01 | 0.026 | −2.60E-04 | 9.69E-07 | |
| Runoff (m3/s) | W1 | −0.74 | 0 | 0.61 | 2.37 | −0.19 | 0.004 |
| Y2 | 0.60 | 0.46 | −3.29 | 7.2 | −0.63 | 0.014 | |
| Old portage | 10.00 | −3.24 | 0.19 | −0.001 | 7.37E-07 | 6.49E-09 | |
| Independence | 5.31 | 0 | 0.001 | 1.58E-05 | 1.67E-10 | N/A |
Note: λ1 parameter for ln(X); λ2 parameter for X; λ3 parameter for X2; λ4 parameter for X3; and λ5 parameter for X4.

Table 5.
Relative differences between sample moments and those obtained from entropy-based distribution.
| Variables | Watersheds | E[ln(X)] | E[X] | E[X2] | E[X3] | E[X4] |
|---|---|---|---|---|---|---|
| Rainfall (mm) | W1 | −2.39E-05 | −8.79E-07 | −8.61E-09 | −5.84E-08 | 3.09E-07 |
| Y2 | −6.33E-05 | −4.51E-06 | −7.51E-08 | −6.13E-08 | −1.97E-08 | |
| Old portage | −6.75E-03 | −9.34E-03 | −1.74E-02 | −4.17E-02 | N/A | |
| Independence | −4.39E-05 | 2.01E-06 | −8.16E-08 | −5.30E-09 | −4.05E-08 | |
| Runoff (m3/s) | W1 | −8.07E-03 | 2.88E-04 | 5.36E-07 | 2.98E-04 | 7.06E-03 |
| Y2 | 5.62E-02 | −3.02E-03 | −1.64E-03 | −3.07E-03 | −2.00E-02 | |
| Old Portage | −9.47E-10 | 1.50E-11 | 5.98E-09 | 1.34E-08 | 2.07E-08 | |
| Independence | −2.34E-02 | −3.57E-03 | −8.31E-03 | −2.90E-02 | N/A |
Further, the goodness-of-fit, i.e., RMSE [Equation (18)], the K-S goodness-of-fit test [Equation (19)], and the A-D goodness-of-fit test [Equation (20)] were applied to examine whether the maximum entropy-based probability distribution may appropriately represent the underlining univariate rainfall and runoff probability distributions. The P-value was approximated using Miller’s approximation for the K-S goodness-of-fit test and Monte Carlo simulation with parametric bootstrap resampling procedure (10,000 parametric bootstrap samples) for the A-D goodness of fit test. The test results in Table 6 indicate that the P-value calculated from both the K-S and A-D goodness-of-fit tests was much higher than the critical level α = 0.05. So the null hypothesis cannot be rejected, that is, the maximum entropy-based probability distribution can appropriately represent the univariate rainfall/runoff probability distributions. The RMSE results in Table 6 show that the corresponding error is also small. In addition, to compare graphically, the maximum entropy-based PDF is compared with the frequency histograms (Figure 2 and Figure 3), which indicate the proposed maximum entropy-based probability density function is able to capture the shape of the frequency histogram.

Table 6.
Goodness-of-fit statistics for univariate rainfall and discharge analysis.
| Variables | Watersheds | K-S Statistics | AD statistics | RMSE | ||||
|---|---|---|---|---|---|---|---|---|
| H* | Statistics | P-value | H* | Statistics | P-Value | |||
| Rainfall (mm) | W1 | 0 | 0.07 | 0.92 | 0 | 0.19 | 0.99 | 3.49 |
| Y2 | 0 | 0.07 | 0.89 | 0 | 0.23 | 0.98 | 3.62 | |
| Old portage | 0 | 0.10 | 0.64 | 0 | 0.66 | 0.60 | 2.99 | |
| Independence | 0 | 0.08 | 0.81 | 0 | 0.37 | 0.88 | 2.03 | |
| Runoff (m3/s) | W1 | 0 | 0.08 | 0.77 | 0 | 0.53 | 0.71 | 6.22 |
| Y2 | 0 | 0.06 | 0.97 | 0 | 0.61 | 0.64 | 6.84 | |
| Old portage | 0 | 0.08 | 0.78 | 0 | 0.39 | 0.86 | 4.70 | |
| Independence | 0 | 0.08 | 0.79 | 0 | 0.57 | 0.67 | 15.83 | |
* The null hypothesis cannot be rejected if H = 1.
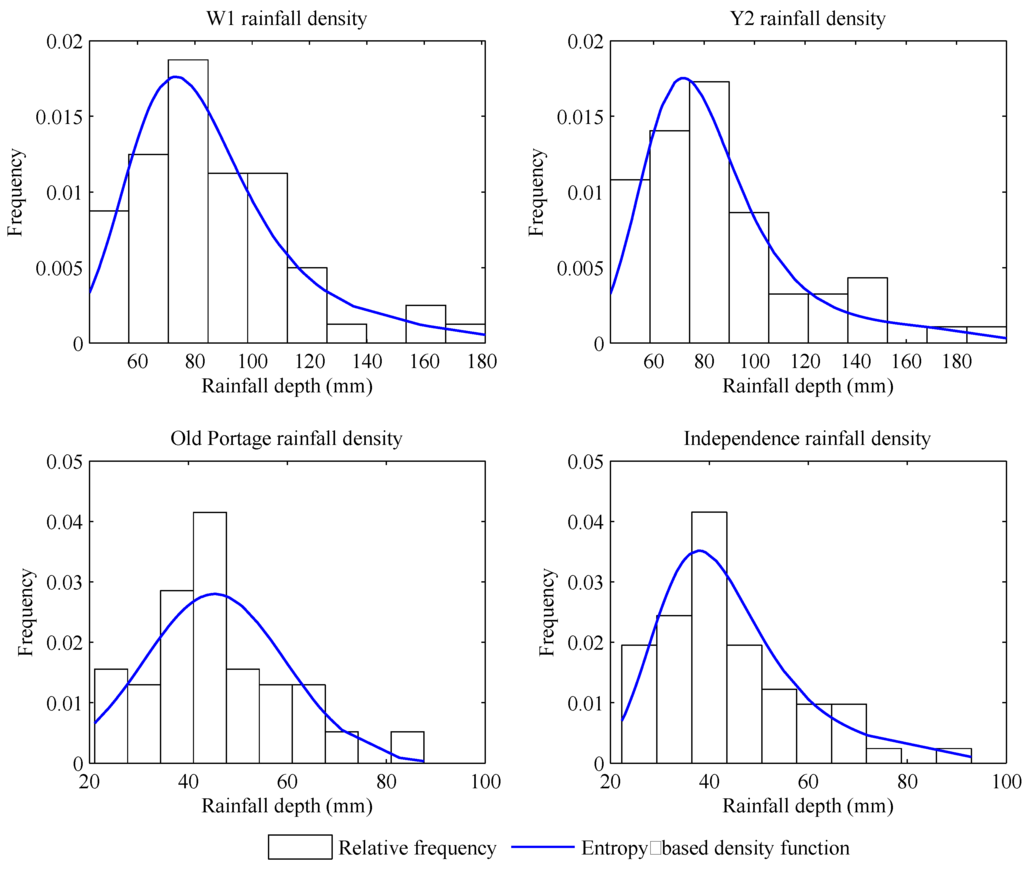
Figure 2.
Rainfall depth probability density function.
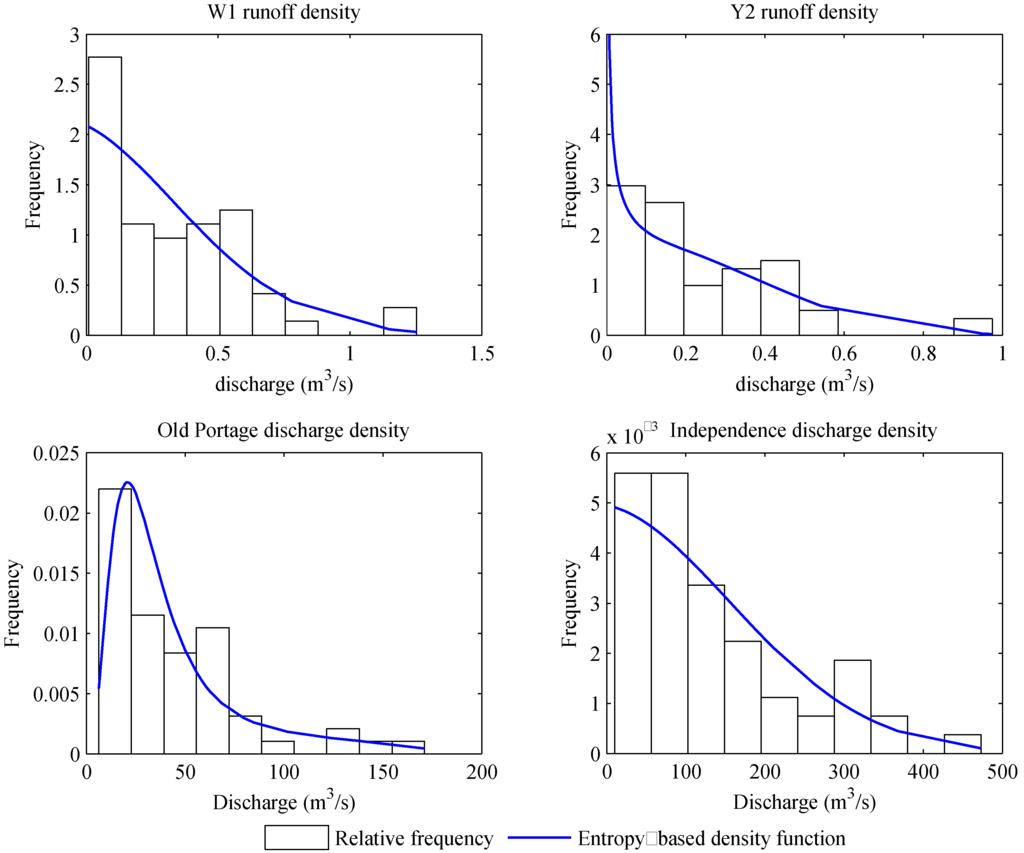
Figure 3.
Discharge probability density function.
Thus, from both the formal goodness-of-fit statistics and graphical comparison for univariate rainfall and runoff random variables, the univariate entropy-based distribution derived represents the PDF of rainfall and runoff variables well. It is worth stating that the appropriate identification of univariate rainfall and runoff distribution plays an important role in the study of joint and conditional return period in case of extreme behavior of rainfall and runoff variables.
5.3. Bivariate Rainfall and Runoff Distribution
Considering rainfall and runoff as continuous random variables, the copula theory was applied to capture the dependence with a unique copula function C [Equation (12)]. Table 7 lists sample Kendall’s τ and Spearman’s ρ rank coefficients of correlation. Results showed that overall there existed positive dependence structure for all the watersheds studied. It is therefore appropriate to apply the copula functions listed in Appendix I. The parameters of the copula function were estimated using the Pseudo-Maximum Likelihood method in which the empirical marginal distribution was applied. Table 8 lists the parameters estimated and the corresponding maximum Log-Likelihood (LL). Table 8 indicates that Galambos copula, belonging to the extreme value copula family, reached the largest maximum LL for watersheds W1, Y2 and Old Portage. However, the Frank copula reached the largest maximum LL for Independence watershed.

Table 7.
Rank correlation of coefficients for rainfall and discharge variables.
| Watersheds | Kendall’s tau | Spearman’s rho |
|---|---|---|
| W1 | 0.454 | 0.632 |
| Y2 | 0.475 | 0.646 |
| Old Portage | 0.276 | 0.394 |
| Independence | 0.397 | 0.564 |

Table 8.
Estimated copula parameters for bivariate rainfall and discharge analysis.
| Copula | Estimated parameters | Likelihood | Estimated parameters | Likelihood |
|---|---|---|---|---|
| W1 | Y2 | |||
| Clayton | 0.85 | 7.10 | 0.88 | 6.93 |
| Gumbel-Hougaard | 1.73 | 13.98 | 1.86 | 17.16 |
| Frank | 4.40 | 12.26 | 4.55 | 12.92 |
| Joe | 2.10 | 13.56 | 2.42 | 17.02 |
| A12 | 1.17 | 8.44 | 1.24 | 9.38 |
| BB1[a] | (8.65E-6, 1.73) | 13.98 | (2.03E-4, 1.86) | 17.15 |
| BB5[b] | (1.21, 0.73) | 14.52 | (1.47, 0.54) | 17.21 |
| BB7[c] | (1, 0.85) | 7.10 | (1, 0.88) | 6.93 |
| Galambos | 1.04 | 14.54 | 1.16 | 17.30 |
| Plackett | 6.03 | 11.38 | 7.08 | 12.72 |
| Old Portage | Independence | |||
| Clayton | 0.62 | 4.30 | 0.96 | 8.55 |
| Gumbel-Hougaard | 1.39 | 5.64 | 1.52 | 7.79 |
| Frank | 2.64 | 4.92 | 4.15 | 10.71 |
| Joe | 1.53 | 4.83 | 1.63 | 5.29 |
| A12 | 1 | 2.97 | 1.05 | 8.65 |
| BB1 | (0.20, 1.29) | 5.89 | (0.57, 1.24) | 9.20 |
| BB5 | (1.06, 0.60) | 6 | (1.19, 0.53) | 8.22 |
| BB7 | (1, 0.62) | 4.30 | (1, 0.96) | 8.55 |
| Glambos | 0.67 | 6.02 | 0.80 | 8.22 |
| Plackett | 3.28 | 4.81 | 5.83 | 10.23 |
Note: [a] when θ1 → 0 converge to Gumbel-Hougaard copula; [b] when θ1 = 1 BB5 copula is Galambos copula; [c] whenθ1 = 1 BB7 copula is the Clayton copula.
In order to better assess the copula functions estimated using the Pseudo-Maximum Likelihood method, the formal goodness-of-fit analysis was performed to test whether the given copula function may appropriately model the joint distribution using the goodness-of-fit test based on the integral probability transformation discussed in Section 4. The Cramér-von Mises test statistic was calculated using Equations (21–23). The corresponding P-value was approximated using Equations (24–26) with 10,000 parametric bootstrap samples. Table 9 lists the test statistics and the corresponding P-values forall the copula functions studied. It indicates: (i) the copula functions, reaching the maximum LL, can appropriately measure the full dependence of the rainfall and runoff variables, (ii) for the Independence watershed, the Plackett copula reached a much higher P-value than did the Frank copula, and there exists minimal differences for the maximum LL calculated from the Frank and Plackett copulas (4.5%). Thus, the Galambos copula can be applied to represent the joint distribution for W1, Y2 and Old Portage watersheds, and the Plackett copula can be applied to represent the joint distribution for Independence watershed. Figure 4 and Figure 5 compare the empirical PDF (CDF) and the parametric PDF (CDF) determined from the fitted copula function for experimental watersheds, i.e., W1 and Y2, and Cuyahoga River watershed, i.e., Old Portage and Independence. The figures indicate that: (i) there clearly exists an upper tail dependence for experimental watersheds W1 and Y2 (joint PDF in Figure 4), (ii) the upper tail dependence for Old portage is not as significant as that of experimental watersheds, and (iii) there is no clear evidence of upper tail dependence for Independence which is an interesting finding through the study of the annual maximum daily rainfall amount and corresponding daily discharge. The findings for watersheds at Old Portage and Independence may be explained by the natural flow of the stream affected by flow diversion, storage reservoirs, and power plants located in the watersheds (USGS).

Table 9.
Goodness-of-fit statistics for copulas.
| Copula | Goodness-of-fit statistics | |||
|---|---|---|---|---|
| Sn | P-value | Sn | P-value | |
| W1 | Y2 | |||
| Clayton | 0.19 | 0.05 | 0.21 | 0.04 |
| Gumbel-Hougaard | 8.57 | 0.59 | 8.72 | 0.52 |
| Frank | 0.05 | 0.63 | 0.08 | 0.33 |
| Joe | 0.07 | 0.50 | 0.03 | 0.93 |
| A12 | 0.15 | 0.07 | 0.20 | 0.02 |
| BB1 | 0.05 | 0.78 | 0.06 | 0.52 |
| BB5 | 7.74 | 0.44 | 7.71 | 0.54 |
| BB7 | 8.48 | 0 | 8.40 | 0 |
| Galambos | 7.70 | 0.52 | 7.64 | 0.72 |
| Plackett | 8.10 | 0.05 | 8.03 | 0.10 |
| Old Portage | Independence | |||
| Clayton | 0.06 | 0.75 | 0.14 | 0.15 |
| Gumbel-Hougaard | 5.49 | 0.45 | 5.49 | 0.45 |
| Frank | 0.06 | 0.64 | 0.07 | 0.42 |
| Joe | 0.12 | 0.26 | 0.30 | 0.01 |
| A12 | 0.13 | 0.22 | 0.11 | 0.23 |
| BB1 | 0.05 | 0.80 | 0.10 | 0.19 |
| BB5 | 8.15 | 0.06 | 7.89 | 0.24 |
| BB7 | 8.96 | 0 | 7.92 | 0 |
| Galambos | 7.52 | 0.81 | 7.95 | 0.19 |
| Plackett | 7.83 | 0.30 | 7.51 | 0.82 |
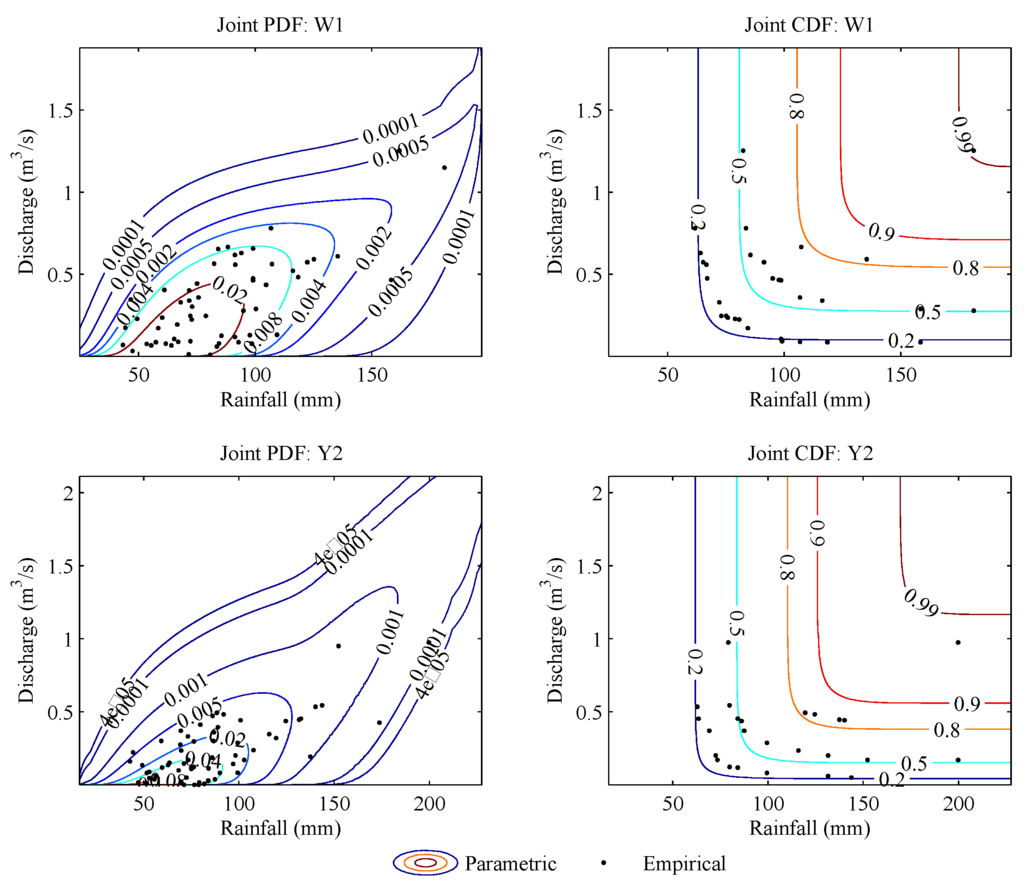
Figure 4.
Comparison of empirical PDF and CDF versus parametric PDF and CDF of the best fitted copula function for experimental watersheds: W1 and Y2.
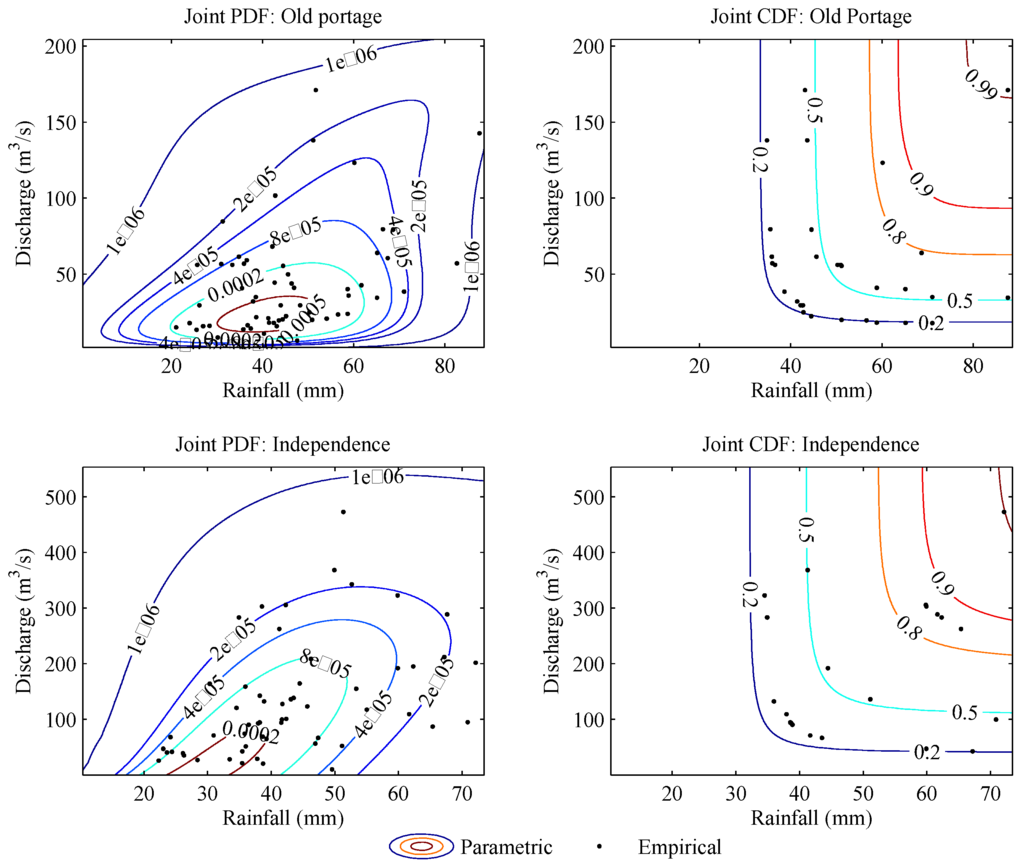
Figure 5.
Comparison of empirical PDF and CDF versus parametric PDF and CDF of the best fitted copula function for Cuyahoga River watershed: Old Portage and Independence.
To further assess the above findings numerically, the upper tail dependence coefficient was calculated from both the empirical copula and the copula function candidates (Appendix II). Equations (14a–c) were applied to determine the upper tail dependence coefficient nonparametrically from the empirical copula where the thresholds k in Equations (14a,b) were determined by applying the plateau-finding algorithm [10]. The equations listed in Appendix II were applied to determine the upper tail dependence coefficient for the copula functions. Table 10 lists the results of the upper tail dependence coefficient. It shows that the differences are relatively small from the nonparametric estimation (the maximum relative difference being around 10% comparing Equations (14a,b) with Equation (14c) for W1, Y2 and Old Portage watersheds. For Independence watershed, the upper tail dependence coefficient was estimated to be close to 0 from Equations (14a,b), however it reached around 0.43 if Equation (14c) was applied. Again comparing with the graphical finding (Figure 5), Equation (14c) cannot be applied to estimate the upper tail dependence coefficient for Independence watershed, due to the strong underlining assumption of empirical copula approximating the extreme value copula.
To this end, the conclusion is that the extreme value copula can be applied to assess the upper tail dependence for W1, Y2 and Old Portage watersheds uwing the Galambos copula. No upper tail dependence was found for Independence watershed and the Plackett copula can be reasonably applied. Thus, in what follows, the Galambos and Plackett copula were applied to study the joint (and conditional) return periods.

Table 10.
Estimated upper tail dependence coefficient.
| Tail dependence | LOG [a] | SEC[a] | CFG[b] | LOG | SEC | CFG |
|---|---|---|---|---|---|---|
| W1 | Y2 | |||||
| Empirical | 0.53 | 0.56 | 0.50 | 0.58 | 0.58 | 0.56 |
| Clayton | 0 | 0 | ||||
| Gumbel-Hougaard | 0.51 | 0.55 | ||||
| Frank | 0 | 0 | ||||
| Joe | 0.61 | 0.67 | ||||
| A12 | 0.19 | 0.25 | ||||
| BB1 | 0.51 | 0.55 | ||||
| BB5 | 0.51 | 0.55 | ||||
| BB7 | 0 | 0 | ||||
| Galambos | 0.51 | 0.55 | ||||
| Placektt | 0 | 0 | ||||
| Old Portage | Independence | |||||
| Empirical | 0.36 | 0.32 | 0.35 | −0.01 | 0.02 | 0.43 |
| Clayton | 0 | 0 | ||||
| Gumbel-Hougaard | 0.35 | 0.42 | ||||
| Frank | 0 | 0 | ||||
| Joe | 0.43 | 0.47 | ||||
| A12 | 0 | 0.07 | ||||
| BB1 | 0.29 | 0.25 | ||||
| BB5 | 0.36 | 0.42 | ||||
| BB7 | 0 | 0 | ||||
| Galambos | 0.36 | 0.42 | ||||
| Plackett | 0 | 0 | ||||
Note: [a] with b = 1 with threshold; [b] no threshold needed.
5.4. Return Period of Rainfall and Runoff Events
In rainfall and runoff frequency analysis as well as other multivariate hydrologic frequency analyses, the purpose is to estimate the joint and conditional return period (joint and conditional exceedance probabilities) of the extreme events for risk analysis and to provide a framework for engineering design. Following the discussion in Section 3.4, the rainfall and runoff events with given joint and conditional return periods were studied.
5.4.1. Joint Return Period of Rainfall and Runoff Events
The joint return period (i.e., 25-, 50-, and 100-yr) for the “AND” case was determined following [32] using the most-likely design realization [Equation (15)] discussed in Section 3.4.1. Using Old Portage watershed as an example, Figure 6 shows the procedure for the identification of critical layer and the corresponding rainfall and runoff event (x*, y*). Considering the Galambos copula belonging to the extreme value copula family, the parametric Kendall distribution is given as:
where θ is the parameter, i.e., Kendall correlation of coefficient.
Graphically, it is seen that the empirical Kendall distribution matches the parametric Kendall distribution function for the Galambos copula fairly well especially for the upper tail (Figure 6a). Figure 6b provides the graphical link for the identification of t which results in the joint K(t) being equal to the nonexceedance probability of 25-, 50-, and 100-year joint return periods. The identified t’s are the cumulative probability for the identified critical layer shown in Figure 6c. Using 100-year joint return period as an example, Figure 6d plots the negative log-likelihood of function [Equation (15b)]. The critical event is then estimated by finding the minimum of the negative log-likelihood function. It is worth noting that in case of the Plackett copula applied to the Independence watershed, the Kendall distribution of the Plackett copula needs to be estimated using Monte Carlo simulation with the parametric bootstrap sampling technique as discussed in Section 4.2.
Table 11 lists the critical rainfall and runoff events with joint return period of 25-, 50-, and 100-year. The joint return period study indicates that the rainfall and runoff variables for all four watersheds are positively quadrant dependent (PQD) [28] as:
or equivalently:
and for illustration purposes, for Old Portage watershed, the exceedance probabilities for rainfall events with joint return periods of 25-, 50-, and 100-year are 0.05, 0.02, and 0.01; the right side of Equation (28a) is calculated as: 0.023, 0.004 and 0.001, respectively.
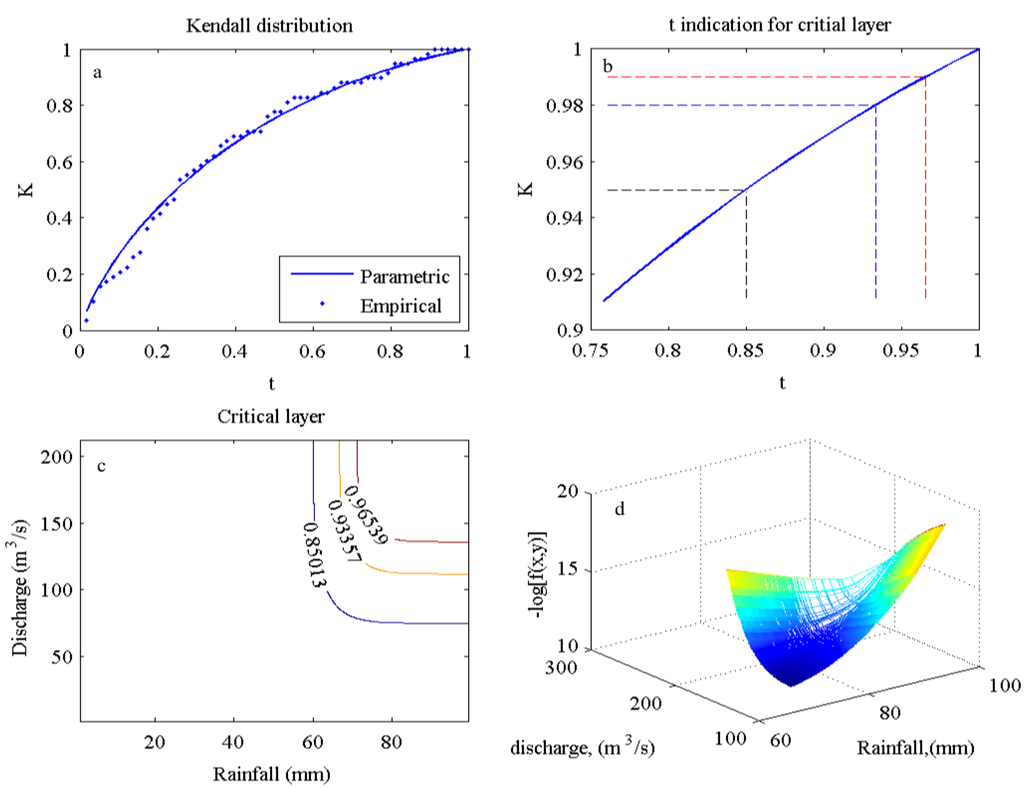
Figure 6.
(a) Kendall distribution plot, (b,c) critical layer identification for 50- and 100-year event, (d) critical rainfall and runoff event for return period = 100-year as example.

Table 11.
Rainfall (mm) and runoff (m3/s) estimated for ‘AND’ case for the return period of 25-, 50-, and 100-year.
| Joint return period | 25-year | 50-year | 100-year | |||
|---|---|---|---|---|---|---|
| Rainfall | Runoff | Rainfall | Runoff | Rainfall | Runoff | |
| W1 | 122.13 | 0.69 | 145.79 | 0.88 | 161.27 | 1.01 |
| Y2 | 126.06 | 0.51 | 157.31 | 0.66 | 176.19 | 0.84 |
| Old Portage | 60.09 | 74.75 | 66.75 | 111.8 | 71.25 | 135.94 |
| Independence | 54.59 | 237.13 | 60.84 | 296.35 | 64.38 | 329.38 |
5.4.2. Conditional Return Period of Runoff Events of Given Rainfall Events
As discussed in Section 3.4.2, both cases were studied for conditional return period analysis. The critical runoff events (y*) of given conditional return periods are estimated from daily rainfall amount. Table 12 lists the daily rainfall amount with univariate return period of 25-, 50-, and 100-year estimated from fitted entropy-based univariate distribution. Then the conditional return period of Case I (i.e., was estimated using Equation (16) and that of Case II (i.e., is estimated using Equation (17). Table 13 lists the runoff events obtained for Cases I and II with the conditional return periods of 25-, 50-, and 100-year.

Table 12.
25-, 50-, and 100-year daily rainfall amount (mm) from univariate frequency analysis.
| Watersheds | Return period | ||
|---|---|---|---|
| 25-year | 50-year | 100-year | |
| W1 | 142.87 | 163.59 | 174.83 |
| Y2 | 155.04 | 178.58 | 189.97 |
| Old Portage | 68.75 | 74.57 | 78.44 |
| Independence | 64.72 | 69.37 | 71.31 |

Table 13.
Daily Runoff (m3/s) estimated based on Cases I and II for the return period of 50- and 100-year with 50- and 100-year daily rainfall amount (mm).
| Watersheds | Return period | ||
|---|---|---|---|
| 25-year | 50-year | 100-year | |
| Case I | |||
| W1 | 1.37 | 1.64 | 1.8 |
| Y2 | 1.1 | 1.32 | 1.46 |
| Old Portage | 183.09 | 202.49 | 212.28 |
| Independence | 429.12 | 481.02 | 508.52 |
| Case II | |||
| W1 | 1.14 | 1.36 | 1.51 |
| Y2 | 0.89 | 1.08 | 1.21 |
| Old Portage | 164.54 | 186.32 | 198.06 |
| Independence | 417.64 | 477.16 | 507.03 |
Using Old Portage as an example, Figure 7 plots the conditional exceedance probabilities for both cases. Figure 7 indicates that Equation (16) and Equations (17) are nondecreasing functions of given rainfall event for all runoff events. It further indicates that rainfall and runoff variables hold right tail increasing (RTI, for case I) and stochastic increasing (SI, for case II) properties. The same results are reached for the other two watersheds modeled by the Galambos copula as well (i.e., W1, Y2).
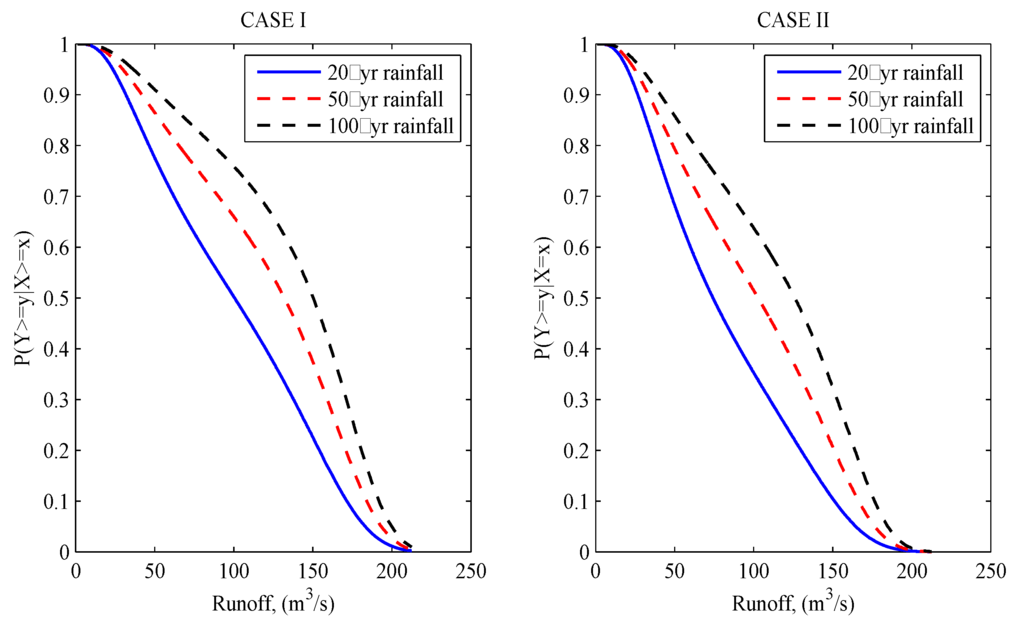
Figure 7.
Conditional exceedance probability estimated for Cases I and II with watershed Old Portage as an example.
On the other hand, Figure 8 plots the conditional exceedance probabilities for Independence watershed. One may note the minimal difference in exceedance probabilities (return periods) obtained by conditioning on the rainfall events of different return periods for cases I and II. This finding again indicates the RTI and SI properties do not hold for Independence watershed.
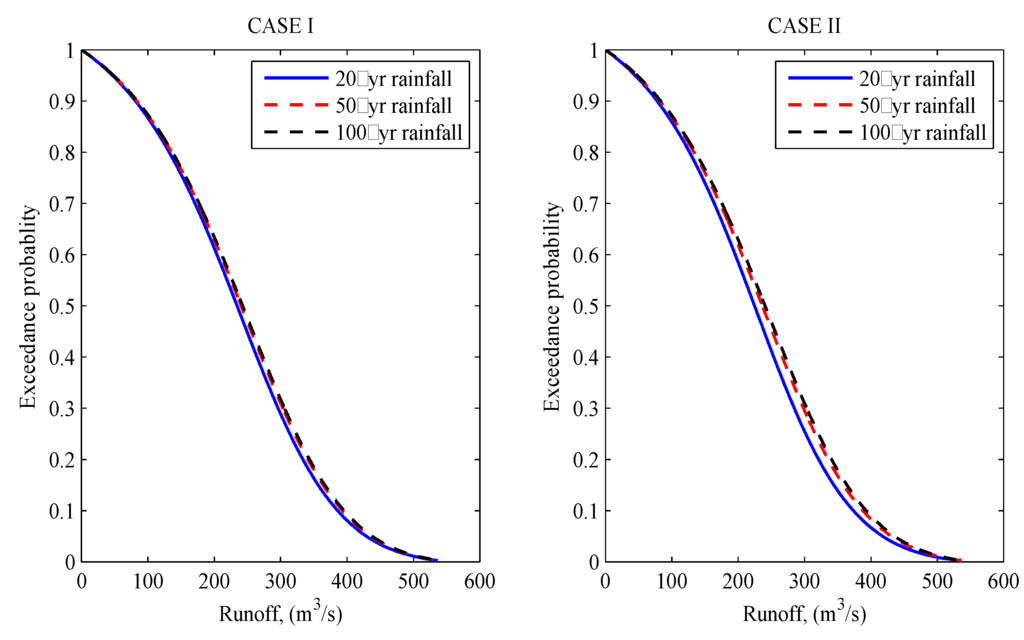
Figure 8.
Conditional exceedance probability for Cases I and II with watershed Independence as an example.
6. Conclusions
This study investigates the relationship between annual maximum daily rainfall amount and the corresponding daily runoff (discharge) using maximum entropy and copula theories to address the questions arising from the assumptions in the commonly applied approaches and to better estimate risk. The maximum entropy theory is applied to derive the univariate rainfall and runoff distributions. The joint distribution of rainfall and runoff is studied using the copula method. The following conclusions are drawn from the study:
- (1)
- The rainfall and runoff variables are fat tailed except for rainfall variable at Old Portage and runoff variable at Independence. Thus, except for these two cases, the fourth non-central moment is necessary to be considered as one of the constraints for the derivation of maximum entropy-based distribution. The maximum entropy-based univariate distribution can successfully model the rainfall and runoff variables, and it also provides the universal solution for the univariate rainfall and runoff frequency analysis.
- (2)
- The copula functions capturing the positive dependence structure may appropriately model the bivariate rainfall and runoff distribution. The Galambos copula (belonging to extreme value copula family) appropriately models the dependence between rainfall and runoff variables for watersheds W1, Y2 and Old Portage based on the MLE and formal goodness-of-fit statistics. Similarly, the Plackett copula appropriately models the dependence for watershed Independence.
- (3)
- Upper tail dependence is found for watersheds W1, Y2, and Old Portage, and the nonparametric/parametric estimation of upper tail dependence coefficient indicates that the Galambos copula may again model the extreme events which in turn can be applied to study the joint and conditional return periods for these 3 watersheds.
- (4)
- No upper tail dependence is found for watershed Independence. It may be explained by the natural flow of the stream affected by diversion, storage reservoirs and power plants located in the watersheds. The fitted Plackett copula can be applied to study the joint and conditional return periods for watershed Independence.
- (5)
- The positive dependence structure and joint return period (“AND” case) study of the rainfall and runoff variables show that rainfall and runoff are positive quadrant dependent.
- (6)
- For watersheds W1, Y2, and Old Portage, Case I conditional return period indicates the right tail increasing (RTI) property, and Case II conditional return period indicates the stochastic increasing (SI) property. These findings are in agreement with the upper tail dependence identified for the above three watersheds.
- (7)
- For watershed Independence, Case I and II conditional return periods indicate that there does not exist RTI or SI (i.e., with given rainfall events of different return periods, the conditional exceedance probability exhibits minimal difference). This finding is in agreement with no upper tail dependence found for the watershed.
In summary, the study provides an appropriate framework to link the maximum entropy theory and copula theory in multivariate frequency analysis. This framework may lead to a better study of both univariate and multivariate studies and permit a better estimation of risk and better engineering design (e.g., runoff of a given rainfall event in this study). With different types of watersheds, the study shows that for experimental watersheds (well maintained and minimal human activity induced changes), the dependence and tail dependence structure between rainfall and runoff variables tend to follow the law of natural rainfall and runoff process. For the watersheds Old Portage and Independence belonging to Cuyahoga River basin, even though the positive dependence structure still holds for the whole dataset analyzed, the upper tail dependence is significantly lower. In case of watershed Old Portage, the upper tail dependence is in the range of [0.3, 0.4], and for Independence, there is no upper tail dependence existing. This may be explained by the intensity of human activity induced hydrological response changes. This finding provides an insight that one needs to pay attention to the real world situation when applying the copulas belonging to extreme value copula family (e.g., commonly applied Gumbel-Houggard copula as an example) to study the annual maximum multivariate hydrological time series.
Appendix I

Table S1.
Selected copula family for analysis.
| Copulas | Parameters | ||
|---|---|---|---|
| One-parameter Archimedean Copula[b] | Clayton | ||
| Gumbel-Hougaard[a] | |||
| Frank | |||
| Joe[c] | |||
| A12 | |||
| Two-parameter Archimedean Copula[c] | BB1 | ||
| BB5 | |||
| BB7 | |||
| Extreme value Copula | Galambos | ||
| Others | Plackett | ||
Note: [a] also belongs to the extreme value copula; [b] refer to [44]; [c] refer to [49].
Appendix II

Table S2.
Tail dependence coefficient for different copulas.
| Copulas | UTD | LTD | |
|---|---|---|---|
| One-parameter Archimedean copula | Clayton | 0 | |
| Frank | 0 | 0 | |
| Joe | 0 | ||
| Gumbe-Hougaard | 0 | ||
| A12 | |||
| Two-parameter Archimedean copula | BB1 | ||
| BB5 | 0 | ||
| BB7 | |||
| Extreme value copula | Galambos | 0 | |
| Others | Plackett | 0 | 0 |
References
- Haan, C.T.; Wilson, B.N. Another look at the joint probability of rainfall and runoff. In Hydrologic Frequency Modeling, Proceedings of the International Symposium on Flood Frequency and Risk Analyses, Baton Rouge, LA, USA, May 1986; D. Reidel Publishing Company: Boston, MA, USA, 1987; pp. 555–569. [Google Scholar]
- Singh, K.; Singh, V.P. Derivation of bivariate probability density functions with exponential marginals. Stoch. Hydrol. Hydraul. 1991, 5, 55–68. [Google Scholar] [CrossRef]
- Yue, S.; Ouarda, T.B.M.J.; Bobée, B.; Legendre, P.; Bruneau, P. The Gumbel mixed model for flood frequency analysis. J. Hydrol. 1999, 226, 88–100. [Google Scholar] [CrossRef]
- Yue, S. A bivariate extreme value distribution applied to flood frequency analysis. Nord. Hydrol. 2001, 32, 49–64. [Google Scholar]
- Yue, S. The bivariate lognormal distribution to model a multivariate flood episode. Hydrol. Processes 2001, 14, 2575–2588. [Google Scholar] [CrossRef]
- Bárdossy, A.; Pegram, G.G.S. Copula based multisite model for daily precipitation simulations. Hydrol. Earth Syst. Sci. 2009, 13, 2299–2314. [Google Scholar] [CrossRef]
- Evin, G.; Favre, A.-C. A new rainfall model based on the Neyman-Scott process using cubic copulas. Water Resour. Res. 2008, 44, W03433. [Google Scholar] [CrossRef]
- De Michele, C.; Salvadori, G.; Canossi, M.; Petaccia, A.; Rosso, R. Bivariate statsitical approach to check adequacy of dam spillway. J. Hydro. Eng. 2005, 10, 1084–0699. [Google Scholar]
- Favre, A.-C.; Adlouni, E.; Perreault, L.; Monge, N.T.; Bobée, B. Multivariate hydrological frequency analysis using copulas. Water Resour. Res. 2004, 40, W01101. [Google Scholar] [CrossRef]
- Genest, C.; Favre, A.-C.; Béliveau, J.; Jacques, C. Metaelliptical copulas and their use in frequency analysis of multivariate hydrological data. Water Resour. Res. 2007, 43, W09401. [Google Scholar] [CrossRef]
- Genest, C.; Favre, A.-C. Everything you always wanted to know about copula modeling but were afraid to ask. J. Hydro. Eng. 2007, 12, 347–368. [Google Scholar] [CrossRef]
- Grimaldi, S.; Serinaldi, F. Asymmetric copula in multivariate flood frequency analysis. Adv. Water resour. 2006, 29, 1155–1167. [Google Scholar] [CrossRef]
- Kao, S.-C.; Govindaraju, R.S. A Bivariate frequency analysis of extreme rainfall with implications for design. J. Geophys. Res. 2007, 112, D13119. [Google Scholar] [CrossRef]
- Kao, S.-C.; Govindaraju, R.S. Probabilistic structure of storm surface runoff considering the dependence between average intensity and storm duration of rainfall events. Water Resour. Res. 2007, 43, W06410. [Google Scholar] [CrossRef]
- Serinaldi, F.; Bonaccroso, B.; Cancelliere, A.; Grimaldi, S. Probabilistic characterization of drought properties through copulas. J. Phys. Chem. Earth 2009, 34, 596–605. [Google Scholar] [CrossRef]
- Song, S.; Singh, V.P. Meta-elliptical copulas for drought frequency analysis of periodic hydrologic data. Stoch. Environ. Res. Risk Assess 2010, 24, 425–444. [Google Scholar] [CrossRef]
- Song, S.; Singh, V.P. Frequency analysis of droughts using the Plackett copula and parameter estimation by genetic algorithm. Stoch. Environ. Res. Risk Assess 2010, 24, 783–805. [Google Scholar] [CrossRef]
- Vandenberghe, S.; Verhoest, N.E.C.; de Baets, B. Fitting bivariate copulas to the dependence structure between storm characteristics: A detailed analysis based on 105 year 10 min rainfall. Water Resour. Res. 2010, 46, W01512. [Google Scholar] [CrossRef]
- Vandenberghe, S.; Verhoest, N.E.C.; Onof, C.; de Baets, B. A comparative copula-based bivariate frequency analysis of observed and simulated storm events: A case study on Bartlett-Lewis modeled rainfall. Water Resour. Res. 2011, 47, W07529. [Google Scholar] [CrossRef]
- Wang, C.N.; Chang, N.-B.; Yeh, G.-T. Copula-based flood frequency (COEF) analysis at the confluences of river systems. Hydrol. Process. 2009, 23, 1471–1486. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Bivariate flood frequency analysis using the copula method. J. Hydrol. Eng. 2006, 11, 150–164. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Bivariate rainfall frequency distributions using Archimedean copulas. J. Hydrol. 2007, 332, 93–109. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Gumbel-Hougaard copula for trivariate rainfall frequency analysis. J. Hydrol. Eng. 2007, 12, 409–419. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Trivariate flood frequency analysis using the Gumbel-Hougaard copula. J. Hydrol. Eng. 2007, 12, 431–439. [Google Scholar] [CrossRef]
- Agrawal, D.; Singh, J.K.; Kumar, A. Maximum Entropy-based Conditional Probability Distribution Runoff Model. Biosystem Eng. 2005, 90, 103–113. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P. Single-site monthly streamflow simulation using entropy theory. Water Resour. Res. 2011, 47, W09528. [Google Scholar] [CrossRef]
- Krstanovic, P.F.; Singh, V.P. A Real-Time Flood Forecasting Model Based on Maximum-Entropy Spectral Analysis: I. Development. Water Resour. Mgmt. 1993, 7, 109–129. [Google Scholar] [CrossRef]
- Krstanovic, P.F.; Singh, V.P. A Real-Time Flood Forecasting Model Based on Maximum-Entropy Spectral Analysis: II. Application. Water Resour. Mgmt. 1993, 7, 131–151. [Google Scholar] [CrossRef]
- Singh, V.P.; Krstanovic, P.F. A stochastic model for sediment yield using the principle of maximum entropy. Water Resour. Res. 1987, 23, 78l–793. [Google Scholar] [CrossRef]
- Chang, T.P. Wind speed and power density analysis based on mixture weibull and maximum entropy distributions. Int. J. Appl. Sci. Eng. 2010, 8, 39–46. [Google Scholar]
- Papalexiou, S.M.; Koutsoyiannis, D. Entropy based derivation of probability distributions: A case study to daily rainfall. Adv. Water Resour. 2012, 45, 51–57. [Google Scholar] [CrossRef]
- Singh, V.P. Entropy-Based Parameter Estimation in Hdyrology; Kluwer Academic Publishers: Boston, MA, USA, 1998. [Google Scholar]
- Singh, V.P. Entropy theory for derivation of infiltration equations. Water Resour. Res. 2010, 46, W03527. [Google Scholar] [CrossRef]
- Singh, V.P. Entropy theory for movement of moisture in soils. Water Resour. Res. 2010, 46, W03516. [Google Scholar] [CrossRef]
- Singh, V.P. Derivation of rating curves using entropy theory. Trans. ASABE 2010, 53, 1811–1821. [Google Scholar]
- Singh, V.P. Hydrologic synthesis using entropy theory: Review. J. Hydrol. Eng. 2011, 16, 421–433. [Google Scholar] [CrossRef]
- Shannon, C.E. The mathematical theory of communications. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Jaynes, E. Information theory and statistical mechanics, I. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Jaynes, E. Information theory and statistical mechanics, II. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Kapur, J.N. Maximum Entropy Models in Science and Engineering, 1st ed.; John Wiley & Sons INC.: New York, NY, USA, 1989. [Google Scholar]
- Kapur, J.N.; Kesavan, H.K. Entropy Optimization Principles with Applications, 1st ed.; Academic Press: Boston, MA, USA, 1992. [Google Scholar]
- Zellner, A.; Highfield, R.A. Calculation of maximum entropy distributions and approximation of marginal posterior distributions. J. Econometrics 1988, 37, 95–209. [Google Scholar] [CrossRef]
- Sklar, A. Fonctions de repartition à n dimensions et leurs marges. Publ. Inst. Statist. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas, 2nd ed.; Springer Science+Business Media, Inc: New York, NY, USA, 2006. [Google Scholar]
- Poulin, A.; Huard, D.; Favre, A.-C.; Pugin, S. Important of tail dependence in bivariate frequency analysis. J. Hydrol. Eng. 2007, 12, 394–403. [Google Scholar] [CrossRef]
- Abberger, K. A simple graphical method to explore tail dependence in stock-return pairs. Appl. Financial Economics 2005, 15, 43–51. [Google Scholar] [CrossRef]
- Frahm, G.; Junker, M.; Schmidt, R. Estimating the tail dependence coefficient: properties and pitfalls. Insur. Math. Econ. 2005, 37, 80–100. [Google Scholar] [CrossRef]
- Cole, S.; Heffernan, J.; Tawn, J. Dependence measures for extreme value analysis. Extremes 1999, 2, 339–365. [Google Scholar] [CrossRef]
- Joe, H. Multivariate Models and Dependence Concepts, 1st ed.; Chapman & Hall/CRC: New York, USA, 1997. [Google Scholar]
- Capéraà, P.; Fougéres, A.-L.; Genest, C. Bivariate distributions with given extreme value attractor. J. Multivariate Anal. 1997, 72, 567–577. [Google Scholar] [CrossRef]
- Salvadori, G.; de Michele, C.; Durante, F. On the return period and design in a multivariate framework. Hydrol. Earth Syst. Sci. 2011, 15, 3293–3305. [Google Scholar] [CrossRef]
- Miller, L.H. Table of percentage points of Kolmogorov statistics. J. Am. Stat. Assoc. 1956, 51, 111–121. [Google Scholar] [CrossRef]
- NIST. Engineering statistics handbook. Available online: http://www.itl.nist.gov/div898/handbook/ (accessed on 12 May 2012).
- Genest, C.; Quessy, J.-F.; R Rémillard, B. Goodness-of-fit procedures for copula models based on the integral probability transformation. Scand. J. Stat. 2006, 33, 337–366. [Google Scholar] [CrossRef]
- Genest, C.; Rémillard, B.; Beaudoin, D. Goodness-of-fit tests for copulas: A review and a power study. Insur. Math. Econ. 2009, 44, 199–213. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).