Some New Results on the Wiretap Channel with Side Information

Abstract

In this paper, the model of wiretap channel has been reconsidered for the case that the main channel is controlled by channel state information (side information), and it is available at the transmitter in a noncausal manner (termed here noncausal side information) or causal manner (termed here causal side information). Inner and outer bounds are derived on the capacity-equivocation regions for the noncausal and causal manners, and the secrecy capacities for both manners are described and bounded, which provide the best transmission rate with perfect secrecy. Moreover, for the case that the side information is available at the transmitter in a memoryless manner (termed here memoryless side information), both the capacity-equivocation region and the secrecy capacity are determined. The results of this paper extend the previous work on wiretap channel with noncausal side information by providing an outer bound on the capacity-equivocation region. In addition, we find that the memoryless side information can not help to obtain the same secrecy capacity as that of the causal case, and this is different from the well known fact that the memoryless manner can achieve the capacity of the channel with causal side information.

1. Introduction

The concept of the wiretap channel was first introduced by A.D. Wyner [1]. It is a kind of degraded broadcast channel. The wiretapper knows the encoding scheme used at the transmitter and the decoding scheme used at the legitimate receiver, see Figure 1. The object is to describe the rate of reliable communication from the transmitter to the legitimate receiver, subject to a constraint of the equivocation to the wiretapper.

Figure 1. The model of wiretap channel.

Figure 1. The model of wiretap channel.

After the publication of A.D. Wyner’s work, I. Csisz$\acute{a}$r and J. Körner [2] investigated a more general situation: the broadcast channels with confidential messages. It is clear that A.D. Wyner’s wiretap channel is a special case of the model of I. Csisz$\acute{a}$r and J. Körner, in a manner that the main channel is less noisy than the wiretap channel. Furthermore, S.K. Leung-Yan-Cheong and M.E. Hellman studied the Gaussian wiretap channel (GWC) [3], and showed that its secrecy capacity was the difference between the main channel capacity and the overall wiretap channel capacity (the cascade of main channel and wiretap channel).

The coding for channels with causal (past and current) side information at the encoder was first investigated by C.E. Shannon [4] in 1958. After that, in order to solve the problem of coding for a computer memory with defective cells, N.V. Kuznetsov and B.S. Tsybakov [5] considered a channel in the presence of non-causal side information at the transmitter. They provided some coding techniques without determination of the capacity. The capacity was found in 1980 by S. I. Gel’fand and M. S. Pinsker [6]. Furthermore, Max H.M. Costa [7] investigated a power constrained additive noise channel, where part of the noise is known at the transmitter as side information. This channel is also called dirty paper channel. Based on the dirty paper channel, C. Mitrpant et al. [8] studied the Gaussian wiretap channel with side information, and provided an inner bound on the capacity-equivocation region. Furthermore, Y. Chen et al. [9] investigated the discrete memoryless wiretap channel with noncausal side information, and also provided an inner bound on the capacity-equivocation region. Note that the coding scheme of [9] is a combination of those in [1,6]. Chen et al. [9] generalize Mitrpant et al.’s work [8] by extending the Gaussian channel to the discrete memoryless channel (DMC), i.e., the result of [8] can be obtained from that of [9]. Recently, N. Merhav [10] studied a variation of the wiretap channel, and obtained the capacity-equivocation region, where both the legitimate receiver and the wiretapper have access to some leaked symbols from the source, but the channels for the wiretapper are more noisy than the legitimate receiver, which shares a secret key with the encoder.

In this paper, we study the model of wiretap channel with side information, see Figure 2. The transition probability distribution of the main channel depends on a channel state information $V^N$, which is available at the encoder in a noncausal or causal manner. The wiretapper can get a degraded version of the symbols $Y^N$ via a wiretap channel. Both the main channel and the wiretap channel are discrete memoryless channels.

Figure 2. Wiretap channel with side information.

Figure 2. Wiretap channel with side information.

Inner and outer bounds are derived on the capacity-equivocation regions for the noncausal and causal manners (the inner bound for the noncausal manner is in fact equivalent to that of [9]), and the secrecy capacity for both manners is described and bounded. Moreover, for the case that the side information is available at the transmitter in a memoryless manner (at time i, the encoder is only allowed to use the side information $V_i$), both the capacity-equivocation region and the secrecy capacity are determined. In Shannon’s well known paper [4], it shows that the optimal way to achieve the capacity of the channel with causal side information is to use $V_i$ instead of $V^i$ for the channel encoder. Then, it is natural to think about whether the memoryless side information can help to obtain the same secrecy capacity as that of the wiretap channel with causal side information, and this is also our motivation on the study of the memoryless model.

Compared with [9], the inner bound on the capacity-equivocation region for the noncausal manner of this paper, in fact, is equivalent to the achievable region in [9]. However, the region provided in this paper is easier to understand than that of [9].

The remainder of this paper is organized as follows. In Section 2, we present the basic definitions and the main results on the capacity-equivocation regions. In Section 3, we prove the outer bounds on the capacity-equivocation regions for noncausal and causal manners, and provide the converse proof of the capacity-equivocation region for the memoryless manner. The inner bound for causal manner and the direct part of the capacity-equivocation region for the memoryless manner are proved in Section 4. Final conclusions are presented in Section 5.

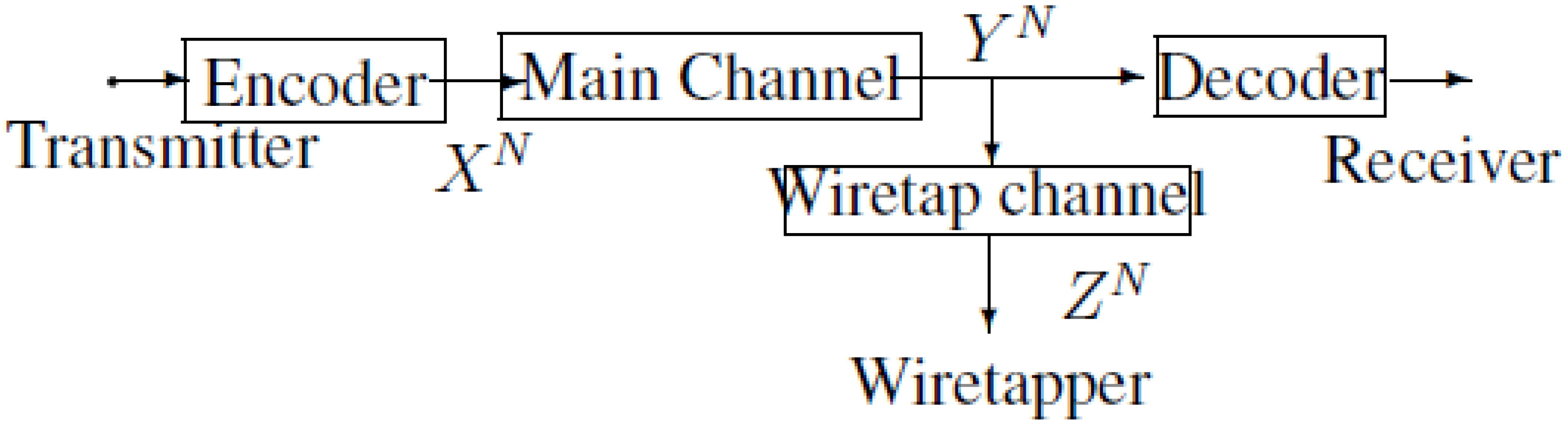
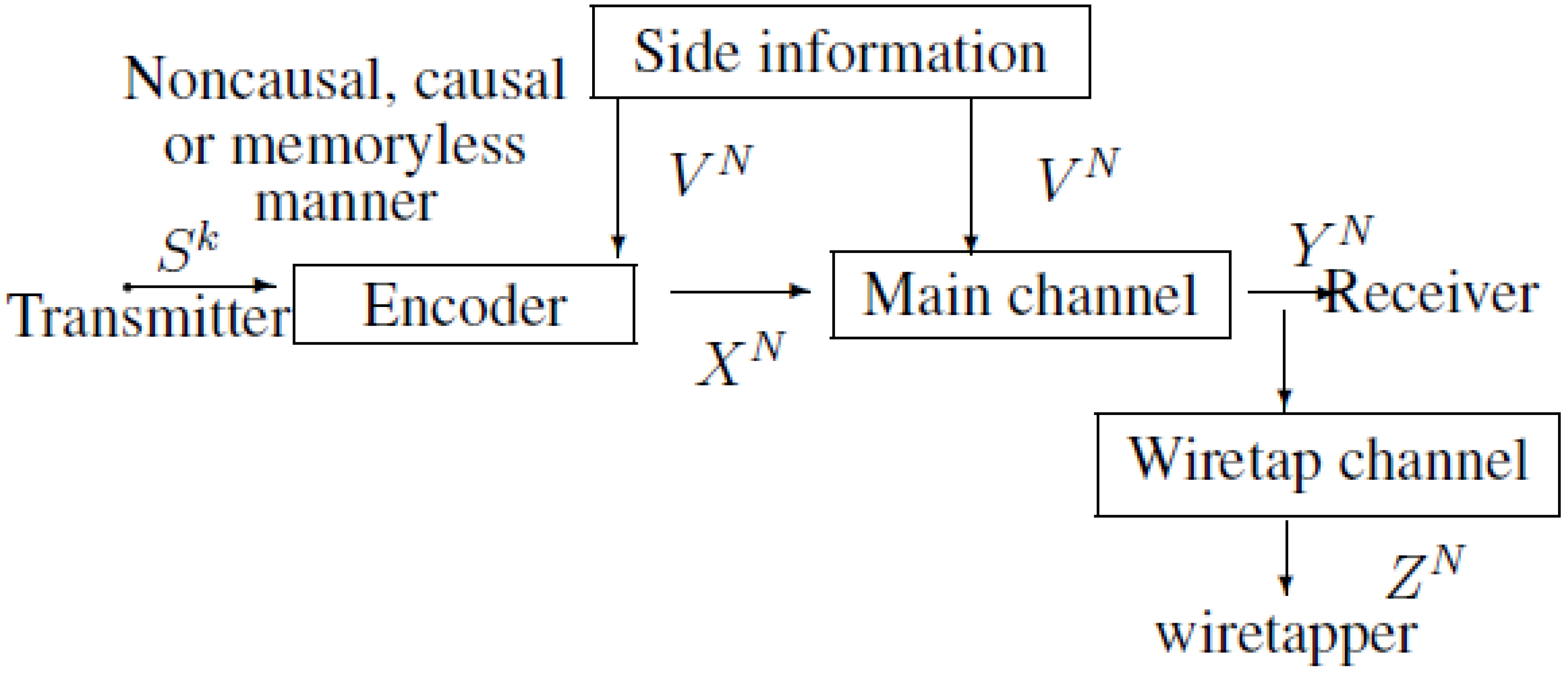
2. Notations, Definitions and the Main Results

Throughout the paper, random variables, sample values and alphabets are denoted by capital letters, lower case letters and calligraphic letters, respectively. A similar convention is applied to the random vectors and their sample values. For example, $U^N$ denotes a random N-vector $(U_1,\dots ,U_N)$, and $u^N=(u_1,\dots ,u_N)$ is a specific vector value in ${\mathcal{U}}^N$ that is the Nth Cartesian power of $\mathcal{U}$. $U_i^N$ denotes a random $N-i+1$-vector $(U_i,\dots ,U_N)$, and $u_i^N=(u_i,\dots ,u_N)$ is a specific vector value of $U_i^N$. Let $p_V(v)$ denote the probability mass function $Pr\{V=v\}$.

In this section, the model of Figure 2 is considered in three parts. The model of Figure 2 with noncausal side information is described in Section 2.1, the causal side information is described in Section 2.2, and the memoryless side information is described in Section 2.3, see the following.

2.1. The Model of Figure 2 with Noncausal Side Information

In this subsection, a description of the wiretap channel with noncausal side information is given by Definitions 1–4. The inner and outer bounds on the capacity-equivocation region $\mathcal{C}$ composed of all achievable $(R,d)$ pairs are given in Theorem 1 and Theorem 2, respectively, where the achievable $(R,d)$ pair is defined in Definition 5.

Definition 1 

(encoder) The source $S^k$ is defined as $(S_1,S_2,\dots ,S_k)$, where $S_i(1\le i\le k)$ are i.i.d. random variables that take values in the finite set $\mathcal{S}$. Then $H(S^k)=k{H}_S$, where $H_S=H(S_i)$ for $1\le i\le k$. The side information $V^N$ is the output of a discrete memoryless source $P_V(·)$, and it is available at the encoder in a noncausal manner. $V^N$ is independent of $S^k$.

The inputs of the encoder are $S^k$ and $V^N$, while the output is $X^N$. The encoder $f^N$ is a matrix of conditional probabilities $f^N(x^N|s^k,v^N)$, where $x^N\in {\mathcal{X}}^N$, $s^k\in {\mathcal{S}}^k$, $v^N\in {\mathcal{V}}^N$, ${\sum }_{x^N}{f}^N(x^N|s^k,v^N)=1$, and $f^N(x^N|s^k,v^N)$ is the probability that the source $s^k$ and the side information $v^N$ are encoded as the channel input $x^N$.

Definition 2 

(main channel) The main channel is a DMC with finite input alphabet $\mathcal{X}\times \mathcal{V}$, finite output alphabet $\mathcal{Y}$, and transition probability $Q_M(y|x,v)$, where $x\in \mathcal{X},v\in \mathcal{V},y\in \mathcal{Y}$. $Q_M(y^N|x^N,v^N)={\prod }_{n=1}^N{Q}_M(y_n|x_n,v_n)$. The inputs of the main channel are $X^N$ and $V^N$, while the output is $Y^N$.

Definition 3 

(wiretap channel) The wiretap channel is also a DMC with finite input alphabet $\mathcal{Y}$, finite output alphabet $\mathcal{Z}$, and transition probability $Q_W(z|y)$, where $y\in \mathcal{Y},z\in \mathcal{Z}$. The input and output of the wiretap channel are $Y^N$ and $Z^N$, respectively. The equivocation to the wiretapper is defined as

$$\Delta =\frac{H(S^k|Z^N)}{H(S^k)}$$

(2.1)

The cascade of the main channel and the wiretap channel is another DMC with transition probability

$$Q_{MW}(z|x,v)=\sum _{y\in \mathcal{Y}}{Q}_W(z|y)Q_M(y|x,v)$$

(2.2)

Let $C_{MW}$ be the capacity of the channel $Q_{MW}$.

Note that, $(S^k,V^N)\to (X^N,V^N)\to Y^N\to Z^N$ is a Markov chain in the model of Figure 2.

Definition 4 

(decoder) The decoder is a mapping $f_D:{\mathcal{Y}}^N\to {\mathcal{S}}^k$, with input $Y^N$ and output ${\widehat{S}}^k=f_D(Y^N)$. Let $P_e$ be the error probability, and it is defined as $Pr\{S^k\ne {\widehat{S}}^k\}$.

Definition 5 

(achievable $(R,d)$ pair in the model of Figure 2) A pair $(R,d)$ (where $R,d>0$) is called achievable if, for any $ϵ>0$, there exists an encoder-decoder $(N,k,\Delta ,P_e)$ such that

$$\frac{H_{S}k}{N}\ge R-ϵ,\Delta \ge d-ϵ,P_e\le ϵ$$

(2.3)

The capacity-equivocation region $\mathcal{C}$ is a set composed of all achievable $(R,d)$ pairs. Inner and outer bounds on $\mathcal{C}$ are respectively provided in the following Theorem 1 and Theorem 2.

Theorem 1 

The capacity-equivocation region $\mathcal{C}$ of the wiretap channel with noncausal side information satisfies ${\mathcal{R}}_i\subseteq \mathcal{C}$, where

$$\begin{array}{ccc}& & {\mathcal{R}}_i=\{(R,d):0\le d\le 1\hfill \\ & & 0\le R\le I(U;Y)-I(U;V)\hfill \\ & & Rd\le min\{I(U;Y)-I(U;Z),I(U;Y)-I(U;V)\}\}\hfill \end{array}$$

where the random variables U, X, V, Y and Z satisfy the following Markov chain,

$$U\to (X,V)\to Y\to Z$$

Remark 1 

There are some notes on Theorem 1, see the following.

• The range of the random variable U satisfies

  $$\parallel \mathcal{U}\parallel \le \parallel \mathcal{X}\parallel \parallel \mathcal{V}\parallel +3$$

  The proof is similar to that of Theorem 2, and it is omitted here.
• The region ${\mathcal{R}}_i$, in fact, is equivalent to the achievable region in [9], however, it is easier to understand than that of [9]. The proof of Theorem 1 is a combination of Gel’fand–Pinsker’s technique [6] and Wyner’s random binning method [1], and we omit it here.
• Secrecy capacity
  The points in ${\mathcal{R}}_i$ for which $d=1$ are of considerable interest, which imply the perfect secrecy $H(S^k)=H(S^k|Z^N)$. Clearly, we can easily bound the secrecy capacity $C_s$ of the model of Figure 2 with noncausal side information by

  $$maxmin\{I(U;Y)-I(U;Z),I(U;Y)-I(U;V)\}\le C_s\le max(I(U;Y)-I(U;V))$$

  (2.4)

Theorem 2 

The capacity-equivocation region $\mathcal{C}$, as defined above, satisfies $\mathcal{C}\subseteq {\mathcal{R}}_o$, where

$$\begin{array}{ccc}& & {\mathcal{R}}_o=\{(R,d):0\le d\le 1\hfill \\ & & 0\le R\le I(U;Y)-I(U;V)\hfill \\ & & Rd\le I(U;Y)-I(K;Z|A)\}\hfill \end{array}$$

where the random variables U, K, A, X, V, Y and Z satisfy the following Markov chains,

$$(U,K,A)\to (X,V)\to Y\to Z$$

$$(K,A)\to U\to Y\to Z$$

and A may be assumed to be a (deterministic) function of K (these are directly from the definitions of the random variables U, K, A, X, V, Y and Z, see Equations (3.18), (3.19), (3.20) and (3.21)).

Remark 2 

There are some notes on Theorem 2, see the following.

• The ranges of the random variables U, K and A satisfy

  $$\parallel \mathcal{A}\parallel \le \parallel \mathcal{X}\parallel \parallel \mathcal{V}\parallel$$

  $$\parallel \mathcal{K}\parallel \le {\parallel \mathcal{X}\parallel }^2{\parallel \mathcal{V}\parallel }^2$$

  $$\parallel \mathcal{U}\parallel \le {\parallel \mathcal{X}\parallel }^2{\parallel \mathcal{V}\parallel }^2(\parallel \mathcal{X}\parallel \parallel \mathcal{V}\parallel +1)$$

  The proof is in Appendix 5.
• Observing the formula $Rd\le I(U;Y)-I(K;Z|A)$ in Theorem 2, we have

  $$\begin{array}{ccc}\hfill I(U;Y)-I(K;Z|A)& {=}^{(a)}& I(U;Y)-H(Z|A)+H(Z|K)\hfill \\ & \ge & I(U;Y)-H(Z)+H(Z|K)\hfill \\ & \ge & I(U;Y)-H(Z)+H(Z|K,U)\hfill \\ & {=}^{(b)}& I(U;Y)-H(Z)+H(Z|U)=I(U;Y)-I(U;Z)\hfill \end{array}$$

  (2.5)

  where (a) is from the fact that A may be assumed to be a (deterministic) function of K, and (b) is from the Markov chain $K\to U\to Y\to Z$. Then it is easy to see that ${\mathcal{R}}_i\subseteq {\mathcal{R}}_o$.

2.2. The Model of Figure 2 with Causal Side Information

The model of Figure 2 with causal side information is similar to the model with noncausal side information in Section 2.1, except that the side information $V^N$ in Definition 1 is known to the encoder in a causal manner, i.e., at the i-th time ($1\le i\le N$), the output of the encoder $x_i=f_i(s^k,v^i)$, where $v^i=(v_1,v_2,\dots ,v_i)$ and $f_i$ is the probability that the source $s^k$ and the side information $v^i$ are encoded as the channel input $x_i$ at time i. Define

$$f^N(x^N|s^k,v^N)=\prod _{i=1}^N{f}_i(x_i|s^k,v^i)$$

(2.6)

Inner and outer bounds on the capacity-equivocation region ${\mathcal{C}}_c$ for the model of Figure 2 with causal side information are respectively provided in the following Theorem 3 and Theorem 4.

Theorem 3 

The capacity-equivocation region ${\mathcal{C}}_c$ satisfies ${\mathcal{R}}_{ci}\subseteq {\mathcal{C}}_c$, where

$$\begin{array}{ccc}& & {\mathcal{R}}_{ci}=\{(R,d):0\le d\le 1\hfill \\ & & 0\le R\le I(U;Y)\hfill \\ & & Rd\le I(U;Y)-I(U;Z)\}\hfill \end{array}$$

where the random variables U, X, V, Y and Z satisfy the following Markov chain,

$$U\to (X,V)\to Y\to Z$$

Remark 3 

There are some notes on Theorem 3, see the following.

• The range of the random variable U satisfies

  $$\parallel \mathcal{U}\parallel \le \parallel \mathcal{X}\parallel \parallel \mathcal{V}\parallel +1$$

  The proof is similar to that in Theorem 2, and it is omitted here.
• Secrecy capacity
  The points in ${\mathcal{R}}_{ci}$ for which $d=1$ are of considerable interest, which imply the perfect secrecy $H(S^k)=H(S^k|Z^N)$. Clearly, we can easily bound the secrecy capacity $C_s^c$ of the model of Figure 2 with causal side information by

  $$max(I(U;Y)-I(U;Z))\le C_s^c\le maxI(U;Y)$$

  (2.7)

Theorem 4 

The capacity-equivocation region ${\mathcal{C}}_c$ satisfies ${\mathcal{C}}_c\subseteq {\mathcal{R}}_{co}$, where

$$\begin{array}{ccc}& & {\mathcal{R}}_{co}=\{(R,d):0\le d\le 1\hfill \\ & & 0\le R\le I(U;Y)\hfill \\ & & Rd\le I(U;Y)-I(K;Z|A)\}\hfill \end{array}$$

where the random variables U, K, A, X, V, Y and Z satisfy the following Markov chains,

$$(U,K,A)\to (X,V)\to Y\to Z$$

$$(K,A)\to U\to Y\to Z$$

and A may be assumed to be a (deterministic) function of K (these are directly from the definitions of the random variables U, K, A, X, V, Y and Z, see Equations (3.18), (3.19), (3.20) and (3.21)).

Remark 4 

There are some notes on Theorem 4, see the following.

• The ranges of the random variables U, K and A satisfy

  $$\parallel \mathcal{A}\parallel \le \parallel \mathcal{X}\parallel \parallel \mathcal{V}\parallel$$

  $$\parallel \mathcal{K}\parallel \le {\parallel \mathcal{X}\parallel }^2{\parallel \mathcal{V}\parallel }^2$$

  $$\parallel \mathcal{U}\parallel \le {\parallel \mathcal{X}\parallel }^3{\parallel \mathcal{V}\parallel }^3$$

  The proof is similar to that of Theorem 2, and it is omitted here.
• Since the causal side information is a special case of the noncausal manner, the outer bound ${\mathcal{R}}_{co}$ can be directly obtained from ${\mathcal{R}}_o$ by using the fact that U is independent of V.
• Note that $I(U;Y)-I(K;Z|A)\ge I(U;Y)-I(U;Z)$ (the proof is the same as that in Remark 2), and therefore, it is easy to see that ${\mathcal{R}}_{ci}\subseteq {\mathcal{R}}_{co}$

2.3. The Model of Figure 2 with Memoryless Side Information

The model of Figure 2 with memoryless side information is similar to the model with causal side information in Section 2.2, except that the side information $V^N$ in Definition 1 is known to the encoder in a memoryless manner, i.e., at the i-th time ($1\le i\le N$), the output of the encoder $x_i=f_i(s^k,v_i)$, where $f_i$ is the probability that the source $s^k$ and the side information $v_i$ are encoded as the channel input $x_i$ at time i. Define

$$f^N(x^N|s^k,v^N)=\prod _{i=1}^N{f}_i(x_i|s^k,v_i)$$

(2.8)

The capacity of the main channel for the memoryless case is determined by C. E. Shannon [4],

$$C_M=\underset{p_{X|U,V}(x|u,v)p_U(u)}{max}I(U;Y)$$

(2.9)

where $U\to (X,V)\to Y$ is a Markov chain and $\parallel \mathcal{U}\parallel \le \parallel \mathcal{X}\parallel \parallel \mathcal{V}\parallel +1$. The proof of $\parallel \mathcal{U}\parallel \le \parallel \mathcal{X}\parallel \parallel \mathcal{V}\parallel +1$ is similar to that of Theorem 2, and it is omitted here.

A function ${\Gamma }^{{}^{\prime }}(R)$ used for describing the capacity-equivocation region composed of all achievable $(R,d)$ pairs in the model of Figure 2 with memoryless side information is defined in Definition 6.

Definition 6 

(function ${\Gamma }^{{}^{\prime }}(R)$) For $R\ge 0$, let

$$\rho (R)=\{p_{X|U,V}(x|u,v)p_U(u):I(U;Y)\ge R\}$$

(2.10)

It is easy to see that $\rho (R)$ is empty for $R>C_M$, where $C_M$ is the capacity of the main channel, see Equation (2.9). For $0\le R\le C_M$, denote

$${\Gamma }^{{}^{\prime }}(R)=\underset{p_{X|U,V}(x|u,v)p_U(u)\in \rho (R)}{sup}I(U;Y)-I(U;Z)$$

(2.11)

The following Lemma 1 provides some properties about ${\Gamma }^{{}^{\prime }}(R)$. The proof of Lemma 1 is in Appendix 5.

Lemma 1 

The quantity ${\Gamma }^{{}^{\prime }}(R)$, where $0\le R\le C_M$, satisfies the following properties:

(i) 

The “supremum” in the definition of ${\Gamma }^{{}^{\prime }}(R)$ is, in fact, a maximum, i.e., for each R, there exists a mass function $p_{X|U,V}(x|u,v)p_U(u)\in \rho (R)$ such that $I(U;Y)-I(U;Z)={\Gamma }^{{}^{\prime }}(R)$.

(ii) 

${\Gamma }^{{}^{\prime }}(R)$ is a concave function of R.

(iii) 

${\Gamma }^{{}^{\prime }}(R)$ is non-increasing in R.

(iv) 

${\Gamma }^{{}^{\prime }}(R)$ is continuous in R.

Our problem in the model of Figure 2 with memoryless side information is to characterize the capacity-equivocation region ${\mathcal{C}}_m$ composed of all achievable $(R,d)$ pairs. The following Theorem 5 gives a characterization of the capacity-equivocation region ${\mathcal{C}}_m$, which is proved in the remaining sections. The secrecy capacity is defined in Remark 5 (see Equation (2.12)), which is bounded by the Formula (2.14).

Theorem 5 

The capacity-equivocation region ${\mathcal{C}}_m$ is equal to ${\mathcal{R}}^{*}$, where

$$\begin{array}{ccc}& & {\mathcal{R}}^{*}=\{(R,d):0\le d\le 1\hfill \\ & & 0\le R\le C_M\hfill \\ & & Rd\le {\Gamma }^{{}^{\prime }}(R)\}\hfill \end{array}$$

Remark 5 

There are some notes on Theorem 5, see the following.

• Comparison with A. D. Wyner’s wiretap channel [1]
  The main channel capacity $C_M$ denoted by Equation (2.9) in Theorem 1 is different from that of [1]. When the channel state information V is a constant, the model of Figure 2 reduces to A. D. Wyner’s wiretap channel [1]. Substituting V by a constant and U by X into Equations (2.9), (2.10) and (2.11), the characters $C_M$, $\rho (R)$, ${\Gamma }^{{}^{\prime }}(R)$ and the region ${\mathcal{R}}^{*}$ are the same as those of [1].
• Secrecy capacity
  A transmission rate $C_s^{{}^{\prime }}$ denoted by

  $$C_s^{{}^{\prime }}=\underset{(R,1)\in {\mathcal{R}}^{*}}{max}R$$

  (2.12)

  is called the secrecy capacity in the model of Figure 2 with memoryless side information. Furthermore, $C_s^{{}^{\prime }}$ is the unique solution of the equation

  $$C_s^{{}^{\prime }}={\Gamma }^{{}^{\prime }}(C_s^{{}^{\prime }})$$

  (2.13)

  and satisfies

  $$0\le {\Gamma }^{{}^{\prime }}(C_M)\le C_s^{{}^{\prime }}\le {\Gamma }^{{}^{\prime }}(0)$$

  (2.14)
  Proof 1 (Proof of Equations (2.13) and (2.14)) Firstly, since ${\Gamma }^{{}^{\prime }}(0)>0$, ${\Gamma }^{{}^{\prime }}(C_M)-C_M\le 0$ and ${\Gamma }^{{}^{\prime }}(R)-R$ is a non-increasing function of R, then there exists a unique $C^{*}\in (0,C_M]$ such that ${\Gamma }^{{}^{\prime }}(C^{*})-C^{*}=0$ and $(C^{*},1)\in {\mathcal{R}}^{*}$. Secondly, if $(R_1,1)\in {\mathcal{R}}^{*}$, then $R_1\le {\Gamma }^{{}^{\prime }}(R_1)$, so that ${\Gamma }^{{}^{\prime }}(R_1)-R_1\ge 0$. Since ${\Gamma }^{{}^{\prime }}(R)-R$ is a non-increasing function of R, we conclude that $R_1\le C^{*}$. Thus $C^{*}$ is the maximum of those $R_1$ in which $(R_1,1)\in {\mathcal{R}}^{*}$, i.e., $C^{*}$ is the secrecy capacity $C_s^{{}^{\prime }}$ in the model of Figure 2 with memoryless side information. By using the Formula (2.13), and the non-increasing property of ${\Gamma }^{{}^{\prime }}(·)$ (see Lemma 1 (iii)), we get Equation (2.14). The proof is completed.
• Note that in Equation (2.14), we have $C_s^{{}^{\prime }}\le {\Gamma }^{{}^{\prime }}(0)$, which implies that $C_s^{{}^{\prime }}\le max(I(U;Y)-I(U;Z))$. Also note that for the causal model, the secrecy capacity satisfies $max(I(U;Y)-I(U;Z))\le C_s^c\le maxI(U;Y)$ (see Equation (2.7).
  Then, it is easy to see that the memoryless manner for the encoder can not help to obtain the same secrecy capacity as that of the wiretap channel with causal side information.

3. Proof of Theorem 2, Theorem 4 and Converse Half of Theorem 5

3.1. Proof of Theorem 2

Suppose $(R,d)$ is achievable, i.e., for any given $ϵ>0$, there exists an encoder-decoder $(N,k,\Delta ,P_e)$ such that

$$\frac{H_{S}k}{N}\ge R-ϵ,\Delta \ge d-ϵ,P_e\le ϵ$$

Then we will show the existence of random variables $(U,K,A)\to (X,V)\to Y\to Z$ such that

$$0\le d\le 1$$

(3.1)

$$0\le R\le I(U;Y)-I(U;V)$$

(3.2)

$$Rd\le I(U;Y)-I(K;Z|A)$$

(3.3)

3.1.1. Proof of Equation (3.1)

$$d-ϵ\le \Delta =\frac{H(S^k|Z^N)}{H(S^k)}\le \frac{H(S^k)}{H(S^k)}=1$$

Letting $ϵ\to 0$, we have $d\le 1$.

3.1.2. Proof of Equations (3.2) and (3.3)

The Formulas (3.2) and (3.3) are proved by Lemma 2, see the following.

Lemma 2 

The random vectors $S^k$, $Y^N$, $Z^N$ and the random variables U, K, A, Y, Z of Theorem 2 satisfy:

$$\frac{1}{N}H(S^k)\le I(U;Y)-I(U;V)+\delta (P_e)$$

(3.4)

$$\frac{1}{N}H(S^k|Z^N)\le I(U;Y)-I(K;Z|A)+\delta (P_e)$$

(3.5)

where $\delta (P_e)=h(P_e)+P_{e}log(|\mathcal{S}|-1)$. Note that $h(P_e)=-P_{e}log{P}_e-(1-P_e)log(1-P_e)$

Substituting $H(S^k)=k{H}_S$, $\frac{H(S^k|Z^N)}{H(S^k)}=\Delta$ and Equation (2.3) into Equations (3.4) and (3.5), it is easy to see that

$$R-ϵ\le I(U;Y)-I(U;V)+\delta (ϵ)$$

(3.6)

$$(R-ϵ)(d-ϵ)\le I(U;Y)-I(K;Z|A)+\delta (ϵ)$$

(3.7)

Letting $ϵ\to 0$ and using the fact that $\delta (ϵ)\to 0$ as $ϵ\to 0$, the Formulas (3.2) and (3.3) are obtained.

It remains to prove Lemma 2, see the following.

Proof 2 

(Proof of Lemma 2) The Formula (3.4) is from Equations (3.8), (3.10) and (3.22). The Formula (3.5) is proved by Equations (3.9), (3.10), (3.14), (3.22) and (3.26).

<Part i> We begin with the left parts of the inequalities Equations (3.4) and (3.5), see the following.

$$\begin{array}{ccc}\hfill \frac{1}{N}H(S^k)& =& \frac{1}{N}(I(S^k;Y^N)+H(S^k|Y^N))\hfill \\ & \stackrel{(1)}{\le }& \frac{1}{N}(I(S^k;Y^N)+k\delta (P_e))\hfill \\ & \le & \frac{1}{N}I(S^k;Y^N)+\delta (P_e)\hfill \end{array}$$

(3.8)

$$\begin{array}{ccc}\hfill \frac{1}{N}H(S^k|Z^N)& \stackrel{(2)}{\le }& \frac{1}{N}(H(S^k|Z^N)+k\delta (P_e)-H(S^k|Y^N))\hfill \\ & =& \frac{1}{N}(H(S^k|Z^N)+k\delta (P_e)-H(S^k|Y^N)+H(S^k)-H(S^k))\hfill \\ & =& \frac{1}{N}(I(S^k;Y^N)-I(S^k;Z^N))+\delta (P_e)\hfill \end{array}$$

(3.9)

where (1) and (2) follow from the Fano’s inequality.

<Part ii> The character $\frac{1}{N}I(S^k;Y^N)$ in Formulas (3.8) and (3.9) can be bounded by Equation (3.10), see the following.

$$\begin{array}{ccc}\hfill \frac{1}{N}I(S^k;Y^N)& \stackrel{(a)}{=}& \frac{1}{N}(I(S^k;Y^N)-I(S^k;V^N))\hfill \\ & =& \frac{1}{N}\sum _{i=1}^N(I(S^k;Y_i|Y^{i-1})-I(S^k;V_i|V_{i+1}^N))\hfill \\ & =& \frac{1}{N}\sum _{i=1}^N(H(Y_i|Y^{i-1})-H(Y_i|Y^{i-1},S^k)-H(Y_i|Y^{i-1},S^k,V_{i+1}^N)+H(Y_i|Y^{i-1},S^k,V_{i+1}^N)\hfill \\ & & -I(S^k;V_i|V_{i+1}^N))\hfill \\ & =& \frac{1}{N}\sum _{i=1}^N(I(Y_i;S^k,V_{i+1}^N|Y^{i-1})-I(Y_i;V_{i+1}^N|Y^{i-1},S^k)-I(S^k;V_i|V_{i+1}^N))\hfill \\ & =& \frac{1}{N}\sum _{i=1}^N(I(Y_i;S^k,V_{i+1}^N|Y^{i-1})-I(Y_i;V_{i+1}^N|Y^{i-1},S^k)-H(V_i|V_{i+1}^N)\hfill \\ & & +H(V_i|V_{i+1}^N,S^k)-H(V_i|V_{i+1}^N,S^k,Y^{i-1})+H(V_i|V_{i+1}^N,S^k,Y^{i-1}))\hfill \\ & =& \frac{1}{N}\sum _{i=1}^N(I(Y_i;S^k,V_{i+1}^N|Y^{i-1})-I(Y_i;V_{i+1}^N|Y^{i-1},S^k)-I(V_i;S^k,Y^{i-1}|V_{i+1}^N)\hfill \\ & & +I(V_i;Y^{i-1}|V_{i+1}^N,S^k))\hfill \\ & \stackrel{(b)}{=}& \frac{1}{N}\sum _{i=1}^N(I(Y_i;S^k,V_{i+1}^N|Y^{i-1})-I(V_i;S^k,Y^{i-1}|V_{i+1}^N))\hfill \\ & =& \frac{1}{N}\sum _{i=1}^N(H(Y_i|Y^{i-1})-H(Y_i|Y^{i-1},S^k,V_{i+1}^N)-H(V_i|V_{i+1}^N)+H(V_i|V_{i+1}^N,S^k,Y^{i-1}))\hfill \\ & \stackrel{(c)}{\le }& \frac{1}{N}\sum _{i=1}^N(H(Y_i)-H(Y_i|Y^{i-1},S^k,V_{i+1}^N)-H(V_i)+H(V_i|V_{i+1}^N,S^k,Y^{i-1}))\hfill \\ & =& \frac{1}{N}\sum _{i=1}^N(I(Y_i;S^k,V_{i+1}^N,Y^{i-1})-I(V_i;S^k,Y^{i-1},V_{i+1}^N))\hfill \end{array}$$

(3.10)

Formula (a) follows from the fact that $S^k$ is independent of $V^N$.

Formula (b) is from

$$\sum _{i=1}^{N}I(Y_i;V_{i+1}^N|Y^{i-1},S^k)=\sum _{i=1}^{N}I(V_i;Y^{i-1}|V_{i+1}^N,S^k)$$

(3.11)

Formula (c) follows from that $V^N$ is composed of N i.i.d. random variables.

Proof 3 

(Proof of Equation (3.11)) Since the left part of Equation (3.11) is equal to

$$\sum _{i=1}^{N}I(Y_i;V_{i+1}^N|Y^{i-1},S^k)=\sum _{i=1}^N\sum _{j=i+1}^{N}I(Y_i;V_j|Y^{i-1},S^k,V_{j+1}^N)$$

(3.12)

and the right part of Equation (3.11) is equal to

$$\begin{array}{ccc}\hfill \sum _{i=1}^{N}I(V_i;Y^{i-1}|V_{i+1}^N,S^k)& =& \sum _{i=1}^N\sum _{j=1}^{i-1}I(V_i;Y_j|V_{i+1}^N,S^k,Y^{j-1})\hfill \\ & =& \sum _{j=1}^N\sum _{i=1}^{j-1}I(V_j;Y_i|S^k,V_{j+1}^N,Y^{i-1})\hfill \\ & =& \sum _{i=1}^N\sum _{j=i+1}^{N}I(V_j;Y_i|S^k,V_{j+1}^N,Y^{i-1})\hfill \end{array}$$

(3.13)

The Formula (3.11) is verified by Equations (3.12) and (3.13).

<Part iii> The character $\frac{1}{N}I(S^k;Z^N)$ in Formula (3.9) can be bounded by the following Equation (3.14).

$$\begin{array}{ccc}\hfill \frac{1}{N}I(S^k;Z^N)& \stackrel{(1)}{=}& \frac{1}{N}(I(S^k;Z^N)-I(S^k;V^N))\hfill \\ & =& \frac{1}{N}\sum _{i=1}^N(I(S^k;Z_i|Z^{i-1})-I(S^k;V_i|V_{i+1}^N))\hfill \\ & =& \frac{1}{N}\sum _{i=1}^N(H(Z_i|Z^{i-1})-H(Z_i|Z^{i-1},S^k)-H(Z_i|Z^{i-1},S^k,V_{i+1}^N)+H(Z_i|Z^{i-1},S^k,V_{i+1}^N)\hfill \\ & & -I(S^k;V_i|V_{i+1}^N))\hfill \\ & =& \frac{1}{N}\sum _{i=1}^N(I(Z_i;S^k,V_{i+1}^N|Z^{i-1})-I(Z_i;V_{i+1}^N|Z^{i-1},S^k)-I(S^k;V_i|V_{i+1}^N))\hfill \\ & =& \frac{1}{N}\sum _{i=1}^N(I(Z_i;S^k,V_{i+1}^N|Z^{i-1})-I(Z_i;V_{i+1}^N|Z^{i-1},S^k)-H(V_i|V_{i+1}^N)\hfill \\ & & +H(V_i|V_{i+1}^N,S^k)-H(V_i|V_{i+1}^N,S^k,Z^{i-1})+H(V_i|V_{i+1}^N,S^k,Z^{i-1}))\hfill \\ & =& \frac{1}{N}\sum _{i=1}^N(I(Z_i;S^k,V_{i+1}^N|Z^{i-1})-I(Z_i;V_{i+1}^N|Z^{i-1},S^k)-I(V_i;S^k,Z^{i-1}|V_{i+1}^N)\hfill \\ & & +I(V_i;Z^{i-1}|V_{i+1}^N,S^k))\hfill \\ & \stackrel{(2)}{=}& \frac{1}{N}\sum _{i=1}^N(I(Z_i;S^k,V_{i+1}^N|Z^{i-1})-I(V_i;S^k,Z^{i-1}|V_{i+1}^N))\hfill \\ & =& \frac{1}{N}\sum _{i=1}^N(H(Z_i|Z^{i-1})-H(Z_i|Z^{i-1},S^k,V_{i+1}^N)-H(V_i|V_{i+1}^N)+H(V_i|V_{i+1}^N,S^k,Z^{i-1}))\hfill \\ & \stackrel{(3)}{=}& \frac{1}{N}\sum _{i=1}^N(H(Z_i|Z^{i-1})-H(Z_i|Z^{i-1},S^k,V_{i+1}^N)-H(V_i)+H(V_i|V_{i+1}^N,S^k,Z^{i-1}))\hfill \\ & \ge & \frac{1}{N}\sum _{i=1}^N(H(Z_i|Z^{i-1})-H(Z_i|Z^{i-1},S^k,V_{i+1}^N)-H(V_i)+H(V_i|V_{i+1}^N,S^k,Z^{i-1},Y^{i-1}))\hfill \\ & \stackrel{(4)}{=}& \frac{1}{N}\sum _{i=1}^N(H(Z_i|Z^{i-1})-H(Z_i|Z^{i-1},S^k,V_{i+1}^N)-H(V_i)+H(V_i|V_{i+1}^N,S^k,Y^{i-1}))\hfill \end{array}$$

(3.14)

Formula (1) is from the fact that $S^k$ is independent of $V^N$.

Formula (2) follows from

$$\sum _{i=1}^{N}I(Z_i;V_{i+1}^N|Z^{i-1},S^k)=\sum _{i=1}^{N}I(V_i;Z^{i-1}|V_{i+1}^N,S^k)$$

(3.15)

Formula (3) is from the fact that $V_i$ is independent of $V_{i+1}^N$.

Formula (4) is from the Markov chain $V_i\to (V_{i+1}^N,S^k,Y^{i-1})\to Z^{i-1}$.

Proof 4 

(Proof of Equation (3.15)) Since the left part of Equation (3.15) is equal to

$$\sum _{i=1}^{N}I(Z_i;V_{i+1}^N|Z^{i-1},S^k)=\sum _{i=1}^N\sum _{j=i+1}^{N}I(Z_i;V_j|Z^{i-1},S^k,V_{j+1}^N)$$

(3.16)

and the right part of Equation (3.15) is equal to

$$\begin{array}{ccc}\hfill \sum _{i=1}^{N}I(V_i;Z^{i-1}|V_{i+1}^N,S^k)& =& \sum _{i=1}^N\sum _{j=1}^{i-1}I(V_i;Z_j|V_{i+1}^N,S^k,Z^{j-1})\hfill \\ & =& \sum _{j=1}^N\sum _{i=1}^{j-1}I(V_j;Z_i|S^k,V_{j+1}^N,Z^{i-1})\hfill \\ & =& \sum _{i=1}^N\sum _{j=i+1}^{N}I(V_j;Z_i|S^k,V_{j+1}^N,Z^{i-1})\hfill \end{array}$$

(3.17)

The Formula (3.15) is verified by Equations (3.16) and (3.17).

<Part iv>(single letter) To complete the proof, we introduce an random variable J, which is independent of $S^k$, $X^N$, $V^N$, $Y^N$ and $Z^N$. Furthermore, J is uniformly distributed over $\{1,2,\dots ,N\}$. Define

$$A=(Z^{J-1},J)$$

(3.18)

$$K=(Z^{J-1},V_{J+1}^N,S^k,J)$$

(3.19)

$$U=(Y^{J-1},V_{J+1}^N,S^k,J)$$

(3.20)

$$X=X_J,Y=Y_J,Z=Z_J,V=V_J$$

(3.21)

<Part v> Then Equation (3.10) can be rewritten as

$$\begin{array}{ccc}\hfill \frac{1}{N}I(S^k;Y^N)& \le & \frac{1}{N}\sum _{i=1}^N(I(Y_i;S^k,V_{i+1}^N,Y^{i-1})-I(V_i;S^k,Y^{i-1},V_{i+1}^N))\hfill \\ & =& \frac{1}{N}\sum _{i=1}^N(I(Y_i;S^k,V_{i+1}^N,Y^{i-1}|J=i)-I(V_i;S^k,Y^{i-1},V_{i+1}^N|J=i))\hfill \\ & =& I(Y_J;S^k,V_{J+1}^N,Y^{J-1}|J)-I(V_J;S^k,Y^{J-1},V_{J+1}^N|J)\hfill \\ & \stackrel{(a)}{\le }& I(Y_J;S^k,V_{J+1}^N,Y^{J-1},J)-I(V_J;S^k,Y^{J-1},V_{J+1}^N,J)\hfill \\ & \le & I(U;Y)-I(U;V)\hfill \end{array}$$

(3.22)

where (a) is from the fact that $V_J$ is independent of J, i.e., $p(V_J=v,J=i)=p(V_J=v)p(J=i)$.

Proof 5 

(Proof of $p(V_J=v,J=i)=p(V_J=v)p(J=i)$) Since $V^N$ is the output of a discrete memoryless source $p_V(v)$, then we have

$$p(V_i=v)=p(V=v)$$

(3.23)

From <Part iv>, we know that the random variable J is independent of $V^N$, and therefore,

$$\begin{array}{ccc}\hfill p(V_J=v,J=i)& =& p(V_i=v,J=i)\hfill \\ & =& p(V_i=v)p(J=i)\hfill \\ & {=}^{(1)}& P(V=v)p(J=i)\hfill \end{array}$$

(3.24)

where (1) follows from Equation (3.23).

On the other hand, the probability $p(V_J=v)$ can be calculated as follows,

$$\begin{array}{ccc}\hfill p(V_J=v)& =& \sum _{i=1}^{N}p(V_J=v,J=i)=\sum _{i=1}^{N}p(V_i=v,J=i)\hfill \\ & {=}^{(a)}& \sum _{i=1}^{N}p(V_i=v)p(J=i)\hfill \\ & {=}^{(b)}& \sum _{i=1}^{N}p(V=v)p(J=i)\hfill \\ & =& p(V=v)\sum _{i=1}^{N}p(J=i)=p(V=v)\hfill \end{array}$$

(3.25)

where (a) is from the fact that J is independent of $V^N$, the Formula (b) is from Equation (3.23).

By using Equations (3.24) and (3.25), it is easy to verify that $V_J$ is independent of J, completing the proof.

<Part vi> Analogously, Equation (3.14) can be rewritten as

$$\begin{array}{ccc}\hfill \frac{1}{N}I(S^k;Z^N)& =& \frac{1}{N}\sum _{i=1}^N(H(Z_i|Z^{i-1})-H(Z_i|Z^{i-1},S^k,V_{i+1}^N)-H(V_i)+H(V_i|V_{i+1}^N,S^k,Y^{i-1}))\hfill \\ & =& \frac{1}{N}\sum _{i=1}^N(H(Z_i|Z^{i-1},J=i)-\hfill \\ & & H(Z_i|Z^{i-1},S^k,V_{i+1}^N,J=i)-H(V_i|,J=i)+H(V_i|V_{i+1}^N,S^k,Y^{i-1},J=i))\hfill \\ & =& {}^{(a)}H(Z_J|Z^{J-1},J)-H(Z_J|Z^{J-1},S^k,V_{J+1}^N,J)-H(V_J)+H(V_J|V_{J+1}^N,S^k,Y^{J-1},J)\hfill \\ & =& H(Z|A)-H(Z|K,A)-H(V)+H(V|U)\hfill \\ & =& I(K;Z|A)-I(U;V)\hfill \end{array}$$

(3.26)

where (a) follows from the fact that $V_J$ is independent of J.

Substituting Equations (3.22) and (3.26) into Equations (3.8) and (3.9), Lemma 2 is proved.

The Markov chains $(U,K,A)\to (X,V)\to Y\to Z$ and $(K,A)\to U\to Y\to Z$ are easily verified by Equations (3.18), (3.19), (3.20) and (3.21).

The proof of Theorem 2 is completed.

3.2. Proof of Theorem 4

Suppose $(R,d)$ is achievable, i.e., for any given $ϵ>0$, there exists an encoder-decoder $(N,k,\Delta ,P_e)$ such that

$$\frac{H_{S}k}{N}\ge R-ϵ,\Delta \ge d-ϵP_e\le ϵ$$

Then we will show the existence of random variables $(U,K,A)\to (X,V)\to Y\to Z$ such that

$$0\le d\le 1$$

(3.27)

$$0\le R\le I(U;Y)$$

(3.28)

$$Rd\le I(U;Y)-I(K;Z|A)$$

(3.29)

The Formula (3.27) is from

$$d-ϵ\le \Delta =\frac{H(S^k|Z^N)}{H(S^k)}\le \frac{H(S^k)}{H(S^k)}=1$$

. Letting $ϵ\to 0$, we have $d\le 1$.

Since the model of Figure 2 with causal side information is a special case of the model of Figure 2 with noncausal side information, the Formulas (3.28) and (3.29) are obtained from Equations (3.2) and (3.3), respectively, see the following.

Proof 6 

(Proof of Equation (3.28)) The parameter R of Equation (3.28) can be written as follows,

$$\begin{array}{ccc}\hfill R-ϵ& \le & \frac{H(S^k)}{N}\hfill \\ & {\le }^{(a)}& \delta (P_e)+\frac{1}{N}\sum _{i=1}^N(H(Y_i)-H(Y_i|Y^{i-1},S^k,V_{i+1}^N)-H(V_i)+H(V_i|Y^{i-1},S^k,V_{i+1}^N))\hfill \\ & {\le }^{(b)}& \delta (ϵ)+H(Y)-H(Y|U)\hfill \\ & =& I(U;Y)+\delta (ϵ)\hfill \end{array}$$

(3.30)

where (a) follows from Equations (3.8) and (3.10), and the Formula (b) is from the definitions of Y, U, see Equations (3.20) and (3.21), and $V_i$ is independent of $(Y^{i-1},S^k,V_{i+1}^N)$.

Letting $ϵ\to 0$, the proof of Equation (3.28) is completed.

Proof 7 

(Proof of Equation (3.29)) The parameter $Rd$ of Equation (3.29) satisfies

$$\begin{array}{ccc}\hfill (R-ϵ)(d-ϵ)& \le & \frac{H(S^k|Z^N)}{N}\hfill \\ & {\le }^{(a)}& \frac{1}{N}I(S^k;Y^N)-\frac{1}{N}I(S^k;Z^N)+\delta (P_e)\hfill \\ & {\le }^{(b)}& \frac{1}{N}\sum _{i=1}^N(I(Y_i;S^k,V_{i+1}^N,Y^{i-1})-I(V_i;S^k,Y^{i-1},V_{i+1}^N)-\hfill \\ & & H(Z_i|Z^{i-1})+H(Z_i|Z^{i-1},S^k,V_{i+1}^N)+H(V_i)-H(V_i|V_{i+1}^N,S^k,Y^{i-1}))+\delta (P_e)\hfill \\ & {=}^{(c)}& \frac{1}{N}\sum _{i=1}^N(I(Y_i;S^k,V_{i+1}^N,Y^{i-1})-H(Z_i|Z^{i-1})+H(Z_i|Z^{i-1},S^k,V_{i+1}^N)+\delta (P_e)\hfill \\ & {\le }^{(d)}& I(U;Y)-I(K;Z|A)+\delta (ϵ)\hfill \end{array}$$

(3.31)

where (a) follows from Equation (3.9), the Formula (b) is from Equations (3.10) and (3.14), the Formula (c) is from the fact that $V_i$ is independent of $(Z^{i-1},Y^{i-1},S^k,V_{i+1}^N)$, the Formula (d) is from the definitions of Y, Z, U, K, A, see Equations (3.18), (3.19), (3.20) and (3.21). Letting $ϵ\to 0$, the proof of Equation (3.29) is completed.

The proof of Theorem 4 is completed.

3.3. Converse Half of Theorem 5

In this subsection, we establish the converse theorem of Theorem 5: the region ${\mathcal{C}}_m$ which is composed of all achievable $(R,d)$ pairs is contained in the set ${\mathcal{R}}^{*}$, i.e., ${\mathcal{C}}_m\subseteq {\mathcal{R}}^{*}$.

Suppose $(R,d)\in {\mathcal{C}}_m$, i.e., for any given $ϵ>0$, there exists an encoder-decoder $(N,k,\Delta ,P_e)$ such that

$$\frac{H_{S}k}{N}\ge R-ϵ,\Delta \ge d-ϵ,P_e\le ϵ$$

Then we will show that $(R,d)\in {\mathcal{R}}^{*}$, i.e., $(R,d)$ satisfies the following conditions

$$0\le R\le C_M,0\le d\le 1\mathrm{and}Rd\le {\Gamma }^{{}^{\prime }}(R)$$

The proof of $R\le C_M$ and $d\le 1$ is obvious, and it is omitted here. It only needs to prove $Rd\le {\Gamma }^{{}^{\prime }}(R)$, see the following.

The following Lemma 3 provides a Markov chain used in the remaining of this subsection. The proof of Lemma 3 is in Appendix 5.

Lemma 3 

In the model of Figure 2, the random variable $Z_i$ and the random vectors $S^k$ and $Y^{i-1}$ ($1\le i\le N$) form the following Markov chain:

$$Y^{i-1}\to S^k\to Z_i$$

The proof of $Rd\le {\Gamma }^{{}^{\prime }}(R)$ is considered in the following five steps:

(i) Show that

$$H(S^k)\Delta \le I(S^k;Y^N|Z^N)+k\delta (P_e)$$

(ii) In the right part of step (i), show that

$$I(S^k;Y^N|Z^N)\le \sum _{n=1}^N(I(U_n;Y_n|Y^{n-1})-I(U_n;Z_n|Y^{n-1}))$$

(iii) In the right part of step (ii), show that

$$\frac{1}{N}\sum _{n=1}^N(I(U_n;Y_n|Y^{n-1})-I(U_n;Z_n|Y^{n-1}))\le {\Gamma }^{{}^{\prime }}(\frac{1}{N}\sum _{n=1}^{N}I(U_n;Y_n|Y^{n-1}))$$

(iv) A property about the variable of the function ${\Gamma }^{{}^{\prime }}(·)$ in step (iii) is

$$\frac{k}{N}(H_S-\delta (P_e))\le \frac{1}{N}\sum _{n=1}^{N}I(U_n;Y_n|Y^{n-1})$$

(v) Substituting step (ii), step (iii) and step (iv) into step (i), we have

$$Rd\le {\Gamma }^{{}^{\prime }}(R)$$

3.3.1. Proof of Step (i)

By using Fano’s inequality,

$$H(S^k|Z^N,Y^N)\le H(S^k|Y^N)\le k\delta (P_e)$$

(3.32)

where $\delta (P_e)=h(P_e)+P_{e}log(|\mathcal{S}|-1)$.

Then we have

$$\begin{array}{ccc}\hfill H(S^k)\Delta & =& H(S^k|Z^N)\hfill \\ & \le & H(S^k|Z^N)+k\delta (P_e)-H(S^k|Z^N,Y^N)\hfill \\ & =& k\delta (P_e)+I(S^k;Y^N|Z^N)\hfill \end{array}$$

(3.33)

Thus, the proof of step (i) is completed.

3.3.2. Proof of Step (ii)

$$\begin{array}{ccc}\hfill I(S^k;Y^N|Z^N)& =& H(S^k|Z^N)-H(S^k|Y^N,Z^N)\hfill \\ & {=}^{(a)}& H(S^k|Z^N)-H(S^k|Y^N)\hfill \\ & =& I(S^k;Y^N)-I(S^k;Z^N)\hfill \\ & =& H(Y^N)-H(Y^N|S^k)-H(Z^N)+H(Z^N|S^k)\hfill \\ & =& \sum _{n=1}^N(H(Y_n|Y^{n-1})-H(Y_n|Y^{n-1},S^k)-H(Z_n|Z^{n-1})+H(Z_n|Z^{n-1},S^k))\hfill \\ & {\le }^{(b)}& \sum _{n=1}^N(H(Y_n|Y^{n-1})-H(Y_n|Y^{n-1},S^k,V_{n+1}^N)-H(Z_n|Z^{n-1},Y^{n-1})+H(Z_n|S^k))\hfill \\ & {=}^{(c)}& \sum _{n=1}^N(H(Y_n|Y^{n-1})-H(Y_n|Y^{n-1},S^k,V_{n+1}^N)-H(Z_n|Y^{n-1})+H(Z_n|S^k,Y^{n-1}))\hfill \\ & {=}^{(d)}& \sum _{n=1}^N(H(Y_n|Y^{n-1})-H(Y_n|Y^{n-1},S^k,V_{n+1}^N)-H(Z_n|Y^{n-1})+H(Z_n|S^k,Y^{n-1},V_{n+1}^N))\hfill \\ & {=}^{(e)}& \sum _{n=1}^N(H(Y_n|Y^{n-1})-H(Y_n|Y^{n-1},U_n)-H(Z_n|Y^{n-1})+H(Z_n|U_n,Y^{n-1}))\hfill \\ & =& \sum _{n=1}^N(I(U_n;Y_n|Y^{n-1})-I(U_n;Z_n|Y^{n-1}))\hfill \end{array}$$

(3.34)

where Formula (a) follows from $S^k\to Y^N\to Z^N$, see Lemma 3 in Appendix 5. Formula (b) follows from the fact that $V_{n+1}^N$ is independent of $Y_n,Y^{n-1},S^k$. Formula (c) follows from $Z^{n-1}\to Y^{n-1}\to Z_n$ and $Y^{n-1}\to S^k\to Z_n$ (see Lemma 2). Formula (d) follows from the fact that $V_{n+1}^N$ is independent of $Z_n,Y^{n-1},S^k$. Formula (e) follows from the definition that $U_n=(S^k,Y^{n-1},V_{n+1}^N)$, and this is coincident with the definition of U used in the converse proof of Equation (2.9).

The proof of step (ii) is completed.

3.3.3. Proof of Step (iii)

The proof of step (iii) is considered in two parts. The first part is for some definitions, and the second part is for the main proof.

• For $n=2,3,\dots ,N$, and any $y^{n-1}\in {\mathcal{Y}}^{n-1}$, let

  $${\alpha }_n(y^{n-1})=I(U_n;Y_n|Y^{n-1}=y^{n-1})$$

  (3.35)

  Denote

  $${\alpha }_1=I(U_1;Y_1)$$

  (3.36)

  It follows from the definition of $\rho (R)$ in Equation (2.10) that the distribution $p_1$, defined by

  $$p_1=Pr\{X_1=x|U_1=u,V_1=v\}Pr\{U_1=u\},u\in \mathcal{U}x\in \mathcal{X},v\in \mathcal{V}$$

  (3.37)

  belongs to $\rho ({\alpha }_1)$. Similarly, for $2\le n\le N$, let

  $$p_{n,y^{n-1}}=Pr\{X_n=x|U_n=u,V_n=v,Y^{n-1}=y^{n-1}\}Pr\{U_n=u|Y^{n-1}=y^{n-1}\}$$

  (3.38)

  where $u\in \mathcal{U},x\in \mathcal{X},v\in \mathcal{V},y^{n-1}\in {\mathcal{Y}}^{n-1}$. Then it is easy to see that $p_{n,y^{n-1}}\in \rho ({\alpha }_n(y^{n-1}))$. Thus, from the definition of ${\Gamma }^{{}^{\prime }}(R)$ in Equation (2.11),

  $${\Gamma }^{{}^{\prime }}({\alpha }_1)\ge I(U_1;Y_1)-I(U_1;Z_1)$$

  (3.39)

  and for $2\le n\le N$, $y^{n-1}\in {\mathcal{Y}}^{n-1}$,

  $${\Gamma }^{{}^{\prime }}({\alpha }_n(y^{n-1}))\ge I(U_n;Y_n|Y^{n-1}=y^{n-1})-I(U_n;Z_n|Y^{n-1}=y^{n-1})$$

  (3.40)
• By using the Formulas (3.35) and (3.40), the proof of step (iii) is as follows,

  $$\begin{array}{ccc}& & \frac{1}{N}\sum _{n=1}^N(I(U_n;Y_n|Y^{n-1})-I(U_n;Z_n|Y^{n-1}))\hfill \\ & =& \frac{1}{N}\sum _{n=1}^N\sum _{y^{n-1}\in {\mathcal{Y}}^{n-1}}Pr\{Y^{n-1}=y^{n-1}\}(I(U_n;Y_n|Y^{n-1}=y^{n-1})-I(U_n;Z_n|Y^{n-1}=y^{n-1}))\hfill \\ & {\le }^{(a)}& \frac{1}{N}\sum _{n=1}^N\sum _{y^{n-1}\in {\mathcal{Y}}^{n-1}}Pr\{Y^{n-1}=y^{n-1}\}{\Gamma }^{{}^{\prime }}({\alpha }_n(y^{n-1}))\hfill \\ & {\le }^{(b)}& {\Gamma }^{{}^{\prime }}(\frac{1}{N}\sum _{n=1}^N\sum _{y^{n-1}\in {\mathcal{Y}}^{n-1}}Pr\{Y^{n-1}=y^{n-1}\}{\alpha }_n(y^{n-1}))\hfill \\ & {=}^{(c)}& {\Gamma }^{{}^{\prime }}(\frac{1}{N}\sum _{n=1}^{N}I(U_n;Y_n|Y^{n-1}))\hfill \end{array}$$

  where Formula (a) follows from the inequality Equation (3.40). Formula (b) follows from the concavity of ${\Gamma }^{{}^{\prime }}(R)$[Lemma 1 (ii)]. Formula (c) follows from the definition Equation (3.35).

The proof of step (iii) is completed.

3.3.4. Proof of Step (iv)

$$\begin{array}{ccc}\hfill \frac{1}{N}\sum _{n=1}^{N}I(U_n;Y_n|Y^{n-1})& =& \frac{1}{N}\sum _{n=1}^N(H(U_n|Y^{n-1})-H(U_n|Y^{n-1},Y_n))\hfill \\ & {=}^{(a)}& \frac{1}{N}\sum _{n=1}^N(H(V_{n+1}^N,S^k|Y^{n-1})-H(V_{n+1}^N,S^k|Y^{n-1},Y_n))\hfill \\ & {=}^{(b)}& \frac{1}{N}\sum _{n=1}^N(H(V_{n+1}^N)+H(S^k|V_{n+1}^N,Y^{n-1})-H(V_{n+1}^N)-H(S^k|V_{n+1}^N,Y^{n-1},Y_n))\hfill \\ & =& \frac{1}{N}\sum _{n=1}^{N}I(S^k;Y_n|V_{n+1}^N,Y^{n-1})\hfill \\ & =& \frac{1}{N}\sum _{n=1}^N(H(Y_n|V_{n+1}^N,Y^{n-1})-H(Y_n|V_{n+1}^N,Y^{n-1},S^k))\hfill \\ & {=}^{(c)}& \frac{1}{N}\sum _{n=1}^N(H(Y_n|Y^{n-1})-H(Y_n|Y^{n-1},S^k))\hfill \\ & =& \frac{1}{N}(H(Y^N)-H(Y^N|S^k))\hfill \\ & =& \frac{1}{N}I(S^k;Y^N)\hfill \\ & =& \frac{1}{N}(H(S^k)-H(S^k|Y^N))\hfill \\ & {\ge }^{(d)}& \frac{1}{N}(k{H}_S-k\delta (P_e))\hfill \end{array}$$

where Formula (a) follows from the definition that $U_n=(S^k,Y^{n-1},V_{n+1}^N)$. Formulas (b) and (c) follow from the fact that $V_{n+1}^N$ is independent of $Y_n,Y^{n-1},S^k,V_n$. Formula (d) follows from $H(S^k)=k{H}_S$ and the Fano’s inequality.

The proof of step (iv) is completed.

3.3.5. Proof of Step (v)

Substituting step (ii), step (iii), step (iv) into step (i), and using the non-increasing property of ${\Gamma }^{{}^{\prime }}(R)$[Lemma 1 (iii)], it is easy to see that

$$\frac{k{H}_S\Delta -k\delta (P_e)}{N}\le {\Gamma }^{{}^{\prime }}(\frac{k{H}_S-k\delta (P_e)}{N})$$

(3.41)

By using the definition of achievable $(R,d)$ pair, i.e., $\Delta \ge d-ϵ$, $\frac{H_{S}k}{N}\ge R-ϵ$, $P_e\le ϵ$, and the fact that $\delta (P_e)\le \delta (ϵ)$, we know from Equation (3.41) that

$$\begin{array}{ccc}\hfill (R-ϵ)(d-ϵ)-\delta (ϵ)& \le & \frac{k{H}_S\Delta -k\delta (P_e)}{N}\hfill \\ & \le & {\Gamma }^{{}^{\prime }}(\frac{k{H}_S-k\delta (P_e)}{N})\hfill \\ & {\le }^{(a)}& {\Gamma }^{{}^{\prime }}(R-ϵ-\delta (ϵ))\hfill \end{array}$$

(3.42)

where the formula (a) follows from the non-increasing property of ${\Gamma }^{{}^{\prime }}(R)$ [Lemma 1 (iii)]. In Equation (3.42), letting $ϵ\to 0$ and invoking the continuity of ${\Gamma }^{{}^{\prime }}(R)$ [Lemma 1 (iv)] yield $Rd\le {\Gamma }^{{}^{\prime }}(R)$. The proof of step (v) is completed.

The converse part of Theorem 5 is proved.

4. Proof of Theorem 3 and Direct Half of Theorem 5

In this section, all logarithms are taken to the base 2.

4.1. Proof of Theorem 3

In this subsection, we will show the achievability of the region ${\mathcal{R}}_{ci}$, and we only need to prove that the pair $(R,d=\frac{I(U;Y)-I(U;Z)}{R})$ is achievable.

4.1.1. Coding Construction

Given the pair $(R,d=\frac{I(U;Y)-I(U;Z)}{R})$, let k and N satisfy $\frac{H_{S}k}{N}=R=I(U;Y)-\gamma$, where γ satisfies $0\le \gamma {\le }^{(a)}I(U;Z)$, and (a) is from $d=\frac{I(U;Y)-I(U;Z)}{R})\le 1$ and $R=I(U;Y)-\gamma$.

A separated source-channel coding method is provided. The source encoder is a mapping

$${\mathcal{S}}^k\to \mathcal{W}=\{1,2,\dots ,2^{k{H}_S(1+k^{-\frac{1}{4}})}\}$$

with the input $S^k$ and the output W.

Generate a random code-book composed of $2^{N(I(U;Y)-{\gamma }_1)}$ codewords of $u^N$ (${\gamma }_1$ is a small fixed positive number), and each of them is i.i.d. generated according to $p_U(u)$. Divide the code-book into $2^{k{H}_S(1+k^{-\frac{1}{4}})}$ bins, and each bin corresponds to a specific value in $\mathcal{W}$. There are $2^{NI(U;Y)-N{\gamma }_1-k{H}_S(1+k^{-\frac{1}{4}})}$ codewords in each bin. Note that

$$\begin{array}{ccc}& & NI(U;Y)-N{\gamma }_1-k{H}_S(1+k^{-\frac{1}{4}})=NI(U;Y)-N{\gamma }_1-NR-NR{k}^{-\frac{1}{4}}\hfill \\ & =& NI(U;Y)-N{\gamma }_1-N(I(U;Y)-\gamma )-NR{k}^{-\frac{1}{4}}\hfill \\ & =& N\gamma -N{\gamma }_1-NR{k}^{-\frac{1}{4}}\hfill \\ & {\le }^{(1)}& NI(U;Z)-N{\gamma }_1-NR{k}^{-\frac{1}{4}}\le NI(U;Z)\hfill \end{array}$$

(4.1)

where (1) is from $0\le \gamma \le I(U;Z)$. For a given w, randomly choose a codeword in bin w to transmit.

The $x^N$ is generated according to a new discrete memoryless channel (DMC) with inputs $u^N$, $v^N$, and output $x^N$. The transition probability of this new DMC is $p_{X|U,V}(x|u,v)$. Furthermore, we have

$$p_{X^N|U^N,V^N}(x^N|u^N,v^N)=\prod _{i=1}^N{p}_{X|U,V}(x_i|(u_i,v_i)$$

(4.2)

For given $y^N$, the legitimate receiver tries to find a sequence $u^N$ such that $(u^N,y^N)\in T_{UY}^N({ϵ}^{**})$. If there exists one sequence, put out the corresponding index $\widehat{w}$ of the bin, else declare a decoding error. Then, by using the mapping ${\mathcal{S}}^k\to \mathcal{W}$, put out the corresponding source ${\widehat{s}}^k$.

4.1.2. Proof of $\frac{H_{S}k}{N}\ge R-ϵ$, $P_e\le ϵ$, and $\Delta \ge d-ϵ$

By using the above definitions, it is easy to verify that $\frac{H_{S}k}{N}=R\ge R-ϵ$.

Then, observing the construction of $U^N$, it is easy to see that the codewords of $U^N$ is upper-bounded by $2^{NI(U;Y)}$. Since the main channel can be viewed as an ordinary DMC with input $U^N$ and output $Y^N$, from the standard channel coding theorem, we have $Pr\{W\ne \widehat{W}\}\to 0$ as the coding length $N\to \infty$. From the source coding theorem, we have $Pr\{S^k\ne {\widehat{S}}^k\}\to 0$ as $k=\frac{NR}{H_S}\to \infty$. So we can choose sufficiently large N to satisfy $Pr\{S^k\ne {\widehat{S}}^k\}+Pr\{W\ne \widehat{W}\}\le ϵ$, thus $P_e\le ϵ$ is proved.

It remains to show that $\Delta \ge d-ϵ$, see the following.

4.1.3. Proof of $\Delta \ge \frac{I(U;Y)-I(U;Z)}{R}-ϵ$

Since

$$\begin{array}{ccc}\hfill \frac{H(S^k)\Delta }{N}& =& \frac{1}{N}H(S^k|Z^N)=\frac{1}{N}(H(S^k,Z^N)-H(Z^N))\hfill \\ & =& \frac{1}{N}(H(S^k,Z^N,U^N)-H(U^N|S^k,Z^N)-H(Z^N))\hfill \\ & =& \frac{1}{N}(H(Z^N|S^k,U^N)+H(S^k)+H(U^N|S^k)-H(U^N|S^k,Z^N)-H(Z^N))\hfill \\ & {=}^{(a)}& \frac{1}{N}(H(Z^N|U^N)+H(S^k)+H(U^N|S^k)-H(U^N|S^k,Z^N)-H(Z^N))\hfill \\ & =& \frac{1}{N}(H(S^k)+I(U^N;Z^N|S^k)-I(U^N;Z^N))\hfill \\ & =& \frac{1}{N}(H(S^k)+H(Z^N|S^k)-H(Z^N|S^k,U^N)-I(U^N;Z^N))\hfill \\ & {\ge }^{(b)}& \frac{1}{N}(H(S^k)+H(Z^N|S^k,W)-H(Z^N|U^N)-I(U^N;Z^N))\hfill \\ & {=}^{(c)}& \frac{1}{N}(H(S^k)+H(Z^N|W)-H(Z^N|U^N,W)-I(U^N;Z^N))\hfill \\ & =& \frac{1}{N}(H(S^k)+I(U^N;Z^N|W)-I(U^N;Z^N))\hfill \\ & {\ge }^{(d)}& I(U;Y)-{\gamma }_1-R{k}^{-\frac{1}{4}}-\delta ({ϵ}^{**})-I(U;Z)\hfill \end{array}$$

(4.3)

where (a), (b) and (c) follow from $S^k\to W\to U^N\to Z^N$, (d) is from $\frac{H(S^k)}{N}=R=I(U;Y)-\gamma$,

$$\begin{array}{ccc}\hfill H(U^N|W)& =& \sum _{i=1}^{M}Pr\{W=i\}H(U^N|W=i)\hfill \\ & =& \sum _{i=1}^{M}Pr\{W=i\}log{2}^{NI(U;Y)-N{\gamma }_1-k{H}_S(1+k^{-\frac{1}{4}})}\hfill \\ & =& NI(U;Y)-N{\gamma }_1-k{H}_S(1+k^{-\frac{1}{4}})\hfill \\ & =& NI(U;Y)-N{\gamma }_1-k{H}_S-NR{k}^{-\frac{1}{4}}\hfill \end{array}$$

(4.4)

and the fact that given W and $Z^N$, there are $2^{NI(U;Y)-N{\gamma }_1-k{H}_S(1+k^{-\frac{1}{4}})}$ codewords left for the wiretapper, and therefore, by using Equation (4.1) and the standard channel coding theorem, we have $H(U^N|W,Z^N)\le N\delta ({ϵ}^{**})$, where ${ϵ}^{**}$ is an arbitrary small positive number. Then for sufficiently large N, choosing ${ϵ}^{**}$, ${\gamma }_1$ , $R{k}^{-\frac{1}{4}}$ such that ${\gamma }_1+R{k}^{-\frac{1}{4}}+\delta ({ϵ}^{**})\le ϵR$, and using $\frac{H(S^k)}{N}=R$, we have $\Delta \ge \frac{I(U;Y)-I(U;Z)}{R}-ϵ$. The proof for $\Delta \ge d-ϵ$ is completed.

The proof of Theorem 3 is completed.

4.2. Proof of the Direct Half of Theorem 5

In this subsection we establish the direct part of Theorem 5 (about existence), i.e., ${\mathcal{R}}^{*}\subseteq {\mathcal{C}}_m$. Suppose $(R,d)\in {\mathcal{R}}^{*}$, i.e., $(R,d)$ satisfies the following conditions:

$$0\le R\le C_M,0\le d\le 1\mathrm{and}Rd\le {\Gamma }^{{}^{\prime }}(R)$$

We will show that $(R,d)\in \mathcal{R}$, that is to say, $(R,d)$ is achievable, i.e., for any given $ϵ>0$, there exists an encoder-decoder $(N,k,\Delta ,P_e)$ such that

$$\frac{H_{S}k}{N}\ge R-ϵ,\Delta \ge d-ϵ,P_e\le ϵ$$

A sufficient condition of the corresponding proof is to show that the $(R,d)$ pair satisfying

$$Rd={\Gamma }^{{}^{\prime }}(R)$$

(4.5)

is achievable, see the remaining of this section. The construction of the code is introduced in Section 4.2.1. For any given $ϵ>0$, the proofs of $\frac{H_{S}k}{N}\ge R-ϵ$ and $\Delta \ge d-ϵ$ are given in Section 4.2.2. Section 4.2.3 is about $P_e\le ϵ$.

4.2.1. Code Construction

The existence of the encoder-decoder is under the sufficient condition $Rd={\Gamma }^{{}^{\prime }}(R)$. Let k and N satisfy $\frac{H_{S}k}{N}=R$. Choose a probability mass function $Pr\{X^{*}=x|U^{*}=u,V=v\}Pr\{U^{*}=u\}$ such that $I(U^{*};Y^{*})\ge R$ and $I(U^{*};Y^{*})-I(U^{*};Z^{*})={\Gamma }^{{}^{\prime }}(R)$, where $U^{*}$ and V are the inputs of the channel encoder, while $X^{*}$ is the output, $Y^{*}$ and $Z^{*}$ are the respective outputs of the main channel and the wiretap channel.

A separated source-channel coding method is provided. The source encoder is a mapping ${\mathcal{S}}^k\to \{1,2,\dots ,M\}$, with the input $S^k$ and the output W. According to the specific value of W, generate $M_1$ codewords $\{u^N(w,m):1\le w\le M,1\le m\le M_2\}$ i.i.d. according to $Pr\{U^{*}=u\}$, where $M_1=2^{NI(U^{*};Y^{*})}$, $M=2^{k{H}_S(1+k^{-\frac{1}{4}})}$ and $M_2=\frac{M_1}{M}=2^{NI(U^{*};Y^{*})-k{H}_S(1+k^{-\frac{1}{4}})}$ (note that $\frac{1}{N}log{M}_2\le I(U^{*};Z^{*})-ϵ$, and this is from the similar argument in [1], p. 1377).

For a given w, there is a corresponding subcode $C_w=\{u^N(w,1),\dots ,u^N(w,M_2)\}$. Randomly choose a codeword $u^N(w,m)$ from $C_w$ to transmit.

The $x^N$ is generated according to a new discrete memoryless channel (DMC) with inputs $u^N(w,m)$, $v^N$, and output $x^N$. The transition probability of this new DMC is $p_{X^{*}|U^{*},V}(x|u,v)$. Furthermore, we have

$$p_{X^N|U^N,V^N}(x^N|u^N(w,m),v^N)=\prod _{i=1}^N{p}_{X^{*}|U^{*},V}(x_i|(u_i,v_i)$$

(4.6)

The inputs of the main channel are $x^N$ and $v^N$, while the output is $y^N$. In the decoding scheme, for given $y^N$, try to find a codeword $u^N(\widehat{w},\widehat{m})$ such that $(u^N(\widehat{w},\widehat{m}),y^N)\in T_{UY}^N({ϵ}^{****})$. If there is one or more such codeword, choose one and put out the corresponding $\widehat{w}$. According to $\widehat{w}$ and the mapping $F_D:\{1,2,\dots ,M\}\to {\mathcal{S}}^k$, put out the corresponding ${\widehat{s}}^k$.

4.2.2. Proofs of $\frac{H_{S}k}{N}\ge R-ϵ$ and $\Delta \ge d-ϵ$

Since $\frac{H_{S}k}{N}=R$, it is easy to see that $\frac{H_{S}k}{N}\ge R-ϵ$ for any $ϵ>0$. It remains to show that $\Delta \ge d-ϵ$, see the Formulas (4.7), (4.8), (4.12), (4.16) and (4.18).

$$\begin{array}{ccc}\hfill \frac{H(S^k)\Delta }{N}& =& \frac{1}{N}H(S^k|Z^N)=\frac{1}{N}(H(S^k,Z^N)-H(Z^N))\hfill \\ & =& \frac{1}{N}(H(S^k,Z^N,U^N)-H(U^N|S^k,Z^N)-H(Z^N))\hfill \\ & =& \frac{1}{N}(H(Z^N|S^k,U^N)+H(S^k)+H(U^N|S^k)-H(U^N|S^k,Z^N)-H(Z^N))\hfill \\ & {=}^{(a)}& \frac{1}{N}(H(Z^N|U^N)+H(S^k)+H(U^N|S^k)-H(U^N|S^k,Z^N)-H(Z^N))\hfill \\ & =& \frac{1}{N}(H(S^k)+I(U^N;Z^N|S^k)-I(U^N;Z^N))\hfill \\ & =& \frac{1}{N}(H(S^k)+H(Z^N|S^k)-H(Z^N|S^k,U^N)-I(U^N;Z^N))\hfill \\ & {\ge }^{(b)}& \frac{1}{N}(H(S^k)+H(Z^N|S^k,W)-H(Z^N|U^N)-I(U^N;Z^N))\hfill \\ & {=}^{(c)}& \frac{1}{N}(H(S^k)+H(Z^N|W)-H(Z^N|U^N,W)-I(U^N;Z^N))\hfill \\ & =& \frac{1}{N}(H(S^k)+I(U^N;Z^N|W)-I(U^N;Z^N))\hfill \end{array}$$

(4.7)

where (a), (b) and (c) follow from $S^k\to W\to U^N\to Z^N$. Then, we will estimate the two characters $I(U^N;Z^N|W)$ and $I(U^N;Z^N)$, respectively.

• $$I(U^N;Z^N|W)\ge log{M}_2-h(\overline{\lambda })-\overline{\lambda }log{M}_2$$

  (4.8)

  where $\overline{\lambda }={\sum }_{i=1}^{M}Pr\{W=i\}{\lambda }_i$, and ${\lambda }_i$ is the resulting error probability of a code $C_i=\{c^N(i,1),\dots ,c^N(i,M_2)\}$ used on the channel $Q_{MW}$.

Proof 8 

(Proof of Equation (4.8))

$$I(U^N;Z^N|W)=H(U^N|W)-H(U^N|W,Z^N)$$

(4.9)

$$\begin{array}{ccc}\hfill H(U^N|W)& =& \sum _{i=1}^{M}Pr\{W=i\}H(U^N|W=i)\hfill \\ & =& \sum _{i=1}^{M}Pr\{W=i\}log{M}_2\hfill \\ & =& log{M}_2\hfill \end{array}$$

(4.10)

$$\begin{array}{ccc}\hfill H(U^N|W,Z^N)& =& \sum _{i=1}^{M}Pr\{W=i\}H(U^N|W=i,Z^N)\hfill \\ & {\le }^{(a)}& \sum _{i=1}^{M}Pr\{W=i\}(h({\lambda }_i)+{\lambda }_{i}log{M}_2)\hfill \\ & {\le }^{(b)}& h(\sum _{i=1}^{M}Pr\{W=i\}{\lambda }_i)+\sum _{i=1}^{M}Pr\{W=i\}{\lambda }_{i}log{M}_2\hfill \\ & {=}^{(c)}& h(\overline{\lambda })+\overline{\lambda }log{M}_2\hfill \end{array}$$

(4.11)

Formula (a) follows from the Fano’s inequality. Formula (b) follows from the concavity of $h(·)$. Formula (c) follows from the definition of $\overline{\lambda }={\sum }_{i=1}^{M}Pr\{W=i\}{\lambda }_i$.

Substituting Equations (4.10) and (4.11) into Equation (4.9), we get Equation (4.8).

• Since $U^N$ is composed of N i.i.d. random variables with probability mass function $Pr\{U^{*}=u\},u\in \mathcal{U}$, and $V^N$ is available at the encoder in a memoryless case, we have

  $$\begin{array}{ccc}\hfill \frac{1}{N}I(U^N;Z^N)& =& \frac{1}{N}\sum _{n=1}^{N}I(U_n;Z_n)\hfill \\ & =& I(U^{*};Z^{*})\hfill \end{array}$$

  (4.12)

Substituting $\frac{H(S^k)}{N}=R$, Equations (4.8) and (4.12) into Equation (4.7),

$$R\Delta \ge \frac{H(S^k)}{N}+\frac{log{M}_2}{N}-\frac{h(\overline{\lambda })}{N}-\frac{\overline{\lambda }log{M}_2}{N}-I(U^{*};Z^{*})$$

(4.13)

For $H(S^k)=k{H}_S$ and $log{M}_2=NI(U^{*};Y^{*})-k{H}_S(1+k^{-\frac{1}{4}})$, the Formula (4.13) can be written as follows,

$$R\Delta \ge I(U^{*};Y^{*})-\frac{k{H}_S}{N}{k}^{-\frac{1}{4}}-\frac{h(\overline{\lambda })}{N}-\frac{\overline{\lambda }log{M}_2}{N}-I(U^{*};Z^{*})$$

(4.14)

Since $\frac{k{H}_S}{N}=R$ and $I(U^{*};Y^{*})-I(U^{*};Z^{*})={\Gamma }^{{}^{\prime }}(R)$, we know from Equation (4.14) that

$$R\Delta \ge {\Gamma }^{{}^{\prime }}(R)-R{k}^{-\frac{1}{4}}-\frac{h(\overline{\lambda })}{N}-\frac{\overline{\lambda }log{M}_2}{N}$$

(4.15)

$R{k}^{-\frac{1}{4}}+\frac{h(\overline{\lambda })}{N}+\frac{\overline{\lambda }log{M}_2}{N}$ in the right part of Equation (4.15) is estimated as follows. Since the channel $Q_{MW}$ can be viewed as an ordinary DMC with input $U^N$ and output $Z^N$, by using the similar argument in [1], p. 1377, $\overline{\lambda }\to 0$ as the coding length $N\to \infty$. So with sufficiently large N, we choose N to satisfy

$$R{k}^{-\frac{1}{4}}+\frac{h(\overline{\lambda })}{N}+\frac{\overline{\lambda }log{M}_2}{N}\le ϵR$$

(4.16)

Substituting Equation (4.16) into Equation (4.15),

$$R\Delta \ge {\Gamma }^{{}^{\prime }}(R)-ϵR$$

(4.17)

Then by using Equation (4.5), Formula (4.17) can be rewritten as

$$\Delta \ge \frac{{\Gamma }^{{}^{\prime }}(R)}{R}-ϵ=d-ϵ$$

(4.18)

The proof of $\Delta \ge d-ϵ$ is completed.

4.2.3. Proof of $P_e\le ϵ$

$P_e=Pr\{S^k\ne {\widehat{S}}^k\}\le Pr\{S^k\ne F_D(W)\}+Pr\{W\ne \widehat{W}\}$. Since the main channel can be viewed as an ordinary DMC with input $U^N$ and output $Y^N$, from the standard channel coding theorem, we have $Pr\{W\ne \widehat{W}\}\to 0$ as the coding length $N\to \infty$. From the source coding theorem, we have $Pr\{S^k\ne F_D(W)\}\to 0$ as $k=\frac{NR}{H_S}\to \infty$. So we can choose sufficiently large N to satisfy $Pr\{S^k\ne F_D(W)\}+Pr\{W\ne \widehat{W}\}\le ϵ$, thus $P_e\le ϵ$. The proof is completed.

5. Conclusions

In this paper, we study the model of wiretap channel with side information. Inner and outer bounds are derived on the capacity-equivocation regions for the noncausal and causal manners (the inner bound for the noncausal manner is in fact equivalent to that of [9]), and the secrecy capacities for both manners are described and bounded. Moreover, for the case that the side information is available at the transmitter in a memoryless manner, both the capacity-equivocation region and the secrecy capacity are determined.