Wavelet q-Fisher Information for Scaling Signal Analysis
Abstract
:1. Introduction
2. Wavelet Analysis of Scaling Processes
2.1. Scaling Processes
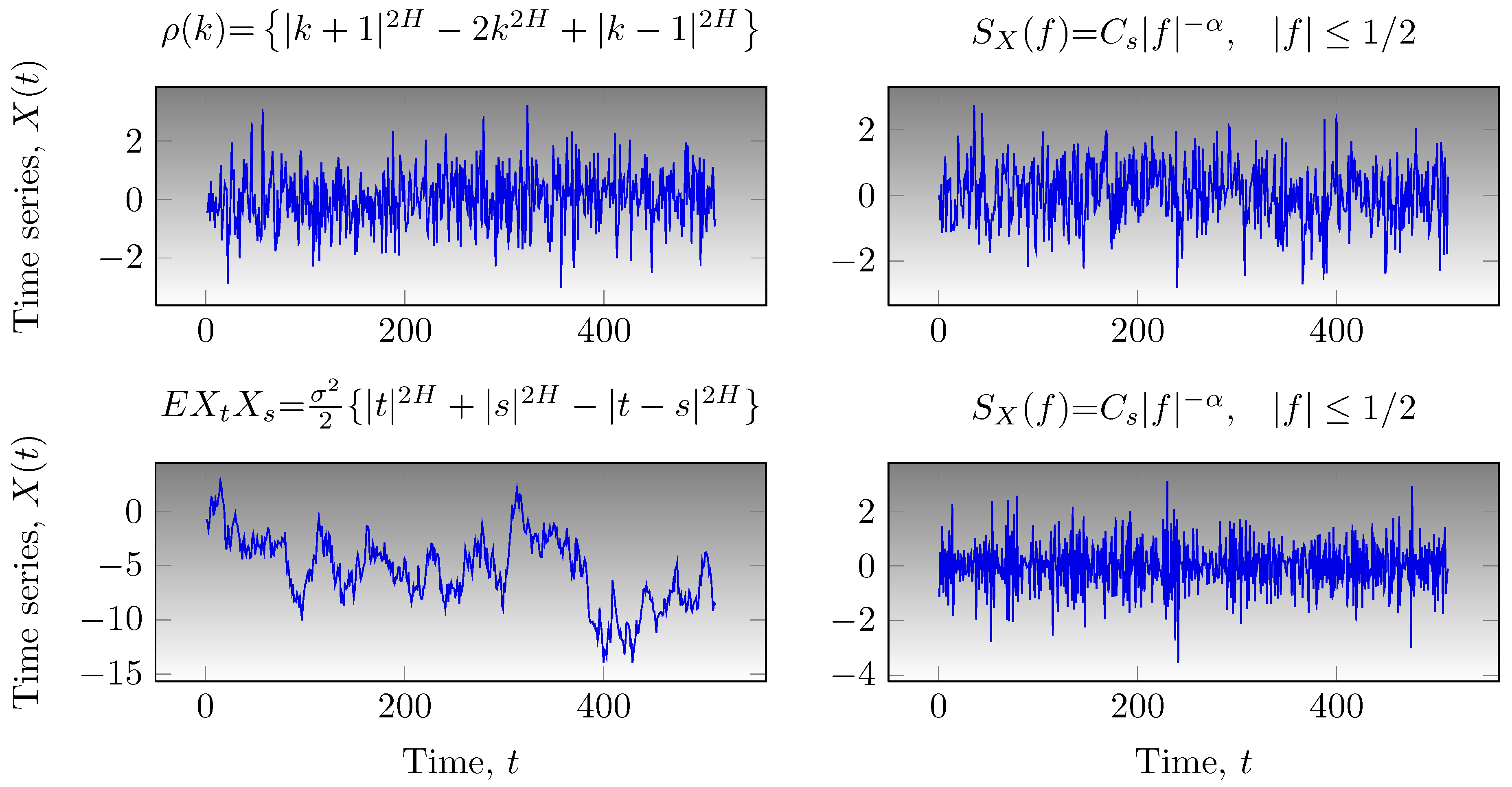
2.2. Wavelet Analysis of Scaling Signals
| Type of scaling process | Associated wavelet spectrum or variance |
|---|---|
| Long-memory process | , |
| Self-similar process | |
| Hsssi process | |
| dPPL process |
3. Wavelet q-Fisher Information of Signals
3.1. Time-Domain Fisher’s Information Measure
3.2. Wavelet q-Fisher Information
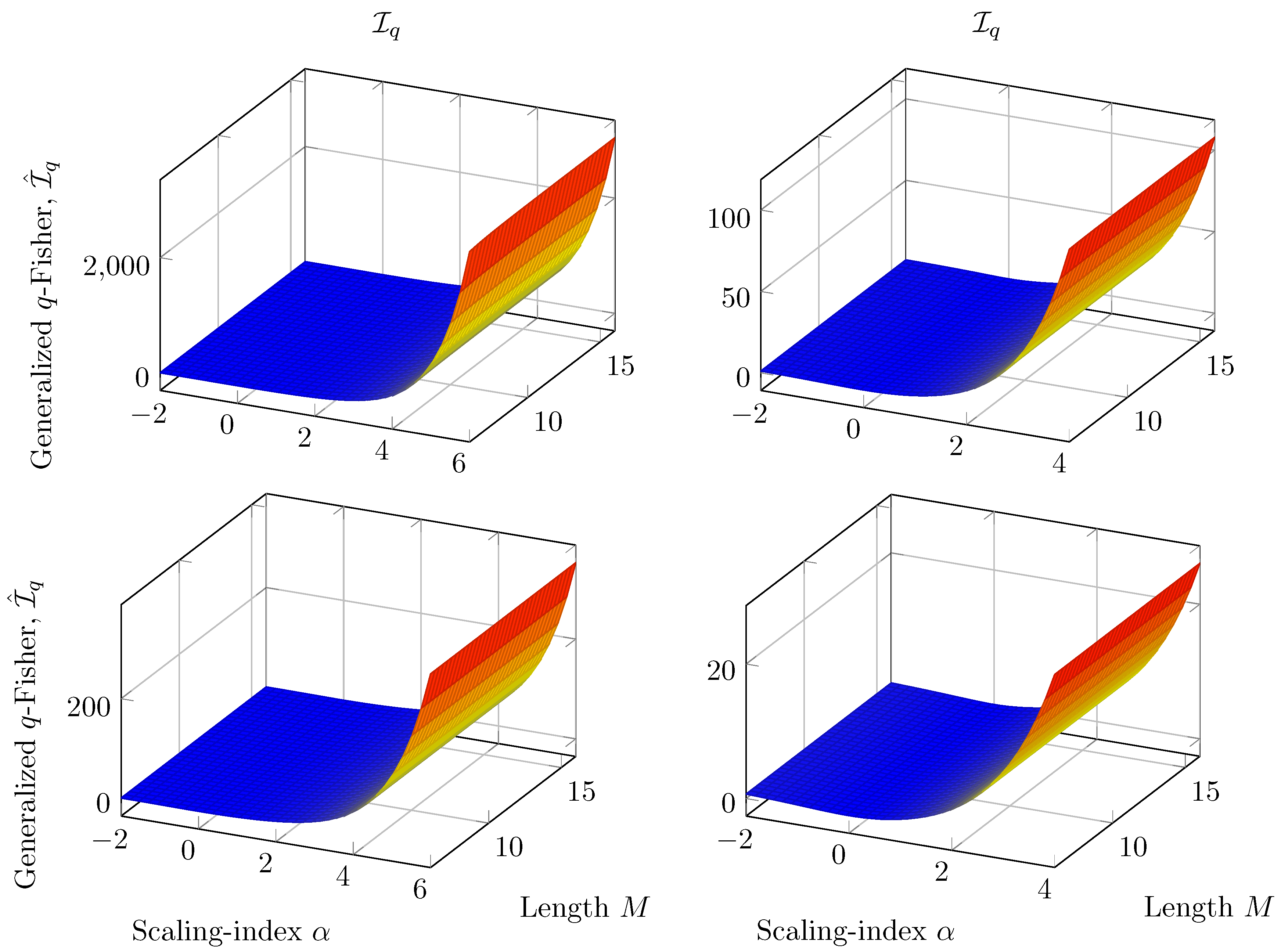
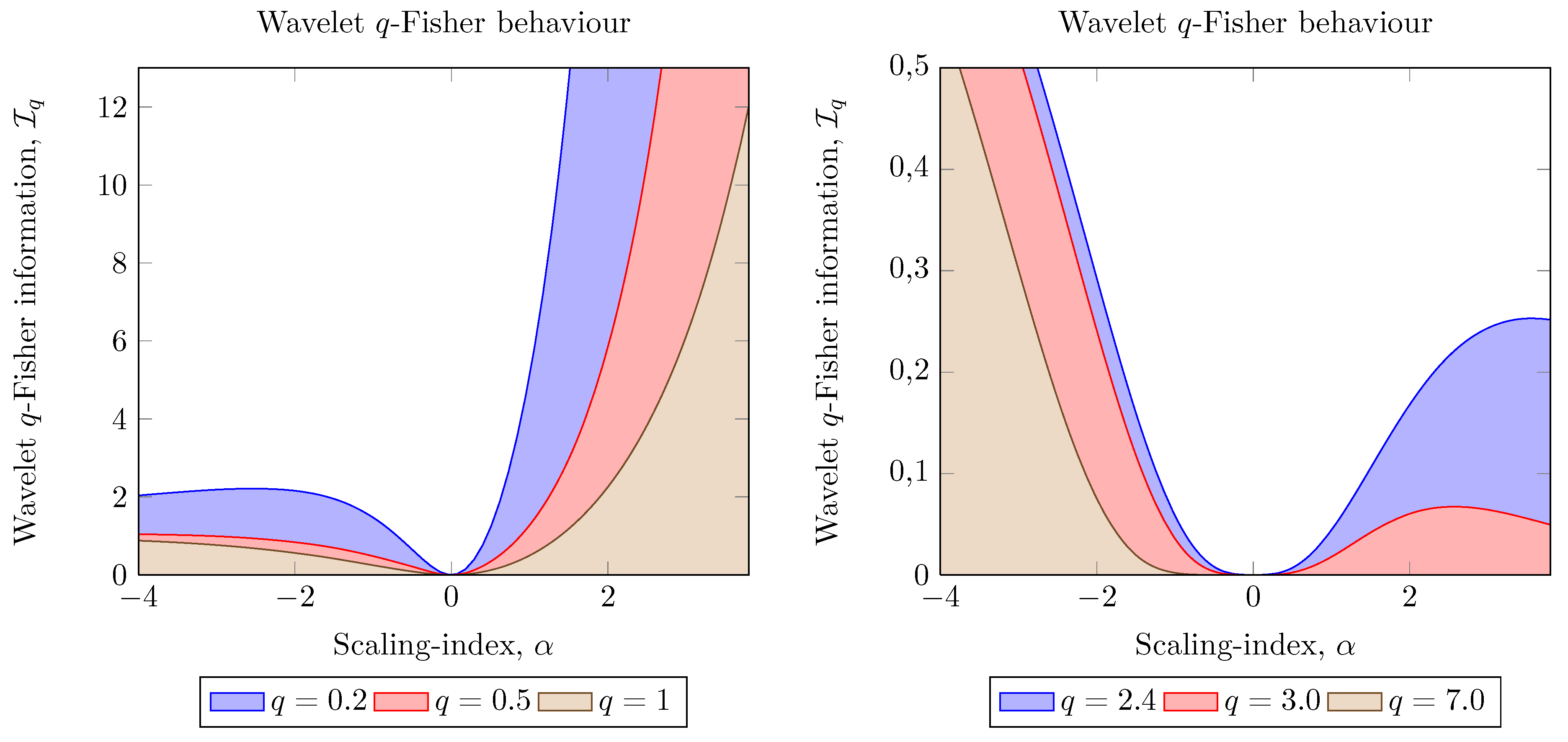
3.3. Applications of Wavelet Fisher’s Information Measure

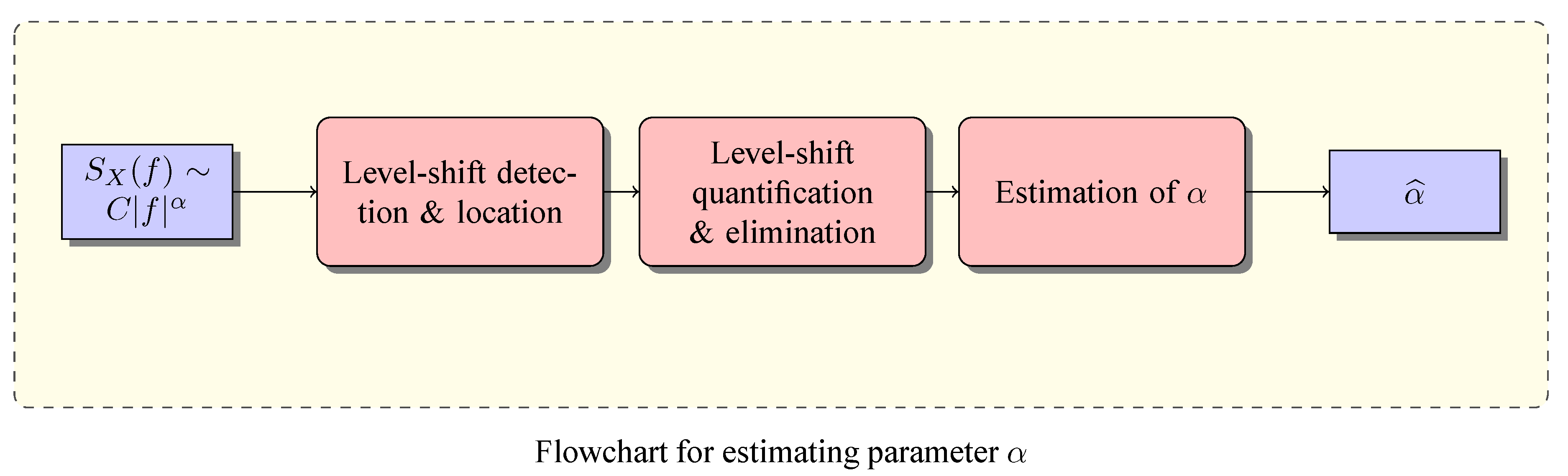
4. Level-Shift Detection Using Wavelet q-Fisher Information
4.1. The Problem of Level-Shift Detection
4.2. Level-Shift Detection Using Wavelet q-Fisher Information
5. Results and Discussion
5.1. Analysis of fGn Signals with Single Level-Shifts
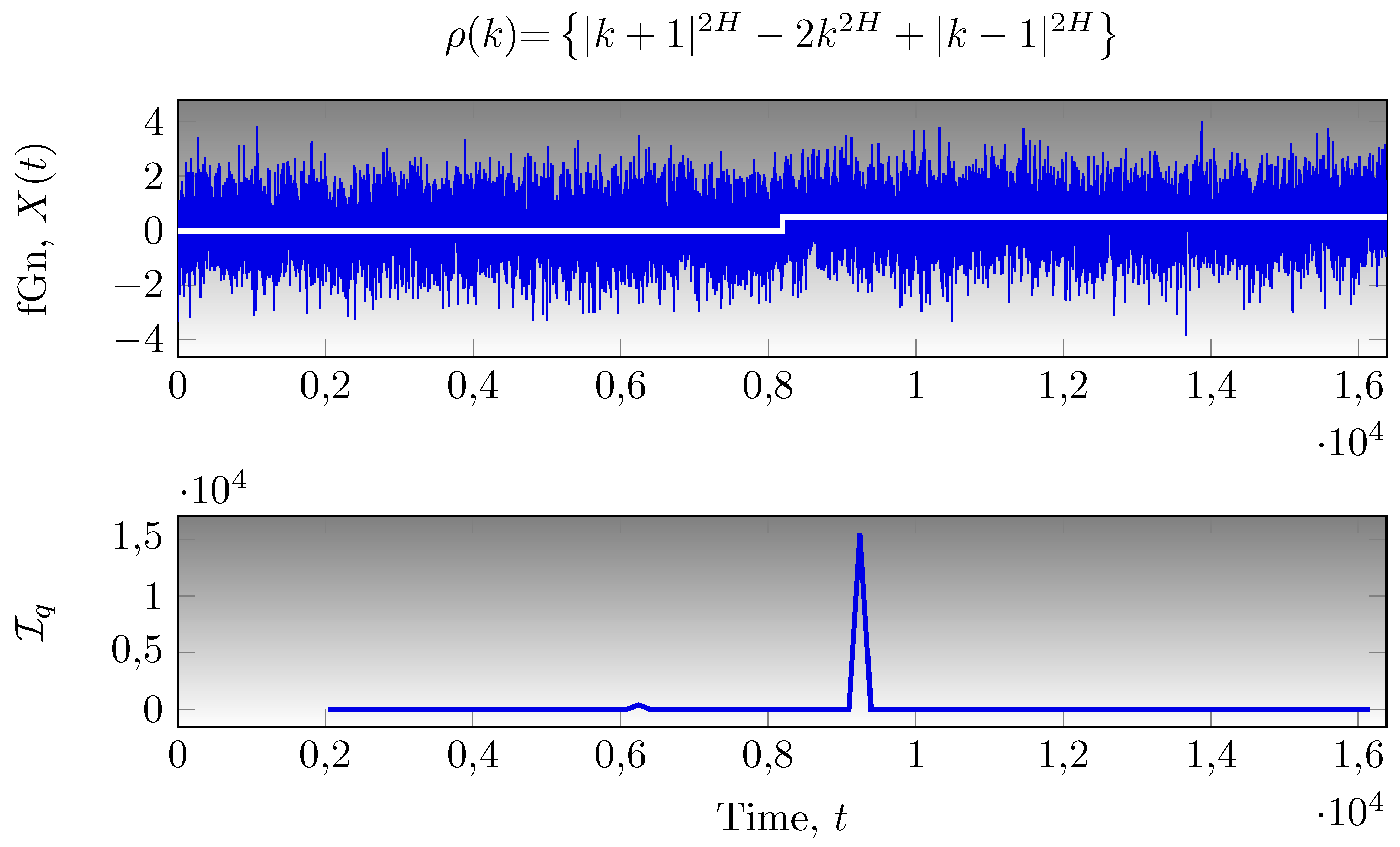
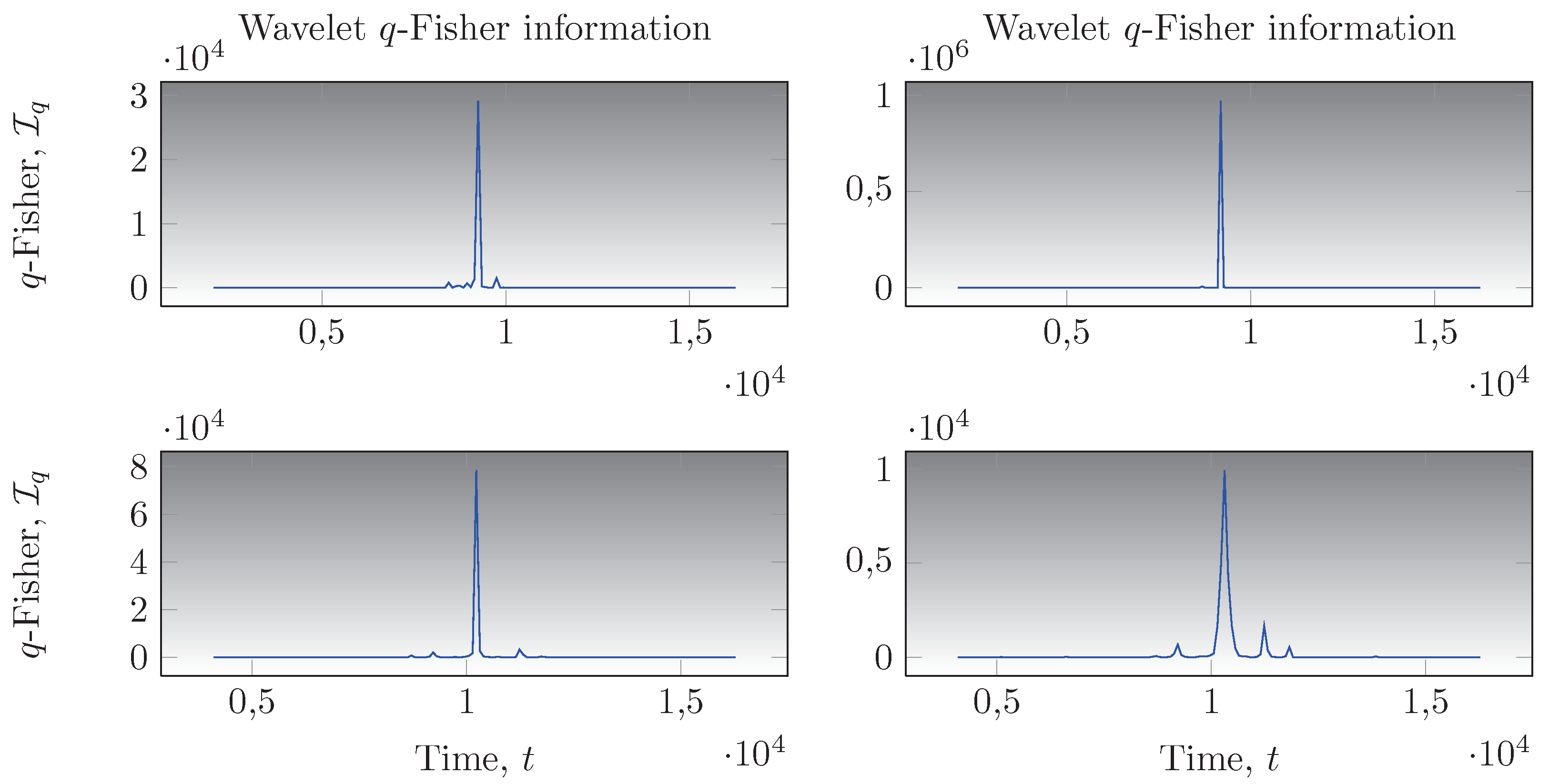

5.2. Comparison with Other Methods
| Statistics | Breakpoint detection using fGn signals | |||||
|---|---|---|---|---|---|---|
| Nominal H | ||||||
| Bai & Perron algorithm | Wavelet FIM Bai & Perron | |||||
| 0.3 | 0.5 | 0.7 | 0.3 | 0.5 | 0.7 | |
| BIAS | 456.1 | |||||
| σ | 4.41 | 32.2 | 569 | 138 | 256 | 562 |
| 4.37 | 31.64 | 722.33 | 484.1 | 551.1 | 706.4 | |
| μ | 2048 | 2048 | 1591 | 2512 | 2538 | 2487 |
| 2040 | 2000 | 646 | 2184 | 2104 | 1444 | |
| 2058 | 2186 | 2159 | 2844 | 3624 | 3624 | |
5.3. Application to H.263 Video Traces

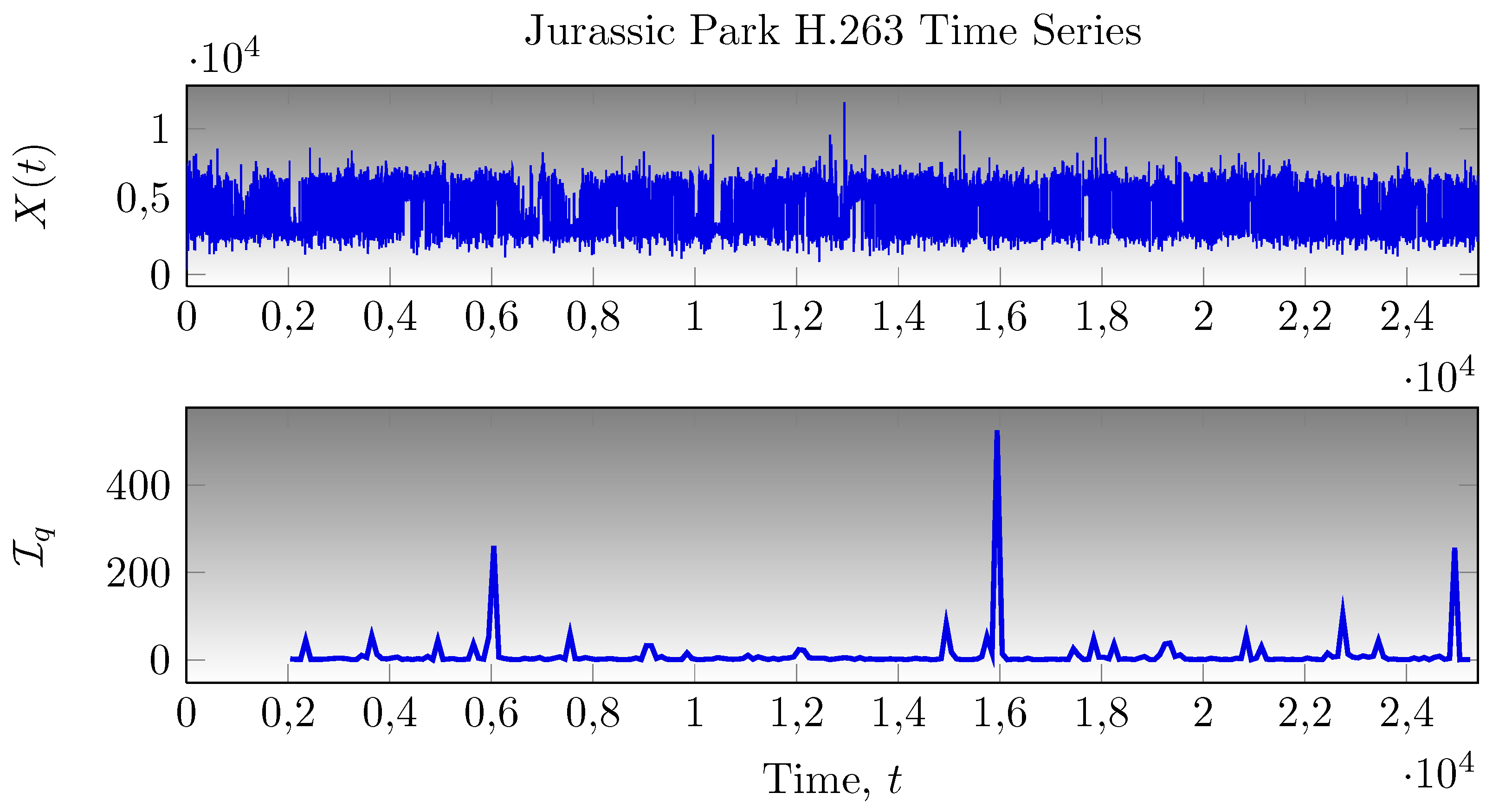

6. Conclusions
Acknowledgements
References
- Leland, W.E.; Taqqu, M.S.; Willinger, W.; Wilson, D. On the self-similar nature of ethernet traffic (extended version). IEEE/ACM Trans. Netw. 1994, 2, 1–15. [Google Scholar] [CrossRef]
- Paxson, V.; Floyd, S. Wide area traffic: The failure of poisson modeling. IEEE/ACM Trans. Netw. 1995, 3, 226–244. [Google Scholar] [CrossRef]
- Lee, I.W.C.; Fapojuwo, A.O. Stochastic processes for computer network traffic modelling. Comput. Commun. 2005, 29, 1–23. [Google Scholar] [CrossRef]
- Beran, J. Statistical methods for data with long-range dependence. Stat. Sci. 1992, 7, 404–416. [Google Scholar] [CrossRef]
- Beran, J.; Sherman, R.; Taqqu, M.S.; Willinger, W. Long-range dependence in variable-bit-rate video traffic. IEEE Trans. Commun. 1995, 43, 1566–1579. [Google Scholar] [CrossRef]
- Fitzek, F.H.P.; Reisslein, M. MPEG-4 and H.263 video traces for network performance evaluation. IEEE Netw. 2001, 15, 40–54. [Google Scholar] [CrossRef]
- Shen, H.; Zhu, Z.; Lee, T. Robust estimation of the self-similarity parameter in network traffic using the wavelet transform. Signal Process. 2007, 87, 2111–2124. [Google Scholar] [CrossRef]
- Stoev, S.; Taqqu, M.S.; Park, C.; Marron, J.S. On the wavelet spectrum diagnostic for Hurst parameter estimation in the analysis of internet traffic. Comput. Netw. 2005, 48, 423–445. [Google Scholar]
- Ramirez-Pacheco, J.; Torres-Roman, D. Cosh window behaviour of wavelet Tsallis q-entropies in signals. Electron. Lett. 2011, 47, 186–187. [Google Scholar] [CrossRef]
- Eke, A.; Hermán, P.; Bassingthwaighte, J.B.; Raymond, G.; Percival, D.B.; Cannon, M.; Balla, I.; Ikrényi, C. Physiological time series: Distinguishing fractal noises and motions. Pflugers Arch. 2000, 439, 403–415. [Google Scholar] [CrossRef] [PubMed]
- Plastino, A.; Plastino, A.R.; Miller, H.G. Tsallis nonextensive themostatistics and Fisher’s information measure. Phys. A 1997, 235, 557–588. [Google Scholar] [CrossRef]
- Samorodnitsky, G.; Taqqu, M. Stable Non-Gaussian Random Processes: Stochastic Models with Infinite Variance; Chapman & Hall/CRC Press: New York, NY, USA, 1994. [Google Scholar]
- Beran, J. Statistics for Long-Memory Processes; Chapman & Hall/CRC Press: New York, NY, USA, 1994. [Google Scholar]
- Mandal, S.; Arfin, S.K.; Sarpeshkar, R. Sub-pHz MOSFET 1/f noise measurements. Electron. Lett. 2009, 45, 81–82. [Google Scholar] [CrossRef]
- Serinaldi, F. Use and misuse of some Hurst parameter estimators applied to stationary and non-stationary financial time series. Phys Stat Mech Appl. 2010, 389, 2770–2781. [Google Scholar] [CrossRef]
- Malamud, B.D.; Turcotte, D.L. Self-affine time series: Measures of weak and strong persistence. J. Statist. Plann. Inference 1999, 80, 173–196. [Google Scholar] [CrossRef]
- Gallant, J.C.; Moore, I.D.; Hutchinson, M.F.; Gessler, P. Estimating the fractal dimension of profiles: A comparison of methods. Math. Geol. 1994, 26, 455–481. [Google Scholar] [CrossRef]
- Ramirez Pacheco, J.; Torres Román, D.; Toral Cruz, H. Distinguishing stationary/nonstationary scaling processes using wavelet Tsallis q-entropies. Math. Probl. Eng. 2012, 2012, 1–18. [Google Scholar] [CrossRef]
- Ramirez-Pacheco, J.; Torres-Román, D.; Rizo-Dominguez, L.; Trejo-Sánchez, J.; Manzano-Pinzón, F. Wavelet Fisher’s information of signals. Entropy 2011, 13, 1648–1663. [Google Scholar] [CrossRef]
- Bai, J.; Perron, P. Computation and analysis of multiple structural change models. J. Appl. Econom. 2003, 18, 1–22. [Google Scholar] [CrossRef]
- Percival, D.B. Stochastic models and statistical analysis for clock noise. Metrologia 2003, 40, S289. [Google Scholar] [CrossRef]
- Mandelbrot, B.; Van Ness, J.W. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Flandrin, P. Wavelet analysis and synthesis of fractional Brownian motion. IEEE Trans. Inform. Theor. 1992, 38, 910–917. [Google Scholar] [CrossRef]
- Lowen, S.B.; Teich, M.C. Estimation and simulation of fractal stochastic point processes. Fractals 1995, 3, 183–210. [Google Scholar] [CrossRef]
- Hudgins, L.; Friehe, C.A.; Mayer, M.E. Wavelet transforms and atmospheric turbulence. Phys. Rev. Lett. 1993, 71, 3279–3283. [Google Scholar] [CrossRef] [PubMed]
- Cohen, A.; Kovacevic, J. Wavelets: The mathematical background. Proc. IEEE 1996, 84, 514–522. [Google Scholar] [CrossRef]
- Abry, P.; Veitch, D. Wavelet analysis of long-range dependent traffic. IEEE Trans. Inform. Theor. 1998, 44, 2–15. [Google Scholar] [CrossRef]
- Veitch, D.; Abry, P. A wavelet based joint estimator of the parameters of long-range dependence. IEEE Trans. Inform. Theor. 1999, 45, 878–897. [Google Scholar] [CrossRef]
- Bardet, J.M. Statistical study of the wavelet analysis of fractional brownian motion. IEEE Trans. Inform. Theor. 2002, 48, 991–999. [Google Scholar] [CrossRef]
- Pesquet-Popescu, B. Statistical properties of the wavelet decomposition of certain non-Gaussian self-similar processes. Signal Process. 1999, 75, 303–322. [Google Scholar] [CrossRef]
- Martin, M.T.; Penini, F.; Plastino, A. Fisher’s information and the analysis of complex signals. Phys. Stat. Mech. Appl. 1999, 256, 173–180. [Google Scholar] [CrossRef]
- Martin, M.T.; Perez, J.; Plastino, A. Fisher information and non-linear dynamics. Phys. Stat. Mech. Appl. 2001, 291, 523–532. [Google Scholar] [CrossRef]
- Telesca, L.; Lapenna, V.; Lovallo, M. Fisher information measure of geoelectrical signals. Phys. Stat. Mech. Appl. 2005, 351, 637–644. [Google Scholar] [CrossRef]
- Romera, E.; Sánchez-Moreno, P.; Dehesa, J.S. The Fisher information of single-particle systems with a central potential. Chem. Phys. Lett. 2005, 414, 468–472. [Google Scholar] [CrossRef]
- Luo, S. Quantum Fisher information and uncertainty relation. Lett. Math. Phys. 2000, 53, 243–251. [Google Scholar] [CrossRef]
- Vignat, C.; Bercher, J.-F. Analysis of signals in the Fisher–Shannon information plane. Phys. Lett. A 2003, 312, 27–33. [Google Scholar] [CrossRef]
- Frieden, B.R.; Hughes, R.J. Spectral 1/f noise derived from extremized physical information. Phys. Rev. E 1994, 49, 2644–2649. [Google Scholar] [CrossRef]
- Perez, D.G.; Zunino, L.; Garavaglia, M.; Rosso, O.A. Wavelet entropy and fractional Brownian motion time series. Phys. Stat. Mech. Appl. 2006, 365, 282–288. [Google Scholar] [CrossRef]
- Zunino, L.; Perez, D.G.; Garavaglia, M.; Rosso, O.A. Wavelet entropy of stochastic processes. Phys. Stat. Mech. Appl. 2007, 379, 503–512. [Google Scholar] [CrossRef]
- Kowalski, A.M.; Plastino, A.; Casas, M. Generalized complexity and classical quantum transition. Entropy 2009, 11, 111–123. [Google Scholar] [CrossRef] [Green Version]
- Quiroga, R.Q.; Rosso, O.A.; Basar, E.; Schurmann, M. Wavelet entropy in event-related potentials: A new method shows ordering of EEG oscillations. Biol. Cybern. 2001, 84, 291–299. [Google Scholar] [CrossRef] [PubMed]
- Borges, E.P. A possible deformed algebra and calculus inspired in nonextensive thermostatistics. Phys. Stat. Mech. Appl. 2004, 340, 95–101. [Google Scholar] [CrossRef]
- Eke, A.; Hermán, P.; Kocsis, L.; Kozak, L.R. Fractal characterization of complexity in temporal physiological signals. Physiol. Meas. 2002, 23, R1–R38. [Google Scholar] [CrossRef] [PubMed]
- Deligneres, D.; Ramdani, S.; Lemoine, L.; Torre, K.; Fortes, M.; Ninot, G. Fractal analyses of short time series: A re-assessment of classical methods. J. Math. Psychol. 2006, 50, 525–544. [Google Scholar] [CrossRef]
- Castiglioni, P.; Parato, G.; Civijian, A.; Quintin, L.; Di Rienzo, M. Local scale exponents of blood pressure and heart rate variability by detrended fluctuation analysis: Effects of posture, exercise and aging. IEEE Trans. Biomed. Eng. 2009, 56, 675–684. [Google Scholar] [CrossRef] [PubMed]
- Esposti, F.; Ferrario, M.; Signorini, M.G. A blind method for the estimation of the Hurst exponent in time series: Theory and methods. Chaos 2008, 18, 033126–033126-8. [Google Scholar] [CrossRef] [PubMed]
- Rea, W.; Reale, M.; Brown, J.; Oxley, L. Long-memory or shifting means in geophysical time series? Math. Comput. Simulat. 2011, 81, 1441–1453. [Google Scholar] [CrossRef]
- Capelli, C.; Penny, R.N.; Rea, W.; Reale, M. Detecting multiple mean breaks at unknown points with Atheoretical Regression Trees. Math. Comput. Simulat. 2008, 78, 351–356. [Google Scholar] [CrossRef]
- Davies, R.B.; Harte, D.S. Tests for Hurst effect. Biometrika 1987, 74, 95–101. [Google Scholar] [CrossRef]
- Cannon, M.; Percival, D.B.; Caccia, D.C.; Raymond, G.; Bassingthwaighte, J.B. Evaluating scaled windowed variance for estimating the hurst coefficient of time series. Phys. Stat. Mech. Appl. 1996, 241, 606–626. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ramírez-Pacheco, J.; Torres-Román, D.; Argaez-Xool, J.; Rizo-Dominguez, L.; Trejo-Sanchez, J.; Manzano-Pinzón, F. Wavelet q-Fisher Information for Scaling Signal Analysis. Entropy 2012, 14, 1478-1500. https://doi.org/10.3390/e14081478
Ramírez-Pacheco J, Torres-Román D, Argaez-Xool J, Rizo-Dominguez L, Trejo-Sanchez J, Manzano-Pinzón F. Wavelet q-Fisher Information for Scaling Signal Analysis. Entropy. 2012; 14(8):1478-1500. https://doi.org/10.3390/e14081478
Chicago/Turabian StyleRamírez-Pacheco, Julio, Deni Torres-Román, Jesús Argaez-Xool, Luis Rizo-Dominguez, Joel Trejo-Sanchez, and Francisco Manzano-Pinzón. 2012. "Wavelet q-Fisher Information for Scaling Signal Analysis" Entropy 14, no. 8: 1478-1500. https://doi.org/10.3390/e14081478
APA StyleRamírez-Pacheco, J., Torres-Román, D., Argaez-Xool, J., Rizo-Dominguez, L., Trejo-Sanchez, J., & Manzano-Pinzón, F. (2012). Wavelet q-Fisher Information for Scaling Signal Analysis. Entropy, 14(8), 1478-1500. https://doi.org/10.3390/e14081478




