Deterministic Thermal Reservoirs
Abstract
:1. Introduction
2. The Generalized Gibbs Relation: Kinetic Theory
3. The Model System
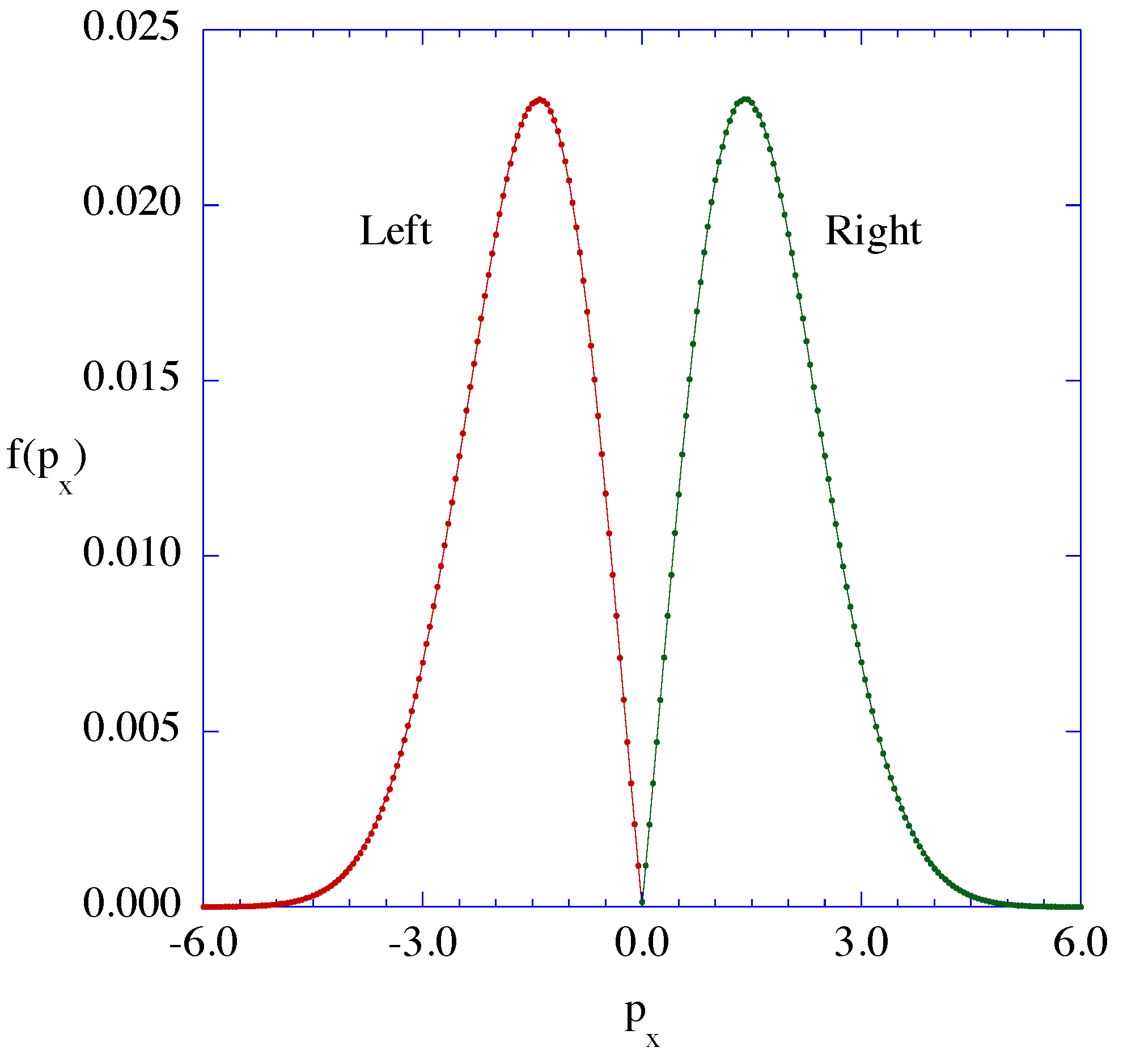
3.1. System Dynamics
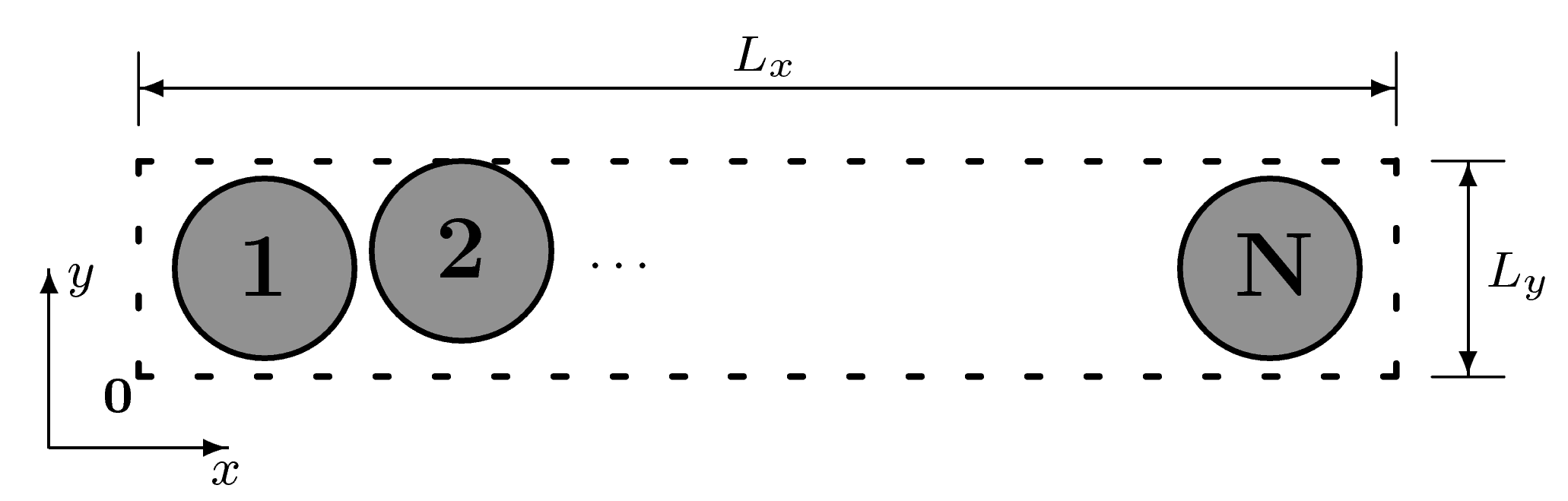
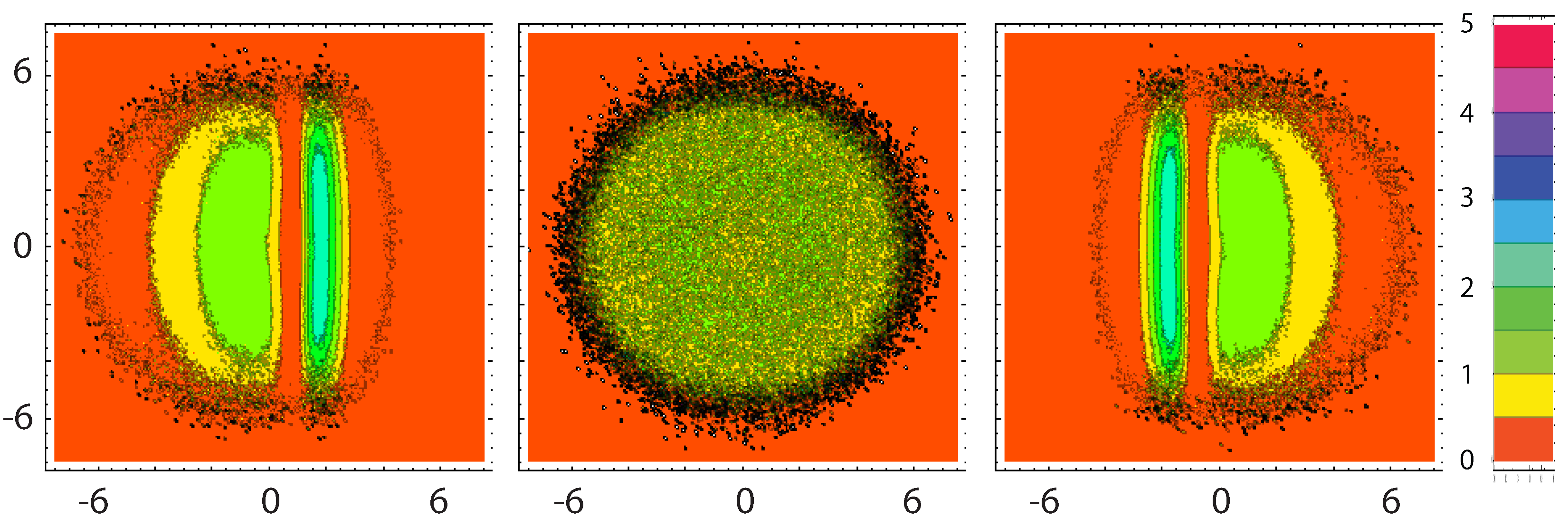
3.2. Energy Balance
| N | ||||
|---|---|---|---|---|
| 80 | ||||
| 160 | ||||
| 320 | ||||
| 640 | ||||
| 1280 | − | − |
| N | α | β | γ | T |
|---|---|---|---|---|
| 80 | ||||
| 160 | ||||
| 320 | ||||
| 640 |
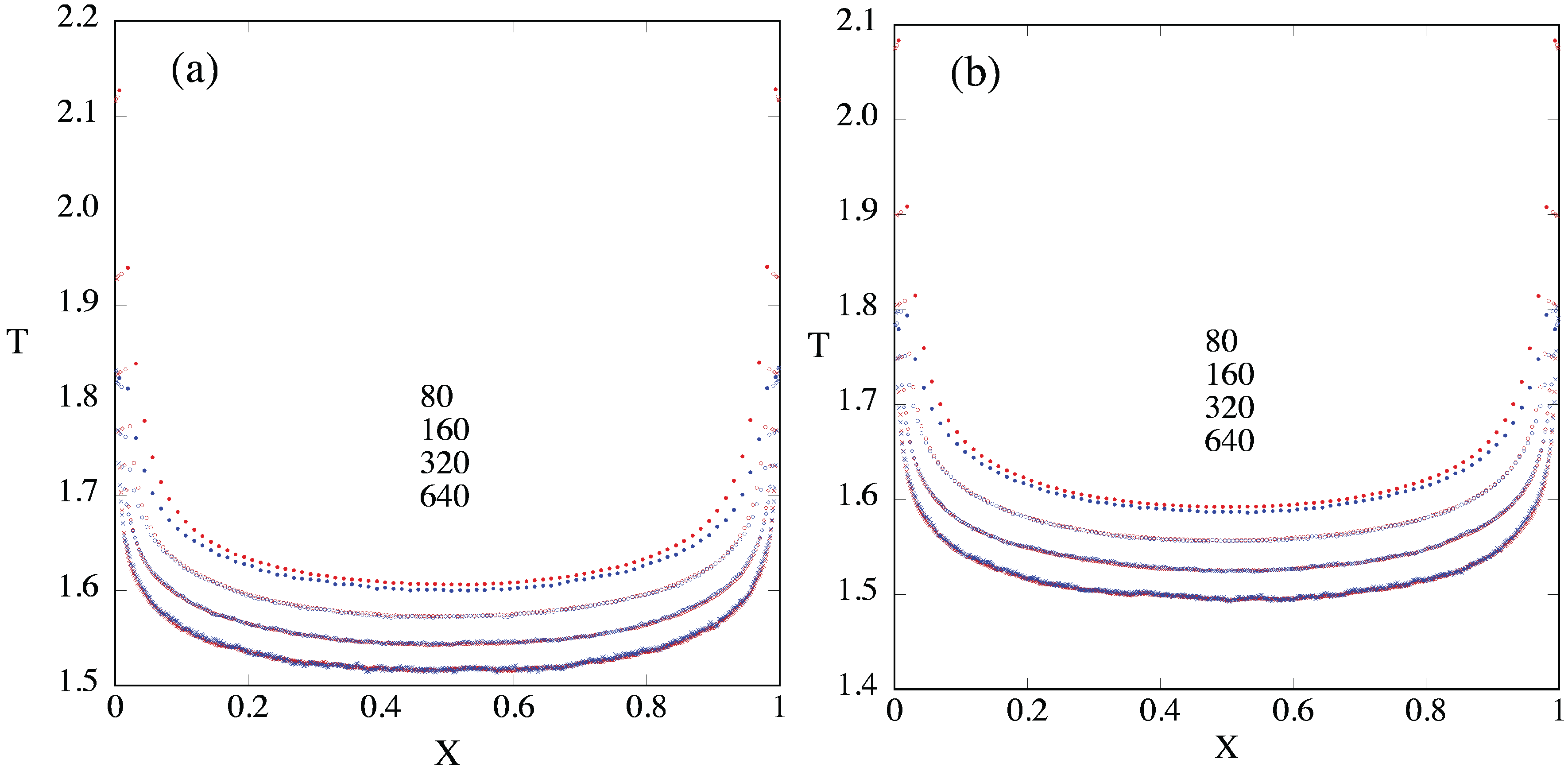
3.3. Temperature Profiles
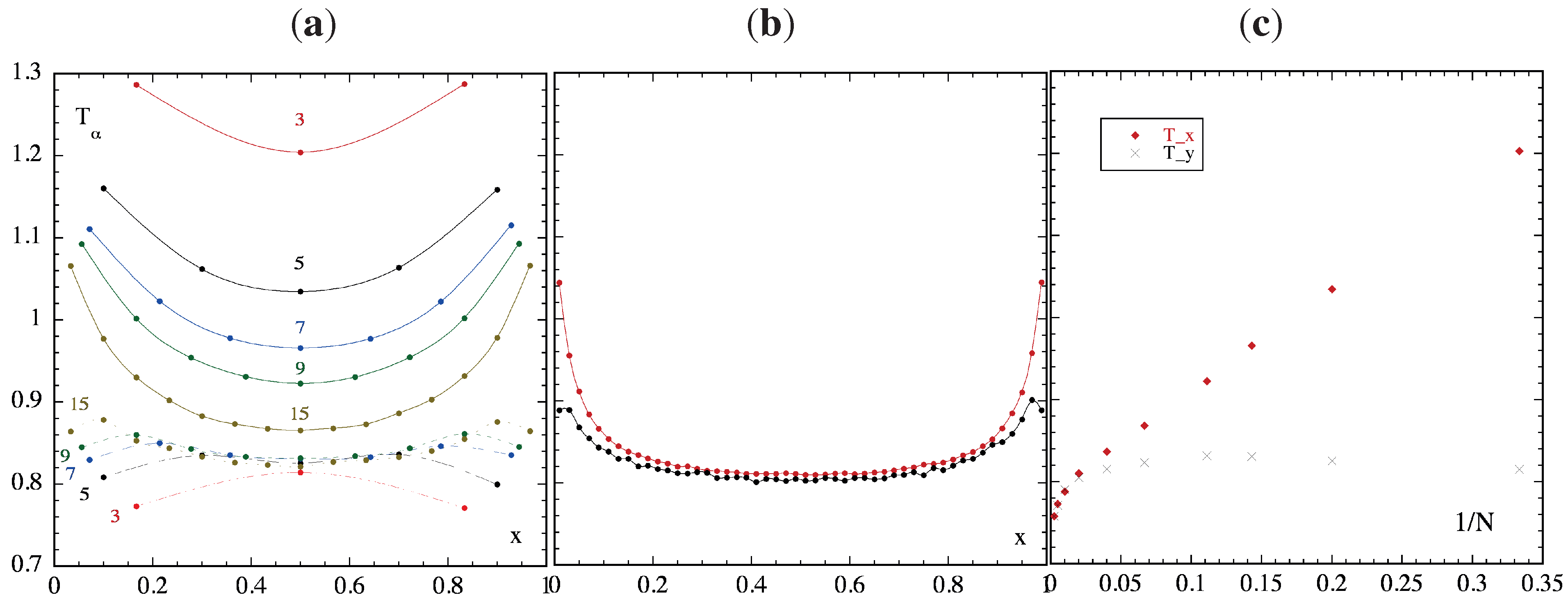
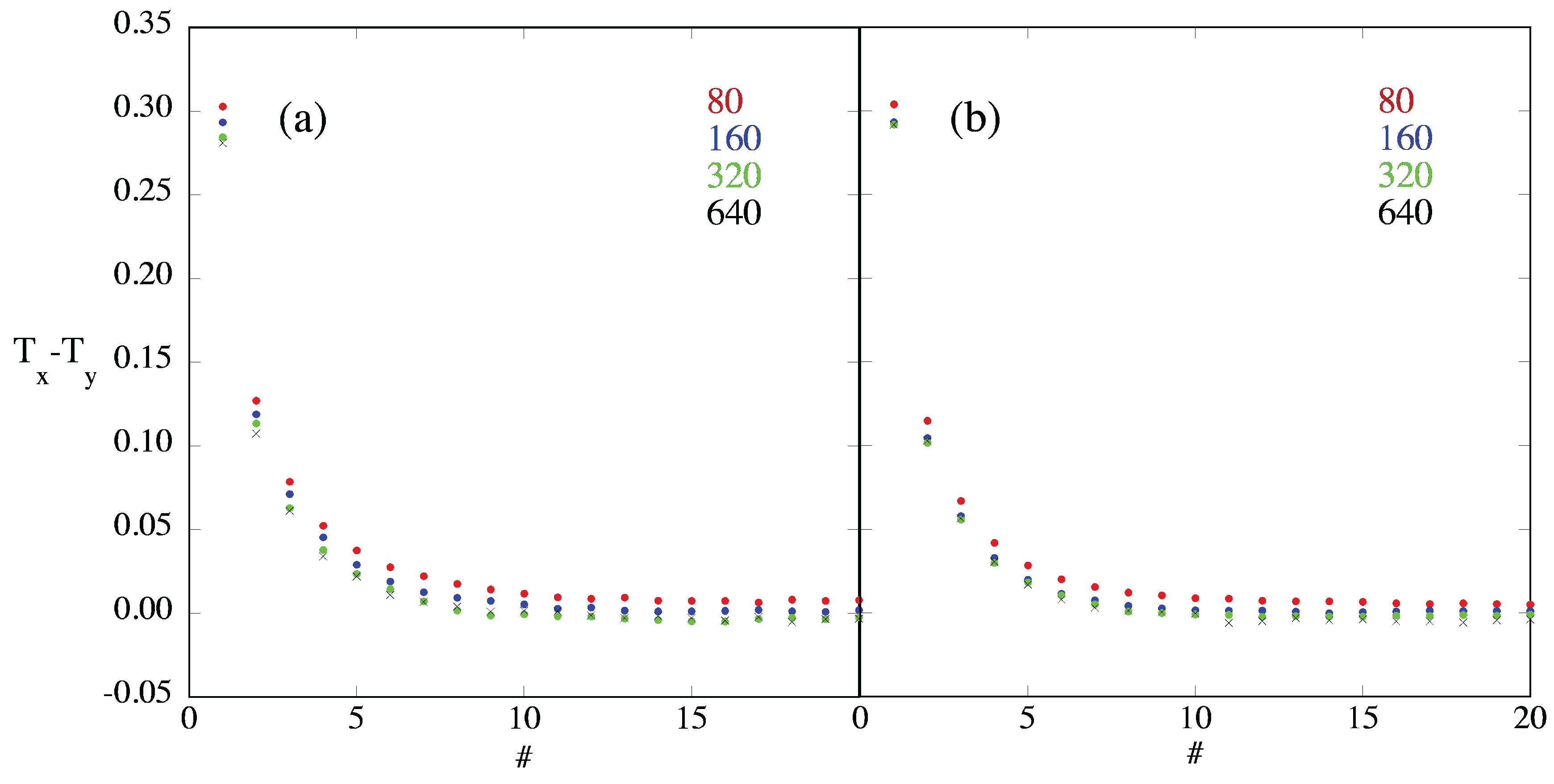
3.4. Temperature Differences and Equilibration
4. Entropy
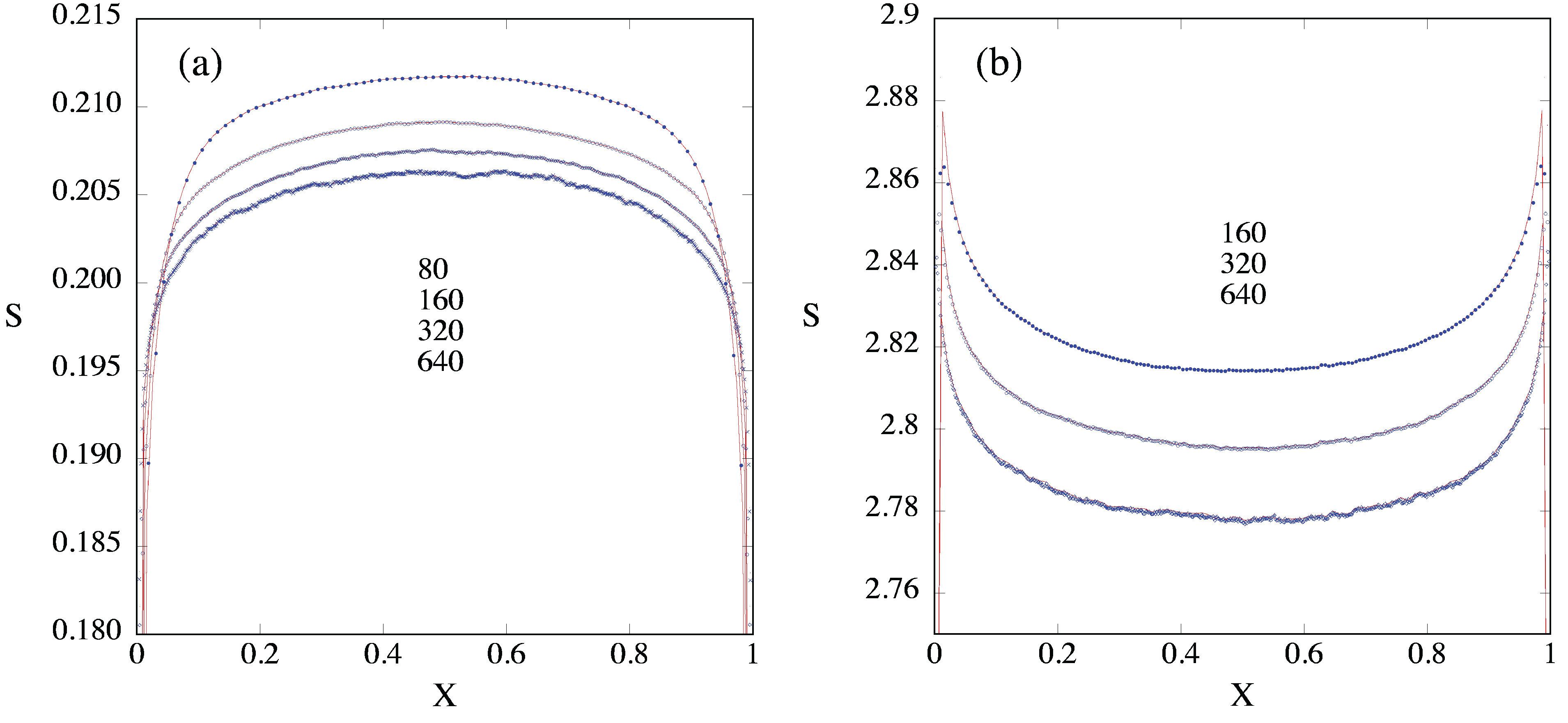
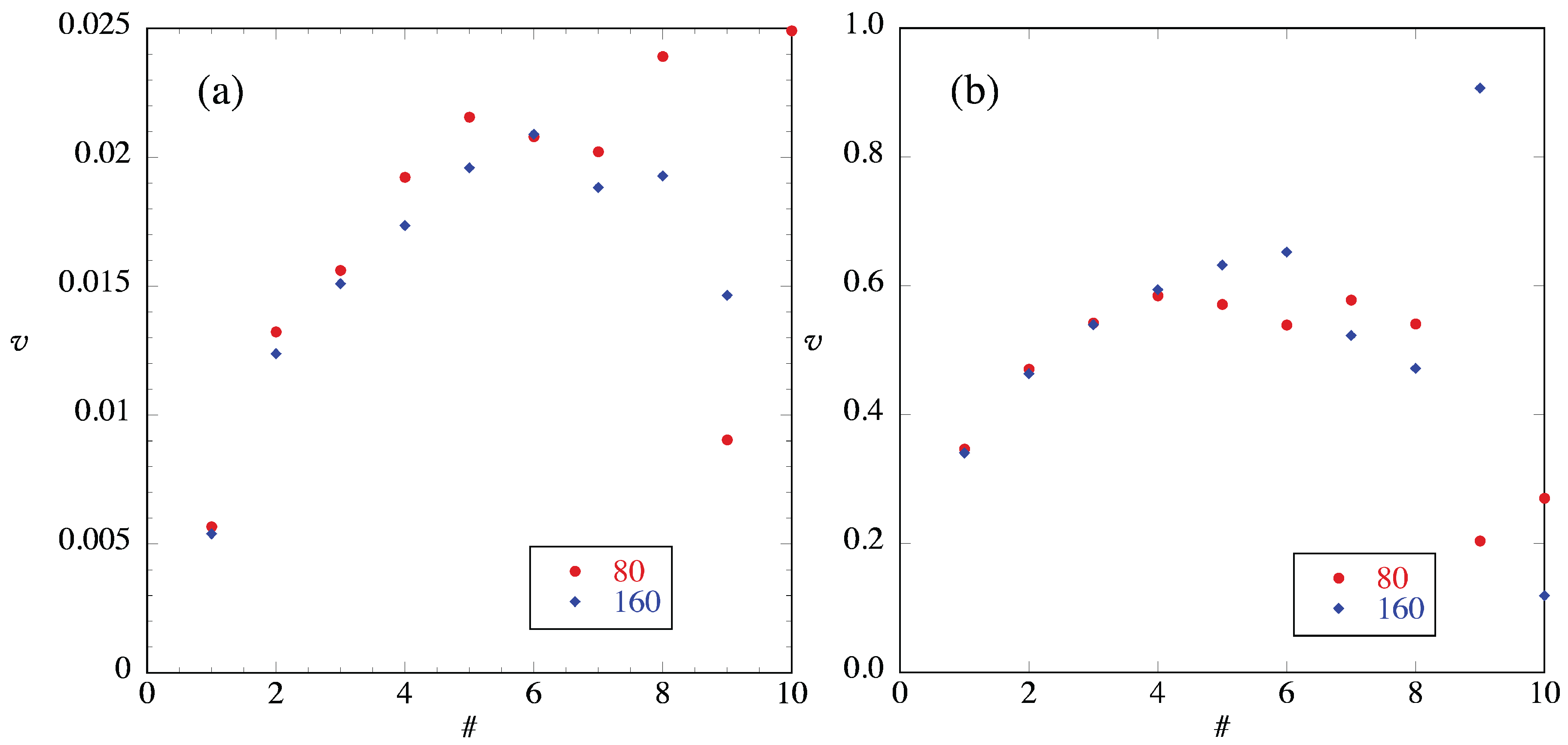
4.1. Entropy Production and Flux Near Reservoirs

| N | ||
|---|---|---|
| 80 | ||
| 160 | ||
| 320 | ||
| 640 |
5. Conclusions
References
- Hatano, T.; Sasa, S. Steady-state thermodynamics of Langevin systems. Phys. Rev. Lett. 2001, 86, 3463. [Google Scholar] [CrossRef] [PubMed]
- Morriss, G.P.; Rondoni, L. On a definition of temperature in equilibrium and nonequilibrium systems. Phys. Rev. E 1999, 59, 5. [Google Scholar] [CrossRef]
- Baranyai, A. Numerical temperature measurement in far from equilibrium model systems. Phys. Rev. E 2000, 61, 3306. [Google Scholar] [CrossRef]
- Baranyai, A. Temperature of nonequilibrium steady-state systems. Phys. Rev. E 2000, 62, 5989. [Google Scholar] [CrossRef]
- Jou, D.; Casas-Vazquez, J.; Lebon, G. Extended Irreversible Thermodynamics; Springer: Berlin, Germany, 2001. [Google Scholar]
- Ottinger, H.C. Beyond Equilibrium Thermodynamics; Wiley: New York, NY, USA, 2005. [Google Scholar]
- Ritort, F. Resonant nonequilibrium temperatures. J. Phys. Chem. B 2005, 109, 6787. [Google Scholar] [CrossRef] [PubMed]
- Garriga, A.; Ritort, F. Mode-dependent nonequilibrium temperature in aging systems. Phys. Rev. E 2005, 72, 031505. [Google Scholar] [CrossRef]
- Shokef, Y.; Shulkind, G.; Levine, D. Isolated nonequilibrium systems in contact. Phys. Rev. E 2007, 76, 030101. [Google Scholar] [CrossRef]
- Lepri, S.; Livi, R.; Politi, A. Thermal conduction in classical low-dimensional lattices. Phys. Rep. 2003, 377, 1. [Google Scholar] [CrossRef]
- Evans, D.J.; Morriss, G.P. Statistical Mechanics of Nonequilibrium Liquids, 2nd ed.; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Morriss, G.P.; Chung, T.; Angstmann, C. Thermal contact. Entropy 2008, 10, 786. [Google Scholar] [CrossRef]
- Lumpkin, M.E.; Saslow, W.M.; Visscher, W.M. One-dimensional Kapitza conductance: Comparison of the phonon mismatch theory with computer experiments. Phys. Rev. B 1978, 17, 4295. [Google Scholar] [CrossRef]
- Kim, C.S.; Morriss, G.P. Local entropy in a quasi-one-dimensional heat transport. Phys. Rev. E 2009, 80, 061137. [Google Scholar] [CrossRef]
- McLennan, J.A. Introduction to Non-equilibrium Statistical Mechanics; Prentice-Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Zwanzig, R. Nonequilibrium Statistical Mechanics; Oxford University Press: New York, NY, USA, 2001. [Google Scholar]
- Born, M.; Green, H.S. A general Kinetic Theory of Liquids; Cambridge University Press: London, UK, 1949; pp. 14–17. [Google Scholar]
- Cercignani, C. The Boltzmann Equation and Its Applications; Spinger-Verlag: New York, NY, USA, 1988. [Google Scholar]
- Dorfman, J.R.; van Beijeren, H. The kinetic theory of gases. In Statistical Mechanics, Part B: Time-Dependent Processes; Berne, B., Ed.; Plenum: New York, NY, USA, 1977. [Google Scholar]
- Taniguchi, T.; Morriss, G.P. Boundary effects in the stepwise structure of the Lyapunov spectra for quasi-one-dimensional systems. Phys. Rev. E 2003, 68, 026218. [Google Scholar] [CrossRef]
- Taniguchi, T.; Morriss, G.P. Lyapunov modes for a nonequilibrium system with a heat flux. Comptes Rendus Physique 2007, 8, 625. [Google Scholar] [CrossRef]
- Deutsch, J.M.; Narayan, O. One-dimensional heat conductivity exponent from a random collision model. Phys. Rev. E 2003, 68, 010201. [Google Scholar] [CrossRef]
- Deutsch, J.M.; Narayan, O. Correlations and scaling in one-dimensional heat conduction. Phys. Rev. E 2003, 68, 041203. [Google Scholar] [CrossRef]
- Eckmann, J.P.; Young, L.S. Temperature profiles in Hamiltonian heat conduction. Europhys. Lett. 2004, 68, 790. [Google Scholar] [CrossRef]
- Evans, D.J.; Morriss, G.P. Statistical Mechanics of Nonequilibrium Liquids, 2nd ed.; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Bright, J.N.; Evans, D.J.; Searles, D.J. New observations regarding deterministic, time-reversible thermostats and Gauss’s principle of least constraint. J. Chem. Phys. 2005, 122, 194106. [Google Scholar] [CrossRef] [PubMed]
- Evans, D.J.; Searles, D.J.; Williams, S.R. Musings on thermostats. J. Chem. Phys. 2010, 133, 104106. [Google Scholar] [CrossRef] [PubMed]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Morriss, G.P.; Truant, D. Deterministic Thermal Reservoirs. Entropy 2012, 14, 1011-1027. https://doi.org/10.3390/e14061011
Morriss GP, Truant D. Deterministic Thermal Reservoirs. Entropy. 2012; 14(6):1011-1027. https://doi.org/10.3390/e14061011
Chicago/Turabian StyleMorriss, Gary P., and Daniel Truant. 2012. "Deterministic Thermal Reservoirs" Entropy 14, no. 6: 1011-1027. https://doi.org/10.3390/e14061011
APA StyleMorriss, G. P., & Truant, D. (2012). Deterministic Thermal Reservoirs. Entropy, 14(6), 1011-1027. https://doi.org/10.3390/e14061011




