Some Further Results on the Minimum Error Entropy Estimation

Abstract

The minimum error entropy (MEE) criterion has been receiving increasing attention due to its promising perspectives for applications in signal processing and machine learning. In the context of Bayesian estimation, the MEE criterion is concerned with the estimation of a certain random variable based on another random variable, so that the error’s entropy is minimized. Several theoretical results on this topic have been reported. In this work, we present some further results on the MEE estimation. The contributions are twofold: (1) we extend a recent result on the minimum entropy of a mixture of unimodal and symmetric distributions to a more general case, and prove that if the conditional distributions are generalized uniformly dominated (GUD), the dominant alignment will be the MEE estimator; (2) we show by examples that the MEE estimator (not limited to singular cases) may be non-unique even if the error distribution is restricted to zero-mean (unbiased).

2. MEE Estimator for Generalized Uniformly Dominated Conditional Distributions

Before presenting the main theorem of this section, we give the following definitions.

Definition 1: Let $\mathit{ℱ}=\left\{f_t(x):{ℝ}^n\to {ℝ}_{+},t\in \mathbb{T}\right\}$ be a set of nonnegative, integrable functions, where $\mathbb{T}$ denotes an index set (possibly uncountable). Then $\mathit{ℱ}$ is said to be uniformly dominated in $x\in {ℝ}^n$ if and only if $\forall \epsilon \in \left[0,\infty \right)$, there exists a measurable set $D_{\epsilon }\subset {ℝ}^n$, satisfying $\lambda (D_{\epsilon })=\epsilon$ and:

$${\displaystyle \underset{D_{\epsilon }}{\int }{f}_t\left(x\right)dx}=\underset{A:\lambda (A)=\epsilon }{\sup }{\displaystyle \underset{A}{\int }{f}_t\left(x\right)dx},\forall t\in \mathbb{T}$$

(3)

where $\lambda$ is Lebesgue measure. The set $D_{\epsilon }$ is called the $\epsilon$-volume dominant support of $\mathit{ℱ}$.

Definition 2: The nonnegative, integrable function set $\mathit{ℱ}$ is said to be generalized uniformly dominated (GUD) in $x\in {ℝ}^n$ if and only if there exists a function $\pi :\mathbb{T}\to {ℝ}^n$, such that ${\mathit{ℱ}}_{\pi }$ is uniformly dominated, where:

$${\mathit{ℱ}}_{\pi }=\left\{f_t^{\pi }:f_t^{\pi }\left(x\right)=f_t\left(x+\pi (t)\right),t\in \mathbb{T}\right\}$$

(4)

The function $\pi (t)$ is called the dominant alignment of $\mathit{ℱ}$.

Remark 1: The dominant alignment is, obviously, non-unique. If $\pi (t)$ is a dominant alignment of $\mathit{ℱ}$, then $\forall c\in {ℝ}^n$, $\pi (t)+c$ will also be a dominant alignment of $\mathit{ℱ}$.

When regarding $y$ as an index parameter, the conditional PDF $p(x|y)$ will represent a set of nonnegative and integrable functions, that is:

$$\mathit{𝒫}=\left\{p(x|y):{ℝ}^n\to {ℝ}_{+},y\in {ℝ}^m\right\}$$

(5)

If the above function set is (generalized) uniformly dominated in $x\in {ℝ}^n$, then we say that the conditional PDF $p(x|y)$ is (generalized) uniformly dominated in $x\in {ℝ}^n$.

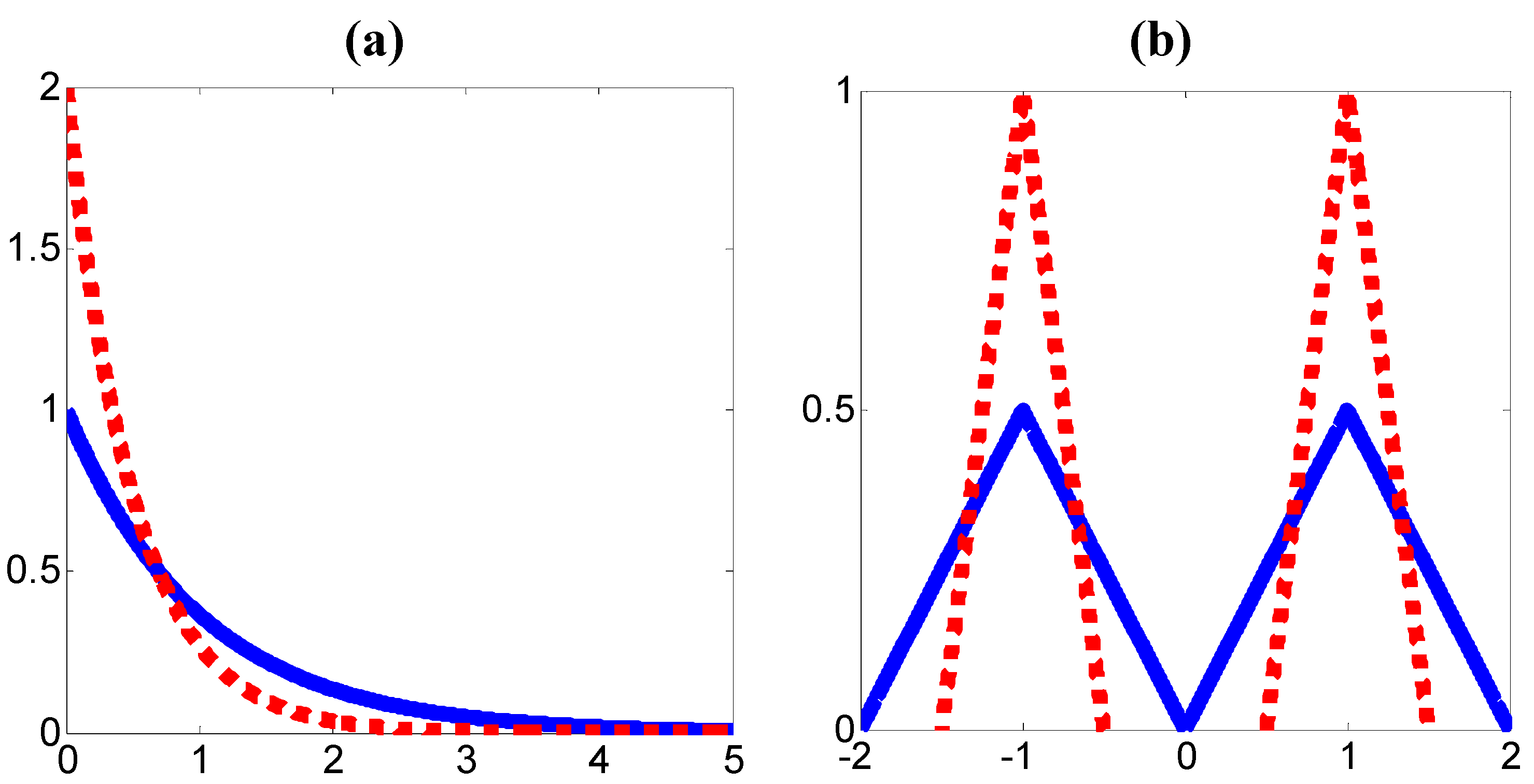
Remark 2: The GUD is much more general than CSUM. Actually, if the conditional PDF is CSUM, it must also be GUD (with the conditional mean as the dominant alignment), but not vice versa. In Figure 1 we show two examples where two PDFs (solid and dotted lines) are uniformly dominated but not CSUM.

Figure 1. Uniformly dominated PDFs: (a) non-symmetric, (b) non-unimodal.

Theorem 1: Assume the conditional PDF $p(x|y)$ is generalized uniformly dominated in $x\in {ℝ}^n$, with dominant alignment $\pi (y)$. If $H(X-\pi (Y))$ exists (here “exists” means “exists in the extended sense” as defined in [19]) then $H(X-\pi (Y))\le H(X-g(Y))$ for all $g:{ℝ}^m\to {ℝ}^n$ for which $H(X-g(Y))$ also exists.

Proof of Theorem 1: The proof presented below is similar to that of the Theorem 1 in [19], except that the discretization procedure is avoided. In the following, we give a brief sketch of the proof, and consider only the case $n=1$ (the proof can be easily extended to $n>1$). First, one needs to prove the following proposition.

Proposition 1: Assume that the function $f(x|y)$, $x\in ℝ$, $y\in {ℝ}^m$ (not necessarily a conditional PDF) satisfies the following conditions:

(1)

non-negative, continuous, and integrable in $x\in ℝ$ for each $y\in {ℝ}^m$;

(2)

generalized uniformly dominated in $x$, with dominant alignment $\pi (y)$;

(3)

uniformly bounded in $(x,y)$.

Then for any $g:{ℝ}^m\to ℝ$, we have:

$$H\left(f^{\pi }\right)\le H\left(f^g\right)$$

(6)

where $H\left(f\right)=-{\displaystyle {\int }_{ℝ}f(x)\log f(x)dx}$ (here we extend the entropy definition to nonnegative $L^1$ functions), and:

$$\{\begin{array}{l}{f}^{\pi }(x)={\displaystyle {\int }_{{ℝ}^m}f(x+\pi (y)|y)dF(y)}\\ f^g(x)={\displaystyle {\int }_{{ℝ}^m}f(x+g(y)|y)dF(y)}\end{array}$$

(7)

Remark 3: It is easy to verify that ${\displaystyle \int f^{\pi }dx}={\displaystyle \int f^{g}dx}\le {\sup }_{(x,y)}f\left(x|y\right)<\infty$ (not necessarily ${\displaystyle \int f^{\pi }dx}=1$).

Proof of Proposition 1: The above proposition can be readily proved using the following two lemmas.

Lemma 1 [19]: Assume the nonnegative function $h:ℝ\to \left[0,\infty \right)$ is bounded, continuous, and integrable, and define the function $O_h(z)$ by ($\lambda$ is Lebesgue measure):

$$O_h(z)=\lambda \left\{x:h(x)\ge z\right\}$$

(8)

Then the following results hold:

(a)

Define $m^h(x)=\sup \left\{z:O_h(z)\ge x\right\}$, $x\in \left(0,\infty \right)$, and $m^h(0)={\sup }_{x}h(x)$. Then $m^h(x)$ is continuous and non-increasing on $\left[0,\infty \right)$, and $m^h(x)\to 0$ as $x\to \infty$.

(b)

For any function $G:\left[0,\infty \right)\to ℝ$ with ${\displaystyle {\int }_{ℝ}\left|G\left(h(x)\right)\right|dx}<\infty$

$${\displaystyle {\int }_{ℝ}G\left(h(x)\right)dx}={\displaystyle {\int }_0^{\infty }G\left(m^h(x)\right)dx}$$

(9)

(c)

For any $x_0\in \left[0,\infty \right)$

$${\displaystyle {\int }_0^{x_0}{m}^h(x)dx}=\underset{A:\lambda (A)=x_0}{\sup }{\displaystyle {\int }_{A}h(x)dx}$$

(10)

Proof of Lemma 1: See [19].

Remark 4: Denote $m^{\pi }=m^{f^{\pi }}$, and $m^g=m^{f^g}$. Then by Lemma 1, we have $H(m^{\pi })=H(f^{\pi })$ and $H(m^g)=H(f^g)$ (let $G(x)=-x\log x$). Therefore, to prove Proposition 1, it suffices to prove:

$$H(m^{\pi })\le H(m^g)$$

(11)

Lemma 2: Functions $m^{\pi }$ and $m^g$ satisfy:

(a)

$${\displaystyle {\int }_0^{\infty }{m}^{\pi }(x)dx}={\displaystyle {\int }_0^{\infty }{m}^g(x)dx}<\infty$$

(12)

(b)

$${\displaystyle {\int }_0^{\epsilon }{m}^g(x)dx}\le {\displaystyle {\int }_0^{\epsilon }{m}^{\pi }(x)dx},\forall \epsilon \in \left[0,\infty \right)$$

(13)

Proof of Lemma 2: (a) comes directly from the fact ${\displaystyle \int f^{\pi }dx}={\displaystyle \int f^{g}dx}<\infty$. We only need to prove (b). We have:

$$\begin{array}{l}\underset{A:\lambda (A)=\epsilon }{\sup }{\displaystyle {\int }_A{f}^g(x)dx}\\ =\underset{A:\lambda (A)=\epsilon }{\sup }{\displaystyle {\int }_A{\displaystyle {\int }_{{ℝ}^m}f(x+g(y)|y)dF(y)}dx}\\ =\underset{A:\lambda (A)=\epsilon }{\sup }{\displaystyle {\int }_{{ℝ}^m}{\displaystyle {\int }_{A}f(x+g(y)|y)dx}dF(y)}\\ \le {\displaystyle {\int }_{{ℝ}^m}\left\{\underset{A:\lambda (A)=\epsilon }{\sup }{\displaystyle {\int }_{A}f(x+g(y)|y)dx}\right\}dF(y)}\\ ={\displaystyle {\int }_{{ℝ}^m}\left\{{\displaystyle {\int }_{D_{\epsilon }}f(x+\pi (y)|y)dx}\right\}dF(y)}\\ ={\displaystyle {\int }_{D_{\epsilon }}{\displaystyle {\int }_{{ℝ}^m}f(x+\pi (y)|y)dF(y)}dx}\\ =\underset{A:\lambda (A)=\epsilon }{\sup }{\displaystyle {\int }_A{\displaystyle {\int }_{{ℝ}^m}f(x+\pi (y)|y)dF(y)}dx}\\ =\underset{A:\lambda (A)=\epsilon }{\sup }{\displaystyle {\int }_A{f}^{\pi }(x)dx}\end{array}$$

(14)

where $D_{\epsilon }$ is the $\epsilon$-volume dominant support of $f(x+\pi (y)|y)$. By Lemma 1 (c):

$$\{\begin{array}{l}{\displaystyle {\int }_0^{\epsilon }{m}^g(x)dx}=\underset{A:\lambda (A)=\epsilon }{\sup }{\displaystyle {\int }_A{f}^g(x)dx}\\ {\displaystyle {\int }_0^{\epsilon }{m}^{\pi }(x)dx}=\underset{A:\lambda (A)=\epsilon }{\sup }{\displaystyle {\int }_A{f}^{\pi }(x)dx}\end{array}$$

(15)

Thus $\forall \epsilon \in \left[0,\infty \right)$, we have ${\displaystyle {\int }_0^{\epsilon }{m}^g(x)dx}\le {\displaystyle {\int }_0^{\epsilon }{m}^{\pi }(x)dx}$:

Q.E.D (Lemma 2)

We are now in position to prove (11):

$$\begin{array}{l}H\left(m^g\right)=-{\displaystyle {\int }_0^{\infty }{m}^g(x)\log m^g(x)dx}\\ ={\displaystyle {\int }_0^{\infty }{m}^g(x){\displaystyle {\int }_0^{-\log m^g(x)}dy}}dx\\ ={\displaystyle {\int }_0^{\infty }\left({\displaystyle {\int }_0^{\infty }{m}^g(x)\mathbb{I}\left[y\le -\log m^g(x)\right]dy}\right)dx}\\ ={\displaystyle {\int }_0^{\infty }\left({\displaystyle {\int }_{\inf \left\{x:-\log m^g(x)\ge y\right\}}^{\infty }{m}^g(x)dx}\right)dy}\\ \stackrel{Lemma2}{\ge }{\displaystyle {\int }_0^{\infty }\left({\displaystyle {\int }_{\inf \left\{x:-\log m^g(x)\ge y\right\}}^{\infty }{m}^{\pi }(x)dx}\right)dy}\\ =-{\displaystyle {\int }_0^{\infty }{m}^{\pi }(x)\log m^g(x)dx}\\ \stackrel{(a)}{\ge }-{\displaystyle {\int }_0^{\infty }{m}^{\pi }(x)\log m^{\pi }(x)dx}\\ =H(m^{\pi })\end{array}$$

(16)

where $\mathbb{I}[.]$ denotes the indicator function, and (a) follows from $\forall x>0$, $-\log x\ge 1-x$, that is:

$$\begin{array}{l}-{\displaystyle {\int }_0^{\infty }{m}^{\pi }(x)\log m^g(x)dx}+{\displaystyle {\int }_0^{\infty }{m}^{\pi }(x)\log m^{\pi }(x)dx}\\ =-{\displaystyle {\int }_0^{\infty }{m}^{\pi }(x)\log \left(\frac{m^g(x)}{m^{\pi }(x)}\right)dx}\\ \ge {\displaystyle {\int }_0^{\infty }{m}^{\pi }(x)\left(1-\frac{m^g(x)}{m^{\pi }(x)}\right)dx}\\ ={\displaystyle {\int }_0^{\infty }{m}^{\pi }(x)dx}-{\displaystyle {\int }_0^{\infty }{m}^g(x)dx}\stackrel{Lemma2}{=}0\end{array}$$

(17)

In the above proof, we adopt the convention $0\cdot \infty =0$.

Q.E.D (Proposition 1)

Now the proof of Proposition 1 has been completed. To finish the proof of Theorem 1, we have to remove the conditions of continuity and uniform boundedness imposed in Proposition 1. This can be easily accomplished by approximating $p(x|y)$ by a sequence of functions $\left\{f_n(x|y)\right\}$, $n=1,2,\cdots$, which satisfy these conditions. The remaining proof is omitted here, since it is exactly the same as the last part of the proof for Theorem 1 in [19].

Q.E.D (Theorem 1)

Example 1: Consider an additive noise model:

$$X=\phi \left(Y\right)+\xi$$

(18)

where $\xi$ is an additive noise that is independent of $Y$. In this case, we have $p\left(x|y\right)=p_{\xi }\left(x-\phi (y)\right)$, where $p_{\xi }(.)$ denotes the noise PDF. It is clear that $p\left(x|y\right)$ is generalized uniformly dominated, with dominant alignment $\pi (y)=\phi (y)$. According to Theorem 1, we have $H\left(X-\phi (Y)\right)\le H\left(X-g(Y)\right)$. In fact, this result can also be proved by:

$$\begin{array}{l}H\left(X-\phi (Y)\right)=H\left(\xi \right)\\ \stackrel{(b)}{\le }H\left(\xi +\left(\phi (Y)-g(Y)\right)\right)\\ =H\left(X-g(Y)\right)\end{array}$$

(19)

where (b) comes from the fact that $\xi$ and $\left(\phi (Y)-g(Y)\right)$ are independent (For independent random variables $X$ and $Y$, the inequality $H(X+Y)\ge \max \left\{H(X),H(Y)\right\}$ holds). In this example, the conditional PDF $p\left(x|y\right)$ is, obviously, not necessarily CSUM.

Example 2: Suppose the joint PDF of random variables $X$, $Y$ ($X,Y\in ℝ$) is:

$$p\left(x,y\right)=\exp \left(1-x\exp (y)\right)$$

(20)

where $y\ge 0$, $x\exp (y)\ge 1$. Then the conditional PDF $p\left(x|y\right)$ will be:

$$\begin{array}{l}p\left(x|y\right)=\frac{p\left(x,y\right)}{p\left(y\right)}\\ =\frac{\exp \left(1-x\exp (y)\right)}{{\displaystyle {\int }_{\exp (-y)}^{\infty }\exp \left(1-x\exp (y)\right)dx}}\\ =\exp \left(1-x\exp (y)+y\right)\end{array}$$

(21)

One can easily verify that the above conditional PDF is non-symmetric but generalized uniformly dominated, with dominant alignment $\pi (y)=\exp (-y)$ (the ε-volume dominant support of $p(x+\pi (y)|y)$ is $D_{\epsilon }=\left[0,\epsilon \right]$). By Theorem 1, the function $\exp (-y)$ is the minimizer of error entropy.

3. Non-Uniqueness of Unbiased MEE Estimation

Because entropy is shift-invariant, the MEE estimator is obviously non-unique. In practical applications, in order to yield a unique solution, or to meet the desire for small error values, the MEE estimator is usually restricted to be unbiased, that is, the estimation error is restricted to be zero-mean [15]. The question of interest in this paper is whether the unbiased MEE estimator is unique. In [20], it has been shown that, for the singular case (in which the error entropy approaches minus infinity), the unbiased MEE estimation may yield non-unique (even infinitely many) solutions. In the following, we present two examples to show that this result still holds even for nonsingular case.

Example 3: Let the joint PDF of $X$ and $Y$ ($X,Y\in ℝ$) be a mixed-Gaussian density [20]:

$$p\left(x,y\right)=\frac{1}{4\pi \sqrt{1-{\rho }^2}}\left\{\exp \left\{\frac{-\left(y^2-2\rho y(x-\mu )+{(x-\mu )}^2\right)}{2\left(1-{\rho }^2\right)}\right\}+\exp \left\{\frac{-\left(y^2+2\rho y(x+\mu )+{(x+\mu )}^2\right)}{2\left(1-{\rho }^2\right)}\right\}\right\}$$

(22)

where $\mu >0$, $0\le \left|\rho \right|<1$. The conditional PDF of $X$ given $Y$ will be:

$$p\left(x|y\right)=\frac{1}{2\sqrt{2\pi \left(1-{\rho }^2\right)}}\left\{\exp \left(-\frac{{\left(x-\mu -\rho y\right)}^2}{2\left(1-{\rho }^2\right)}\right)+\exp \left(-\frac{{\left(x+\mu +\rho y\right)}^2}{2\left(1-{\rho }^2\right)}\right)\right\}$$

(23)

$\forall y\in ℝ$, $p\left(x|y\right)$ is symmetric around zero (but not unimodal in x). It can be shown that for some values of $\mu$, $\rho$, the MEE estimator of $X$ based on $Y$ does not equal zero (see [20], Example 3). In these cases, the MEE estimator will be non-unique, even if the error’s PDF is restricted to zero-mean (unbiased) distribution. This can be proved as follows:

Let $g^{*}$ be an unbiased MEE estimator of $X$ based on $Y$. Then $-g^{*}$ will also be an unbiased MEE estimator, because:

$$\begin{array}{l}{p}^{g^{*}}(x)={\displaystyle {\int }_{ℝ}p(x+g^{*}(y)|y)dF(y)}\\ \stackrel{(c)}{=}{\displaystyle {\int }_{ℝ}p(-x-g^{*}(y)|y)dF(y)}\\ =p^{-g^{*}}(-x)\end{array}$$

(24)

where (c) comes from the fact that $p\left(x|y\right)$ is symmetric around zero, and further:

$$\begin{array}{l}H\left(p^{g^{*}}\right)=-{\displaystyle {\int }_{-\infty }^{\infty }{p}^{g^{*}}(x)\log p^{g^{*}}(x)dx}\\ =-{\displaystyle {\int }_{-\infty }^{\infty }{p}^{-g^{*}}(-x)\log p^{-g^{*}}(-x)dx}\\ =-{\displaystyle {\int }_{-\infty }^{\infty }{p}^{-g^{*}}(x)\log p^{-g^{*}}(x)dx}\\ =H\left(p^{-g^{*}}\right)\end{array}$$

(25)

If the unbiased MEE estimator is unique, then we have $g^{*}=-g^{*}\Rightarrow g^{*}=0$, which contradicts the fact that $g^{*}$ does not equal zero. Therefore, the unbiased MEE estimator must be non-unique. Obviously, the above result can be extended to more general cases. In fact, we have the following proposition.

Proposition2: The unbiased MEE estimator will be non-unique if the conditional PDF $p\left(x|y\right)$ satisfies:

(1)

Symmetric in $x\in {ℝ}^n$ around the conditional mean $\mu (y)=E\left[X|Y=y\right]$ for each $y\in {ℝ}^m$;

(2)

There exists a function $\zeta :{ℝ}^m\to {ℝ}^n$ such that $\zeta (Y)\ne \mu (Y)$, $H\left(X-\zeta (Y)\right)\le H\left(X-\mu (Y)\right)$.

Proof: Similar to the proof presented above (Omitted).

In the next example, we show that, for some particular situations, there can be even infinitely many unbiased MEE estimators.

Example 4: Suppose$Y$ is a discrete random variable with Bernoulli distribution:

$$\mathrm{Pr}(Y=0)=\mathrm{Pr}(Y=1)=0.5$$

(26)

The conditional PDF of $X$ given $Y$ is (see Figure 2):

$$p\left(x|Y=0\right)=\{\begin{array}{l}\frac{1}{2a}if\left|x\right|\le a\\ 0other\end{array}$$

$$p\left(x|Y=1\right)=\{\begin{array}{l}\frac{1}{a}if\left|x\right|\le \frac{1}{2}a\\ 0other\end{array}$$

where $a>0$. Note that the above conditional PDF is uniformly dominated in $x$.

Figure 2. Conditional PDF of $X$ given $Y$: (a) $p(x|Y=0)$, (b) $p(x|Y=1)$.

Given an estimator $\widehat{X}=g(Y)$, the error’s PDF will be:

$$p^g(x)=\frac{1}{2}\left\{p\left(x+g(0)|Y=0\right)+p\left(x+g(1)|Y=1\right)\right\}$$

(27)

Let $g$ be an unbiased estimator, then ${\displaystyle {\int }_{-\infty }^{\infty }x{p}^g(x)dx}=0$, and hence $g(0)=-g(1)$. In the following, we assume $g(0)\ge 0$ (due to symmetry, one can obtain similar results for $g(0)<0$), and consider three cases:

Case 1: $0\le g(0)\le \frac{1}{4}a$. In this case, the error PDF is:

$$p^g(x)=\{\begin{array}{l}\frac{1}{4a},-a-g(0)\le x<-\frac{a}{2}+g(0)\\ \frac{3}{4a},-\frac{a}{2}+g(0)\le x\le \frac{a}{2}+g(0)\\ \frac{1}{4a},\frac{a}{2}+g(0)<x\le a-g(0)\end{array}$$

(28)

Then the error entropy can be calculated as:

$$H\left(p^g(x)\right)=-\frac{3}{4}\log \left(3\right)+\log \left(4a\right)$$

(29)

Case 2: $\frac{1}{4}a<g(0)\le \frac{3}{4}a$. In this case, we have:

$$p^g(x)=\{\begin{array}{l}\frac{1}{4a},-a-g(0)\le x<-\frac{a}{2}+g(0)\\ \frac{3}{4a},-\frac{a}{2}+g(0)\le x\le a-g(0)\\ \frac{1}{2a},a-g(0)<x\le \frac{a}{2}+g(0)\end{array}$$

(30)

And hence:

$$H\left(p^g(x)\right)=\left(-\frac{9}{8}+\frac{3g(0)}{2a}\right)\log \left(3\right)+\left(\frac{1}{4}-\frac{g(0)}{a}\right)\log \left(2\right)+\log \left(4a\right)$$

(31)

Case 3: $g(0)>\frac{3}{4}a$. In this case:

$$p^g(x)=\{\begin{array}{l}\frac{1}{4a},-a-g(0)\le x\le a-g(0)\\ \frac{1}{2a},-\frac{a}{2}+g(0)\le x\le \frac{a}{2}+g(0)\end{array}$$

(32)

Thus:

$$H\left(p^g(x)\right)=-\frac{1}{2}\log \left(2\right)+\log \left(4a\right)$$

(33)

One can easily verify that the error entropy achieves its minimum value when $0\le g(0)\le a/4$ (the first case). There are, therefore, infinitely many unbiased estimators that minimize the error entropy.

4. Conclusion

Two issues involved in the minimum error entropy (MEE) estimation have been studied in this work. The first issue is about which estimator minimizes the error entropy. In general there is no explicit expression for the MEE estimator unless some constraints on the conditional distribution are imposed. In the past, several researchers have shown that, if the conditional density is conditionally symmetric and unimodal (CSUM), then the conditional mean (or median) will be the MEE estimator. We extend these results to a more general case, and show that if the conditional densities are generalized uniformly dominated (GUD), then the dominant alignment will minimize the error entropy. The second issue is about the non-uniqueness of the unbiased MEE estimation. It has been shown in a recent paper that for the singular case (in which the error entropy approaches minus infinity), the unbiased MEE estimation may yield non-unique (even infinitely many) solutions. In this work, we show by examples that this result still holds even for nonsingular case.