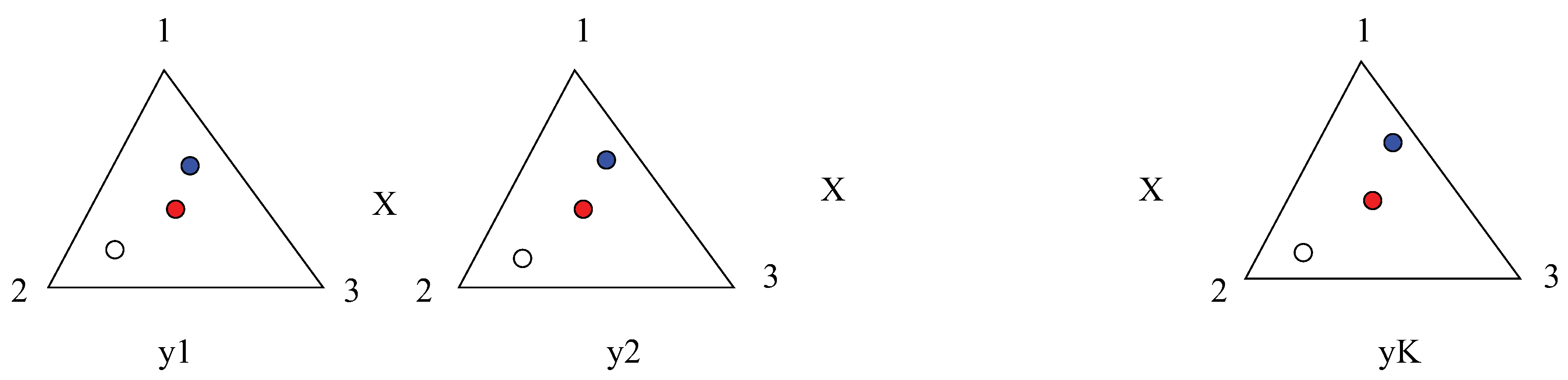The Mathematical Structure of Information Bottleneck Methods

Abstract

Information Bottleneck-based methods use mutual information as a distortion function in order to extract relevant details about the structure of a complex system by compression. One of the approaches used to generate optimal compressed representations is by annealing a parameter. In this manuscript we present a common framework for the study of annealing in information distortion problems. We identify features that should be common to any annealing optimization problem. The main mathematical tools that we use come from the analysis of dynamical systems in the presence of symmetry (equivariant bifurcation theory). Through the compression problem, we make connections to the world of combinatorial optimization and pattern recognition. The two approaches use very different vocabularies and consider different problems to be “interesting". We provide an initial link, through the Normalized Cut Problem, where the two disciplines can exchange tools and ideas.

1. Introduction

Our goal in this paper is to investigate the mathematical structure of Information Distortion methods. There are several approaches to computing the best quantization of the data, and they differ in the algorithms used, the data they are applied to, and the functions that are optimized by the algorithms. We will concentrate on the annealing method applied to two different functions: the Information Bottleneck cost function [1] and the Information Distortion function [2]. By formalizing a common framework in which to study these two problems, we will exhibit common features of, as well as differences between, the two cost functions. Moreover, the differences and commonalities we will highlight are based on the underlying structural properties of these systems rather then on the philosophy behind their derivation. All results that we present are valid for any system characterized by a probability distribution and in this sense they present fundamental structural results.

On a more concrete level, our goal is to understand why the annealing algorithms now in use work as well as they do, but also to suggest improvements to these algorithms. Some results which have been observed numerically are not expected when applying annealing to a general cost function. We want to ask what is the special feature of these systems that cause such results.

Our final goal is to provide a bridge between the world of combinatorial optimization and pattern recognition, and the world of dynamical systems in mathematics. These two areas have different goals, different sets of “natural questions” and, perhaps most crucially, different vocabularies. We want this manuscript to contribute to bridging this gap, as we believe that both sides have developed interesting and powerful techniques that can be used to expand the knowledge of the other side.

We close by introducing the optimization problems we will study. Both approaches attempt to characterize a system of interest $(\mathit{X},\mathit{Y})$ defined by a probability $p(\mathit{X},\mathit{Y})$ by quantizing (discretizing) one of the variables ($\mathit{Y}$ here) into a reproduction variable $\mathit{T}$ with few elements. One of the problems stems from the Information Distortion approach to neural coding [2,3],

$$\underset{q\in \Delta }{max}{F}_H\left(q\right):=\mathit{H}\left(T\right|Y)+\beta \mathit{I}(X;T)$$

(1)

where $\mathit{H}(·)$ is the conditional entropy, and $\mathit{I}(·;·)$ is the mutual information [4]. The other problem is from the Information Bottleneck approach to clustering [1,5,6]

$$\underset{q\in \Delta }{max}{F}_I\left(q\right):=-\mathit{I}(T;Y)+\beta \mathit{I}(X;T)$$

(2)

which has been used for document classification [7,8], gene expression [9], neural coding [10,11], stellar spectral analysis [12], and image time-series data mining [13].

The variables (quantizers) q are conditional probabilities $q:=q\left(t\right|y)$ and Δ is the space of all appropriate conditional probabilities. We will explain all of the details in the main text, but we want to sketch the basic idea of the annealing approach here. Since both functions $\mathit{H}\left(T\right|Y)$ and $-\mathit{I}(T;Y)$ are concave, when $\beta =0$, both problems (1) and (2) admit a homogeneous solution $q\left(t\right|y)=1/N$, where N is the number of elements in $\mathit{T}$. Starting at this solution and increasing β slowly, the optimal solution, or quantizer, q will undergo a series of phase transitions (bifurcations) as a function of β. We will show that the parameter β, at which the first phase transition takes place, does not depend on the number of elements in the reproduction variable $\mathit{T}$. Annealing in the temperature-like parameter β terminates either at some predefined finite value of β, or goes to $\beta =\infty$. It is this process and its phase transitions that we consider in this contribution.

1.1. Outline of the Mathematical Contributions

In Section 2 we start with the optimization problems and identify the space of variables over which optimization takes place. Since these variables are constrained, we use Lagrange multipliers to eliminate equality constraints. We also present some results about convexity and concavity of the cost functions.

Our first main question is whether the approach of deterministic annealing [14] can be used for these optimization problems. Rose and his collaborators have shown that, if the distortion function in certain class of optimization problems is taken to be the Euclidean distance, the phase transitions of the annealing function can be computed explicitly. More precisely, the first phase transition can be computed explicitly, since the quantizer value is known and only the value of the temperature at which this quantizer loses stability has to be computed. In general, an implicit formula relating critical temperature and the critical quantizer at which phase transition occurs can be computed.

In Section 4 we will show that the same calculations can be done for our optimization problems. We relate the critical value of β at which the uniform quantizer $q_{\frac{1}{N}}$ loses stability to a certain eigenvalue problem. This problem can be solved effectively off-line and thus the annealing procedure can start from this value of β rather then at $\beta =0$. As a consequence, we also show that in both optimization problems considered here, the quantizer $q_{\frac{1}{N}}$ is a local maximum for all $\beta \in [0,1]$. In complete analogy with deterministic annealing, our results extend beyond phase transitions off $q_{\frac{1}{N}}$. As we show in Section 5, the aforementioned eigenvalue problem implicitly relates all critical values of the parameter β to critical values of the quantizer q.

We study more closely the first phase transition in Section 6. We show that the eigenvector corresponding to this phase transition solves the Approximate Normalized Cut problem for some graphs with vertices corresponding to elements of Y. These graphs have considerable intuitive appeal.

In [15,16,17] we studied the subsequent phase transitions more closely, using bifurcation theory with symmetries. We summarize the main results here as well. The symmetry of our problems comes from the fact that the cost function is invariant under the relabeling of the elements of the representation variable T. Such a symmetry is characterized by the permutation group $S_N$ and its subgroups. Since this is a structural symmetry, it does not require the symmetry of the underlying probability distribution $p(\mathit{X},\mathit{Y})$. These results are valid for arbitrary probability distributions.

2. Mathematical Formulation of the Problem

The variables q over which the optimization takes place are conditional probabilities $q\left(t\right|y)$. In order for the problems (1) and (2) to be well defined, we must fix the number of elements of T. Let this number be N and let the number of elements in Y be K. Then there are $NK$ conditional probabilities $q\left(t\right|y)$ which satisfy

$$\sum _{t}q\left(t\right|y)=1\mathrm{for}\mathrm{all}y$$

(3)

These equations form an equality constraint on the maximization problems (1) and (2). We also have to satisfy inequality constraints $q\left(t\right|y)\ge 0$ since $q\left(t\right|y)$ are probabilities. We notice that, for a fixed y, the space of admissible values $q\left(t\right|y)$ is the unit $N-1$ simplex ${\Delta }^{N-1}$ in ${\mathbf{R}}^N$. We denote this simplex as ${\Delta }_y$, to also indicate that it is related to variable y, and suppressing the dimension for simplicity of notation. It follows from (3) that the set of all admissible values of $q\left(t\right|y)$ is a product of such simplices (see Figure 1), which we call Δ,

$$\Delta :={\Delta }_{y_1}\times {\Delta }_{y_2}\times \dots \times {\Delta }_{y_K}$$

Figure 1. The space Δ of admissible vectors q can be represented as a product of simplices, one simplex for each $y_i\in Y$. The figure shows the case when the reproduction variable T has three elements ($N=3$). Each triangle represents a unit simplex in ${\mathbf{R}}^3$ and the constraint $q\left(1\right|y_i)+q\left(2\right|y_i)+q\left(3\right|y_i)=1,q\left(t\right|y_i)\ge 0$. The green point represents the position of a particular q. To clarify the illustration: The part of q in simplex 4, $q\left(t\right|3)$, is almost deterministic (shown at a vertex), while the next q, $q\left(t\right|4)$ is almost uniform (shown almost at the center of simplex 4).

At this point we want to comment on a successful implementation of the annealing algorithm by Slonim and Tishby [6]. In their approach they start the annealing procedure with $N=2$ at $q\left(t\right|y)=$ for all $t=1,2$ and y at $\beta =0$. After increasing β they split $q\left(t\right|y)$, for $t=1,2$, into two parts, $q\left(t^1\right|y)$ and $q\left(t^2\right|y)$ by setting

$$q\left(t^1\right|y)=q\left(1\right|y)(\frac{1}{2}+ϵ\alpha (t,y)),q\left(t^2\right|y)=q\left(1\right|y)(\frac{1}{2}-ϵ\alpha (t,y))$$

where $\alpha (t,y)$ is random perturbation and ϵ is small. If under the fixed point iteration at new value of β the values $q\left(t^1\right|y)$ and $q\left(t^2\right|y)$ converge to the same value ($1/4$ in this case), then the process is repeated; if, on the other hand, these values diverge, a presence of a bifurcation is asserted. Note, that this process changes N from 2 to 4 repeatedly. This changes the optimization problem, because the space of admissible quantizers q doubled. It is not clear a priori that phase transition detected in problem with $2K$ variables also occurs at the same value of β in problem with $4K$ variables. Numerically, however, this seems to be the case not only at the first phase transition, but at every phase transition. One of the results of Section 4 will be an explanation of this phenomena. We will show that the parameter β, at which the first phase transition takes place, does not depend on the number of elements in the reproduction variable T. This provides a justification for Slonim’s algorithm, at least for the first phase transition.

Since the optimization problems (1) and (2) are constrained, we first form the Lagrangian,

$$\mathcal{L}=F+\sum _{k=1}^K{\lambda }_k\left(\sum _{t=1}^{N}q\left(t\right|y_k)-1\right)$$

(4)

which incorporates the vector of Lagrange multipliers λ, imposed by the equality constraints from the constraint space Δ. Here $F=F_H$ for (1) or $F=F_I$ for (2),

Lemma 2.1

The function $\mathit{H}\left(T\right|Y)$ is a strictly concave function of $q\left(t\right|y)$ and the functions $\mathit{I}(X;T)$ and $\mathit{I}(Y;T)$ are convex, but not strictly convex, functions of $q\left(t\right|y)$.

Proof. 

For concavity of $\mathit{H}\left(T\right|Y)$ and convexity of $\mathit{I}(Y;T)$, see [2]. Proof of the convexity of $\mathit{I}(X;T)$ is analogous.

This Lemma implies that for $\beta =0$ in both (1) and (2), there is a trivial solution $q\left(t\right|y)=1/N$ for all t and y. We denote this solution as $q_{\frac{1}{N}}$.

What we want to emphasize here is that $\mathit{I}(Y;T)$ and $\mathit{I}(X;T)$ are not strictly convex functions. Recall that a function f is convex provided

$$sf\left(\mathit{u}\right)+(1-s)f\left(\mathit{v}\right)\le f(s\mathit{u}+(1-s\mathit{v}\left)\right)$$

(5)

for all u, v, and $0\le s\le 1$. The function f is strictly convex if the inequality in (5) is strict for u ≠ v and $0<s<1$.

To show that $\mathit{I}(Y;T)$ is not strictly convex, we take $q\left(t\right|y_k)=a_t$ independent on k (see Figure 2). In order for this q to satisfy $q\in \Delta$ we require that numbers $a_t$ are chosen with ${\sum }_t{a}_t=1$. Using the facts that $p(y,t)=q\left(t\right|y\left)p\right(y)$ and $p\left(t\right)={\sum }_{y}p(y,t)=a_t{\sum }_{y}p\left(y\right)$, we evaluate at $q=q_a$ the function

$$\begin{array}{ccc}\hfill \mathit{I}(T;Y)& =& \sum _{y,t}p(y,t)log\frac{p(y,t)}{p\left(y\right)p\left(t\right)}\hfill \\ & =& \sum _{y,t}{a}_{t}p\left(y\right)log\frac{a_{t}p\left(y\right)}{p\left(y\right)a_t}\hfill \\ & =& 0\hfill \end{array}$$

This implies that in Δ there is an $N-1$ dimensional linear space spanned by vectors $a=(a_1,a_2,\dots ,a_N)$ with ${\sum }_t{a}_t=1$, such that for all q in this space $\mathit{I}(T;Y)\left(q\right)=0$. Since $\mathit{I}(T;Y)\ge 0$, this function does not have a unique minimum and thus is not strictly convex.   ☐

Figure 2. The function $I(T;Y)$ is not strictly convex. There are three vectors q depicted in the figure. The red point in the middle of each simplex represents the point $q_{\frac{1}{N}}$ with $N=3$. The blue point and the white points have the property that $q\left(t\right|y)$ does not depend on y, only on t. At all three points the function $I(T;Y)$ is equal to zero.

This result has consequences for the function $F_I\left(q\right)$. As we will see in Lemma 3.1, $F_I\left(q\right)=0$ at all points where $\mathit{I}(T;X)\left(q\right)=0$. This lack of strict convexity has important consequences for phase transitions for $F_I$. Since $\mathit{H}\left(T\right|Y)$ is strictly concave, this problem will not affect the function $F_H$.

Maxima of (1) and (2) are critical points of the Lagrangian, that is, points q where the gradient of (4) is zero. We now switch our search from maxima to critical points of the Lagrangian. Obviously, minima and saddle points are also critical points and therefore we must always check whether a given critical point is indeed a maximum of the original problem (1) or (2). We want to use the language of bifurcation theory which deals with qualitative changes in the structure of system dynamics given by differential equations or maps. Therefore we will now reformulate the optimization problems (1) and (2) as a system of differential equations under a gradient flow,

$$\begin{array}{c}\hfill \left(\begin{array}{c}\dot{q}\\ \dot{\lambda }\end{array}\right)={\nabla }_{q,\lambda }\mathcal{L}(q,\lambda ,\beta )\end{array}$$

(6)

In this equation, the $NK\times 1$ vector q representing the quantizer, and the $K\times 1$ vector of the Langrange multipliers (see Equation (4)) are viewed as functions of some independent variable s, which parameterizes curves of solutions $\left(q\right(s),\lambda (s\left)\right)$ to either (1) or (2). Thus, the derivatives implicit in $(\dot{q},\dot{\lambda })$ are with respect to s. The critical points of the Lagrangian are the equilibria of (6), since those are the places where the gradient of Ł is equal to zero. By the same token, the maxima of (1) and (2) correspond to stable (in q) equilibria of the gradient flow (6). More technically, these are points for which the Hessian $d^{2}F$ is negative definite on the kernel of the Jacobian of the constraints [18,19].

As β increases from 0, the solution $q_{\frac{1}{N}}$ is initially a maximum of (1) and (2). We are interested in the smallest value of β, say $\beta ={\beta }^{*}$, where $q_{\frac{1}{N}}$ ceases to be a maximum. This corresponds to a change in the number of critical points in the neighborhood of $q_{\frac{1}{N}}$ as β passes through $\beta ={\beta }^{*}$. The value ${\beta }^{*}$ is called a bifurcation value and the new sets of critical points emanating from $q_{\frac{1}{N}}$ are called bifurcating branches. This question can be posed at any other point besides $q_{\frac{1}{N}}$ as well: When do such bifurcations happen? We will formulate the answer in the language of differential equations. If the linearization of the flow at equilibrium has eigenvalues with nonzero real part, the implicit function theorem implies that this equilibrium exists for all values of the parameter in a small neighbourhood. Since the number of equilibria then does not change locally, this implies that a bifurcation does not occur at such a point. Therefore, a necessary condition for bifurcation is that the real part of some eigenvalue of the linearization of the flow at an equilibrium crosses zero [20]. Therefore, we need to consider eigenvalues of the $(NK+K)\times (NK+K)$ Hessian $d^2\mathcal{L}$. Since $d^2\mathcal{L}$ is a symmetric matrix, bifurcation can only be caused by one of its real eigenvalues crossing zero, and therefore we must find values of $(q,\beta )$ at which $d^2\mathcal{L}$ is singular, or, equivalently, has a nontrivial kernel.

The form of $d^2\mathcal{L}$ is simple:

$$d^2\mathcal{L}=\left[\begin{array}{cccc}{B}_1& 0& \dots & I\\ 0& B_2& \dots & I\\ ⋮& ⋮& ⋮& ⋮\\ 0& \dots & B_N& I\\ I& I& \dots & 0\end{array}\right]$$

where I is the identity matrix and $B_i$ is

$$B_i:=\frac{{\partial }^2\mathcal{L}}{\partial q\left(t_i\right|y_k)\partial q\left(t_i\right|y_l)}=\frac{{\partial }^{2}F}{\partial q\left(t_i\right|y_k)\partial q\left(t_i\right|y_l)}$$

The block diagonal matrix consisting of all matrices $B_i$ represents the matrix of second derivatives (Hessian) of F.

In [15,17] we showed that there are two types of generic bifurcations: saddle-node, in which a set of equilibria emerge simultaneously, and pitchfork-like, in which new equilibria emanate from an existing equilibrium. The first kind of bifurcation corresponds to a value of β, and corresponding q, for which $d^2\mathcal{L}$ is singular, but $d^{2}F$ is non-singular; the second kind of bifurcation happens at β and q where $d^{2}F$ is singular. Our primary focus here is on bifurcations off $q_{\frac{1}{N}}$, and more generally off an existing branch, we will focus on the second kind of bifurcation. Therefore, we will investigate only the case in which the eigenvalues of the smaller $NK\times NK$ Hessians $d^2{F}_H$ and $d^2{F}_I$ are zero to determine the location of pitchfork-like bifurcations.

2.1. Derivatives

In order to simplify notation we will denote

$$q_{\nu k}:=q(t=\nu |y=y_k)$$

To determine $d^2{F}_H$ and $d^2{F}_I$ from (1) and (2), we need to determine the quantities $d^2\mathit{H}\left(T\right|Y)$, $d^2\mathit{I}(X;T)$ and $d^2\mathit{I}(Y;T)$. The first two were computed in [2]:

$$\begin{array}{c}\hfill \frac{{\partial }^2\mathit{H}\left(T\right|Y)}{\partial q_{\eta l}\partial q_{\nu k}}=-\frac{1}{ln2}\frac{p\left(y_k\right)}{q_{\nu k}}{\delta }_{\nu \eta }{\delta }_{kl}\end{array}$$

(7)

and

$$\begin{array}{c}\hfill \frac{{\partial }^2\mathit{I}(X;T)}{\partial q_{\eta l}\partial q_{\nu k}}=\frac{{\delta }_{\nu \eta }}{ln2}\left(\sum _i\frac{p(x_i,y_k)p(x_i,y_l)}{{\sum }_k{q}_{\nu k}p(x_i,y_k)}-\frac{p\left(y_k\right)p\left(y_l\right)}{{\sum }_k{q}_{\nu k}p\left(y_k\right)}\right)\end{array}$$

(8)

where ${\delta }_{\nu \eta }=1$ if $\nu =\eta$ and zero otherwise. We computed the derivative of the term $-d^2\mathit{I}(Y;T)$ in [19]

$$\frac{-{\partial }^2\mathit{I}(Y;T)}{\partial q_{\eta l}\partial }=\frac{{\delta }_{\nu \eta }}{ln2}\left(\frac{p\left(y_k\right)p\left(y_l\right)}{p\left(\nu \right)}-\frac{{\delta }_{lk}p\left(y_k\right)}{}\right)$$

(9)

The formulas (7)–(9) show that we can factor ${\delta }_{\nu \eta }$ out of both $d^2{F}_H=d^2\mathit{H}\left(T\right|Y)+\beta d^2\mathit{I}(X;T)$ and $d^2{F}_I=-d^2\mathit{I}(Y;T)+\beta d^2\mathit{I}(X;T)$. This implies that the $NK\times NK$ matrices $d^2{F}_H$ and $d^2{F}_I$ are block diagonal, with N blocks, with each $K\times K$ block $B_i$ corresponding to a particular value (class) of the reconstruction variable $\mathit{T}$.

2.2. Symmetries

The optimization problems (1) and (2) have symmetry. We capitalize on this symmetry to solve these problems better. The symmetries arise from the structure of $q\in \Delta$ and from the form of the functions $F_H$ and $F_I$: permuting subvectors $q_{\nu }$ does not change the value of $F_H$ and $F_I$. This symmetry is characterized as an invariance under the action of the permutation group, $S_N$, or one of its subgroups $S_{l_1}\times S_{l_2}\times \dots \times S_{l_z}$, $\sum l_k=N$ .

We will capitalize upon the symmetry of $S_N$ by using the Equivariant Branching Lemma to determine the bifurcations of stationary points, which includes local solutions, to (1) and (2).

In [15] we clarified the bifurcation structure for a larger class of constrained optimization problems of the form

$$\underset{q\in \Delta }{max}F(q,\beta )$$

as long as F satisfies the following:

Proposition 2.2

The function $F(q,\beta )$ is of the form

$$F(q,\beta )=\sum _{\nu =1}^{N}f(q_{\nu },\beta )$$

for some smooth scalar function f, where the vector $q\in \Delta \subset {\mathbf{R}}^{NK}$ is decomposed into N subvectors $q_{\nu }\in {\mathbf{R}}^K$.

The annealing problems (1) and (2) satisfy this Proposition. Any F satisfying Proposition 2.2 has the following properties.

• F is $S_N$-invariant, where the action of $S_N$ on q permutes the subvectors $q_{\nu }$ of q.
• The $NK\times NK$ Hessian $d^{2}F$ is block diagonal, with $N,$$K\times K$ blocks.

3. The Kernel at a Bifurcation

In this section we investigate and compare the kernels of the $NK\times NK$ Hessians $d^2{F}_I$ and $d^2{F}_B$.

3.1. The Kernel of the Information Bottleneck

Our first observation is that $F_I$ is highly degenerate as a consequence of the fact that both $\mathit{I}(Y;T)$ and $\mathit{I}(X;T)$ are not strictly convex in q.

Lemma 3.1

Select a collection of numbers $a_1,\dots ,a_K$ such that $a_i\ge 0$ and ${\sum }_{i=1}^K{a}_i=1$. Let $q_a\in {\mathbf{R}}^{NK}$ be a vector consisting of vectors $q_a^j\in {\mathbf{R}}^N$, $j=1,\dots K$ such that $q_a^j$ is a constant vector with entries $a_j$. In other words, select $q\left(t\right|y)=a_t$ independent on y. Then

$$F_I\left(q_a\right)=F_I(q_{\frac{1}{N}})=0for all \beta$$

Proof. 

We evaluate at $q=q_a$ the function

$$\begin{array}{ccc}\hfill -\mathit{I}(T;Y)+\beta \mathit{I}(T;X)& =& -\sum _{y,t}p(y,t)log\frac{p(y,t)}{p\left(y\right)p\left(t\right)}+\beta \sum _{x,t}p(x,t)log\frac{p(x,t)}{p\left(x\right)p\left(t\right)}\hfill \\ & =& -\sum _{y,t}{a}_{t}p\left(y\right)log\frac{a_{t}p\left(y\right)}{p\left(y\right)a_t}+\beta \sum _{x,t,y}q\left(t\right|y)p(x,y)log\frac{{\sum }_{y}q\left(t\right|y)p(x,y)}{p\left(x\right)a_t}\hfill \\ & =& \beta \sum _{x,t,y}q\left(t\right|y)p(x,y)log\frac{a_t{\sum }_{y}p(x,y)}{p\left(x\right)a_t}\hfill \\ & =& 0\hfill \end{array}$$

Since $q_{\frac{1}{N}}$ is a particular case of $q_a$, the Lemma is proved.    ☐

Now we prove a generalization of this Lemma. We will say that q has symmetry described by $S_{l_1}\times S_{l_2}\times \dots \times S_{l_z}$ (a subgroup of $S_N$) if

$$q={(q_1,\dots ,q_1,q_2\dots q_2,\dots ,q_z,\dots ,q_z)}^T$$

(10)

where z is the total number of “blocks" of sub-vectors, with the sub-vector $q_i$ repeating $l_i$ times in the $i^{th}$ block. At such vector q, the matrix $d^{2}F$ has z groups of blocks $B_i$, and all blocks in each group are identical. In particular, the first $l_1$ blocks $B_1=\dots =B_{l_1}$ are the same, then next $l_2$ blocks are the same, and so on.

Theorem 3.2

Consider an arbitrary pair $(q,\beta )$, where q admits a symmetry $S_{l_1}\times S_{l_2}\times \dots \times S_{l_z}$. Then, at a fixed value of β, there is a linear manifold of dimension

$$(l_1-1)+(l_2-1)+\dots +(l_z-1)$$

passing through q, such that the function $F_I$ is constant on this manifold.

Proof. 

The quantizer q must take the form given by (10). Let

$$w={(c_1{q}_1,c_2{q}_1,\dots ,c_{l_1}{q}_1,q_2\dots q_2,\dots ,q_z,\dots ,q_z)}^T$$

where the constants $c_i$ are nonnegative and ${\sum }_i{c}_i=l_1$. We will show that

$$F_I\left(q\right)=F_I\left(w\right)$$

We separate $F_I\left(w\right)$ into two parts

$$\begin{array}{ccc}\hfill F_I\left(w\right)& =& -\sum _{y,t}p(y,t)log\frac{p(y,t)}{p\left(y\right)p\left(t\right)}+\beta \sum _{x,t}p(x,t)log\frac{p(x,t)}{p\left(x\right)p\left(t\right)}\hfill \\ & =& \sum _{t\le l_1}\left[-\sum _{y}p(y,t)log\frac{p(y,t)}{p\left(y\right)p\left(t\right)}+\beta \sum _{x}p(x,t)log\frac{p(x,t)}{p\left(x\right)p\left(t\right)}\right]\hfill \\ & +& \sum _{t>l_1}\left[-\sum _{y}p(y,t)log\frac{p(y,t)}{p\left(y\right)p\left(t\right)}+\beta \sum _{x}p(x,t)log\frac{p(x,t)}{p\left(x\right)p\left(t\right)}\right]\hfill \\ & =& F_I^1\left(w\right)+F_I^2\left(w\right)\hfill \end{array}$$

Since the vectors w and q agree for all $t>l_1$ we have

$$F_I^2\left(q\right)=F_I^2\left(w\right)$$

Observe first that

$$\begin{array}{ccc}\hfill F_I^1\left(y\right)& =& -\sum _{y,t\le l_1}{q}_1\left(t\right|y)p\left(y\right)log\frac{q_1\left(t\right|y)p\left(y\right)}{p\left(y\right)p\left(t\right)}+\beta \sum _{x,y,t\le l_1}{q}_1\left(t\right|y)p(x,y)log\frac{{\sum }_y{q}_1\left(t\right|y)p(x,y)}{p\left(x\right)p\left(t\right)}\hfill \\ & =& l_1\left(-\sum _y{q}_1\left(t\right|y)p\left(y\right)log\frac{q_1\left(t\right|y)p\left(y\right)}{p\left(y\right)p\left(t\right)}+\beta \sum _{x,y,}{q}_1\left(t\right|y)p(x,y)log\frac{{\sum }_y{q}_1\left(t\right|y)p(x,y)}{p\left(x\right)p\left(t\right)}\right)\hfill \\ & =& l_1{G}^1\left(y\right)\hfill \end{array}$$

where $G^1\left(y\right)$ is the function inside the parentheses on the last line. Now we evaluate $F_I^1\left(w\right)$

$$\begin{array}{ccc}\hfill F_I^1\left(w\right)& =& -\sum _{y,t\le l_1}{c}_t{q}_1\left(t\right|y)p\left(y\right)log\frac{c_t{q}_1\left(t\right|y)p\left(y\right)}{p\left(y\right)c_{t}p\left(t\right)}+\beta \sum _{x,y,t\le l_1}{c}_t{q}_1\left(t\right|y)p(x,y)log\frac{c_t{\sum }_y{q}_1\left(t\right|y)p(x,y)}{p\left(x\right)c_{t}p\left(t\right)}\hfill \\ & =& -\sum _{t\le l_1}{c}_t\sum _{y}p(t,y)log\frac{p(t,y)}{p\left(y\right)p\left(t\right)}+\beta \sum _{t\le l_1}{c}_t\sum _{x,y}{q}_1\left(t\right|y)p(x,y)log\frac{{\sum }_y{q}_1\left(t\right|y)p(x,y)}{p\left(x\right)p\left(t\right)}\hfill \\ & =& \sum _{t\le l_1}{c}_t{G}^1\left(y\right)\hfill \end{array}$$

Since ${\sum }_{t\le l_1}{c}_t=l_1$ by assumption, we have $F_I^1\left(y\right)=F_I^1\left(w\right)$ and therefore

$$F_I\left(w\right)=F_I\left(y\right)$$

Since ${\sum }_{t\le l_1}{c}_t=1$, the solutions w form a $l_1-$dimensional linear manifold. The same argument can be applied to $q_2,\dots ,q_z$ to finish the proof.    ☐

Now we spell out the consequences of this degeneracy for $dimker{d}^2{F}_I$. Since the manifolds of constant value of $F_I$ are linear, the second derivative along these manifolds must vanish. Note that in Theorem 3.2 we required that the solutions lie in Δ. Therefore, $ker{d}^2\mathcal{L}$ must vanish along this manifold, rather then $ker{d}^2{F}_I$. In the following paragraphs, our first two results are concerned with $ker{d}^2{F}_I$, the third—with $ker{d}^2\mathcal{L}$.

First we will show the result for a single block of ${}_I$.

Lemma 3.3

Fix an arbitrary quantizer q and an arbitrary class ν. Then the $K\times 1$ vector $q_{\nu }:=q(\mathit{T}=\nu |Y)$ is in the kernel of the ${\nu }^{th}$ block $B_{\nu }$ of $d^2{F}_I$ for any value of β.

Proof. 

To show that the vector $q_{\nu }$, defined in the statement of the Lemma, is in the kernel of $d^2{F}_I^{\nu }\left(q\right)$, the ${\nu }^{th}$-block of $d^2{F}_I$, we compute the $l^{th}$ row of this matrix. From (8) and (9) we see that

$$\begin{array}{ccc}\hfill {\left[d^2{F}_I^{\nu }{q}_{\nu }\right]}_l& =& \frac{1}{ln2}\left(\sum _k\frac{p\left(y_l\right)p\left(y_k\right)}{p\left(\nu \right)}-\sum _k{\delta }_{lk}\frac{p\left(y_k\right)}{}\right)\hfill \\ & & +\frac{\beta }{ln2}\sum _k\left(\sum _i\frac{p(x_i,y_k)p(x_i,y_l)}{p(x_i,\nu )}-\frac{p\left(y_k\right)p\left(y_l\right)}{p\left(\nu \right)}\right)\hfill \\ & =& \frac{1}{ln2}(p\left(y_l\right)-p\left(y_l\right))+\frac{\beta }{ln2}(\sum _i\frac{p(x_i,y_l)}{p(x_i,\nu )}\sum _{k}p(y_k,x_i)\hfill \\ & & -\frac{p\left(y_l\right)}{p\left(\nu \right)}\sum _{k}p\left(y_k\right))\hfill \\ & =& \frac{\beta }{ln2}\left(\sum _{i}p(x_i,y_l)-p\left(y_l\right)\right)=\mathbf{0}\hfill \end{array}$$

This shows that $q_{\nu }$ is in the kernel of block ν of $d^2{F}_I$.    ☐

Corollary 3.4

For an arbitrary pair $(q,\beta )$, the dimension of $ker{d}^2{F}_I$ is at least N, the number of classes of T.

Proof. 

Given $q_{\nu }$ as in Lemma 3.3, we define vectors ${{\{}_i\}}_{i=1}^N\in {\mathbf{R}}^{NK}$ by

$$\begin{array}{c}\hfill {}_1=\left(\begin{array}{c}{q}_1\\ \mathbf{0}\\ \mathbf{0}\\ ⋮\\ \mathbf{0}\end{array}\right),{}_2=\left(\begin{array}{c}\mathbf{0}\\ q_2\\ \mathbf{0}\\ ⋮\\ \mathbf{0}\end{array}\right),...,{}_N=\left(\begin{array}{c}\mathbf{0}\\ \mathbf{0}\\ \mathbf{0}\\ ⋮\\ q_N\end{array}\right)\end{array}$$

By Lemma 3.3, ${{\{}_i\}}_{i=1}^N\in ker{d}^2{F}_I(q,\beta )$. Clearly these vectors are linearly independent.    ☐

Now we investigate the consequences of Theorem 3.4 for the dimensionality of the kernel of $d^2\mathcal{L}$.

Theorem 3.5

Consider an arbitrary pair $(q,\beta )$, where q admits a symmetry $S_{l_1}\times S_{l_2}\times \dots \times S_{l_z}$. Then the dimension of $ker{d}^2{\mathcal{L}}_I$ at such point is at least

$$d\left(q\right):=(l_1-1)+(l_2-1)+\dots +(l_z-1)$$

Proof. 

Since q admits the stated symmetry it has the form (10). There are $l_1-1$ vectors of the form

$$\mathit{v}\left(1\right):={\mathit{u}}_1-{\mathit{u}}_l,l=2,\dots ,l_1.$$

Direct computation shows that, since ${\mathit{u}}_i\in ker{d}^2{F}_I$, each vector $\mathit{v}\left(1\right)\in ker{d}^2\mathcal{L}$. Similar argument shows that there are $l_i-1$ vectors $\left(i\right)\in ker{d}^2\mathcal{L}$ for $i=2,\dots ,z$.    ☐

Corollary 3.6

If q has no symmetry, i.e., $q=(q_1,q_2,\dots ,q_K)$ and all $q_i\ne q_j$ for $i\ne j$, then the dimension of $ker{d}^2{\mathcal{L}}_I$ is $d\left(q\right)=0$. In other words, $d^2{\mathcal{L}}_I$ is non-singular.

Lemma 3.7

At a phase transition $(q,\beta )$ of system (2) we have $dimker{d}^2{\mathcal{L}}_I\ge d\left(q\right)+1$.

Proof. 

This follows from the fact that the degeneracy of the kernel of dimension $d\left(q\right)$ is a consequence of the existence of a $d\left(q\right)$-dimensional manifold of solutions on which $F_I$ is constant. The existence of kernel with this dimension therefore does not indicate a phase transition. For that, the kernel must be at least $d\left(q\right)+1$-dimensional.    ☐

3.2. The Kernel of the Information Distortion

We want to contrast the degeneracy of $d^2{F}_I$ with the non-degeneracy of $d^2{F}_H$.

Theorem 3.8

There is no value of q such that the matrix $d^2{F}_H(q,\beta )$ is singular for all β in some interval.

Proof. 

If $\exists q$ such that for each β in some interval I, $d^2{F}_H$ is singular, then

$$\left(d^2\mathit{H}\left(T\right|Y)+\beta d^2\mathit{I}(T;Y)\right)W\left(\beta \right)=\mathbf{0}$$

for some $NK\times 1$ vector valued function $W\left(\beta \right)$. Thus, $\frac{1}{\beta }W\left(\beta \right)=-{\left(d^2\mathit{H}\left(T\right|Y)\right)}^{-1}{d}^2\mathit{I}(T;Y)W\left(\beta \right)$, from which it follows that $W\left(\beta \right)$ is a $\frac{1}{\beta }$-eigenvector of the fixed matrix $-{\left(d^2\mathit{H}\left(T\right|Y)\right)}^{-1}{d}^2\mathit{I}(T;Y)$ for every $\beta \in I$. This is a contradiction, since $-{\left(d^2\mathit{H}\left(T\right|Y)\right)}^{-1}{d}^2\mathit{I}(T;Y)$ has at most $NK$ distinct eigenvalues.    ☐

Lemma 3.9

At the phase transition $(q,\beta )$ for system (1) we have $dimker{d}^2{L}_H\ge 1$.

4. Bifurcations off the Uniform Solution

In this section we want to illustrate the close analogy between Deterministic Annealing with Euclidean distortion function and Information Distortion. Our goal is to find values of $(q,\beta )$ for which the problems (1) and (2) undergo phase transition. Given the joint probability distribution $p(x,y)$, we can find the values of β explicitly for $q=1/N$ in terms of eigenvalues of a certain stochastic matrix. Secondary phase transitions that occur at values of $q\ne 1/N$ cannot be computed explicitly and we must resort to numerical continuation along the branches of equilibria. An eigenvalue problem, implicitly relating quantities $q\ne 1/N$ and β at which phase transition occurs, can still be obtained. This is completely analogous to results of Rose [14] for a different class of optimization problems.

We start by deriving a general eigenvalue problem which computes the pair $(q,\beta )$. We seek to compute $(q,\beta )$ for which the $NK\times NK$ matrix of second derivatives $d^{2}F$ has a nontrivial kernel. This is a necessary condition for a bifurcation to occur. We first discuss the Hessian of (1), $d^2{F}_H:=d^2{F}_H(q,\beta )$, evaluated at q and at some value of the annealing parameter β. Thus, we need to find pairs $(q,\beta )$ where $d^2{F}_H$ has a nontrivial kernel. For that, we solve the system

$$d^2{F}_H\mathit{w}=(d^2\mathit{H}\left(T\right|Y)+\beta d^2\mathit{I}(X;T\left)\right)\mathit{w}=0$$

(11)

for any nontrivial $\mathit{w}\in {\mathbf{R}}^{NK}$. We rewrite (11) as an eigenvalue problem,

$${(-d^2\mathit{H}\left(T\right|Y))}^{-1}{d}^2\mathit{I}(X;T)\mathit{w}=\frac{1}{\beta }\mathit{w}$$

(12)

Since $-\mathit{I}(Y;T)=\mathit{H}\left(T\right|Y)-\mathit{H}\left(T\right)$, then, for the Hessian $d^2{F}_I$, we find pairs $(q,\beta )$ for which

$$d^2{F}_I\mathit{w}=(d^2\mathit{H}\left(T\right|Y)-d^2\mathit{H}(T)+\beta d^2\mathit{I}(X;T\left)\right)\mathit{w}=0$$

Multiplying by ${(-d^2\mathit{H}\left(T\right|Y))}^{-1}$ leads to a generalized eigenvalue problem

$${(-d^2\mathit{H}\left(T\right|Y))}^{-1}{d}^2\mathit{I}(X;T)\mathit{w}=(I-{(-d^2\mathit{H}(T|Y))}^{-1}{d}^2\mathit{H}(T))\frac{1}{\beta }\mathit{w}$$

(13)

Since $d^2\mathit{H}\left(T\right|Y)$ is diagonal, we can explicitly compute the inverse

$${[{(-d^2\mathit{H}(T|Y))}^{-1}]}_{\left(\nu k\right),\left(\eta l\right)}={\delta }_{\eta \nu }{\delta }_{lk}ln2\frac{q_{vk}}{p\left(y_k\right)}.$$

(14)

Next, we compute the explicit forms of the $NK\times NK$ matrices

$$U\left(q\right):={(-d^2\mathit{H}\left(T\right|Y))}^{-1}{d}^2\mathit{I}(X;T)$$

and

$$A\left(q\right):={(-d^2\mathit{H}\left(T\right|Y))}^{-1}{d}^2\mathit{H}(T)$$

Since both of these matrices are block diagonal, with one block corresponding to a class of $\mathit{T}$, we will compute the ${\nu }^{th}$ block of these matrices. Using (7)–(9) we get that the ${(l,k)}^{th}$ element of the ${\nu }^{th}$ block of $U\left(q\right)$ is

$$u_{lk}^{\nu }:=\sum _i\frac{p(x_i,y_k)p(x_i,y_l)}{p(x_i,\nu )p\left(y_l\right)}{q}_{\nu l}-\frac{p\left(y_k\right)}{p\left(\nu \right)}{q}_{\nu l}$$

and the ${(l,k)}^{th}$ element of the ${\nu }^{th}$ block of $A\left(q\right)$ is

$$a_{lk}^{\nu }:=\frac{p\left(y_k\right)q_{\nu l}}{p\left(\nu \right)}$$

(15)

We observe that the matrix $U\left(q\right)$ can be written as $U\left(q\right)=Q\left(q\right)-A\left(q\right)$, where the ${(l,k)}^{th}$ element of the ${\nu }^{th}$ block of matrix $Q\left(q\right)$ is

$$r_{lk}^{\nu }:=\sum _i\frac{p(x_i,y_k)p(x_i,y_l)q_{\nu l}}{p(x_i,\nu )p\left(y_l\right)}$$

(16)

Therefore the problems (12) and (13) become generalized eigenvalue problems,

$$\left(Q\right(q)-A(q\left)\right)\mathit{w}=\lambda \mathit{w}\mathrm{for}\mathrm{system} \left(1\right)$$

(17)

and

$$\left(Q\right(q)-A(q\left)\right)\mathit{w}=(I-A(q\left)\right)\lambda \mathit{w}\mathrm{for}\mathrm{system} \left(2\right)$$

(18)

respectively.

In the eigenvalue problems (17) and (18), the matrices $Q\left(q\right)$ and $A\left(q\right)$ change with q. On the other hand, we know that for all $\beta \in [0,\widehat{\beta })$ for some $\widehat{\beta }>0$, both problems (1) and (2) have a maximum at the uniform solution $q_{\frac{1}{N}}$ [19], i.e., when $q\left(t\right|y)=1/N$ for all t and y. We now determine when this extremum ceases to be the maximum.

We evaluate matrices $Q\left(q\right)$ and $A\left(q\right)$ at $q_{\frac{1}{N}}$ to get

$$r_{lk}^{\nu }=\sum _i\frac{p(x_i,y_k)p(x_i,y_l)}{p\left(x_i\right)p\left(y_l\right)}=\sum _{i}p\left(y_k\right|x_i)p\left(x_i\right|y_l)$$

and

$$a_{lk}^{\nu }=p\left(y_k\right)$$

Let $\mathbf{1}$ be a vector of ones in ${\mathbf{R}}^N$. We observe that

$$A(q_{\frac{1}{N}})\mathbf{1}=\mathbf{1}$$

and that the $l^{th}$ component of $Q(q_{\frac{1}{N}})\mathbf{1}$

$$\begin{array}{ccc}\hfill {[Q(q_{\frac{1}{N}})\mathbf{1}]}_l& =& \sum _k\sum _{i}p\left(y_k\right|x_i)p\left(x_i\right|y_l)\hfill \\ & =& \sum _{i}p\left(x_i\right|y_l)\sum _{k}p\left(y_k\right|x_i)\hfill \\ & =& \sum _{i}p\left(x_i\right|y_l)\hfill \\ & =& 1\hfill \end{array}$$

Therefore, we obtain one particular eigenvalue-eigenvector pair $(0,\mathbf{1})$ of the eigenvalue problems (17) and (18):

$$Q(q_{\frac{1}{N}})-A(q_{\frac{1}{N}})\mathbf{1}=0\mathrm{and}Q(q_{\frac{1}{N}})-A(q_{\frac{1}{N}})\mathbf{1}=0=(I-A(q_{\frac{1}{N}}))\mathbf{1}$$

Since the eigenvalue λ corresponds to $1/\beta$, this solution indicates a bifurcation at $\beta =\infty$. We are interested in finite values of β.

Theorem 4.1

Let $1={\lambda }_1\ge {\lambda }_2\ge {\lambda }_3\dots {\lambda }_K$ be eigenvalues of a block of the matrix $Q(q_{\frac{1}{N}})$. Then the solution $q_{\frac{1}{N}}$ of the maximization problems (1) and (2) ceases to be a maximum at $\beta =\frac{1}{{\lambda }_2}$. The corresponding eigenvector to ${\lambda }_2$ (and all ${\lambda }_k$ for $k\ge 2$) is perpendicular to the vector $p:={(p\left(y_1\right),p\left(y_2\right),\dots ,p\left(y_n\right))}^T$.

Proof. 

We note first that the range of matrix $A(q_{\frac{1}{N}})$ is the linear space spanned by vector $\mathbf{1}$, and its kernel is the linear space

$$W:=\{\mathit{w}\in {\mathbf{R}}^N|⟨\mathit{p},\mathit{w}⟩=0\}$$

where $\mathit{p}=(p\left(y_1\right),\dots ,p\left(y_n\right))$.

We now check that the space W is invariant under the matrix $Q(q_{\frac{1}{N}})$, which means that $Q(q_{\frac{1}{N}})W\subset W$. It will then follow that all eigenvectors of $Q(q_{\frac{1}{N}})-A(q_{\frac{1}{N}})$, except $\mathbf{1}$, belong to W and are actually eigenvectors of $Q(q_{\frac{1}{N}})$ alone. So, assume $\mathit{w}=(w_1,\dots ,w_N)\in W$, which means

$$\sum _k{w}_{k}p\left(y_k\right)=0$$

We compute the l-th element ${[Q(q_{\frac{1}{N}})\mathit{w}]}_l$ of vector $Q(q_{\frac{1}{N}})\mathit{w}$:

$${[Q(q_{\frac{1}{N}})\mathit{w}]}_l=\sum _k\sum _{i}p\left(y_k\right|x_i)p\left(x_i\right|y_l)w_k$$

The vector $Q(q_{\frac{1}{N}})\mathit{w}$ belongs to W if, and only if, its dot product with p is zero. We compute the dot product

$$\begin{array}{ccc}\hfill Q(q_{\frac{1}{N}})\mathit{w}·\mathit{p}& =& \sum _{l,i,k}p\left(y_k\right|x_i)p\left(x_i\right|y_l)w_{k}p\left(y_l\right)\hfill \\ & =& \sum _{i,k}p\left(y_k\right|x_i)w_k\sum _{l}p\left(x_i\right|y_l)p\left(y_l\right)\hfill \\ & =& \sum _k{w}_k\sum _{i}p\left(y_k\right|x_i)p\left(x_i\right)\hfill \\ & =& \sum _k{w}_{k}p\left(y_k\right)\hfill \end{array}$$

The last expression is zero, since $w\in W$.

This shows that all other eigenvectors of $Q(q_{\frac{1}{N}})-A(q_{\frac{1}{N}})$, except $\mathbf{1}$, belong to W and are eigenvectors of $Q(q_{\frac{1}{N}})$ alone. Since bifurcation values β are reciprocal to eigenvalues ${\lambda }_i$, the result follows.    ☐

Corollary 4.2

The value β at which the first phase transition occurs does not depend on the number of classes, N. It only depends on the properties of the matrix Q.

Observe that, since $d^{2}F$ has N identical blocks at $q_{\frac{1}{N}}$ and each block has a zero eigenvalue at $\beta =1/{\lambda }_i$, we get that

$$dimker{d}^2{F}_H\ge N$$

at such a value of β. This is a consequence of the symmetry. For the Information Bottleneck function $F_I$, as a consequence of Lemma 3.4, each block has a zero eigenvalue for any value of β. At the instance of the first phase transition at $(q_{\frac{1}{N}},\beta =1/{\lambda }_i)$, each block of $F_I$ admits an additional zero eigenvalue, and therefore

$$dimker{d}^2{F}_I\ge 2N$$

Notice that the matrix $Q(q_{\frac{1}{N}})$ is transpose of a stochastic matrix, since the sum of all elements in the $l^{th}$ row,

$$\sum _k\sum _{i}p\left(y_k\right|x_i)p\left(x_i\right|y_l)=1$$

Therefore all eigenvalues satisfy $-1\le {\lambda }_i\le 1$. In particular, ${\lambda }_2\le 1$. This proves

Corollary 4.3

For both problems (1) and (2), the solution $q_{\frac{1}{N}}$ is stable for all $\beta \in [0,1]$.

Remark 4.4

The matrix $Q:=Q(q_{\frac{1}{N}})$ has an interesting structure and interpretation (see Figure 3). Let G be a graph with vertices $y_k$ and let the oriented edge $y_l\to y_k$ have a weight ${\sum }_{i}p\left(y_k\right|x_i)p\left(x_i\right|y_l)$. The matrix Q is the transpose of a Markov transition matrix on the elements $\left\{y_k\right\}$. The weight attached to each edge is a sum of all the contributions along all the paths $y_l\to x_i\to y_k$ over all i. This structure is key to associating the annealing problem to the normalized cut problem discussed in Section 6.

Figure 3. The graph G with vertices labelled by elements of Y. The oriented edges in G have weights obtained from the weights in the graph of the joint distribution $p(X,Y)$. The weight of the solid edge in G is computed by summing the edges on the left side of the picture.

5. Bifurcations in the General Case

To find the discrete values of the pairs $(q,\lambda )$ that solve the eigenvalue problems (17) and (18) for a general value of q, we transform the problems (17) and (18) one more time. Let C be a block diagonal matrix of size $NK\times NK$ whose ${\nu }^{th}$ block is a $K\times K$ diagonal matrix, $\mathrm{diag}\left(p\left(y_k\right)\right)$. Instead of the eigenvalue problem (17), we consider

$$C(Q\left(q\right)-A\left(q\right))C^{-1}\mathit{w}=\lambda \mathit{w}$$

(19)

and instead of the problem (18), we consider

$$C(Q\left(q\right)-A\left(q\right))C^{-1}\mathit{w}=C(I-A)C^{-1}\lambda \mathit{w}$$

(20)

Clearly, these problems have the same eigenvalues as the problems (17) and (18) respectively, and the eigenvectors are related via the diagonal matrix C.

Let

$$V\left(q\right):=CQ\left(q\right)C^{-1}\mathrm{and}B\left(q\right):=CA\left(q\right)C^{-1}$$

Then the ${(l,k)}^{th}$ element of the ${\nu }^{th}$ block of the $NK\times NK$ matrix $V\left(q\right)$ is

$$v_{lk}^{\nu }:=\sum _i\frac{p(x_i,y_k)p(x_i,y_l)q_{\nu l}}{p(x_i,\nu )p\left(y_k\right)}$$

(21)

and for the $NK\times NK$ matrix B, we have that

$$b_{lk}^{\nu }=\frac{p(\nu ,y_l)}{p\left(\nu \right)}$$

(22)

Lemma 5.1

The matrix $V\left(q\right)$ is stochastic for any value of q.

Proof. 

We sum the $k^{th}$ column of $V\left(q\right)$ to get

$$\begin{array}{ccc}\hfill \sum _l{v}_{lk}& =& \sum _l\sum _i\frac{p(x_i,y_k)p(x_i,y_l)q_{\nu l}}{p(x_i,\nu )p\left(y_k\right)}\hfill \\ & =& \sum _i\frac{p(x_i,y_k)}{p(x_i,\nu )p\left(y_k\right)}\sum _{l}p(x_i,y_l)q_{\nu l}\hfill \\ & =& \sum _i\frac{p\left(x_i\right|y_k)p\left(y_k\right)}{p(x_i,\nu )p\left(y_k\right)}\sum _{l}p\left(x_i\right|y_l)p(y_l,\nu )\hfill \\ & =& \sum _i\frac{p\left(x_i\right|y_k)}{p(x_i,\nu )}p(x_i,\nu )\hfill \\ & =& \sum _{i}p\left(x_i\right|y_k)\hfill \\ & =& 1\hfill \end{array}$$

☐

Lemma 5.2

The ${\nu }^{th}$ block of the matrices in the eigenvalue problems (19) and (20) have solutions $\{\lambda =0,P_{\nu }={(p(y_1,\nu ),\dots ,p(y_K,\nu ))}^T\}$ that correspond to the eigenvalue-eigenvector pair $(1,P_{\nu })$ of the stochastic matrix $V^{\nu }\left(q\right)$, the ${\nu }^{th}$ block of the $NK\times NK$ matrix $V\left(q\right)$. All other eigenvalues are eigenvalues of the problem

$$V^{\nu }\left(q\right)u=\lambda u$$

and the corresponding eigenvectors lie in the space $W^{\nu }=\{u\in {\mathbf{R}}^K|{\sum }_j{\left[u\right]}_j=0\}$.

Proof. 

To show the first part of the Lemma, we multiply the $l^{th}$ row of ${\nu }^{th}$ block of $V\left(q\right)-B\left(q\right)$ by the vector $P_{\nu }:={(p(y_1,\nu ),\dots ,p(y_K,\nu ))}^T$. We get

$$\begin{array}{ccc}\hfill {(V\left(q\right)-B\left(q\right))}^{\nu }{P}_{\nu }& =& \sum _{i,k}\frac{p(x_i,y_k)p(x_i,y_l)q_{\nu l}p(y_k,\nu )}{p(x_i,\nu )p\left(y_k\right)}-\sum _k\frac{p\left(y_l\right)q_{\nu l}p(y_k,\nu )}{p\left(\nu \right)}\hfill \\ & =& \sum _i\frac{p(x_i,y_l)q_{\nu l}}{p\left(x_i\right|\nu )p\left(\nu \right)}\sum _k\frac{p\left(x_i\right|y_k)p\left(y_k\right)p(y_k,\nu )}{p\left(y_k\right)}\hfill \\ & & -\frac{p\left(y_l\right)q_{\nu l}}{p\left(\nu \right)}\sum _{k}p(y_k,\nu )\hfill \\ & =& \sum _i\frac{p(x_i,y_l)q_{\nu l}}{p\left(x_i\right|\nu )}p\left(x_i\right|\nu )-p\left(y_l\right)q_{\nu l}\hfill \\ & =& q_{\nu l}\sum _{i}p(x_i,y_l)-p\left(y_l\right)q_{\nu l}=0\hfill \\ & =& 0\hfill \end{array}$$

(23)

Observe that the above computation shows that $V^{\nu }\left(q\right)P_{\nu }=P_{\nu }$, and so $P_{\nu }$ is a 1-eigenvector of the stochastic matrix $V^{\nu }\left(q\right)$. This finishes the first part of the proof.

To prove the second case, we will show that $W^{\nu }=ker{B}^{\nu }\left(q\right)$ and that $W^{\nu }$ is invariant under $V^{\nu }\left(q\right)$. To see that $W^{\nu }=ker{B}^{\nu }\left(q\right)$, it is enough to realize that every row of $B^{\nu }\left(q\right)$ is a multiple of 1, the $K\times 1$ vector of ones. In other words, $b_{kl}^{\nu }$ from (22) is independent of k. Clearly, 1 is perpendicular to $W^{\nu }$. Since the range of $B^{\nu }\left(q\right)$ is one-dimensional, $dimker{B}^{\nu }\left(q\right)=K-1$. It follows easily that

$$ker{B}^{\nu }\left(q\right)=W^{\nu }$$

(24)

To finish the proof, we show that W is invariant under any stochastic matrix, and in particular to the matrix $V^{\nu }\left(q\right)$. Let S be a $K\times K$ stochastic matrix. Then, if $\mathit{w}\in W$ then

$$Sw={(s_{1,1}{\left[\mathit{w}\right]}_1+\dots +s_{1,K}{\left[\mathit{w}\right]}_K,s_{2,1}{\left[\mathit{w}\right]}_1+\dots +s_{2,K}{\left[\mathit{w}\right]}_K,\dots ,s_{K,1}{\left[\mathit{w}\right]}_1+\dots +s_{K,K}{\left[\mathit{w}\right]}_K)}^T.$$

Adding up the elements in vector Sw, we get

$$\begin{array}{ccc}\hfill \sum _{i}S{\left[\mathit{w}\right]}_i& =& s_{1,1}{\left[\mathit{w}\right]}_1+\dots +s_{1,K}{\left[\mathit{w}\right]}_K+\dots s_{K,1}{\left[\mathit{w}\right]}_1+\dots +s_{K,K}{\left[\mathit{w}\right]}_K\hfill \\ & =& (s_{1,1}+\dots +s_{K,1}){\left[\mathit{w}\right]}_1++\dots +(s_{1,K}+\dots +s_{K,K}){\left[\mathit{w}\right]}_K\hfill \\ & =& {\left[\mathit{w}\right]}_1+{\left[\mathit{w}\right]}_2+\dots +{\left[\mathit{w}\right]}_K=0,\hfill \end{array}$$

(25)

and so $S\mathit{w}\in W$.    ☐

Theorem 5.3

Fix an arbitrary $q\in \Delta$. Let $1={\lambda }_1={\lambda }_2=...={\lambda }_N\ge {\lambda }_{N+1}\ge {\lambda }_{N+2}\dots \ge {\lambda }_{KN}$ be a union of eigenvalues of the stochastic matrices $V^{\nu }\left(q\right)$ for all ν. Then the values of β for which $d^2{F}_H\left(q\right)$ has a nontrivial kernel (or where $dimker{d}^2{F}_I\left(q\right)\ge d\left(q\right)+1$, see Lemma 3.5) are

$$\frac{1}{{\lambda }_{N+1}}\le \frac{1}{{\lambda }_{N+2}}\le \dots \le \frac{1}{{\lambda }_{KN}}$$

Proof. 

The only difference between $d^2{F}_H$ and $d^2{F}_I$ is the N dimensional kernel of the latter matrix. Therefore we will only consider $d^2{F}_H$ in this proof.

As discussed above, $d^2{F}_H\left(q\right)$ has a nontrivial kernel if and only if there is a block which has a nontrivial kernel. We will use the previous Lemma to discuss such a block.

Note that $\lambda =0$ corresponds to $\beta =\infty$, and so this scenario is unimportant for the bifurcation structure of the problems (1) and (2).

Since $W^{\nu }$ is a $K-1$ dimension invariant subspace of ${\mathbf{R}}^K$, there must be $K-1$ eigenvectors of $V^{\nu }\left(q\right)$ in $W^{\nu }$. The 0-eigenvector $P_{\nu }$ is not in $W^{\nu }$, so all other eigenvectors not corresponding to $\lambda =0$ must be in $W^{\nu }$. Since $V^{\nu }\left(q\right)$ is stochastic and $\lambda =0$ corresponds to the eigenvalue 1 of $V^{\nu }\left(q\right)$, then the β values at which bifurcation occurs are reciprocals to the eigenvalues of $V^{\nu }\left(q\right)$ for each ν. That means $\beta \le 1$. Since there are N blocks, there will be at least N eigenvalues of $d^2{F}_H\left(q\right)$ equal to 1.    ☐

We used Theorem 5.3 to determine the β values where bifurcations occur from the uniform solution branch $(q_{\frac{1}{N}},\beta )$. The results are presented in Figure 4.

Figure 4. Theorem 5.3 can be used to determine the β values where bifurcations can occur from $(q_{\frac{1}{N}},\beta )$. A joint probability space on the random variables $(X,Y)$ was constructed from a mixture of four Gaussians as in [2]. For this data set, and for either $F=F_H$ or $F=F_I$, we predict bifurcation from the branch $(q_{\frac{1}{4}},\beta )$, at each of the 15 β values given in this figure. By Theorem 4.1, $q_{\frac{1}{4}}$ ceases to be a solution at $\beta \approx 1.038706$.

6. Normalized Cuts and the Bifurcation off $q_{\frac{1}{N}}$

There is a vast literature devoted to problems of clustering. Many clustering problems can be formulated in the language of graph theory. Objects which one desires to cluster are represented as a set of nodes V of a graph $G=(V,E)$, and the weights w associated to edges represent the degree of similarity of two adjacent nodes. Finding a good clustering in such a formulation is equivalent to finding a cut in the graph G, which divides the set of nodes V into sets representing individual clusters. A cut in the graph is simply a collection of edges that are removed from the graph.

A bi-partitioning of the graph is the problem in which a cut divides the graph into two parts, A and B. We define

$$cut(A,B)=\sum _{u\in A,v\in B}w(u,v)$$

(26)

There are efficient algorithms to solve minimal cut problem, where one seeks a partition into sets A and B with minimal cut value. When using the minimal cut as a basis for a clustering algorithm, one often finds that the minimal cut is achieved by separating one node from the rest of the graph G. Including more edges into the cut increases the cost, hence these singleton solutions will be favored.

To counteract that, Shi and Malik [21] studied image segmentation problems and proposed a clustering based on minimizing the normalized cut (Ncut):

$$Ncut(A,B)=\frac{cut(A,B)}{assoc(A,V)}+\frac{cut(A,B)}{assoc(B,V)}$$

(27)

where

$$assoc(A,V)=\sum _{u\in A,t\in V}w(a,t)$$

Shi and Malik [21] have shown that the problem of minimizing the normalized cut is NP-complete. However, they proposed an approximate solution, which can be found efficiently. We briefly review their argument: Let

$$d\left(i\right)=\sum _{j}w(i,j)$$

be the total connection from node i to all other nodes. Let $n=\left|V\right|$ be the number of nodes in the graph and let D be an $n\times n$ diagonal matrix with values $d\left(i\right)$ on the diagonal. Let W be an $n\times n$ symmetric matrix with

$$W(i,j)=w_{ij}$$

Let x be an indicator vector with $x_i=1$ if node i is in A, and $x_i=-1$ otherwise. Then Shi and Malik [21] show that the minimal cut can be computed by minimizing the Rayleigh quotient over a discrete set of admissible vectors y:

$$\underset{x}{min}Ncut\left(x\right)=\underset{y}{min}\frac{y^T(D-W)y}{y^{T}Dy}$$

(28)

with components of y satisfying $y_i\in \{1,-b\}$ for some constant b, and under the additional constraint

$$y^{T}D\mathbf{1}=0$$

(29)

If one relaxes the first constraint $y_i\in \{1,-b\}$ and allows for a real valued vector y, then the problem is computationally tractable. The computation of the real valued vector y is the basis of the Approximate normalized cut. Once this vector is computed, vertices of G which correspond to positive entries of y will be assigned to the set A, and vertices which correspond to negative entries of y will be assigned to the set B. The relaxed problem is solved by the solution of a generalized eigenvalue problem,

$$(D-W)y=\mu Dy$$

(30)

that satisfies the constraint (29). We repeat here an argument of Shi and Malik’s [21], which shows that (28) with the constraint (29) is solved by the second smallest eigenvector of the problem (30). In fact, the smallest eigenvalue of (30) is zero and corresponds to an eigenvector $y_0=\mathbf{1}$. The argument starts with rewriting (30) as

$$D^{-1/2}(D-W)D^{-1/2}z=\mu z$$

and realizing that $z_0=D^{1/2}\mathbf{1}$ is a 0-eigenvector of this equation. Further, since $D^{-1/2}(D-W)D^{-1/2}$ is symmetric, all other eigenvectors are perpendicular to $z_0$. Translating back to problem (30), one gets the corresponding vector $y_0$ and all other eigenvectors satisfying $y^{T}D\mathbf{1}=0$. We want to observe that this is the only place when the symmetry of matrix W is used.

In Theorem 4.1 we showed that the bifurcating direction v of one block of $d^{2}F$ is the eigenvector corresponding to the second largest eigenvalue of a stochastic matrix Q. In Remark 4.4 we interpreted the matrix $Q^T$ as a transition matrix of a Markov chain and we associated a directed graph G to this Markov chain. The graph G had vertices labelled by the elements of Y and the weight of the edge $y_l\to y_k$ was defined by

$${\left[Q\right]}_{lk}=\sum _{x}p\left(y_k\right|x)p\left(x\right|y_l)$$

Note that these weights are not symmetric. We will symmetrize the graph G by multiplying the weight matrix $Q:=Q(q_{\frac{1}{N}})$ by a diagonal matrix $C=diag\left(p\left(y_k\right)\right)$. The resulting graph H (Figure 5) has a weight matrix $CQ$ whose $l{k}^{th}$ element is

$$\sum _{x}p\left(y_k\right|x)p\left(x\right|y_l)p\left(y_l\right)=\sum _x\frac{p(y_k,x)p(x,y_l)}{p\left(x\right)}$$

(31)

We form an undirected graph H with vertices labelled by elements of Y and the edge weight $w_{lk}$ given by (31).

Figure 5. Graph G on the left is an oriented graph. We obtain unoriented graph H on the right by multiplying all edges emanating from $y_i$ by $p\left(y_i\right)$. In the figure all weighs along solid edges are multiplied by $p\left(y_1\right)$ and all weights along the dashed edges are multiplied by $p\left(y_2\right)$.

The following Theorem, relating the bifurcating direction $v_2$ of matrix Q to the solution of the Approximate Normalized Cut of graph H, was proved in [22]. We use the notation of Theorem 4.1

Theorem 6.1

([22]) The eigenvector $v_2$, along which the solution $q=1/N$ bifurcates at ${\beta }_2=1/{\lambda }_2$, induces the Approximate Normal Cut of the graph H.

This Theorem shows that the bifurcating eigenvector solves the Approximate Normal Cut for the graph H, rather than the original graph G. This suggest an important inverse problem. Given a graph H for which we want to compute the Approximate Normal Cut, can we construct the graph G (given by the set of vertices, edges and weights), such that the bifurcating eigenvector would compute the Approximate Normal Cut for H? This problem, which is beyond the scope of this paper, was addressed in [22], where an annealing algorithm was designed to compute the Approximate Normal Cut using these techniques. The reader is referred to the original paper for more details.

Remark 6.2

In [15] we show that the bifurcating direction for $d^2{\mathcal{L}}_H$ at the first phase transition from $q_{\frac{1}{N}}$ is a vector of the form

$$\mathit{u}:={((N-1)v,-v,\dots ,-v)}^T$$

where $v:=v_2$ is the second eigenvector of the block $B_1$ (all the block are identical by symmetry). In this expression $v\in {\mathbf{R}}^N$ and there are K vectors of size K in vector $\mathit{u}$. Then the quantizer q shortly after passing a bifurcation value of β has the form

$$q=q_{\frac{1}{N}}+ϵ\mathit{u}$$

(32)

Let us denote by A the set of $y_i$ such that the i-th component of v is negative, and by B the set of $y_i$ such that the i-th component of v is positive. Note that A and B correspond to the Approximate Ncut for both graphs G and H. If we verbalize $q\left(t\right|y)$ as “the probability that y belongs to class t”, then (32) shows that, after bifurcation

• the probability that $y\in A$ belongs to class 1 is less than $1/N$ and the probability that it belongs to classes $2,\dots ,N$ is more then $1/N$;
• the probability that $y\in B$ belongs to class 1 is more than $1/N$ and the probability that it belongs to classes $2,\dots ,N$ is less then $1/N$.

This describes the correspondence between the first bifurcation and Approximate Ncut.

7. Conclusions

The main goal of this contribution was to show that information-based distortion annealing problems have an interesting mathematical structure. The most interesting aspects of that mathematical structure are driven by the symmetries present in the cost functions—their invariance to actions of the permutation group $S_N$, represented as relabeling of the reproduction classes. The second mathematical structure that we used successfully was bifurcation theory, allowing us to identify and study the discrete points at which the character of the solutions to the cost function changed. The combination of those two tools allowed us to compute explicitly in Section 4 the value of the annealing parameter β at which the initial maximum $q_{\frac{1}{N}}$ of (1) and (2) loses stability. We concluded that, for a fixed system $p(\mathit{X},\mathit{Y})$, this value is the same for both problems, that it does not depend on the number of elements of the reproduction variable $\mathit{T}$ and that it is always greater than 1. In Section 5 we further introduced an eigenvalue problem which links together the critical values of β and q for phase transition off arbitrary intermediate solutions.

Even though the cost functions $F_I$ and $F_H$ have similar properties, they also differ in some important aspects. We have shown that the function $F_I$ is degenerate since its constitutive functions $\mathit{I}(Y;T)$ and $\mathit{I}(X;T)$ are not strictly convex. That introduces additional invariances that are always preserved, which makes phase transitions more difficult to detect, and post-transition directions more difficult to determine. Specifically, in addition to actions by the group of symmetries, the cost function $F_I$ is invariant to altering a solution by a vector in the ever-present kernel (identified in Corollary 3.4). In contrast, $F_H$ is strictly convex except at points of phase transitions. The theory we developed allows us to identify bifurcation directions, and determine their stability. Despite the presence of a high dimensional null space at bifurcations, the symmetries restrict the allowed transitions to multiple 1-dimensional transition, all related by group transformations.

Finally, in Section 6 we showed that the direction in which a phase transition occurs can be linked to an Approximate Normalized Cut problem of graphs arising naturally from the data structure given by $p(\mathit{X},\mathit{Y})$. This connection will allow future studies of information distortion methods to include powerful approximate techniques developed in Graph Theory. It will also allow the transition of the methods we developed here into tools that may be used to create new approximations for the Approximate Normalized Cut problem.

Previously we have shown that for both problems the global optimum ($\beta \to \infty$) is deterministic [3], and that the combinatorial search for the solution is NP-complete [23]. The main problem that still remains unresolved is whether the global optimum can always be achieved by the annealing process from the uniform starting solution. Proving this may be equivalent to stating that $NP=P$, so it is unlikely. However, the relatively straightforward annealing problem, when combined with the power of equivariant bifurcation theory, may be a fruitful method for approaching $NP$-hard problems.