Entropy Stress and Scaling of Vital Organs over Life Span Based on Allometric Laws
Abstract
:1. Introduction and Literature Review
2. Rationale and Objective
3. Analysis
- Lifetime energy expenditure (LSEE) and entropy generation (LSEGk) of each organ k, where k = B, H, K, L and the remainder R
- Specific lifetime energy expenditure, LSEEM, (kJ/kg body mass) and specific entropy generation, LSEGM, (kJ/{kg body mass K}) whole body
- The % contribution by the each organ k to the overall energy consumption and % contribution by each organ to the total entropy generation of the whole body.
3.1. Life Span Energy Expenditure of Body in Terms of Energy Expenditure of Vital Organs
| Organ, k | ck | dk | ek | fk+ | W Contrib* | |
|---|---|---|---|---|---|---|
| Brain | 0.01100 | 0.76 | 21.620 | −0.14 | 11.93 | 14.0 |
| Heart | 0.00630 | 0.98 | 43.113 | −0.12 | 25.89 | 3.31 |
| Kidneys | 0.00893 | 0.85 | 33.414 | −0.08 | 23.79 | 6.16 |
| Liver | 0.03300 | 0.87 | 33.113 | −0.27 | 10.52 | 9.20 |
| Rest, without BHKL | 0.93900 | 1.01 | 1.446 | −0.17 | 0.70 | 49.2 |
| Nutrients | Formulae | M, kg/kmol | St.O2, kg/kg | RQ | HHV kJ/kg | HHVO2 kJ/kg O2 | ΔHC° at 37°C MJ/kmol | hf MJ/kmol | s°298 kJ/kmol K | ΔGc° MJ/kmol | ΔGM° MJ/kmol | ΔSc° kJ/kmol K | Metabol. eff. % | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Glucose | C6H12O6 | 180 | 1.066 | 1.0 | 15630 | 14665 | −2815 | −1260 | 212.0 | −2895 | 1.03 | −1790 | 259.5 | 38.2 |
| Fat | C16H32O2 | 256 | 2.869 | 0.7 | 39125 | 13635 | −10035 | −835 | 452.4 | −9840 | 0.98 | −3125 | −630.1 | 32.2 |
| Protein or Albumin | C72H112N2O22S (*1) | 1390 | 2.07 | 0.8 | 28893 (*3) | 13944 | −4480 | |||||||
| Protein | C4.57H9.03N1.27 O2.25S0.046 (*2) | 119 | 1.54 | 0.8 | 22790 | 14705 | −2720 | −384 | −2665 | 0.98 | −163.8 | 10.4 | ||
| Protein [40] | C4.98 H9.8 N1.4O2.5 | 117.3 | 1.413 | 0.83 | 19000 [41] | 13475 |
3.2. Life Span Entropy Generation (LSEG) in Terms of Entropy Generation of Vital Organs
3.3. Availability Analysis
3.3.1. Assumptions
- (a)
- The macronutrients or main nutrient groups CH, F and P are modeled using glucose, palmitic acid, and average amino acids composition respectively.
- (b)
- The ηn, where n=CH, F and P are different for every nutrient but remain constant over time/age.
- (c)
- The ATP, which is equivalent to work in thermodynamics, does not create irreversibility.
- (d)
- Energy requirements are related to body mass mB(t); statistical data on normal growth of body mB (t) with age from the Summary Report 2007, US National Center for Environmental Assessment [33].
- (e)
- Life span of whole species could be defined since the birth and death are well defined; however it is difficult to define the life span of organs. Thus, only extent of degradation of organs is presented in terms of entropy generated during average life span.
- (f)
- The Gibbs free energy change of nutrients during metabolism, ΔGc,n is a function of temperature, pressure and mole fraction is approximately same as ΔGc,n°, i.e., ΔGc,n ≈ ΔGc,n° which implies that nutrients, oxidants, CO2 and H2O exists as pure species in the reactants and products.
- (g)
- In thermodynamic literature, the ratio of varies from 1.0 to 1.02 for most hydrocarbon fuels of general formulae CxHy when lower heat value is used for the enthalpy of combustion of nutrient n. This is consistent with the findings of Brzustowski and Brena, who showed that the ratio of fuel availability to lower heat value ranges from 1.04 to 1.07 [32]. When higher heating values are used for the same fuels, the ratio varies from 0.9 to 0.96 for HC and from 0.98 to 1.03 for CH, and F. Hence,
- (h)
- While general derivations assume that metabolic efficiency depends upon organ k, age (t) and type of nutrients (j) being oxidized, the quantitative results assume a weighted metabolic efficiency independent of organ k and age (t).
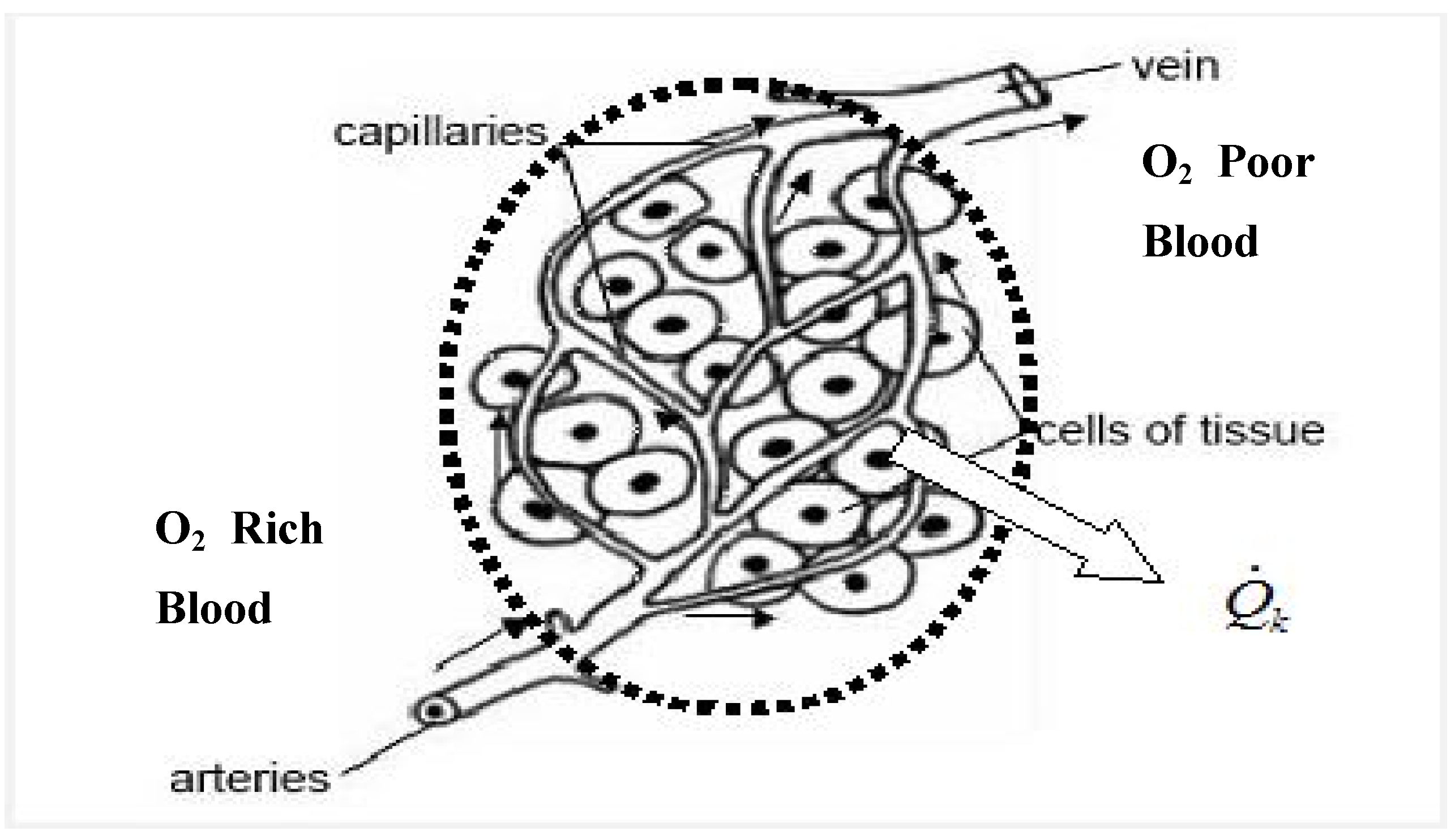
3.3.2. Irreversibility of Organs and Heat Transfer from Organs
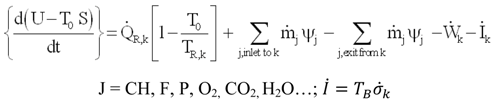
3.3.3. Lifespan Energy Expenditure and Entropy Generation of Organs and Contribution by Organs to the Body
| Parameter | Y | Fk | Remarks |
|---|---|---|---|
| Life Time Specific Entropy Generation of organ k | Equation (34) | ||
| Life Time Entropy Generation contribution by organ k to unit mass of body | Equation (34) with fk replaced by (fk+dk-1) | k,M,st = ckek mB,st (fk+dk−1) | |
| Life Time Entropy Generation contribution by organ k to whole body | Equation (34) with fk replaced by (fk+dk) | k, st = ckek mB,st(fk+dk) | |
| Life Time Specific metabolic energy release by organ k | Equation (34) | ||
| Life Time metabolic energy contribution by organ k to unit mass of body | Equation (34) with fk replaced by (fk+dk-1) | ||
| Life Time metabolic energy contribution by organ k to whole body | Equation (34) with fk replaced by (fk+dk) |
4. Results and Discussion
4.1. Nutrient Data
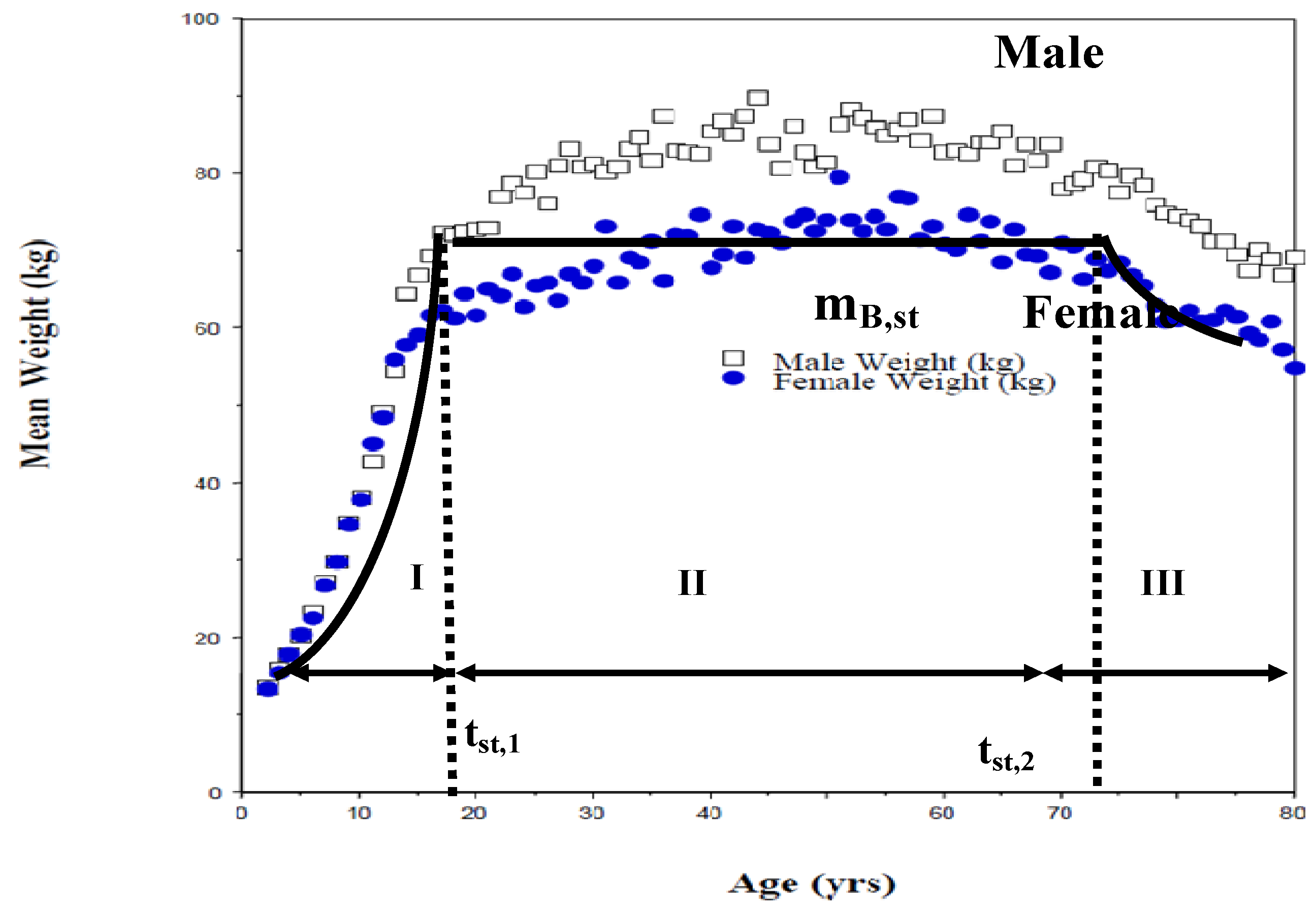
4.2. Growth Data
- Period I: tbirth<t< tst, 1, tst, 1 = 24 yrs, mB, st = 84 kg, {mB/mBst} = {t/tst, 1}°.75
- Period II: 24 < t < 75; mB = mBst = 84 kg, tlife = 75 years
- A short period of small weight loss (period III) after 70 yrs and prior to death was ignored.
4.3. Results
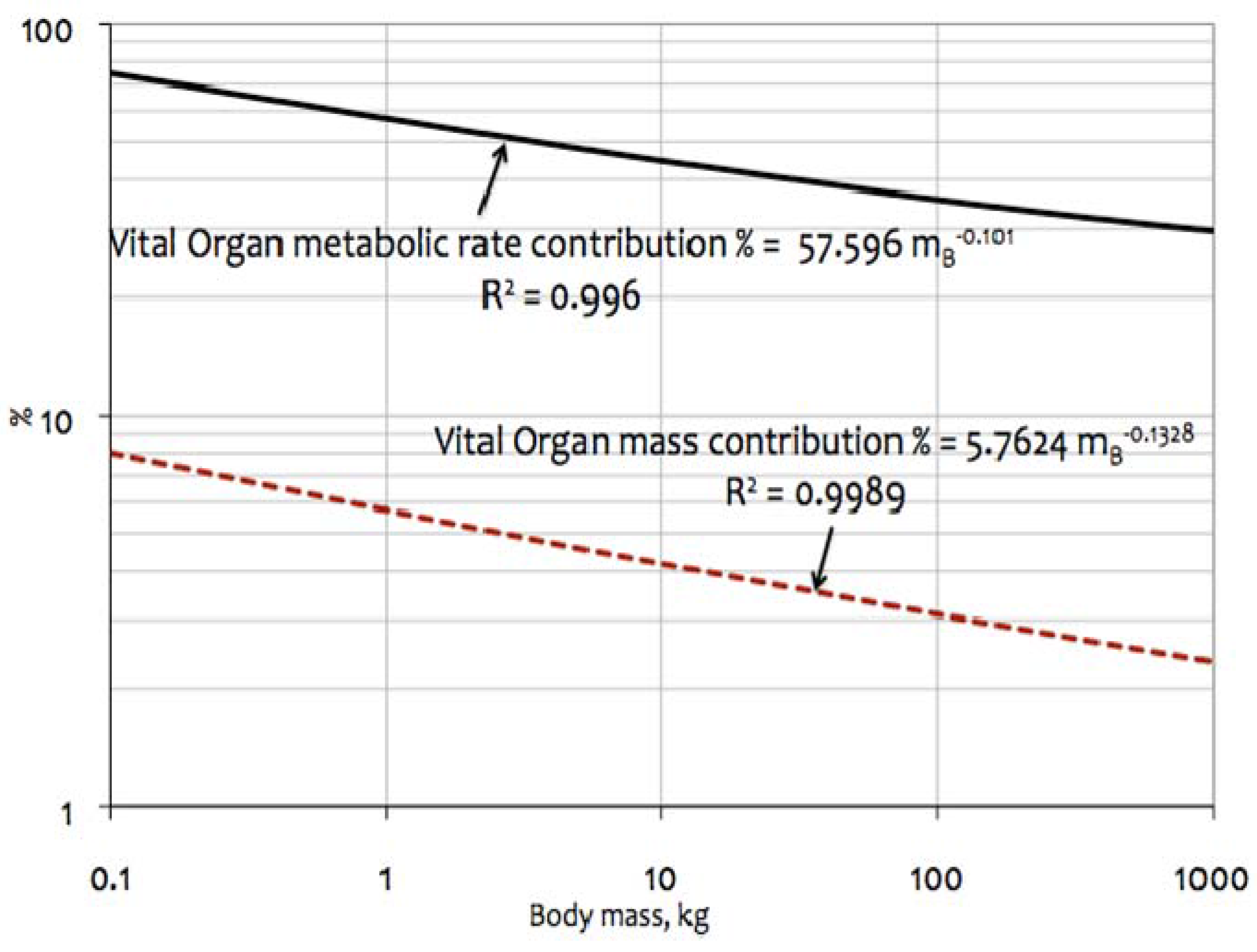
4.3.1. % Contribution by Vital Organs (BHKL) to Overall Metabolic Rates
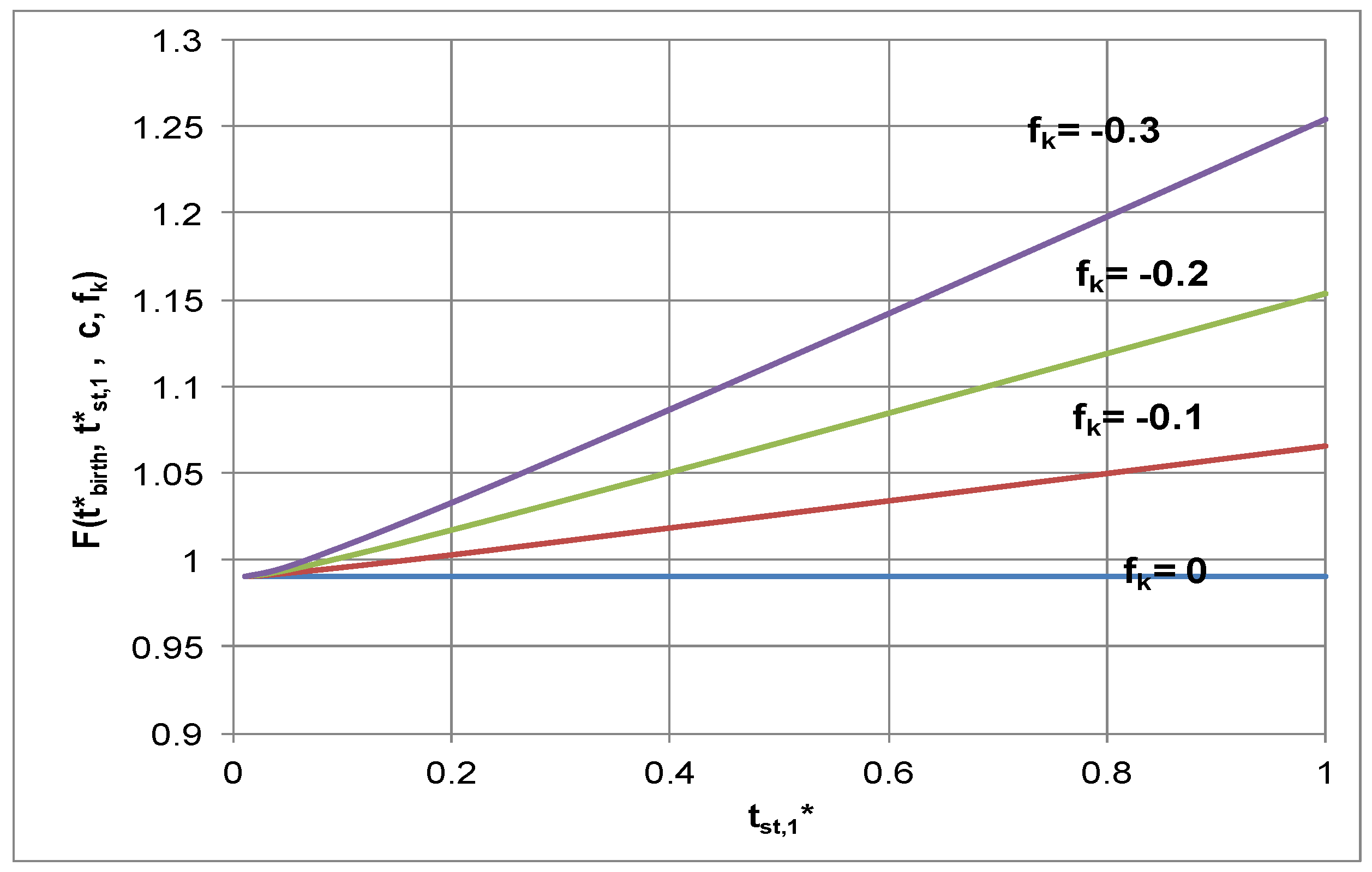
4.3.2. Growth Correction Factor, F
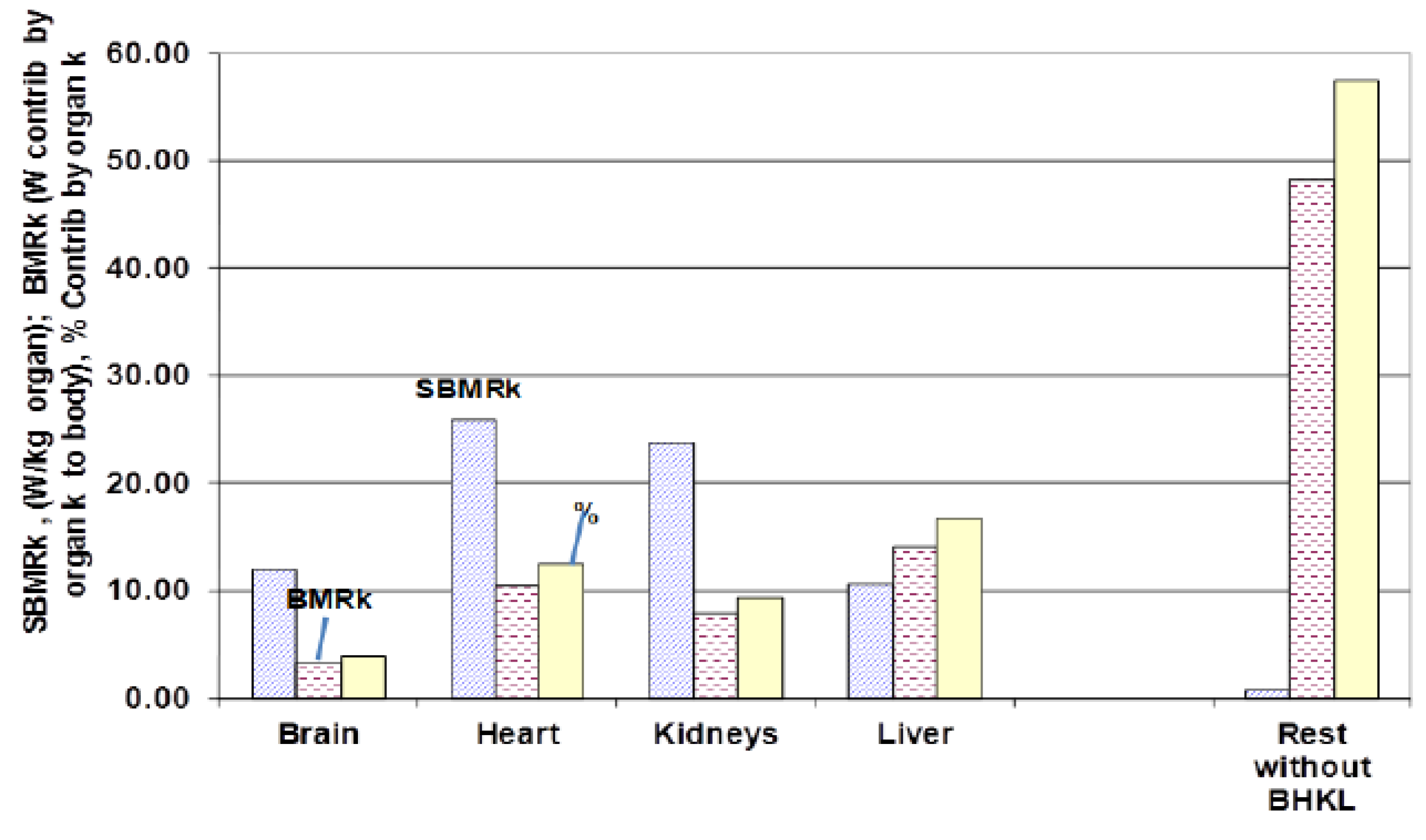
4.3.3. Specific Basal Metabolic Contribution (SBMRk) by Organ k, tst* = tst,/tlife
4.3.4. Lifespan Specific Energy Expenditure (LSEEM)
| % Nutrient consumed for metabolism, CH: F: P = | 55:30:15 |
| Computed Fraction of O2 by nutrient “n”, fO2, n. See Equation (24) = | 0.349:0.513: 0.138 |
| Average metabolic Efficiency computed by Equation (24) = | 31.3% |
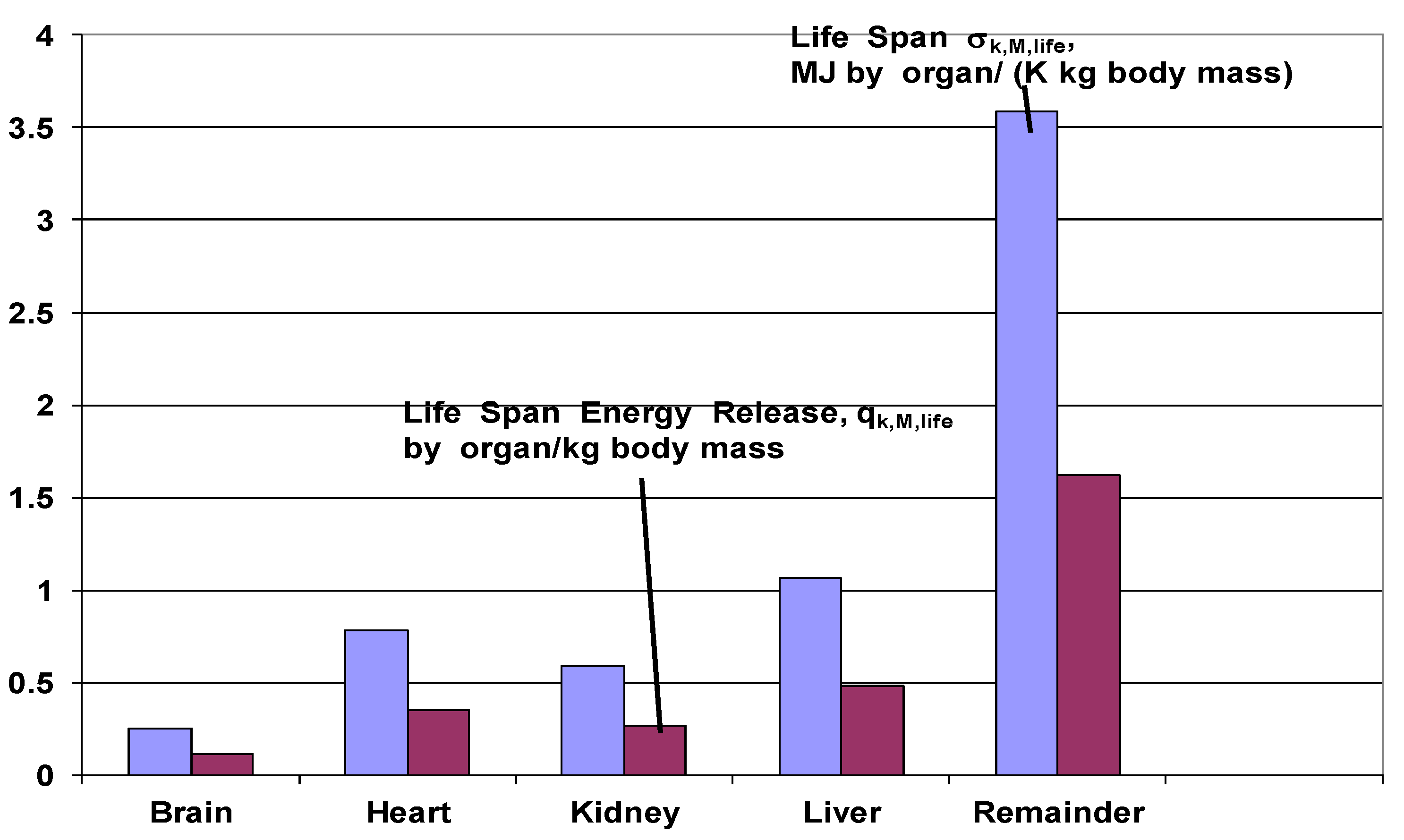
| Organ | MJ/(kg body·K) | MJ/kg body |
|---|---|---|
| Sigma contrib. | Metabolic contrib. | |
| Brain | 0.252 | 114 |
| Heart | 0.784 | 352 |
| Kidney | 0.589 | 266 |
| Liver | 1.069 | 480 |
| Remainder | 3.610 | 1620 |
| Sum | 6.304 | 2832 |
4.3.5. Life Span Organ Entropy Generation
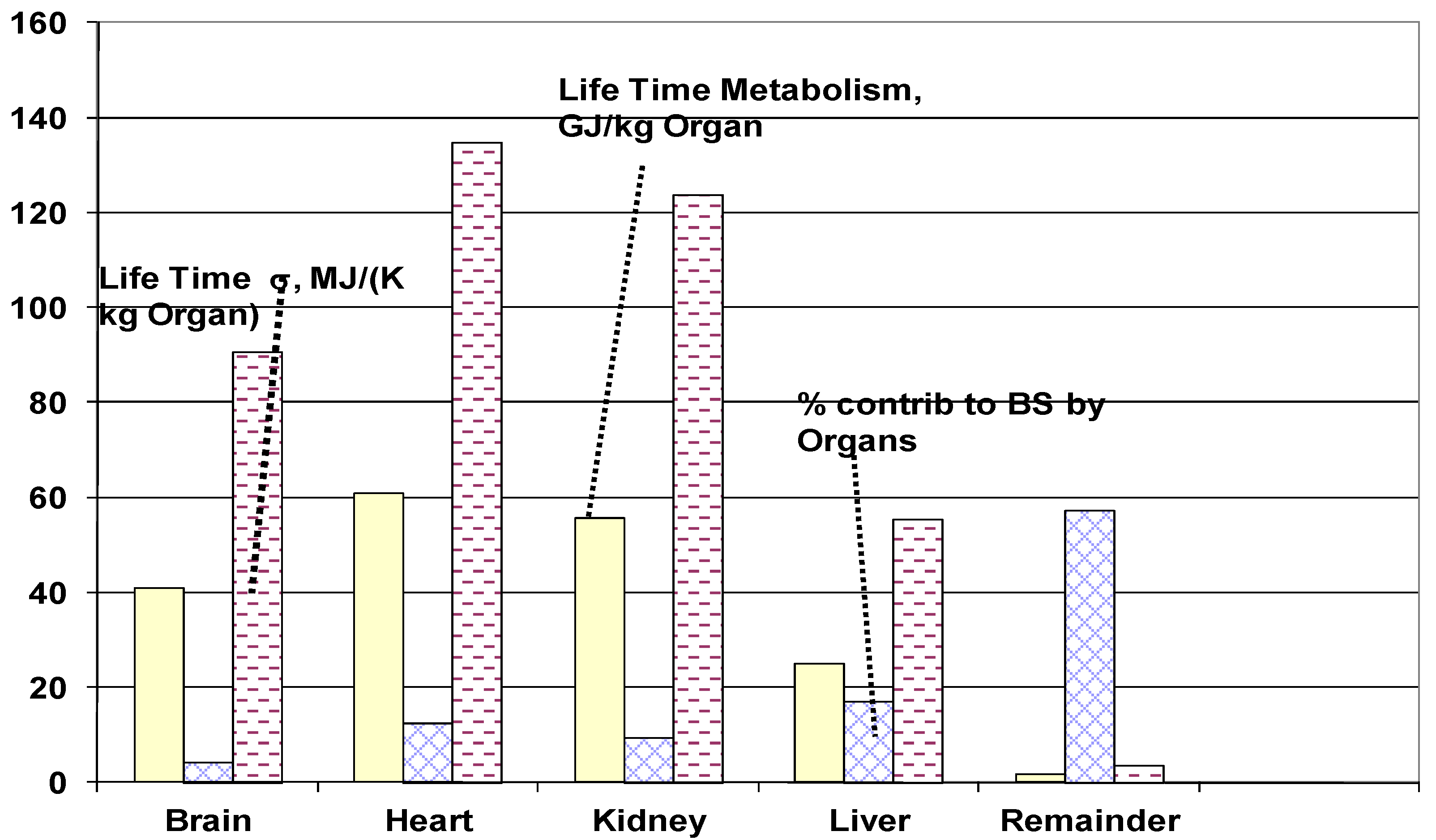
4.3.6. Life span Specific Entropy Generation of Whole Body
4.3.7. Effect of Nutrients
4.3.8. Relation to Life Span
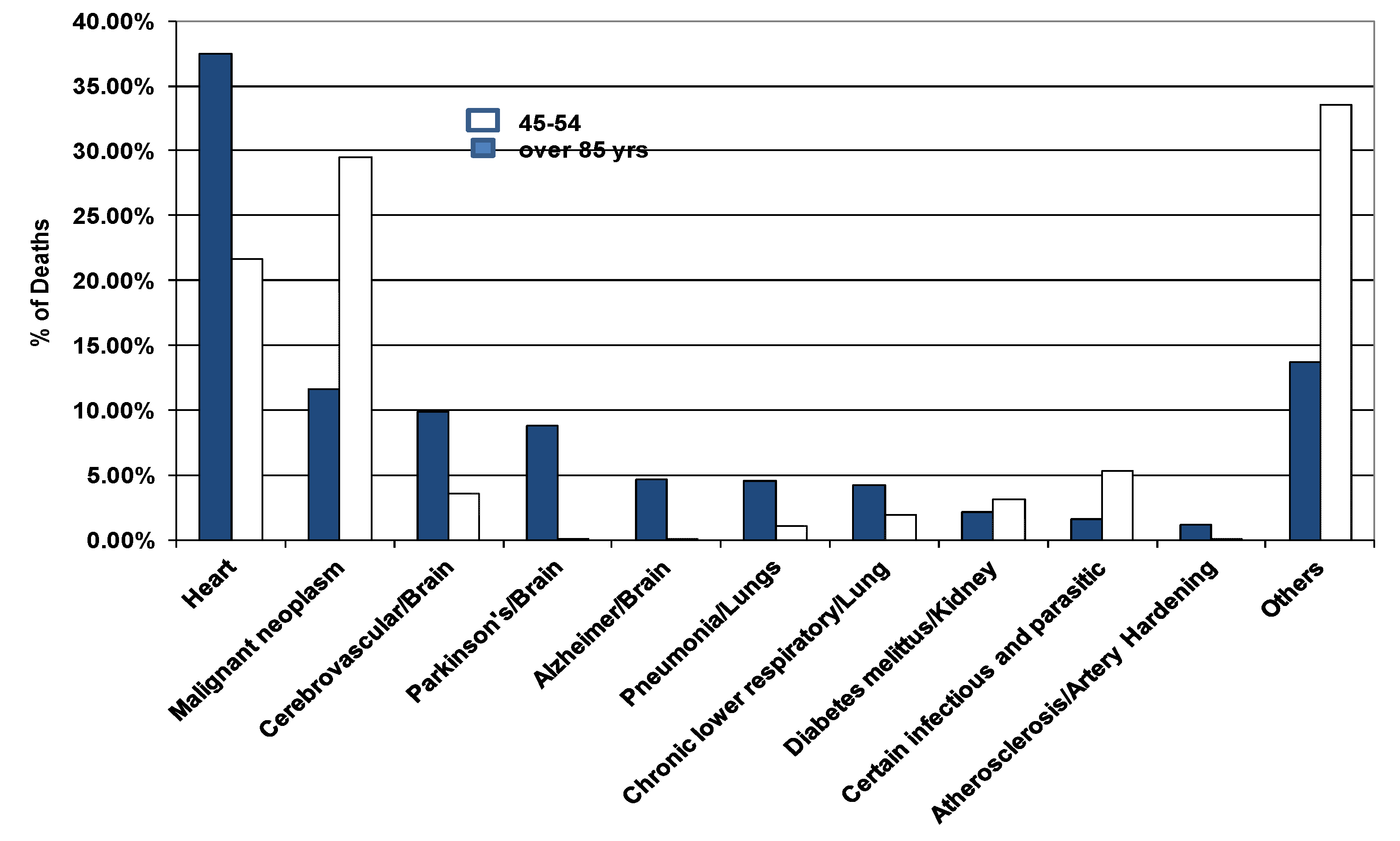
- Looking at data on people living longer than 85 years, heart is cited as #1 cause agreeing with current entropy stress level [2]
- According to current hypothesis, the next organ must be kidney; however cancer is the statistical number 2 cause of death (Figure 2). Recently, Germaine Wong and her colleagues collected data from 3654 Australians within the age group 49–97 years over 10 year period and observed that decreased kidney function leads to an increased risk of developing cancer [38]. Chronic kidney disease is common in people with cardio-vascular disease. Kidney function is also related to progression to cardio-vascular disease; chronic kidney disease is a risk factor in other chronic diseases such as infections and cancer [38].
- Since ROS concentrations are generally higher with increased TB (i.e., metabolism which results in fraction of energy converted into heat) and hence, shorter life span, then decreased TB must lead to prolonged lifespan. “On November 2006, a team of scientists from the Scripps Research Institute reported that transgenic mice which had body temperature 0.3–0.5 °C lower than normal mice indeed lived longer than normal mice.” [39]. Lifespan was 12% longer for males and 20% longer for females. Mice were allowed to eat as much as they wanted. However they had indicated that the effects of such a genetic change in body temperature on longevity are harder to study in humans.
- The third cause happens to be brain as predicted by the MREG model.
- The effect of change in nutrient composition and metabolic efficiency on n (t) are apparent from Equation (17); when n= P, ηn is low (e.g., proteins), and hence n (t) is higher indicating high protein diet leads to highest metabolic heat and irreversibility. It has been shown by Kapahi and his group that life spans of fruit flies are extended by using low protein diet [37].
5. Conclusions
- (1)
- The first and second laws of thermodynamics including availability analyses were applied to the vital organs of biological systems.
- (2)
- It is shown that that the sum of lifetime entropy generation contribution by all the vital organs to each unit body mass is .
- (3)
- The lifetime specific entropy generation of vital organs for 84 kg person is estimated as follows (MJ/ {kg of organ·K}): Bran: 62.4, Heart = 135.4, Kidney: 124.1, Liver: 55.5, Rest of organs: 3.7. The vital organ under most severe stress was found to be heart in agreement with leading cause of natural death.
- (4)
- The total lifetime contribution by all the vital organs to each unit body mass is .
- (5)
- The heart-normalized entropy stress (NESH) values are: Heart: 1.0, Kidney: 0.92, Brain: 0.46, Liver: 0.41, Rest of BS: 0.027. If normalized to rest of body (R), NESR, heart: 37, Kidney: 34, Brain: 17, Liver: 15, Rest of BS: 1.0; so heart will fail first followed by kidney and other organs in order. Supporting data is provided.
- (6)
- It is possible to estimate lifespan entropy stress just by measuring metabolic rate at the standard weight age (after which weight remains constant), and assuming that allometric laws are valid for organs.
- (7)
- Since ROS concentrations are generally higher with increased TB and hence, shorter life span, then decreased TB must lead to prolonged lifespan.
Acknowledgements
Acronyms
| ADP | Adenosine di-phosphate |
| AMDR/AI | Adequate macronutrient distribution range/Adequate Intake |
| ATP | Adenosine tri-phosphate |
| BHKL | Brain, heart, kidney, liver |
| BMR | Basal Metabolic Rate |
| BS | Biological system |
| CCE | Cell copy error |
| CDC | Center for Disease Control and Prevention |
| CH | Carbohydrate |
| CR | Calorie restriction diet |
| CSA | Chemist Standard Atmosphere, 0 °C, 101 kPa |
| DRI | Dietary reference intake |
| EER | Energy expenditure requirements |
| EER | Estimated energy requirements |
| HHV | Higher or gross heating value, |
| HHVO2, n | higher heating value per unit mass of stoichiometric oxygen of nutrient n |
| LSEG | Lifetime specific entropy generation (J/kg K) |
| LSEE | Lifetime specific Energy Expenditure (J/kg) |
| LSEH | Lifetime specific energy released as heat |
| ME | Metabolic efficiency |
| MREG | Modified Rate of Entropy Generation |
| NES | Normalized Entropy Stress |
| REG | Rate of Entropy Generation |
| ROL | Rate of Living Theory |
| ROS | Radical Oxygen Species |
| SATP | Standard Atmospheric temperature and pressure (25 C, 1 atm) |
| SBMR | Specific Basal Metabolic Rate, (W/kg K) |
| US FNB | US Food and Nutrition Board |
| VLSF | Vital life sustaining functions |
Nomenclature
| E | Energy, kJ |
| F | Growth Correction factor |
| G | Gibbs free energy, kJ |
| h | Enthalpy, kJ/kg |
| I | Irreversibility I, kJ |
Irreversibility rate, kJ/s | |
| m | Mass, kg |
| mB | Body mass |
| mk | Mass of organ k |
Mass flow rate of nutrient n in organ k | |
Consumption rate of oxygen by nutrient n in organ k | |
| P | Protein |
| Q | Heat |
Heat transfer rate due to metabolic heat release
at organ k | |
Specific metabolic energy release rate from organ k per unit mass of organ k | |
Energy release rate of organ k contributed to the unit mass of body | |
| S | Entropy , kJ/ K |
| s | Specific Entropy, kJ/kg K |
| TB | Body temperature, K |
| t | Time or age |
| tst | Time to reach steady weight |
| U | Internal energy |
| WK | Work delivered by metabolism at organ k |
| C° | Gibbs free Energy for combustion |
| M° | Gibbs free Energy for metabolism ( with ATP production) |
| °ATP | Gibbs free energy |
Greek Symbols
| η | metabolic efficiency |
| σ | Entropy generation, kJ/K |
| σ M,k | Entropy contribution to unit mass of body by whole organ k |
Entropy generation rate per unit body mass (W/kg body mass K) | |
Specific entropy generation rate of organ k (W/{K kg of k}) | |
| Ψ | Stream availability, kJ/kg |
| νO2,n | Stoichiometric oxygen mass per unit mass of nutrient n |
| ηn,k | metabolic efficiency of nutrient n in organ k |
Superscript
| 0 | Atmospheric conditions |
| B,ref | Reference mass for body |
| C | Combustion |
| k | Organ k |
| life | Life Span |
| m | Specific referring to unit mass of organ |
| M | Specific referring to unit mass of body |
| n | Nutrient (n) |
| P-R | Difference of value from products to reactants |
| J | Nutrient j |
| P | Products |
| R | Reactants |
| St | Steady |
General Notes
Appendix
A1. Alternate Allometric Relations
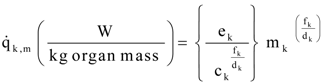
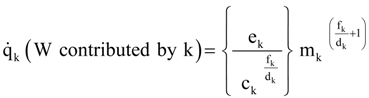
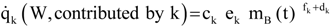

A2. Integration:

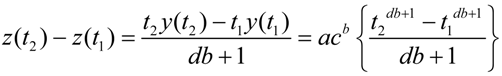
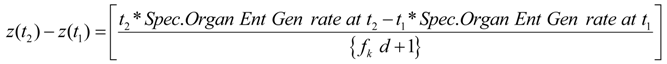

References
- Olshansky, S.J.; Carnes, B.A. Quest for Immortality: Science at Frontiers of Aging; W.W. Nortons: New York, NY, USA, 2001. [Google Scholar]
- National Center for Health Statistics, 2001 Data Warehouse on Trends in Health and Aging. extensive data from http://www.cdc.gov/nchs/nvss/mortality_public_use_data.htm.
- Ebersole, P.; Hess, P.; Schmidt, L.A. Towards Healthy Aging-Human Needs and Nursing, 6th ed.; Mosby Inc.: London, UK, 2003. [Google Scholar]
- Schrodinger, E. What Is Life? Cambridge University Press: Cambridge, UK, 1944; p. 194. [Google Scholar]
- Azbel, M.Y. Universal Biological Scaling and Mortality. Proc. Nat. Acad. Sci. USA 1994, 91, 453–457. [Google Scholar] [CrossRef]
- Kirkwood, T.B.L. Evolution of Ageing. Nature 1977, 270, 301–304. [Google Scholar] [CrossRef] [PubMed]
- Hofman, M.A. Energy, Metabolism, Brain Size and Longevity in Mammals. Quart. Rev. Biol. 1983, 58, 495–512. [Google Scholar] [CrossRef] [PubMed]
- Hofman, M.A. Evolution of brain size in neonatal and adult placental mammals: a theoretical approach. J. Theor. Biol. 1983, 105, 317–332. [Google Scholar] [CrossRef]
- Pearl, R. The Biology of Death: Being a Series of Lectures Delivered at the Lowell Institute in Boston in December 1920; J. B. Lippincott & Co.: Philadelphia, PA, USA, 1922. [Google Scholar]
- Speakman, J.R. Body size, energy metabolism and lifespan-A Review. J. Exp. Biol. 2005, 208, 1717–1730. [Google Scholar] [CrossRef] [PubMed]
- Julie, A.M.; George, S.R.; Beasley, T.M.; Tilmont, E.M.; Handy, A.M.; Herbert, R.L.; Longo, D.L.; Allison, D.B.; Young, J.E.; Bryant, M.; et al. Impact of caloric restriction on health and survival in rhesus monkeys from the NIA study. Nature 2012. [Google Scholar] [CrossRef]
- Annamalai, K.; Puri, I. Combustion Science and Engineering; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- DNA Repair at Encyclopedia of Aging. Available online: http://www.encyclopedia.com/doc/1G2-3402200112.html/ (accessed on 12 August 2012).
- Beckman, A. Free Radical Theory of Aging Matures. Phys. Rev. 1998, 78, 547–581. [Google Scholar]
- Hershey, D.; Wang, H. A New Age-Scale for Humans; Lexington Books: New York, USA, 1980. [Google Scholar]
- Silva, C.A.; Annamalai, K. Entropy generation and human aging: lifespan entropy and effect of diet composition and caloric restriction diets. J. Thermodyn. 2009, 186723. [Google Scholar] [CrossRef]
- Batato, M.; Deriaz, O.; Jequier, E.; Borel, L. Second Law Analysis of the Human Body. In Proceedings of Florence World Energy Research Symposium, Firenze, Italy, May 1990.
- Aoki, I. Entropy Flow and Entropy Production in the Human Body in Basal Conditions. J. Theor. Biol. 1989, 141, 11–21. [Google Scholar] [CrossRef]
- Aoki, I. Effects of Exercise and Chills on Entropy Production in Human Body. J. Theor. Biol. 1990, 145, 421–428. [Google Scholar] [CrossRef]
- Aoki, I. Entropy production in human lifespan: a thermodynamical measure for aging. Age 1994, 1, 29–31. [Google Scholar] [CrossRef]
- Rahman, M.A. A novel Method for Estimating the Entropy Generation in a Human Body. Therm. Sci. 2007, 11, 75–92. [Google Scholar] [CrossRef]
- Flyod, R.A.; West, M.; Hensley, K. Oxidative Biochemical Markers Cluse To Understanding Aging In Long Lived Species. Exp. Gerontol. 2001, 36, 619–640. [Google Scholar] [CrossRef]
- Walford, R.L. Calorie Restriction, Eat Less, Eat Better, Live Longer. LE Magazine, Febuary 1998. [Google Scholar]
- Wang, Z.; Heshka, S.; Gallagher, D.; Boozer, C.; Kotler, D.P.; Heymsfield, S. Resting energy expenditure-fat-free mass relationship: new insights provided by body composition modeling. Am. J. Physiol. Endocrinol. Metab. 2000, 279, E539–E545. [Google Scholar] [PubMed]
- Wang, Z.; Timothy, P.; O’Connor, S.H.; Steven, B.H. The Reconstruction of Kleiber’s Law at the Organ-Tissue Level. J. Am. Soc. Nutr. Sci. 2001, 131, 2967–2970. [Google Scholar]
- Calder, W.A., III. Size, Function, and Life History; Dover: New York, NY, USA, 1996. [Google Scholar]
- Elia, M. Organ and tissue contribution to metabolic rate. In Energy Metabolism: Tissue Determinants and Cellular Corollaries; Kinney, J.M., Tucker, H.N., Eds.; Raven: New York, NY, USA, 1992; pp. 61–80. [Google Scholar]
- Gallagher, D.; Belmonte, D.; Deurenberg, P.; Wang, Z.; Krasnow, N.; Pi-Sunyer, F.X.; Heymsfield, S.B. Organ tissue mass measurement allows modeling of resting energy expenditure and metabolically active tissue mass. Am. J. Physiol. 1998, 275, E249–E258. [Google Scholar] [PubMed]
- Annamalai, K.; Puri, I.; Jog, M. Advanced Thermodynamics Engineering, 2nd ed.; Taylor and Francis: Boca Raton, FL, UAS, 2011; Chapter 14; p. 1096. [Google Scholar]
- Silva, C.; Annamalai, K. Entropy generation and human aging: lifespan entropy and effect of physical activity level. Entropy 2008, 10, 100–123. [Google Scholar] [CrossRef]
- Cardiovascular System at Wikibooks. Available online: http://en.wikibooks.org/wiki/Anatomy_and_Physiology_of_Animals/Cardiovascular_System/Blood_circulation (accessed on 23 December 2010).
- Brzustowski, T.A.; Brena, A. Second law analyses of energy processes. IV–The exergy of hydrocarbon fuels, Second Law analysis of Energy Processes. Trans. Canad. Soc. Mech. Eng. 1986, 10, 121–128. [Google Scholar]
- National Center for Environmental Assessment, Office of Research and Development, U.S. Environmental Protection Agency. Summary Report of a Peer Involvement Workshop on the Development of an Exposure Factors Handbook for the Aging, Arlington, VA, USA, 14–15 February, 2007.
- Health Survey at the National Archives. Available online: http://www.dh.gov.uk/en/Publicationsandstatistics/PublishedSurvey/HealthSurveyForEngland/Healthsurveyresults/DH_4001334 (accessed on 15 December 2010).
- Snyder, W.S.; Cook, M.J. Report of the task group on reference men. International Commission on Radiological Protection, 1975; Pergamon Press: Oxford, UK.
- Dietary Reference Intakes for Energy, Carbohydrate, Fiber, Fat, Fatty Acids, Cholesterol, Protein, and Amino Acids (Macronutrients); National Academy Press: Washington, DC, USA, 2002.
- Edman, U.; Garcia, A.M.; Busuttil, R.; Sorensen, D.; Lundell, M.; Kapahi, P.; Vijg, J. Lifespan extension by dietary restriction is not linked to protection against somatic DNA damage in Drosophila melanogaster. Aging Cell 2009, 8, 331–338. [Google Scholar] [CrossRef] [PubMed]
- Wong, G.; Hayen, A.; Chapman, J.; Webster, A.; Wang, J.; Mitchell, P.; Craig, J. Association of CKD and Cancer Risk in Older People. Clin. J. Am. Soc. Nephrol. 2009. [Google Scholar] [CrossRef] [PubMed]
- Conti, B.; Sanchez-Alavez, M.; Winsky-Sommere, R.; Morale, M.C.; Lucero, J. Transgenic Mice with a Reduced Core Body Temperature Have an Increased Life Span. Science 2006, 314, 825–828. [Google Scholar] [CrossRef] [PubMed]
- Madya, C.; Keutenedjian, E.; de Oliveira, S., Jr. Human body exergy metabolism. In Proceedings Of Ecos 2012–The 25th International Conference on Efficiency, Cost, Optimization, Simulation And Environmental Impact Of Energy Systems, Perugia, Italy, 26–29 June 2012.
- Hayne, D.T. Biological Thermodynamics. Cambridge University Press: London, UK, 2008. [Google Scholar]
- American Society of Heating, Refrigerating and Air-Conditioning Engineers. Physiological principles and thermal comfort. In Handbook of Fundamentals; ASHRAE: Atlanta, GA, USA, 1993; pp. 1–29. [Google Scholar]
- Annamalai, K. Group Combustion of Char Particles and Metabolism in Large Organs. In Spring Technical Meeting of the Central States Section of the Comb. Inst., Dayton, OH, USA, 22–24 April 2012. Paper No. 12S-130.
- Suarez, R.K.; Charles, A.D. Review: Multi-level regulation and metabolic scaling. J. Exp. Biol. 2005, 208, 1627–1634. [Google Scholar] [CrossRef] [PubMed]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Annamalai, K.; Silva, C. Entropy Stress and Scaling of Vital Organs over Life Span Based on Allometric Laws. Entropy 2012, 14, 2550-2577. https://doi.org/10.3390/e14122550
Annamalai K, Silva C. Entropy Stress and Scaling of Vital Organs over Life Span Based on Allometric Laws. Entropy. 2012; 14(12):2550-2577. https://doi.org/10.3390/e14122550
Chicago/Turabian StyleAnnamalai, Kalyan, and Carlos Silva. 2012. "Entropy Stress and Scaling of Vital Organs over Life Span Based on Allometric Laws" Entropy 14, no. 12: 2550-2577. https://doi.org/10.3390/e14122550





