The Effect of Thermal Radiation on Entropy Generation Due to Micro-Polar Fluid Flow Along a Wavy Surface
Abstract
:1. Introduction
2. Mathematical Formulation
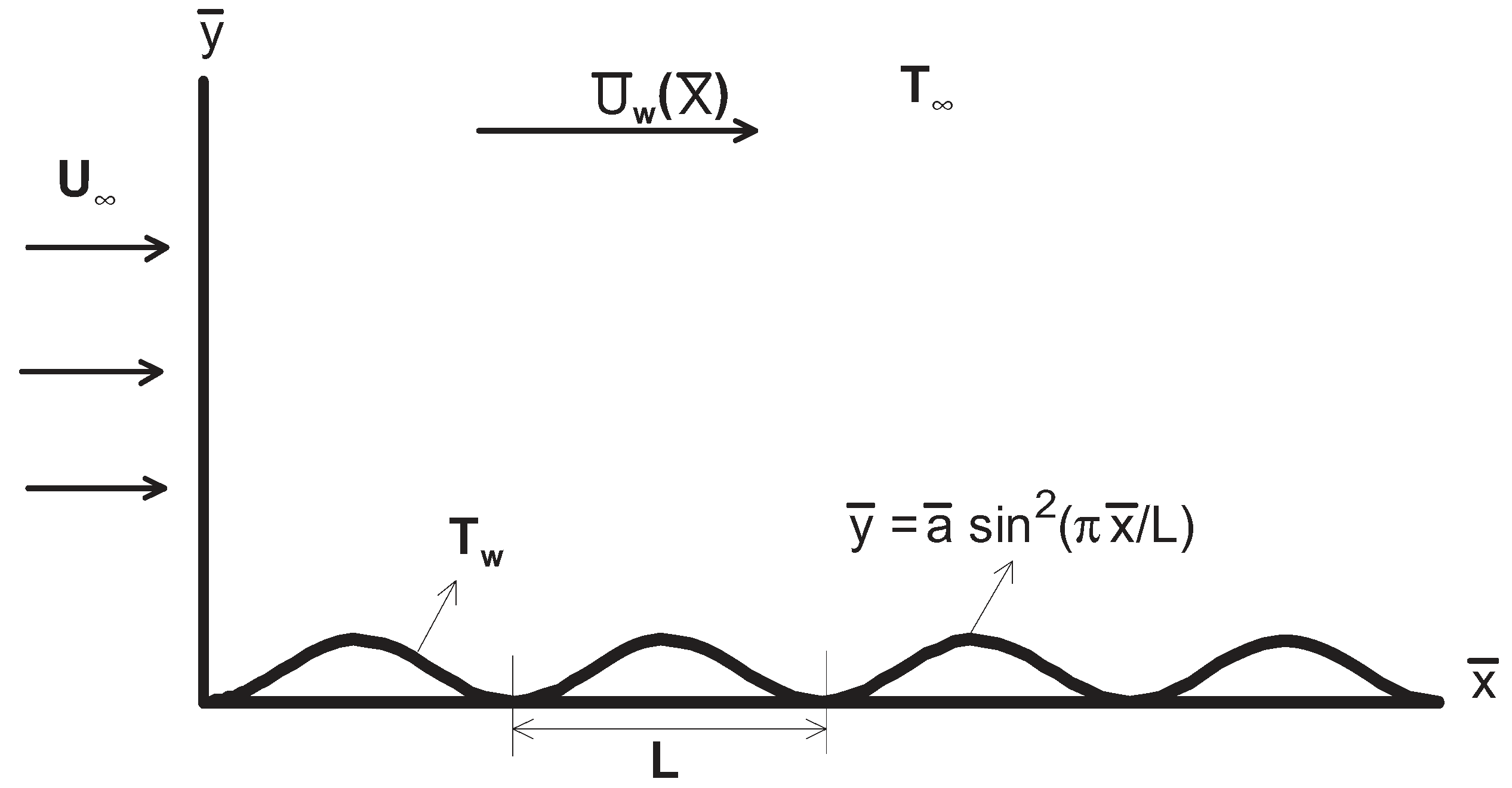
3. Numerical Method
| u | ||
| θ | ||
| N | ||
4. Results and Discussion
| x = 0.16 | x = 4 | x = 0.16 | x = 4 | |
| Steady state solutions: Pr = 0.73, α= 0.002, , | ||||
| 100 × 20 | 0.393842 | 0.379809 | 1.131646 | 0.968401 |
| 100 × 50 | 0.394535 | 0.376537 | 1.131432 | 0.960356 |
| 100 × 150 | 0.394248 | 0.375848 | 1.129922 | 0.958338 |
| 25 × 50 | 0.394550 | 0.377982 | 1.132669 | 0.959618 |
| 50 × 50 | 0.394376 | 0.375799 | 1.130772 | 0.956972 |
| 100 × 50 | 0.394393 | 0.376083 | 1.130753 | 0.959037 |
| 100 × 75 (*) | 0.391625 | 0.378118 | 1.123619 | 0.960467 |
| 100 × 200 (*) | 0.393746 | 0.376413 | 1.127222 | 0.959405 |
| (*): Uniform grid (y direction); | ||||
| The forms for both local heat transfer rate and local skin friction coefficient are obtained from Wang and Chen [10]. | ||||
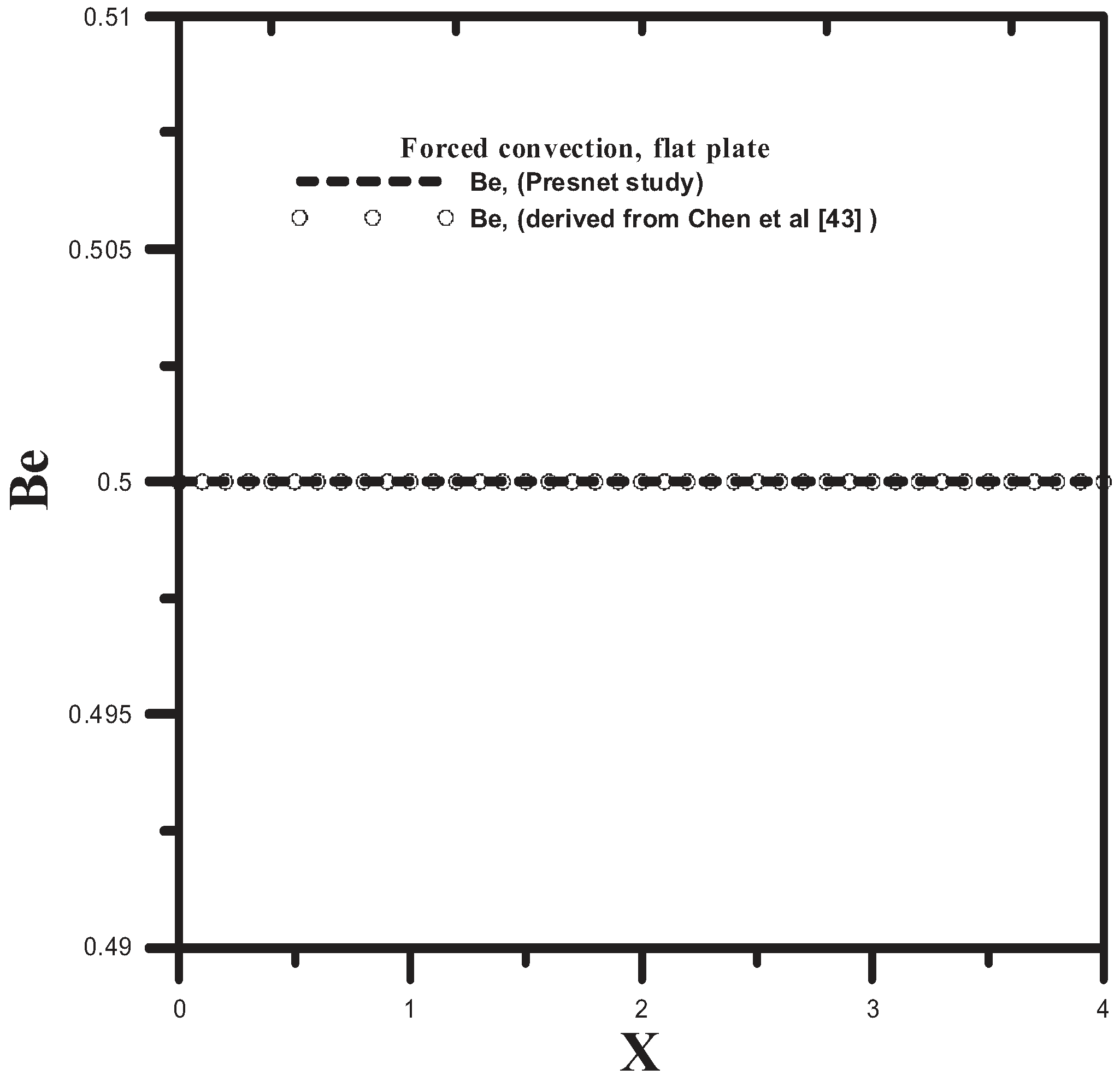

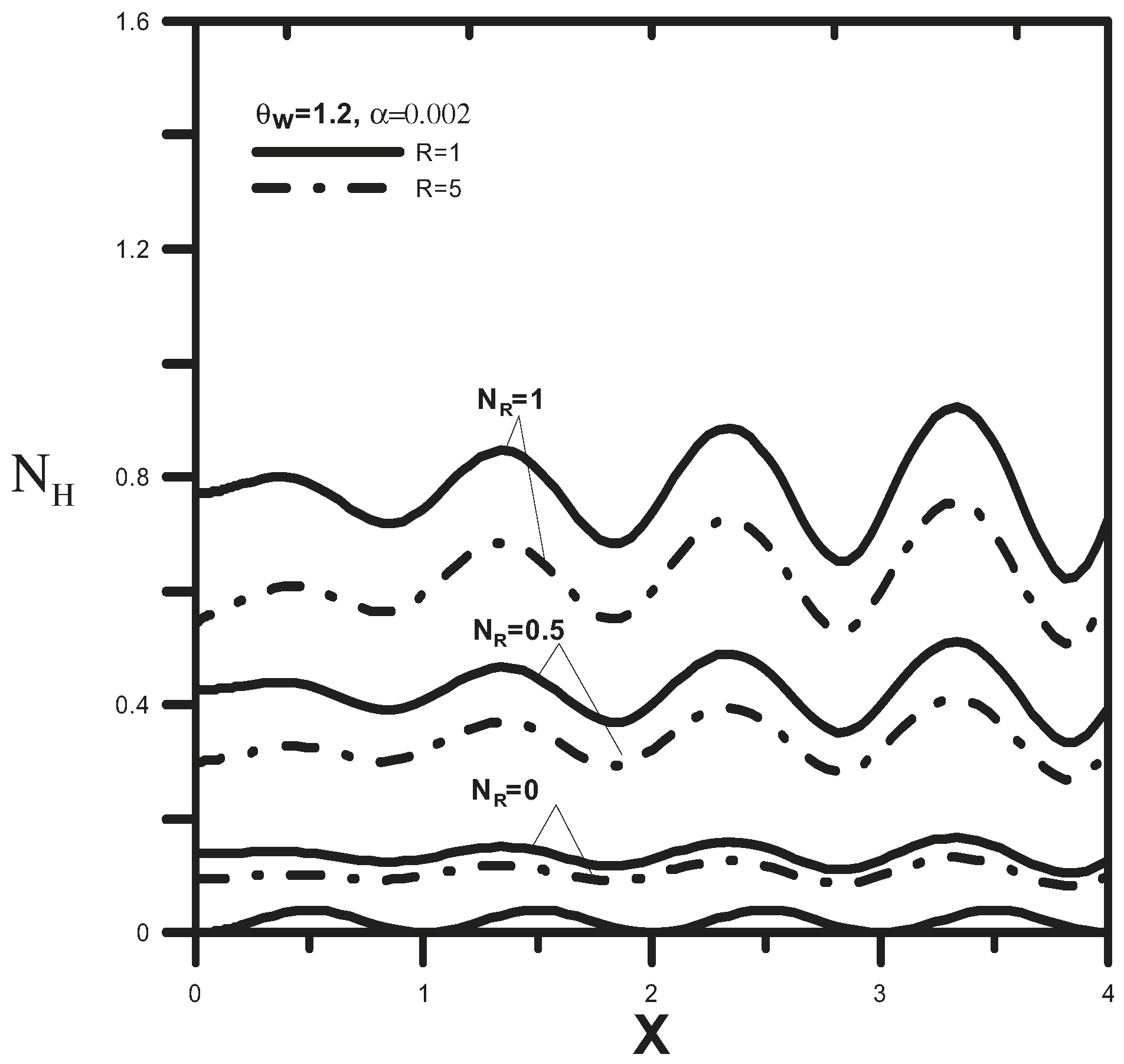
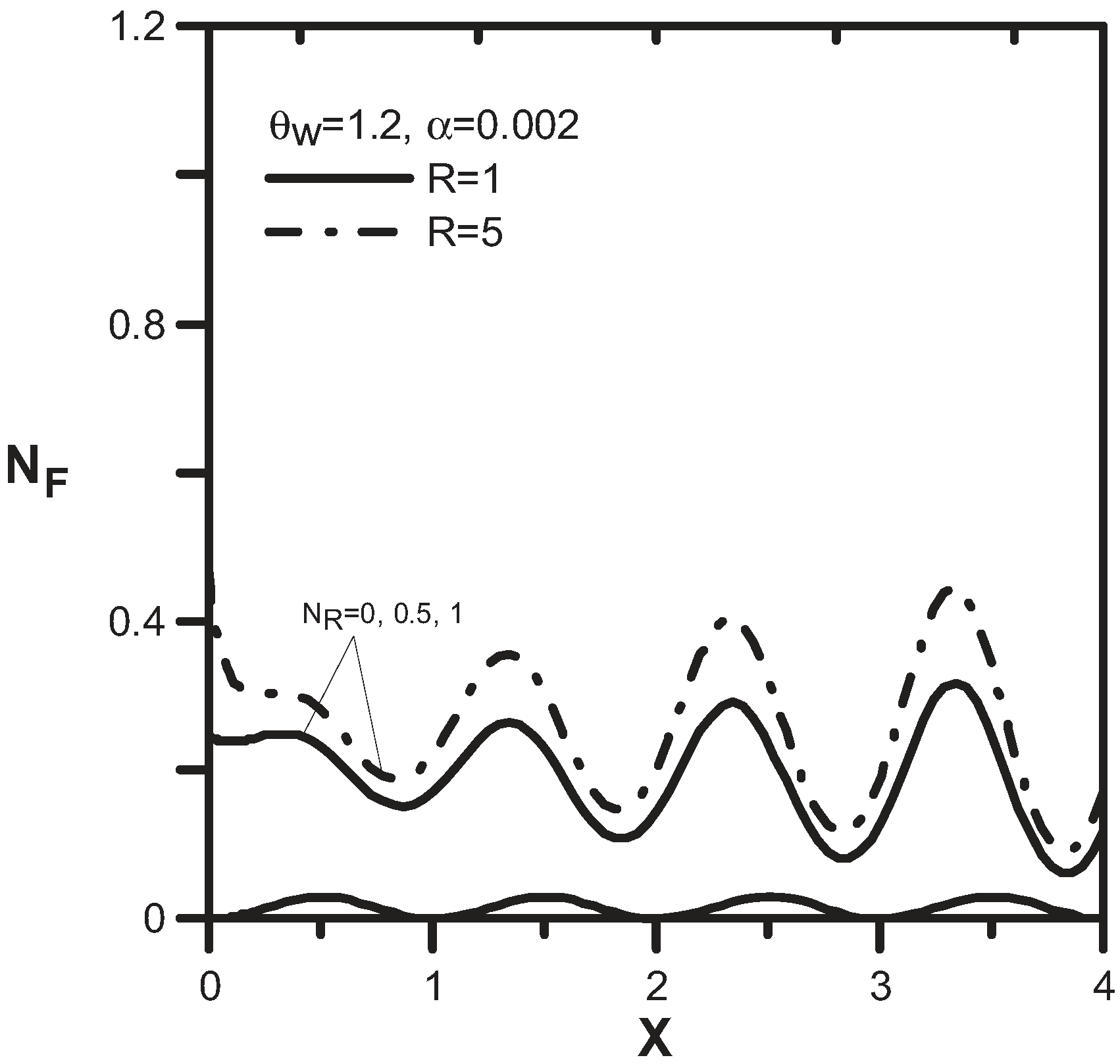
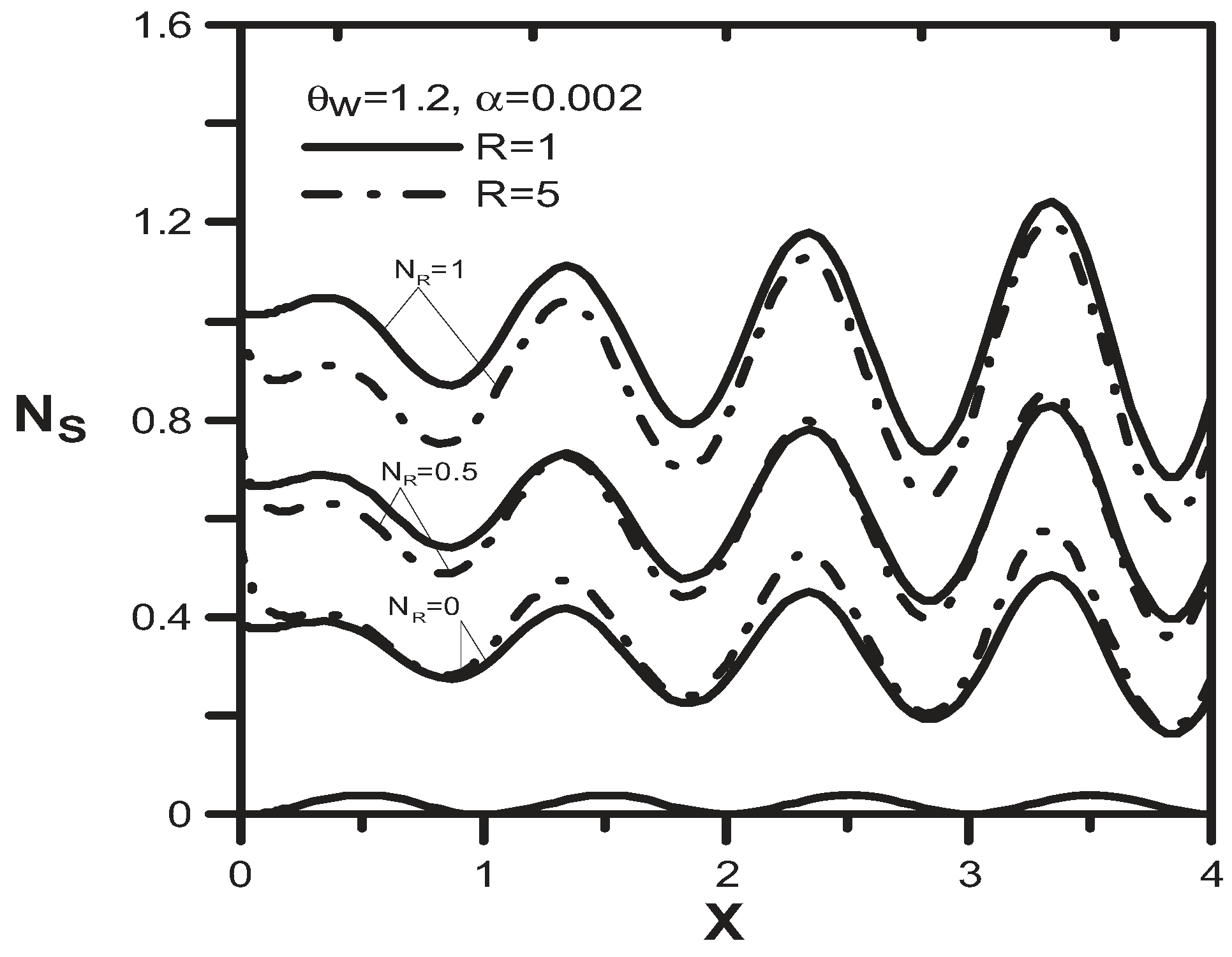

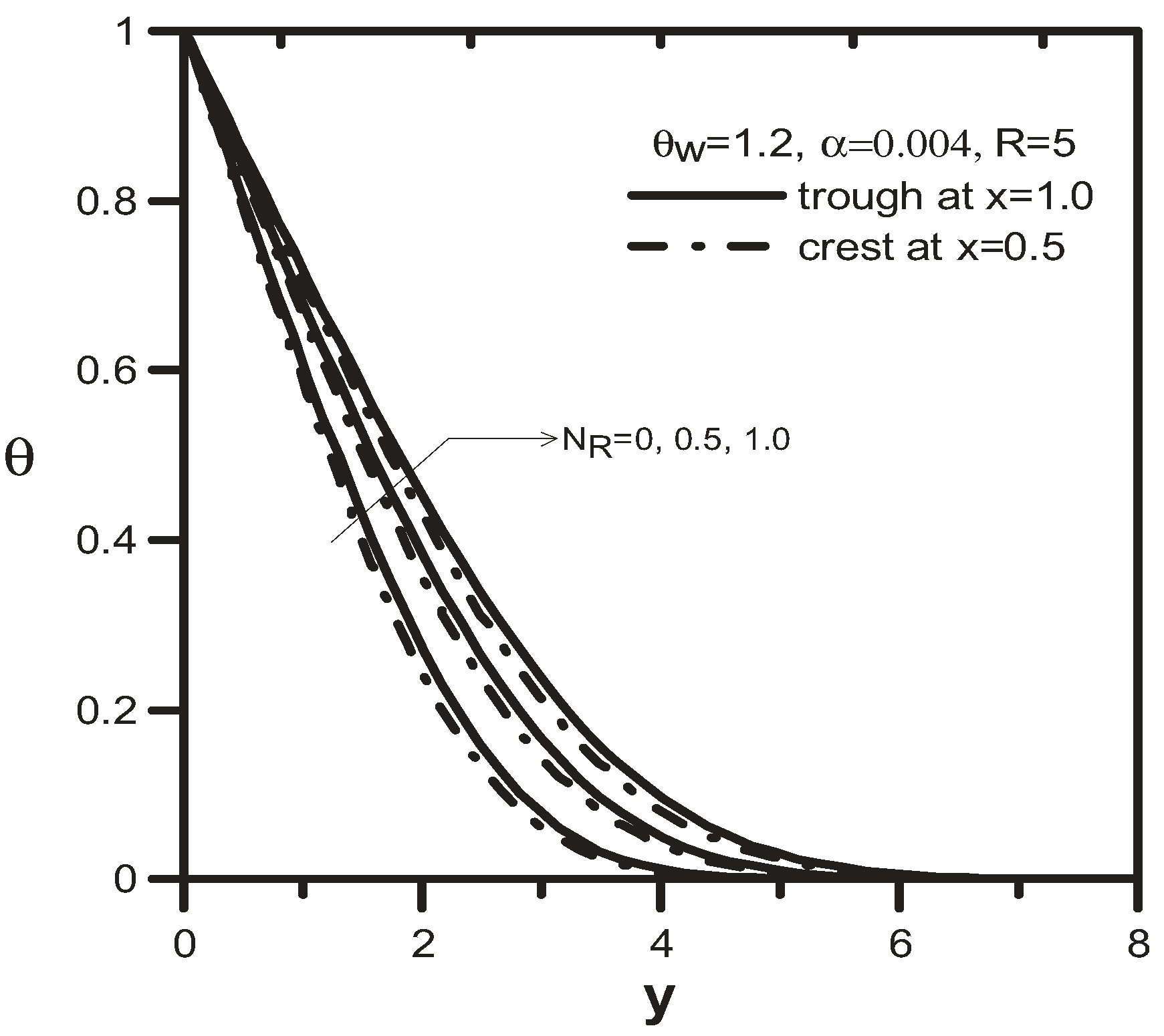
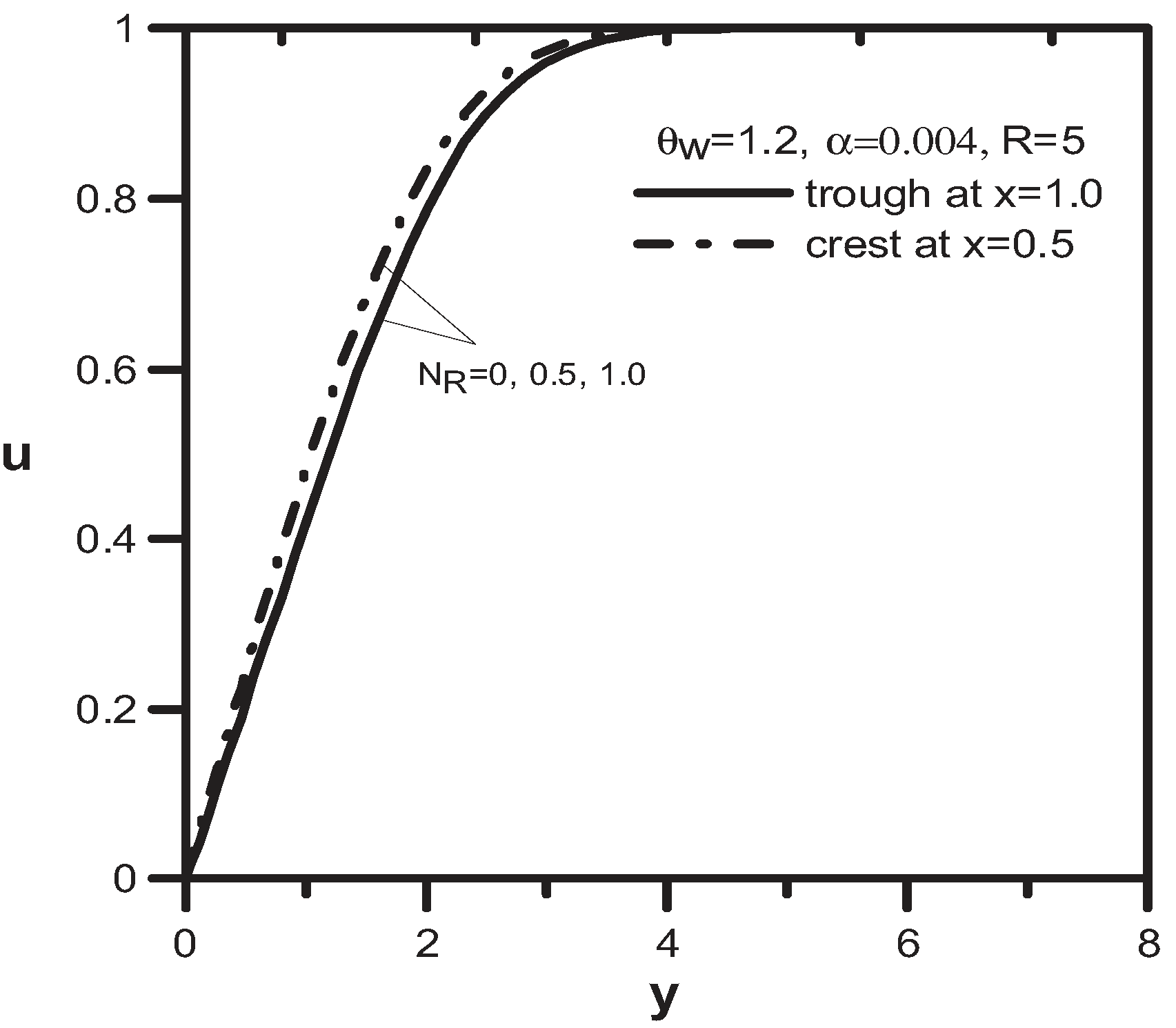
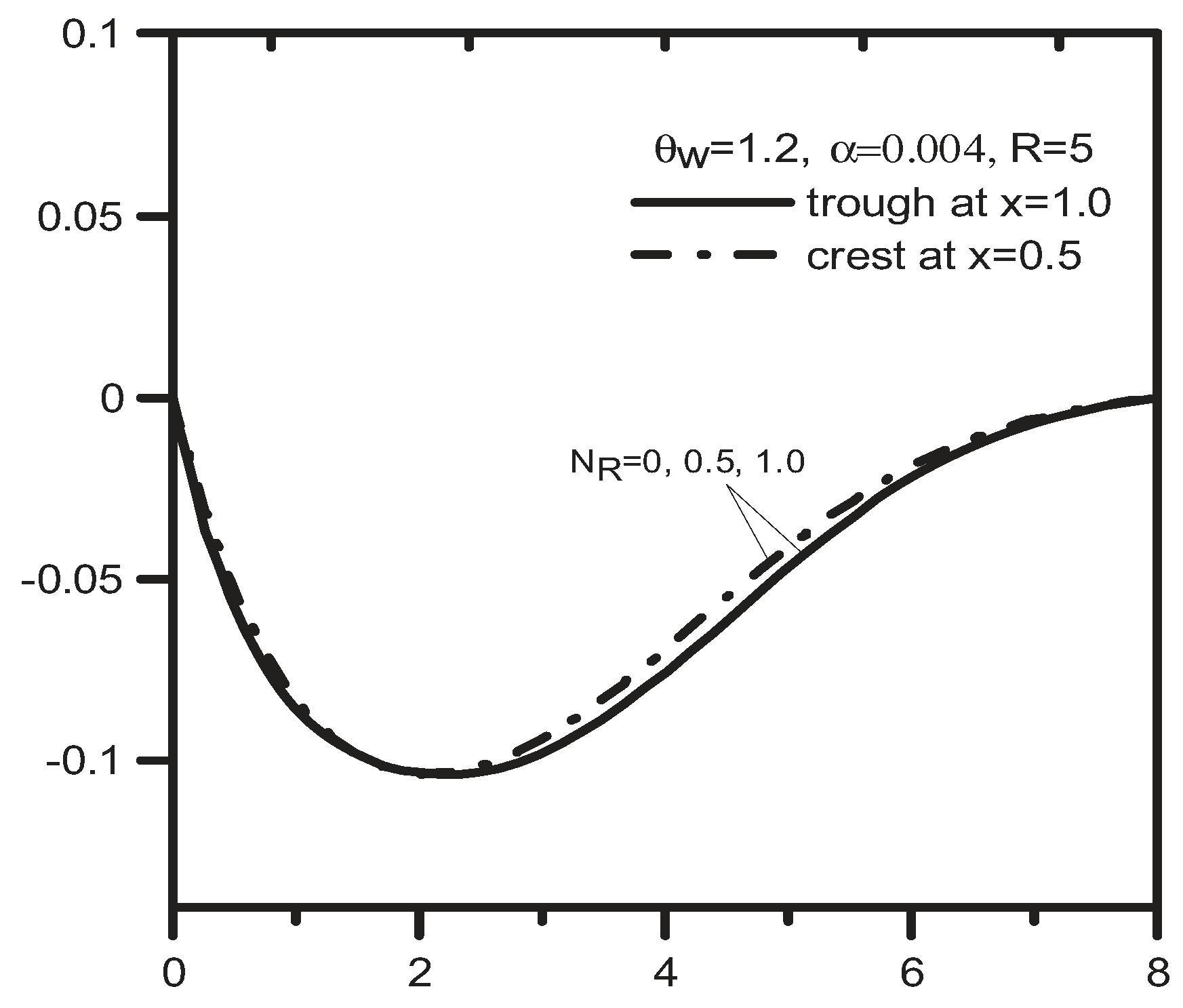
5. Conclusions
Nomenclature
Amplitude of wavy surface | |
Dimensionless material parameter | |
Bejan number | |
Brinkman number | |
Skin-friction coefficient | |
Heat transfer coefficient | |
Microinertia density | |
Thermal Conductivity | |
Characteristic length | |
Dimensionless microrotation | |
Entropy generation due to fluid friction | |
Entropy generation due to heat transfer | |
Entropy generation number | |
Radiation-conduction parameter | |
Pressure | |
Prandtl number | |
Vortex viscosity parameter | |
Radiation heat flux | |
Reynolds number | |
Surface geometry function | |
x component of velocity of the inviscid flow evaluated at surface | |
Dimensionless x component of velocity | |
Temperature | |
Dimensionless y component of velocity | |
| , | Axial and transverse (Cartesian) coordinates, respectively |
Greek Symbols
Wavy amplitude-wavelength ratio | |
The mean extinction coefficient | |
Thermal expansion coefficient of fluid | |
Spin-gradient viscosity | |
Dimensionless temperature | |
Vortex viscosity | |
Material parameter | |
Dynamic viscosity | |
Kinematic viscosity | |
Density of fluid | |
Dimensionless temperature difference |
Subscripts
Wall surface | |
Free stream condition |
Superscripts
| - | Dimensional variables |
| ~, ^ | Dimensionless quantity |
| ′ | Derivative with respect to x |
Acknowledgments
References
- Yao, L.S. Natural convection along a vertical wavy surface. ASME J. Heat Trans. 1983, 105, 465–468. [Google Scholar] [CrossRef]
- Yao, L.S. A note on Prandtl’s transposition theorem. ASME J. Heat Trans. 1988, 100, 507–508. [Google Scholar] [CrossRef]
- Moulic, S.G.; Yao, L.S. Natural convection along a vertical wavy surface with uniform heat flux. ASME J. Heat Trans. 1989, 111, 1106–1108. [Google Scholar] [CrossRef]
- Yao, L.S. Natural convection along a vertical complex wavy surface. Int. J. Heat Mass Trans. 2006, 49, 281–286. [Google Scholar] [CrossRef]
- Wang, C.C.; Chen, C.K. Forced convection in a wavy-wall channel. Int. J. Heat Mass Trans. 2002, 45, 2587–2595. [Google Scholar] [CrossRef]
- Ariman, T.; Turk, M.A.; Sylvester, N.D. Microcontinuum fluid mechanics, a review. Int. J. Eng. Sci. 1973, 11, 905–930. [Google Scholar] [CrossRef]
- Ariman, T.; Turk, M.A.; Sylvester, N.D. Applications of microcontinuum fluid mechanics. Int. J. Eng. Sci. 1974, 12, 273–293. [Google Scholar] [CrossRef]
- Eringen, A.C. Theory of micropolar fluids. J. Math. Mech. 1966, 16, 1–18. [Google Scholar] [CrossRef]
- Eringen, A.C. Theory of thermomicro fluids. J. Math. Anal. Appl. 1972, 38, 480–496. [Google Scholar] [CrossRef]
- Wang, C.C.; Chen, C.K. Forced convection in micropolar fluid flow over a wavy surface. Numer. Heat Trans. 2000, 37, 271–279. [Google Scholar] [CrossRef]
- Wang, C.C.; Chen, C.K. Transient force and free convection along a vertical wavy surface in micropolar fluids. Int. J. Heat Mass Trans. 2001, 44, 3241–3251. [Google Scholar] [CrossRef]
- Lien, F.S.; Chen, T.M.; Chen, C.K. Analysis of a free-convection micropolar boundary layer about a horizontal permeable cylinder at a non-uniform thermal condition. ASME J. Heat Trans. 1990, 112, 504–506. [Google Scholar] [CrossRef]
- Lien, F.S.; Chen, C.K.; Cleaver, J.W. Analysis of natural convection flow of micropolar fluid about a sphere with blowing and suction. ASME J. Heat Trans. 1986, 108, 967–970. [Google Scholar] [CrossRef]
- Yang, Y.T.; Chen, C.K.; Lin, M.T. Natural convection of non-Newtonian fluids along a wavy vertical plate including the magnetic field effect. Int. J. Heat Mass Trans. 1996, 39, 2831–2842. [Google Scholar] [CrossRef]
- Chen, C.K.; Yang, Y.T.; Lin, M.T. Transient free convection of non-Newtonian fluids along a wavy vertical plate including the magnetic field effect. Int. J. Heat Fluid Flow 1996, 17, 604–612. [Google Scholar] [CrossRef]
- Wang, C.C.; Chen, C.K. Mixed convection boundary layer flow of non-Newtonian fluids along vertical wavys plates. Int. J. Heat Fluid Flow 2002, 23, 831–839. [Google Scholar] [CrossRef]
- Lien, F.S.; Chen, C.K.; Cleaver, J.W. Radiation effect on conjugated forced convection-conduction analysis of heat Trans. in a plate fin. AIAA J. 1985, 23, 1645–1647. [Google Scholar]
- Rosseland, S. Theoretical Astrophysics; Oxford University Press: London, UK, 1936. [Google Scholar]
- Novotny, J.L.; Yang, K.T. The interaction of thermal radiation in optically thick boundary layers. ASME J. Heat Trans. 1967, 192, 309–312. [Google Scholar] [CrossRef]
- Cheng, E.H.; Ozisic, M.N. Radiation with free convection in an absorbing, emitting and scattering medium. Int. J. Heat Mass Trans. 1972, 15, 1243–1252. [Google Scholar] [CrossRef]
- Hossain, M.A.; Takhar, H.S. Radiation effect on mixed convection along a vertical plate with uniform surface temperature. Heat Mass Trans. 1996, 31, 243–248. [Google Scholar] [CrossRef]
- Elsayed, M.M.; Fathalah, K.A. Natural convection over a vertical fiat plate due to absorption of thermal radiation. Heat Mass Trans. 1985, 19, 121–129. [Google Scholar]
- Hooman, K.; Hooman, F.; Mohebpour, S.R. Entropy generation for forced convection in a porous channel with isoflux or isothermal walls. Int. J. Exer. 2008, 5, 78–96. [Google Scholar] [CrossRef]
- Makinde, O.D. Entropy-generation analysis for variable-viscosity channel flow with non-uniform wall temperature. Appl. Energ. 2008, 85, 384–393. [Google Scholar] [CrossRef]
- Makinde, O.D.; Anwar, B.O. On inherent irreversibility in a reactive hydromagnetic channel flow. J. Therm. Sci. 2010, 19, 72–79. [Google Scholar] [CrossRef]
- Erbay, L.B.M.; Yalçın, M.M.; Ercan, M.S. Entropy generation in parallel plate microchannels. Heat Mass Trans. 2007, 43, 729–739. [Google Scholar] [CrossRef]
- Makinde, O.D. Thermodynamic second law analysis for a gravity driven variable viscosity liquid film along an inclined heated plate with convective cooling. J. Mech. Sci. Technol. 2010, 24, 899–908. [Google Scholar] [CrossRef]
- Paoletti, S.; Rispoli, F.; Sciubba, E. Calculation of exergetic losses in compact heat exchanger passages. ASME AES 1989, 10, 21–29. [Google Scholar]
- Antar, M.A.; El-Shaarawi, M.A.I. Entropy generation due to forced convection fluid flow about a solid sphere. Int. J. Exer. 2008, 5, 97–114. [Google Scholar] [CrossRef]
- Chen, C.K.; Su, Y.F. Exergetic efficiency optimization for an irreversible Brayton refrigeration cycle. Int. J. Therm. Sci. 2005, 44, 303–310. [Google Scholar] [CrossRef]
- Cheng, C.Y.; Chen, C.K. Efficiency optimizations of an irreversible Brayton heat engine. Trans. ASME J. Energ. Resour. Technol. 1998, 120, 143–148. [Google Scholar] [CrossRef]
- Su, Y.F.; Chen, C.K. Analysis and optimisation of an irreversible Brayton refrigeration cycle using exergy concept. Int. J. Exer. 2008, 5, 470–486. [Google Scholar] [CrossRef]
- Erbay, L.B.; Göktun, S.; Yavuz, H. Optimal design of the regenerative gas turbine engine with isothermal heat addition. Int. J. Appl. Energ. 2001, 68, 249–264. [Google Scholar] [CrossRef]
- Aziz, A.; Makinde, O.D. Entropy generation minimization design of a two-dimensional orthotropic convection Pin Fin. Int. J. Exer. 2010, 7, 579–592. [Google Scholar] [CrossRef]
- Hsu, P.T.; Chen, C.K.; Wang, C.C. Mixed convection of micropolar fluids along a vertical wavy surface. Acta Mech. 2000, 144, 231–247. [Google Scholar] [CrossRef]
- Moulic, S.G.; Yao, L.S. Mixed convection along a vertical wavy surface. ASME J. Heat Trans. 1989, 111, 974–978. [Google Scholar] [CrossRef]
- Bejan, A. A study of entropy generation in fundamental convective heat Transfer. ASME J. Heat Trans. 1979, 101, 718–725. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation through Heat and Fluid Flow; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Mahmud, S.; Fraser, R.A. The second law analysis in fundamental convective heat Trans. problems. Int. J. Therm. Sci. 2003, 42, 177–186. [Google Scholar] [CrossRef]
- Rubin, S.G.; Graves, R.A. Viscous flow solution with a cubic Spline approximation. Comput. Fluid. 1975, 1, 1–36. [Google Scholar] [CrossRef]
- Wang, P.; Kahawita, R. Numerical integration of partial differential equations using cubic spline. Int. J. Comput. Math. 1983, 13, 271–286. [Google Scholar] [CrossRef]
- Çengel, Y.A. Heat and Mass Transfer: A Practical Approach; McGraw-Hill: New York, NY, USA, 2004. [Google Scholar]
- Chen, C.K.; Yang, Y.T.; Chang, K.H. Entropy generation of laminar-forced convection along the wavy surface. Int. J. Exer. 2010, 7, 564–578. [Google Scholar] [CrossRef]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chen, C.-K.; Yang, Y.-T.; Chang, K.-H. The Effect of Thermal Radiation on Entropy Generation Due to Micro-Polar Fluid Flow Along a Wavy Surface. Entropy 2011, 13, 1595-1610. https://doi.org/10.3390/e13091595
Chen C-K, Yang Y-T, Chang K-H. The Effect of Thermal Radiation on Entropy Generation Due to Micro-Polar Fluid Flow Along a Wavy Surface. Entropy. 2011; 13(9):1595-1610. https://doi.org/10.3390/e13091595
Chicago/Turabian StyleChen, Cha’o-Kuang, Yue-Tzu Yang, and Kuei-Hao Chang. 2011. "The Effect of Thermal Radiation on Entropy Generation Due to Micro-Polar Fluid Flow Along a Wavy Surface" Entropy 13, no. 9: 1595-1610. https://doi.org/10.3390/e13091595




