1. Introduction
During the course of time the problem of how to quantize gravity has been approached in various ways by a number of authors. Despite the great diversity in their opinions, there is at least one point where all serious physicists specializing in quantum gravity will agree: whatever the forthcoming generally accepted quantum theory of gravitation may be, it should be able to provide a statistical, microscopic interpretation to the so-called
Hawking effect. According to this effect black holes are not completely black, but they emit radiation with a characteristic temperature, which for a Schwarzschild black hole with Schwarzschild mass
M is given by the Hawking temperature
Even though the Hawking effect was discovered already about 35 years ago as a straightforward consequence of the quantum theory of fields in curved spacetime [
1], we may safely say that nobody really understands it. Why does a black hole radiate? Is the radiation of a black hole a somewhat similar process as is the radiation of ordinary matter, where the atoms of the matter perform jumps between different quantum states and, as a consequence, photons are emitted? If so, what are the “atoms” of spacetime which are supposed to constitute, among other things, black holes? What are their quantum states? Obviously, questions of this kind take us to the very foundations of the concepts of space and time. What is the proper microscopic description of space and time?
When considering these questions we need a microscopic model of a black hole which, even if not necessarily correct, at least allows us to address our questions in precise terms. We are going to construct such a model in this paper for the Schwarzschild black hole. Whenever we go over from a microscopic, statistical description of any system to its macroscopic, thermodynamical description, the key role is played by the
partition function
of the system. In Equation (
2)
n labels the possible different total energies
of the system,
β is the inverse temperature of the system, and
is the number of states associated with the same total energy
. We construct a microscopic model of what we call as a “stretched horizon” of a Schwarzschild black hole, and we write the partition function of the Schwarzschild black hole from the point of view of an observer on its stretched horizon. Using our partition function we obtain, among other things, the Hawking effect, and provide it with a statistical, microscopic interpretation.
We begin our considerations in
Section 2 with a definition of the concept of stretched horizon of the Schwarzschild black hole. In broad terms, our stretched horizon may be described as a space-like two-sphere just outside of the event horizon of the hole. An observer at rest with respect to the stretched horizon has a certain proper acceleration, and we require that when the Schwarzschild mass of the hole is changed, its stretched horizon will also change, but in such a way that the proper acceleration of the observer stays unchanged. In other words, we require that no matter what may happen to the black hole, an observer on the stretched horizon will always feel the one and the same proper acceleration. One finds, quite remarkably, that if such an observer is initially close to the event horizon of the black hole, he will stay close to the event horizon even when the Schwarzschild mass of the hole is changed. In this respect our notion of stretched horizon really makes sense.
The partition function
of Equation (
2) involves the concept of energy. Unfortunately, the concept of energy is very problematic in general relativity. Nevertheless, it turns out possible to define, beginning from the so-called Brown-York energy [
2], the notion of energy of the Schwarzschild black hole from the point of view of an observer on its stretched horizon. The resulting expression for the energy turns out to be, in SI units,
where
a is the proper acceleration of an observer on the stretched horizon, and
A is the area of the horizon. Since the proper acceleration
a is assumed to be a constant, the energy of the hole depends, from the point of view of an observer on the stretched horizon, on the area
A of the horizon only.
To consider the microscopic origin of the Hawking effect we need an appropriate microscopic model of the stretched horizon. Simple models are often the best models, and in this paper we shall settle in a model that can hardly be challenged in simplicity. We shall assume that the stretched horizon consists of a finite number of discrete constituents, each of them contributing to the stretched horizon an area, which is a non-negative integer times a constant. More precisely, we write the area of the stretched horizon, in SI units, as:
In this equation
N is the number of the constituents,
are non-negative integers determining their quantum states,
α is a number to be determined later, and
is the Planck length. We shall not specify what the constituents of the stretched horizon actually are. Since each constituent contributes a certain area to the stretched horizon, we shall call the quantum states of the constituents determined by the quantum numbers
as their
area eigenstates [
3].
After introducing our model in
Section 2 we shall proceed, in
Section 3, to the calculation of the partition function of the Schwarzschild black hole. Following the commonly accepted—although still unproved—wisdom that the quantum states of a black hole are somehow encoded in its horizon [
4,
5,
6], we shall assume that for each stationary quantum state of a black hole there exists a unique quantum state, determined by the quantum numbers
, of its stretched horizon. The calculation of the partition function is based on what we shall call as a
statistical postulate of our model. According to this postulate the microscopic states of the black hole are identified with the combinations of the non-vacuum area eigenstates of the constituents of its stretched horizon. Equations (3) and (4) imply that the possible energies of the black hole are, from the point of view of an observer on its stretched horizon, of the form:
where
Hence it follows from the statistical postulate that the number of microscopic states associated with the same energy
is the same as is the number of ways of expressing a given positive integer
n as a sum of at most
N positive integers
. More precisely, it is the number of ordered strings
, where
,
for all
and
. This number, which depends on
n and
N only, gives the function
in Equation (
2), and it may be calculated explicitly. It is most gratifying that the resulting partition function
of the Schwarzschild black hole may be also calculated explicitly, yielding a surprisingly simple expression:
where we shall call the temperature
as the
characteristic temperature of the hole.
All thermodynamical properties of the Schwarzschild black hole will follow, in our model, from the partition function of Equation (
8). In
Section 4 we shall consider the dependence of the energy of the hole on its absolute temperature
T. The most important outcome of those considerations is a result, which will be investigated in details in
Section 5, that when
, the Schwarzschild black hole performs a
phase transition, where the constituents of its stretched horizon jump, in average, from the vacuum to the second excited states. More precisely we shall see, in the large
N limit, that when
, all constituents of the stretched horizon, except one, are in vacuum, whereas when
T is slightly higher than
, the constituents are, in average, in the second excited states. Since the constituents are in vacuum, when
, there is no black hole with a temperature less than its characteristic temperature
, and in this sense the characteristic temperature
is the lowest possible temperature a Schwarzschild black hole may have. Choosing
in Equation (
9) one finds in the leading approximation, when using the natural units, where
:
This is the lowest possible temperature measured by an observer on the stretched horizon of the Schwarzschild black hole with Schwarzschild mass
M, and
r is the radial Schwarzschild coordinate of that observer. In our model one may interpret the effective, non-zero temperature of the black hole as an outcome of a thermal radiation emitted by the hole, when the constituents of its stretched horizon perform transitions from the excited states to the vacuum. The factor
is the blue shift factor of the temperature, and using the Tolman relation (see, for example, [
7]) one finds that when the possible backscattering effects of the radiation from the spacetime geometry are neglected, the temperature measured by an observer at a faraway infinity for the radiation emitted by the black hole is, in SI units,
which is exactly the Hawking temperature
of Equation (
1). Hence we may really obtain the Hawking effect from our model, and provide it with a microscopic, statistical interpretation.
Closely related to the Hawking effect is the so-called
Bekenstein-Hawking entropy law, which states that black hole possesses entropy which, in the natural units, is one-quarter of its event horizon area
or, in SI units [
8],
In
Section 6 we shall consider, beginning from the partition function
of Equation (
8), the entropic properties of the Schwarzschild black hole. Since the stretched horizon lies just outside of the event horizon of the Schwarzschild black hole, we may equate, for all practical purposes, the stretched horizon area
A of the hole with its even horizon area
. We shall show in
Section 6 that when
, the Bekenstein-Hawking entropy law of Equation (
13) is exactly reproduced, except that
has been replaced with
A. However, if
, the situation is somewhat different. When
T is slightly greater than
, the black hole has just performed a phase transition, where the constituents of its stretched horizon have jumped from the vacuum to the second excited states, and the stretched horizon possesses a
critical area
which has been obtained from Equation (
4) by putting
and
. If
then
, and one may obtain for the black hole entropy an expression:
This expression provides a modification, involving logarithmic terms, of the Bekenstein-Hawking entropy law. As one may observe, the Bekenstein-Hawking entropy law of Equation (
13) is exactly reproduced, when
.
We shall close our discussion in
Section 7 with some concluding remarks. Unless otherwise stated, we shall always use the natural units, where
.
4. Energy vs. Temperature
After finding in Equation (
61) an explicit expression for the partition function of the Schwarzschild black hole from the point of view of an observer on its stretched horizon, we are now prepared to obtain expressions for various thermodynamical quantities of the hole. The first of them is the average energy
of the hole in a given temperature
. Using Equation (
61) we find:
It turns out useful to define the average energy of the hole per a constituent:
and we get, assuming that
N is very large:
where
When obtaining Equation (
66) we have approximated
by 1. It should be noted that the quantity
may not be interpreted as the average energy of an individual constituent of the stretched horizon. The constituents of the stretched horizon are presumably Planck size objects, and at the Planck length scales the concept of energy simply does not make sense. However, using the quantity
we may consider the distribution of the constituents on different quantum states as a function of the inverse temperature
β. Using Equations (48), (58) and (65) we find that the average value
of the quantum numbers
determining the quantum states of individual constituents is related to
such that
Since the constituents of the stretched horizon are presumably Planck size objects, one may expect that for real, astrophysical black holes the number N of the constituents is enormous. For instance, if the mass of a black hole is a few solar masses, its Schwarzschild radius is a few kilometers, and N is around . When investigating the properties of the stretched horizon we may therefore consider, in practice, the limit where N goes to infinity. In this limit the properties of the quantity depend crucially on whether the absolute temperature T of the stretched horizon is greater or less than the characteristic temperature .
If
, the quantity
in the natural units. As a consequence,
is positive, and it vanishes in the limit, where
. One also finds that the quantity
, and hence the quantity
in the denominator of
goes towards the positive infinity, when
. So we find that
will vanish in this limit as well, and we get an important result:
whenever
. This means that all constituents of the stretched horizon are, in average, in vacuum, when
. When
, we must consider the limit, where both
and
N go towards the positive infinity. In this limit the first term inside the brackets in Equation (
64) goes towards unity, whereas the second term will vanish. Hence we find that when
, the total energy of the hole is, in SI units,
. The fact that the energy is non-zero even, when
implies that the Schwarzschild black hole may never, according to our model, vanish completely, but at least a Planck size remnant is left in behind. The result is a straightforward consequence of the statistical postulate, which implies that at least one of the constituents of the stretched horizon is in a non-vacuum state. It is possible to construct well-defined quantum-mechanical models of the Schwarzschild black hole, where the ground state energy is non-zero [
16]. The possible evaporation of the Planck size remnant, together with the consequent solution of the information loss problem in black hole physics has been considered in [
22,
23].
When
, the quantity
and
. As a consequence, the quantity
in the denominator of
will vanish in the limit, where
. The quantity
will also vanish in this limit, and hence it follows from Equations (66), (67) and (68) that we may write, in effect,
whenever
.
Of particular interest is the high temperature limit, where the absolute temperature
. In this limit
is very small, and because
where
denotes the terms, which are of the order
, or higher, Equation (
72) implies:
where
denotes the terms, which are of the order
or higher. Hence we find, using Equations (65) and (72), that in the high temperature limit the energy
E of the Schwarzschild black hole from the point of view of an observer on its stretched horizon takes, in SI units, the form:
So we have managed to obtain a result, which holds for almost any system in a high enough temperature. The thermal energy of almost any system may be written, in a high temperature limit, in the form:
where
N is the number of the constituents of the system, and
γ is a pure number, which depends on the number of the physical degrees of freedom possessed by an individual constituent of the system. For instance, the solids obey, as a very good approximation, the Dulong-Petit law (see, for example, [
24]):
where
N is the number of the constituents (atoms, molecules or ions) of the solid. In our model each constituent of the stretched horizon possesses exactly one physical degree of freedom, which is described by the quantum number
. Hence Equation (
75) is something one might expect, and it may therefore be used as a consistency check of our model.
5. Phase Transition and the Hawking Effect
So far we have considered the properties of the average energy of the Schwarzschild black hole from the point of view of an observer on its stretched horizon, when the temperature T of the hole is either smaller or greater than the characteristic temperature . When the temperature of the hole is very close to the characteristic temperature , something very peculiar happens to its energy.
It has been shown in
Appendix B that when
, the average energy per a constituent of the stretched horizon is, in SI units,
and that
where
denotes the terms, which are of the order
, or less. Hence we observe that when the number
N of the constituents becomes very large,
goes towards the positive infinity. Putting in another way, this means that increase in energy does not change the temperature of the Schwarzschild black hole, when
. In other words, the Schwarzschild black hole undergoes a
phase transition at the characteristic temperature
. Putting
in Equation (
72), which gives the quantity
in the large
N limit, whenever
, we find that during this phase transition
jumps from zero to the value
which gives the latent heat per a constituent in the phase transition.
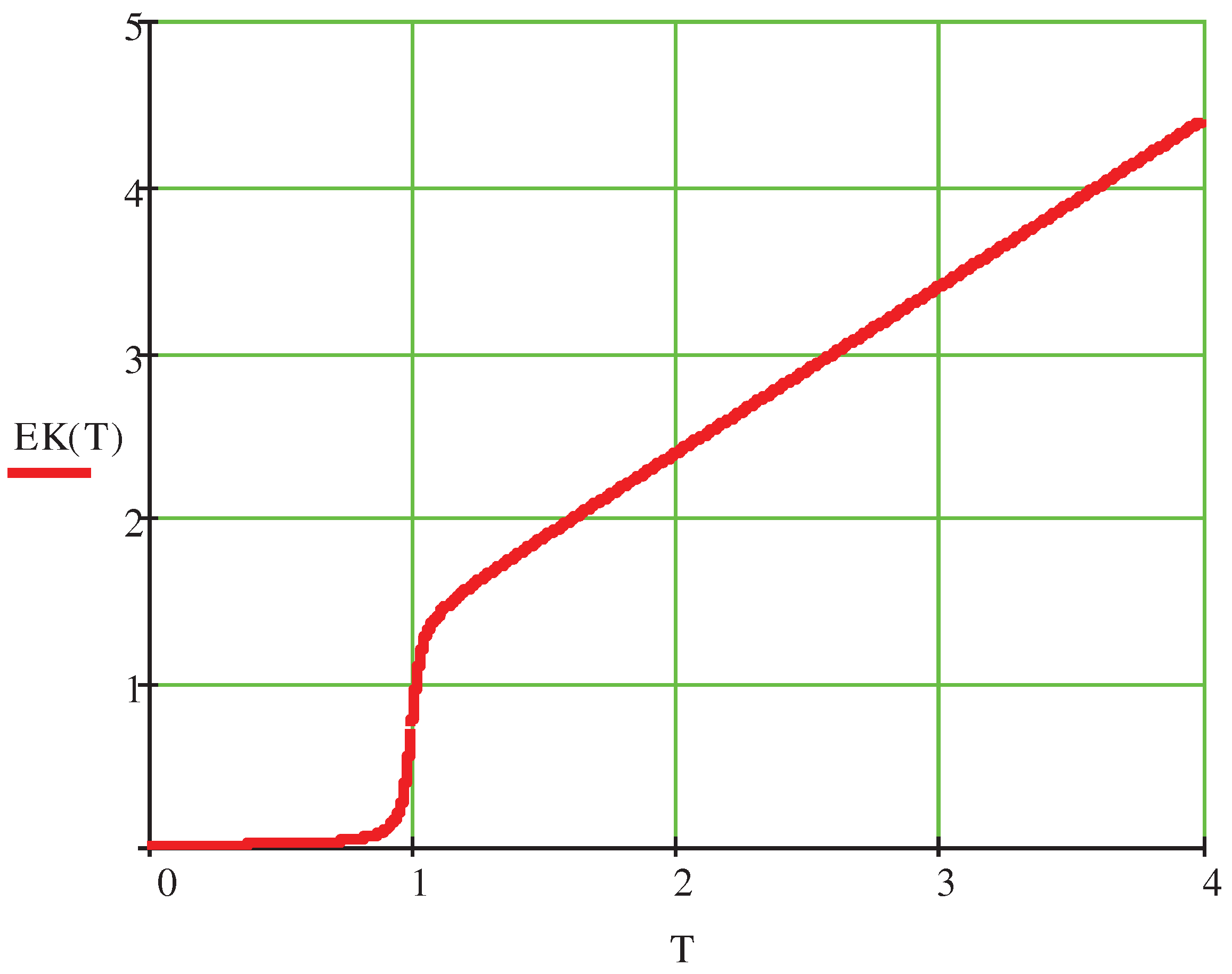
The results obtained above are confirmed by numerical investigations. In
Figure 1 we have made a plot of
as a function of the absolute temperature
T, when
. When
,
is practically zero. However, when
, the curve
becomes practically vertical. When
T is slightly greater than
,
is approximately
, which is about the same as
. Finally, the dependence of
on
T becomes approximately linear, when
.
Figure 1.
The average energy of the Schwarzschild black hole per a constituent of its stretched horizon as a function of the absolute temperature T, when the number of the constituents of the stretched horizon is . The absolute temperature T has been expressed in the units of , and the average energy in the units of . If , is effectively zero, which means that the constituents of the stretched horizon (except one) are in vacuum. When , the curve is practically vertical, which indicates a phase transition at the temperature . During this phase transition the constituents of the stretched horizon are excited from the vacuum to the second excited states. The latent heat per a constituent corresponding to this phase transition is . When , the curve is approximately linear.
Figure 1.
The average energy of the Schwarzschild black hole per a constituent of its stretched horizon as a function of the absolute temperature T, when the number of the constituents of the stretched horizon is . The absolute temperature T has been expressed in the units of , and the average energy in the units of . If , is effectively zero, which means that the constituents of the stretched horizon (except one) are in vacuum. When , the curve is practically vertical, which indicates a phase transition at the temperature . During this phase transition the constituents of the stretched horizon are excited from the vacuum to the second excited states. The latent heat per a constituent corresponding to this phase transition is . When , the curve is approximately linear.
The most important implication of the observed phase transition at the characteristic temperature
is that it
predicts the Hawking effect: The result that
is practically zero, when
, and then suddenly jumps to
, when
, indicates that the characteristic temperature
is the lowest possible temperature a black hole may have. If the temperature
T of the black hole were less than its characteristic temperature
, all of the constituents of its stretched horizon, except one, would be in vacuum, and there would be no black hole. Using Equations (20) and (58) we find that the characteristic temperature
may be written in terms of the Schwarzschild mass
M and the Schwarzschild radial coordinate
r of an observer on the stretched horizon as:
On the stretched horizon
r is approximately
, and hence an observer just outside of the event horizon measures a temperature
for the black hole. As a consequence of the non-zero temperature of the hole, thermal radiation comes out of the hole, and if the possible backscattering effects of the radiation from the spacetime geometry are neglected, the Tolman relation (see, for example, [
7]) implies that an observer at the asymptotic space-like infinity measures for the radiation a temperature
or, in SI units,
Hence it follows that if we fix the so far undetermined constant
α to be
then
where
is the Hawking temperature of the hole [
1]. So we have managed to show that according to our model the Schwarzschild black hole has, from the point of view of a distant observer, a certain non-zero temperature which, with the choice (
85) for the constant
α, agrees with the Hawking temperature
of the hole. In this sense our model predicts the Hawking effect. One may consider the determination of the constant
α from the requirement that the model must reproduce the Hawking effect, rather than from an
ab initio calculation as a weakness of our model. However, such an
ab initio calculation is unattainable as far as the proper quantum theory of gravity is still lacking.
If the temperature of the environment of a black hole is, from the point of view of an observer on the stretched horizon, less than the characteristic temperature , the hole begins to emit thermal radiation to its surroundings. As a consequence, the black hole evaporates away, and our model enables us to investigate what happens during this evaporation.
Suppose that at the onset of the evaporation the temperature of the hole is slightly greater than its characteristic temperature
. In that case the energy
per a constituent of the stretched horizon agrees with the latent heat
per a constituent given by Equation (
80). Since the average value
taken by the quantum numbers
is related to
as in Equation (
70), we find that
at the onset of the evaporation. This means that when the evaporation begins, all of the constituents of the stretched horizon are, in average, on the second excited state. During the evaporation the constituents descent to lower quantum states until, finally, all constituents, except one, are in vacuum, and the only remaining constituent is in the first excited state. It should be noted that from the point of view of an observer on the stretched horizon the temperature of the hole remains the same during the whole process of evaporation. That is because the proper acceleration
a of our observer is, by definition, a constant, and the characteristic temperature
depends on the proper acceleration
a according to Equation (
58). Hence we find that constant proper acceleration implies constant temperature, and there is not any dramatic increase in the black hole temperature during the final stages of its evaporation. The temperature remains the same all the time, and the black hole simply fades away, leaving a Planck-size remnant in behind.
6. Entropy vs. Horizon Area
If we know the partition function
of a system, we are able to calculate its entropy. In general, the energy
E, absolute temperature
T and the entropy
S of any system obey the relationship:
where
is the Helmholtz free energy of the system. Hence the entropy of the system may be written, in the natural units, as:
Using Equations (61) and (64) we therefore find that according to our model, the entropy of the Schwarzschild black hole when written in terms of its inverse temperature
β takes the form:
One immediately observes that in the limit, where
and hence
, the entropy of the hole vanishes:
which means that the black hole obeys the third law of thermodynamics. More generally, it turns out useful to define a quantity
which gives the entropy per a constituent of the stretched horizon. We find:
where, in the large
N limit:
If
, then
, and the quantity
goes towards the positive infinity in the large
N limit. As a consequence, we get:
whenever
. If
, then
, and the quantity
goes towards zero in the large
N limit. Hence we have:
whenever
. So we find that in the large
N limit there is a discrete jump in the values taken by
at the phase transition temperature
, and the magnitude of this jump is given by the right hand side of Equation (
99).
A really interesting question is in which way does the entropy
S of the Schwarzschild black hole depend on its event horizon area. Equation (
72) implies that when
, the quantity
depends on the average energy
per a constituent of its stretched horizon such that
and on the energy
of the hole as:
Employing Equations (41), (58) and (85) we find that the stretched horizon area
A of the hole may be expressed in terms of its energy
E, in the natural units, as:
and hence
where we have defined the
critical area
which gives the area taken by the stretched horizon, when
T is slightly greater than
. Indeed, Equation (
103) implies:
When
, the constituents of the stretched horizon are, in average, in the second excited states. In SI units
may be written in terms of the Planck length
as:
Substituting the right hand side of Equation (
103) for
in Equation (
99) we find that in the large
N limit we have:
whenever
. Hence the entropy
takes, by means of Equation (
104), the form:
or, in SI units:
Since the stretched horizon of the Schwarzschild black hole lies just outside of its event horizon, we may equate the stretched horizon area
A of the hole with its event horizon area. It is interesting to see what happens to the black hole entropy when
. When
, the hole has just undergone the phase transition, where the constituents of its stretched horizon have, in average, jumped from the vacuum to the second excited states, and the temperature
T of the hole is slightly above of its characteristic temperature
. Putting
in Equation (
109) we get:
which is exactly the Bekenstein-Hawking entropy law [
8]. We have thus achieved one of our main goals: We have been able to obtain the Bekenstein-Hawking entropy law for the Schwarzschild black hole from its partition function which, in turn, followed from a specific microscopic model of its stretched horizon. It should be stressed, however, that our derivation of the Bekenstein-Hawking entropy law holds only if the horizon area of the Schwarzschild black hole agrees with its critical area
and the temperature
T of the hole is slightly higher than its characteristic temperature
. If
T is appreciably greater than
, and thus
A is appreciably greater than
, the simple proportionality between the area and the entropy predicted by the Bekenstein-Hawking entropy law for the Schwarzschild black hole will no longer hold, and the Bekenstein-Hawking entropy law must be replaced by Equation (
109). Since the characteristic temperature
measured by an observer on the stretched horizon of the Schwarzschild black hole corresponds to the Hawking temperature
of Equation (
87) measured by a faraway observer, we may thus conclude that the Bekenstein-Hawking entropy law holds only if the temperature of the hole is, from the point of view of a faraway observer, very close to its Hawking temperature, but not otherwise.
So far we have managed to obtain, in Equation (
109), an expression for the black hole entropy, when
and
. When
, the constituents of its stretched horizon are effectively in vacuum, and the black hole, as well as its entropy, will effectively vanish. It is very interesting to investigate what will happen to the black hole entropy during the phase transition where
and its horizon area is
less than its critical area
. It is a general property of any system that its entropy
S is related to its energy
E and inverse temperature
β such that
Actually, this is the
definition of the concept of temperature in terms of the concepts of energy and entropy. Since the proper acceleration
a of the observer is assumed to be a constant, we get, using Equation (
41):
Equations (58) and (85) imply that when
, the inverse temperature of the hole is, in natural units,
and hence it follows from Equations (
111) and (
112) that
or
which, again, is the Bekenstein-Hawking entropy law in the natural units. So we have managed to show that whenever
, the entropy of the Schwarzschild black hole obeys the Bekenstein-Hawking entropy law.
Before closing our discussion on the entropy of the Schwarzschild black hole we point out yet another interesting feature of our model. It has been shown in
Appendix B that when
, the energy of the hole from the point of view of an observer on its stretched horizon is exactly [
25]
Hence it follows from Equations (
102) and (
115) that when
, the entropy of the Schwarzschild black hole may be written in terms of
N, the number of the constituents of the stretched horizon, as:
Putting in another way, this means that when the temperature
T of the hole is exactly the same as its characteristic temperature
—which means that its temperature from the point of view of a faraway observer agrees with its Hawking temperature
—each constituent of the stretched horizon carries, in average, exactly one bit of information. In this sense our model seems to reproduce at least in some respects Wheeler’s famous “it from bit” proposal, which states in very broad terms that in the utmost fundamental level, the laws of physics should be reducible to the properties of some fundamental constituents each carrying exactly one bit of information [
26].
7. Discussion
In this paper we have considered the statistical and the thermodynamical properties of the Schwarzschild black hole from the point of view of an observer on its “stretched horizon”, or a space-like two-sphere, where the Schwarzschild coordinate r was assumed to be slightly greater than the Schwarzschild radius of the hole. The stretched horizon was assumed to consist of a finite number of discrete, Planck-size constituents, each of them contributing an area, which is an integer times a constant, to the total area of the stretched horizon. Assuming that the quantum states of the Schwarzschild black hole are encoded in the quantum states of the constituents of its stretched horizon, we wrote the partition function of the hole. It turned out that the partition function may be calculated explicitly, yielding a surprisingly simple, analytic expression. Our partition function implied, among other things, the Hawking effect, and the Bekenstein-Hawking entropy law, which states that the black hole entropy is, in the natural units, one-quarter of its event horizon area. The entropy of the hole was found to agree with the Bekenstein-Hawking entropy, when the temperature of the hole agrees, from the point of view of a faraway observer, with the Hawking temperature of the hole. Using our partition function, however, it is possible to obtain expressions for the mass and the temperature of the hole even when its temperature differs from its Hawking temperature. The Hawking temperature is the lowest possible temperature of a black hole, but if the hole is in a heat bath with a temperature higher than its Hawking temperature, its entropy will differ from its Bekenstein-Hawking entropy.
The most interesting feature of our model is that it provides a microscopic interpretation to the Hawking effect: The Hawking effect is a consequence of a phase transition performed by a black hole. At a certain characteristic temperature , which is proportional to the proper acceleration a of an observer on the stretched horizon, the black hole undergoes a phase transition, where the microscopic constituents of its stretched horizon descend, in average, from the second excited states to the vacuum. During this phase transition the black hole emits radiation with the characteristic temperature until, finally, all constituents of its stretched horizon, except one, are in vacuum, and there is no more a black hole. Since the constituents of the stretched horizon are in vacuum, whenever , the characteristic temperature is, from the point of view of an observer on the stretched horizon, the lowest possible temperature a black hole may have. The characteristic temperature involves a certain constant of proportionality, and with an appropriate choice of that constant one finds that at the asymptotic space-like infinity the temperature corresponds to the Hawking temperature of the black hole. In other words, the phase transition of the black hole takes the place, from the point of view of a faraway observer at rest with respect to the hole, at its Hawking temperature, which is the same as is the temperature of the radiation emitted by the hole during the phase transition.
Even though our simple model of the Schwarzschild black hole meets with some success, it deserves some critique as well. The crucial point of our investigations was the counting of states. The counting of states was based on what we called as “statistical postulate”. The statistical postulate implied that if we denote the number of the constituents of the stretched horizon by
N, then the number of the microscopic states associated with the same total energy
of a black hole is the same as is the number of the ordered strings
of positive integers
such that
and
. The positive integers
determine the quantum states of the constituents of the stretched horizon, and it is important to note that with this identification of microscopic states different combinations of the
same quantum numbers represent different microscopic states. In this sense the counting of states in our model is in marked contrast with the counting of states in, say, the approaches to black hole thermodynamics based on loop quantum gravity [
27], where different combinations of the same quantum states of the individual constituents represent the same microscopic state.
Indeed, the idea that different combinations of the same quantum states of the individual constituents should represent the same overall, microscopic state of a system might appear very attractive, at least in the first sight. In that case the constituents of the stretched horizon would behave in the same way as a system of identical bosons, where interchange of two bosons keeps the overall quantum state of the system unchanged. But then again, why should the Planck scale constituents of the stretched horizon act like identical bosons? The symmetry of the quantum state of a system of identical bosons under interchanges of the bosons follows from the Spin-Statistics Theorem which, in turn, may be traced back to the symmetry properties of flat spacetime. There are no grounds to believe that spacetime at the Planck length scale would possess symmetries in any way akin to those of flat spacetime. Rather, the contrary is the case. When constituents in different quantum states are interchanged, the properties of the stretched horizon are also changed. Hence there are no grounds to believe that the constituents of the stretched horizon would behave like bosons either.
Another piece of criticism against our model may be addressed on the form of our partition function. In a well known work (see, for example, [
28]) based on the Euclidean path integral approach to quantum gravity it was shown by Hawking that in the leading approximation the partition function of the Schwarzschild black hole should be, in the natural units, of the form:
where
is an appropriate normalization constant. The problem is that our partition function in Equation (
61) seems to be nowhere near of the partition function (
118) obtained by Hawking. Is our partition function totally wrong?
To begin with, we note that in Equation (
61) the partition function has been written from the point of view of an observer on the stretched horizon, whereas the partition function in Equation (
118) has been written from the point of view of an observer at rest at a faraway infinity. Hence there is really nothing strange in the fact that the partition functions (61) and (118) are very different. It is simply what one expects.
Nevertheless, there does exist a connection between the partition functions Equation (
61) and (
118). Since the energy of any system is
, we find that (
118) may be written equivalently as:
From the point of view of a faraway observer at rest with respect to the black hole the energy
E may be identified with the Schwarzschild mass
M of the hole, and hence Equation (
118) simply states that Schwarzschild black hole has, in the leading approximation, the temperature
which is the Hawking temperature
of the hole. However, this is exactly what the partition function (
61) is telling us as well: It implies that even if we dropped the temperature of the external heat bath of the hole close to the absolute zero, the hole would still have a temperature which, from the point of view of a faraway observer, equals with its Hawking temperature. We may therefore view the right hand side of Equation (
118) as an effective partition function of a black hole in the limit, where the temperature of the external heat path is close to zero. An advantage of the partition function (
61) is that it enables us to consider the thermodynamical properties of the Schwarzschild black hole even when the temperature of the external heat bath exceeds the Hawking temperature of the hole.
As we have learned, the characteristic temperature
defined in Equation (
58) plays a crucial role in our model. If we put
in Equation (
58), we find, in the natural units,
or, in SI units:
It is interesting that
is exactly the
Unruh temperature measured by an observer with proper acceleration
a [
29]. The result suggests that a microscopic model essentially similar to the one used for a microscopic interpretation of the Hawking effect in this paper could possibly be used to interpret the so-called Unruh effect as well. According to this effect an observer in a uniformly accelerating motion will detect particles even when all inertial observers detect a vacuum. The effective temperature of the radiation of the particles measured by an accelerating observer is the Unruh temperature, and hence the Unruh temperature is the lowest possible temperature an accelerating observer may detect in the same way as the Hawking temperature is the lowest possible temperature of a black hole [
30]. One expects the emission of the Unruh radiation to involve processes in the microscopic structure of spacetime, which are somewhat similar to those taking place in the Hawking radiation.
To provide a microscopic interpretation to the Unruh effect one only needs to replace the stretched horizon of the Schwarzschild black hole by a spacelike two-surface propagating in spacetime close to the Rindler horizon of an accelerated observer. In other words, the stretched Schwarzschild horizon is replaced by a sort of “stretched Rindler horizon”. Postulating that any finite part with area A of the “stretched Rindler horizon” consists, like the stretched Schwarzschild horizon, of a finite number of discrete constituents and possesses, in the natural units, energy (a is the proper acceleration of the observer on the stretched Rindler horizon), one finds that results identical to those obtained for the stretched Schwarzschild horizon may be obtained for the stretched Rindler horizon as well: At the temperature the stretched Rindler horizon performs a phase transition, where its constituents jump, in average, from the vacuum to the second excited states, and the entropy of any finite part of the stretched Rindler horizon is . Hence the Unruh temperature is the lowest temperature an accelerated observer may measure, and we have found, in the context of this simple model, a microscopic interpretation of the Unruh effect. The most questionable step in our chain of reasoning was the association of the concept of energy with the stretched Rindler horizon in the same way as we associated the concept of energy with the Schwarzschild black hole from the point of view of an observer on the stretched Schwarzschild horizon. Lots of work must still be done to clarify this point.
It seems that somewhat similar reasoning could be applied for an extension of our analysis for Kerr-Newman black holes as well. As the first step one finds such space-like two-surfaces just outside of the event horizon of the Kerr-Newman black hole, where the proper acceleration
. A two-surface of this kind will then serve as the stretched horizon of the hole. As the second step one finds the constraint between the infinitesimal changes in the mass
M, electric charge
Q and the angular momentum
J of the Kerr-Newman black hole such that no matter what may happen to the hole, the proper acceleration
a on the stretched horizon will always stay the same. The third step is to establish an expression, beginning from the concept of Brown-York energy, for the energy of the Kerr-Newman hole from the point of view of an observer on its stretched horizon. If one is able to show that this energy takes, in the natural units, the form
, where
A is the area of the stretched horizon, the calculation of the partition function of the Kerr-Newman black hole proceeds in the same way as for the Schwarzschild black hole. One assumes that the stretched horizon consists of
N discrete constituents such that its area may be written in terms of non-negative integers
as in Equation (
4). The resulting partition function should be, when written in terms of the inverse temperature
β and the constant
α, the same as for the Schwarzschild black hole. One expects this partition function to imply that from the point of view of an observer at the space-like infinity the lowest possible temperature of the hole is, in the natural units,
, where
κ is the surface gravity on the event horizon, and that the entropy of the hole is one-quarter of its event horizon area. The technical details of the procedure outlined above, however, are pretty complicated, and they will be left in the forthcoming publications.
An essential feature of our model is its extreme simplicity. Indeed, in our model the counting of the microscopic states, which is the key question in the consideration of the statistical physics of any system, boils down to the elementary problem of in how many ways a given positive integer may be expressed as a sum of a given number of integers. It remains to be seen whether any results of our model will survive in the more advanced attempts to approach the problems in the thermodynamics of black holes by means of the microphysics of spacetime. An advantage of our model is that it allows us to address these problems in precise terms.