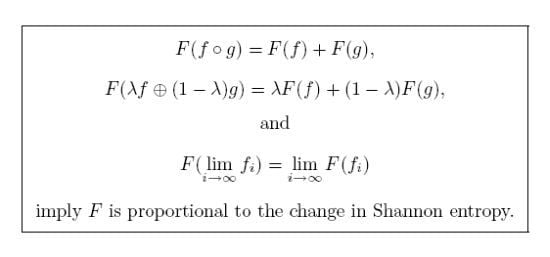A Characterization of Entropy in Terms of Information Loss

Abstract

There are numerous characterizations of Shannon entropy and Tsallis entropy as measures of information obeying certain properties. Using work by Faddeev and Furuichi, we derive a very simple characterization. Instead of focusing on the entropy of a probability measure on a finite set, this characterization focuses on the “information loss”, or change in entropy, associated with a measure-preserving function. Information loss is a special case of conditional entropy: namely, it is the entropy of a random variable conditioned on some function of that variable. We show that Shannon entropy gives the only concept of information loss that is functorial, convex-linear and continuous. This characterization naturally generalizes to Tsallis entropy as well.

1. Introduction

The Shannon entropy [1] of a probability measure p on a finite set X is given by:

$$H\left(p\right)=-\sum _{i\in X}{p}_{i}ln\left(p_i\right)$$

There are many theorems that seek to characterize Shannon entropy starting from plausible assumptions; see for example the book by Aczél and Daróczy [2]. Here we give a new and very simple characterization theorem. The main novelty is that we do not focus directly on the entropy of a single probability measure, but rather, on the change in entropy associated with a measure-preserving function. The entropy of a single probability measure can be recovered as the change in entropy of the unique measure-preserving function onto the one-point space.

A measure-preserving function can map several points to the same point, but not vice versa, so this change in entropy is always a decrease. Since the second law of thermodynamics speaks of entropy increase, this may seem counterintuitive. It may seem less so if we think of the function as some kind of data processing that does not introduce any additional randomness. Then the entropy can only decrease, and we can talk about the “information loss” associated with the function.

Some examples may help to clarify this point. Consider the only possible map $f:\{a,b\}\to \left\{c\right\}$. Suppose p is the probability measure on $\{a,b\}$ such that each point has measure $1/2$, while q is the unique probability measure on the set $\left\{c\right\}$. Then $H\left(p\right)=ln2$, while $H\left(q\right)=0$. The information loss associated with the map f is defined to be $H\left(p\right)-H\left(q\right)$, which in this case equals $ln2$. In other words, the measure-preserving map f loses one bit of information.

On the other hand, f is also measure-preserving if we replace p by the probability measure $p^{\prime }$ for which a has measure 1 and b has measure 0. Since $H\left(p^{\prime }\right)=0$, the function f now has information loss $H\left(p^{\prime }\right)-H\left(q\right)=0$. It may seem odd to say that f loses no information: after all, it maps a and b to the the same point. However, because the point b has probability zero with respect to $p^{\prime }$, knowing that $f\left(x\right)=c$ lets us conclude that $x=a$ with probability one.

The shift in emphasis from probability measures to measure-preserving functions suggests that it will be useful to adopt the perspective of category theory [3], where one has objects and morphisms between them. However, the reader need only know the definition of “category” to understand this paper.

Our main result is that Shannon entropy has a very simple characterization in terms of information loss. To state it, we consider a category where a morphism $f:p\to q$ is a measure-preserving function between finite sets equipped with probability measures. We assume F is a function that assigns to any such morphism a number $F\left(f\right)\in [0,\infty )$, which we call its information loss. We also assume that F obeys three axioms. If we call a morphism a “process” (to be thought of as deterministic), we can state these roughly in words as follows. For the precise statement, including all the definitions, see Section 2.

(i)

Functoriality. Given a process consisting of two stages, the amount of information lost in the whole process is the sum of the amounts lost at each stage:

$$F(f\circ g)=F\left(f\right)+F\left(g\right)$$

(ii)

Convex linearity. If we flip a probability-λ coin to decide whether to do one process or another, the information lost is λ times the information lost by the first process plus $(1-\lambda )$ times the information lost by the second:

$$F(\lambda f\oplus (1-\lambda \left)g\right)=\lambda F\left(f\right)+(1-\lambda )F\left(g\right)$$

(iii)

Continuity. If we change a process slightly, the information lost changes only slightly: $F\left(f\right)$ is a continuous function of f.

Given these assumptions, we conclude that there exists a constant $c\ge 0$ such that for any $f:p\to q$, we have

$$F\left(f\right)=c\left(H\right(p)-H(q\left)\right)$$

The charm of this result is that the first two hypotheses look like linear conditions, and none of the hypotheses hint at any special role for the function $-plnp$, but it emerges in the conclusion. The key here is a result of Faddeev [4] described in Section 4.

For many scientific purposes, probability measures are not enough. Our result extends to general measures on finite sets, as follows. Any measure on a finite set can be expressed as $\lambda p$ for some scalar λ and probability measure p, and we define $H\left(\lambda p\right)=\lambda H\left(p\right)$. In this more general setting, we are no longer confined to taking convex linear combinations of measures. Accordingly, the convex linearity condition in our main theorem is replaced by two conditions: additivity ($F(f\oplus g)=F\left(f\right)+F\left(g\right)$) and homogeneity ($F\left(\lambda f\right)=\lambda F\left(f\right)$). As before, the conclusion is that, up to a multiplicative constant, F assigns to each morphism $f:p\to q$ the information loss $H\left(p\right)-H\left(q\right)$.

It is natural to wonder what happens when we replace the homogeneity axiom $F\left(\lambda f\right)=\lambda F\left(f\right)$ by a more general homogeneity condition:

$$F\left(\lambda f\right)={\lambda }^{\alpha }F\left(f\right)$$

for some number $\alpha >0$. In this case we find that $F\left(f\right)$ is proportional to $H_{\alpha }\left(p\right)-H_{\alpha }\left(q\right)$, where $H_{\alpha }$ is the so-called Tsallis entropy of order α.

2. The Main Result

We work with finite sets equipped with probability measures. All measures on a finite set X will be assumed nonnegative and defined on the σ-algebra of all subsets of X. Any such measure is determined by its values on singletons, so we will think of a probability measure p on X as an X-tuple of numbers $p_i\in [0,1]$ ($i\in X$) satisfying $\sum p_i=1$.

Definition 1. Let $\mathtt{FinProb}$ be the category where an object $(X,p)$ is given by a finite set X equipped with a probability measure p, and where a morphism $f:(X,p)\to (Y,q)$ is a measure-preserving function from $(X,p)$ to $(Y,q)$, that is, a function $f:X\to Y$ such that

$$q_j=\sum _{i\in f^{-1}\left(j\right)}{p}_i$$

for all $j\in Y$.

We will usually write an object $(X,p)$ as p for short, and write a morphism $f:(X,p)\to (Y,q)$ as simply $f:p\to q$.

There is a way to take convex linear combinations of objects and morphisms in $\mathtt{FinProb}$. Let $(X,p)$ and $(Y,q)$ be finite sets equipped with probability measures, and let $\lambda \in [0,1]$. Then there is a probability measure

$$\lambda p\oplus (1-\lambda )q$$

on the disjoint union of the sets X and Y, whose value at a point k is given by

$${(\lambda p\oplus (1-\lambda )q)}_k=\left\{\begin{array}{cc}\lambda p_k\hfill & \text{if}k\in X\hfill \\ (1-\lambda )q_k\hfill & \text{if}k\in Y\hfill \end{array}\right.$$

Given morphisms $f:p\to p^{\prime }$ and $g:q\to q^{\prime }$, there is a unique morphism

$$\lambda f\oplus (1-\lambda )g:\lambda p\oplus (1-\lambda )q⟶\lambda p^{\prime }\oplus (1-\lambda )q^{\prime }$$

that restricts to f on the measure space p and to g on the measure space q.

The same notation can be extended, in the obvious way, to convex combinations of more than two objects or morphisms. For example, given objects $p\left(1\right),\dots ,p\left(n\right)$ of $\mathtt{FinProb}$ and nonnegative scalars ${\lambda }_1,\dots ,{\lambda }_n$ summing to 1, there is a new object ${⨁}_{i=1}^n{\lambda }_{i}p\left(i\right)$.

Recall that the Shannon entropy of a probability measure p on a finite set X is

$$H\left(p\right)=-\sum _{i\in X}{p}_{i}ln\left(p_i\right)\in [0,\infty )$$

with the convention that $0ln\left(0\right)=0$.

Theorem 2. Suppose F is any map sending morphisms in $\mathtt{FinProb}$ to numbers in $[0,\infty )$ and obeying these three axioms:

(i) 

Functoriality:

$$F(f\circ g)=F\left(f\right)+F\left(g\right)$$

(1)

whenever $f,g$ are composable morphisms.

(ii) 

Convex linearity:

$$F(\lambda f\oplus (1-\lambda \left)g\right)=\lambda F\left(f\right)+(1-\lambda )F\left(g\right)$$

(2)

for all morphisms $f,g$ and scalars $\lambda \in [0,1]$.

(iii) 

Continuity: F is continuous.

Then there exists a constant $c\ge 0$ such that for any morphism $f:p\to q$ in $\mathtt{FinProb}$,

$$F\left(f\right)=c\left(H\right(p)-H(q\left)\right)$$

where $H\left(p\right)$ is the Shannon entropy of p. Conversely, for any constant $c\ge 0$, this formula determines a map F obeying Conditions (i)–(iii).

We need to explain Condition (iii). A sequence of morphisms

$$(X_n,p\left(n\right))\stackrel{f_n}{\to }(Y_n,q\left(n\right))$$

in $\mathtt{FinProb}$ converges to a morphism $(X,p)\stackrel{f}{\to }(Y,q)$ if:

• for all sufficiently large n, we have $X_n=X$, $Y_n=Y$, and $f_n\left(i\right)=f\left(i\right)$ for all $i\in X$;
• $p\left(n\right)\to p$ and $q\left(n\right)\to q$ pointwise.

We define F to be continuous if $F\left(f_n\right)\to F\left(f\right)$ whenever $f_n$ is a sequence of morphisms converging to a morphism f.

The proof of Theorem 2 is given in Section 5. First we show how to deduce a characterization of Shannon entropy for general measures on finite sets.

The following definition is in analogy to Definition 1:

Definition 3. Let $\mathtt{FinMeas}$ be the category whose objects are finite sets equipped with measures and whose morphisms are measure-preserving functions.

There is more room for maneuver in $\mathtt{FinMeas}$ than in $\mathtt{FinProb}$: we can take arbitrary nonnegative linear combinations of objects and morphisms, not just convex combinations. Any nonnegative linear combination can be built up from direct sums and multiplication by nonnegative scalars, which are defined as follows.

• For direct sums, first note that the disjoint union of two finite sets equipped with measures is another object of the same type. We write the disjoint union of $p,q\in \mathtt{FinMeas}$ as $p\oplus q$. Then, given morphisms $f:p\to p^{\prime }$, $g:q\to q^{\prime }$ there is a unique morphism $f\oplus g:p\oplus q\to p^{\prime }\oplus q^{\prime }$ that restricts to f on the measure space p and to g on the measure space q.
• For scalar multiplication, first note that we can multiply a measure by a nonnegative real number and get a new measure. So, given an object $p\in \mathtt{FinMeas}$ and a number $\lambda \ge 0$ we obtain an object $\lambda p\in \mathtt{FinMeas}$ with the same underlying set and with ${\left(\lambda p\right)}_i=\lambda p_i$. Then, given a morphism $f:p\to q$, there is a unique morphism $\lambda f:\lambda p\to \lambda q$ that has the same underlying function as f.

This is consistent with our earlier notation for convex linear combinations.

We wish to give some conditions guaranteeing that a map sending morphisms in $\mathtt{FinMeas}$ to nonnegative real numbers comes from a multiple of Shannon entropy. To do this we need to define the Shannon entropy of a finite set X equipped with a measure p, not necessarily a probability measure. Define the total mass of $(X,p)$ to be

$$\parallel p\parallel =\sum _{i\in X}{p}_i$$

If this is nonzero, then p is of the form $\parallel p\parallel \overline{p}$ for a unique probability measure space $\overline{p}$. In that case we define the Shannon entropy of p to be $\parallel p\parallel H\left(\overline{p}\right)$. If the total mass of p is zero, we define its Shannon entropy to be zero.

We can define continuity for a map sending morphisms in $\mathtt{FinMeas}$ to numbers in $[0,\infty )$ just as we did for $\mathtt{FinProb}$, and show:

Corollary 4. Suppose F is any map sending morphisms in $\mathtt{FinMeas}$ to numbers in $[0,\infty )$ and obeying these four axioms:

(i) 

Functoriality:

$$F(f\circ g)=F\left(f\right)+F\left(g\right)$$

whenever $f,g$ are composable morphisms.

(ii) 

Additivity:

$$F(f\oplus g)=F\left(f\right)+F\left(g\right)$$

(3)

for all morphisms $f,g$.

(iii) 

Homogeneity:

$$F\left(\lambda f\right)=\lambda F\left(f\right)$$

(4)

for all morphisms f and all $\lambda \in [0,\infty )$.

(iv) 

Continuity: F is continuous.

Then there exists a constant $c\ge 0$ such that for any morphism $f:p\to q$ in $\mathtt{FinMeas}$,

$$F\left(f\right)=c\left(H\right(p)-H(q\left)\right)$$

where $H\left(p\right)$ is the Shannon entropy of p. Conversely, for any constant $c\ge 0$, this formula determines a map F obeying Conditions (i)–(iv).

Proof. Take a map F obeying these axioms. Then F restricts to a map on morphisms of $\mathtt{FinProb}$ obeying the axioms of Theorem 2. Hence there exists a constant $c\ge 0$ such that $F\left(f\right)=c\left(H\right(p)-H(q\left)\right)$ whenever $f:p\to q$ is a morphism between probability measures. Now take an arbitrary morphism $f:p\to q$ in $\mathtt{FinMeas}$. Since f is measure-preserving, $\parallel p\parallel =\parallel q\parallel =\lambda$, say. If $\lambda \ne 0$ then $p=\lambda \overline{p}$, $q=\lambda \overline{q}$ and $f=\lambda \overline{f}$ for some morphism $\overline{f}:\overline{p}\to \overline{q}$ in $\mathtt{FinProb}$; then by homogeneity,

$$F\left(f\right)=\lambda F\left(\overline{f}\right)=\lambda c(H\left(\overline{p}\right)-H\left(\overline{q}\right))=c(H\left(p\right)-H\left(q\right)).$$

If $\lambda =0$ then $f=0f$, so $F\left(f\right)=0$ by homogeneity. So $F\left(f\right)=c\left(H\right(p)-H(q\left)\right)$ in either case. The converse statement follows from the converse in Theorem 2. ☐

3. Why Shannon Entropy Works

To prove the easy half of Theorem 2, we must check that $F\left(f\right)=c\left(H\right(p)-H(q\left)\right)$ really does determine a functor obeying all the conditions of that theorem. Since all these conditions are linear in F, it suffices to consider the case where $c=1$. It is clear that F is continuous, and Equation (1) is also immediate whenever $g:m\to p$, $f:p\to q$, are morphisms in $\mathtt{FinProb}$:

$$F(f\circ g)=H\left(m\right)-H\left(q\right)=H\left(p\right)-H\left(q\right)+H\left(m\right)-H\left(p\right)=F\left(f\right)+F\left(g\right)$$

The work is to prove Equation (2).

We begin by establishing a useful formula for $F\left(f\right)=H\left(p\right)-H\left(q\right)$, where as usual f is a morphism $p\to q$ in $\mathtt{FinProb}$. Since f is measure-preserving, we have

$$q_j=\sum _{i\in f^{-1}\left(j\right)}{p}_i$$

So

$$\begin{array}{cc}\hfill \sum _j{q}_{j}ln{q}_j& =\sum _j\sum _{i\in f^{-1}\left(j\right)}{p}_{i}ln{q}_j\hfill \\ & =\sum _j\sum _{i\in f^{-1}\left(j\right)}{p}_{i}ln{q}_{f\left(i\right)}\hfill \\ & =\sum _i{p}_{i}ln{q}_{f\left(i\right)}\hfill \end{array}$$

where in the last step we note that summing over all i that map to j and then summing over all j is the same as summing over all i. So,

$$\begin{array}{cc}\hfill F\left(f\right)& =-\sum _i{p}_{i}ln{p}_i+\sum _j{q}_{j}ln{q}_j\hfill \\ & =\sum _i(-p_{i}ln{p}_i+p_{i}ln{q}_{f\left(i\right)})\hfill \end{array}$$

and thus

$$F\left(f\right)=\sum _{i\in X}{p}_{i}ln\frac{q_{f\left(i\right)}}{p_i}$$

(5)

where the quantity in the sum is defined to be zero when $p_i=0$. If we think of p and q as the distributions of random variables $x\in X$ and $y\in Y$ with $y=f\left(x\right)$, then $F\left(f\right)$ is exactly the conditional entropy of x given y. So, what we are calling “information loss” is a special case of conditional entropy.

This formulation makes it easy to check Equation (2),

$$F(\lambda f\oplus (1-\lambda \left)g\right)=\lambda F\left(f\right)+(1-\lambda )F\left(g\right)$$

simply by applying (5) on both sides.

In the proof of Corollary 4 (on $\mathtt{FinMeas}$), the fact that $F\left(f\right)=c\left(H\right(p)-H(q\left)\right)$ satisfies the four axioms was deduced from the analogous fact for $\mathtt{FinProb}$. It can also be checked directly. For this it is helpful to note that

$$H\left(p\right)=\parallel p\parallel ln\parallel p\parallel -\sum _i{p}_{i}ln\left(p_i\right)$$

(6)

It can then be shown that Equation (5) holds for every morphism f in $\mathtt{FinMeas}$. The additivity and homogeneity axioms follow easily.

4. Faddeev’s Theorem

To prove the hard part of Theorem 2, we use a characterization of entropy given by Faddeev [4] and nicely summarized at the beginning of a paper by Rényi [5]. In order to state this result, it is convenient to write a probability measure on the set $\{1,\cdots ,n\}$ as an n-tuple $p=(p_1,\cdots ,p_n)$. With only mild cosmetic changes, Faddeev’s original result states:

Theorem 5. (Faddeev) Suppose I is a map sending any probability measure on any finite set to a nonnegative real number. Suppose that:

(i) 

I is invariant under bijections.

(ii) 

I is continuous.

(iii) 

For any probability measure p on a set of the form $\{1,\cdots ,n\}$, and any number $0\le t\le 1$,

$$I\left((t{p}_1,(1-t)p_1,p_2,\cdots ,p_n)\right)=I\left((p_1,\cdots ,p_n)\right)+p_{1}I\left((t,1-t)\right)$$

(7)

Then I is a constant nonnegative multiple of Shannon entropy.

In Condition (i) we are using the fact that given a bijection $f:X\to X^{\prime }$ between finite sets and a probability measure on X, there is a unique probability measure on $X^{\prime }$ such that p is measure-preserving; we demand that I takes the same value on both these probability measures. In Condition (ii), we use the standard topology on the simplex

$${\Delta }^{n-1}=\left\{(p_1,\dots ,p_n)\in {\mathbb{R}}^n|p_i\ge 0,\sum _i{p}_i=1\right\}$$

to put a topology on the set of probability distributions on any n-element set.

The most interesting condition in Faddeev’s theorem is (iii). It is known in the literature as the “grouping rule” ([6], Section 2.179)or “recursivity” ([2], Section 1.2.8). It is a special case of “strong additivity” ([2], Section 1.2.6), which already appears in the work of Shannon [1] and Faddeev [4]. Namely, suppose that p is a probability measure on the set $\{1,\cdots ,n\}$. Suppose also that for each $i\in \{1,\dots ,n\}$, we have a probability measure $q\left(i\right)$ on a finite set $X_i$. Then $p_{1}q\left(1\right)\oplus \cdots \oplus p_{n}q\left(n\right)$ is again a probability measure space, and the Shannon entropy of this space is given by the strong additivity formula:

$$H\left(p_{1}q\left(1\right)\oplus \cdots \oplus p_{n}q\left(n\right)\right)=H\left(p\right)+\sum _{i=1}^n{p}_{i}H\left(q\left(i\right)\right)$$

This can easily be verified using the definition of Shannon entropy and elementary properties of the logarithm. Moreover, Condition (iii) in Faddeev’s theorem is equivalent to strong additivity together with the condition that $I\left(\right(1\left)\right)=0$, allowing us to reformulate Faddeev’s theorem as follows:

Theorem 6. Suppose I is a map sending any probability measure on any finite set to a nonnegative real number. Suppose that:

(i) 

I is invariant under bijections.

(ii) 

I is continuous.

(iii) 

$I\left(\right(1\left)\right)=0$, where $\left(1\right)$ is our name for the unique probability measure on the set $\left\{1\right\}$.

(iv) 

For any probability measure p on the set $\{1,\cdots ,n\}$ and probability measures $q\left(1\right),\dots ,q\left(n\right)$ on finite sets, we have

$$I(p_{1}q\left(1\right)\oplus \cdots \oplus p_{n}q\left(n\right))=I\left(p\right)+\sum _{i=1}^n{p}_{i}I\left(q\left(i\right)\right)$$

Then I is a constant nonnegative multiple of Shannon entropy. Conversely, any constant nonnegative multiple of Shannon entropy satisfies Conditions (i)–(iv).

Proof. Since we already know that the multiples of Shannon entropy have all these properties, we just need to check that Conditions (iii) and (iv) imply Faddeev’s equation (7). Take $p=(p_1,\dots ,p_n)$, $q\left(1\right)=(t,1-t)$ and $q\left(i\right)=\left(1\right)$ for $i\ge 2$: then Condition (iv) gives

$$I\left((t{p}_1,(1-t)p_1,p_2,\dots ,p_n)\right)=I\left((p_1,\dots ,p_n)\right)+p_{1}I\left((t,1-t)\right)+\sum _{i=2}^n{p}_{i}I\left(\left(1\right)\right)$$

which by Condition (iii) gives Faddeev’s equation.

It may seem miraculous how the formula

$$I(p_1,\cdots ,p_n)=-c\sum _i{p}_{i}ln{p}_i$$

emerges from the assumptions in either Faddeev’s original Theorem 5 or the equivalent Theorem 6. We can demystify this by describing a key step in Faddeev’s argument, as simplified by Rényi [5]. Suppose I is a function satisfying the assumptions of Faddeev’s result. Let

$$\varphi \left(n\right)=I\left(\frac{1}{n},\cdots ,\frac{1}{n}\right)$$

equal I applied to the uniform probability measure on an n-element set. Since we can write a set with $nm$ elements as a disjoint union of m different n-element sets, Condition (iv) of Theorem 6 implies that

$$\varphi \left(nm\right)=\varphi \left(n\right)+\varphi \left(m\right)$$

The conditions of Faddeev’s theorem also imply

$$\underset{n\to \infty }{lim}(\varphi (n+1)-\varphi \left(n\right))=0$$

and the only solutions of both these equations are

$$\varphi \left(n\right)=clnn$$

This is how the logarithm function enters. Using Condition (iii) of Theorem 5, or equivalently Conditions (iii) and (iv) of Theorem 6, the value of I can be deduced for probability measures p such that each $p_i$ is rational. The result for arbitrary probability measures follows by continuity.

5. Proof of the Main Result

Now we complete the proof of Theorem 2. Assume that F obeys Conditions (i)–(iii) in the statement of this theorem.

Recall that $\left(1\right)$ denotes the set $\left\{1\right\}$ equipped with its unique probability measure. For each object $p\in \mathtt{FinProb}$, there is a unique morphism

$${!}_p:p\to \left(1\right)$$

We can think of this as the map that crushes p down to a point and loses all the information that p had. So, we define the “entropy” of the measure p by

$$I\left(p\right)=F\left({!}_p\right)$$

Given any morphism $f:p\to q$ in $\mathtt{FinProb}$, we have

$${!}_p={!}_q\circ f$$

So, by our assumption that F is functorial,

$$F\left({!}_p\right)=F\left({!}_q\right)+F\left(f\right)$$

or in other words:

$$F\left(f\right)=I\left(p\right)-I\left(q\right)$$

(8)

To conclude the proof, it suffices to show that I is a multiple of Shannon entropy.

We do this by using Theorem 6. Functoriality implies that when a morphism f is invertible, $F\left(f\right)=0$. Together with (8), this gives Condition (i) of Theorem 6. Since ${!}_{\left(1\right)}$ is invertible, it also gives Condition (iii). Condition (ii) is immediate. The real work is checking Condition (iv).

Given a probability measure p on $\{1,\dots ,n\}$ together with probability measures $q\left(1\right),\dots ,q\left(n\right)$ on finite sets $X_1,\dots ,X_n$, respectively, we obtain a probability measure ${⨁}_i{p}_{i}q\left(i\right)$ on the disjoint union of $X_1,\dots ,X_n$. We can also decompose p as a direct sum:

$$p\cong \underset{i}{⨁}{p}_i\left(1\right)$$

(9)

Define a morphism

$$f=\underset{i}{⨁}{p}_i{!}_{q\left(i\right)}:\underset{i}{⨁}{p}_{i}q\left(i\right)\to \underset{i}{⨁}{p}_i\left(1\right)$$

Then by convex linearity and the definition of I,

$$F\left(f\right)=\sum _i{p}_{i}F\left({!}_{q\left(i\right)}\right)=\sum _i{p}_{i}I\left(q\left(i\right)\right)$$

But also

$$F\left(f\right)=I\left(\underset{i}{⨁}{p}_{i}q\left(i\right)\right)-I\left(⨁p_i\left(1\right)\right)=I\left(\underset{i}{⨁}{p}_{i}q\left(i\right)\right)-I\left(p\right)$$

by (8) and (9). Comparing these two expressions for $F\left(f\right)$ gives Condition (iv) of Theorem 6, which completes the proof of Theorem 2.

6. A Characterization of Tsallis Entropy

Since Shannon defined his entropy in 1948, it has been generalized in many ways. Our Theorem 2 can easily be extended to characterize one family of generalizations, the so-called “Tsallis entropies”. For any positive real number α, the Tsallis entropy of order α of a probability measure p on a finite set X is defined as:

$$H_{\alpha }\left(p\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{\alpha -1}\left(1-\sum _{i\in X}{p}_i^{\alpha }\right)}\hfill & \mathrm{if}\alpha \ne 1\hfill \\ {\displaystyle -\sum _{i\in X}{p}_{i}ln{p}_i}\hfill & \mathrm{if}\alpha =1\hfill \end{array}\right.$$

The peculiarly different definition when $\alpha =1$ is explained by the fact that the limit ${lim}_{\alpha \to 1}{H}_{\alpha }\left(p\right)$ exists and equals the Shannon entropy $H\left(p\right)$.

Although these entropies are most often named after Tsallis [7], they and related quantities had been studied by others long before the 1988 paper in which Tsallis first wrote about them. For example, Havrda and Charvát [8] had already introduced a similar formula, adapted to base 2 logarithms, in a 1967 paper in information theory, and in 1982, Patil and Taillie [9] had used $H_{\alpha }$ itself as a measure of biological diversity.

The characterization of Tsallis entropy is exactly the same as that of Shannon entropy except in one respect: in the convex linearity condition, the degree of homogeneity changes from 1 to α.

Theorem 7. Let $\alpha \in (0,\infty )$. Suppose F is any map sending morphisms in $\mathtt{FinProb}$ to numbers in $[0,\infty )$ and obeying these three axioms:

(i) 

Functoriality:

$$F(f\circ g)=F\left(f\right)+F\left(g\right)$$

whenever $f,g$ are composable morphisms.

(ii) 

Compatibility with convex combinations:

$$F(\lambda f\oplus (1-\lambda )g)={\lambda }^{\alpha }F\left(f\right)+{(1-\lambda )}^{\alpha }F\left(g\right)$$

for all morphisms $f,g$ and all $\lambda \in [0,1]$.

(iii) 

Continuity: F is continuous.

Then there exists a constant $c\ge 0$ such that for any morphism $f:p\to q$ in $\mathtt{FinProb}$,

$$F\left(f\right)=c(H_{\alpha }\left(p\right)-H_{\alpha }\left(q\right))$$

where $H_{\alpha }\left(p\right)$ is the order α Tsallis entropy of p. Conversely, for any constant $c\ge 0$, this formula determines a map F obeying Conditions (i)–(iii).

Proof. We use Theorem V.2 of Furuichi [10]. The statement of Furuichi’s theorem is the same as that of Theorem 5 (Faddeev’s theorem), except that Condition (iii) is replaced by

$$I\left((t{p}_1,(1-t)p_1,p_2,\cdots ,p_n)\right)=I\left((p_1,\cdots ,p_n)\right)+p_1^{\alpha }I\left((t,1-t)\right)$$

and Shannon entropy is replaced by Tsallis entropy of order α. The proof of the present theorem is thus the same as that of Theorem 2, except that Faddeev’s theorem is replaced by Furuichi’s. ☐

As in the case of Shannon entropy, this result can be extended to arbitrary measures on finite sets. For this we need to define the Tsallis entropies of an arbitrary measure on a finite set. We do so by requiring that

$$H_{\alpha }\left(\lambda p\right)={\lambda }^{\alpha }{H}_{\alpha }\left(p\right)$$

for all $\lambda \in [0,\infty )$ and all $p\in \mathtt{FinMeas}$. When $\alpha =1$ this is the same as the Shannon entropy, and when $\alpha \ne 1$, we have

$$H_{\alpha }\left(p\right)=\frac{1}{\alpha -1}\left({\left(\sum _{i\in X}{p}_i\right)}^{\alpha }-\sum _{i\in X}{p}_i^{\alpha }\right)$$

(which is analogous to (6)). The following result is the same as Corollary 4 except that, again, the degree of homogeneity changes from 1 to α.

Corollary 8. Let $\alpha \in (0,\infty )$. Suppose F is any map sending morphisms in $\mathtt{FinMeas}$ to numbers in $[0,\infty )$, and obeying these four properties:

(i) 

Functoriality:

$$F(f\circ g)=F\left(f\right)+F\left(g\right)$$

whenever $f,g$ are composable morphisms.

(ii) 

Additivity:

$$F(f\oplus g)=F\left(f\right)+F\left(g\right)$$

for all morphisms $f,g$.

(iii) 

Homogeneity of degree:

$$F\left(\lambda f\right)={\lambda }^{\alpha }F\left(f\right)$$

for all morphisms f and all $\lambda \in [0,\infty )$.

(iv) 

Continuity: F is continuous.

Then there exists a constant $c\ge 0$ such that for any morphism $f:p\to q$ in $\mathtt{FinMeas}$,

$$F\left(f\right)=c(H_{\alpha }\left(p\right)-H_{\alpha }\left(q\right))$$

where $H_{\alpha }$ is the Tsallis entropy of order α. Conversely, for any constant $c\ge 0$, this formula determines a map F obeying Conditions (i)–(iv).

Proof. This follows from Theorem 7 in just the same way that Corollary 4 follows from Theorem 2. ☐