1. Introduction
Mesh simplification is the process of reducing the number of polygons used in the surface while keeping the overall shape, volume and boundaries preserved as much as possible (see
Figure 1). This reduction is necessary when complex three-dimensional scenes are required, that is, where a high geometric complexity is managed because geometry can lead to bottlenecks. Simplification techniques reduce the load on the graphics processing unit or GPU.
Figure 1.
Simplification example. (a) Original Model. 49694 triangles. (b) Model simplified to 12% with our algorithm using TVMI (). 6285 triangles.
Figure 1.
Simplification example. (a) Original Model. 49694 triangles. (b) Model simplified to 12% with our algorithm using TVMI (). 6285 triangles.
Simplification methods make use of a simplification operation and an error metric. The simplification operation gives the way in which geometry will be removed, while the error metric establishes the order in which the simplification steps will be performed.
Different criteria have been used for the purpose of simplifying polygonal meshes. The first simplification methods only considered the geometric information of the objects to establish the simplification order. These methods are fast and normally produce simplified objects with a good geometric closeness, which is suitable for some applications such as CAD/CAM, collision detection, and mesh signal processing. However, the most common use of simplification is to produce a model that is visually similar to the original. This is crucial for applications such as vehicle simulations, architectural walkthroughs, virtual reality and visualization. During the last years, methods that take visual information into account have also appeared. These methods increase simplification in those parts of the objects that are not visible for the user. They consider not only geometric properties of the models, but also visual aspects in the scene. Visual methods are usually slower than geometry-based methods. Most visual methods often work by locating several cameras around the object in order to preserve the most visually relevant areas. Many articles about simplification techniques have appeared in the literature, some surveys can be found in [
1,
2]. Recently, theoretic information measures, such as entropy and mutual information, have been applied for simplifying polygonal meshes [
3,
4]. These measures capture the information about the structure of the mesh. This approach has proven to lead to very good results in visual simplification. Others visual methods in the literature such as [
5,
6] also indirectly preserve some structural information, but that is not their main goal. Other more accurate measures designed to measure the structure of the mesh could improve the results of existing visual methods.
In this paper, we present a study and a comparison of the use of different information-theoretic measures for polygonal mesh simplification. The discrete entropy and mutual information [
7] and their Havrda–Charvát–Tsallis generalizations [
8,
9] have been applied to mesh simplification. We demonstrate that these measures are useful for simplifying three-dimensional polygonal meshes. In addition, we compare the results obtained with different parameters of these generalized formulas and with other simplifications from the geometry-based method presented in [
10] and from the image-based method presented in [
5] using its metric. We also present a qualitative comparison using the root-mean-square error (RMSE). We must emphasize that the use of the information-theoretic measures analyzed in this paper produces a better preservation of the structural appearance of the models. The visual simplification approach by Lindstrom and Turk [
5] only considers a pixel-to-pixel error which may suffer from problems in translation, rotation or scaling of the images. This method preserves some structural information but we show in this work that our measures designed to measure that information are able to outperform its results.
We have extended the viewpoint-driven simplification approach [
4,
11] in order to include those generalized information-theoretic measures. This simplification method uses the edge collapse operation as the simplification operation. In order to measure the error committed by a decimation operation, this approach uses a set of cameras regularly distributed surrounding the object. This error will give the associated cost to each edge of the object. This will establish the simplification order. The edge collapse operation is a simplification operation that removes an edge returning a vertex at each simplification step. All the neighboring triangles must be retriangulated after this operation in order to avoid the appearance of holes.
The remainder of this paper is organized as follows.
Section 2 reviews some related work in mesh simplification and in viewpoint information measures. In
Section 3, we review the viewpoint-driven simplification approach and extend the framework with new viewpoint information measures based on Tsallis entropy.
Section 4 shows the results of our experiments and a comparison with a geometry-based simplification method. Finally, in
Section 5 we summarize our work and propose some future work.
3. Simplification Algorithm
In this section, we review the viewpoint-driven approach [
4,
11] and extend its simplification algorithm to include new measures based on Tsallis Entropy [
9,
25]. The main idea of our approach is to define a function that measures the difference of information captured by a set of viewpoints before and after a simplification operation. The simplification operation reduces the complexity of the model by removing an item of the mesh. This difference of information will give us the cost of the simplification operation.
To reduce the complexity of a model, the algorithm uses the edge collapse operation. There are two slightly different edge collapse operations. One is known as
edge collapse while the other is known as
half edge collapse. Given an edge
e joining vertices
u and
v, the edge collapse operation replaces
e,
u and
v for a new vertex
r, while the half edge collapse operation pulls
v into
u, disappearing
e and leaving
u in place. In both cases the operation removes the edge
e along with the two polygons adjacent to it (see
Figure 2).
Figure 2.
The two possible half edge collapses for the edge highlighted with a thicker line. Triangles in grey will be removed.
Figure 2.
The two possible half edge collapses for the edge highlighted with a thicker line. Triangles in grey will be removed.
Naturally, the surface that results from an edge collapse deviates from the initial surface by some amount, and since the goal of simplification is to reduce the number of polygons while retaining the overall look of the surface as much as possible, it is necessary to measure such a deviation. Some methods attempt to measure the total deviation from the initial surface to the completely simplified surface, for example, by tracking an accumulated error while keeping a history of the simplification changes. Other methods attempt to measure only the cost of each individual edge collapse (the local deviation introduced by a single simplification step) and plan the entire process as a sequence of steps of increasing cost [
4,
10,
11,
13,
14,
17].
This iterative algorithm proceeds in two stages. In the first stage, an initial collapse cost is assigned to each and every edge in the surface. Then in the second stage, edges are processed in order of increasing cost. Collapsed edges are replaced by a vertex and the collapse cost of all the edges now incident on the replacement vertex is recalculated, affecting the order of the remaining unprocessed edges. Not all edges selected for processing are collapsed. Some can be discarded right away if they do not satisfy certain topological and geometric conditions. Brute force selection of edges can introduce mesh inconsistencies. To avoid artifacts, we consider 2-manifold edges,
i.e., edges that have at most two adjacent polygons, and boundary edges,
i.e., edges having one single adjacent polygon. At each step, all remaining edges are potential candidates for collapsing and the one with the lowest cost is selected. The algorithm maintains an internal data structure (a priority queue) which allows each edge to be processed in increasing cost order. After applying an edge collapse, the remaining edges that should be recalculated are simply marked as dirty. In the next iteration, if the edge extracted from the heap is dirty, it is simply discarded. Then, its cost is recomputed and it is inserted again into the heap. This heuristic was introduced in [
26] to avoid unnecessary edge collapse costs.
Given an edge collapse
, note that the cost of collapsing vertex
u to
v may be different than the cost of collapsing
v to
u. To determine the best half edge collapse, the algorithm would need to render both possibilities and compute their error. But this penalizes the temporal cost due to the number of framebuffer readings needed to get the projected areas of the polygons of the model. To avoid this, the approach by Melax [
27] which considers polygon normals is followed. Before rendering the model, the two different half edge collapses,
and
, are performed and the change in curvature around the local region is measured. Finally, the half edge collapse that produces a minor change in curvature is applied. Then, the simplification deviation is computed only for that half edge collapse. The algorithm ends when it reaches the desired number of polygons.
The cost of a simplification operation in the algorithm is determined by the chosen error metric. In the next section, we introduce two new error metrics used to measure the cost of a simplification operation.
3.1. Error Metrics
Recently, viewpoint entropy and viewpoint mutual information have been applied to polygonal simplification [
3,
11]. As it has been shown, both measures are sensitive to the variation of the projected area distribution of the polygons and, thus, are useful to evaluate the visual distortion degree caused by the simplification process. Now, we introduce two new generalizations for viewpoint entropy and viewpoint mutual information based on Tsallis entropy [
9,
25], viewpoint T-entropy and viewpoint T-mutual information.
3.1.1. Viewpoint Generalized Entropy
Rényi [
28] and Havrda and Charvát [
8] introduced, respectively, two different forms of generalized entropies. In both cases, the Shannon entropy is a particular case of these generalized entropies when the entropic index is equal to 1. We consider here the so-called Tsallis entropy to define the viewpoint generalized entropy.
Given a random variable
X with alphabet
and probability distribution
, the T-entropy is defined by
where the parameter
α is called entropic index. The T-entropy recovers the Shannon entropy, calculated using natural logarithms, when
.
We define the viewpoint T-entropy (TVE) for a set of viewpoints V and the set of polygons Z as
where
Z is the random variable that represents the set of polygons
,
is the number of polygons and
(where
is the area of the polygon
i projected over the sphere of directions,
represents the projected area of the background in open scenes, and
is the total projected area of all the polygons over the sphere of directions). Maximum entropy is also obtained when a certain viewpoint can see all the polygons with the same projected area. For extension, the best viewpoint can also be defined as the one that has maximum entropy.
As a conclusion, both Shannon and generalized viewpoint entropies quantify the uniformity of the distribution of the projected polygons. These measures essentially depend on both the number of polygons seen from a viewpoint and the balance of the projected distribution of these polygons. In general, entropy increases with both the number of polygons and the degree of uniformity of the projected distribution of polygons, and decreases in the contrary case.
3.1.2. Viewpoint Generalized Mutual Information
From the Tsallis mutual information introduced by Taneja [
29] and Tsallis [
25], we will define the viewpoint generalized mutual information.
The Tsallis mutual information
between two discrete random variables
X and
Y (with alphabets
,
, probability distributions
,
, and joint distribution
) is defined as
where
α is the entropic index.
From this equation, the T-mutual information between
V and
Z is defined by
where
is the viewpoint T-mutual information (TVMI). This definition recovers VMI when
.
As we have seen, the Tsallis information measures introduced in this section represent an extension of the Shannon information measures, since these are included as particular cases. The sensitivity of the Tsallis information measures for polygonal simplification can be evaluated by modifying the parameter α. This parameter allows us to adjust the T-entropy and the T-mutual information so that these measures maximally capture the distortion produced by the polygonal simplification.
3.2. Edge Collapse Cost
Given an object and a set of viewpoints, TVMI and TVE express the accessible information about the object from a given viewpoint
v. The variation in any of those measures for each viewpoint can provide us with an error metric to guide the simplification process. Therefore, the
simplification error deviation for an edge collapse
e from all viewpoints
V is defined by
where
represents either viewpoint T-mutual information (TVMI) or viewpoint T-entropy (TVE) before edge collapse
e and
afterward.
3.3. Implementation Issues
Both TVMI and TVE can be calculated iteratively. We can benefit from this property to speed up their calculation. Our measures are computed from the projected areas of the polygons of the model. In order to compute the projected areas of the polygons of the model from a viewpoint
v we render the model and perform a pixel-to-pixel analysis, this means that the bottleneck in our algorithm mainly resides in the memory transfer cost. The model is rendered using OpenGL’s
vertex buffer object and
framebuffer object extensions. To reduce this overload, instead of analyzing the whole image, we restrict the area of reading to a small window that only includes the polygons adjacent the edge collapse. To obtain this window, first the bounding box of the edge collapse is determined and then projected onto the screen. This method reduces the temporal cost, but may lead to some slight loss of quality, because after an edge collapse some hidden polygons might appear and their contribution to the formula was not measured [
4,
11]. The background is considered to be another polygon, and thus the total projected area is always the image resolution. Moreover, only a few polygons change after an edge collapse. Therefore, either TVMI or TVE can be computed at the beginning of the simplification process for the entire object and then their initial values can be successively updated. This feature was exploited in our current implementation.
Edge collapse
e with the lowest deviation
(
10) is chosen at every simplification step. It is important to determine several parameters such as the number of viewpoints and image resolution, since the quality of the results may change. We performed measurements with 20 regularly distributed viewpoints and rendered 256 × 256 resolution images. More viewpoints can increase quality, but also significantly raise the temporal cost [
4,
11].
At each step, in principle, the collapse cost should be evaluated for the entire set of remaining edges. But not every edge collapse has to affect all the remaining edges. So, we only choose a small group of edges surrounding the edge collapse to recalculate their cost. These edges are the ones that are adjacent to the vertices adjacent to the vertex
v resulting from a half-edge collapse. If the whole set of edges of the model is considered the temporal cost is increased considerably, but the results are not clearly better [
4,
11].
4. Results and Discussion
We show the results of our experiments carried out with four models, the Galo, the Skull, the Brush and the Junk. The Skull, Brush and Junk belong to the De Espona 3D Models Collection for 3DS Max [
30]. We compared our results with those obtained with QSlim [
10,
17] a well-known algorithm for surface simplification, which is freely available at [
31]. The QSlim algorithm is a technique for surface simplification based on a quadric error metric for measuring vertex-to-plane distances. Its error metric is related to curvature. In this paper we used the latest QSlim version 2.1. In addition, we compared our results with our implementation of the image-driven simplification approach (IDS) [
5]. This algorithm is a surface simplification algorithm which tries to produce approximation according to visual similarity, not to geometric similarity as in the QSlim algorithm. The image-driven simplification approach guides the simplification process by the root mean square error (RMSE), a per-pixel-difference image metric. For IDS we used the same parameters used in TVMI and TVE, that is, 20 viewpoints, 256 × 256 images and the half edge collapse as the decimation operation. We render the images for IDS during the simplification in flat (per triangle) shading. We did not presimplify the models using a geometric simplification technique (for instance, the geometry-driven “memoryless” method [
13,
14]) prior to using IDS as the authors carried out in their experiments. Instead, we directly simplified the original models using our own implementation of IDS without a previous simplification stage. In order to determine the visual quality of the approximations we also used RMSE between a set of multiple images of the original and the simplified model taken from a sphere of camera positions. This time, we used the 24 vertices of the small rhombicuboctahedron as camera positions, 512 × 512 images and flat shading. Both the resolution and the position and number of cameras were deliberately different from the configuration used in our simplification algorithm to perform a more accurate comparison. The RMSE metric does not reflect well how the differences between two images are perceived. A metric that considers how the human visual system (HVS) works, that is, a perceptually motivated metric would be more appropriate for mesh simplification. We think that this would be a relevant area for future research. In our simplification method (TVE and TVMI) we used the vertices of a regular dodecahedron (20 viewpoints) and 256 × 256 images. All tests were run on a Mac Pro Intel Xeon 2.8 GHz CPU with 4 GB of RAM and an NVIDIA 8800GT 512 MB GPU under Windows Vista SP2.
Table 1 illustrates the visual error measured with RMSE and the simplification time for the three models tested. Clearly both TVMI and TVE achieve better results in visual quality than the geometric approach (QSlim). Moreover, both TVMI and TVE improve the results of the IDS algorithm. In case of the Junk model, we obtain an improvement over QSlim about 30% and 21% over IDS. The QSlim algorithm is faster than our simplification method. In fact, QSlim is one of the fastest surface simplification techniques in the literature. However, QSlim’s metric is purely geometric and does not take into account the visibility of the models. In general, geometric simplification methods are quite faster than those based on some kind of measure of visibility. Nevertheless, simplification is an off-line preprocessing often carried out only once. Hence, simplification times are not so relevant as the final quality of the approximations. IDS shows simplification times similar to TVMI and TVE. The difference in visual quality between TVMI and TVE was very little in our tests. TVE accomplished the best results in the Skull and the Junk models but the difference was around 1%. Viewpoint entropy tends to balance the area of the polygons that remain after an edge collapse operation. In principle, this may be more adequate for models that have polygons of the same size with very few flat regions. Viewpoint mutual information considers the mean visibility of the polygons from the set of viewpoints and usually improves the results of viewpoint entropy when a model has many flat regions, because it is capable of increasing the simplification in those regions more than viewpoint entropy. In the Brush model, TVMI achieved better results than TVE because the model has many flat regions.
Table 1.
Visual error (RMSE) and simplification time (seconds) for all models simplified with QSlim, IDS, TVE and TVMI.
Table 1.
Visual error (RMSE) and simplification time (seconds) for all models simplified with QSlim, IDS, TVE and TVMI.
| Model | Triangles | QSlim | IDS | TVE | TVMI |
|---|
| Original | Final | RMSE | Time | RMSE | Time | α | RMSE | Time | α | RMSE | Time |
|---|
| Galo | 6592 | 600 | 11.82 | 0.07 | 8.65 | 162.44 | 1.5 | 7.53 | 271.26 | 0.5 | 7.88 | 296.97 |
| Skull | 9934 | 1784 | 11.06 | 0.08 | 11.05 | 360.78 | 1 | 10.31 | 285.80 | 0.5 | 10.37 | 343.74 |
| Brush | 20698 | 1200 | 15.49 | 0.11 | 14.86 | 863.13 | 1 | 13.56 | 683.75 | 0.5 | 13.47 | 822.36 |
| Junk | 61242 | 6212 | 13.66 | 0.50 | 11.73 | 2436.04 | 1 | 10.58 | 1929.76 | 0.5 | 10.73 | 2320.98 |
Figure 3 shows the results for the Galo model. As shown in this figure, TVE, TVMI and IDS achieve better visual results than QSlim. Clearly, the comb and tale are retained better with TVE, TVMI and IDS than with QSlim. Besides, the silhouette of the model is preserved better in both TVE and TVMI than in IDS. TVE maintains the wattle better than TVMI reducing slightly the visual error.
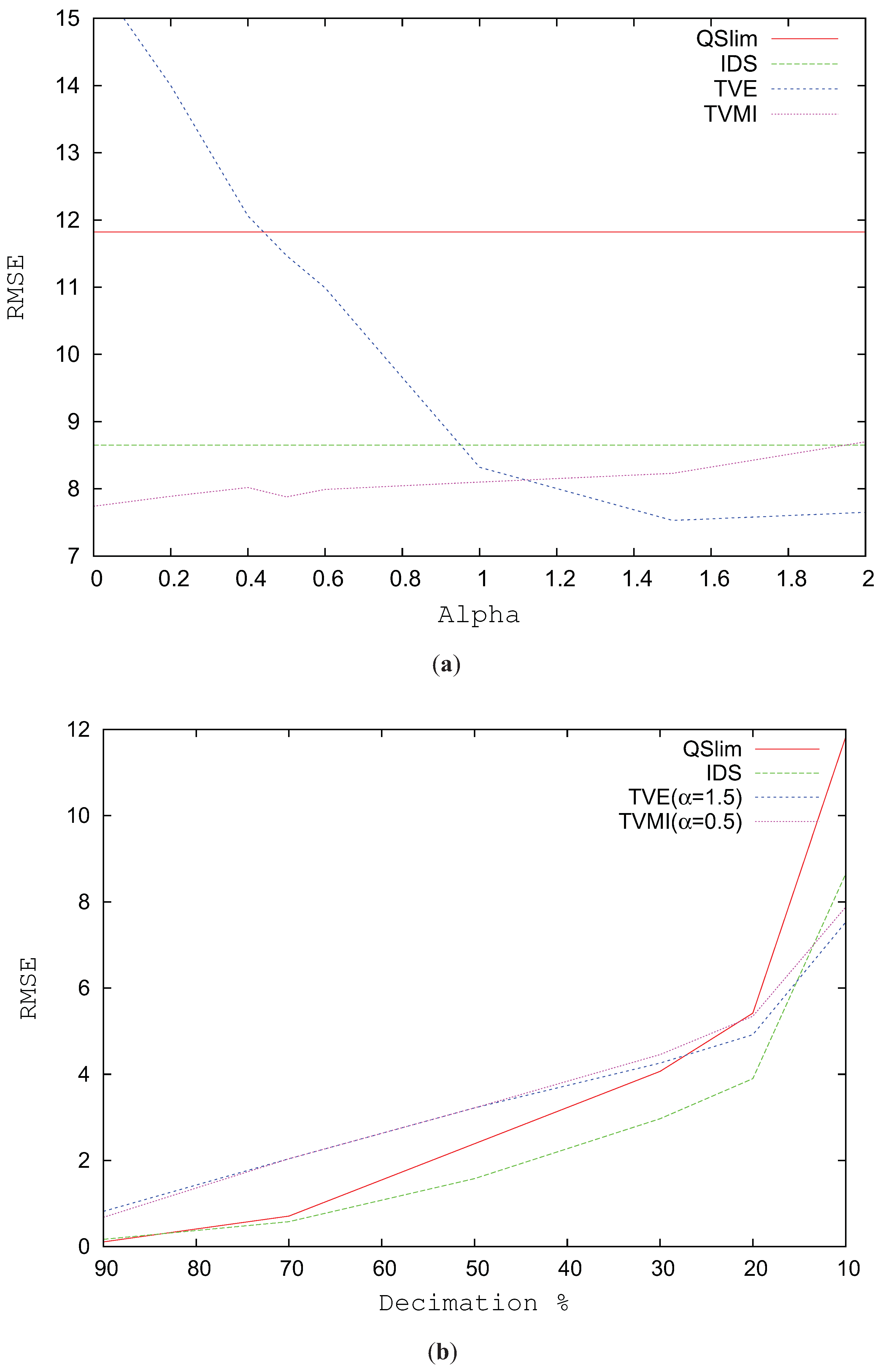
Figure 4a analyzes the RMSE for the Galo model simplified to 600 triangles using alpha values between 0 and 2. The best results for TVMI in this model are obtained when
and for TVE when
. TVE slightly improves the results of TVMI (around 4%). In the case of TVE, alpha values less than 1 considerably increase the visual error. However, TVE with
accomplishes an improvement (around 10%) over TVE with
.
Figure 4b analyzes the RMSE for the Galo model progressively changing the level of simplification. As depicted in this figure, the great enhancement comes when the model complexity is reduced over 20%. For values from 90% to 30%, that is, the model is not very simplified, IDS and QSlim show better values in visual similarity than TVMI and TVE. However, over 20% both TVE and TVMI clearly improve the results of IDS and QSlim.
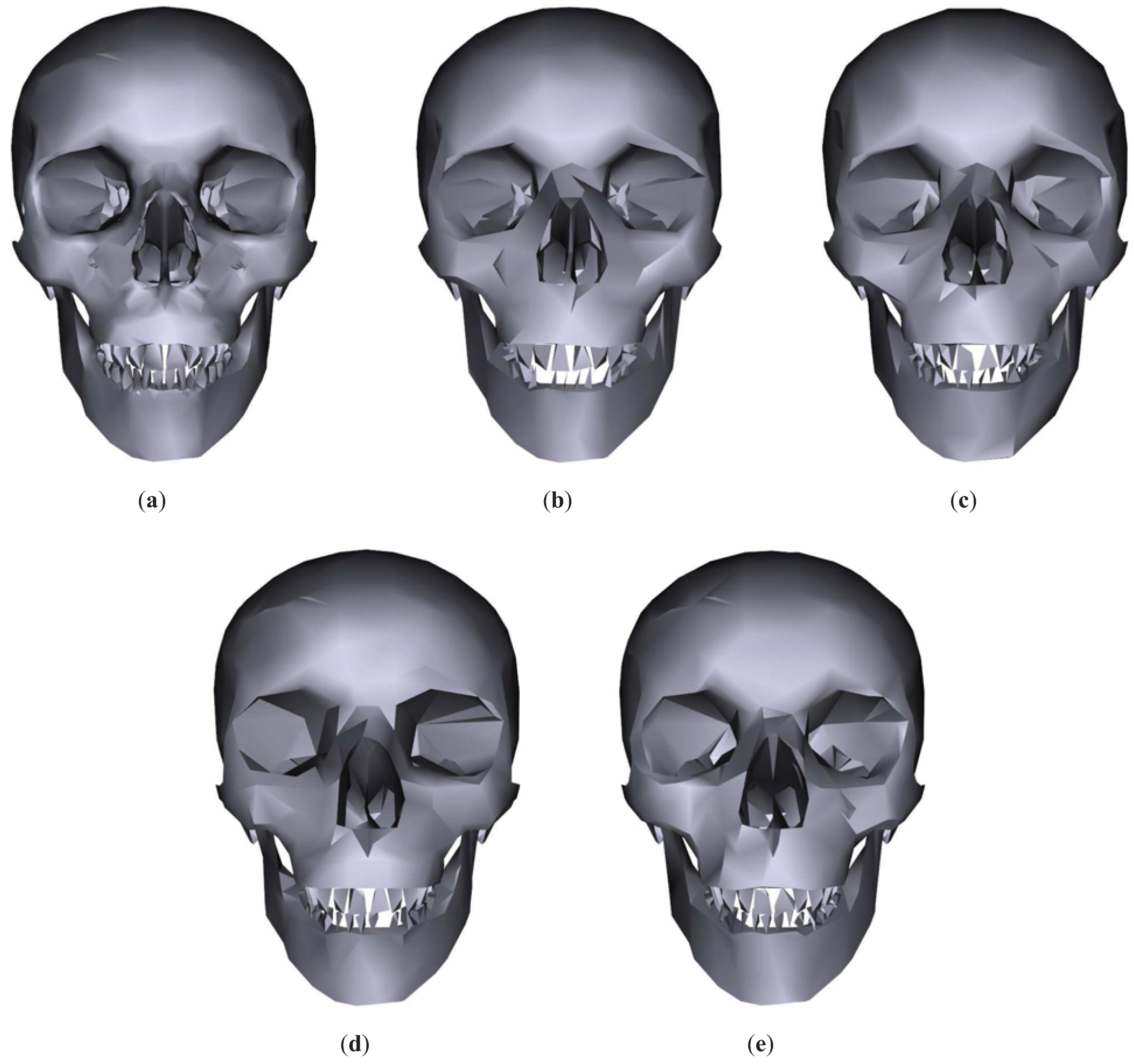
Figure 5 shows the results for the Skull model. As shown in this figure, TVMI, IDS and TVE achieve better visual results than QSlim. Specially, it can be appreciated (see
Figure 6) that the teeth are retained better with TVMI, IDS and TVE than with QSlim. As pointed out earlier, our simplification technique considers the visibility of the polygons, and the mouth region in the Skull model has a great impact on visibility. Also, we can see that the silhouette of the model is preserved better in both TVMI and TVE than in IDS. In fact, this is one of the reasons why IDS shows a similar global quality than QSlim, although as shown in
Figure 6, IDS has lower error in the teeth region than QSlim.
Figure 3.
Galo model. (a) Original model. T = 6592. (b) QSlim. T = 600. (c) IDS. T = 600. (d) TVE(). T = 600. (e) TVMI(). T = 600. T indicates the number of triangles. Different approximations of Galo model obtained with QSlim, IDS, TVE and TVMI. The original model is shown in (a). TVE and TVMI preserve the comb and tail better than QSlim and IDS.
Figure 3.
Galo model. (a) Original model. T = 6592. (b) QSlim. T = 600. (c) IDS. T = 600. (d) TVE(). T = 600. (e) TVMI(). T = 600. T indicates the number of triangles. Different approximations of Galo model obtained with QSlim, IDS, TVE and TVMI. The original model is shown in (a). TVE and TVMI preserve the comb and tail better than QSlim and IDS.
Figure 4.
RMSE for Galo model. (a) RMSE vs. different alpha values. T = 600. (b) Decimation %. High percentage values indicate that the model has been simplified slightly. Low values correspond to a very coarse model.
Figure 4.
RMSE for Galo model. (a) RMSE vs. different alpha values. T = 600. (b) Decimation %. High percentage values indicate that the model has been simplified slightly. Low values correspond to a very coarse model.
Figure 5.
Skull model. (a) Original model. T = 9934. (b) QSlim. T = 1784. (c) IDS. T = 1784. (d) TVE (). T = 1783. (e) TVMI (). T = 1784. Different approximations of Skull model obtained with QSlim, IDS, TVE and TVMI. The original model is shown in (a).
Figure 5.
Skull model. (a) Original model. T = 9934. (b) QSlim. T = 1784. (c) IDS. T = 1784. (d) TVE (). T = 1783. (e) TVMI (). T = 1784. Different approximations of Skull model obtained with QSlim, IDS, TVE and TVMI. The original model is shown in (a).
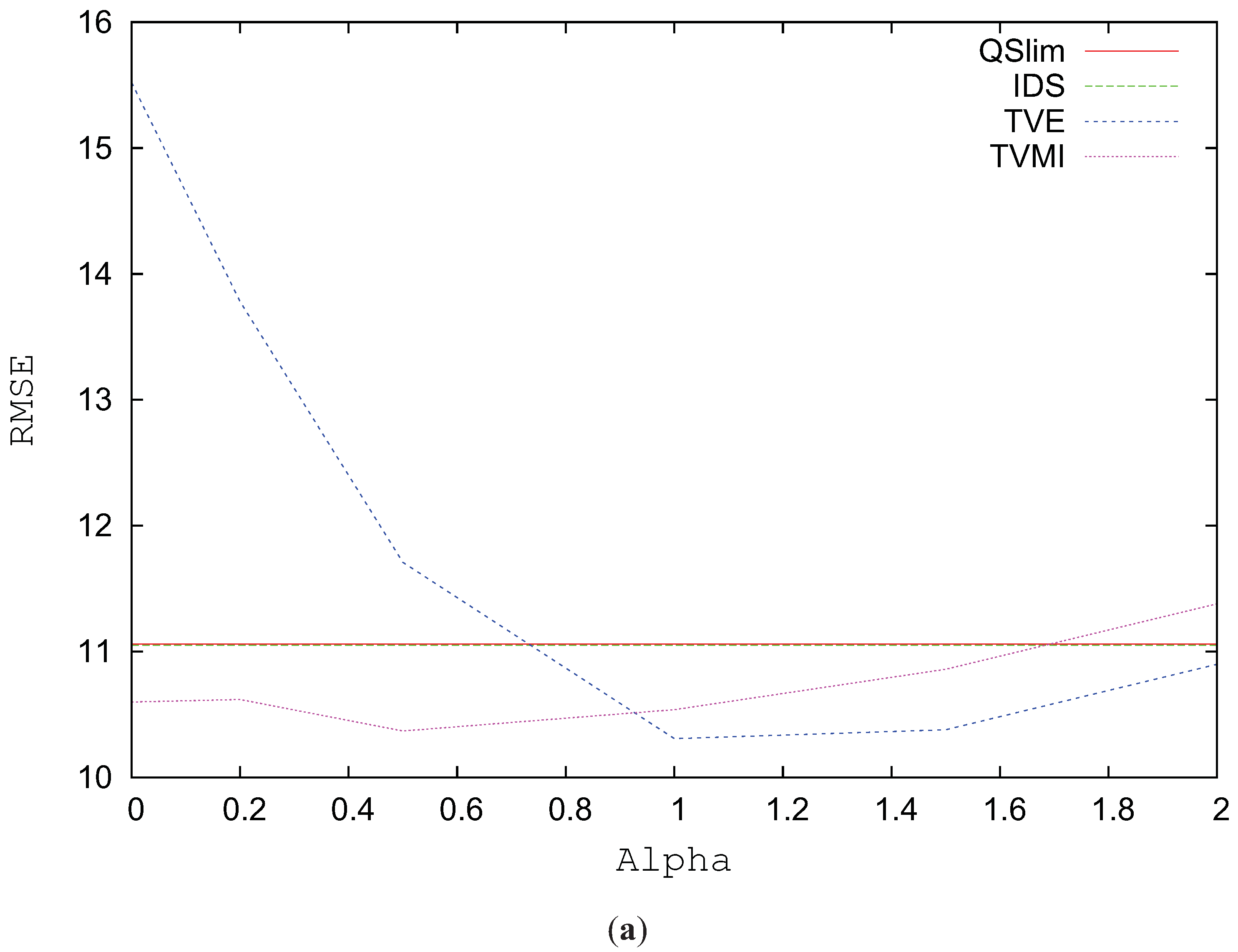
Figure 7a analyzes the RMSE for the Skull model simplified to 1784 triangles using alpha values between 0 and 2. The best results for TVMI in this model are obtained when
and for TVE when
. In the case of TVE, lower values for alpha considerably increase the visual error. However, TVMI with
accomplished and improvement (around 2%) over TVMI with
.
Figure 7b analyzes the RMSE for the Skull model progressively changing the level of simplification. As depicted in this figure, the true enhancement comes when the model complexity is reduced over 40%. For values from 90% to 40%, that is, the model is not very simplified, QSlim shows similar values in visual similarity than TVMI, TVE and IDS.
Figure 6.
Close-ups of Skull model. (a) Original model. (b) QSlim. T = 1784. RMSE = 47.58. (c) IDS. T = 1784. RMSE = 42.05. (d) TVE (). T = 1783. RMSE = 42.53. (e) TVMI (). T = 1784. RMSE = 40.24. These images show that the region around the mouth, especially the teeth in the lower junk, is preserved better in TVMI, IDS and TVE than in QSlim. In the bottom row, difference images are shown. These difference images were produced by superimposing the simplified image over the original image. Here black signifies no difference, while red corresponds to maximum difference.
Figure 6.
Close-ups of Skull model. (a) Original model. (b) QSlim. T = 1784. RMSE = 47.58. (c) IDS. T = 1784. RMSE = 42.05. (d) TVE (). T = 1783. RMSE = 42.53. (e) TVMI (). T = 1784. RMSE = 40.24. These images show that the region around the mouth, especially the teeth in the lower junk, is preserved better in TVMI, IDS and TVE than in QSlim. In the bottom row, difference images are shown. These difference images were produced by superimposing the simplified image over the original image. Here black signifies no difference, while red corresponds to maximum difference.
Figure 7.
RMSE for Skull model. (a) RMSE vs. different alpha values. T = 1784. (b) Decimation %.
Figure 7.
RMSE for Skull model. (a) RMSE vs. different alpha values. T = 1784. (b) Decimation %.
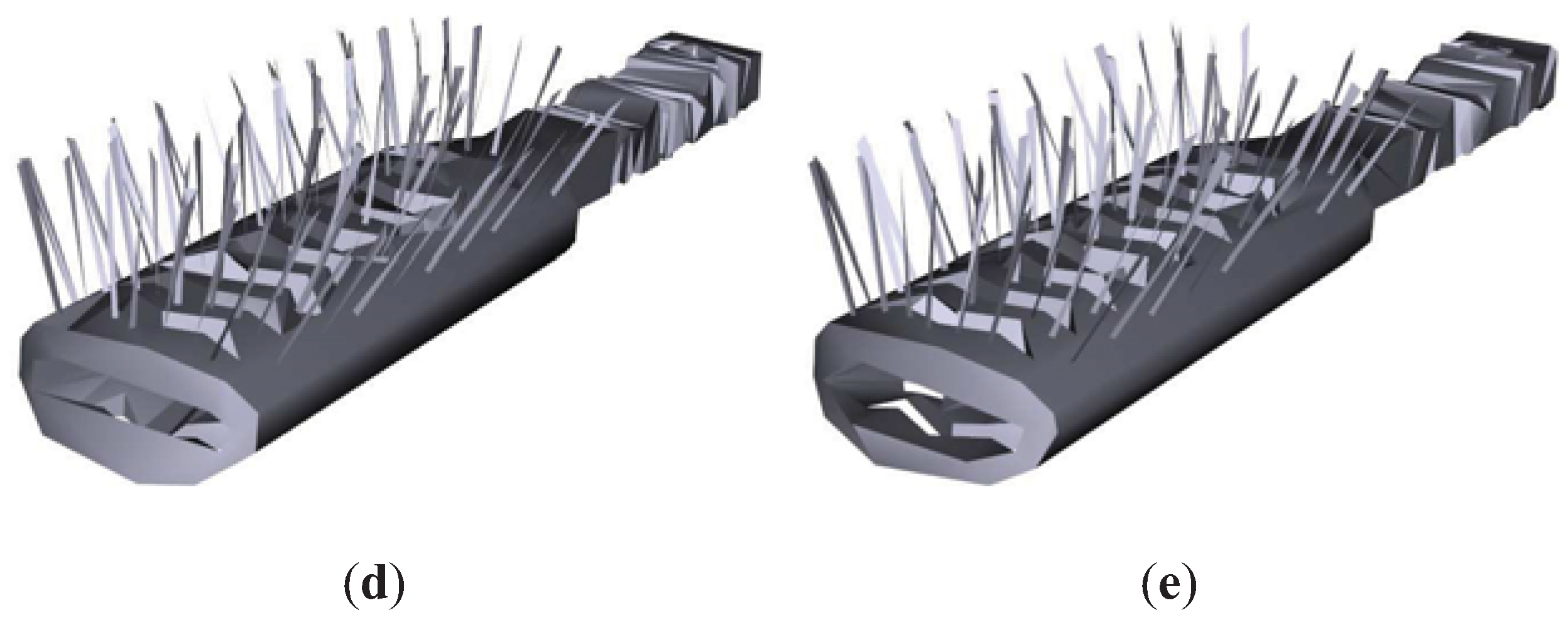
Figure 8 shows the results for the Brush model. As can be appreciated, TVMI, IDS and TVE achieve better visual results than QSlim. TVMI, IDS and TVE are able to retain the brush pins better than QSlim. As we mentioned earlier, QSlim does not consider the visibility of the model, thus it fails in the pins. Logically, other regions that have less visibility are preserved better in QSlim than in IDS, TVE and TVMI, for instance, the brush handle. Both TVE and TVMI achieve better visual results than IDS because they maintain more pins in the brush.
Figure 8.
Brush model. (a) Original model. T = 20698. (b) QSlim. T = 1200. (c) IDS. T = 1199. (d) TVE (). T = 1199. (e) TVMI (). T = 1199. Different approximations of Brush model obtained with QSlim, IDS, TVE and TVMI. The original model is shown in (a). The results show that our measures (TVE and TVMI) are capable of retaining more polygons in the brush pins than IDS and QSlim.
Figure 8.
Brush model. (a) Original model. T = 20698. (b) QSlim. T = 1200. (c) IDS. T = 1199. (d) TVE (). T = 1199. (e) TVMI (). T = 1199. Different approximations of Brush model obtained with QSlim, IDS, TVE and TVMI. The original model is shown in (a). The results show that our measures (TVE and TVMI) are capable of retaining more polygons in the brush pins than IDS and QSlim.
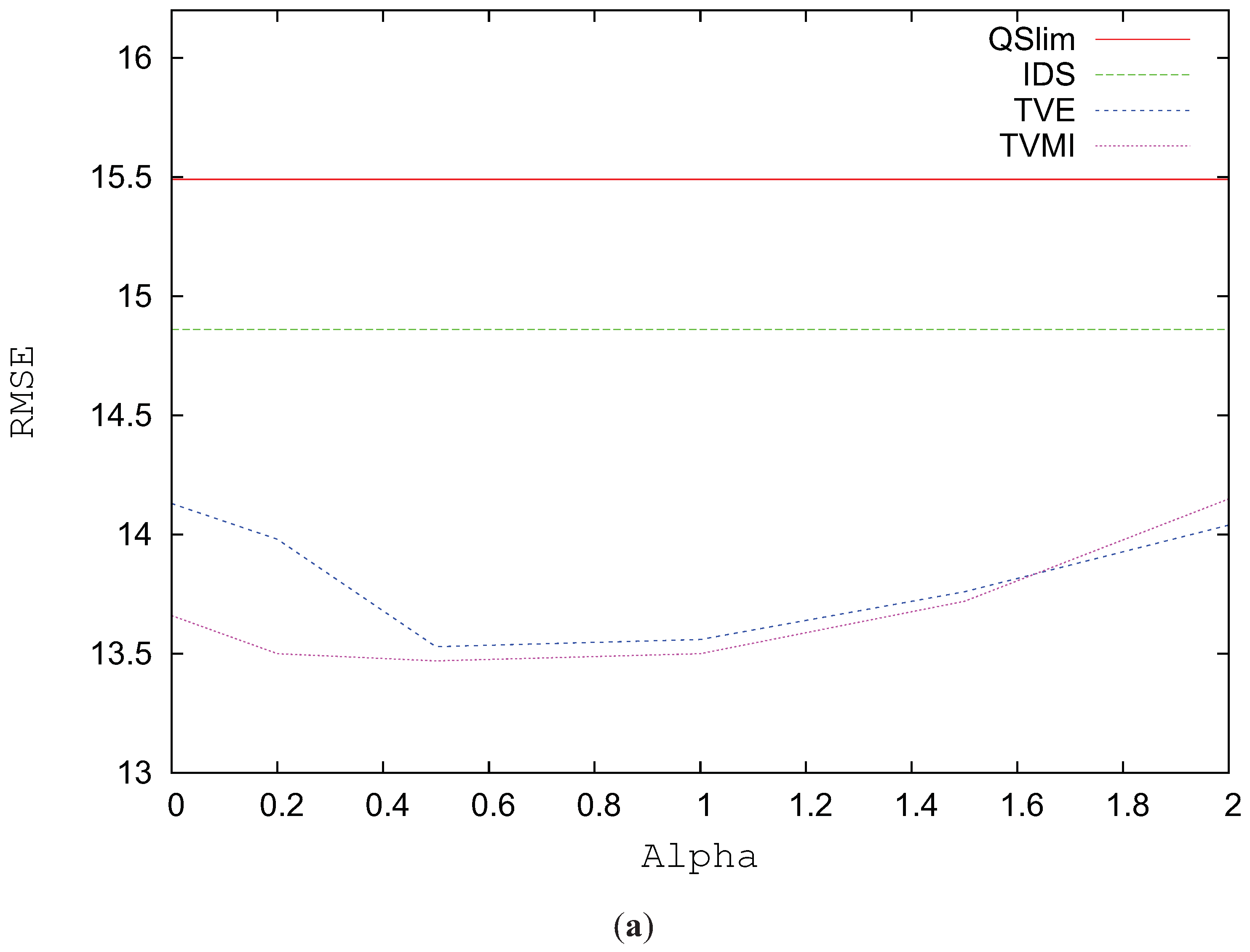
Figure 9a depicts the RMSE for the Brush model simplified to 1200 triangles using alpha values between 0 and 2. The best visual results in this model are obtained when
for both TVE and TVMI. In the case of TVE, lower values for alpha considerably increase the visual error. In this model TVMI achieves an improvement around 1% over VMI (TVMI (
)) and TVE, and around 1% over VE (TVE (
)). The difference in visual quality between TVE and TVMI is very little in this model (about %1).
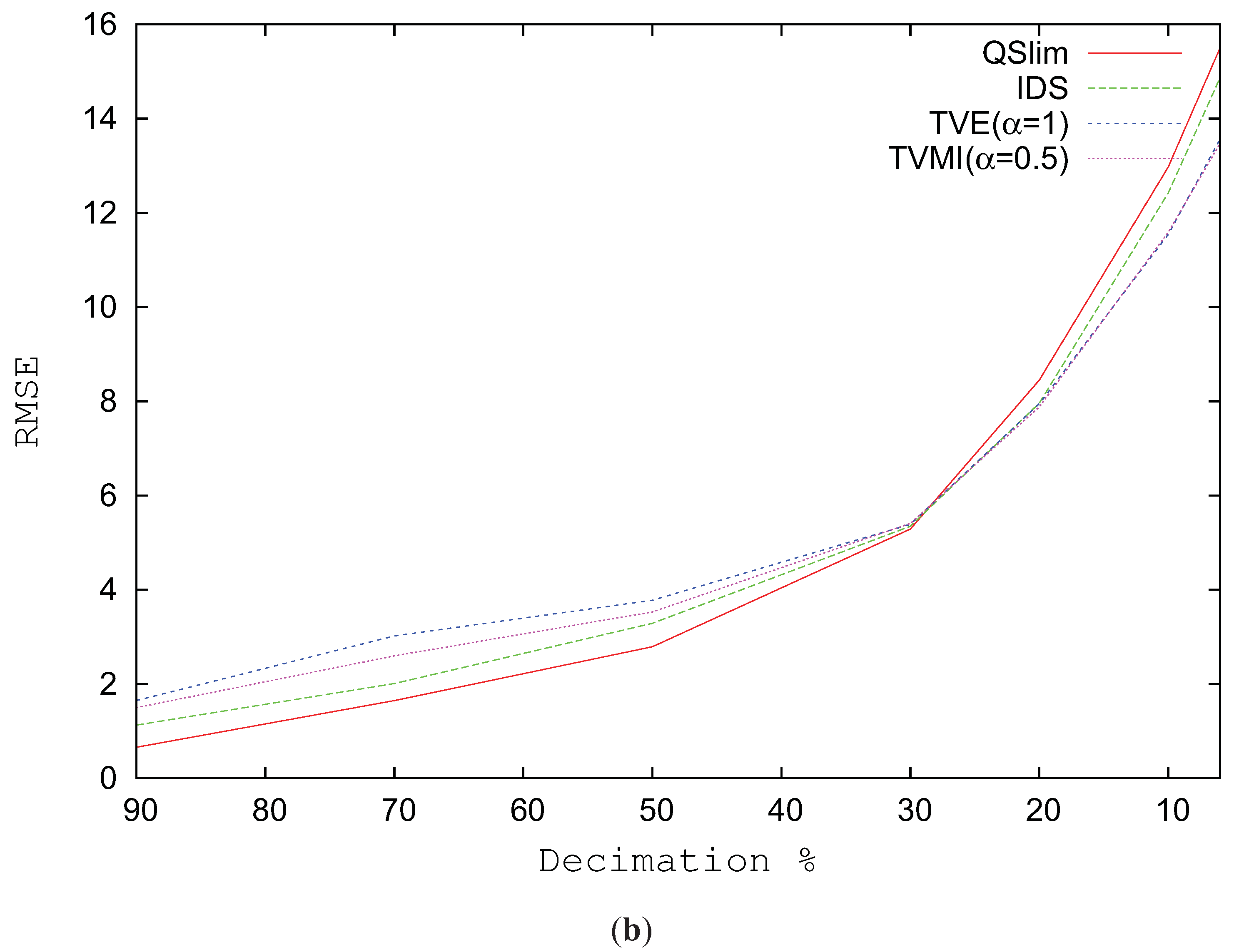
Figure 9b depicts the RMSE for the Brush model progressively changing the level of simplification. The real improvement in visual similarity comes when the model complexity is reduced over 30%. When the model is not very simplified, QSlim shows better values in visual quality than TVMI, TVE and IDS.
Figure 9.
RMSE for Brush model. (a) RMSE vs. different alpha values. T = 1200. (b) Decimation %.
Figure 9.
RMSE for Brush model. (a) RMSE vs. different alpha values. T = 1200. (b) Decimation %.
Figure 10 shows the results for the Junk model. Both TVE and TVMI achieve the best visual results. TVMI, TVE and IDS were able to retain many ropes, whereas QSlim could not. Nevertheless, QSlim preserves the ship’s sails better than IDS. We measured RMSE in
Figure 10b (QSlim) was
and in
Figure 10c (IDS) was
. This means that for this particular view, QSlim accomplished better visual results than IDS, although the global RMSE for the model is lower in IDS than QSlim (see
Table 1).
Figure 11 shows some close-ups of the ship’s bow, clearly we can see that TVMI and TVE obtained the best results. QSlim and IDS present more red regions than TVMI and TVE. The red pixels indicate visual error in the image.
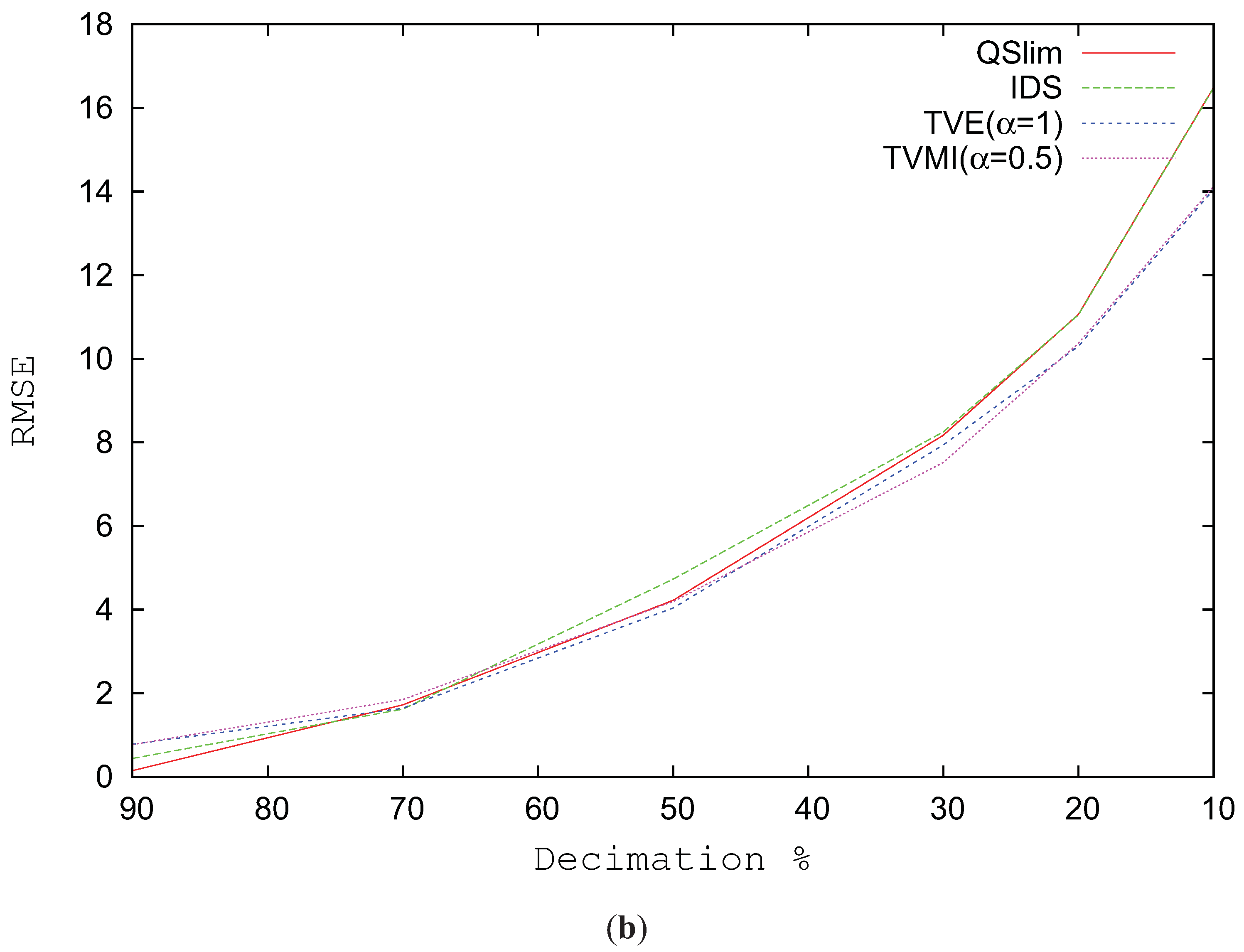
Figure 12a depicts the RMSE for the Junk model simplified to 6212 triangles using alpha values between 0 and 2. The best visual results in this model are obtained when
for TVMI and when
for TVE. Similar to the Skull and Brush models, lower values for alpha considerably increase the visual error for TVE. In this model TVMI achieves an improvement around 2% over VMI (TVMI (
)). The difference in visual quality between TVE and TVMI is very little in this model (around 1%). As shown in
Table 1, TVE obtains the best results in visual similarity among the methods tested for this model.
Figure 12b depicts the RMSE for the Junk model progressively changing the level of simplification. When the model complexity is reduced over 50%, all the visual methods tested (TVMI, TVE and IDS) obtained better visual quality than QSlim. But similar to our previous experiments, when the model is not very simplified, QSlim shows better results.
Figure 10.
Junk model. (a) Original model. T = 61242. (b) QSlim. T = 6212. (c) IDS. T = 6211. (d) TVE (). T = 6218. (e) TVMI (). T = 6219. Different approximations of Junk model obtained with QSlim, IDS, TVE and TVMI. The original model is shown in (a). All the visual simplifications (IDS, TVE and TVMI) preserve the ropes better than the purely geometric simplification (QSlim). The silhouette of the model is retained better with TVE and TVMI than with IDS, see for example the sail at the ship’s stern in (c).
Figure 10.
Junk model. (a) Original model. T = 61242. (b) QSlim. T = 6212. (c) IDS. T = 6211. (d) TVE (). T = 6218. (e) TVMI (). T = 6219. Different approximations of Junk model obtained with QSlim, IDS, TVE and TVMI. The original model is shown in (a). All the visual simplifications (IDS, TVE and TVMI) preserve the ropes better than the purely geometric simplification (QSlim). The silhouette of the model is retained better with TVE and TVMI than with IDS, see for example the sail at the ship’s stern in (c).
Figure 11.
Close-ups of Junk model. (a) Original model. (b) QSlim. T = 6212. RMSE = 30.15. (c) IDS. T = 6211. RMSE = 28.18. (d) TVE (). T = 6218. RMSE = 27.46. (e) TVMI (). T = 6219. RMSE = 26.59. The ropes, some masts and poles are retained better in TVE, TVMI and IDS than in QSlim. TVE (see (e)) achieves an improvement about 6% over IDS (see (c)) and over 14% over QSlim (see (b)).
Figure 11.
Close-ups of Junk model. (a) Original model. (b) QSlim. T = 6212. RMSE = 30.15. (c) IDS. T = 6211. RMSE = 28.18. (d) TVE (). T = 6218. RMSE = 27.46. (e) TVMI (). T = 6219. RMSE = 26.59. The ropes, some masts and poles are retained better in TVE, TVMI and IDS than in QSlim. TVE (see (e)) achieves an improvement about 6% over IDS (see (c)) and over 14% over QSlim (see (b)).
Figure 12.
RMSE for Junk model. (a) RMSE vs. different alpha values. T = 6212. (b) Decimation %.
Figure 12.
RMSE for Junk model. (a) RMSE vs. different alpha values. T = 6212. (b) Decimation %.
5. Conclusions and Future Work
In this paper, we have presented an extension to the viewpoint-driven simplification approach [
4,
11]. The viewpoint-driven simplification approach belongs to those simplification methods whose main goal is to produce approximations according to visual appearance. We have incorporated two new generalized information-theoretic viewpoint selection measures, viewpoint T-entropy and viewpoint T-mutual information into the viewpoint-driven simplification algorithm. These generalized measures include Shannon Information Theory as a special case. Tsallis measures have a parameter
α, when
they recover the usual Shannon entropy and mutual information. These measures give information about the structure of the model and produce high quality approximations when applied to mesh simplification, because they do not suffer from problems such as image distortion and affine transformations that pixel-wise metrics have.
Furthermore, we have compared our results with two different simplification approaches well-known in the computer graphics literature. The geometric approach, QSlim [
10,
17], based on quadrics, a measure related to curvature, and the visual approach, image-based simplification (IDS) [
5], which uses a metric based on pixel differences among a set of render images, the root mean square error (RMSE). We also used RMSE for the quality evaluation due to its simplicity and efficiency and because it can give us an idea of visual similarity of the simplified models. For future work, it would be very interesting to develop other metrics based on computational models of human vision and perceptual factors in order to measure the quality of the approximations in simplification. As shown in our tests, using the generalized measures (TVE and TVMI) in the viewpoint-driven method clearly improves the quality of the resulting approximations compared to geometric decimation methods and even in visual simplification methods as image-based simplification. Our metrics are able to capture structural information from the models, which leads to better simplification, and this is especially noticeable when the complexity of the models is considerably reduced. In addition, our results show that our Tsallis-based measures (TVE and TVMI) slightly enhance the results of the Shannon-based measures, VE and VMI, when applied to mesh decimation.
One important fact that can be inferred from our tests is that when models are not very simplified, the geometric approach in simplification does give superior quality. We think that this is because purely geometry-based methods such as QSlim simplify all the very small polygons first, which has a very low impact on the visual quality of the mesh. Visual simplification methods such as IDS and ours remove hidden regions first and these regions might have some collateral effects on other parts of the models. The visual approach in mesh decimation is really interesting when models are simplified drastically. A hybrid approach would be more adequate in terms of time efficiency, because visual simplification methods are quite slow compared to the geometric ones.
Instead of selecting an entropic index
α heuristically by experiments, an approach similar to [
32] could be applied in which the entropic index
α is obtained systematically by a least-squares estimation.
The current implementation of the viewpoint-driven simplification algorithm is slow, for future work it would be very useful to exploit the parallelism of the new GPU architectures in order to accelerate the rendering stages. With these new architectures, even the metrics can be calculated in the GPU. This would avoid the traffic between the GPU and the CPU, which is where the bottleneck mainly resides.