1. Introduction
Cells are intrinsically noisy biochemical reactors; low reactant numbers can lead to significant statistical fluctuations in molecule numbers and reaction rates [
1,
2,
3]. Fluctuations in the concentrations of a regulatory protein can propagate through a genetic cascade [
4]. Therefore, stochastic mechanisms are ubiquitous in biological systems. Biochemical reactions that involve small numbers of molecules are intrinsically noisy, being dominated by large concentration fluctuations. Although deterministic models can predict the average network behaviour, they fail to incorporate the stochastic characteristic of gene expression, thereby limiting their relevance when single cell behaviors deviate from the population average [
5,
6]. Recent experiments have measured this variation for thousands of different proteins reveal a linear relationship between variance and mean level of expression for much of the proteome [
7,
8].
Understanding random noises in gene networks is crucial for understanding signal fidelity in nature gene networks and designing noise-tolerant gene circuits. The concept of entropy arose in classical theoretical physics as describing a measure of randomness or disorder. The second law of thermodynamics states that the entropy of a closed systems increases with time. This is in effect a statistical law and in principle describes the most likely behaviour of the physical system. However, many phenomena of biology violate the second law of thermodynamics. For example, animals and plants are all developed from an embryo. Obviously, there should exist some mechanisms in biological systems to counteract the increase of entropy. In the biological world, the genetic program of a living cell is determined by a complex web of gene networks. The proper execution of this genetic program relies on faithful signal propagation from one gene to other genes. This process may be hindered by stochastic fluctuations arising from gene expression, because some of components in these genetic circuits are present at low number, which makes fluctuations in concentrations unavoidable. Additionally, reaction rates can fluctuate because of stochastic variation in global pool of housekeeping genes or because of fluctuations in environmental conditions that affect all genes. For example, fluctuations in number of available polymerases or in any factor that alters the cell growth rate will change reaction rates for all genes. Thus, it underscores the significance of entropy as a fundamental invariant of biological systems. However, stochastic fluctuations may also serve as a means of decision making during cell differentiation [
9]. Therefore, the study of entropy about the random events in biological systems is far more important than in physical systems. Recently, this entropy study involves quite complex mathematical stochastic processes and pervades both medicine and biology.
Even in clonal cell populations and under the most uniform experimental conditions, considerable variation is observed in the rates of development morphology and the concentration of each molecular species in each cell [
9]. The molecular-level phenomena that produce these differences are deeply rooted in the statistical mechanical behavior of so-called “small” (or nanoscale) chemical systems, where concentrations of reacting species are extremely low and, consequently, fluctuations and noises in reaction rates are large [
9]. Many genetic regulatory reactions occur at just such low concentrations. Genetic regulatory circuit designs use redundancy, feedback loops and other features to produce the needed determinism in outcome for circuits constructed from such inherent noisy elements. Information theory was introduced as a method for assessing the uncertainty in the state of a system via an entropy measure [
9,
10,
11,
12,
13,
14,
15]. In a series of papers [
16,
17,
18], information theory has been used to calibrate model parameters of transcriptional regulatory network, to use an incomplete transcriptional regulatory model and to estimate the associated uncertainties based on the inaccuracies in the observed data and the model used. The probability density
p for the values of the set Λ of model parameters and the time course
T(
t) of gene expression microarray data can be represented by information theory formulation as
p =
p(
T(
t),Λ). We can construct
p by specifying the model parameter set Λ to maximize the entropy
S = -
pln(
p). In [
19], the principle of entropy maximization is also used to infer genetic interaction networks from gene expression patterns. In [
17], the basin entropy, which was first introduced in [
15] to measure the uncertainty of future behavior of a random state, can be estimated from time series and is therefore also applicable to random Boolean gene networks. In this work, the entropy of complex relevant components of Boolean gene networks is considered as a function of their connectivity,
i.e., basin entropy is a parameter for the dynamic uncertainty or information storage capacity of a gene network as well as the average transient time in random relevant components as a function of their connectivity. Critical Boolean networks balance robustness against random perturbation with complex asymptotic attractor dynamics [
17]. In [
20], the basin entropy is considered as a quantity of the size distribution of the basins of attraction for a Boolean network. The authors use the basin entropy and distance to reference attractor to represent perturbed dynamics in random biological network models [
20].
Dynamics of cell tissues with coupled stochastic gene networks are described by a two-dimensional regular square lattice of identical cells [
21], each a three-dimensional compartment with a gene regulatory network and a toggle switch. The dynamics are driven by a delayed stochastic simulation algorithm, nearest neighbor cells are coupled by normally distributed time-delayed reactions allowing interchange of proteins, and gene expression is a multiple time-delayed reaction. The synchronization of cells’ protein expression levels is measured by their time series entropy. It is observed that fluctuations in protein concentrations of coupled cells were far smaller than for uncoupled cells. Therefore, coupling between cells, which will decrease entropy, can also be useful to reduce noise in gene regulatory network dynamics. As cells are coupled strongly, a stable or synchronization state emerges. This case shows that coupling mechanism is able to create tissues by decreasing entropy [
21]. In [
22], based on the maximum entropy linear discriminant analysis between normal/tumoral prostates, a multivariable gene expression analysis method is used to reveal functional connectivity changes in dependent networks which are related to cell transformation as biomarkers. Entropy is also employed to model sexual dimorphism in growth hormone secretary dynamics by unequal auto-negative feedback [
23]. A mathematical modeling has been used to study feedback regulation in lactose operon by bifurcation and entropy method via comparing experimental data [
24]. The metabolism of a cell can be viewed as a weighted sum of elementary modes [
25]. It is shown that individual weights are inversely correlated with entropy generated by the operation of the used pathways defined in elementary modes. This suggests that evolution develops cellular regulatory patterns that permit diversity of pathways while favoring efficient pathways are with low entropy generation. Such correlation provides a rational way of estimating metabolic fluxes of
Escherichia coli (
E. coli) based on thermodynamic properties of elementary modes [
25]. Based on time series data with random noises, gene regulatory networks are inferred by using the minimum description length principle [
26]. The attenuation and amplification of molecular noises in genetic regulatory networks are discussed from the perspective of H
∞ filtering [
27].
In recent years, several probabilistic graphical models are used to study regulatory programs of gene networks. Some gene regulatory networks can be represented by a class of piecewise affine network model [
28,
29]. Geometric uncertain properties of these symbolic dynamic can be described by topological entropy [
28]. The location of the regulators in the modular network regulation program and their conditional entropy may be used to prioritize regulators for functional validation, and the combination of the bottom-up clustering strategy with the conditional entropy-based assignment of regulators can improve the handling of missing or hidden regulators [
30]. A package based on four entropy estimators is provided for inferring large transcriptional gene networks using mutual information [
30]. An entropy characterization of protein interaction networks and cellular robustness is discussed from network topology and dynamical processes [
11]. The analysis shows that knockouts of proteins with large contribution to network entropy are preferentially lethal. It underscores the significance of entropy as a fundamental invariant of the dynamical network, and as a measure of structure and dynamical properties of gene networks [
11].
Recently, based on S-system model, a new measure of the robustness of biochemical networks is provided according to the smallest singular value of system matrix [
31],
i.e., the uncertainties less than the smallest singular value could be tolerated from the worst-case point of view. A gene circuit design is also provided to improve the filtering ability of stochastic gene network to tolerate more intrinsic parameter fluctuations and to attenuate more extrinsic noises [
32]. An analysis of the stability of the cell cycle network of
Schizosaccharomyces pombe (
S. pombe) is given through the computation of an entropy parameter [
33]. In cell cycle, cell differentiation is a complex process governed by the timely activation of genes resulting in a specific phenotype or observable physical change. A systematic approach using a combination of entropy, pair-wise dependency and Bayesian approach is used to gain insight into dependencies and underlying gene network structure in stem cell differentiation [
34]. For more general gene networks, the robust stabilization is discussed from the H
∞ stabilization perspective to tolerate intrinsic random molecular noises and extrinsic random molecular noises [
35,
36].
It is observed that the period and the amplitude of oscillations are more dispersed and oscillations become less coherent when the fluctuations increase [
37]. It is also found that the entropy production of the whole network, characterizing the dissipation costs from the combined effects of both landscapes and fluxes, decreases when the fluctuation decreases [
37]. These observations on entropy can help in designing robust gene networks with intrinsic random parameter fluctuations. The robustness analysis of
E. coli metabolic network is given based on how to decrease the entropy production of whole network [
38]. An entropy mechanism is provided to generate highly cooperative and specific binding from protein phosphorylation [
39]. How to decrease the effects of intrinsic random noises, extrinsic random disturbances and process delay of engineered circuit is discussed from the robust stabilization and H
∞ filtering perspectives, simultaneously [
10,
40,
41,
42,
43,
44,
45].
Synthetic biology is the engineering of artificial biological systems to fulfill a particular purpose in the host cell [
7,
8,
46]. Synthetic biology is foreseen to have important applications in biotechnology and medicine, and is expected to contribute significantly to a better understanding of the functioning of complex biological systems. However, the development of synthetic gene networks is still difficult and most newly created gene networks are non-function due to random parameter uncertainties, random disturbances and functional variations of intra- and extra- cellular environments. How to design a robust synthetic gene network that works properly in a host cell under these intrinsic random parameter uncertainties and external random disturbances is the most important topic in synthetic biology. Recently, a tuning algorithm of robust synthetic gene network is proposed to tolerate random noises [
47]. A game theory is applied to the robust synthetic gene networks when the random noises with uncertain or unknown statistics is considered as a player to distort the gene network and the gene network is considered as another player to eliminate the effect of random noise [
48]. In [
49], random parameter fluctuations and environmental random disturbances are modeled into the stochastic dynamic equation of synthetic gene network, and four design specifications are also proposed in design procedure to efficiently tolerate random parameter fluctuations and attenuate the random disturbances on the synthetic gene network in the host cell [
49]. In evolution, the random transmission of genes from parent to offspring implies that the study of evolution as a genetic process must allow for this randomness [
36,
50,
51]. In the evolutionary process, the random transmission and random mutation of genes provide the diversities for natural selection. Gene networks need to robustly evolve under these random gene transmission and gene mutation to meet the natural selection [
36,
50,
51,
52]. Therefore, the robust stability in network evolutionary process is a natural selection force. Genetic networks adjust their kinetic parameters by gene mutations to meet the natural selection. This intrinsic robustness of a genetic network can enable co-option, so that new traits (or corresponding new genetic networks) can be generated in the evolutionary process [
36]. The underlying principles of natural selection in network evolution can be discussed from the systems biology perspective [
52,
53]. A stochastic dynamic process is given to discuss robust genetic regulatory networks in the evolutionary process from the viewpoint of nonlinear stochastic regulation theory [
50,
54,
55,
56,
57,
58,
59,
60].
2. On the Entropy Measure of Gene Regulatory Networks
First, for simplicity, we consider a linear nominal gene regulatory network with the following stoichiometric equation:
where
X0(t) = [
X01(
t)…
X0n(
t)]
T,
.
X0(
t) denotes the nominal gene expressions of
n genes and
S0 denotes the stoichiometric matrix, which collects all the kinetic parameters and decay rates of gene regulatory network.
In vivo, the kinetic parameters and decay rates in
S0 suffer from the random parameter fluctuations due to gene expression fluctuations in binding, transcription, splicing and translation processes:
where
S0,ij denotes the nominal parameters; Δ
Sl,ij denotes the amplitude of random kinetic parameter fluctuations;
nl(
t) is a white noise with zero mean and unit variance,
i.e., Δ
Sl,ij denotes the deterministic parts of the corresponding parameter variations, and
nl(
t) absorbs the stochastic property of intrinsic parameter fluctuations.
n1(
t),
n2(
t),…,
nL(
t) are independent stochastic sources of random parameter fluctuations, where covariances are given as:
in which
δ(
t,
τ) denotes the delta function,
i.e.,
δ(
t,
τ) = 1 if
t =
τ and
δ(
t,
τ) = 0 if
. In other words, Δ
Sl,ij denotes the corresponding standard deviation of the stochastic parameter fluctuationsΔ
Sl,ijnl(
t) from the random source
nl(
t). The reason why
nl(
t) in (2) are assumed to be zero mean with unit variance is that the mean of
nl(
t) could be merged in the nominal
S0,ij and the variance can be absorbed in Δ
Sl,ij in (2). Therefore, without loss of generality,
nl(
t) are assumed white noises with zero mean and unit variance.
Suppose the gene regulatory network in (1) suffers the following random intrinsic parameter fluctuation and extrinsic disturbance
in vivo [
32,
35,
40,
41,
42,
49,
52]:
where
and
v(
t) = [
v1(
t) …
vi(
t)…
vn(
t)]
T.
Remark 1: Sl denotes the parameter fluctuation matrix infected by the random source, nl(t), for example, the alternative splicing in gene expression process. If the ij-th component of S0 is free of parameter fluctuation due to random source, nl(t), then ΔSl,ij in S is zero. In (4), there are L random fluctuation sources. G denotes the coupling matrix from environmental disturbances to the gene network. vi(t) denotes the environmental molecular disturbance on gene i due to upstream genes’ regulations or interactions with cellular context.
For the convenience of analysis and design, the stochastic gene regulatory network can be represented by the following equivalent Itô stochastic differential equation [
32,
35,
40,
41,
42,
49,
52]:
where
wl(
t) is a standard Wiener process or Brownian motion with
dwl(
t) =
nl(
t)
dt. The term
denotes the stochastic parameter fluctuations due to
L random sources. Obviously,
in vivo, a linear gene regulatory network under random parameter fluctuations and external disturbance can be represented by the stochastic system in (5).
Let us denote the fluctuation of a perturbed gene network in (5) from its nominal system in (1) as:
Then we get the fluctuation dynamic equation as:
Since
in (7) is a stochastic process, it is not easy to consider it as a measure of randomness (or entropy) of stochastic regulatory network. Let us define the measure of randomness of the stochastic fluctuation equation of gene regulatory network as:
where
denotes the covariance matrix of
.
By Itô’s formula [
57] and with
, we get the following equation for randomness:
where
denotes the covariance matrix of
X(
t) and
Rv denotes the covariance of external noise.
From the randomness equations in both (8) and (9), it is seen that the randomness or entropy of stochastic gene network is mainly due to Rv of the covariance matrix of external random noise and due to the intrinsic random parameter fluctuations.
In the nonlinear gene regulatory network case, the nominal system in (1) is modified as [
61]:
where
f(
X0) denotes the nonlinear regulation function vector.
For the nonlinear stochastic gene regulatory network with intrinsic random parameter fluctuation and external random disturbance
in vivo, (5) is modified as [
42]:
Then, for the nonlinear stochastic gene regulatory network in (11), the randomness dynamic equation in (9) should be modified as:
Based on the Gaussian distribution assumption, the probability function of stochastic gene regulatory networks can be described by:
Another randomness measure,
i.e., entropy, is defined as [
9,
10,
11,
12,
13,
14]:
Therefore, the randomness and entropy of nonlinear stochastic regulatory network in (11) can be measured by (8) and (15), respectively. Even several researches have used the maximum entropy method to estimate parameters of some gene regulatory networks by several iterative searching methods [
13,
14,
16,
17,
18,
19]. In general, it is not easy to measure the randomness or entropy from (8) or (15) by directly solving the randomness differential equations in (11)-(13). It is still difficult to get insight into the systematic characteristics of gene networks from (8) and (15) for the designs of systems and synthetic biology. However, the effect of intrinsic parameter fluctuations
is state-dependent, and it will influence the stability of stochastic gene regulatory network. Further, the external random disturbance will corrupt the gene regulatory network. For more insight and easy computation, the interplaying between randomness (or entropy) and robustness of stochastic gene network should be discussed more from the systematic and filtering point of view. More detailed analysis about the effect of stochastic intrinsic random noise and extrinsic random disturbance on the gene regulatory network and the robustness of gene regulatory network to attenuate the effect of the intrinsic noise and extrinsic disturbance to counteract the entropy in biological systems will be discussed in the following section.
3. Measurement of Robust Stability and Filtering Ability for Stochastic Gene Regulatory Networks
Consider the nonlinear stochastic gene regulatory network in (11) with intrinsic random parameter fluctuations and external random disturbance. Suppose a phenotype near a stable equilibrium point
xe is of interest. For the convenience of analysis, the origin of nonlinear stochastic gene network in (11) is shifted to
xe. In such a situation, if the shifted nonlinear stochastic system is robustly stable at the origin, then the equilibrium point of interest is also equivalently robustly stable. This will simplify the analysis procedure of robust stability and filtering of gene regulatory networks. Let us denote
, then we get the following shifted stochastic system [
26]:
i.e., the origin
of the stochastic gene network in (16) is at the equilibrium
xe of the original stochastic system in (11).
The stochastic gene regulatory network in (16) is said “robust stabilization” if the stochastic parameter fluctuations
could be tolerated at the equilibrium point
or
X(
t) =
xe. The attenuation level of external disturbance
v(
t) by the gene regulatory network can be measured by the following H
∞ filtering ability [
35,
40,
55,
56,
57,
58]:
where E(・) denotes the expectation of (・),
i.e., the effect of
v(
t) on
is less than or equal to
ρ2 from the energy point of view or the attenuation level
ρ is the upper bound of the filtering ability of the gene network.
Before further analysis of robust stabilization and filtering problem of the stochastic gene network in (16), we first consider only the robust stabilization to tolerate intrinsic stochastic parameter fluctuation in (16) in the case free of external disturbance (
i.e.,
),
i.e.:
Since the stochastic parameter fluctuation in (18) is state-dependent, they will influence the stability of the stochastic system in (18) [
57,
58]. From the theory of stochastic stability [
57], the stochastic gene network in (18) with
v(
t) = 0 is assumed with asymptotical stability in probability,
i.e.,
as
t→∞, if the expectation of the time derivative of Lyapunov (energy) function
is negative [
57],
i.e.:
where
is the Lyapunov (energy) function of the stochastic regulatory gene network in (18). The inequality in (19) means that on average the energy function of stochastic gene network decreases with time and will asymptotically converge to
or
X(
t)→
xe in probability in the case
v(
t) = 0, or the stochastically asymptotical stability is achieved.
In the case , only the H∞ disturbance attenuation level in (17) can be measured because the asymptotical stability in probability (or stochastically asymptotical stability) can not be achieved due to the continuous interference of stochastic external disturbances, i.e., or X(t)→xe, can not be achieved in probability as t→∞ and the stochastic deviation from xe (i.e., ) due to stochastic external disturbances can only be attenuated below a level ρ, which is the upper bound of the filtering ability of stochastic gene network of (16).
First, let us consider the robust stabilization of stochastic gene network in the case
v(
t) = 0 in (18). Based the stochastic stability condition in (19), we get the following robust stability result [
27].
Proposition 1: The stochastic gene network in (18) is asymptotically stable in probability if the following Hamilton-Jacobi inequality (HJI) has a position solution
:
i.e., the intrinsic stochastic parameter fluctuations in (18) could be asymptotically tolerated by the gene regulatory network if the above inequality holds.
Remark 2: If the gene regulatory network is free of intrinsic parameter fluctuations and external disturbance, based on HJI in (20), the asymptotical stability for the initial condition is guaranteed by the existence of the positive solution to . Obviously, the asymptotical stability in probability for the intrinsic stochastic parameter fluctuation case in the stochastic system (18) needs more stability robustness to overcome the second term in (20). More effort is needed to solve in (20) than the case of free stochastic parameter fluctuation.
If the stochastic gene network in (16) needs to tolerate the stochastic parameter fluctuations and attenuate stochastic external disturbances below an attenuation level
ρ simultaneously, then we get the following result [
27].
Proposition 2: If the following HJI has a positive solution
then (a) the stochastic gene network in (16) can achieve both the robust stochastic stabilization to tolerate intrinsic random parameter fluctuation and the attenuation level
ρ in (17); and (b) if the stochastic gene network is free of stochastic external disturbances,
i.e.,
, then the stochastic gene network will asymptotically converge to
or
X(
t)→
xe in probability.
Remark 3: (i) Comparing (21) with (20), it is more difficult to find a positive solution
to solve (21) than (20) because two extra-terms
and
due to the attenuation of stochastic external disturbance in (17). (ii) Since
ρ is the upper bound of the random disturbance attenuation in (17), the optimal disturbance attenuation level
ρ0 of the stochastic gene regulatory network in (11) or (16) could be found by solving the following constrained optimization problem [
27,
32]:
i.e.,
ρ0 is a stochastic disturbance attenuation measure or the filtering ability of a stochastic gene network to attenuate the stochastic disturbance
v(
t) in (16) under robust stabilization to tolerate intrinsic parameter fluctuation at
xe. If
ρ0<1, then the stochastic external disturbance is attenuated by the gene regulatory network. If
ρ0>1, then the stochastic external disturbance is amplified by the gene regulatory network. In some cases, extrinsic noise is enhanced by some gene networks [
9]. (iii) If the Wiener noises
wl(
t) in (16) are replaced by the mutually independent Poisson noises
pl(
t) with mean E[
pl(
t)] =
λlt and variance var[
pl(
t)] =
λlt as follows:
Then HJI in (21) should be modified as:
which is much more complex to solve.
In general, it is very difficult to solve HJI in (20) for robust stabilization against the intrinsic stochastic parameter fluctuation or (22) for the filtering ability of stochastic extrinsic noise attenuation. At present, there is no good method to solve the nonlinear partial differential HJI analytically or numerically. In this situation, the global linearization technique is employed to transform the nonlinear stochastic gene network in (16) to an interpolation of a set of locally linearized gene networks to simplify the analysis of robust stabilization and noise filtering ability of stochastic gene network.
By the global linearization method [
42,
62], if all the global linearizations are bounded by a polytope consisting of
M vertices as:
where
C0 denotes the convex hull of the polytope with
M vertices defined in (25), then the state trajectories
of the shifted stochastic gene network in (16) will belong to the convex combination of the state trajectories of the following
M linearized stochastic gene networks derived from the vertices of the polytope [
42]:
By the global linearization theory [
42], if (25) holds, then every trajectory of nonlinear stochastic gene network in (16) is a trajectory of a convex combination of
M linearized gene networks in (26). Therefore, if we can prove that the convex combination of
M linearized gene networks in (26) can tolerate intrinsic stochastic parameter fluctuations and attenuate external stochastic disturbances at a level
ρ0, then the original nonlinear stochastic gene network in (16) will have the same robust stabilization and disturbance attenuation property. The convex combination of M linearized gene networks in (26) can be written as [
42,
62]:
where the interpolation function
satisfies
and
,
i.e., the trajectory of nonlinear gene network in (16) could be represented by the interpolated gene network in (27), which is the convex combination of
M linearized gene networks in (26).
In the case of free external disturbance in (16), the global linearization approach is given by:
Remark 4: (i) Recently, Takagi-Sugeno (T-S) fuzzy model has been also employed to interpolate several linear systems at local regions to approximate the nonlinear stochastic system through smooth fuzzy membership functions [
55]. Therefore, in the fuzzy interpolation case, the interpolated system in (27) could be represented by a T-S fuzzy system when
in (27) are replaced by fuzzy basis functions as follows [
54,
55]:
where
are fuzzy basis functions with
and
. (ii) In general,
in (27) could be any interpolation function, for example, cubic spline functions.
For the global linearization system in (28) with only stochastic parameter fluctuations, we get the following results [
27,
41].
Proposition 3: If the following linear matrix inequalities have a positive symmetric solution
P>0
then the stochastic parameter fluctuations in (28) or (18) can be tolerated by the stochastic gene network,
i.e., the stochastic gene network is asymptotically robustly stable in probability for
xe under the parameter fluctuations.
Remark 5: If the linear matrix inequalities (LMIs) in (30) are changed to the following:
with a positive symmetric solution
P>0, then only robust stability in probability can be achieved and asymptotical stability in probability to
xe is to be achieved.
For the stochastic gene network with stochastic parameter fluctuations and external disturbances in (27) or (16), we get the following result [
27,
41].
Proposition 4: Suppose the following inequalities have a positive solution
P>0
then (i) the random parameter fluctuations are tolerated and the external random disturbance is attenuated below a level
ρ in (17); and (ii) If the stochastic gene network is free of external disturbance,
i.e.,
, then the stochastic asymptotical stability to
xe is achieved.
Remark 6: (i) Since there are two extra-terms in (32) than in (30) due to the consideration of the attenuation of stochastic external disturbances, it should be more difficult to solve (32) than (30). Therefore, the stochastic gene network should be with more robust stability to tolerate the random parameter fluctuations and to attenuate the random external disturbance, simultaneously. (ii) The inequalities in (32) are the quadratic inequalities of
P, it is not easy to solve
P>0 for (32), directly. By Schur complements [
62], they could be transformed to the following equivalent LMIs:
i.e., if the LMIs in (33) have a positive symmetric solution
P>0, then the stochastic gene network can tolerate random parameter fluctuations and attenuate environmental random noises to a level
ρ. (iii) By the fuzzy interpolation technique in (29), we can obtain the similar results, except the linearized parameters
Fi ,
Fli and
Gi are of different values by the interpolation of the fuzzy bases
[
35]. By the global linearization in (27) or fuzzy interpolation in (29) the optimal disturbance attenuation level or the filtering ability
ρ0 of the stochastic gene network in (22) can be measured by solving the following LMI constrained optimization [
27,
41]:
This constrained optimization for measuring the noise filtering ability
ρ0 of stochastic gene network can be achieved by decreasing
ρ in (33) until there doesn’t exist a positive solution
P>0 via the software algorithm of LMI toolbox in Matlab [
62].
Remark 7: (i) From (33), if the eigenvalues of the linearized systems matrices
S0Fi are more negative,
i.e., in the far left-hand side of s-complex domain, then the stochastic gene network has more robust stability to tolerate random parameter fluctuations. From (32), if
ρ is small,
i.e., to attenuate more environmental disturbances, the eigenvalues of
S0Fi of stochastic gene network should be in more far the left-hand s-complex domain in order to attenuate environmental random noises to a small level
ρ. (ii) Recently, the filtering ability and enhancing ability of random noises in neural firing system are also discussed in [
63]. It is found that the activation random noise is filtered but the Na
+ and K
+ channel noises are enhanced.
The dynamic system of a biochemical network can also be represented in the following S-system [
61,
64]:
where
x1(
t), …,
xn+m(
t) are metabolites, such as substrates, enzymes, factors or products of a biochemical network in which
x1(
t), …,
xn(
t) denote the
n-dependent variables (intermediate metabolites and products), and
xn+1(
t), …,
xn+m(
t) denote the independent variables (initial reactants and enzymes),
αi and
βj denote the rate constants, and
gij and
hij represent the kinetic parameters of the biochemical network. These parameters could be estimated by experimental data or microarray data. Suppose transient time is neglected and for simplicity we shall focus on the randomness and robustness of biochemical network at the steady state case. Consider the steady state of biochemical network in (35), we get [
61]:
Taking the logarithm on both sides of (36), introducing new variables
yj(
t) =
ln[
xj(
t)],
aij =
gij-
hij,
bi =
ln(
βj/
αi) and after some rearrangement, we get [
61]:
The above equations could be represented by the following steady state equation [
61]:
where
YD(
t) = [
y1(
t)…
yn(
t)]
T,
b = [
b1…
bn]
T,
YI(
t) = [
yn+1(
t)…
yn+m(
t)]
T,
and
in which
AD denotes the system matrix of the catalytic interactions among the dependent variables
AD and
AI indicates the catalytic interactions between the dependent variables
YD(
t) and the independent variables
YI(
t) (
i.e., the environmental medium of the metabolic system). From the simple algebraic steady state equation in (38), obviously, the S-system in (35) is an useful model for describing the phenotype of biochemical network [
61]. If the inverse of
AD exists, the steady state (or phenotype) of the biochemical network is solved by [
61]:
The steady state
YD(
t) in (39) is one of the equilibrium points of the nonlinear biochemical network in (35). Actually, there are many equilibrium points for (35), which represent different phenotypes. Only the equilibrium point (or phenotype) in (39) is favored by natural selection in evolution. Actually, a real biochemical network in (35) suffers from random parameter fluctuations and environmental disturbance.
i.e.:
Then the corresponding perturbative steady state of the biochemical network is given by [
31,
61]:
Because the biochemical networks are the backbone of physiological systems of organisms, a biochemical network should be sufficiently robust to tolerate the random parameter fluctuation to maintain its function properly. Then we find the following robust stability of biochemical network in S-system model [
31,
53,
65].
Proposition 5: If the following robustness condition holds:
then the phenotype of stochastically perturbed biochemical network exists as follows:
i.e., if the covariance of random parameter fluctuation Δ
AD(
t) of system matrix is less than
ADADT, then the random parameter fluctuations will be tolerated and the phenotype of biochemical network is only with a small perturbation as (43).
If the robustness condition in (42) is violated, the matrix in here in (43) may not exist and the steady state of perturbed biochemical network in (43) may cease to exist or move to another equilibrium point with a change of the phenotype. The random variations of Δ
b(
t), Δ
YI(
t) and Δ
AI(
t) will influence the phenotypic variation Δ
YD(
t) in (43). Their effects on the phenotype have been discussed by the following sensitivity analysis of biochemical network:
In order to tolerate the random variations Δ
b(
t), Δ
YI(
t) and Δ
AI(
t) to preserve the phenotype of a biochemical network, the sensitivity in (44) should be below some values as follows [
65]:
or equivalently:
where
s1,
s2 and
s3 are some small sensitivity values so that the phenotype
YD(
t)+Δ
YD(
t) of stochastically perturbed biochemical networks would not change too much in (43) in comparison with the nominal values in (39),
i.e., Δ
YD(
t) in (43) should be small enough. The sensitivity criteria in (45) or (46) determine the ranges of sensitivities of phenotype change Δ
YD(
t) to random parameter and environmental fluctuations. For a functional biochemical network, it should satisfy the sensitivity criteria to prevent metabolic concentration from being changed too much by parametric and environmental random changes.
4. Interplay Between Entropy and Robustness in the Evolutionary Process of Gene Networks
Robustness is an ubiquitously observed property of biological systems [
31,
36,
66]. Since world random events arise constantly in biological world, the random transmission of genes from parent to offspring implies that the study of evolution as a genetic process must allow for this randomness. The robustness is considered to be a fundamental feature to balance the entropy of complex evolvable biological systems. It has been pointed out that robustness facilitates evolvability and robust traits are often selected by evolution [
36],
i.e., complex biological systems must be robust against environmental and genetic randomness to be evolvable. Evolution often selects gene networks that might enhance the robustness of organisms [
36]. In the past, most molecular biologists and biochemists assume that random fluctuations in gene networks are due to genetic mutation and natural selection. However, the design principles of gene networks via natural selection in evolution are still in conceptual description but not get in mathematical rules. The investigation of robustness of gene networks in evolution is still in its infancy and needs to be discovered. In fact, robustness allows changes in the structure and components of gene networks owing to intrinsic random noise and extrinsic random disturbances, but specific functions are still maintained [
52,
53].
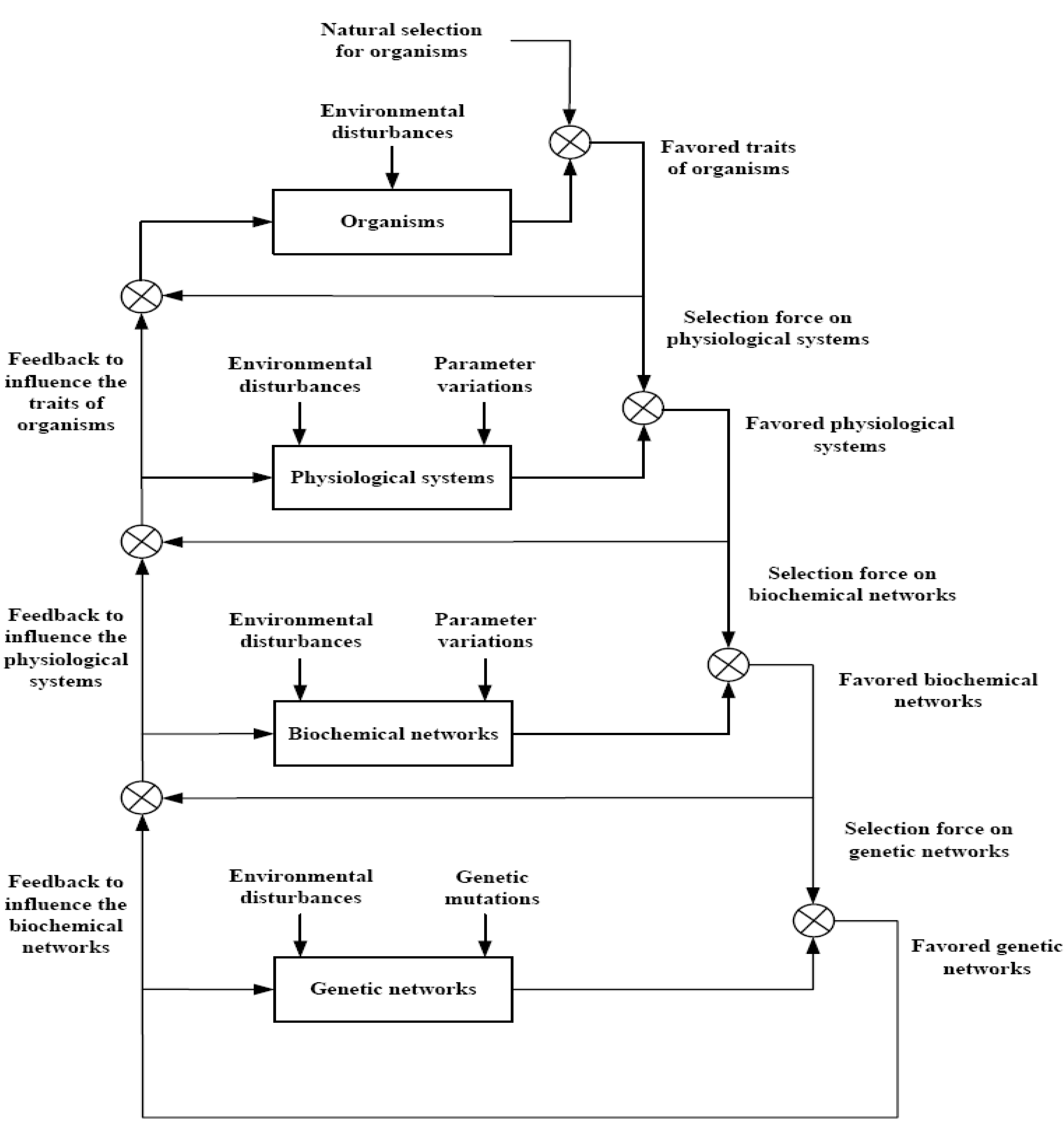
According to the hierarchical network interplaying in
Figure 1 [
52], the high-level selected networks will specify a selection force on lower levels. Just as external environment molds the evolution of local adaptation of organisms by natural selection, the internal biological network environment of population is expected to head to the evolution of local biological networks in a favorable manner [
67]. Once the favored organisms are selected by natural selection, the lower networks have to maintain proper functions of the physiological systems of favored organism. Therefore, the favored organisms are the selection force of the physiological systems. Since biochemical networks are the backbone of the physiological systems of organisms, in order to maintain the favored physiological system by natural selection, a biochemical network should be sufficiently robust to tolerate intrinsic randomness and environmental changes in the evolutionary process. Therefore, the favored physiological systems specify the selection force on biochemical networks. Similarly, in order to maintain the robustness of the favored biochemical networks, gene networks should be designed with enough robustness to tolerate random variations due to random gene mutations in sex-chromosome and filter environmental random noises. On the other hand, changes of lower-level networks will feedback to influence the high-level networks in involution. Therefore, the natural selection actually acts on the interplaying of multiple biological networks. Hence, the revolution of robust adaptive design rules of biological networks by natural selection can gain much insight into the evolutionary mechanisms of biological networks under random intrinsic noises and environmental disturbances. In the evolutionary process, the stochastic gene network can be also represented by (5) but with a more large time scale in evolution. However, the effect of the intrinsic random fluctuations
on the gene network is mainly due to the random genetic mutations of
L genes in the sex-chromosome in the evolutionary process, unlike the random genetic mutations in the autosome of somatic cells in the previous section.
v(
t) denotes the environmental random disturbance in evolution. In this case, the equilibrium point
xe denotes the trait of gene network. As seen in
Figure 1, the genetic network lies at the lowest level of the biological network evolution. In order to maintain the proper function of the favored biochemical network at high-level, the lower-level genetic networks have to function properly. Therefore, in evolution, robust stability is the natural selection force specified by higher-level networks. A stochastic gene network in evolutionary process can be represented as (11) but the random parameter fluctuations are mainly due to genetic mutations of genes in sex-chromosome in the evolutionary process. Further, the time-scale of gene network is much larger in the evolutionary process. Therefore, the robust stability condition of a gene network at the equilibrium point
xe (trait) is the same as (20) except the parameter fluctuations
Sl mainly due to the random gene mutations of sex-chromosome in evolutionary process,
i.e., there should exist a positive solution
for HJI in (20) in the disturbance-free case [
52]. If the gene network can tolerate the intrinsic random fluctuation and can attenuate the environmental disturbance to a level
ρ simultaneously in the evolutionary process, then there should exist a positive solution
in (21) [
52]. Similarly, by the global linearization technique, the robust stability of gene network to tolerate intrinsic genetic mutations in the evolutionary process is guaranteed for a trait if there exists a positive solution
P>0 for LMIs in (31). In this situation, the trait of gene network is kept under gene mutations in evolution. The disturbance filtering ability
ρ0 of a gene network in the evolutionary process could be measured by solving the constrained optimization problem in (34). This could measure the influence of environment on the gene network in the evolution process. Obviously, as remarks 6 and 7, if the eigenvalues of linearized gene networks are all in the far left-hand side of s-complex domain, then a gene network has enough robustness to tolerate intrinsic random genetic mutation and filter environmental random disturbances to keep its trait in evolution to avoid extinction by natural selection. The genetic mutations, which could lead to feedback circuits to improve robustness and noise filtering ability, are favored by natural selection in the evolutionary process. However, some gene mutations, which could make the corresponding parameter fluctuations
Sl and coupling function
g(
X) small, such as those mutations to redundancy, duplicating and self-regulation so that it is not easy to violate robust stability conditions (20)-(21) or (31)-(32), due to these buffers, are also favored by natural selection [
68,
69]. If filtering ability
ρ0<1 in (22) or (34), the eigenvalues of linearized gene networks should be in the far left-hand of s-complex domain side to attenuate the environmental random noises. The trait of this kind of gene networks is more robust in evolution. If
ρ0>1, it is easier for the gene network to satisfy this amplification ability. In this situation, this gene network is much influenced by environmental random noises to easily move toward another equilibrium points (traits) so that the gene network is more adaptive to the environmental changes in the evolutionary process, especially for
ρ0»1, to generate a new trait (or phenotype) to a new environment. This is a tradeoff between the robust stability and the adaptability of gene networks in the evolutionary process [
52,
53].
If the biochemical network in the evolution process is described by the S-system model in (41), the time scale should be enlarged and the parameter fluctuations are mainly due to genetic mutations in the sex-chromosome. Suppose that there exist some random parameter variations Δ
αi(
t), Δ
βi(
t), Δ
hij(
t), Δ
gij(
t) due to random genetic mutations and Δ
YI(
t) due to environmental random disturbances in the evolutionary process. These random parameter variations due to genetic mutations in the sex-chromosome could be considered as design parameters in the evolutionary process. Because the biochemical networks are the backbone of physiological system of organisms, a biochemical network should be sufficiently robust to tolerate the random parameter variations and environmental changes due to genetic mutations to maintain its function properly in the evolutionary process (see
Figure 1). However, if the robustness condition in (42) is violated, the steady state phenotype of the perturbed biochemical network in (43) may not exist or move to another equilibrium point with a change of the trait. The random variations Δ
b(
t), Δ
YI(
t) and Δ
AI(
t) will influence the trait variation Δ
YD(
t) in (34), and their effects on the trait can be obtained from the sensitivities in (44). In general, the perturbed biochemical networks with random parameter variations that violate the robustness criterion in (42) will be eliminated by natural selection. Therefore, the perturbed biochemical network should satisfy the robustness criterion in order to guarantee not to be perturbed too much from its equilibrium point (the normal physiological function) in the evolutionary process. Because the violation of (42) means a lethal genetic mutation, the robustness criterion in (42) is the necessary condition for the survival of biochemical networks under natural selection [
52,
53]. From the robustness criterion in (42), natural selection favors the perturbed biochemical networks with small-variance random genetic mutation,
i.e., with small E[Δ
AD(
t)Δ
ADT(
t)], so that the robustness criterion is not violated. A biochemical network with redundancy and self-regulation can attenuate random fluctuation Δ
AD(
t). Furthermore, a biochemical network with adequate negative feedbacks can increase
ADADT in (42) to tolerate random parameter fluctuations with large variance E[Δ
ADΔ
ADT] in the evolutionary process. These robust adaptive designs with feedbacks are also favored by natural selection in the evolutionary process of biochemical networks. This is why there are so many redundancies, duplicated genes, modularities, self-regulations and feedback pathways in the biochemical networks in organisms [
52,
53,
68,
69,
70]. A scale-free structure could reduce the effect of E[Δ
AD(
t)Δ
ADT(
t)] on the stability of bio-networks and is also favored by natural selection in evolution [
36].
Figure 1.
[
42] The natural selection process on the interplaying of hierarchical biological networks with random parameter fluctuations and environmental disturbance. The high-level biological system selection will become the selection force on low level
biological systems. The natural selection on organisms selects its favored organisms. However, the random parameter fluctuations and stochastic environmental disturbance will influence the natural selection process of gene networks in evolution. Once the favored organisms are selected, the low-level biological networks have to maintain the favored physiological systems of the selected organisms. Hence, these favored organisms become the selection force to select their favored physiological systems. The favored physiological systems will lead to the selection force on biochemical networks. The favored biochemical networks by natural selection will become the selection force on genetic networks. On the other hand, the lower-level selected networks will feedback to influence the higher-level networks in evolution. Therefore, the natural selection actually acts on the interplaying of the multiple bionetworks.
Figure 1.
[
42] The natural selection process on the interplaying of hierarchical biological networks with random parameter fluctuations and environmental disturbance. The high-level biological system selection will become the selection force on low level
biological systems. The natural selection on organisms selects its favored organisms. However, the random parameter fluctuations and stochastic environmental disturbance will influence the natural selection process of gene networks in evolution. Once the favored organisms are selected, the low-level biological networks have to maintain the favored physiological systems of the selected organisms. Hence, these favored organisms become the selection force to select their favored physiological systems. The favored physiological systems will lead to the selection force on biochemical networks. The favored biochemical networks by natural selection will become the selection force on genetic networks. On the other hand, the lower-level selected networks will feedback to influence the higher-level networks in evolution. Therefore, the natural selection actually acts on the interplaying of the multiple bionetworks.
![Entropy 12 01071 g001]()
The sensitivity criteria in (45) and (46) determine the ranges of the sensitivities of phenotype change Δ
YD(
t) to random parameter variations due to genetic mutations and random environmental changes by natural selection in the evolutionary process. For a functional biochemical network, it should satisfy the sensitivity criteria to prevent the metabolic concentration from being changed too much by random genetic mutations and environmental changes. Hence, the steady state (trait) of a biochemical network can be preserved while exposing the random genetic mutations and environmental changes to natural selection in the evolutionary process. The assumption that the three sensitivity criteria in (45) or (46) all hold for natural selection is derived from the fact that biochemical networks are the backbone of physiological systems and cannot be too sensitive to random genetic mutations and environmental changes, especially for some core (conserved) biochemical networks [
52]. Actually, the sensitivity values
si of sensitivity criteria in (45) or (46) are dependent on the biochemical network. If some sensitivity criteria in (45) or (46) are relaxed,
i.e., some of the inequalities in (45) or (46) are with much larger value
si, the phenotype of the biochemical network will be changed quickly with some random genetic mutations and environmental changes and will be more favored by natural selection. In this situation, the traits of biochemical networks are much influenced by random genetic mutation and environmental variations and are more easily toward another equilibrium points (traits) so that they may be more adaptive to environmental changes through random genetic mutations in the evolutionary process. In this case, new traits are more easily generated in order to be more adaptive to the natural selection force on biochemical networks under random genetic mutations and environmental variations in the evolutionary process [
52,
53]. The robustness criterion in (42) and the sensitivity criteria in (45) are called adaptive rules of natural selection on biochemical network via genetic mutations of sex-chromosome in the evolutionary process. There are many perturbed biochemical networks that can satisfy the adaptive rules of natural selection in the evolutionary process. If they are selected by natural selection, there are some differences in trait among these selected biochemical networks with random genetic mutations. After several generations in the evolutionary process, due to co-option of existing biochemical networks, diversities of the biochemical networks with conserved physiological function but with different structures will be developed [
66]. This is the origin of the diversities of biochemical networks within organisms in evolution. However, if the requirements on the robustness in (42) and the sensitivities in (45) are stricter (or more conservative),
i.e., with small
si, only a few solutions (or structures) can be selected by natural selection to meet these requirements. This is the reason why a conserved core biochemical network has less diversity [
53].
5. The Balancing Roles of Entropy and Robustness in the Design of Systems Biology
Consider nonlinear stochastically perturbed gene network in (16). If the nonlinear stochastic gene network in (16) cannot achieve robust stabilization with a prescribed filtering ability
ρ,
i.e., random parameter fluctuations and stochastic disturbance can not be efficiently attenuated, some feedback gene circuits
k should be designed to improve its robust stability and filtering ability [
32,
35]:
By a similar method as
Proposition 2, we get following robust gene circuit design result [
35].
Proposition 6: If we can design some gene circuits so that the following HJI has a positive solution
then the robust stability and filtering ability in (17) is guaranteed,
i.e., the random parameter fluctuation can be tolerated and random disturbance can be efficiently attenuated below a prescribed level
ρ.
However, it is difficult to solve the HJI in (48). The global linearization technique in (25) and (27) is employed to simplify the robust gene circuit design procedure. By the similar way as
Proposition 4, we get the following robust gene circuit design method [
41,
52].
Proposition 7: If we can design some feedback gene circuits
k such that the following LMIs has a positive symmetric solution:
then random parameter fluctuations could be tolerated and random disturbances can be attenuated below a prescribed level
ρ.
By Schur complement [
62], if we can design feedback gene circuit
k so that the following LMIs has a positive matrix solution
P>0:
then random parameter fluctuations can be tolerated and stochastic disturbances can be attenuated below a prescribed level
ρ. Therefore, the robust gene circuit design principle in systems biology is to design some adequate feedback circuits
k so that the LMIs in (50) have a common solution
P>0. The robust design of gene network with random parameter fluctuation, stochastic environmental disturbance and process delays is also discussed in [
40,
41]. The above is an application of evolutionary systems biology to the robust gene network design, with the bio-designer instead of natural selection, selecting
k in the design procedure with a more fast speed genetic searching in computer than genetic mutations in evolution.
If the robust criterion in (42) and sensitivity criteria in (45) are violated by large random parameter fluctuations ΔAD(t), Δb(t) and enzyme change ΔYI(t) due to genetic mutation, environmental changes and diseases. A robust design method can be developed for biochemical networks to improve their robustness to compensate the effect of random parameter fluctuations and to attenuate the effect of random disturbances.
In the S-system model, a robust circuit control design can be developed for a biochemical network in (35) by some feedback control circuits as follows [
65]:
where
denotes a biochemical control circuit via
xk(
t) for regulating the production of
xi(
t) with a kinetic parameter
fik and
denotes a biochemical control circuit via
xk(
t) for regulating the degradation of
xi(
t) with the kinetic parameter
eik. The choice between regulating objects,
xk(
t) and
xi(
t) and the specification of kinetic parameters,
fik and
eik, are to be made according to the feasibility of biochemical circuit linkages to achieve both the robust stability to tolerate random parameter fluctuations Δ
AD(
t) and the desired sensitivities to attenuate the other random parameter fluctuations Δ
b(
t), Δ
AI(
t) and the random disturbance Δ
YI(
t). Since
fik and
eik are the elasticities of the corresponding enzymes in the designed gene control circuits, the implementation of gene control circuits is highly dependent on the specification of elasticities of these enzymes [
65]. Based on the robustness analysis from (35) to (46), a biochemical circuit design scheme for robust control of biochemical networks can be developed in the following. Consider the robust control of the biochemical network in (51). Using a similar procedure from (35) to (46), we obtain:
where the feedback control parameter matrix is defined as:
in which
fik and
eik are the kinetic parameters of the biochemical control circuits to be specified in (51).
By the similar procedure to obtain the robustness criterion in (42), we get the following robust circuit design result.
Proposition 8: If we can design feedback circuits
F such that the following inequality holds:
then the phenotype of the perturbed biochemical network is preserved,
i.e., the circuit control
F can improve the robustness to tolerate the random parameter fluctuation Δ
AD(
t) for a biochemical network.
Similarly, if the desired sensitivity of biochemical networks cannot be achieved to attenuate the random variations of other parameters and stochastic disturbances in (45) or (46), the feedback circuit control
F could be designed as follows [
65]:
with some desired sensitivities
s1,
s2 and
s3 so that the phenotypes of the perturbed biological network will not change too much. According to the above analysis, if we can specify the entries of
fik and
eik of
F in (53) for the biochemical network in (51) to satisfy the requirement of robustness in (54) and the sensitivities in (55), then the biochemical network could tolerate the random parameter variations and stochastic disturbances. These results are potential for application to medical technology and robust design of synthetic biology in future.
6. The Balancing Roles of Entropy and Robustness in Synthetic Biology
Synthetic biology is foreseen to have important applications in biotechnology and medicine and to revolutionize how we conceptualize and approach the engineering of biological systems. In short, synthetic biology is the engineering of artificial biological systems to fulfill a particular purpose. It does so through transformative innovation that makes it possible to build living machines from off-the-shelf chemical ingredients, employing many of the same strategies that electrical engineers use to make computer chips [
44,
71,
72]. Drawing up a set of the powerful techniques for the automated synthesis of DNA molecules and their assembly into genes and microbial genomes, synthetic biology envisions the redesign of nature biological systems for greater efficiency as well as the construction of functional “genetic circuits” and metabolic pathways, which will be inserted into the host cells for practical purposes [
7,
8,
44,
46,
71,
72]. At present, even the construction of networks of inter-regulating genes,
i.e., the so-called genetic regulatory networks, has demonstrated the feasibility of synthetic biology. The design of synthetic gene networks is still a difficult problem and the most newly designed gene networks cannot function properly. These design failures are mainly due to both intrinsic random parameter fluctuation such as gene expression noise, splicing, mutation, thermal fluctuation and extrinsic stochastic disturbances such as changing extra-cellular environments in the host cells [
44]. Therefore, how to design a robust synthetic gene network that can tolerate intrinsic random parameter fluctuations, attenuate extrinsic stochastic disturbance and also function properly in host cells is an important topic of synthetic biology [
48,
49].
For the convenience of illustration, a simple cross-inhibition network shown in
Figure 2 is synthesized with two genes,
a and
b, that code for two repressor proteins,
A and
B. More specifically, protein
B represses the expression of gene
a, while protein
A represses both the expression of gene
b and at higher concentration, the expression of its own gene. This synthetic biology system can be modeled by the following differential equations [
49]:
The state variables
xa and
xb denote the concentrations of proteins
A and
B.
k’s and
γ’s are the kinetic parameters and decay rates, respectively, and
ri(
xi) are the regulation functions, which capture the regulator effect of an effector protein on gene expression and are smooth sigmoidal function (e.g., Hill functions). The simple cross-inhibition synthetic network in (56) can be represented by the following stoichiometic matrix equation:
Figure 2.
A two-genes synthetic network and the inhibition regulation functions ri(xi).
Figure 2.
A two-genes synthetic network and the inhibition regulation functions ri(xi).
However, the stoichiometric matrix in the host cell will suffer from the random parameter fluctuations due to gene expression noises, splicing, mutation and thermal noises:
where Δ
ki and Δ
γi denote the amplitude of fluctuations of stochastic kinetic parameters and decay rate; and
ni(
t) is white noises to denote different random sources. Then, the stochastic synthetic gene network under random parameter fluctuations and stochastic disturbances in the host cell can be represented by:
where
x2(
t) = [
xa(
t)
xb(
t)]
T and
υ2(
t) = [
va(
t)
vb(
t)]
T denote the state vector and external random disturbance vector of the synthetic gene network in the host cell, respectively. These random intrinsic parameter fluctuations and stochastic external disturbances may cause the engineered gene network to be dysfunction in the host cell. The robust synthetic biology design is to choose two kinetic parameters
ka and
kb and two decay rates
γa and
γb in
N2 so that the desired steady state
xad and
xbd can be achieved under random intrinsic parameter fluctuations and stochastic disturbances.
If a synthetic gene network consists of
n genes, then the stochastic gene network of (59) in the host cell can be extended to the following
n-gene network dynamics:
where the state vector
x(
t) = [
x1(
t)…
xn(
t)]
T denotes the concentrations of
n proteins in the synthetic gene network.
N denotes the corresponding stoichiometric matrix of
n-gene network.
Mi,
i = 1,…,
m, denote fluctuation matrices due to independent random noise sources
ni,
i = 1,…,
m, and the elements of
Mi denote standard deviations of the corresponding random parameter fluctuations.
υ(
t) = [
υ1(
t)…
υn(
t)]
T denotes the vector of random environmental disturbances. The stochastic system in (60) is used to mimic the realistic stochastic behavior of a synthetic gene network of
n genes in the host cell. The synthetic network, however, suffers from the random parameter fluctuations and environmental disturbances in the context of the host cell. In [
49], a robust synthetic gene network design has been proposed with the ability not only to tolerate these random parameter fluctuations and to attenuate the stochastic disturbances but also to achieve the desired steady state behaviors via the following four design specifications [
49]:
(i). Kinetic parameters and decay rates in N should be chosen from the following biological feasible range, .
(ii). Stochastic kinetic parameters and decay rate fluctuations with prescribed standard deviations in Mi in the state dependent terms to be tolerated by the synthetic gene network should be specified.
(iii). The desired steady state xd should be achieved, where xd is the desired steady state specified by the designer for some design purposes of the synthetic gene network inserted in the host cell.
(iv). The following prescribed disturbance filtering ability (
i.e., the H
∞ filtering) should be
achieved:
for all random
υ(
t), where
Q≥0 is a symmetric weighting matrix and the vector
xd = [
x1d…
xnd]
T denotes the desired steady states of
n proteins.
In order to simplify the design procedure and to achieve the desired steady state in the specification (iii), let us denote
. Then we get the following shifted stochastic
system from (58):
where
dwi(
t) =
ni(
t)
dt,
i.e., the origin
of the stochastic system in (62) is at the desired steady state
xd of the original stochastic system in (60).
From the stochastic biology system in (62), we
obtain the following robust synthetic gene network design result [
49]
Proposition 9: If some designed kinetic parameters and decay rates in
are chosen such that the following HJI has a positive solution
:
then (a) the stochastic synthetic gene network in (62) can achieve both robust stabilization to tolerate random intrinsic parameter fluctuation and the prescribed attenuation level
ρ on the stochastic disturbances,
i.e., the design specifications (i), (ii) and (iv) are all satisfied; and (b) if the stochastic gene network in (62) is free of stochastic disturbance,
i.e.,
υ(
t) = 0, then the synthetic gene network in (62) will asymptotically converge to
or
x(
t)→
xd in probability, or equivalently, the original stochastic synthetic gene network in (60) will asymptotically converge to the desired steady state
xd in probability,
i.e., the design specification (iii) is achieved.
In general, it is very difficult to specify
to solve HJI in (63) for
via a synthetic method. Therefore, based on the global linearization technique in (25), we get the following design result for robust stochastic synthetic gene network [
49].
Proposition 10: Assume that some design kinetic parameters and decay rates
are chosen such that the following
M inequalities have a common symmetric
positive definite solution
P>0:
then there are two results: (a) The stochastic gene network of (62) in the host cell with random parameter fluctuations and stochastic disturbances will be robustly stabilized to tolerate random parameter fluctuations and also achieves a prescribed attenuation level
ρ on the stochastic disturbance,
i.e., the design specifications (i), (ii) and (iv) are satisfied, and (b) if the synthetic gene network in (62) is free of stochastic disturbance,
i.e.,
υ(
t) = 0, then the stochastic synthetic gene network will asymptotically converge to
in probability, or equivalently, the original synthetic gene network in (62) will asymptotically converge to the desired steady state
xd in probability,
i.e., the design specification (iii) is achieved.
By Schur complement [
62], the inequalities in (64) could be
transformed to the following LMIs:
Therefore, the robust synthetic gene network design problem by specifying
to solve a positive function
for HJI in (63) with a prescribed disturbance attenuation level
ρ is transformed into the problem of specifying
to solve a common
P>0 for a set of inequalities in (64) or equivalently for a set of LMIs in (65). The LMIs in (65) can be efficiently solved by the so-called interior-point method via the LMI toolbox in Matlab [
62].
Remark 8: (i) There are some differences between the robust circuit design in
section 5 and the robust synthetic gene network design in
section 6. The robust circuit design in
section 5 is to construct some gene circuits for an existent gene network to improve its stability robustness to tolerate random parameter fluctuations and attenuate more stochastic disturbances. However, in the robust synthetic gene network design, you should engineer a complete new gene network based on design specifications and then these synthetic gene networks will be inserted into their host cells to perform their functions. In the host cells, they should have enough robust stability to tolerate random parameter fluctuations and attenuate stochastic disturbances from the cellular context of the host cell. (ii) Since the statistics of stochastic disturbances can not be easily measured in the host cell, a robust stochastic gene network design is proposed from the stochastic game theory point of view [
48],
i.e., the stochastic disturbances play a role to maximize the regulation error when the designer plays a role to minimize the worst regulation error. The above robust synthetic gene network designs can only achieve a desired steady state under random parameter noise and disturbance. They can not robustly track a changing reference signals. Recently, a robust optimal reference tracking design method for stochastic synthetic biology system is also developed [
73]. A robust synthetic oscillator with desired amplitude, period and phase is also designed via GA-based design algorithm [
74].