1. Introduction
It is a well-known and celebrated result that the uniform distribution on a finite set can be characterized as having maximal entropy. Jaynes used this idea as a foundation of statistical mechanics [
1], and the Maximum Entropy Principle has become a popular principle for statistical inference [
2,
3,
4,
5,
6,
7,
8]. Often it is used as a method to get prior distributions. On a finite set, for any distributions
P we have
where
H is the Shannon entropy,
D is information divergence, and
U is the uniform distribution. Thus, maximizing
is equivalent to minimizing
. Minimization of information divergence can be justified by the conditional limit theorem by Csiszár [
9, Theorem 4]. So if we have a good reason to use the uniform distribution as prior distribution we automatically get a justification of the Maximum Entropy Principle. The conditional limit theorem cannot justify the use of the uniform distribution itself, so we need something else. Here we shall focus on symmetry.
Example 1. A die has six sides that can be permuted via rotations of the die. We note that not all permutations can be realized as rotations and not all rotations will give permutations. Let G be the group of permutations that can be realized as rotations. We shall consider G as the symmetry group of the die and observe that the uniform distribution on the six sides is the only distribution that is invariant under the action of the symmetry group G.
Example 2. is a commutative group that can be identified with the group of rotations in 2 dimensions. This is the simplest example of a group that is compact but not finite.
For an object with symmetries the symmetry group defines a group action on the object, and any group action on an object defines a symmetry group of the object. A special case of a group action of the group G is left translation of the elements in G. Instead of studying distributions on objects with symmetries, in this paper we shall focus on distributions on the symmetry groups themselves. It is no serious restriction because a distribution on the symmetry group of an object will induce a distribution on the object itself.
Convergence of convolutions of probability measures were studied by Stromberg [
10] who proved weak convergence of convolutions of probability measures. An information theoretic approach was introduced by Csiszár [
11]. Classical methods involving characteristic functions have been used to give conditions for uniform convergence of the densities of convolutions [
12]. See [
13] for a review of the subject and further references.
Finally it is shown that convergence in information divergence corresponds to uniform convergence of the rate distortion function and that weak convergence corresponds to pointwise convergence of the rate distortion function. In this paper we shall mainly consider convolutions as Markov chains. This will give us a tool, which allows us to prove convergence of iid. convolutions, and the rate of convergence is proved to be exponential.
The rest of the paper is organized as follows. In
Section 2 we establish a number of simple results on distortion functions on compact set. These results will be used in
Section 4. In
Section 3 we define the uniform distribution on a compact group as the uniquely determined Haar probability measures. In
Section 4 it is shown that the uniform distribution is the maximum entropy distribution on a compact group in the sense that it maximizes the rate distortion function at any positive distortion level. Convergence of convolutions of a distribution to the uniform distribution is established in
Section 5 using Markov chain techniques, and the rate of convergence is discussed in
Section 6. The group
is used as our running example. We finish with a short discussion.
2. Distortion on compact groups
Let G be a compact group where ∗ denotes the composition. The neutral element will be denoted e and the inverse of the element g will be denoted .
We shall start with some general comments on distortion functions on compact sets. Assume that the group both plays the role as source alphabet and reproduction alphabet. A distortion function is given and we will assume that with equality if and only if We will also assume that the distortion function is continuous.
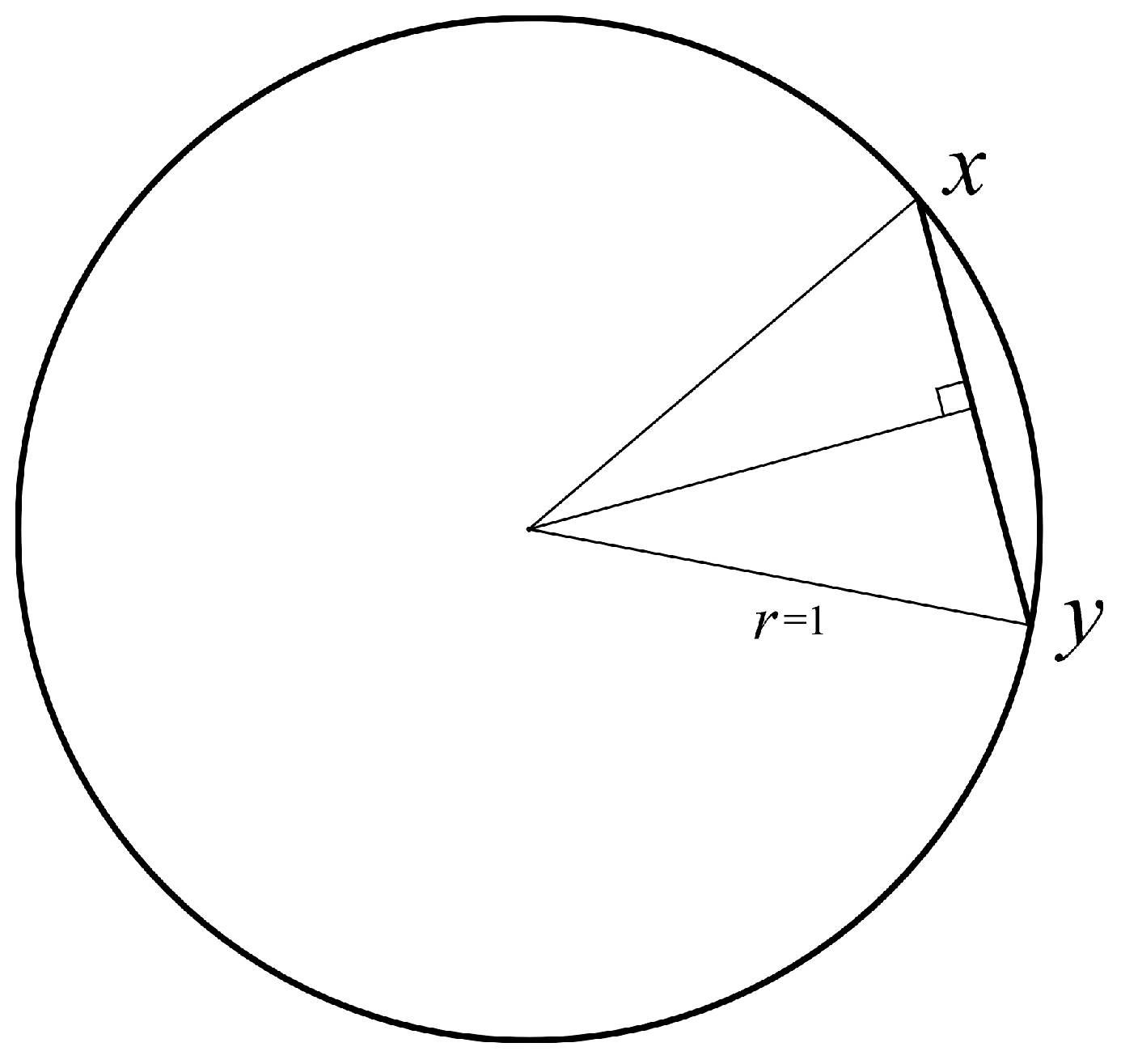
Example 3. As distortion function on we use the squared Euclidean distance between the corresponding points on the unit circle, i.e.This is illustrated in Figure 1.
Figure 1.
Squared Euclidean distance between the rotation angles x and y.
Figure 1.
Squared Euclidean distance between the rotation angles x and y.
The distortion function might be a metric but even if the distortion function is not a metric, the relation between the distortion function and the topology is the same as if it was a metric. One way of constructing a distortion function on a group is to use the squared Hilbert-Smidt norm in a unitary representation of the group.
Theorem 4. If C is a compact set and is a non-negative continuous distortion function such that if and only if , then the topology on C is generated by the distortion balls where and .
Proof. We have to prove that a subset is open if and only if for any there exists a ball that is a subset of B and contains y. Assume that is open and that . Then compact. Hence, the function has a minimum r on and r must be positive because would imply that Therefore
Continuity of d implies that the balls are open. If any point in B is contained in an open ball, then B is a union of open set and open. ☐
The following theorem may be considered as a kind of uniform continuity of the distortion function or as a substitute for the triangular inequality when d is not a metric.
Lemma 5. If C is a compact set and is a non-negative continuous distortion function such that if and only if ,
then there exists a continuous function satisfying such that Proof. Assume that the theorem does not hold. Then there exists
and a net
such that
and
A net in a compact set has a convergent subnet so without loss of generality we may assume that the net
converges to some triple
. By continuity of the distortion function we get
and
which implies
and we have a contradiction. ☐
We note that if a distortion function satisfies (1) then it defines a topology in which the distortion balls are open.
In order to define the weak topology on probability distributions we extend the distortion function from
to
via
where
X and
Y are random variables with values in
C and the infimum is taken all joint distributions on
such that the marginal distribution of
X is
P and the marginal distribution of
Y is
Q. The distortion function is continuous so
has a maximum that we denote
.
Theorem 6. If G is a compact set and is a non-negative continuous distortion function such that if and only if ,
thenfor some continuous function satisfying .
Proof. According to Lemma 5 there exists a function
satisfying (1). We use that
This hold for all
and in particular for
, which proves the theorem. ☐
The theorem can be used to construct the
weak topology on
with
as open balls that generate the topology. We note without proof that this definition is equivalent with the quite different definition of weak topology that one will find in most textbooks.
For a group
G we assume that the distortion function is
right invariant in the sense that for all
a distortion function
d satisfies
A right invariant distortion function satisfies
, so right invariant continuous distortion functions of a group can be constructed from non-negative functions with a minimum in
e.
3. The Haar measure
We use ∗ to denote convolution of probability measures on G. For we shall use to denote the g-translation of the measure P or, equivalently, the convolution with a measure concentrated in g. The n-fold convolution of a distribution P with itself will be denoted . For random variables with values in G one can formulate an analog of the central limit theorem. We recall some facts about probability measures on compact groups and their Haar measures.
Definition 7. Let G be a group. A measure P is said to be a left Haar measure if for any . Similarly, P is said to be a right Haar measure if for any . A measure is said to be a Haar measure if it is both a left Haar measure and a right Haar measure.
Example 8. The uniform distribution on or has density with respect to the Lebesgue measure on .
The functionis a density on a probability distribution P on if the Fourier coefficients are sufficiently small so that f is non-negative. A sufficient condition for f to be non-negative is that .
Translation by y gives a distribution with densityThe distribution P is invariant if and only if f is 1 or, equivalently, all Fourier coefficients are 0.
A measure
P on
G is said to have
full support if the support of
P is
G, i.e.
for any non-empty open set
. The following theorem is well-known [
14,
15,
16].
Theorem 9. Let U be a probability measure on the compact group G. Then the following four conditions are equivalent.
U is a left Haar measure.
U is a right Haar measure.
U has full support and is idempotent in the sense that U ∗ U = U.
There exists a probability measure P on G with full support such that P ∗ U = U.
There exists a probability measure P on G with full support such that U ∗ P = U.
In particular a Haar probability measure is unique.
In [
14,
15,
16] one can find the proof that any locally compact group has a Haar measure. The unique Haar probability measure on a compact group will be called the
uniform distribution and denoted
U. For probability measures
P and
Q the
information divergence from P to Q is defined by
We shall often calculate the divergence from a distribution to the uniform distribution
U, and introduce the notation
For a random variable
X with values in
G we will sometimes write
instead of
when
X has distribution
P.
Example 10. The distribution P with density f given by (2) has Let
G be a compact group with uniform distribution
U and let
F be a closed subgroup of
G. Then the subgroup has a Haar probability measure
and
where
denotes the index of
F in
G. In particular
is finite if and only if
is finite.
4. The rate distortion theory
We will develop aspects of the rate distortion theory of a compact group
G. Let
P be a probability measure on
G. We observe that compactness of
G implies that a covering of
G by distortion balls of radius
contains a finite covering. If
k is the number of balls in a finite covering then
where
is the rate distortion function of the probability measure
P. In particular the rate distortion function is upper bounded. The entropy of a probability distribution
P is given by
. If the group is finite then the uniform distribution maximizes the Shannon entropy
but if the group is not finite then in principle there is no entropy maximizer. As we shall see the uniform distribution still plays the role of entropy maximizer in the sense that the uniform distribution maximize the value
of the rate distortion function for any positive distortion level
. The rate distortion function
can be studied using its convex conjugate
given by
The rate distortion function is then recovered by the formula
The techniques are pretty standard [
17].
Theorem 11. The rate distortion function of the uniform distribution is given bywhere Z is the partition function defined byThe rate distortion function of an arbitrary distribution P satisfies Proof. First we prove a Shannon type lower bound on the rate distortion function of an arbitrary distribution
P on the group. Let
X be a random variable with values in
G and distribution
P, and let
be a random variable coupled with
X such that the mean distortion
equals
δ. Then
Now,
and
where
is the distribution that minimizes divergence under the constraint
when
Y has distribution
. The distribution
is given by the density
where
β is determined by the condition
.
If P is uniform then a joint distribution is obtained by choosing uniformly distributed, and choosing Y distributed according to and independent of . Then is distributed according to and we have equality in (7). Hence the lower bound (7) is achievable for the uniform distribution, which prove the first part of the theorem, and the left inequality in (4).
The joint distribution on that achieved the rate distortion function when X has a uniform distribution, defines a Markov kernel that is invariant under translations in the group. For any distribution P the joint distribution on determined by P and Ψ gives an achievable pair of distortion, and rate that is on the rate distortion curve of the uniform distribution. This proves the right inequality in Equation (4). ☐
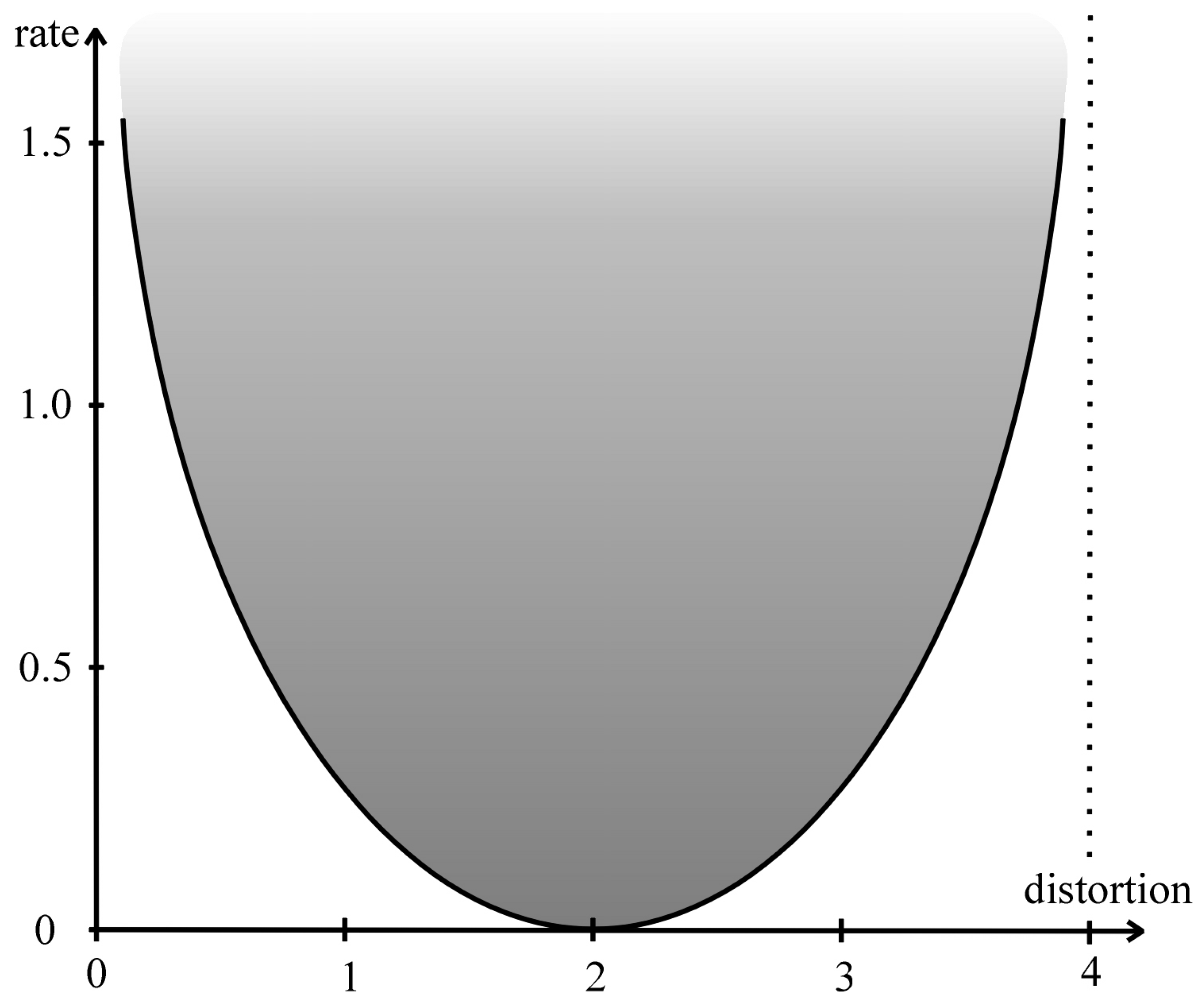
Figure 2.
The rate distortion region of the uniform distribution on is shaded. The rate distortion function is the lower bounding curve. In the figure the rate is measured in nats. The critical distortion equals 2, and the dashed line indicates .
Figure 2.
The rate distortion region of the uniform distribution on is shaded. The rate distortion function is the lower bounding curve. In the figure the rate is measured in nats. The critical distortion equals 2, and the dashed line indicates .
Example 12. For the group the rate distortion function can be parametrized using the modified Bessel functions .
The partition function is given byHence .
The distortion δ corresponding to β is given byand the corresponding rate isThese joint values of distortion and rate can be plotted with β as parameter as illustrated in Figure 2.
The minimal rate of the uniform distribution is achieved when X and are independent. In this case the distortion is . This distortion level will be called the critical distortion and will be denoted . On the interval the rate distortion function is decreasing and the distortion rate function is the inverse of the rate distortion function on this interval. The distortion rate function satisfies:
Theorem 13. The distortion rate function of an arbitrary distribution P satisfiesfor some increasing continuous function satisfying .
Proof. The right hand side follows because
is decreasing in the interval
. Let
X be a random variable with distribution
P and let
Y be a random variable coupled with
X. Let
Z be a random variable coupled with
X such that
. The couplings between
X and
Y, and between
X and
Z can be extended to a joint distribution on
and
Z such that
Y and
Z are independent given
X. For this joint distribution we have
and
We have to prove that
but
so it is sufficient to prove that
and this follows because
. ☐
5. Convergence of convolutions
We shall prove that under certain conditions the n-fold convolutions converge to the uniform distribution.
Example 14. The functionis a density on a probability distribution P on G if the Fourier coefficients are sufficiently small. If and are Fourier coefficients of P and Q then the convolution has densityTherefore the n-fold convolution has densityTherefore each of the Fourier coefficients is exponentially decreasing.
Clearly, if
P is uniform on a proper subgroup then convergence to the uniform distribution on the whole group does not hold. In several papers on this topic [
13,
18, and references therein] it is claimed and “proved” that if convergence does not hold then the support of
P is contained in the coset of a proper normal subgroup. The proofs therefore contain errors that seem to have been copied from paper to paper. To avoid this problem and make this paper more self-contained we shall reformulate and reprove some already known theorems.
In the theory of finite Markov chains is well-known that there exists an invariant probability measure. Certain Markov chains exhibits periodic behavior where a certain distribution is repeated after a number of transitions. All distributions in such a cycle will lie at a fixed distance from any (fixed) measure, where the distance is given by information divergence or total variation (or any other Csiszár
f-divergence). It is also well-known that finite Markov chains without periodic behavior are convergent. In general a Markov chain will converge to a “cyclic” behavior as stated in the following theorem [
19].
Theorem 15. Let Φ be a transition operator on a state space A with an invariant probability measure . If then there exists a probability measure such that and is constant.
We shall also use the following proposition that has a purely computational proof [
20].
Proposition 16. Let be distributions and let Q be a probability distribution on X. Then We denote the set of probability measures on G by .
Theorem 17. Let P be a distribution on a compact group G and assume that the support of P is not contained in any nontrivial coset of a subgroup of G. If is finite then for .
Proof. Let denote the Markov kernel . Then . Thus there exists a probability measure Q on G such that for and such that is constant. We shall prove that .
First we note that
Therefore
for
P almost every
. Thus there exists at least one
such that
. Then
where
.
Let
denote the Markov kernel
Put
According to [
19] this ergodic mean will converge to a distribution
T such that
so that
. Hence we also have that
, i.e.
T is idempotent and therefore supported by a subgroup of
G. We know that
is not contained in any nontrivial subgroup of
G so the support of
T must be
G. We also get
, which together with Theorem 9 implies that
. ☐
By choosing we get the following corollary.
Corollary 18. Let P be a probability measure on the compact group G with Haar probability measure U. Assume that the support of P is not contained in any coset of a proper subgroup of G and is finite. Then for .
Corollary 18 together with Theorem 11 implies the following result.
Corollary 19. Let P be a probability measure on the compact group G with Haar probability measure U. Assume that the support of P is not contained in any coset of a proper subgroup of G and is finite. Then the rate distortion function of converges uniformly to the rate distortion function of the uniform distribution.
We also get weak versions of these results.
Corollary 20. Let P be a probability measure on the compact group G with Haar probability measure U. Assume that the support of P is not contained in any coset of a proper subgroup of G. Then converges to U in the weak topology, i.e. for .
Proof. If we take
then
is finite and
for
. We have
implying that
for
. Now
Therefore
for all
β, which implies that
☐
Corollary 21. Let P be a probability measure on the compact group G with Haar probability measure U. Assume that the support of P is not contained in any coset of a proper subgroup of G and is finite. Then converges to pointwise on the interval for .
Proof. Corollary 20 together with Theorem 13 implies uniform convergence of the distortion rate function for distortion less than . This implies pointwise convergence of the rate distortion function on because rate distortion functions are convex functions. The same argument works in the interval . Pointwise convergence in must also hold because of continuity. ☐
6. Rate of convergence
Normally the rate of convergence will be exponential. If the density is lower bounded this is well-known. We bring a simplified proof of this.
Lemma 22. Let P be a probability distribution on the compact group G with Haar probability measure U. If and is finite, then Proof. First we write
where
S denotes the probability measure
For any distribution
Q on
G we have
Here we have used convexity of divergence. ☐
If a distribution
P has support in a proper subgroup
F then
Therefore
bit implies that
P cannot be supported by a proper subgroup, but it implies more.
Proposition 23. If P is a distribution on the compact group G and bit then is lower bounded by a positive constant.
Proof. The condition
bit implies that
. Hence there exists
such that
. We have
Using the inclusion-exclusion inequalities we get
Hence
for all
.
Combining Theorem 17, Lemma 22, and Proposition 23 we get the following result.
Theorem 24. Let P be a probability measure on a compact group G with Haar probability measure U. If the support of P is not contained in any coset of a proper subgroup of G and is finite then the rate of convergence of to zero is exponential.
As a corollary we get the following result that was first proved by Kloss [
21] for total variation.
Corollary 25. Let P be a probability measure on the compact group G with Haar probability measure U. If the support of P is not contained in any coset of a proper subgroup of G and is finite then converges to U in variation and the rate of convergence is exponential.
Proof. This follows directly from Pinsker’s inequality [
22,
23]
Corollary 26. Let P be a probability measure on the compact group G with Haar probability measure U. If the support of P is not contained in any coset of a proper subgroup of G and is finite, then the densityconverges to 1 point wise almost surely for n tending to infinity.
Proof. The variation norm can be written as
Thus
The result follows by the exponential rate of convergence of
to
U in total variation combined with the Borel-Cantelli Lemma. ☐
7. Discussion
In this paper we have assumed the existence of the Haar measure by referring to the literature. With the Haar measure we have then proved convergence of convolutions using Markov chain techniques. The Markov chain approach can also be used to prove the existence of the Haar measure by simply referring to the fact that a homogenous Markov chain on a compact set has an invariant distribution. The problem about this approach is that the proof that a Markov chain on a compact set has an invariant distribution is not easier than the proof of the existence of the Haar measure and is less known.
We have shown that the Haar probability measure maximizes the rate distortion function at any distortion level. The normal proofs of the existence of the Haar measure use a kind of covering argument that is very close to the techniques found in rate distortion technique. There is a chance that one can get an information theoretic proof of the existence of the Haar measure. It seems obvious to use concavity arguments as one would do for Shannon entropy but, as proved by Ahlswede [
24], the rate distortion function at a given distortion level is not a concave function of the underlying distribution, so some more refined technique is needed.
As noted in the introduction for any algebraic structure A the group can be considered as symmetry group, it it has a compact subgroup for which the results of this paper applies. It would be interesting to extend the information theoretic approach to the algebraic object A itself, but in general there is no known equivalent to the Haar measure for other algebraic structures. Algebraic structures are used extensively in channel coding theory and cryptography so although the theory may become more involved extensions of the result presented in this paper are definitely worthwhile.