1. Introduction
Fourth order diffusion equations arise in many applications such as thin film theory [
1,
2], surface diffusion on solids [
3,
4,
5], interface dynamics [
6,
7,
8], flow in Hele-Shaw cells, and phase field models of multiphase systems [
9]. The simplest prototype is the fourth order diffusion equation with constant coefficients,
ut = −
uxxxx. Although fourth order diffusion equations are dissipative equations, they do not exhibit the smoothing properties usually associated with the very name “diffusion”. Unlike second order diffusion equations, they do not obey a robust maximum principle; one cannot rule out the generation of new extrema in the evolving solutions of standard initial-boundary problems. Indeed, with fourth order evolution we commonly observe the appearance of new structures evolving from smoother initial conditions (e.g. [
1,
5] ). Compared to the familiar smoothing behaviour of second order diffusion, the behaviour of some fourth order equations seems counter-intuitive. Rippling effects and smoothing effects occur in a seemingly ad-hoc manner. Although for fourth order equations, there is no robust maximum principle, entropy production rate may be useful as a simple litmus test. The primary purpose of this paper is to demonstrate that the entropy evolution behaviour of a partial differential equation (PDE) in conservation form, may be readily calculated, allowing it to be easily used as a diagnostic tool to predict smoothing and non-smoothing properties, as well as positivity of solutions with conserved mass. The familiar fourth order diffusion equations do not have increasing Shannon entropy. However, we obtain a new class of nonlinear fourth order diffusion equations that do indeed have this property. These equations also exhibit smoothing properties and they maintain positivity.
A secondary outcome is to show that a single scalar transport equation may be used as a simplified prototype of a thermodynamic system, immediately establishing the equivalence between two statements of the second law of thermodynamics, namely equilibrating heat transport and entropy increase. A system described by a single parabolic equation for a single intensive variable is not a thermodynamic system in the usual technical sense. However, the very purpose of the heat equation is to model the dynamics of heat conduction, which is part of thermodynamics in a practical sense. We can use a single scalar equation to illustrate thermodynamic concepts by constructing from it some entropy density s(x, t) that has a non-negative source density that is not strictly zero. The analogue of an adiabatic process is a time evolution of some scalar quantity T(x, t) governed by a parabolic evolution equation, subject to thermal isolation, represented by zero-flux boundary conditions. In this simplified system, the dynamical law for T(x,t) is specified even in non-equilibrium conditions. This avoids the complication of temperature not even being uniquely defined in more realistic non-equilibrium systems of many interacting particles.
Although the evolution of standard entropy is rarely used as a tool for the analysis of more general PDEs, we demonstrate here that it is in fact quite useful for this purpose. Before we analyse nonlinear fourth order diffusion equations, we first introduce the basic concepts using the very simplest diffusion equation, namely the classical linear heat equation in 1+1 dimensions. Most of the constructions used here can readily be extended to higher spatial dimensions.
2. Basic Concepts: The Linear heat Equation
Consider the classical one-dimensional linear heat equation,
with −∞ ≤
a <
b ≤ ∞. For simplicity, we assume that the domain is a fixed region of constant volume and that the enclosed material has uniform composition and uniform density
ρ. Then we do not need to consider energy transfer due to the work done in compressing the material or in redistributing its components.
The heat equation first arose as a conservation equation
with
q =
ρCV T,
CV being the specific heat, and
k being the thermal conductivity,
k =
ρCV D.
As noted by Lieb and Yngvason [
10], it is remarkable that more than 150 years since the definition of entropy, there is no universally agreed formulation of irreversible thermodynamics of macroscopic systems. In the original definition of Clausius, the entropy S of a closed system is a quantity that has an exact differential
δS =
δQ/T, where
δQ is the infinitesimal increase in heat content during an adiabatic process that notionally connects one equilibrium state to another. For a simplified non-equilibrium system that is described by a single scalar heat conservation equation on a rigid domain with insulated boundary, there can be no change in the total heat content. However, heat will still flow irreversibly from one open subregion to another. For this system, it is possible and convenient to extend the definition of entropy so that it applies to the flow of heat between the open sub-regions, with entropy flux density satisfying
Js =
J/T . This is consistent with the principles of extended thermodynamics [
11]. This prescription can be satisfied by an entropy density
where
Ts, inserted for dimensional consistency, is a natural temperature scale such as the uniform equilibrium temperature of a finite region. From the linear heat equation, one easily derives the reactiondiffusion equation
The entropy source term is non-negative and is zero only for equilibrium states with uniform temperature. The associated total entropy functional S is the continuous analogue of the discrete Burg entropy [
12],
For all non-uniform solutions satisfying zero-flux (perfect insulation) boundary conditions, S increases with time:
A direct connection can be made with information theory since the linear diffusion equation is satisfied also by the probability density function p(x,t) of a particle subjected to Brownian motion (e.g. [
13]). More generally, the positive solutions
u(
x, t) of any nonlinear conservation equation on [
a,
b] × ℜ
+, with constant integral
, may be normalised so that they assume the properties of a probability density
p =
u/U. As a measure of information content, it is convenient to evaluate the Shannon entropy, which is the expected value of
log2(1/
p) [
14]. The Shannon information S has a simple interpretation as the number of binary digits of accuracy in the measurement of a random variable. It is analogous to an extensive thermodynamic variable, having the desirable feature of additivity. That is, if
S1 and
S2 are the entropies of probability densities
p1(
x1) and
p2(
x2) of independent random variables with values in [
a1,
b1] and [
a2,
b2], then the entropy of joint probability density
p1(
x1)
p2(
x2) is
S1 +
S2. The discrete Burg entropy, and more generally, linear combinations of the discrete Burg and discrete Shannon entropies [
12], also have the additivity property. The continuous Burg entropy is additive after all random variables are normalised to take values in [0,1]. In order to consider the information-irreversibility properties of
u(
x, t) =
Up(
x, t), it is sufficient to consider the evolution of the quantity −
u ℓn(
u(
x, t)) whose integral is merely a linear function of the Shannon information,
Henceforth,
log will refer to the natural logarithm and s will refer to the standard entropy density −
u log(
u), where u is the dependent variable under consideration in the primary transport equation. S will refer to the standard entropy which is the integral
For the relationship between Boltzmann’s entropy and Shannon’s information, we refer to [
14].
There are many available choices of Liapunov functionals to indicate irreversibility of the heat equation. With T(x,t) satisfying (1), the variable
v =
f (
T) satisfies the reaction-diffusion equation
This has a non-trivial non-negative source term if and only if
f″(
T) < 0. For those cases, the functional
has the property that for all solutions satisfying zero-flux boundary conditions,
dS/dt ≥ 0. Furthermore,
dS/dt = 0 if and only if T is uniform (thermal equilibrium). This includes the cases
f(
T) =
log(
T) and
f(
T) = −
T log(
T) considered above, as well as the simplest example
f(
T) = −
T2. In that case, -S is simply a multiple of the squared
L2 norm, which is known to decrease because the evolution is contractive. The evolution governed by the linear heat equation is contractive on
L2([
a,
b]) since it is of the form
where
, a self-adjoint contraction operator.
The heat equation cannot be derived from an extremal action principle when the Lagrangian density is defined locally (e.g. [
15] ). However, viewed as a linear mass transport equation for mass concentration
c(
x, t) of a species of particle, it can be generated in another straightforward way from a notional energy functional
with energy density
ε = 0.5
c2. Then the chemical potential per unit mass
µ is given by the variational derivative
δH/δc, which in this case is simply c. The particle drift velocity
vd is then determined by a balance between driving force and linear drag, with resistance coefficient r. Hence the mass flux is
with D=1/r, constant as in Fick’s law. The system is dissipative, since the energy is merely a multiple of the squared
L2 norm, known to be decreasing in time except when it attains its minimum value. The equations for notional energy density
ε and for entropy density
s = −
c log(
c) are
Hence, the production rate of entropy is (1/T) times the dissipation rate of energy. In this sense, s is the entropy density that is thermodynamically conjugate to energy density
ε.
In thermodynamics , an extensive variable S is conjugate to an intensive variable T if the energy cost in increasing S is
δE =
TδS. It is a simple matter to extend this concept to a conjugate triple (
T, s, ε), where s is the locally measured density of S and
ε is the locally measured density of
E. As the notation suggests, one example is the temperature-entropy-enthalpy triple. Another is the volumepressure-work triple, reminiscent of the generalised displacements that do work against the generalised forces of analytical dynamics. Given a scalar evolution equation with dependent variable
T, a pair of locally defined smooth functions (
ε, s), constructed from u and its derivatives, will be said to be an energy-entropy pair if
ε has a source density −
R with
R ≥ 0 and not identically 0, and s has a source density -R/T. For a closed system at uniform temperature, this agrees with the Clausius definition,
but the definition applies locally to the more general situation of an open sub-region having transport through its boundaries and with T non-uniform. Admittedly, in real problems of non-equilibrium thermodynamics, temperature and entropy may not even be well defined. For the present study of scalar partial differential equations, the dependent variable T is taken as primitive.
5. Conclusion
A partial differential equation in conservation form, subject to zero-flux boundary conditions, conserves mass and so its finite-mass solutions may be normalized to take the form of an evolving probability density. From this, the key concept of information irreversibility follows naturally. Irreversibility is traditionally highlighted by monotonicity of a global integral quantity such as the total entropy functional. However, for diagnostic purposes it is more direct to consider a local form of entropy density. From the PDE governing the probability density, we may construct a reaction-diffusion equation for the Shannon entropy density. However, since the current-source decomposition of a reaction-diffusion equation is non-unique, we have had to develop a second key concept, that of an irreducible source term, which is uniquely defined at least for polynomial source terms and which seems to be practically useful as a diagnostic tool. The information irreversibility of the PDE may be analysed directly from the sign of the irreducible fully nonlinear local source term of the entropy density. All second order diffusion equations are information-irreversible. Compared to second order diffusion equations, the entropy behaviour of fourth order equations is quite different. The familiar fourth order diffusion equations that arise in practical applications are not information-irreversible. Contrary to an impression that might easily be formed from the familiar cases, there are some classes of closely related fourth order diffusion equations that are in fact information-irreversible. Information irreversibility seems to be associated with regular smoothing behaviour of solutions, as depicted for example in
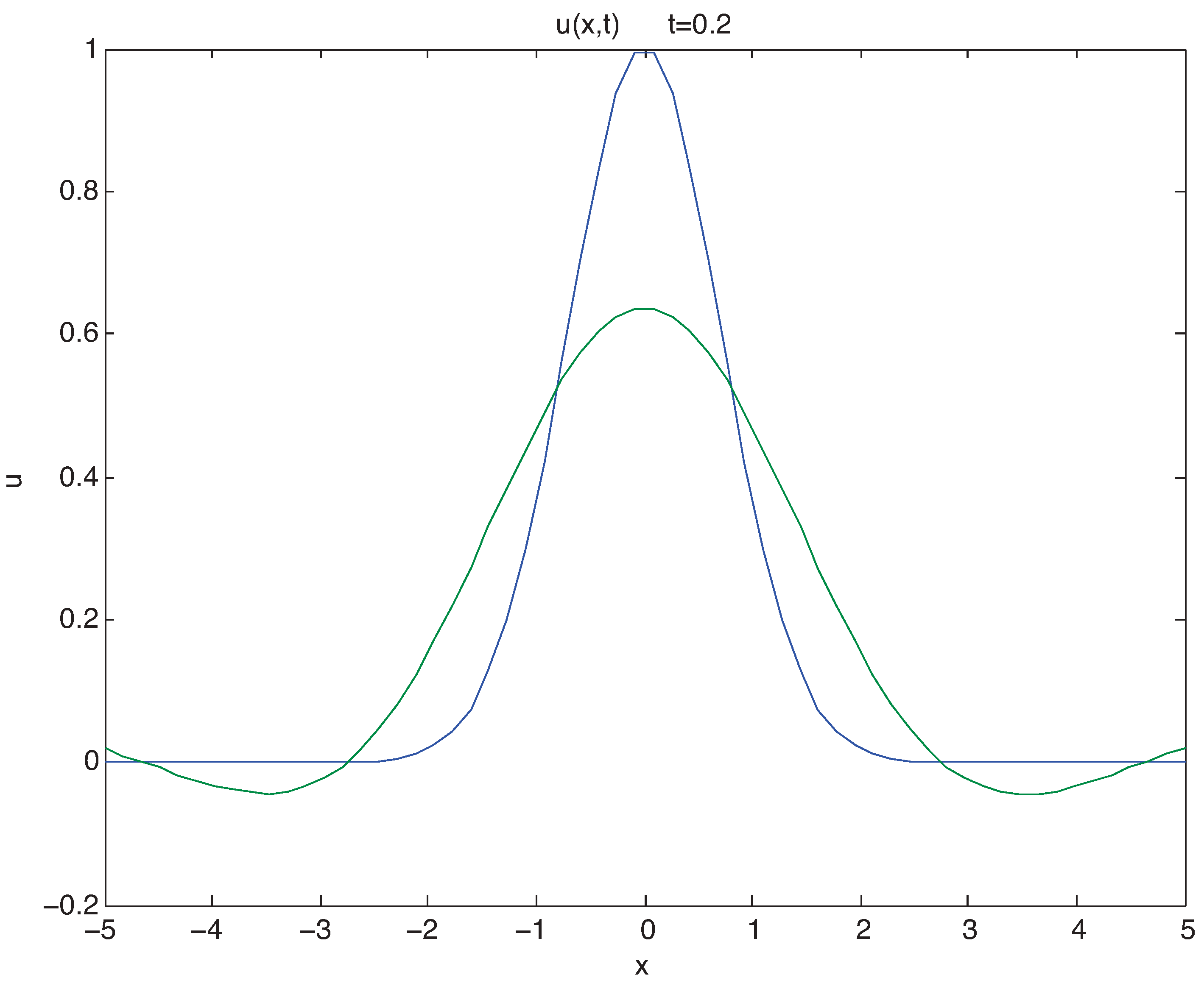
Figure 4. As far as the author is aware, such regular behaviour has not been observed before in the solutions of fourth order evolution equations.
A proof of the uniqueness of the irreducible source term for general functional forms of a reactiondiffusion equation, is given here for the case when the nominal source term is a meromorphic function of the dependent variable and its spatial derivatives. Generally, a monotonic decrease of information is associated with smoothing of ripples. It remains to be seen whether a form of maximum principle might be valid for the restricted class of fourth order nonlinear diffusion equations that obey information irreversibility. In all cases when we have established information-irreversibility, a numerical solution with Gaussian initial conditions maintains positivity and it does not generate new extrema. Conversely, when information is reversible, the solutions generate extrema and they lose positivity. With this limited but suggestive evidence, we conjecture that for zero-flux boundary value problems and positive initial conditions, information-irreversibility implies positivity. It remains to be seen whether additional conditions need to be added before such a conjecture could be established as a true statement.
During the above investigation, we have naturally been led to the concept of a partner entropy that is conjugate to a notional energy density that generates a governing nonlinear PDE. This generalizes the Shannon entropy since the latter is the partner entropy to an energy that generates linear diffusion. However, it is not known if the partner entropy has any use beyond the conceptual. Since the thermodynamic conjugacy of temperature and entropy variables is traditionally defined through an expression for work done, a relation among temperature, entropy and energy variables, it is natural to define a conjugate temperature-entropy-energy triple. One could extend this idea further by applying the Legendre transform of enthalpy with respect to entropy to construct a conjugate temperature-entropy-enthalpy-free energy quadruple but this serves little purpose in the present paper.
In principle, one could define an entropy density even from solutions of PDEs that cannot be expressed in conservation form. However, we have not investigated whether such a concept has any use.