Entropy and Ordering of Hard Rods in One Dimension
Abstract
:1. Introduction
2. Phenomenology of the Tonks gas
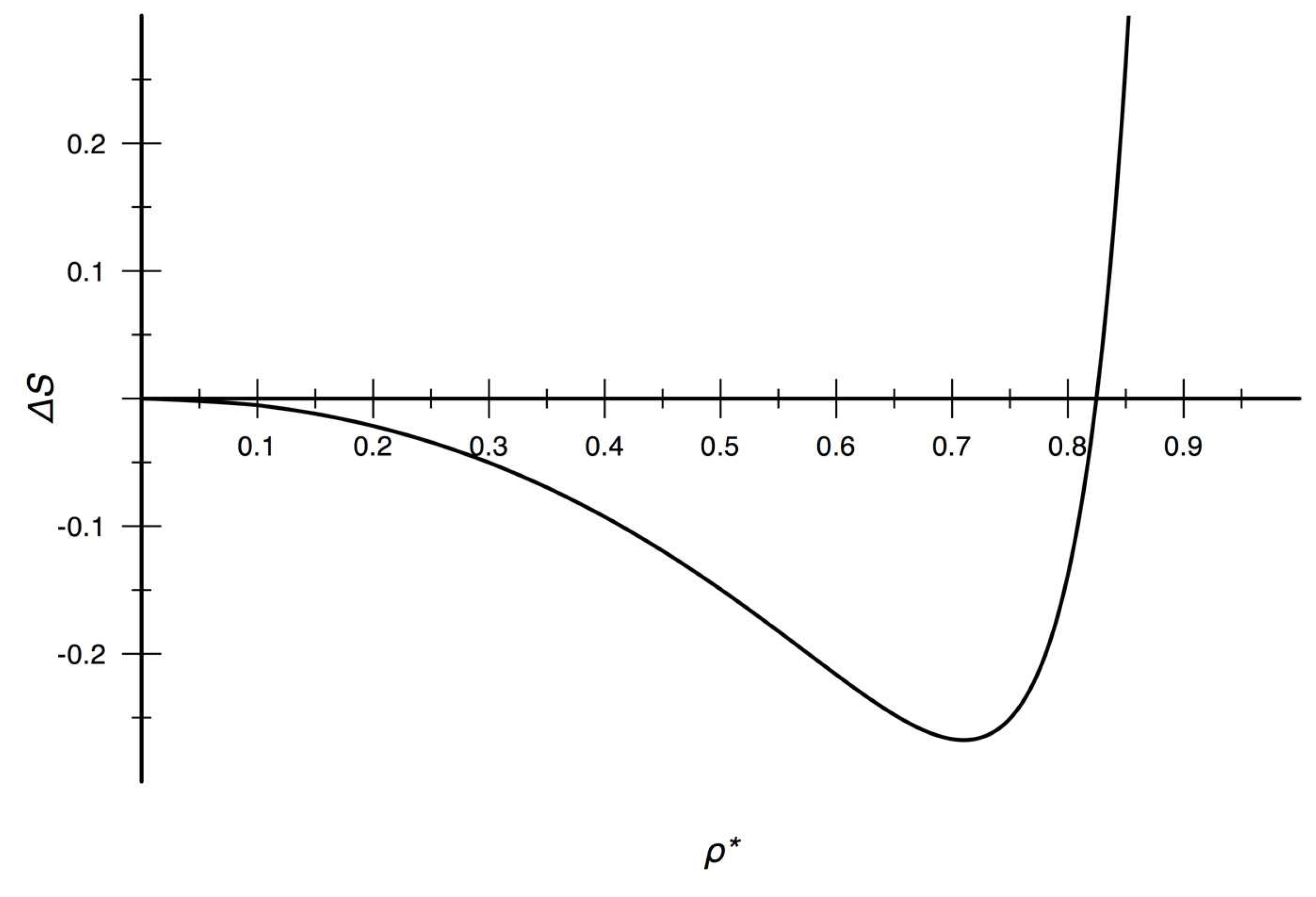
2.1. Residual multiparticle entropy
2.2. Structural properties at high densities
2.3. The unconstrained system versus the single occupancy cell model
3. Three-body correlations, Kirkwood’s coupling and periodic states at high density
4. Conclusions
References
- Green, H.S. The molecular theory of fluids; North-Holland, Amsterdam, 1952. [Google Scholar]
- Nettleton, R.E.; Green, M.S. Expression in terms of molecular distribution functions for the entropy density in an infinite system. The Journal of Chemical Physics 1958, 29(6), 1365–1370. [Google Scholar] [CrossRef]
- Baranyai, A.; Evans, D.J. Direct entropy calculation from computer simulation of liquids. Physical Review A 1989, 40(7), 3817–3822. [Google Scholar] [CrossRef]
- Yvon, J. Correlations and entropy in classical statistical mechanics; Pergamon Press: Oxford, 1969. [Google Scholar]
- Leff, H.S. Entropy differences between ideal and nonideal systems. American Journal of Physics 1969, 37(5), 548–553. [Google Scholar] [CrossRef]
- Baranyai, A.; Evans, D.J. Three-particle contribution to the configurational entropy of simple fluids. Physical Review A 1990, 42(2), 849–857. [Google Scholar] [CrossRef]
- Baranyai, A.; Evans, D.J. On the entropy of the hard sphere fluid. Zeitschrift für Naturforschung A 1991, 46, 27–31. [Google Scholar] [CrossRef]
- Giaquinta, P.V.; Giunta, G. About entropy and correlations in a fluid of hard spheres. Physica A 1992, 187, 145–158. [Google Scholar] [CrossRef]
- Giaquinta, P.V.; Giunta, G.; Prestipino Giarritta, S. Entropy and the freezing of simple liquids. Phys. Rev. A 1992, 45(10), R6966–R6968. [Google Scholar] [CrossRef] [PubMed]
- Caccamo, C.; Giaquinta, P.V.; Giunta, G. Phase diagram of simple fluids: a comprehensive theo-retical approach. Journal of Physics: Condensed Matter 1993, 5(34B), B75–B82. [Google Scholar]
- Cheng, A.; Klein, M.L.; Caccamo, C. Prediction of the phase diagram of rigid C60 molecules. Phys. Rev. Lett. 1993, 71(8), 1200–1203. [Google Scholar] [CrossRef] [PubMed]
- Lomba, E.; Almarza, N.G. Role of the interaction range in the shaping of phase diagrams in simple fluids. The hard sphere Yukawa fluid as a case study. The Journal of Chemical Physics 1994, 100(11), 8367–8372. [Google Scholar] [CrossRef]
- Lomba, E.; López-Martín, J.L.; Cataldo, H.M.; Tejero, C.F. Phase transitions in simple fluids: An application of a one-phase entropic criterion to Lennard-Jones and point Yukawa fluids. Phys. Rev. E 1994, 49(6), 5164–5168. [Google Scholar] [CrossRef]
- Giaquinta, P.V.; Giunta, G.; Malescio, G. Entropy versus correlations in simple fluids: The gas-liquid and freezing transitions. Physica A 1998, 250, 91–102. [Google Scholar] [CrossRef]
- Saija, F.; Prestipino, S.; Giaquinta, P.V. Scaling of local density correlations in a fluid close to freezing. The Journal of Chemical Physics 2001, 115(16), 7586–7591. [Google Scholar] [CrossRef]
- Giaquinta, P.V.; Saija, F. Re-entrant melting in the Gaussian-core model: The entropy imprint. ChemPhysChem 2005, 6(9), 1768–1771. [Google Scholar] [CrossRef] [PubMed]
- Prestipino, S.; Saija, F.; Giaquinta, P.V. Phase diagram of the Gaussian-core model. Physical Review E (Statistical, Nonlinear, and Soft Matter Physics) 2005, 71(5), 050102. [Google Scholar] [CrossRef] [PubMed]
- Saija, F.; Prestipino, S.; Giaquinta, P.V. Evaluation of phenomenological one-phase criteria for the melting and freezing of softly repulsive particles. The Journal of Chemical Physics 2006, 124(24), 244504. [Google Scholar] [CrossRef] [PubMed]
- Saija, F. An entropy-based approach to the freezing of the generalized exponential model. The Journal of Chemical Physics 2008, 128(13), 136101. [Google Scholar] [CrossRef] [PubMed]
- Saija, F. Statistical entropy and clustering in absence of attractive terms in the interparticle potential. Atti della Accademia Peloritana dei Pericolanti - Classe di Scienze Fisiche, Matematiche e Naturali 2008, 86(2), C1A0802002. [Google Scholar]
- Saija, F.; Giaquinta, P.V.; Giunta, G.; Prestipino Giarritta, S. On entropy and ordering in binary hard-sphere mixtures. Journal of Physics: Condensed Matter 1994, 6(46), 9853–9865. [Google Scholar] [CrossRef]
- Saija, F.; Giaquinta, P.V. Statistical entropy of a binary hard-sphere mixture: the low-density limit. Journal of Physics: Condensed Matter 1996, 8(43), 8137–8144. [Google Scholar] [CrossRef]
- Saija, F.; Prestipino, S.; Giaquinta, P.V. Entropy, correlations, and ordering in two dimensions. The Journal of Chemical Physics 2000, 113(7), 2806–2813. [Google Scholar] [CrossRef]
- Prestipino, S.; Giaquinta, P.V. Statistical entropy of a lattice-gas model: Multiparticle correlation expansion. Journal of Statistical Physics 1999, 96(1), 135–167. [Google Scholar] [CrossRef]
- Prestipino, S.; Giaquinta, P.V. Errata: Statistical entropy of a lattice-gas model: Multiparticle correlation expansion. Journal of Statistical Physics 2000, 98(1), 507–509. [Google Scholar] [CrossRef]
- Donato, M.G.; Prestipino, S.; Giaquinta, P.V. Entropy and multi-particle correlations in two-dimensional lattice gases. The European Physical Journal B 1999, 11(4), 621–627. [Google Scholar] [CrossRef]
- Prestipino, S. Analog of surface preroughening in a two-dimensional lattice Coulomb gas. Physical Review E 2002, 66(2), 021602. [Google Scholar] [CrossRef] [PubMed]
- Saija, F.; Pastore, G.; Giaquinta, P. Entropy and fluid-fluid separation in nonadditive hard-sphere mixtures. Journal of Physical Chemistry B 1998, 102(50), 10368–10371. [Google Scholar] [CrossRef]
- Saija, F.; Giaquinta, P. Entropy and fluid-fluid separation in nonadditive hard-sphere mixtures: The asymmetric case. Journal of Physical Chemistry B 2002, 106(8), 2035–2040. [Google Scholar] [CrossRef]
- Saija, F.; Giaquinta, P.V. Monte Carlo simulation and phase behavior of nonadditive hard-core mixtures in two dimensions. The Journal of Chemical Physics 2002, 117(12), 5780–5784. [Google Scholar] [CrossRef]
- Costa, D.; Saija, F.; Giaquinta, P. Angular correlations and statistical entropy of hard spherocylin-ders: the isotropic-nematic transition. Chemical Physics Letters 1998, 283(1-2), 86–90. [Google Scholar] [CrossRef]
- Costa, D.; Saija, F.; Giaquinta, P. Erratum to: “Angular correlations and statistical entropy of hard spherocylinders: the isotropic-nematic transition". Chemical Physics Letters 1999, 290(2), 252–252. [Google Scholar] [CrossRef]
- Costa, D.; Micali, F.; Saija, F.; Giaquinta, P. Entropy and correlations in a fluid of hard sphe-rocylinders: The onset of nematic and smectic order. Journal of Physical Chemistry B 2002, 106(47), 12297–12306. [Google Scholar] [CrossRef]
- Costa, D.; Saija, F.; Giaquinta, P. Smectic ordering of parallel hard spherocylinders: An entropy-based Monte Carlo study. Journal of Physical Chemistry B 2003, 107(35), 9514–9519. [Google Scholar] [CrossRef]
- Prestipino, S.; Giaquinta, P.V. The entropy multiparticle-correlation expansion for a mixture of spherical and elongated particles. Journal of Statistical Mechanics: Theory and Experiment 2004, 2004(09), P09008. [Google Scholar] [CrossRef]
- Saija, F.; Saitta, A.M.; Giaquinta, P.V. Statistical entropy and density maximum anomaly in liquid water. The Journal of Chemical Physics 2003, 119(7), 3587–3589. [Google Scholar] [CrossRef]
- Lord Rayleigh. On the virial of a system of hard colliding bodies. Nature 1891, 45(1152), 80–82. [Google Scholar]
- Herzfeld, K.F.; Goeppert-Mayer, M. On the states of aggregation. The Journal of Chemical Physics 1934, 2(1), 38–45. [Google Scholar] [CrossRef]
- Tonks, L. The complete equation of state of one, two and three-dimensional gases of hard elastic spheres. Phys. Rev. 1936, 50(10), 955–963. [Google Scholar] [CrossRef]
- Lieb, E.H.; Mattis, D.C. (Eds.) Mathematical Physics in One Dimension; Perspectives in Physics; Academic Press: New York, 1966.
- Percus, J.K. Exactly sovable models of classical many-body systems. Lebowitz, J.L., Ed.; In Simple models of equilibrium and nonequilibrium phenomena, volume 13 of Studies in Statistical Mechanics; chapter 1; pp. 1–158. North-Holland Physics Publishing: Amsterdam, 1987. [Google Scholar]
- Salsburg, Z.W.; Zwanzig, R.W.; Kirkwood, J.G. Molecular distribution functions in a one-dimensional fluid. The Journal of Chemical Physics 1953, 21(6), 1098–1107. [Google Scholar] [CrossRef]
- Sells, R.L.; Harris, C.W.; Guth, E. The pair distribution function for a one-dimensional gas. The Journal of Chemical Physics 1953, 21(8), 1422–1423. [Google Scholar] [CrossRef]
- Borzsák, I.; Baranyai, A. On the convergence of Green’s entropy expansion. Chemical Physics 1992, 165(2-3), 227–230. [Google Scholar] [CrossRef]
- Krekelberg, W.P.; Shen, V.K.; Errington, J.R.; Truskett, T.M. Residual multiparticle entropy does not generally change sign near freezing. The Journal of Chemical Physics 2008, 128(16), 161101. [Google Scholar] [CrossRef] [PubMed]
- Hoover, W.G. Computational Statistical Mechanics; Elsevier: Amsterdam, 1991. [Google Scholar]
- Piasecki, J.; Peliti, L. Harmonic properties of hard-sphere crystals: a one-dimensional study. Journal of Physics A: Mathematical and General 1993, 26(19), 4819–4825. [Google Scholar] [CrossRef]
- Barnes, C.D.; Kofke, D.A. Exact solution for the singlet density distributions and second-order correlations of normal-mode coordinates for hard rods in one dimension. The Journal of Chemical Physics 1999, 110, 11390–11398. [Google Scholar] [CrossRef]
- Barnes, C.D.; Kofke, D.A. A comparison of some variational formulas for the free energy as applied to hard-sphere crystals. The Journal of Chemical Physics 2002, 117, 9111–9115. [Google Scholar] [CrossRef]
- Haus, J.W.; Raveché, H.J. Computer studies of dynamics in one dimension: Hard rods. The Journal of Chemical Physics 1978, 68(11), 4969–4976. [Google Scholar] [CrossRef]
- Lovett, R. On the stability of a fluid toward solid formation. The Journal of Chemical Physics 1977, 66(3), 1225–1230. [Google Scholar] [CrossRef]
- Torquato, S.; Lu, B.; Rubinstein, J. Nearest-neighbor distribution functions in many-body systems. Physical Review A 1990, 41(4), 2059–2075. [Google Scholar] [CrossRef]
- Truskett, T.M.; Torquato, S.; Debenedetti, P.G. Density fluctuations in many-body systems. Physical Review E 1998, 58(6), 7369–7380. [Google Scholar] [CrossRef]
- Bishop, M.; Whitlock, P.A.; Klein, D. The structure of hyperspherical fluids in various dimensions. The Journal of Chemical Physics 2005, 122(7), 074508. [Google Scholar] [CrossRef] [PubMed]
- Hoover, W.G.; Alder, B.J. Cell theories for hard particles. The Journal of Chemical Physics 1966, 45(7), 2361–2367. [Google Scholar] [CrossRef]
- Elkoshi, Z.; Reiss, H.; Hammerich, A.D. One-dimensional rigorous hole theory of fluids: Internally constrained ensembles. Journal of Statistical Physics 1985, 41(3-4), 685–709. [Google Scholar] [CrossRef]
- Hirschfelder, J.; Stevenson, D.; Eyring, H. A theory of liquid structure. The Journal of Chemical Physics 1937, 5(11), 896–912. [Google Scholar] [CrossRef]
- Kirkwood, J.G. Statistical mechanics of fluid mixtures. The Journal of Chemical Physics 1935, 3(5), 300–313. [Google Scholar] [CrossRef]
- Kirkwood, J.G.; Monroe Boggs, E. The radial distribution function in liquids. The Journal of Chemical Physics 1942, 10(6), 394–402. [Google Scholar] [CrossRef]
- Cole, G.H.A. Classical fluids and the superposition approximation. Reports on Progress in Physics 1968, 31(2), 419–470. [Google Scholar] [CrossRef]
- Kunkin, W.; Frisch, H.L. Comment on Kirkwood instability. The Journal of Chemical Physics 1969, 50(4), 1817–1818. [Google Scholar] [CrossRef]
- Green, K.A.; Luks, K.D.; MacCarthy, J.E.; Kozak, J.J. The influence of closure on the behaviour of the Yvon-Born-Green equation for a system of hard rods. Molecular Physics 1982, 45(4), 897–913. [Google Scholar] [CrossRef]
- Siders, P.; Kozak, J.J. The Kirkwood superposition approximation for hard rods at high pressure. The Journal of Chemical Physics 1984, 81(10), 4594–4602. [Google Scholar] [CrossRef]


© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Giaquinta, P.V. Entropy and Ordering of Hard Rods in One Dimension. Entropy 2008, 10, 248-260. https://doi.org/10.3390/e10030248
Giaquinta PV. Entropy and Ordering of Hard Rods in One Dimension. Entropy. 2008; 10(3):248-260. https://doi.org/10.3390/e10030248
Chicago/Turabian StyleGiaquinta, Paolo V. 2008. "Entropy and Ordering of Hard Rods in One Dimension" Entropy 10, no. 3: 248-260. https://doi.org/10.3390/e10030248
APA StyleGiaquinta, P. V. (2008). Entropy and Ordering of Hard Rods in One Dimension. Entropy, 10(3), 248-260. https://doi.org/10.3390/e10030248




