1. Introduction
Typically, microstructure observation techniques are critical for advancements in biotechnological research [
1,
2,
3,
4,
5]. To that end, several optical observation techniques that allow observations beyond the diffraction limit [
6,
7,
8] and those that are based on fluorescent staining techniques [
9,
10], such as photoactivated localization microscopy (PALM) and stimulated emission depletion (STED), have been developed and widely used [
11,
12,
13,
14,
15]. However, these techniques require long processing times for information collection and analysis owing to the involved staining process and the object-scanning requirements for image collection.
To mitigate this issue, a method based on speckle interferometry [
16,
17,
18] has been developed [
19]. Instead of the conventional optical observation technique, which analyzes the intensity distribution obtained by imaging the object of interest, this new observation technique achieves super-resolution by analyzing the phase components in the light wavefront captured by an optical microscope [
19].
This new observation method based on phase analysis detects changes in the phase distribution resulting from intentional lateral shifts of the object of interest, and it can observe microstructural shapes beyond the diffraction limit [
20]. To streamline this process, scattered light with multiple ray vectors is used to illuminate the measurement object.
Previously, the validity of this new observation technique was verified using diffraction gratings with known lattice constants as the measurement objects. In this validation, the geometry of the periodic microstructures with dimensions shorter than the diffraction limit of the objective lens used for measurements was obtained. The measurement results were compared with the microstructure results obtained using atomic force microscopy. The comparison results confirmed that the new observation technique was capable of observing structures beyond the diffraction limit [
19].
Subsequently, the validation was extended to randomly distributed microstructures using microsilica spheres with known diameters that exceeded the diffraction limit as the measurement objects [
21]. In the verification of micro-spheres, the result of the microspheres measured by this method was compared with the basic data disclosed by the microsphere manufacturer using statistical processing to demonstrate the effectiveness of this method. Furthermore, another validation based on microcharacters formed using line segments with widths of less than 100 nm with directionality in each element confirmed that the shapes of such microcharacters formed by line segments with line widths exceeding multiple diffraction limits could be detected [
20].
These results confirm that the speckle-interferometry-based microstructural observation technique using phase analysis of light is capable of observing microstructures comprising line widths of approximately 100 nm that exceed the diffraction limit.
Based on these results, it can be assumed that the layered organization within biological tissues apparent in the colored slide images of human cells [
22] can be modeled as a periodic structure such as a diffraction grating, which can be observed using this method. In addition, spherical tissues within living cells can be modeled using a measurement process based on microsilica spheres [
21]. Furthermore, it is assumed that the branch-like tissues in living organisms can be modeled in the form of microcharacters [
20].
Based on the results of virtual biological observation experiments conducted using diffraction gratings, microsilica spheres, and microcharacters, we can infer that living biological tissues with sizes of approximately 100 nm can be observed using the new observation technique. Furthermore, observing the movements of microstructures in biological tissues in the form of moving images may be possible by analyzing and arranging consecutive individual images.
This paper discusses the possible challenges in applying super-resolution technique based on speckle interferometry to the observation of living cellular tissues with complex structures, instead of artificial solid structures such as diffraction gratings, microspheres, and microcharacters; for this, chromosomes produced during cell division in garlic were considered as the measurement objects.
As confirmed by the abovementioned verification results for solid structures, the speckle interferometry-based observation technique for microstructures is capable of observing structures as small as 100 nm. Thus, in this study, garlic chromosomes were selected as the measurement samples because they are cellular tissues that are easy to handle and, thus, can be utilized to identify challenges that may arise when handling living organisms.
Notably, the width of a garlic chromosome is approximately 800 nm, which is approximately on the same scale as the diffraction limit of the optical system used in this study. The cellular-tissue sample-preparation process is also based on traditionally established general processing.
Our results indicate that the super-resolution technique based on speckle interferometry can observe cellular tissues with complex structures that are subjected to conventional cell-fixation treatments similar to solid specimens, such as microspheres and microcharacters.
Therefore, based on the results obtained for solid objects, we hypothesize that biological cellular tissues that are approximately 100 nm in size may be observable using this technique.
However, the shapes of the measured objects were distorted when the cells were subjected to traditional plant-cell fixation treatments, as in the present study.
Thus, it is necessary to develop a method to observe living cells naturally without subjecting them to fixation treatments, along with an optical system that allows horizontal growth of the sample in the culture medium.
3. Results and Discussion
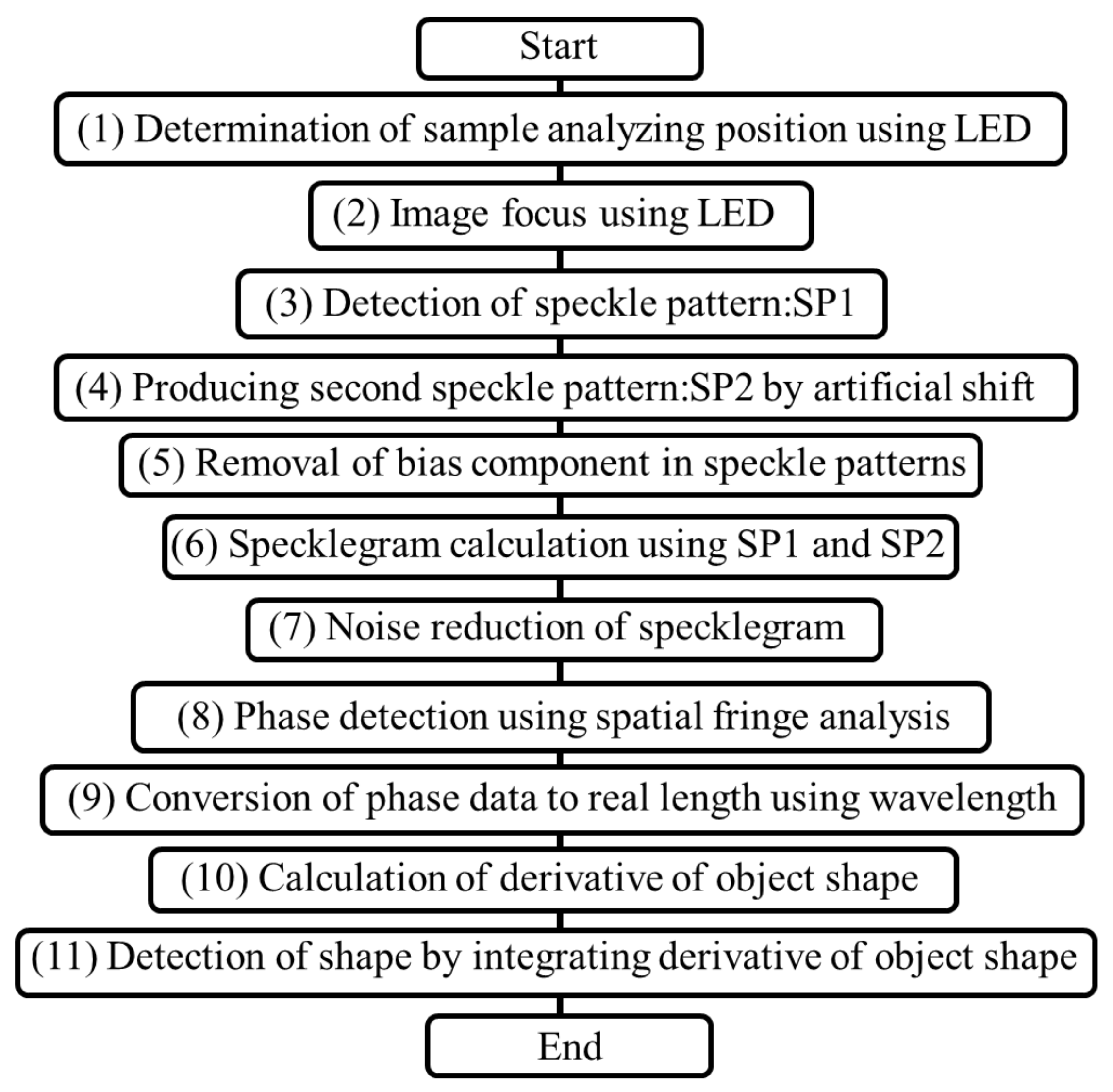
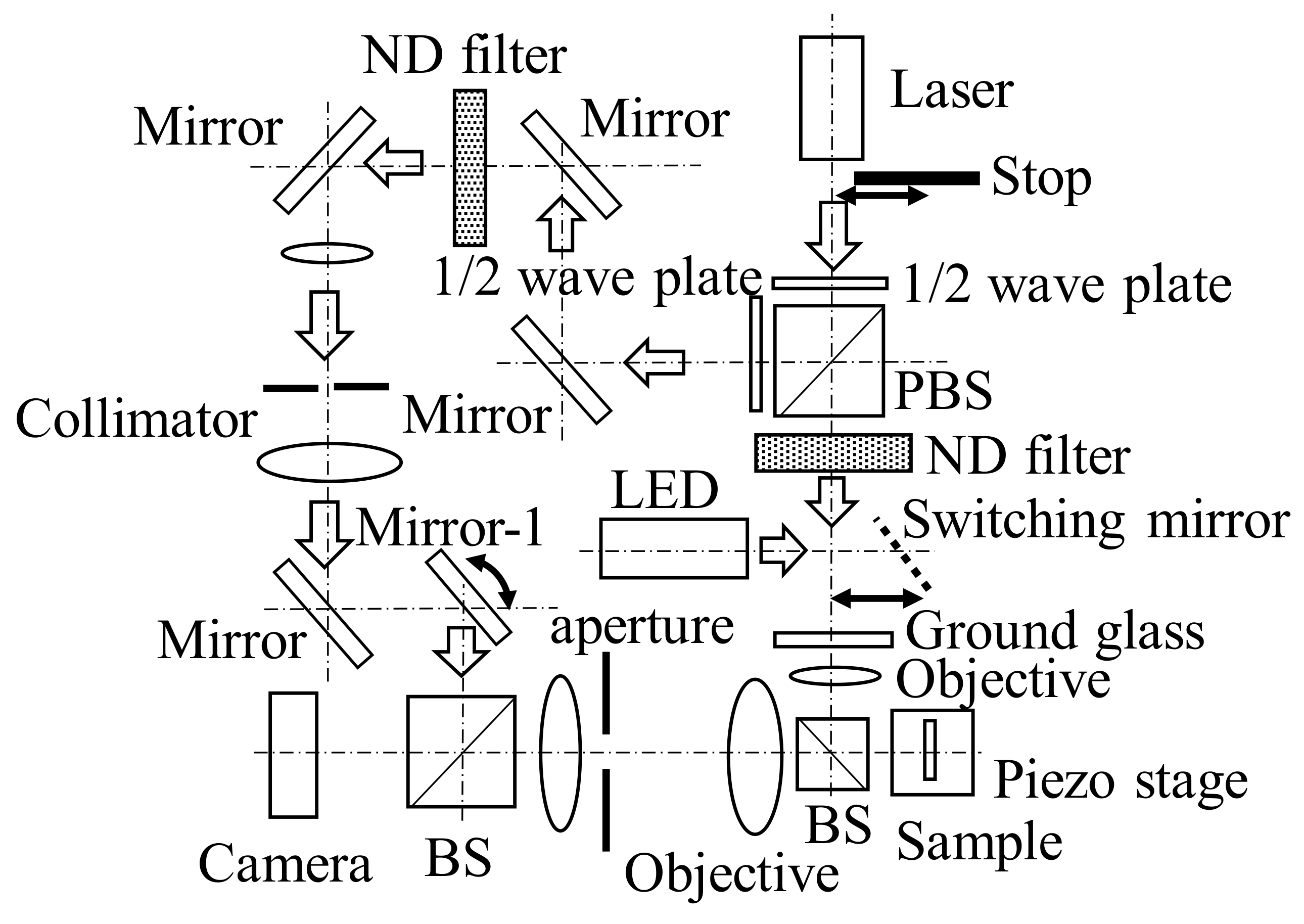
After blocking the laser light by installing a block in the optical path directly in front of the laser light source and after turning on the LED, a switching mirror was inserted into the laser optical path of the optical system, as depicted in
Figure 2. In addition, the sample was precisely positioned on the piezo stage; thus, images could be captured with a focus on the cell tissues. The use of LEDs enabled efficient focusing on cellular tissues, and the observations were not affected by unwanted interference fringes, which are generated in large numbers during laser irradiation.
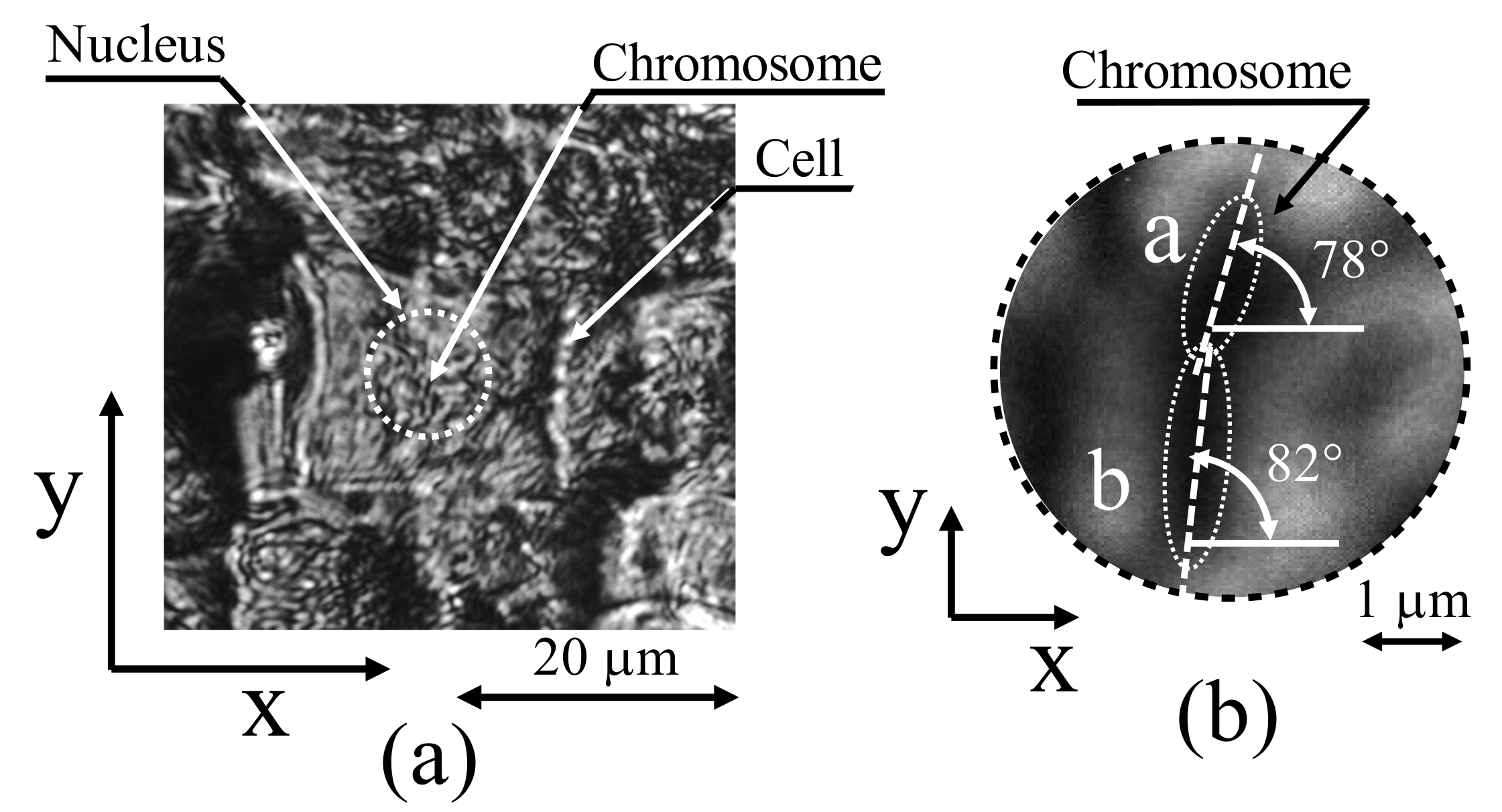
Figure 3b indicates that the garlic-cell tissues were relatively large-approximately 20 μm. By further magnifying the cell tissues using the optical system presented in
Figure 2, the image depicted in
Figure 4a was captured.
At the center of the cell, the nucleus was enclosed by a white dashed line. When the chromosomes scattered inside the nucleus were further magnified, individual stained chromosomes could be observed, as illustrated in
Figure 4b. However, the image is already fuzzy because the chromosomes are approximately the same size as the diffraction limit. Among the chromosomes that were observed in this manner, two chromosomes (a and b shown in
Figure 4b) that were relatively large and easy to observe were selected for further observations of the fine structure.
To observe the 3D structure of chromosomes a and b, depicted in
Figure 4b, the stopping and switching mirrors were released in the optical system, the light source was restored to a laser light source (wavelength: 671 nm), and the area around the cell nucleus was magnified and captured. Accordingly, a speckle pattern was recorded, as depicted in
Figure 5a. Several spherical light speckles were generated by the illumination light passing through the ground glass placed in the optical system [
17]. As stated, a Fourier transform was performed on this speckle pattern, and frequency domain information, shown in
Figure 5b, was recorded [
24]. Here, note that only the signal component was extracted to perform spatial-fringe analysis based on speckle interferometry; the first speckle pattern (SP1) was detected by shifting it by 128 pixels (=1024/8) in the frequency domain to obtain a carrier signal of 8 pixels/period.
In contrast, the speckle pattern depicted in
Figure 5a was shifted horizontally by 3 pixels, which is the optimal shift in this method, to create a virtual speckle pattern, as reported in a previous study [
23]. Subsequently, the signal component was detected in the frequency domain in the same manner, as illustrated in
Figure 5b. SP2 was artificially created based on (4) in the flowchart depicted in
Figure 1. Using this technique of artificially creating a second speckle pattern, 3D analysis could be performed based on only a single speckle pattern, as depicted in
Figure 5a.
Notably, this technique enables one to capture the dynamically changing deformation processes of an object in the form of moving images; this can be accomplished by analyzing the speckle patterns captured sequentially for the object subjected to deformation over time and displaying them in succession. This function is considered essential for biological observations.
The specklegram depicted in
Figure 6a was obtained after the specklegram between SP1 and the carrier component of 8 pixels/cycle were added, and the artificially created SP2 was determined using the process described in a previous study [
23,
27]. In this specklegram, fringe information with a period of 8 pixels was provided for use in subsequent processing based on the spatial-fringe analysis method.
However, as stated, speckles are generally treated as noise components [
25]; therefore, this specklegram contained several noise components owing to the influence of unsolved speckles [
29]. Thus, it was necessary to use a noise-reduction processing method that matched each signal component of the measurement object, as demonstrated in a previous study [
26], where the information of the object was extracted using the directional characteristics exhibited by chromosomes.
As depicted in
Figure 4b, chromosomes a and b were the objects observed using this method. Generally, the origin of the coordinate system for an image captured using an industrial TV camera lies in the upper-left corner, whereas in a computer-processed image, this origin lies in the lower-left corner. In this study, all images were modified such that the origin of the image was positioned in the lower-left corner of the image at the time of capture to reduce complexity, and the passband of the filter was determined.
For example, let us consider the case of a diffraction grating with a saw-tooth wave-shaped cross section along the x-direction and a constant shape along the y-direction. When such a grating is transformed using a Fourier transform, there exists a signal peak in the frequency domain associated with the period of the saw-tooth wave along the x-direction. In addition, the higher-order frequency signal peaks that form the saw-tooth wave shape are lined up along the frequency axis in the x-direction. However, in this study, no signal peaks were noted on the frequency axis in the y-direction because the object shape was unchanged. The signal components along the x- and y-directions were appropriately filtered in the frequency domain to reduce noise, and the inverse Fourier transform was used to reconstruct the original saw-tooth shape.
Notably, when several noise components are present in the frequency domain, as in this study, a filter that can allow the passage of only signal components necessary for reconstruction while eliminating as many noise components as possible is required. The original shape of a figure can be obtained by extracting signals using such a filter and reconstructing them using the inverse Fourier transform. Thus, an appropriate filter is required to perform this task.
Specifically, considering the bandwidth of the filter, detecting the fundamental frequency component of the saw-tooth wave along the x-direction and higher-order signal components up to the highest possible frequency was necessary to reproduce the detailed grating cross section in the frequency domain. Typically, as grating strips extend along the y-direction, the grating figure, as a measurement object, is oriented along the y-direction. This indicates that the filter requires a wide passband up to a high frequency along the x-axis, and its bandwidth must be perpendicular to the shape orientation. Furthermore, if the shape is oriented along the y-direction, it is assumed that the original shape can be reproduced with a narrow passband because the same shape values continue along the y-direction.
Therefore, it is advantageous for a filter that restores the shape of samples using the inverse Fourier transform to have a wide passband along the direction perpendicular to the orientation of the figure and a narrow passband along the direction parallel to the orientation of the figure to eliminate as much noise as possible [
27].
Note that the analysis in this study was primarily based on the observation of cross-sectional shapes of chromosomes; therefore, a filter with a wide frequency band perpendicular to the longitudinal orientation of the chromosomes and a narrow frequency band along the longitudinal orientation of the chromosome was used to eliminate the maximum possible noise. The filter passband was determined according to the concept described in a previous study [
26].
Herein, by performing a Fourier transform on the image depicted in
Figure 6a, a specklegram in the frequency domain was obtained, as illustrated in
Figure 7, which indicated the presence of ample noise.
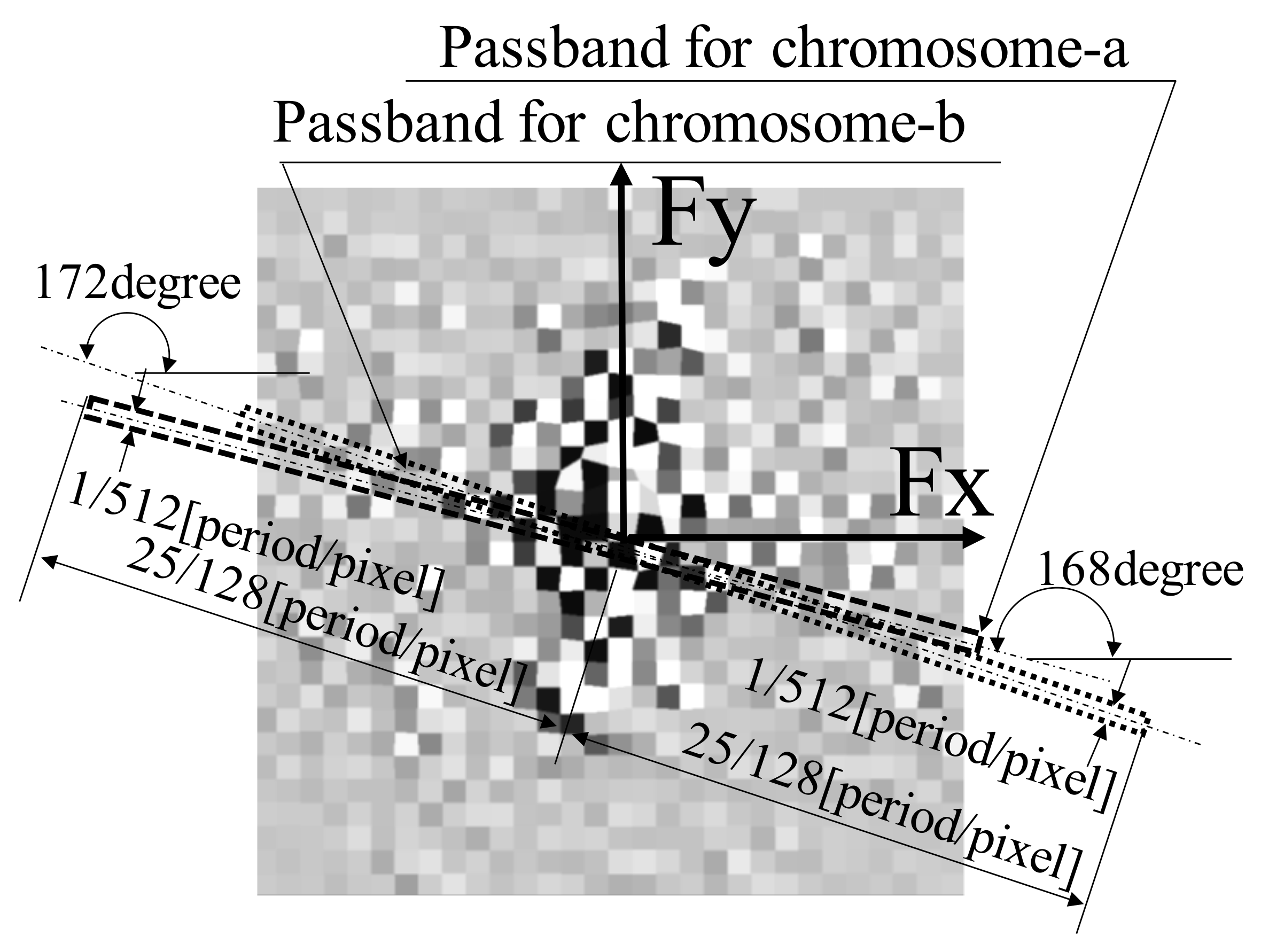
On examining chromosomes a and b, as depicted in
Figure 4b, the orientation of chromosome a was found to be 78° with respect to the horizontal line and that of chromosome b was found to be 82°. Based on this observation, a wide passband was set in the frequency domain along the direction perpendicular to the orientation of the measurement object to detect the signal components of chromosomes a and b, depicted in
Figure 7, as in a previous study [
27]. For chromosomes a and b, the passbands were set with slopes of 168° (=78° + 90°) and 172° (=82° + 90°), respectively. The width of the passband was set to 1/512 period/pixel, and the total length of the passband was set to 25/128 period/pixel. These parameters were set according to the results of a previous study [
27].
Using this filtering process, the specklegram depicted in
Figure 6a was processed as the fringe image shown in
Figure 6b. Furthermore, for the specklegram result illustrated in
Figure 6a, the phase distribution was obtained by analyzing the fringes of the specklegram after filtering, as illustrated in
Figure 6b; this approach reduced the influence of noise using the spatial-fringe analysis method. The camera magnification was set in advance using a reference scale such that 1 pixel of the camera in the optical system corresponded to 40 nm of the actual length.
Therefore, the resulting phase distribution was set to 2π rad for 335.5 nm (half the wavelength of the light source) because the light source wavelength was 671 nm, and the light was double passed. Furthermore, the speckle pattern was shifted by 3 pixels; therefore, the change rate distribution for the shape of the measurement object resulting from the 3 pixels shift (120 nm = 40 nm × 3 pixel) could be obtained by multiplying the phase distribution by (335.5 nm/2 rad)/120 nm, as depicted in (9) and (10) in
Figure 1.
By integrating this rate of change distribution for the shape along two dimensions using the method described in a previous study [
23,
27] and considering that 1 pixel accounted for 40 nm, the surface shape obtained from the contour map shown in
Figure 8b could be realized.
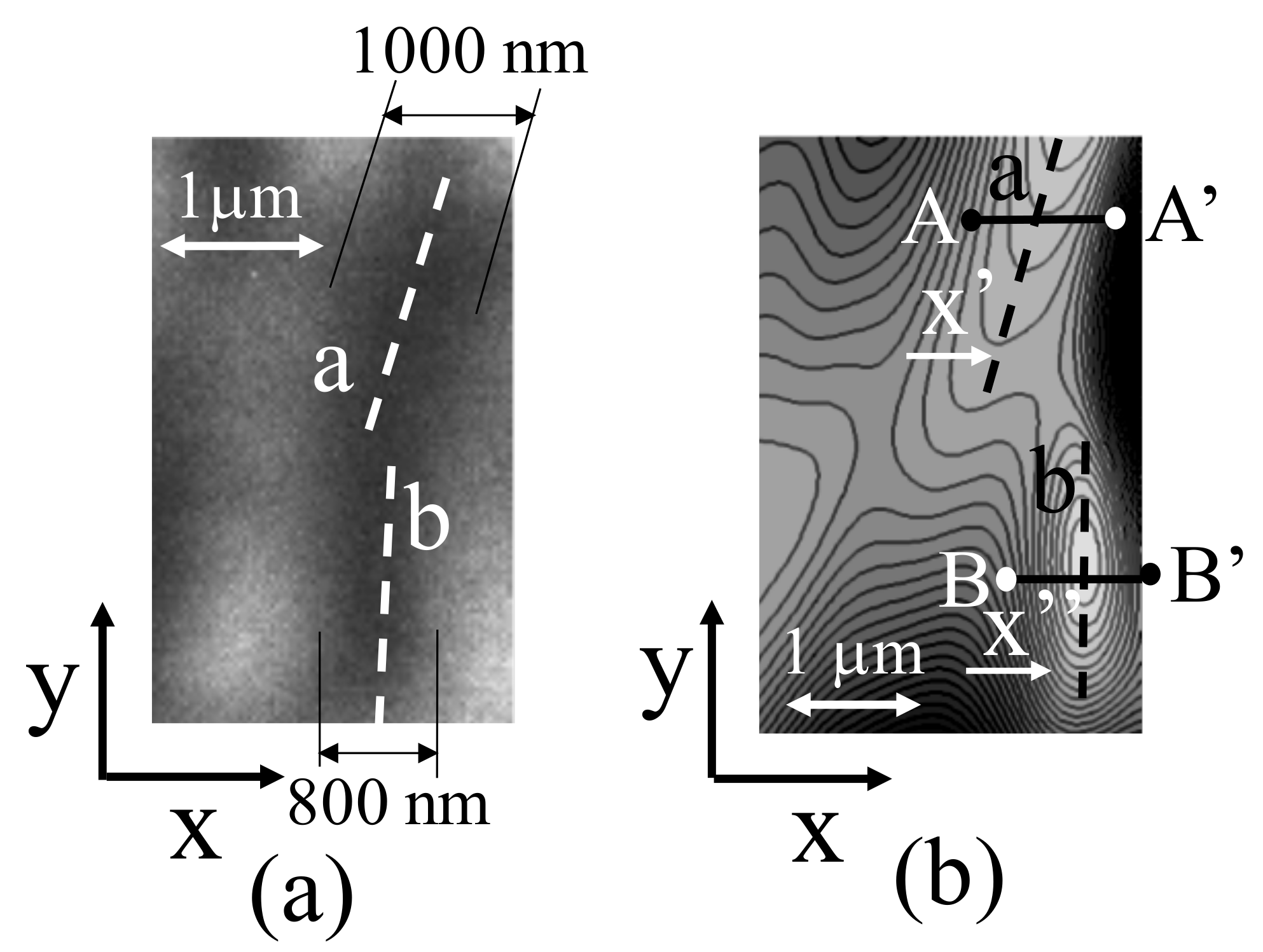
Figure 8a depicts magnified images of chromosomes a and b shown in
Figure 4b, and
Figure 8b illustrates chromosomes a and b in the same positions as those in the measurement results. The chromosomes stained by the carmine acetate solution exhibited widths of approximately 800–1000 nm, as illustrated in
Figure 8a.
Figure 9 depicts the cross-sectional shapes (A-A’ and B-B’) of chromosomes a and b, which are indicated as black dashed lines in
Figure 8b and 3D shapes at the same coordinates in
Figure 8a.
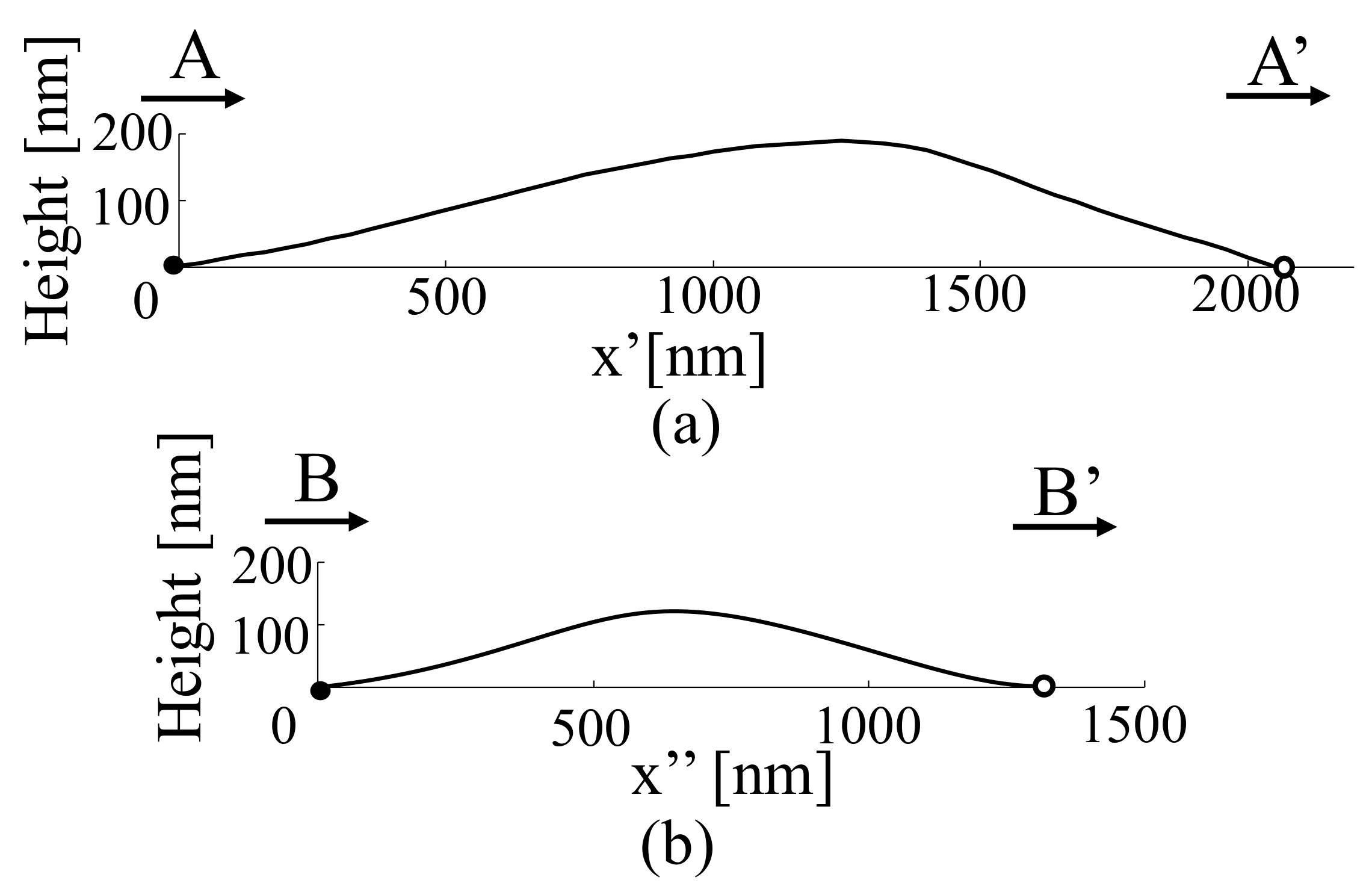
Along the A-A’ cross section of the chromosome shown in
Figure 9a, the width of the chromosome is greater than 1000 nm, as indicated in
Figure 8a. The observation of the chromosome cross section in the form of a 3D shape indicates that the height was approximately 200 nm, which suggests that the chromosome was a flattened tissue. If the chromosome cross section is considered to be approximately elliptical (not necessarily circular), the chromosome cross section depicted in
Figure 9a is a heavily condensed tissue, which may have resulted from the processing during chromosome-sample preparation.
Similarly, chromosome b, shown in
Figure 9b, is slightly narrower than chromosome a, and the height of the 3D cross section is approximately 130 nm. Both chromosomes have structures that would be more circular naturally; however, condensation is assumed to have occurred during the sample-preparation process, thus altering their shapes. The presence of chromosomes in the samples produced by the traditional sample-preparation process can be confirmed by staining and observing the samples using an optical microscope; however, the samples are considered highly distorted biological tissues. Therefore, it is necessary to develop a new sample-preparation method that does not deform the tissue or depend on conventional sample-preparation methods to realize biological observations.
The observations of structures with dimensions of 100 nm in solid samples, such as microspheres and microcharacters, along with the observations of other plant-cell structures with complex organizations, suggest that this technique may play an important role in the biotechnology field as a super-resolution technique.
Based on the numerous results discussed in this paper, peripheral technologies, such as optical-system fabrication, sample fabrication methods, and sample holding methods, will be developed in the future for the effective use of the speckle interferometry-based super-resolution technology in the field of biotechnology.