Electronic, Structural, Mechanical, and Thermodynamic Properties of CoYSb (Y = Cr, Mo, W) Half-Heusler Compounds as Potential Spintronic Materials
Abstract
:1. Introduction
2. Computational Details
3. Results
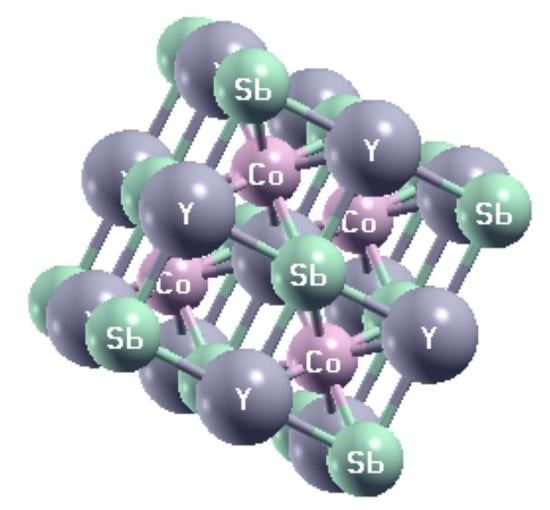
3.1. Structural Properties
3.2. Magnetic Properties
3.3. Electronic Band Structure
3.4. Mechanical Properties
3.5. Thermodynamic Properties
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kieven, D.; Klenk, R.; Naghavi, S.; Felser, C.; Gruhn, T. I-II-V half-Heusler compounds for optoelectronics: Ab initio calculations. Phys. Rev. 2010, B81, 075208. [Google Scholar] [CrossRef]
- Wurmehl, S.; Fecher, G.H.; Kandpal, H.C.; Kseno-fontov, V.; Felser, C.; Lin, H.J.; Morais, J. Geometric, electronic, and magnetic structure of Co2FeSi: Curie temperature and magnetic moment measurements and calculations. Phys. Rev. B 2005, 72, 184434. [Google Scholar] [CrossRef] [Green Version]
- Wolf, S.A.; Awschalom, D.D.; Buhrman, R.A.; Daughton, J.M.; von Molnar, S.; Roukes, M.L.; Chtchelkanova, A.Y.; Treger, D.M. Spintronics: A spin-based electronics vision for the future. Science 2001, 294, 1488–1495. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roy, A.; Bennett, J.W.; Rabe, K.M.; Vanderbilt, D. Half-Heusler semiconductors as piezoelectrics. Phys. Rev. Lett. 2012, 109, 037602. [Google Scholar] [CrossRef] [Green Version]
- Xiao, D.; Yao, Y.; Feng, W.; Wen, J.; Zhu, W.; Chen, X.Q.; Stocks, G.M.; Zhang, Z. Half-Heusler compounds as a new class of three-dimensional topological insulators. Phys. Rev. Lett. 2010, 105, 096404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, H.; Wray, L.A.; Xia, Y.; Xu, S.; Jia, S.; Cava, R.J.; Bansil, A.; Hasan, M.Z. Half-Heusler ternary compounds as new multifunctional experimental platforms for topological quantum phenomena. Nat. Mater. 2010, 9, 546–549. [Google Scholar] [CrossRef] [Green Version]
- Zeeshan, M.; Singh, H.K.; den Brink, J.V.; Kandpal, H.C. Ab initio design of new cobalt based half-Heusler materials for thermoelectric application. Phys. Rev. Mater. 2017, 1, 075407. [Google Scholar] [CrossRef] [Green Version]
- Minami, S.; Fumiyuki, I.; Yo, M.P.; Mineo, S. First-Principle study on thermoelectric properties of half-Heusler compound CoMSb (M= Sc, Ti, V, Cr and Mn). Appl. Phys. Lett. 2018, 113, 032403. [Google Scholar] [CrossRef] [Green Version]
- Li, S.D.; Yuan, Z.R.; Lu, L.Y.; Liu, M.M.; Huang, Z.G.; Zhang, F.M.; Du, Y.W. Effect of annealing on the magnetic entropy change of CoMnSb alloy. Mater. Sci. Eng. A 2006, 428, 332. [Google Scholar] [CrossRef]
- Larson, P.; Mahanti, S.D.; Kanatzidis, M.G. Structural stability of Ni-containing half-Heusler compounds. Phys. Rev. B 2000, 62, 12754. [Google Scholar] [CrossRef] [Green Version]
- Mancoff, F.B.; Bobo, J.F.; Richter, O.E.; Bessho, K.; Johnson, P.R.; Sinclair, R.; Nix, W.D.; White, R.; Clemens, B.M. Growth and characterization of epitaxial NiMnSb/PtMnSb C1b Heusler alloy superlattices. J. Mater. Res. 1999, 14, 1560. [Google Scholar] [CrossRef]
- De Groot, R.A.; Mueller, F.M.; van Engen, P.G.; Buschow, K.H.J. New class of materials: Half-metallic ferromagnets. Phys. Rev. Lett. 1983, 50, 2024. [Google Scholar] [CrossRef] [Green Version]
- Galanakis, I.; Mavropoulos, P.; Dederichs, P.H. Electronic structure and Slater Pauling behaviour in half-metallic Heusler alloys calculated from first principles. J. Phys. D 2006, 39, 765. [Google Scholar] [CrossRef]
- Nanda, B.R.K.; Dasgupta, J.I. Electronic structure and magnetism in half-Heusler compounds. Phys. Condens. Matter 2003, 15, 73077323. [Google Scholar] [CrossRef]
- Kanpal, H.C.; Felse, C.; Seshadri, R. Covalent bonding and the nature of band gaps in some half-Heusler compounds. J. Phys. D Appl. Phys. 2006, 39, 776. [Google Scholar] [CrossRef]
- Zhong-Yu, Y.; Li, S.; Meng-Mei, P.; Shu-Juan, S. First-principle studies of half-metallicities and magnetisms of the semi-Heusler alloys CoCrTe and CoCrSb. Acta Phys. Sin. 2016, 65, 127501. [Google Scholar] [CrossRef]
- Tobola, J.; Pierre, J. Electronic phase diagram of the XTZ (X= Fe, Co, Ni; T= Ti, V, Zr, Nb, Mn; Z= Sn, Sb) semi-Heusler compounds. J. Alloys Compd. 2000, 296, 243. [Google Scholar] [CrossRef]
- Kulkova, S.E.; Eremeev, S.V.; Kakeshita, T.; Kulkov, S.S.; Rudenski, G.E. The electronic structure and magnetic properties of full-and half-Heusler alloys. Mater. Trans. 2006, 47, 604. [Google Scholar] [CrossRef] [Green Version]
- Scandolo, S.; Giannozzi, P.; Cavaoni, C.; de Gironcoli, S.; Pasquarello, A.; Baroni, S. First-principles codes for computational crystallography in the Quantum-ESPRESSO package. Z. Krist. 2005, 220, 574579. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Available online: https://dalcorso.github.io/thermopw (accessed on 29 November 2021).
- Corso, A.D. Elastic constants of beryllium: A first-principles investigation. J. Phys. Condens. Matter 2016, 28, 075401. [Google Scholar] [CrossRef] [PubMed]
- Wyckoff, R.W.G. Crystal Structures, Crystal Structures, 2nd ed.; John Wiley and Sons: Hoboken, NJ, USA, 1963; Volume 1. [Google Scholar]
- Murnaghan, F.D. The Compressibility of Media under Extreme Pressures. Proc. Natl. Acad. Sci. USA 1944, 30, 244. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kubler, J. First principle theory of metallic magnetism. Phys. B+C 1984, 127, 257. [Google Scholar] [CrossRef]
- Galanakis, I.; Dederichs, P.H.; Mavropoulous, P.H. Slater-Pauling behavior and origin of the half-metallicity of the full-Heusler alloys. Phys. Rev. B 2002, 66, 174429. [Google Scholar] [CrossRef] [Green Version]
- Page, Y.L.; Saxe, P. Symmetry-general least-squares extraction of elastic data for strained materials from ab initio calculations of stress. Phys. Rev. B 2002, 65, 104104. [Google Scholar] [CrossRef]
- Born, M.; Huang, K. Dynamical Theory of Crystal Lattices. Dynamical Theory of Crystal Lattices; Oxford Clarendon Press: Oxford, UK, 1956; pp. 120–156. [Google Scholar]
- Voigt, W. Lehrbuck der Kristallphysik; B. B. Teubner: Leipzig, Germany, 1928; p. 739. [Google Scholar]
- Reuss, A.; Angew, Z. Calculation of the centrifugal limit of mixed crystals due to the plasticity condition for single crystals. Math. Mech. 1929, 9, 49. [Google Scholar]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Lond. 1952, 65, 349. [Google Scholar] [CrossRef]
- Huntington, H.B. Solid State Physics, F. Seitz and D. Properties of Engineering Ceramics; Kriegel, W., Palmour, H., Eds.; Academic Press Inc.: New York, NY, USA, 1958; Volume 7. [Google Scholar]
- Pugh, S.F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos. Mag. 1954, 45, 823. [Google Scholar] [CrossRef]
- Rakesh, J.; Jain, V.k.; Chandra, A.R.; Jain, V.; Lakshmi, N. Joural of Superconductivity and Magnetism; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Zener, C. Elasticity and Anelasticity of Metals; University of Chicago Press: Chicago, UK, 1948. [Google Scholar]
- Degheidy, A.R.; Elkenany, E.B. Electronic, optical, and mechanical properties of BN, AlN, and InN with zinc-blende structure under pressure. Chin. Phys. 2017, 26, 086103. [Google Scholar] [CrossRef]
- Gupta, D.C.; Ghosh, S.J. First-principal study of full Heusler alloys Co2VZ (Z = As, In). Magn. Magn. Mater. 2017, 435, 107–116. [Google Scholar] [CrossRef]
- Fu, H.; Li, D.; Peng, F.; Gao, T.; Cheng, X. Ab initio calculations of elastic constants and thermodynamic properties of NiAl under high pressures. Comput. Mater. Sci. 2008, 44, 774–778. [Google Scholar] [CrossRef]
- Anderson, O.L. A simplified method for calculating the Debye temperature from elastic constants. J. Phys. Chem. Solids 1963, 24, 909. [Google Scholar] [CrossRef]
- Fine, M.E.; Brown, L.D.; Marcus, H.L. Elastic constants versus melting temperature in metals. Scr. Metall. 1984, 18, 951–956. [Google Scholar] [CrossRef]







| Structural Phase | X | Y | Z |
|---|---|---|---|
| Type I | 4c | 4b | 4a |
| Type II | 4b | 4a | 4c |
| Type III | 4a | 4c | 4b |
| Alloys | Calculations | Structural Phase | (Å) | B (GPa) | B | (Ry) |
|---|---|---|---|---|---|---|
| CoCrSb | This work | Type I | 5.848 | 121.4 | 4.66 | −757.944 |
| other calculations | ||||||
| Type II | 6.031 | 97.6 | 4.33 | −757.856 | ||
| Type III | 5.935 | 98.6 | 4.71 | −757.869 | ||
| CoMoSb | Type I | 5.937 | 152.2 | 4.62 | −873.598 | |
| other calculations | ||||||
| Type II | 6.134 | 124.1 | 4.13 | −873.484 | ||
| Type III | 6.140 | 131.6 | 3.94 | −873.520 | ||
| CoWSb | Type I | 5.939 | 164.9 | 4.32 | −1269.888 | |
| Type II | 6.133 | 138.7 | 4.01 | −1269.758 | ||
| Type III | 6.145 | 148.2 | 3.81 | −1269.819 |
| () | Calculations | Structural Phase | Co | Y | Sb | Void | Total |
|---|---|---|---|---|---|---|---|
| CoCrSb | This work | Type I | −0.4473 | 2.3766 | −0.0573 | 0.138 | 2.01 |
| other calculations | |||||||
| Type II | −0.4917 | 3.0659 | −0.0625 | 0.328 | 2.84 | ||
| Type III | 1.1219 | 1.8089 | −0.0177 | 0.01169 | 3.03 | ||
| CoMoSb | Type I | 0.6685 | 0.9017 | −0.0148 | 0.2346 | 1.79 | |
| Type II | 1.0329 | 0.4100 | 0.0136 | 0.0435 | 1.20 | ||
| Type III | 0.9274 | 0.0711 | 0.0297 | 0.0082 | 1.02 | ||
| other calculations | |||||||
| CoWSb | Type I | 1.0274 | 1.2957 | −0.0285 | 0.1955 | 2.49 | |
| Type II | 0.8804 | 0.1896 | −0.0178 | 0.0078 | 1.06 | ||
| Type III | 1.6376 | 0.4698 | 0.0133 | 0.0293 | 2.15 |
| Compound | Calculations | Band Gap (eV) | HM Gap (ev) | SP % |
|---|---|---|---|---|
| CoCrSb | This work | 0.81 | 0.21 | 100 |
| others | ||||
| CoMoSb | 0.32 | 72 | ||
| others | ||||
| CoWSb | 33 |
| Calculated Properties | CoCrSb | CoMoSb | CoWSb |
|---|---|---|---|
| (GPa) | 202.83 | 250.02 | 264.14 |
| (GPa) | 79.61 | 117.98 | 131.46 |
| (GPa) | 55.11 | 42.30 | 30.16 |
| (GPa) | 123.22 | 132.04 | 123.68 |
| + 2 (GPa) | 362.04 | 485.97 | 527.05 |
| B (GPa) | 120.66 | 161.99 | 175.68 |
| G (GPa) | 57.63 | 50.59 | 41.61 |
| E (GPa) | 149.19 | 137.45 | 115.64 |
| A | 0.49 | 0.64 | 0.45 |
| 0.29 | 0.36 | 0.39 | |
| Pugh’s ratio | 2.09 | 3.20 | 4.22 |
| Compound | (m/s) | (m/s) | (m/s) | (K) | (K) |
|---|---|---|---|---|---|
| CoCrSb | 5027.79 | 2723.03 | 3037.67 | 354.68 | 1751.73 ± 300 |
| CoMoSb | 5105.36 | 2397.30 | 2688.55 | 308.93 | 2030.62 ± 300 |
| CoWSb | 4459.49 | 1891.93 | 2113.76 | 243.05 | 2114.07 ± 300 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uto, O.T.; Adebambo, P.O.; Akinlami, J.O.; Kenmoe, S.; Adebayo, G.A. Electronic, Structural, Mechanical, and Thermodynamic Properties of CoYSb (Y = Cr, Mo, W) Half-Heusler Compounds as Potential Spintronic Materials. Solids 2022, 3, 22-33. https://doi.org/10.3390/solids3010002
Uto OT, Adebambo PO, Akinlami JO, Kenmoe S, Adebayo GA. Electronic, Structural, Mechanical, and Thermodynamic Properties of CoYSb (Y = Cr, Mo, W) Half-Heusler Compounds as Potential Spintronic Materials. Solids. 2022; 3(1):22-33. https://doi.org/10.3390/solids3010002
Chicago/Turabian StyleUto, Oghenekevwe Timothy, Paul Olufunso Adebambo, Johnson Oluwafemi Akinlami, Stephane Kenmoe, and Gboyega Augustine Adebayo. 2022. "Electronic, Structural, Mechanical, and Thermodynamic Properties of CoYSb (Y = Cr, Mo, W) Half-Heusler Compounds as Potential Spintronic Materials" Solids 3, no. 1: 22-33. https://doi.org/10.3390/solids3010002
APA StyleUto, O. T., Adebambo, P. O., Akinlami, J. O., Kenmoe, S., & Adebayo, G. A. (2022). Electronic, Structural, Mechanical, and Thermodynamic Properties of CoYSb (Y = Cr, Mo, W) Half-Heusler Compounds as Potential Spintronic Materials. Solids, 3(1), 22-33. https://doi.org/10.3390/solids3010002