Coherent Phase States in the Coordinate and Wigner Representations
Abstract
:1. Introduction
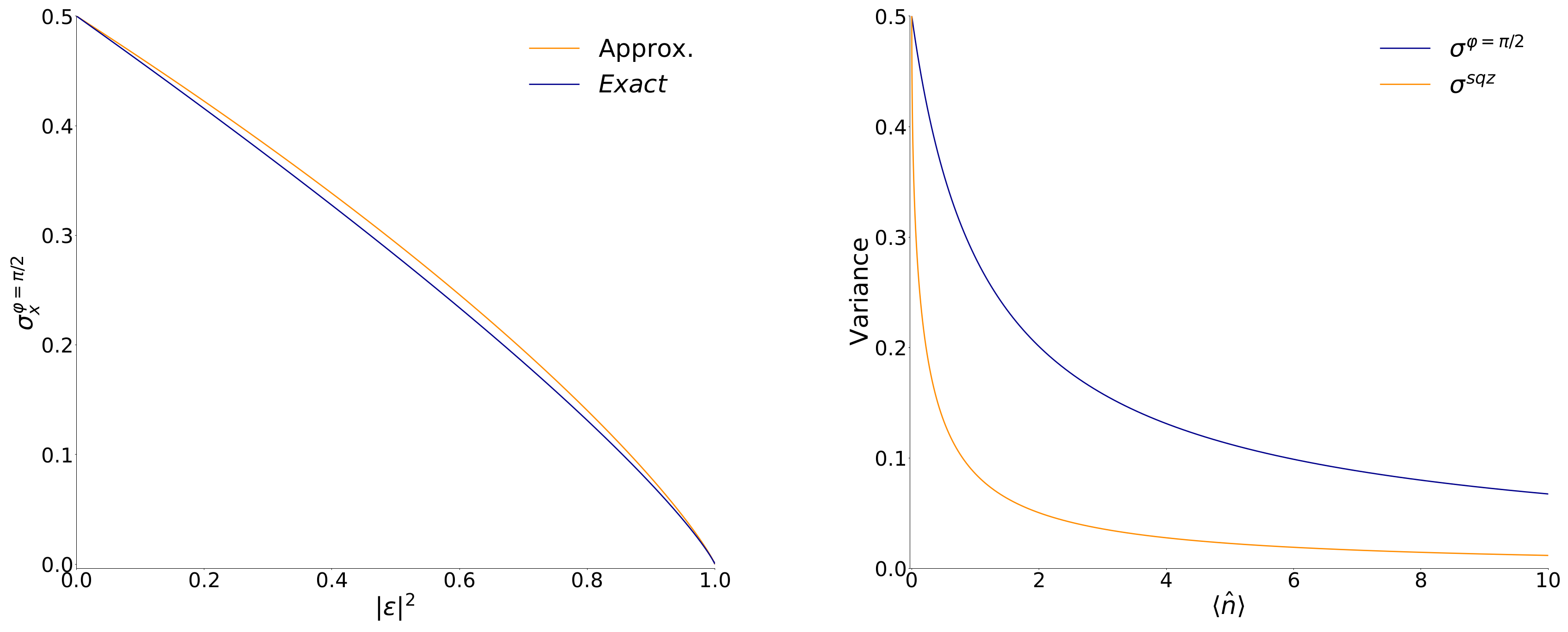
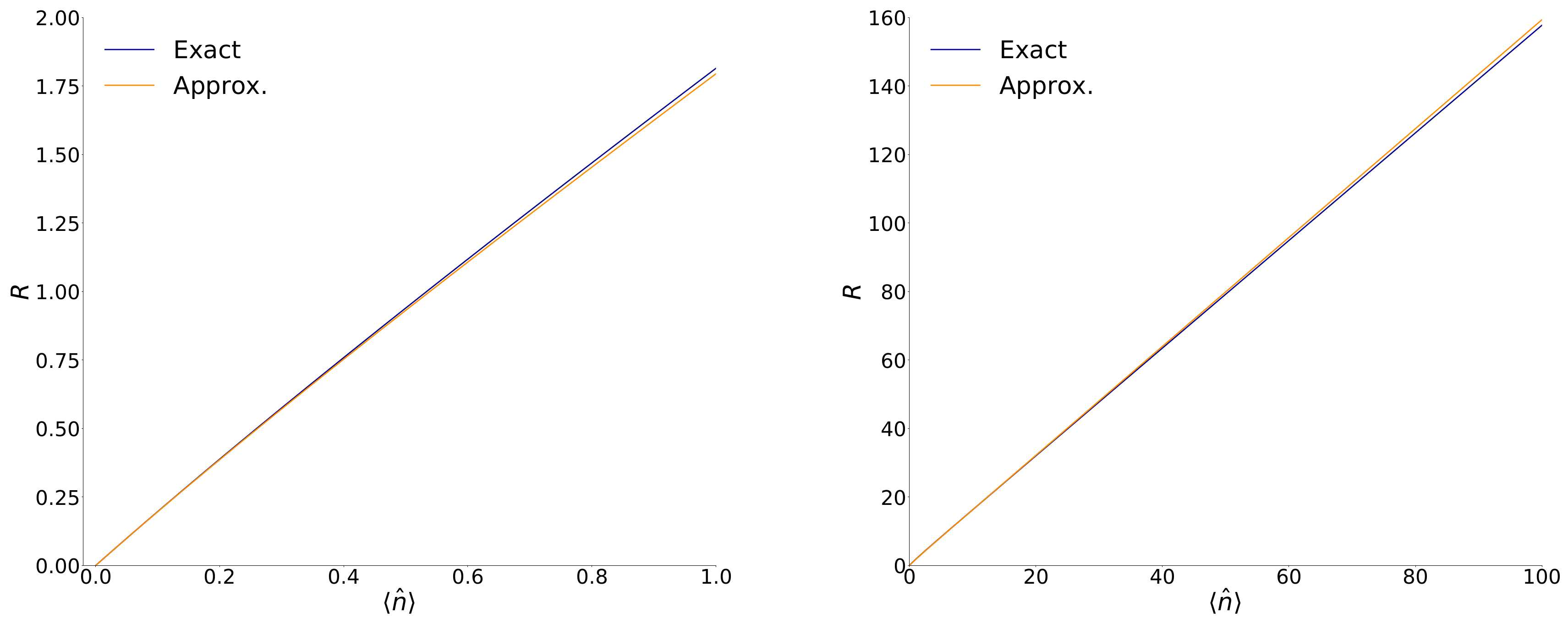
2. Quadrature Mean Values, Variances, and the Robertson–Schrödinger Uncertainty Product
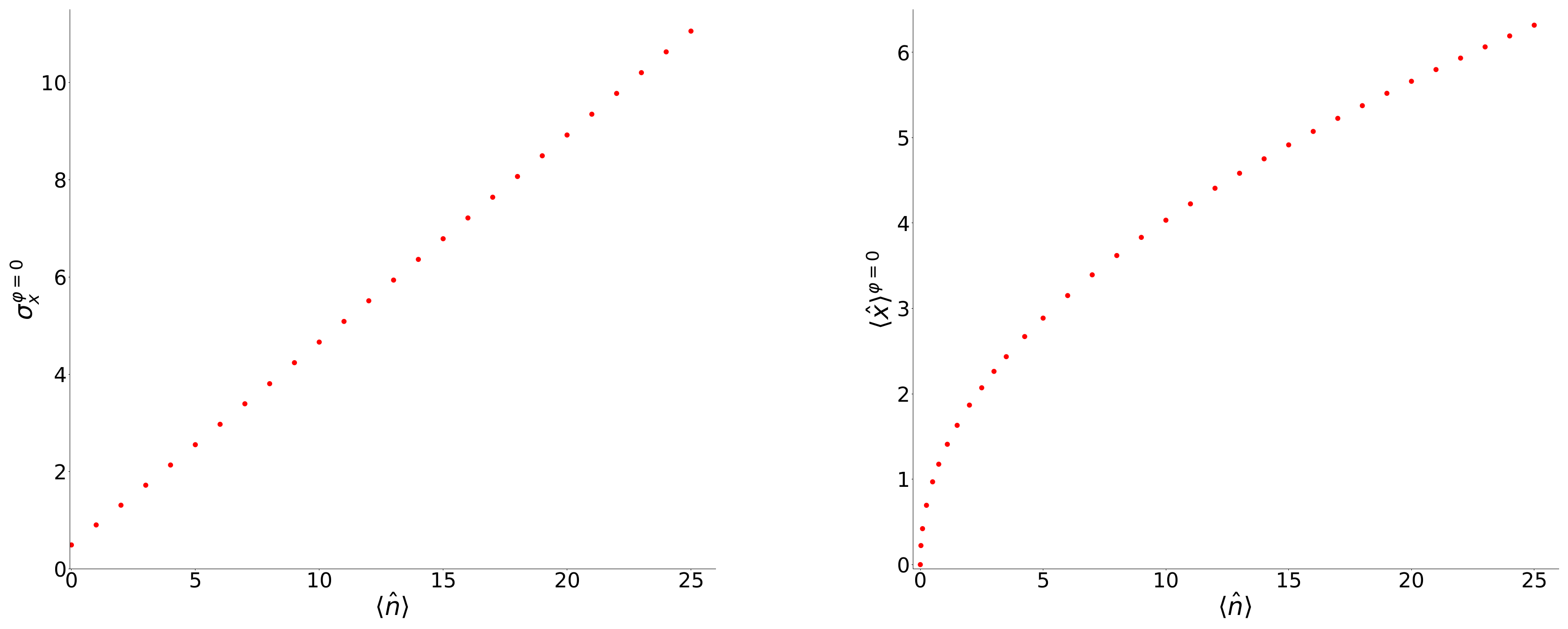
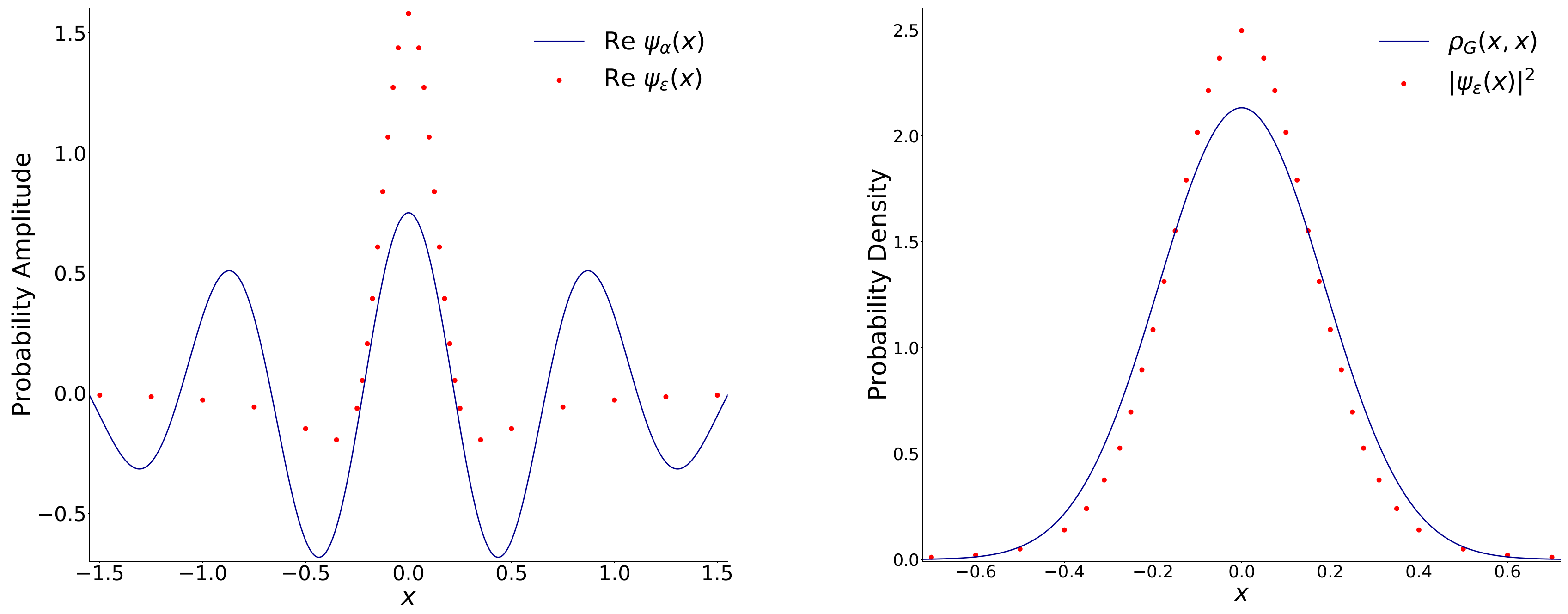
3. Wave Function and Probability Density
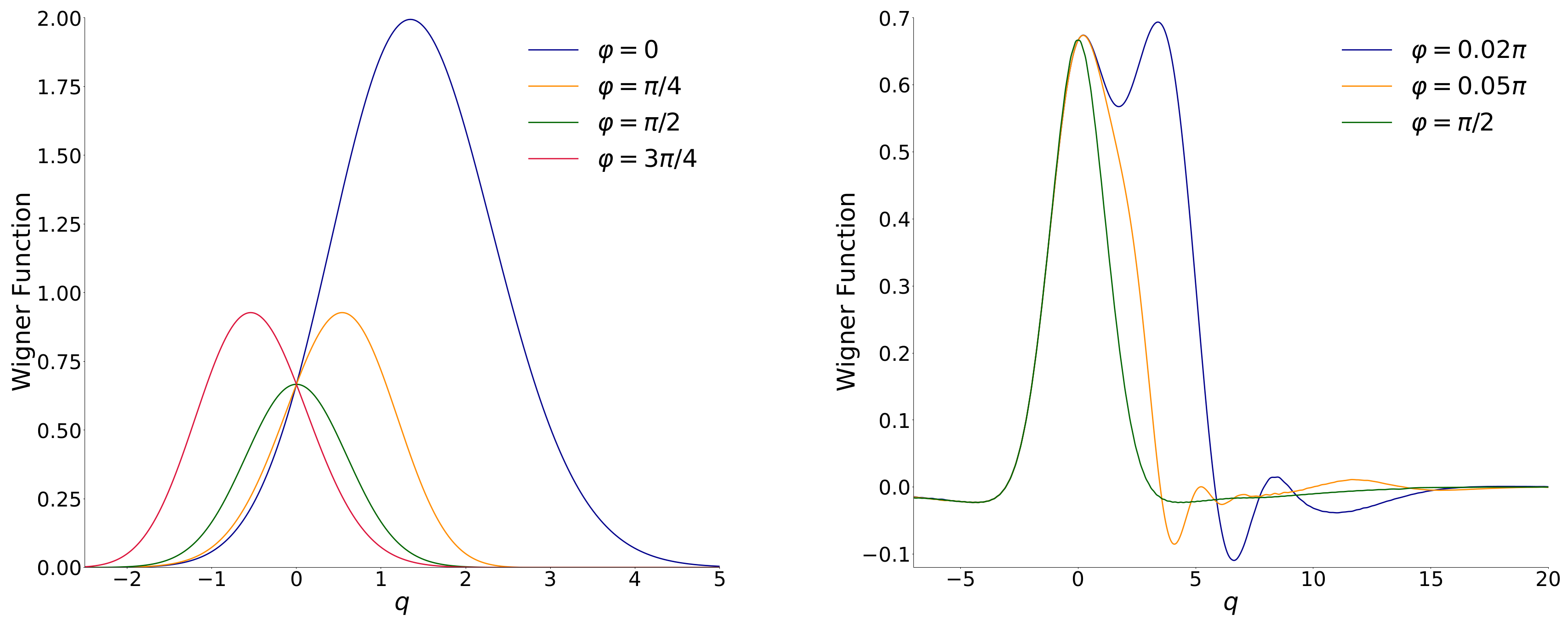
4. Wigner Function
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
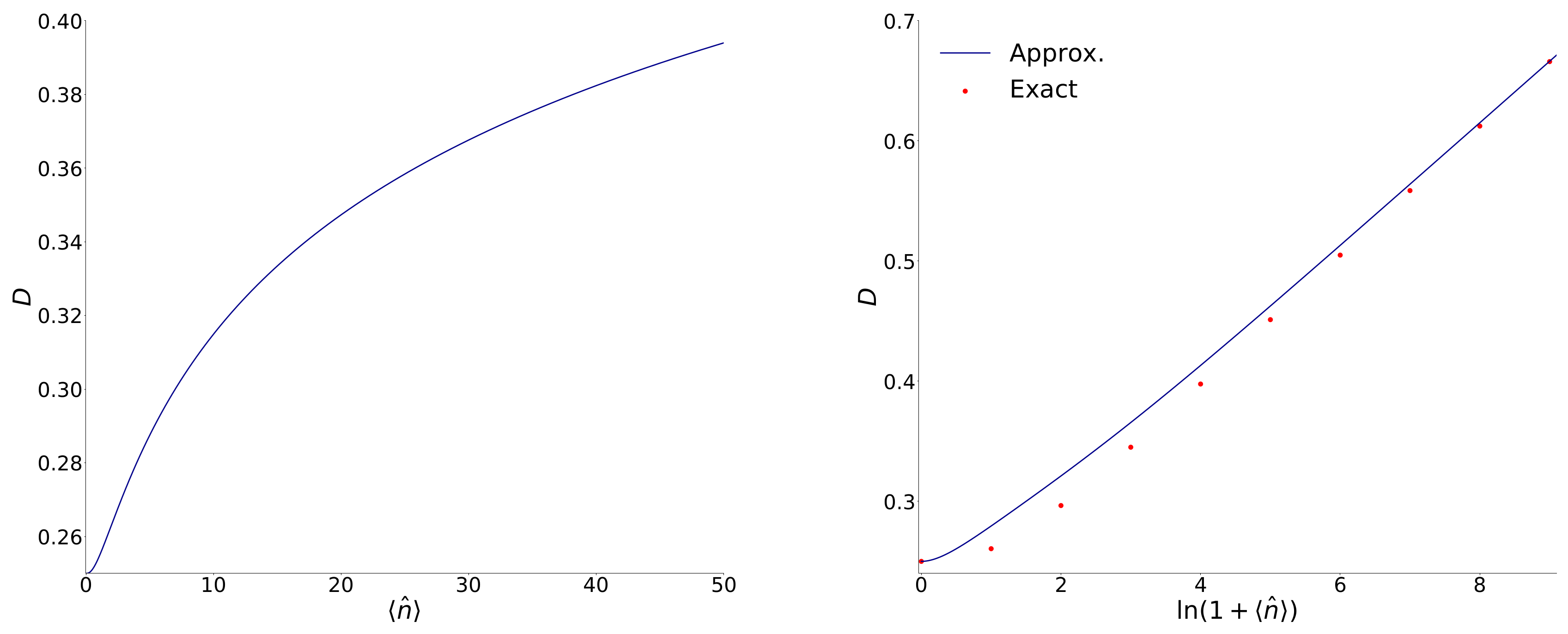
Appendix A. Calculations of the Gaussianity
References
- London, F. Über die Jacobischen Transformationen der Quantenmechanik. Z. Phys. 1926, 37, 915–925. [Google Scholar] [CrossRef]
- Carruthers, P.; Nieto, M. The phase-angle variables in quantum mechanics. Rev. Mod. Phys. 1968, 40, 411–440. [Google Scholar] [CrossRef] [Green Version]
- Garrison, J.C.; Wong, J. Canonically conjugate pairs, uncertainty relations, and phase operators. J. Math. Phys. 1970, 11, 2242–2249. [Google Scholar] [CrossRef]
- Loudon, R. Quantum Theory of Light; Oxford Univ. Press: Oxford, UK, 1973. [Google Scholar]
- Paul, H. Phase of a microscopic electromagnetic field and its measurement. Fortschr. Phys. 1974, 22, 657–689. [Google Scholar] [CrossRef]
- Lévy-Leblond, J.-M. Who is afraid of nonhermitian operators? A quantum description of angle and phase. Ann. Phys. 1976, 101, 319–341. [Google Scholar] [CrossRef]
- Bergou, J.; Englert, B.-G. Operators of the phase. Fundamentals. Ann. Phys. 1991, 209, 479–505. [Google Scholar] [CrossRef]
- Popov, V.N.; Yarunin, V.S. Photon phase operator. Theor. Math. Phys. 1991, 89, 1292–1297. [Google Scholar] [CrossRef]
- Vogel, W.; Schleich, W. Phase distribution of a quantum state without using phase states. Phys. Rev. A 1991, 44, 7642–7646. [Google Scholar] [CrossRef]
- Noh, J.W.; Fougères, A.; Mandel, L. Operational approach to the phase of a quantum field. Phys. Rev. A 1992, 45, 424–442. [Google Scholar] [CrossRef]
- Lukš, A.; Peřinová, V. Presumable solutions of quantum phase problem and their flaws. Quant. Opt. 1994, 6, 125–167. [Google Scholar] [CrossRef]
- Lynch, R. The quantum phase problem: A critical review. Phys. Rep. 1995, 256, 367–437. [Google Scholar] [CrossRef]
- Dubin, D.A.; Hennings, M.A.; Smith, T.B. Mathematical aspects of quantum phase. Int. J. Mod. Phys. B 1995, 9, 2597–2687. [Google Scholar] [CrossRef]
- Tanaš, R.; Miranowicz, A.; Gantsog, T. Quantum phase properties of nonlinear optical phenomena. In Progress in Optics; Wolf, E., Ed.; North Holland: Amsterdam, The Netherlands, 1996; Volume XXXV, pp. 355–446. [Google Scholar]
- Royer, A. Phase states and phase operators for the quantum harmonic oscillator. Phys. Rev. A 1996, 53, 70–108. [Google Scholar] [CrossRef] [PubMed]
- Bužek, V.; Hillery, M. Operational phase distributions via displaced squeezed states. J. Mod. Opt. 1996, 43, 1633–1651. [Google Scholar] [CrossRef]
- Klimov, A.B.; Chumakov, S.M. Gaussians on the circle and quantum phase. Phys. Lett. A 1997, 235, 7–14. [Google Scholar] [CrossRef]
- Pegg, D.T.; Barnett, S.M. Tutorial review: Quantum optical phase. J. Mod. Opt. 1997, 44, 225–264. [Google Scholar] [CrossRef]
- Peřinová, V.; Lukš, A.; Peřina, J. Phase in Optics; World Scientific: Singapore, 1998. [Google Scholar]
- Luis, A.; Sanchez-Soto, L.L. Quantum phase difference, phase measurements and Stokes operators. In Progress in Optics; Wolf, E., Ed.; North Holland: Amsterdam, The Netherlands, 2000; Volume 41, pp. 421–481. [Google Scholar]
- Vorontsov, Y.I. The phase of an oscillator in quantum theory. What is it ’in reality’? Physics–Uspekhi 2002, 45, 847–868. [Google Scholar] [CrossRef]
- Kastrup, H.A. Quantization of the optical phase space S2 = {φ mod 2π,I > 0} in terms of the group SO↑(1,2). Fortschr. Phys. 2003, 51, 975–1134. [Google Scholar] [CrossRef] [Green Version]
- Aragão, A.; Avelar, A.T.; Baseia, B. States of the quantized electromagnetic field with highly concentrated phase distribution. Phys. Lett. A 2004, 331, 366–373. [Google Scholar] [CrossRef]
- Varró, S. Regular phase operator and SU(1,1) coherent states of the harmonic oscillator. Phys. Scr. 2015, 90, 074053. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The quantum theory of the emission and absorption of radiation. Proc. Roy. Soc. London. A 1927, 114, 243–265. [Google Scholar]
- London, F. Winkelvariable und kanonische Transformationen in der Undulationsmechanik. Z. Phys. 1927, 40, 193–210. [Google Scholar] [CrossRef]
- Susskind, L.; Glogower, J. Quantum mechanical phase and time operator. Physics 1964, 1, 49–61. [Google Scholar] [CrossRef] [Green Version]
- Nieto, M.M. Quantum phase and quantum phase operators: Some physics and some history. Phys. Scr. 1993, T48, 5–12. [Google Scholar] [CrossRef]
- Lerner, E.C. Harmonic-oscillator phase operators. Nuovo Cim. B 1968, 56, 183–186. [Google Scholar] [CrossRef]
- Eswaran, K. On generalized phase operators for the quantum harmonic oscillator. Nuovo Cim. B 1970, 70, 1–11. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Klimov, A.B. Exactly solvable model of oscillator with nonpolynomial interaction and zeros of Bessel functions. In Anales de Fisica, Monografias, Proceedings of the XIX International Colloquium on Group Theoretical Methods in Physics, Salamanca, Spain, 29 June–4 July 1992; Mateos Guilarte, J., del Olmo, M.A., Santander, M., Eds.; CIEMAT/RSEF: Madrid, Spain, 1993; Volume 1, pp. 321–324. [Google Scholar]
- Ban, M. Quantum phase superoperator and antinormal ordering of the Susskind–Glogower phase operators. Phys. Lett. A 1995, 199, 275–280. [Google Scholar] [CrossRef]
- De Oliveira, M.C.; Mizrahi, S.S.; Dodonov, V.V. A consistent quantum model for continuous photodetection processes. J. Opt. B Quantum Semiclass. Opt. 2003, 5, S271–S280. [Google Scholar] [CrossRef]
- Dodonov, A.V.; Mizrahi, S.S.; Dodonov, V.V. Inclusion of nonidealities in the continuous photodetection model. Phys. Rev. A 2007, 75, 013806. [Google Scholar] [CrossRef] [Green Version]
- Kozlovskii, A.V. Fluctuations and a rigorous uncertainty relation of trigonometric operators of the phase and the number of photons of an electromagnetic field for general quantum superpositions of coherent states. Opt. Spectrosc. 2017, 123, 629–641. [Google Scholar] [CrossRef]
- Lerner, E.C.; Huang, H.W.; Walters, G.E. Some mathematical properties of oscillator phase operator. J. Math. Phys. 1970, 11, 1679–1684. [Google Scholar] [CrossRef]
- Ifantis, E.K. States, minimizing the uncertainty product of the oscillator phase operator. J. Math. Phys. 1972, 13, 568–575. [Google Scholar] [CrossRef]
- Aharonov, Y.; Lerner, E.C.; Huang, H.W.; Knight, J.M. Oscillator phase states, thermal equilibrium and group representations. J. Math. Phys. 1973, 14, 746–756. [Google Scholar] [CrossRef]
- Shapiro, J.H.; Shepard, S.R. Quantum phase measurement: A system-theory perspective. Phys. Rev. A 1991, 43, 3795–3818. [Google Scholar] [CrossRef]
- Sudarshan, E.C.G. Diagonal harmonious state representation. Int. J. Theor. Phys. 1993, 32, 1069–1076. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Mizrahi, S.S. Uniform nonlinear evolution equations for pure and mixed quantum states. Ann. Phys. 1995, 237, 226–268. [Google Scholar] [CrossRef]
- Vourdas, A. SU(2) and SU(1;1) phase states. Phys. Rev. A 1990, 41, 1653–1661. [Google Scholar] [CrossRef]
- Agarwal, G.S. Infinite statistics and the relation to a phase operator in quantum optics. Phys. Rev. A 1991, 44, 8398–8399. [Google Scholar] [CrossRef]
- Vourdas, A. Analytic representations in the unit disk and applications to phase state and squeezing. Phys. Rev. A 1992, 45, 1943–1950. [Google Scholar] [CrossRef]
- Hall, M.J.W. Phase resolution and coherent phase states. J. Mod. Opt. 1993, 40, 809–824. [Google Scholar] [CrossRef]
- Vourdas, A.; Brif, C.; Mann, A. Factorization of analytic representations in the unit disc and number-phase statistics of a quantum harmonic oscillator. J. Phys. A Math. Gen. 1996, 29, 5887–5898. [Google Scholar] [CrossRef]
- Obada, A.-S.F.; Yassin, O.M.; Barnett, S.M. Phase properties of coherent phase and generalized geometric states. J. Mod. Opt. 1997, 44, 149–161. [Google Scholar] [CrossRef]
- Paris, M.G.A. Sampling canonical phase distribution. Phys. Rev. A 1999, 60, 5136–5139. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Mizrahi, S.S. Creating quanta with an ‘annihilation’ operator. J. Phys. A Math. Gen. 2002, 35, 8847–8857. [Google Scholar]
- Gerry, C.C.; Bui, T. Approximate phase-coherent states and their generation. Phys. Rev. A 2009, 80, 033831. [Google Scholar] [CrossRef]
- Martín, D.; Luis, A. Nonclassicality in phase by breaking classical bounds on statistics. Phys. Rev. A 2010, 82, 033829. [Google Scholar] [CrossRef] [Green Version]
- Luis, A. Nonclassicality in the statistics of noncommuting observables: Nonclassical states are more compatible than classical states. Phys. Rev. A 2011, 84, 012106. [Google Scholar] [CrossRef] [Green Version]
- Matía-Hernando, P.; Luis, A. Nonclassicality in phase-number uncertainty relations. Phys. Rev. A 2011, 84, 063829. [Google Scholar] [CrossRef] [Green Version]
- Dodonov, V.V. Comparing energy difference and fidelity of quantum states. J. Russ. Laser Res. 2011, 32, 412–421. [Google Scholar] [CrossRef] [Green Version]
- Wünsche, A. Quantum-mechanical cumulant expansions and their application to phase-space and to phase distributions. Phys. Scr. 2015, 90, 074063. [Google Scholar] [CrossRef]
- D’Ariano, G.M.; Macchiavello, C.; Sterpi, N.; Yuen, H.P. Quantum phase amplification. Phys. Rev. A 1996, 54, 4712–4718. [Google Scholar] [CrossRef] [PubMed]
- Becir, A.; Wahiddin, M.R. Phase coherent states for enhancing the performance of continuous variable quantum key distribution. J. Phys. Soc. Jpn. 2012, 81, 034005. [Google Scholar] [CrossRef]
- Shen, L.-T.; Tang, C.-Q.; Shi, Z.; Wu, H.; Yang, Z.-B.; Zheng, S.-B. Squeezed-light-induced quantum phase transition in the Jaynes–Cummings model. Phys. Rev. A 2022, 106, 023705. [Google Scholar] [CrossRef]
- D’Ariano, G.M.; Paris, M.G.A.; Sacchi, M.F. Generation of phase-coherent states. Phys. Rev. A 1998, 57, 4894–4898. [Google Scholar] [CrossRef] [Green Version]
- Baseia, B.; Dantas, C.M.A.; Moussa, M.H.Y. Pure states having thermal photon distribution revisited: Generation and phase-optimization. Phys. A 1998, 258, 203–210. [Google Scholar] [CrossRef]
- Brif, C. Photon states associated with the Holstein–Primakoff realisation of the SU(1;1) Lie algebra. Quant. Semiclass. Opt. 1995, 7, 803–834. [Google Scholar] [CrossRef] [Green Version]
- Chizhov, A.V.; Paris, M.G.A. Phase squeezed states. Acta Phys. Slovaca 1998, 48, 343–348. [Google Scholar]
- Wünsche, A. A class of phase-like states. J. Opt. B Quantum Semiclass. Opt. 2001, 3, 206–218. [Google Scholar] [CrossRef]
- Wünsche, A. Duality of two types of SU(1,1) coherent states and an intermediate type. J. Opt. B Quantum Semiclass. Opt. 2003, 5, S429–S438. [Google Scholar] [CrossRef]
- Mouayn, Z. Phase coherent states with circular Jacobi polynomials for the pseudoharmonic oscillator. J. Math. Phys. 2012, 53, 012103. [Google Scholar] [CrossRef] [Green Version]
- Jagannathan, R.; Khan, S.A. On the deformed oscillator and the deformed derivative associated with the Tsallis q-exponential. Int. J. Theor. Phys. 2020, 59, 2647–2669. [Google Scholar] [CrossRef]
- Sivakumar, S. Studies on nonlinear coherent states. J. Opt. B Quantum Semiclass. Opt. 2000, 2, R61–R75. [Google Scholar] [CrossRef]
- Obada, A.-S.F.; Darwish, M. Partial phase state as a nonlinear coherent state and some of its properties. J. Mod. Opt. 2004, 51, 209–222. [Google Scholar] [CrossRef]
- Matos Filho, R.L.; Vogel, W. Nonlinear coherent states. Phys. Rev. A 1996, 54, 4560–4563. [Google Scholar] [CrossRef]
- Man’ko, V.I.; Marmo, G.; Sudarshan, E.C.G.; Zaccaria, F. f-oscillators and nonlinear coherent states. Phys. Scr. 1997, 55, 528–541. [Google Scholar]
- Klauder, J.R. The action option and a Feynman quantization of spinor fields in terms of ordinary c-numbers. Ann. Phys. 1960, 11, 123–168. [Google Scholar] [CrossRef]
- Glauber, R.J. Photon correlations. Phys. Rev. Lett. 1963, 10, 84–86. [Google Scholar] [CrossRef] [Green Version]
- Sudarshan, E.C.G. Equivalence of semiclassical and quantum mechanical descriptions of statistical light beams. Phys. Rev. Lett. 1963, 10, 277–279. [Google Scholar] [CrossRef]
- Schrödinger, E. Der stetige Übergang von der Mikro- zur Makromechanik. Naturwissenschaften 1926, 14, 664–666. [Google Scholar] [CrossRef]
- Marhic, M.E.; Kumar, P. Squeezed states with a thermal photon distribution. Opt. Commun. 1990, 76, 143–146. [Google Scholar] [CrossRef]
- Schrödinger, E. Zum Heisenbergschen Unschärfeprinzip. In Sitzungsberichte der Preussischen Akademie der Wissenschaften. Physikalisch-Mathematische Klasse; VERLAG DER AKADEMIE DER WISSENSCHAFTEN: Berlin, Germany, 1930; pp. 296–303. [Google Scholar]
- Robertson, H.P. A general formulation of the uncertainty principle and its classical interpretation. Phys. Rev. 1930, 35, 667. [Google Scholar]
- Dodonov, V.V. Universal integrals of motion and universal invariants of quantum systems. J. Phys. A Math. Gen. 2000, 33, 7721–7738. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Man’ko, O.V. Universal invariants of quantum-mechanical and optical systems. J. Opt. Soc. Am. A 2000, 17, 2403–2410. [Google Scholar] [CrossRef]
- De Freitas, M.C.; Dodonov, V.V. Non-Gaussianity of four-photon superpositions of Fock states. Quantum Rep. 2021, 3, 350–365. [Google Scholar] [CrossRef]
- Genoni, M.G.; Paris, M.G.A.; Banaszek, K. Measure of the non-Gaussian character of a quantum state. Phys. Rev. A 2007, 76, 042327. [Google Scholar] [CrossRef]
- Hudson, R.L. When is the Wigner quasi-probability density non-negative? Rep. Math. Phys. 1974, 6, 249–252. [Google Scholar] [CrossRef]
- Groenewold, H.J. On the principles of elementary quantum mechanics. Physica 1946, 12, 405–460. [Google Scholar] [CrossRef]
- Bartlett, M.S.; Moyal, J.E. The exact transition probabilities of quantum-mechanical oscillator calculated by the phase-space method. Proc. Cambr. Phil. Soc. 1949, 45, 545–553. [Google Scholar] [CrossRef]
- Cahill, K.E.; Glauber, R.J. Ordered expansions in boson amplitude operators. Phys. Rev. 1969, 177, 1857–1881. [Google Scholar] [CrossRef] [Green Version]
- Dodonov, V.V.; Man’ko, V.I. Phase space eigenfunctions of multidimensional quadratic Hamiltonians. Phys. A 1986, 137, 306–316. [Google Scholar] [CrossRef]
- Erdélyi, A. (Ed.) Bateman Manuscript Project: Higher Transcendental Functions; McGraw-Hill: New York, NY, USA, 1953; Volume II. [Google Scholar]
- Herzog, U.; Paul, H.; Richter, T.H. Wigner function for a phase state. Phys. Scr. 1993, T48, 61–65. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Freitas, M.C.; Dodonov, V.V. Coherent Phase States in the Coordinate and Wigner Representations. Quantum Rep. 2022, 4, 509-522. https://doi.org/10.3390/quantum4040036
de Freitas MC, Dodonov VV. Coherent Phase States in the Coordinate and Wigner Representations. Quantum Reports. 2022; 4(4):509-522. https://doi.org/10.3390/quantum4040036
Chicago/Turabian Stylede Freitas, Miguel Citeli, and Viktor V. Dodonov. 2022. "Coherent Phase States in the Coordinate and Wigner Representations" Quantum Reports 4, no. 4: 509-522. https://doi.org/10.3390/quantum4040036
APA Stylede Freitas, M. C., & Dodonov, V. V. (2022). Coherent Phase States in the Coordinate and Wigner Representations. Quantum Reports, 4(4), 509-522. https://doi.org/10.3390/quantum4040036








