Non-Relativistic Energy Spectra of the Modified Hylleraas Potential and Its Thermodynamic Properties in Arbitrary Dimensions
Abstract
:1. Introduction
2. The Hylleraas Potential (HP) and the Modified Hylleraas Potential (MHP)
3. Solutions of the Schrodinger Equation with Modified Hylleraas Potential
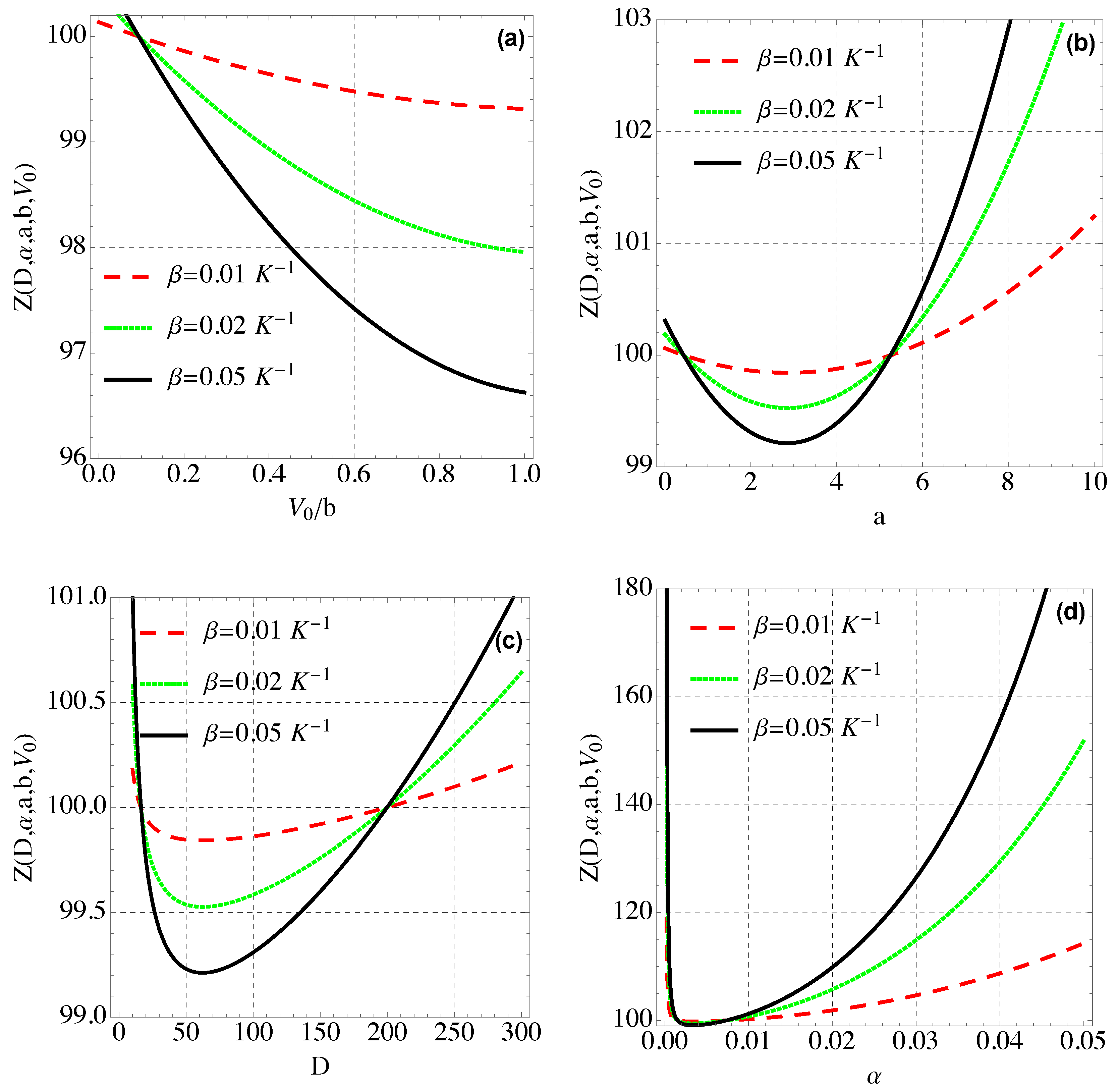
4. Thermal and Magnetic Properties of Modified Hylleraas Potential (MHP)
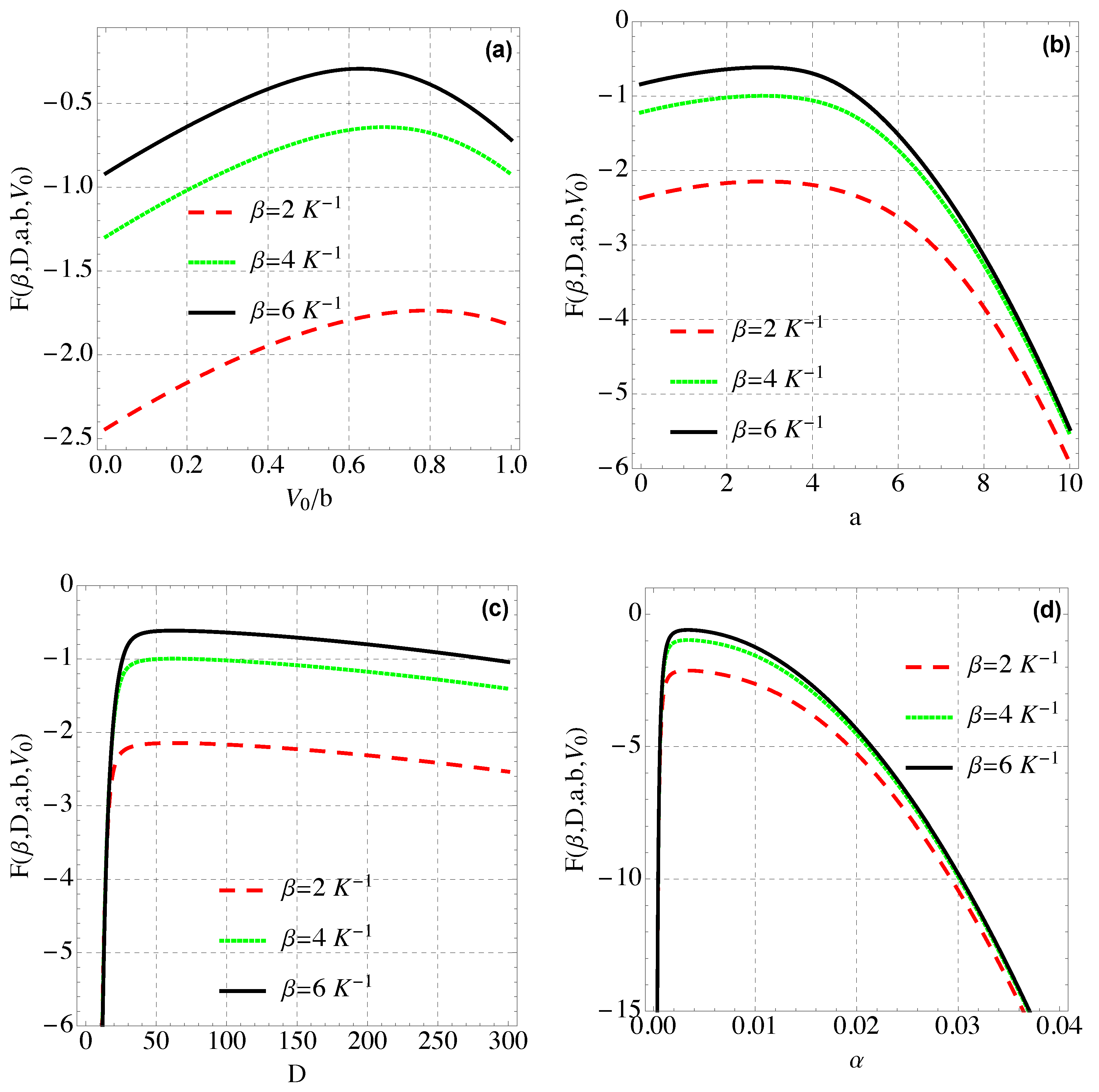
4.1. Free Energy
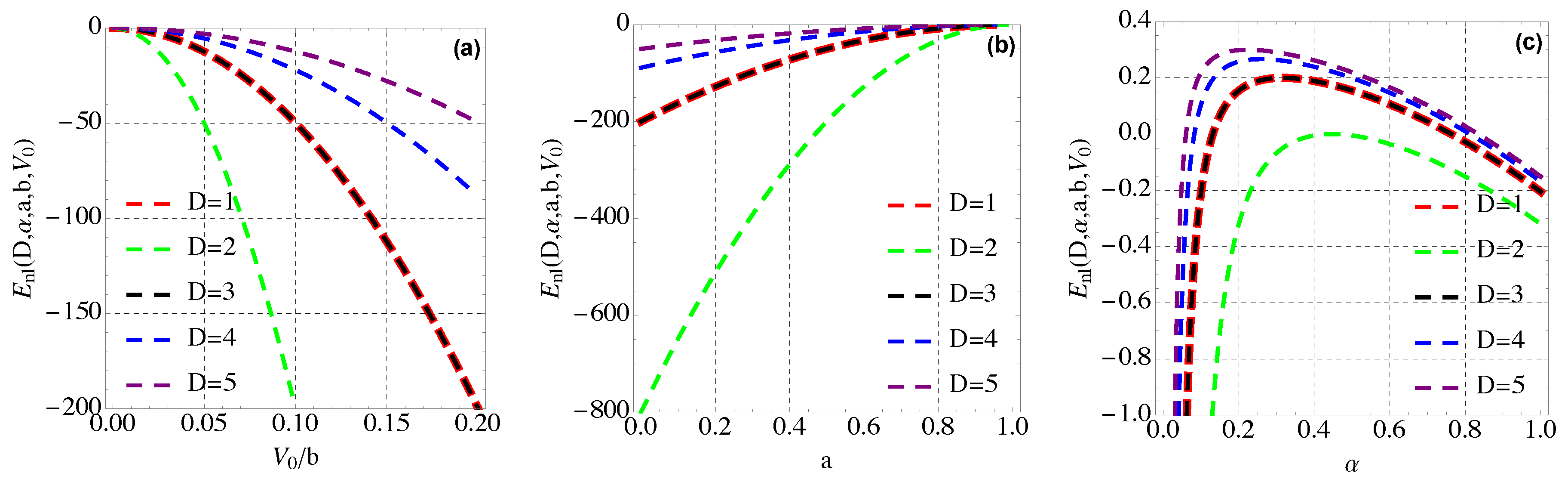
4.2. Mean Energy
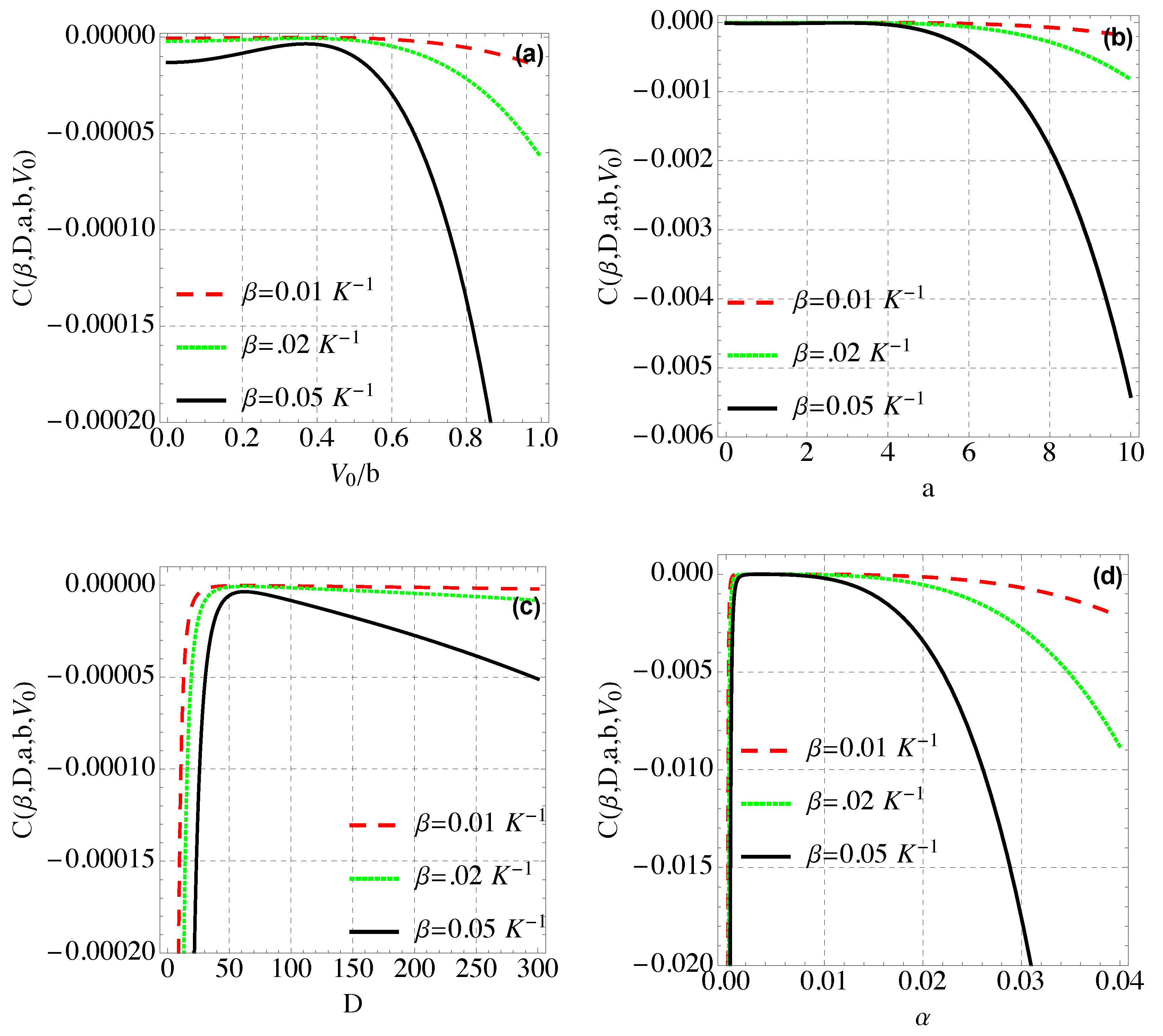
4.3. Spacific Heat Capacity
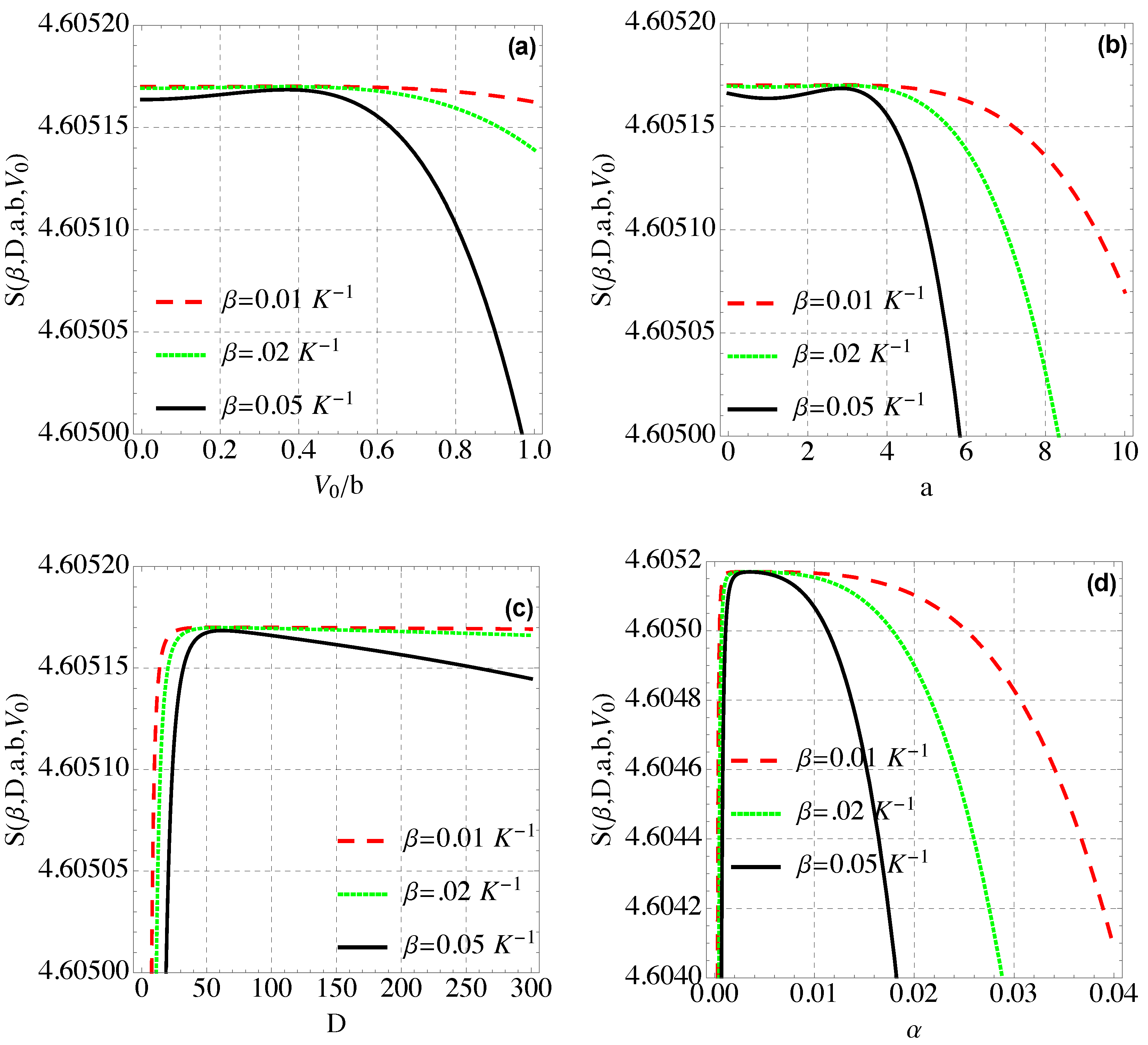
4.4. Entropy
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Schrodinger, E. Quantisation as a problem of characteristic values. Ann. Phys. 1926, 79, 361. [Google Scholar]
- Schrodinger, E. An undulatory theory of the mechanics of atoms and molecules. Phys. Rev. 1926, 28, 1049. [Google Scholar]
- Schrodinger, E. Quantisierung als eigenwertproblem. Ann. Phys. 1926, 385, 437. [Google Scholar] [CrossRef]
- Dong, S.H. Factorization Method in Quantum Mechanics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; Volume 150. [Google Scholar]
- Sakurai, J.J. Modern Quantum Mechanics, revised ed.; Addison Wesley: Boston, MA, USA, 1993. [Google Scholar]
- Antia, A.D.; Essien, I.E.; Umoren, E.B.; Eze, C.C. Solutions of relativistic Klein–Gordon equation with equal scalar and vector shifted Hulthen plus angle dependent potential. Adv. Phys. Theor. Appl. 2015, 47, 45. [Google Scholar]
- Berkdemir, C. Application of the Nikiforov-Uvarov method in quantum mechanics. In Theoretical Concepts of Quantum Mechanics; IntechOpen: London, UK, 2012. [Google Scholar]
- Abu-Shady, M.; Edet, C.O.; Ikot, A.N. Non-relativistic quark model under external magnetic and Aharanov–Bohm (AB) fields in the presence of temperature-dependent confined Cornell potential. Can. J. Phys. 2021, 99, 1024. [Google Scholar] [CrossRef]
- Rajabi, A.A.; Hamzavi, M. Approximate analytical solutions of the perturbed Yukawa Potential with Centrifugal Barrier. Z. Naturforschung A 2013, 68, 454. [Google Scholar] [CrossRef]
- Oyewumi, K.J.; Akinpelu, F.O. Exactly Complete Solutions Pseudoharmonic Potential N-Dimensions. Int. J. Theor. Phys. 2008, 47, 1039. [Google Scholar] [CrossRef]
- Girifalco, L.A.; Weizer, V.G. Application of the Morse potential function to cubic metals. Phys. Rev. 1959, 114, 687. [Google Scholar] [CrossRef]
- Edet, C.O.; Amadi, P.O.; Onyeaju, M.C.; Okorie, U.S.; Sever, R.; Rampho, G.J.; Abdullah, H.Y.; Salih, I.H.; Ikot, A.N. Thermal properties and magnetic susceptibility of Hellmann potential in Aharonov–Bohm (AB) flux and magnetic fields at zero and finite temperatures. J. Low Temp. Phys. 2021, 202, 83. [Google Scholar] [CrossRef]
- Edet, C.O.; Okorie, K.O.; Louis, H.; Nzeata-Ibe, N.A. Any l-state solutions of the Schrodinger equation interacting with Hellmann–Kratzer potential model. Indian J. Phys. 2019, 94, 243. [Google Scholar] [CrossRef]
- Edet, C.O.; Okorie, U.S.; Osobonye, G.; Ikot, A.N.; Rampho, G.J.; Sever, R. Thermal properties of Deng–Fan–Eckart potential model using Poisson summation approach. J. Math. Chem. 2020, 58, 989. [Google Scholar] [CrossRef]
- Okoi, P.O.; Edet, C.O.; Magu, T.O. Relativistic Treatment of the Hellmann-generalized Morse potential. Rev. Mex. Física 2020, 66, 1. [Google Scholar] [CrossRef] [Green Version]
- Antia, A.D.; Ikot, A.N.; Hassanabadi, H.; Maghsoodi, E. Bound state solutions of Klein–Gordon equation with Mobius square plus Yukawa potentials. Indian J. Phys. 2013, 87, 1133. [Google Scholar] [CrossRef]
- Edet, C.O.; Okorie, U.S.; Ngiangia, A.T.; Ikot, A.N. Bound state solutions of the Schrodinger equation for the modified Kratzer potential plus screened Coulomb potential. Indian J. Phys. 2020, 94, 425. [Google Scholar] [CrossRef]
- Ikhdair, S.M.; Sever, R. Relativistic two-dimensional harmonic oscillator plus cornell potentials in external magnetic and AB fields. Adv. High Energy Phys. 2013, 2013, 562959. [Google Scholar] [CrossRef] [Green Version]
- Greene, R.L.; Aldrich, C. Variational wave functions for a screened Coulomb potential. Phys. Rev. A 1976, 14, 2363. [Google Scholar] [CrossRef]
- Serrano, F.A.; Gu, X.Y.; Dong, S.H. Qiang–Dong proper quantization rule and its applications to exactly solvable quantum systems. J. Math. Phys. 2010, 51, 082103. [Google Scholar] [CrossRef]
- Falaye, B.J. Any ℓ-state solutions of the Eckart potential via asymptotic iteration method. Cent. Eur. J. Phys. 2012, 10, 960. [Google Scholar] [CrossRef] [Green Version]
- Oyewumi, K.J.; Titiloye, E.O.; Alabi, A.B.; Falaye, B.J. Bound states of pseudo-harmonic oscillator in the presence of magnetic field. J. Niger. Math. Soc. 2016, 35, 460. [Google Scholar]
- Ikot, A.N. Solution of Dirac equation with generalized hylleraas potential. Commun. Theor. Phys. 2013, 59, 268. [Google Scholar] [CrossRef]
- Ikot, A.N.; Okorie, U.S.; Rampho, G.J.; Abdullah, H.Y. Approximate energy spectra and statistical mechanical functions of some diatomic molecular hydrides. Can. J. Phys. 2021, 99, 253. [Google Scholar] [CrossRef]
- Okorie, U.S.; Ikot, A.N.; Onyeaju, M.C.; Chukwuocha, E.O. A study of thermodynamic properties of quadratic exponential-type potential in D-dimensions. Rev. Mex. Física 2018, 64, 608. [Google Scholar] [CrossRef] [Green Version]
- Onate, C.A.; Ojonubah, J.O. Eigensolutions of the Schrödinger equation with a class of Yukawa potentials via supersymmetric approach. J. Theor. Appl. Phys. 2016, 10, 21. [Google Scholar] [CrossRef] [Green Version]
- Ciftci, H.; Hall, R.L.; Saad, N. Asymptotic iteration method for eigenvalue problems. J. Phys. Math. Gen. 2003, 36, 11807. [Google Scholar] [CrossRef] [Green Version]
- Bayrak, O.; Boztosun, I. Bound state solutions of the Hulthén potential by using the asymptotic iteration method. Phys. Scr. 2007, 76, 92. [Google Scholar] [CrossRef]
- Edet, C.O.; Ikot, A.N. Effects of Topological Defect on the Energy Spectra and Thermo-magnetic Properties of CO Diatomic Molecule. J. Low Temp. Phys. 2021, 203, 84. [Google Scholar] [CrossRef]
- Nikiforov, A.V.; Uvarov, V.B. Special Functions of Mathematical Physics; Birkhauser: Bassel, Switzerland, 1988. [Google Scholar]
- Edet, C.O.; Okoi, A.P.O. Any l-state solutions of the Schrödinger equation for q-deformed Hulthen plus generalized inverse quadratic Yukawa potential in arbitrary dimensions. Rev. Mex. Física 2019, 65, 333. [Google Scholar] [CrossRef] [Green Version]
- Tezcan, C.; Sever, R. A general approach for the exact solution of the Schrödinger equation. Int. J. Theor. Phys. 2009, 48, 337. [Google Scholar] [CrossRef] [Green Version]
- Falaye, B.J.; Ikhdair, S.M.; Hamzavi, M. Formula method for bound state problems. Few-Body Syst. 2015, 56, 63. [Google Scholar] [CrossRef] [Green Version]
- Wentzel, G. Eine verallgemeinerung der quantenbedingungen für die zwecke der wellenmechanik. Z. Phys. 1926, 38, 518. [Google Scholar] [CrossRef]
- Ita, B.I.; Louis, H.; Akakuru, O.U.; Nzeata-Ibe, N.A.; Ikeuba, A.I.; Magu, T.O.; Amos, P.I.; Edet, C.O. Approximate Solution to the Schrödinger Equation with Manning-Rosen plus a Class of Yukawa Potential via WKBJ Approximation Method. Bulg. J. Phys. 2018, 45, 323. [Google Scholar]
- Ma, Z.Q.; Xu, B.W. Exact quantization rule and the invariant. Chin. Acta Phys Sin. 2006, 55, 1571–1579. [Google Scholar] [CrossRef]
- Ma, Z.Q.; Xu, B.W. Quantum correction in exact quantization rules. EPL Europhys. Lett. 2005, 69, 685. [Google Scholar] [CrossRef]
- Ebeling, W.; Sokolov, I. Statistical Thermodynamics and Stochastic Theory of Nonequilibrium Systems; World Scientific Publishing Company: Singapore, 2005; Volume 8. [Google Scholar]
- Pathria, R.K. Statistical Mechanics; Butterworth: Washington, DC, USA, 1996. [Google Scholar]
- Landsberg, P.T. Thermodynamics and Statistical Mechanics; Courier Corporation: North Chelmsford, MA, USA, 2014. [Google Scholar]
- Okorie, U.S.; Edet, C.O.; Ikot, A.N.; Rampho, G.J.; Sever, R. Thermodynamic functions for diatomic molecules with modified Kratzer plus screened Coulomb potential. Indian J. Phys. 2021, 95, 411. [Google Scholar] [CrossRef]
- Ikot, A.N.; Lutfuoglu, B.C.; Ngwueke, M.I.; Udoh, M.E.; Zare, S.; Hassanabadi, H. Klein-Gordon equation particles in exponential-type molecule potentials and their thermodynamic properties in D dimensions. Eur. Phys. J. Plus 2016, 131, 1. [Google Scholar] [CrossRef]
- Ikot, A.N.; Okorie, U.S.; Rampho, G.J.; Amadi, P.O.; Edet, C.O.; Akpan, I.O.; Abdullah, H.Y.; Horchani, R. Klein–gordon equation and nonrelativistic thermodynamic properties with improved screened kratzer potential. J. Low Temp. Phys. 2021, 202, 269. [Google Scholar] [CrossRef]
- Hylleraas, E.A. Energy formula and potential distribution of diatomic molecules. J. Chem. Phys. 1935, 3, 595. [Google Scholar]
- Ikot, A.N.; Awoga, O.A.; Ita, B.I. Exact solutions of the Klein–Gordon equation with Hylleraas potential. Few-Body Syst. 2012, 53, 539. [Google Scholar] [CrossRef]
- Okorie, U.S.; Ikot, A.N.; Edet, C.O.; Rampho, G.J.; Sever, R.; Akpan, I.O. Solutions of the Klein Gordon equation with generalized hyperbolic potential in D-dimensions. J. Phys. Commun. 2019, 3, 095015. [Google Scholar] [CrossRef]
- Edet, C.O.; Ikot, A.N. Analysis of the impact of external fields on the energy spectra and thermo-magnetic properties of N2,I2,CO,NO and HCl diatomic molecules. Mol. Phys. 2021, 119, e1957170. [Google Scholar] [CrossRef]
- Edet, C.O.; Nwbabuzor, P.O.; Ettah, E.B.; Duque, C.A.; Ali, N.; Ikot, A.N.; Mahmoud, S.; Asjad, M. Magneto-transport and thermal properties of the Yukawa potential in cosmic string space-time. Results Phys. 2022, 39, 105749. [Google Scholar] [CrossRef]
- Jia, C.-S.; Wang, C.-W.; Zhang, L.-H.; Peng, X.-L.; Zeng, R.; You, X.-T. Partition function of improved Tietz oscillators. Chem. Phys. Lett. 2017, 676, 150. [Google Scholar] [CrossRef]
- Jia, C.-S.; Zhang, L.-H.; Wang, C.-W. Thermodynamic properties for the lithium dimer. Chem. Phys. Lett. 2017, 667, 211. [Google Scholar] [CrossRef]

| State | ||||||
|---|---|---|---|---|---|---|
| 1s | 0.025 | −7.7003100 | −31.8003000 | −7.7003100 | −3.2225300 | −1.6503100 |
| 0.050 | −1.7012500 | −7.8012500 | −1.7012500 | −0.5568060 | −0.1512500 | |
| 0.075 | −0.5917010 | −3.3583700 | −0.5917010 | −0.0645409 | 0.1249650 | |
| 0.100 | −0.2050000 | −1.8050000 | −0.2050000 | 0.1061110 | 0.2200000 | |
| 2s | 0.025 | −1.6503100 | −3.2225300 | −1.6503100 | −0.9203130 | −0.5225350 |
| 0.050 | −0.1512500 | −0.5568060 | −0.1512500 | 0.0387500 | 0.1431940 | |
| 0.075 | 0.1249650 | −0.0645409 | 0.1249650 | 0.2149650 | 0.2650890 | |
| 0.100 | 0.2200000 | 0.1061110 | 0.2200000 | 0.2750000 | 0.3061110 | |
| 2p | 0.025 | −7.7003100 | −3.2225300 | −1.6503100 | −0.9203130 | −0.5225350 |
| 0.050 | −1.7012500 | −0.5568060 | −0.1512500 | 0.0387500 | 0.1431940 | |
| 0.075 | −0.5917010 | −0.0645409 | 0.1249650 | 0.2149650 | 0.2650890 | |
| 0.100 | −0.2050000 | 0.1061110 | 0.2200000 | 0.2750000 | 0.3061110 | |
| 3s | 0.025 | −0.5225350 | −0.9203130 | −0.5225350 | −0.2819450 | −0.1253130 |
| 0.050 | 0.1431940 | 0.0387500 | 0.1431940 | 0.2069130 | 0.2487500 | |
| 0.075 | 0.2650890 | 0.2149650 | 0.2650890 | 0.2960540 | 0.3166320 | |
| 0.100 | 0.3061110 | 0.2750000 | 0.3061110 | 0.3256120 | 0.3387500 | |
| 3p | 0.025 | −1.6503100 | −0.9203130 | −0.5225350 | −0.2819450 | −0.1253130 |
| 0.050 | −0.1512500 | 0.0387500 | 0.1431940 | 0.2069130 | 0.2487500 | |
| 0.075 | 0.1249650 | 0.2149650 | 0.2650890 | 0.2960540 | 0.3166320 | |
| 0.100 | 0.2200000 | 0.2750000 | 0.3061110 | 0.3256120 | 0.3387500 | |
| 3d | 0.025 | −1.6503100 | −0.9203130 | −0.5225350 | −0.2819450 | −0.1253130 |
| 0.050 | −0.1512500 | 0.0387500 | 0.1431940 | 0.2069130 | 0.2487500 | |
| 0.075 | 0.1249650 | 0.2149650 | 0.2650890 | 0.2960540 | 0.3166320 | |
| 0.100 | 0.2200000 | 0.2750000 | 0.3061110 | 0.3256120 | 0.3387500 | |
| 4s | 0.025 | −0.1253130 | −0.2819450 | −0.1253130 | −0.0175965 | 0.0596875 |
| 0.050 | 0.2487500 | 0.2069130 | 0.2487500 | 0.2777620 | 0.2987500 | |
| 0.075 | 0.3166320 | 0.2960540 | 0.3166320 | 0.3310700 | 0.3416320 | |
| 0.100 | 0.3387500 | 0.3256120 | 0.3387500 | 0.3480860 | 0.3550000 | |
| 4p | 0.025 | −0.5225350 | −0.2819450 | −0.1253130 | −0.0175965 | 0.0596875 |
| 0.050 | 0.1431940 | 0.2069130 | 0.2487500 | 0.2777620 | 0.2987500 | |
| 0.075 | 0.2650890 | 0.2960540 | 0.3166320 | 0.3310700 | 0.3416320 | |
| 0.100 | 0.3061110 | 0.3256120 | 0.3387500 | 0.3480860 | 0.3550000 | |
| 4d | 0.025 | −0.5225350 | −0.2819450 | −0.1253130 | −0.0175965 | 0.0596875 |
| 0.050 | 0.1431940 | 0.2069130 | 0.2487500 | 0.2777620 | 0.2987500 | |
| 0.075 | 0.2650890 | 0.2960540 | 0.3166320 | 0.3310700 | 0.3416320 | |
| 0.100 | 0.3061110 | 0.3256120 | 0.3387500 | 0.3480860 | 0.3550000 | |
| 4f | 0.025 | −0.5225350 | −0.2819450 | −0.1253130 | −0.0175965 | 0.0596875 |
| 0.050 | 0.1431940 | 0.2069130 | 0.2487500 | 0.2777620 | 0.2987500 | |
| 0.075 | 0.2650890 | 0.2960540 | 0.3166320 | 0.3310700 | 0.3416320 | |
| 0.100 | 0.3061110 | 0.3256120 | 0.3387500 | 0.3480860 | 0.3550000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Edet, C.O.; Osang, J.E.; Ali, N.; Agbo, E.P.; Aljunid, S.A.; Endut, R.; Ettah, E.B.; Khordad, R.; Ikot, A.N.; Asjad, M. Non-Relativistic Energy Spectra of the Modified Hylleraas Potential and Its Thermodynamic Properties in Arbitrary Dimensions. Quantum Rep. 2022, 4, 238-250. https://doi.org/10.3390/quantum4030016
Edet CO, Osang JE, Ali N, Agbo EP, Aljunid SA, Endut R, Ettah EB, Khordad R, Ikot AN, Asjad M. Non-Relativistic Energy Spectra of the Modified Hylleraas Potential and Its Thermodynamic Properties in Arbitrary Dimensions. Quantum Reports. 2022; 4(3):238-250. https://doi.org/10.3390/quantum4030016
Chicago/Turabian StyleEdet, Collins Okon, Jonathan E. Osang, Norshamsuri Ali, Emmanuel Paul Agbo, Syed Alwee Aljunid, Rosdisham Endut, Emmanuel B. Ettah, Reza Khordad, Akpan Ndem Ikot, and Muhammad Asjad. 2022. "Non-Relativistic Energy Spectra of the Modified Hylleraas Potential and Its Thermodynamic Properties in Arbitrary Dimensions" Quantum Reports 4, no. 3: 238-250. https://doi.org/10.3390/quantum4030016
APA StyleEdet, C. O., Osang, J. E., Ali, N., Agbo, E. P., Aljunid, S. A., Endut, R., Ettah, E. B., Khordad, R., Ikot, A. N., & Asjad, M. (2022). Non-Relativistic Energy Spectra of the Modified Hylleraas Potential and Its Thermodynamic Properties in Arbitrary Dimensions. Quantum Reports, 4(3), 238-250. https://doi.org/10.3390/quantum4030016









