Secure Quantum Communication Technologies and Systems: From Labs to Markets

Abstract

We provide a broad overview of current quantum communication by analyzing the recent discoveries on the topic and by identifying the potential bottlenecks requiring further investigation. The analysis follows an industrial perspective, first identifying the state or the art in terms of protocols, systems, and devices for quantum communication. Next, we classify the applicative fields where short- and medium-term impact is expected by emphasizing the potential and challenges of different approaches. The direction and the methodology with which the scientific community is proceeding are discussed. Finally, with reference to the European guidelines within the Quantum Flagship initiative, we suggest a roadmap to match the effort community-wise, with the objective of maximizing the impact that quantum communication may have on our society.

1. Introduction

The efforts made in quantum technologies have increased rapidly in recent years, and the number of filed patents and publications have increased together with the number of proposed projects. However, the impact of such technologies on the market remains limited. The reasons for this are several barriers preventing industrial transfer, both technological and related to perception from the industry. Here, we draw a link between existing technologies, protocols, and devices with potential industrial markets, as an attempt to identify where and how quantum technologies may impact relevant market segments. Covered aspects, ranging from enabling technology to market considerations, are illustrated in Figure 1.

The paper is organized as follows. Section 2 introduces quantum key distribution (QKD) systems and networks, based on both discrete and continuous variables, discussing main implementation issues and proposed solutions. Section 3 provides a technological overview of the devices and the sub-systems needed in a QKD system (light sources, detectors, quantum repeaters, and random number generators). Application scenarios are presented in Section 4, along with relevant types of QKD systems and suitable technologies. Section 5, covering market perspectives, discusses the cost factors that may limit or delay the introduction of commercial QKD systems. Section 6 outlines an industrial roadmap based on the considerations above, covering the application scenarios and markets and ongoing public funding efforts. Section 7 gives an overview of the standardization of QKD systems. Finally, Section 8 draws conclusions.

2. Quantum Key Distribution Systems and Networks

Quantum communication is the field of study related to the transmission of quantum states between two or more parties. The most widely accepted applications for quantum communication fall in the field of cryptography, where the laws of quantum mechanics are exploited to secure data, and specifically, to share secret keys between symmetric parties, a technique named quantum key distribution (QKD). The timespan over which humanity has adopted cryptography in some form covers thousands of years. Since the mathematical formalization of cryptosystems, many variants of such systems have been created, all based on difficult mathematical problems, relying on the assumption that nobody could solve them in a realistic amount of time. Such cryptosystems are not really immune from attacks, especially as computation power and theoretical know-how increase, meaning that the probability of being able to decipher encrypted data increases over time. The advent of the new paradigm of quantum computing, where individuals are able to break most of the well-known cyphers, further confirms that just using computationally hard problems to secure data is not enough in the mid-term timescale. More generally, other applications than QKD exist for quantum communication, such as the transfer of quantum states being processed by quantum computers, the transmission of information using techniques such as quantum teleportation, or less known applications such as quantum coin flipping [1], a primitive technique useful in many algorithms. In the following we address the field of secure quantum communications, therefore restricting the paper to the topic of QKD in all its aspects, because it is the technique closest to have an industrial impact.

2.1. Discrete Variable Systems

The discrete variable (DV) approach to QKD has been extensively studied, and most of the testbeds and available commercial devices are of this kind. The underlying idea is that since it is well-known that in quantum mechanical systems any measurement perturbs the system, this feature can be exploited to understand if someone is trying to steal data from the channel.

BB84 is an example of discrete variable quantum key distribution (DV-QKD), where a finite number of polarization bases are used to encode bits. The sender (Alice) generates a random bit (i.e., either a “0” or a “1”) and encodes it in one of two different bases, over a given physical parameter of a photon (typically, polarization). The first basis is used to encode “0” bits and the second base for “1” bits. Since the receiver (Bob) does not know the sender’s basis selection, he measures (after propagation in an optical fiber link) the polarization of the incoming photons by randomly using one of the two possible bases. If he uses the same base as the sender, he will measure the correct bit value; conversely, if he chooses the wrong base, the result of the measurement will give the correct result only with 50% probability. After a long sequence of photons has been exchanged, Alice and Bob compare the bases they have employed to encode and measure each photon, respectively, by communicating via a classical channel. They keep only the bits generated and detected with a matched base, which are said to constitute the sifted keys. In an ideal system without noise, imperfections, and disturbances, the sifted keys are identical and can be used as a private key. Typically, the two polarization bases used by the sender are selected by a polarizer and are rotated 45° about each other. They are called rectilinear (0°, 90°) and diagonal (45°, 135°) bases. At the receiver, a polarization beam splitter (PBS) transforms the polarization encoding into a spatial encoding, so that the photons can be detected using two separate photon avalanche photodetectors (SPAD).

Starting from the BB84 protocol, many variants of QKD protocols have been proposed over the years, but the basic concept has remained the same. We briefly examine some of these protocols without extensively describing them. Incrementally moving from the original BB84 protocol, it is worth noticing that it can be implemented using physical features that differ from polarization. For example, phase encoding is an alternative [2]; the sender uses a Mach–Zehnder interferometer (MZI) to introduce one out of four alternative phase shifts (${\mathsf{\varphi }}_{\mathrm{a}}$), for example ${\mathsf{\varphi }}_{\mathrm{a}}=\left[ 0, \frac{\mathsf{\pi }}{2},\mathsf{\pi } \frac{3}{2}\mathsf{\pi } \right]$, with the first two linked to a “0” bit and the latter to a “1” bit. The receiver uses a second MZI to randomly introduce one out of two phase shifts (${\mathsf{\varphi }}_{\mathrm{b}}$), for example ${\mathsf{\varphi }}_{\mathrm{b}}=\left[ 0, \frac{\mathsf{\pi }}{2}\right]$. The transformation from phase to spatial encoding at the receiver is made on the basis of the differential phase $∆\mathsf{\varphi }={\mathsf{\varphi }}_{\mathrm{a}}-{\mathsf{\varphi }}_{\mathrm{b}}$. Similarly, encoding exploiting the photon spin was proposed in [3,4].

In 1991, the E91 protocols were proposed [5]. This system is similar to BB84 but it uses entangled photons to guarantee the security of the communication, relying on the no-cloning theorem proven by Wooters in 1992 [6]. E91 still uses the polarization to encode information and the same BB84 mechanism to statistically detect an eavesdropper. Entangled photon pairs are distributed among communicating partners, which choose a measurement basis; if two partners choose the same basis, the measured bit will be equal, otherwise the bit is discarded. E91, and its simplified version BBM92, opened a new branch in the taxonomy of the QKD protocols, being entanglement-based as opposed to the so called prepare-and-measure protocols, such as BB84, where photons are encoded (prepared) by the sender and measured by the receiver (measure). The two approaches have been proved to be theoretically equivalent in terms of security guarantee [7].

2.2. Continuous Variable Systems

DV-QKD systems require ad-hoc devices to operate, such as single-photon detectors and single-photon sources. This is a major obstacle to industrialization due to small production volumes (at least during the initial phases of introduction on the market_ and the need to setup a dedicated supply chain. Moreover, the efficient generation, detection, and manipulation of individual photons require cryogenic refrigerated devices. One decade later than the introduction of DV systems, an alternative approach to QKD was proposed [8,9,10]. It is named the continuous variable (CV) approach, since photon parameters assuming continuous values are used.

Continuous variable quantum key distribution (CV-QKD) systems reuse devices already developed for classical optical communication systems and that have been commercially available for decades, such as positive-intrinsic-negative (PIN) photodiodes, reducing system complexity and cost. CV-QKD refers to a family of protocols divided in two macro subclasses, named discrete and gaussian modulation. For a complete description of the topic, interested readers can look at [11].

We can consider CV-QKD as an adaptation of the BB84 protocol to be used with non-discrete characteristics of light. It uses well-studied homodyne detection, transmitting pulses of energy instead of single-photons. In the first proposal, squeezed optical pulses are used. Each pulse can be transmitted over one of the two quadrature components of the complex plane, adding a constant displacement to encode “0” or “1” bits. The receiver then randomly chooses the quadrature component in which to perform measurements, adopting an algorithm analogous to BB84, and keeping only the measures for which the correct quadrature choice was made. If the measure is performed on the correct plane, the result is then Gaussian-distributed with mean value equal to the applied displacement used to decode the bits. A viable alternative to the squeezed states, which are intrinsically hard to generate, is the use of coherent states in the complex plane, which are much easier to generate [12]. The idea remains similar to the exposed one; the difference is that more complex constellations of coherent states can be generated to encode information, such as in [13,14], where four and eight coherent states are used. Alternatively, a Gaussian approach can be adopted, where the displacement the sender introduces between the states follows a Gaussian distribution. The first proposal repeated using squeezed states [15], then many alternatives based on coherent states are proposed, together with practical implementations [16,17,18,19].

Discrete CV-QKD protocols (i.e., using a fixed displacement) are closer to practical implementations and also enable higher distance reach [20]. On the other hand, security features for discrete modulated CV-QKD are harder to proof than Gaussian CV-QKD. The lower the number of states, the harder it is to prove that the protocol is secure. Indeed, in discretizing the signal, finite-size statistical effects progressively become more relevant, increasing the complexity of a theoretical security proof. Many articles exist on the topic of the security of CV-QKD, and a general review is covered in [21]. It is worth to noting that while for DV-QKD many security proofs exist (including non-ideal devices), assuming unlimited computational power and memory [22], the state of the security proofs in the context of CV-QKD is more limited. For the Gaussian approach, the security is guaranteed only for infinite or unpractically long keys.

From an industrial perspective, CV-QKD represents a promising opportunity whenever the reuse of the network infrastructure is important, as well as the integration of the QKD system with a classical network. Its early maturity level and the low number of performed tests and theoretical security proofs, together with its limits in terms of performance and complexity in performing reconciliation, make CV-QKD a longer-term solution compared to DV-QKD.

2.3. Quantum Security and Practical Vulnerability Issues

As the father of information theory, Claude Shannon proved in [23] that for a cryptosystem to be unconditionally secure, the length of the used key cannot be shorter than the data itself. Under these circumstances, the cryptogram used to achieve unconditional security with QKD is well known: it is named a one-time pad, where a simple XOR operation is performed bit-by-bit between data and key. However, given the throughput disparity between current QKD systems (which can achieve Mbit/s speed in the best case, such as in [24]) and classical data communication (which can achieve to Tbit/s speed), one-time pad is not of practical use. This is the reason why many applications use unconditionally secure quantum cryptograms only to share a secret key between partners, which is known to be the most vulnerable part of any encryption system. Once the partners share the secret key, classical symmetric cryptosystems are used to share the data, such as the advanced encryption standard (AES). Symmetrical cryptosystems are very secure and some of them have been studied for their resilience to quantum attacks [25], although it remains to be proven whether they are resistant to any kind of attack by a quantum computer [26]. Hence, the impossibility of performing one-time pad quantum encryption of all data remains a security bottleneck in real-world QKD systems, together with other technological and implementational constraints that we will discuss later in this section.

QKD protocols are known to be unconditionally secure because their security is independent of the amount of information and the computational power of the attacker. However, this statement is true for an ideal system. In practice, as is shown in [27], several assumptions have to be satisfied for the system to be considered unconditionally secure. For example, due to its limited bit rate, QKD is often used in conjunction with classical encryption methods, making the actual security dependent on the technological level of the adversary at the time of the key exchange. Another example of a technological issue is the possible information leakage caused by light emitted by avalanche photodiodes during the breakdown. Moreover, QKD may be vulnerable to beam splitter and trojan horse attacks due to the non-ideality of photon sources and backscattered light, respectively, requiring proper design countermeasures.

A consistent research effort has been devoted to the necessity of achieving unconditional security in practice and to engineering the known protocols for this purpose. For example, single-photon sources implemented by attenuating standalone lasers (a usual choice, due to practical feasibility issues) are vulnerable to a kind of attack called photon number splitting (PNS) [28]. Such non-ideal sources may emit multiple photons instead of exactly one, and these may be used to split the additional photons and extrapolate information without affecting the photons exchanged by “Alice” and “Bob”. A solution aimed at solving source imperfections in BB84 was proposed by Hwang [29], where additional states, called decoy states, are properly designed to be different in power in respect to the data photons and are randomly substituted into the data to understand if someone is sniffing the channel. An unconditional security proof of decoy-state QKD is shown in [30,31].

Decoy states were exploited by Gisin et al. in 2004 [32] to obtain a specific protocol, called the coherent one-way (COW) protocol. Instead of using ideal single-photon sources, which are hard and costly to realize and require cryogenic temperatures, this protocol uses a continuous wave laser as the source, such as the ones used in optical telecom systems. This laser is attenuated to obtain quasi single-photon transmission. Since the optical generation of photons is a statistical process, the number of actual generated photons will be either zero, one, or several photons. The bits are encoded into the arrival times of consecutive pulses, where an empty state followed by a coherent state represents a “0” bit, while the opposite order represents a “1” bit. The decoy states used to prevent PNS attacks are instead represented by consecutive coherent states. This protocol was tested over more than 300 kms in [33,34,35].

Other examples of attacks exploit the physical working principle of the devices in the system, as shown in [28], where they were able to trick the BB84 protocol by injecting power at the detector. Other approaches are reported in [36,37,38]. For this reason, the design trend in new protocols is to achieve device independency (i.e., preventing any security dependency on device implementation and imperfections). The first proposal of this kind of protocols was made in 2012 and is known as measure-device-independent (MDI) protocol [39], where they introduced an intermediate node to which both the partners send their photons. The photons are jointly projected in a base according to the same mechanism as in BB84, but using four maximally entangled Bell states. As in the case of regular QKD, any eavesdropping would lead to a perturbation of the measurement that could be detected by the communicating partners. Since the first proposal of the MDI protocol, many experimental and theoretical works have emerged, improving the distance reach, information rate, robustness, and compatibility with classical optical systems [40,41,42,43,44].

2.4. QKD Networking

Current QKD systems are conceived mainly over point-to-point optical fiber links. This implies the availability of dark fibers at an acceptable access cost and in a multi-user environment; and the deployment of key-regenerated meshed networks, where quantum traffic is inefficiently regenerated at every node, leading to wasted energy and bandwidth resources and negatively impacting on security. Moreover, a separate classical network is still necessary, as required by practical QKD systems not using one-time pad encryption. The ability to support both classical and quantum communication channels on a shared, reconfigurable, transparent wide-area optical network infrastructure is the ultimate condition for the commercial success of QKD systems, but it requires the coexistence of quantum and classical optical channels on the same fiber infrastructure. Examples of experiments running quantum and classical channels on the same fiber are reported in

Table 1. Examples of experiments running quantum and classical channels on the same fiber.

Date	State/Company	Distance (km)	Rate/Wavelength (Gbit/s)/nm	Quantum Wavelength (nm)	Code Rate (bit/s)
1997	United Kingdom/ British Telecom	28	1.2/1550	1300	-
2009	Sweden/Gotheburg University	50	-/1550	1550	11
2012	United Kingdom/ Cambridge University	50	1/1571–1611	1550	507 k
2016	United Kingdom/ Cambridge University	50	100/1547	1529	1.2 M
2017	China/China Telecom Corporation	80–117	80 × 100/1550	1310	1.6 k–1 k
2018	China/China Unicom	66	3600/1550	1310	4.5 k

[45].

Considering that the transmitted optical power in classical optical networks is orders of magnitude higher than for quantum communication, multiplexing classical and quantum signals on the same fiber can result in significant performance impairment for the quantum channel, due to insufficient isolation of optical filters or non-linear propagation effects. In the following, an overview is provided about the main design challenges and guidelines.

The first issue is the link distance: optical fiber loss and photodetection noise limit the distance of the current generation of QKD systems to about 200 km, one order of magnitude less than the distance achieved by classical long-haul systems, which appears to be a challenging goal for QKD systems, even when considering the progress single-photon source, low-noise single-photon detector, and low-loss optical fiber technologies.

Besides the distance challenge, in a mixed quantum–classical network, quantum information must be dynamically routed from the transmitter of any node to the receiver of any other node, as currently happens in classical optical networks, which use tunable lasers and reconfigurable optical add drop multiplexers (ROADMs) for this purpose. ROADMs are based on photonic devices, such as wavelength selective switches (WSSs) and arrayed waveguide gratings (AWGs), which in principle preserve the quantum information. However, their current performance is not specified for quantum channels. For example, the residual crosstalk among different wavelengths could be an issue for the highly sensitive quantum channel, as well as requiring the use of noisy optical amplifiers to compensate for the device loss. The principle operation of a ROADM-based quantum–classical dense wavelength division multiplexing (DWDM) network operating at 1550 nm is reported in [46], where a quantum channel coexists with two simultaneous 200 GHz spaced classical telecom channels. However, as reported in the same paper, Raman and four-wave mixing impairments severally limit the application space of such systems, operating entirely in the 1550 nm window [47,48].

A list of high-level design features to ensure the coexistence of quantum and classical optical channels on the same network infrastructure is provided below:

-

High-isolation (> 100 dB) wavelength division multiplexing (WDM) of quantum and classical channels to remove crosstalk generated by classical channels and spontaneous emission noise generated by optical amplifiers from the quantum channel band.

-

A proper wavelength plan to minimize the transfer of linear and non-linear noise from classical channels into quantum channels.

-

Optical bypass of quantum channels in optical amplifiers and other non-quantum-compatible devices.

-

Signal-format transparent and independent optical switching for quantum and classical channels.

In systems where quantum and classical signals coexist in the same fiber, the noise due to the classical channels must be measured with high accuracy. As a rule of thumb, any in-band noise contribution should be less than the quantum system detector dark noise. For Indium Gallium Arsenide Phosphide (InGaAsP) avalanche photo-diodes (APDs) in Geiger mode, the dark count probability can be as low as 10⁻⁷ over one nanosecond. In order to avoid a negative impact on the performance of a QKD system, the average noise optical power in the quantum band should be less than −138 dBm, corresponding to 1.24 × 10⁷ photons/ns in the 1550 nm band [47]. This rule does not apply to future single-photon detectors, designed to have almost no intrinsic dark counts: in this case, detectors themselves can also be used to measure the noise level with high accuracy.

The noise level must be much lower than the level considered in classical optical communications. Spontaneous emission noise from lasers and optical amplifiers are two examples of noise sources from a classical system. Its typical values, in the order of hundreds of photons/ns at 1550 nm, are incompatible with single-photon quantum communication systems, but they decrease to 10^–2–10⁻³ photons/ns in the 1300 nm region, making quantum–classical coexistence possible using high–isolation optical filters. Deep notch filters used to suppress the noise before the quantum channel insertion, having an adjacent channel isolation of about 75 dB, are an alternative to band duplexers to allow the coexistence of quantum and classical channels in the same 1550 nm band, having the advantage of lower fiber attenuation. However, they need an active control of the central frequency to compensate for any offset from the channel frequency (e.g., due to thermal drift). The filter specifications are even more stringent at the optical demultiplexer, placed before the receiver, where an isolation of about 120 dB is required [49].

Optical filters cannot remove in-band noise, such as that generated by light scattering of classical optical channels, as they propagate in the fiber. Rayleigh and Brillouin scattering add a significant noise contribution only when the quantum channel is very near to the conventional channel and can be mitigated by allocating a frequency gap of at least 100 GHz. Raman scattering noise, which is approximately 200 nm wide, can lead instead to a severe performance impairment and requires a proper wavelength allocation plan and channel optical power control. Coexistence of a quantum channel in the 1300 nm band with four classical DWDM channels with an aggregate power of 2 dBm in the 1550 nm band was demonstrated for a system with a dark count level of 10⁻³ photons/ns over 25 km of standard single mode fiber (SSMF) [50]. Another experiment [51] showed that at least 170 nm of separation are required between the QKD signal and a single 6 dBm conventional channel. System feasibility with a lower separation between quantum and classical channels was experimentally demonstrated with a CV-QKD system [52]. In the experiment, a classical channel at 1550.12 nm was multiplexed with a CV-QD channel at 1530.12 nm. A positive key rate was obtained at 25, 50, and 75 km for classical channel power of 11.5 dBm, 5.5 dBm, and −0.5 dBm, respectively. With a single 0 dBm classical channel at a distance of 25 km, the key rate was 24.11 kbit/s, dropping to 3.16 kbit/s at 50 km. Reducing the classical channel power to −3 dBm, 0.49 kbit/s was obtained over 75 km. The impact of noise sources differing from Raman scattering was analyzed in [52], such as imperfect demultiplexer isolation, Rayleigh scattering, Brillouin backscattering, Brillouin-guided acoustic wave scattering, four-wave mixing, amplified spontaneous emission, sideband photons, and cross-phase modulation. The analysis showed a negligible cumulative contribution to the measured excess noise compared to the Raman scattering noise.

Mitigating the physical impairments is not the only challenge towards an integrated quantum–classical network. Automated network operation is a necessary feature to lower the total cost of ownership to enable the adoption of QKD on a large scale. A proposal to extend the software-defined network (SDN) paradigm to QKD networks is illustrated in [53]. The proposed architecture consists of four layers: an optical layer, where classical channels are switched into optical cross-connects; a separate QKD layer, consisting of interconnected QKD trusted nodes; a control layer, in charge of the concurrent control of classical and quantum channels; and the application layer. A common path computation engine (PCE) for classical and quantum channels takes into account mutually induced penalties and common constraints, such as the total number of wavelengths. The segmentation of a single wavelength channel in multiple time slots to gain spectral efficiency and exploit bandwidth resources across the entire network is also envisaged. In [53], it is assumed that the secret keys for a service request with specific security demands are exchanged between the source and destination nodes at fixed time intervals. Each time interval consists of the channel estimation and calibration time, qubit exchange time, key sifting time, and key distillation time.

Other examples of how the SDN and network function virtualization (NFV) paradigms—widely adopted in classical networks—can be extended to quantum networks, including internet of Things (IoT) [54] and 5G [55] applications, are reported in [55,56,57,58,59,60,61,62,63], further proving the importance of moving from current point-to-point setups to more complex topologies. Furthermore, recent advances in machine learning (ML) can greatly help to improve the automation of QKD systems, whose performance depends of many parameters that must be finely tuned, thereby significantly decreasing operational and maintenance costs. In [61], ML is used in a hybrid classical–quantum network to estimate the channel performance versus various spectrum allocations, launch powers, and channels spacings, and predict the optimal configuration. Similarly, ML-based parameter optimization, such as the choice of intensities and probabilities, is performed in [64].

The synchronization of single-photon gated detectors to the incoming quantum signal is another mandatory feature in practical QKD systems. This can be addressed by recovering the timing from the clock frequency of the digital classical signal or by means of a dedicated synchronization network.

2.5. Closing Remarks on QKD Systems

Most of current quantum communication testbeds and early commercial systems rely on DV-QKD, which was extensively investigated and compared to its competitor, CV-QKD. However, DV-QKD requires dedicated devices, which may forever limit its application to niche markets, which are not too sensitive to costs. CV-QKD potentially overcomes this issue reusing device already developed for classical communication systems. However, while for DV-QKD many security proofs exist, the guaranteed security level of CV-QKD is more uncertain, making it questionable if it is worthwhile to introduce a further encryption layer besides the ones already existing (ranging from physical to packet layers) in classical communications networks.

However, the most serious concern about QKD systems, regardless of whether they are based on discrete or continuous variables, is that they are conceived for short-distance, low-capacity point-to-point links. The ability to support high data rates over long distances remains unsolved. Optical networks where classical and quantum channels coexist are a possible answer, but the achievable performance is far from acceptable, as the experiments discussed in the previous sections show. Spatial division multiplexing (SDM) is another possibility to increase the capacity, splitting and sending the key over parallel multiple fibers or spatial modes. In [65], a 33.6 Mbit/s key rate was achieved over 9.8 km, using a 7-core multicore fiber. SDM may be an interesting technique for data center interconnection, characterized by relatively short point-to-point links and ultra-short chip-to-chip interconnection [66].

It is still too early to declare a winner among the several proposed QKD options, especially considering the early maturity stages of some enabling technologies, such as quantum repeaters, which are the key to extending the link distance. This aspect will be discussed in the next section.

3. Devices for QKD Systems

The development of devices has a key role in the industrialization of QKD, due to the high costs involved and integrability of the solution. Many of the current devices for QKD are still quite bulky. This is the reason why the path of photonic integration, especially using complementary metal oxide semiconductor (CMOS)-compatible silicon photonics, is being pursued to provide enhanced functionalities and miniaturization in platforms that are suitable for mass manufacturing and easy to integrate with existing telecommunication equipment.

The main devices characterizing a QKD systems, as discussed in the following section, are the photon sources and detectors with which to send and receive the quantum states, and the quantum random number generators (QRNG) with which to achieve pure random bit streams. Further, to overcome the distance limitations already mentioned, quantum repeaters represent a fundamental milestone that could take QKD to a higher level, enabling arbitrary long-distance communication.

3.1. Photon Sources

Solid-state, single-photon sources are reviewed in [67]. Ideally, telecommunication-relevant photon sources should work at room temperature, emit information at commonly used wavelengths (850, 1300, or 1500 nm), and be easily integrable with other devices (e.g., silicon photonics modulators) at the cheapest cost. Electrically driven photon emission systems appear to be more suitable for telecommunication, as they are more compact and controllable on chips. Both single photons and entangled photons pairs are suitable, depending on the system requirements and protocol. Room temperature III-V semiconductor lasers integrated on silicon are a short-term viable option. Their main merit is their readiness, but the production process may be expensive for large-scale production.

To realize entangled photon sources at 810 nm or 1550 nm, one may opt for silicon nitride or silicon photonic integrated circuits, respectively, where ring resonators are used for entangled photon-pair emission based on spontaneous four-wave mixing [68].

An integrated weak coherent transmitter at 1550 nm was proposed in [69], based on a monolithically fabricated Indium Phosphide (InP) device comprised of a wavelength-tunable laser, an electro-optic phase modulator (EOPM), and a photodiode. The EOPM is used in multiple interferometers to create intensity modulated and phase-encoded weak coherent signals for multiple protocol QKD.

At 850 nm, the Micius satellite [70] implements space-to-ground BB84 QKD using eight fiber-based laser diodes, of which four are used for signal states and four for decoy states.

In the future, two dimensional materials deposited on silicon may provide true single-photon emissions at room temperature [71].

Regarding weak coherent sources of photons at 1550 nm, III-V lasers, used for single-photon sources or to pump Si microrings for the generation of entangled photons on chips, may be replaced in the future with full group IV photon sources, such as germanium microcavities [72] or Er in silicon or silicon oxide chipsets [73,74], including coupling with resonant rings or cavities.

Single photons can also be generated by defects in materials, such as nitrogen vacancy (NV) centers in diamonds [75] and silicon vacancy (SiV) centers [76].

At 810 nm, one may in the future explore colloidal quantum dots, similar to those used for commercial screens, and 2D materials combined with photonic cavities in silicon nitride.

3.2. Detectors

Single-photon detectors must combine high performance with low cost and with the possibility of integration, for example in the same silicon photonics platform used for manufacturing other components. None of the currently available solutions meet these requirements, and developing radically new components will take many years. A pragmatic strategy is, therefore, to use currently available detectors to demonstrate the correct operation of QKD systems and protocols while waiting for new technologies to be developed. Figure 2 shows different solutions in terms of readiness, cost, operating temperature, degree of integrability, and efficiency for systems operating at 1550 nm. waveguide single-photon avalanche diodes (WG-SPADs) [77,78] are very suitable for mass production and can be monolithically integrated into silicon photonic integrated circuits. WG-SPADs are built around a waveguide, so that light can be easily coupled from the optical circuit into the detector. They operate close to room temperature with obvious advantages in terms of cost. Er-doped silicon devices have been tested to evaluate the photocurrent response [79]. Ge-on-Si SPADs (Ge-SPAD) have a germanium absorption layer and share most of the advantages of WG-SPAD, but they operate at lower temperatures (about −50 °C). Moreover, coupling light from the optical circuit to the detector is not as easy as with WG-SPAD [80]. Using III-V compounds to build a SPAD (III-V SPAD) is currently the most immediately available solution, whereby the integration on the photonic integrated circuit (PIC) is realized by molecular wafer bonding. Compared to Ge direct epitaxial growth on silicon avalanche materials, wafer bonding of III-V SPAD structures onto silicon requires further fabrication steps, such as substrate demounting. Also, electron injection (EI) detectors are fabricated by III-V materials, so they share the same limitations in terms of operating temperature and integrability, but they have no dead time and have the capability to resolve the number of photons simultaneously impinging on the detector [81].

3.3. Quantum Random Number Generators

Random numbers play a crucial role in diverse applications, such as secure communications [69,81,82,83,84], stochastic modelling [85], gambling [86], Monte Carlo simulations [87], and extensive data processing [88]. Unlike pseudo-random numbers that are generated through computational algorithms, true random numbers are generated through physical processes. Randomness is considered “true” if it is provable by information theory [89]. Physical random number generators rely on physical processes that are believed to be random, such as electronic and thermal noise [90], amplified spontaneous emission [91], and chaotic semiconductor lasers [92]. Quantum random number generators (QRNG) are a subset of physical random number generators that derive randomness from quantum mechanical processes and events [93]. The probabilistic nature of quantum mechanics makes QRNG a preferred source for generating true random numbers.

A QRNG is expected to produce uncorrelated and uniformly distributed streams of random data and typically consists of a quantum entropy source block and a post-processing block. The entropy source is a physical system that generates random physical variables, referred to as raw data, and reads them through measurement and detection equipment. In the entropy source, a quantum state is prepared to ensure true randomness and measured to generate the raw random data. In the post-processing stage, an assessment of the degree of randomness of the raw data is made through autocorrelation and estimation of the minimum entropy, which is a measure of the extractable randomness of the raw data. The estimated minimum entropy acts as an input to randomness extractor algorithms and hardware that output nearly true random numbers. The extracted true random numbers are subjected to randomness tests, such as the ones defined by the National Institute of Standards and Technology (NIST); the so called DIEHARD tests, which refer to a widely used suite of methods of assembling and combining uniform random numbers, and then performing statistical tests; and TestU01, a software library, implemented in the ANSI C language, offering utilities for the statistical testing of random number generators.

Optical QRNG implementations have been investigated using different quantum processes, such as entropy sources, including two-path splitting of single photons [94], photon arrival time [95], amplified spontaneous emission [93,94,95,96], detection of vacuum field [97], and phase diffusion and phase noise in laser diodes [98,99,100,101,102,103,104].

The physical principle behind branching path generators is path superposition and subsequent state measurement. The source of randomness is the splitting of weak light beams realized by optical beam splitters or polarization beam splitters (PBS) and detectors. A quantum state with one photon is sent by a weak light source to a balanced beam splitter or a PBS, and detected by the relevant detector. The output path taken by the photon is random and the probability of detection at each detector is the same. The detection on one detector (D0) can be considered as a “0” bit, whereas detection at the other detector (D1) can be considered as a “1” bit, thus generating a random sequence. This type of generator can achieve a rate in the order of Mbit/s. The performance is mainly limited by the detector dead time, which can be improved by using detectors with faster recovery times [94,105].

QRNGs based on photon arrival time exploit randomness in photon detection times (i.e., time of arrival statistics). These QRNGs have timing circuitry in addition to weak photon sources and detectors to keep precise track of each individual detection event or number of clicks in a fixed time window. Within a short time window, photons arriving at the detector from a weak source follow an exponential distribution in time λe^−λt, where λ is the average number of photons per second. The time interval between two photodetection events is the difference of two exponential random variables, which is also exponential [105]. Therefore, the time difference between the arrival times of consecutive pulses can be compared to generate random bits. This type of QRNG can generate random bits at Mbit/s rates. Major design challenges are the time precision and the detector dead time.

In optical communications, strong amplification spontaneous emission (ASE) noise is a limiting factor, but it is a good source of entropy for QRNGs. The main advantage is that ASE provides a readily available strong signal of quantum origin that can be measured with conventional optical devices at fast rates [105]. QRNGs based on amplified spontaneous emission use amplitude fluctuations as entropy sources. Williams et al. [106] demonstrated an ASE-based QRNG that uses a 915 nm pumped erbium/ytterbium co-doped fiber as an optical randomness source. The output ASE spectrum is band-pass-filtered and amplified again by a conventional erbium-doped fiber amplifier (EDFA). A fiber polarization splitter is used to separate the two independent orthogonal polarization components prior to photo-detection. The detected signals in each arm, v1(t) and v2(t), have random amplitude whose distribution depends on the shape of the filter. To generate random bits, the two detected signals are compared at a sampling instant, generating a “1” when v1(t) > v2(t) and a “0” otherwise. Alternative schemes have also been proposed [8]. These devices can achieve generation rates of Gbit/s. The rate of change of amplitude of the ASE field is usually much faster than the speed of the detection mechanism, thus making the speed of the detector the limiting factor for higher generation rates.

QRNGs have also been demonstrated to exploit the fluctuations in the quantum vacuum state [107]. The vacuum state can be considered as a superposition of amplitude quadrature states. These generators use homodyne detection to measure one of the quadrature fluctuations. In homodyne detection, the vacuum state is mixed with a reference field of a local oscillator (LO) laser in a balanced optical beam splitter and photo-detected with balanced detectors at the splitter outputs. The detector outputs are subtracted and processed, generating a current output proportional to the quadrature amplitude of the vacuum field. Its values are a measure of the fundamental uncertainty in the vacuum state. This signal is then digitized and processed to produce random number sequences [105]. The achievable output generation rate is dependent on the characteristics of the local oscillator, the detector noise and bandwidth, and the characteristics of the digitizer. Other challenges are the removal of classical noise and the post-processing complexity. These QRNGs can achieve rates in the Gbit/s range.

Semiconductor laser output field fluctuations are caused by spontaneous emission in the laser cavity. The resultant random phase noise, also referred to as phase diffusion (PD), has a quantum mechanical nature [93] and is exploited to generate random numbers in phase noise-based QRNGs (PN-QRNG). PN-QRNGs basically measure field quadrature fluctuations of phase-randomized weak signal states [23]. This is achieved by translating the random phase fluctuations of the laser into amplitude fluctuations, using an unbalanced Mach Zehnder interferometer (uMZI). Two different schemes have been reported for PN-QRNGs. The first approach directly detects phase fluctuations from a continuous wave laser using a delayed self-heterodyne detection system [98,104], whereas the second scheme strongly modulates the laser in the gain switching regime to produce a pulsed light output. The uMZI delay is matched to the pulse repetition rate to translate the phase difference in successive pulses into amplitude variations [99,100,101]. Pulsing helps to increase the phase diffusion rate for the same mean power, which is proportional to the spontaneous emission rate over the intra-cavity photon number [101]. Compared to other QRNG approaches, generators based on phase diffusion have been shown to provide higher bit rates owing to the use of conventional photodetectors instead of SPADs [103]. In addition, PN-QRNGs are also more robust against detector noise and have been successfully evaluated versus extensive randomness tests, thus ensuring both high data rate and reliability [104]. However, most of these demonstrations use bulk fiber or free space components, which are large, costly, and exhibit long-term instability. Significant reduction in size is essential for the integration into complex systems such as QKD receivers. Similarly, larger size and higher cost reduce scalability and limit widespread commercial use. Instability issues strongly affect the reliability of these devices. To achieve low-cost, scalable solutions, there has been a huge interest in photonic integrated circuit (PIC) technologies for quantum optics recently. A number of on-chip QRNG solutions for well-investigated schemes (referenced above) have been reported in the literature, demonstrating different levels of complexity and using different integration technologies, e.g., Lithium Niobate (LiNbO3) or Indium Phosphide on Silicon (InP/Si) [106,107,108,109,110,111,112,113]. Authors in [106] demonstrated a monolithically integrated QRNG on a Si platform using a light emitting diode (LED) as a quantum entropy source and a SPAD, achieving a 1 Mbit/s rate. Haylock et al. demonstrated a photonic integrated scheme for multiplexed QRNG on a lithium niobate platform to achieve higher generation rates [107]. However, the relatively large footprint of lithium niobate devices restricts widespread use in complex applications. Two fully integrated PN-QRNGs, including entirely passive and active elements and providing Gbit/s rates using InP integration technology, have been demonstrated recently [108,109]. Both these implementations employed accelerated phase diffusion exploiting gain switching in lasers. These schemes use two lasers to reduce correlations between successive pulses. Indium phosphide technology has the advantage of monolithic on-chip integration of active (lasers, photo-detectors) and passive (couplers, multiplexers, etc.) components on a single platform. On the other hand, silicon photonic systems have the advantage of compatibility with cost-effective complementary metal oxide semiconductor (CMOS) processes, hence increasing their deployment prospects in advanced semiconductor applications. Raffaelli et al. [110] demonstrated optical integration of a homodyne detector on a silicon-on-insulator (SOI) chip for QRNG based on vacuum fluctuations and achieved a 1.2 Gbit/s rate. An integrated Gbit/s QRNG based on improved homodyne detection of vacuum fluctuation using a silica planar light circuit was reported in [111]. Raffaelli et al. recently demonstrated another SOI-integrated QRNG based on phase fluctuations from an off-chip laser diode, with all other components integrated on a SOI chip [112]. Rude et al. demonstrated interferometric photo detection on a Si chip using an integrated uMZI interferometer for a quantum entropy source based on accelerated phase diffusion. The input multi-mode interference (MMI) coupler of the uMZI was designed to provide an unbalanced splitting ratio (2% and 98%) and 1 ns delay [113]. Photonic integration certainly helps to provide a more compact uMZI compared to bulky discrete devices. However, the performance is strongly impacted by stability issues associated with long delays in uMZI caused by intrinsic phase noise and temperature drifts, and therefore requires strong stability control [111]. Improved visibility and signal-to-noise ratio (SNR) and higher entropy generation rates (short delays require faster modulation) can be achieved by reducing the waveguide losses and difference in length of the two arms of the uMZI [113].

In conclusion, QRNGs employing different quantum phenomena have been extensively investigated and they can be considered as relatively mature quantum technologies. Photonic chip-based implementations have high potential to reduce cost and footprint and improve scalability for mass production. Although generation rates at the Gbit/s scale have been demonstrated in laboratory environments, real-world implementation is still constrained by practical challenges in the speed of the electronic subsystems and post-processing methods.

3.4. Quantum Repeaters

Quantum repeaters are devices conceived to extend entanglement over space, despite the fundamental limitations of the no-cloning theorem. Their purpose is to cause base-level entanglement over a physical link and coupling entangled links along an end-to-end path. There are two alternative methods to create quantum repeaters: the solid state approach, based on a static buffer memory; and the all-optical approach, without such a static buffer memory. In the following, we focus on solid-state devices. There is a range of proposals based on different physical systems relying on ensembles of atoms, intended to collectively interact with a photon in order to store the quantum information encoded by the photon itself. The purpose of employing an ensemble of atoms instead of a single atom is to increase the cross section (i.e., the probability that the photon interacts with the device). Furthermore, an ensemble of atoms can, in principle, store more than one photon at a time, which is beneficial for increasing the communication rate. There are several elements that are under consideration for creating the mentioned ensemble, among which rare earth embedded in solid state crystals are the most promising. Such elements have the drawback of extreme cryogenic cooling at around 1.5 K, but some of them, such as ytterbium (yttrium orthosilicate, YSO), can offer both operation at the 980 nm wavelength and 1 ms of coherence time, with the advantage of being compatible with telecom systems and having robustness to perturbations of the environment [114,115]. Erbium supports 1550 nm wavelengths but has the disadvantage of having higher sensitivity to such perturbations. Europium shows a coherence time of about 6 h at 2 K [116].

Alternatively, III-V alloy quantum dots have been used to demonstrate entanglement between a single quantum dot spin qubit and a flying (i.e., propagating) photonic qubit [117]. One should note that in all-photonic quantum repeaters, the quantum information is instead encoded and protected in multi-photon entangled states, so they operate, in principle, at room temperature. This approach and the related protocol require only two coupled quantum emitters, as described in [118,119,120].

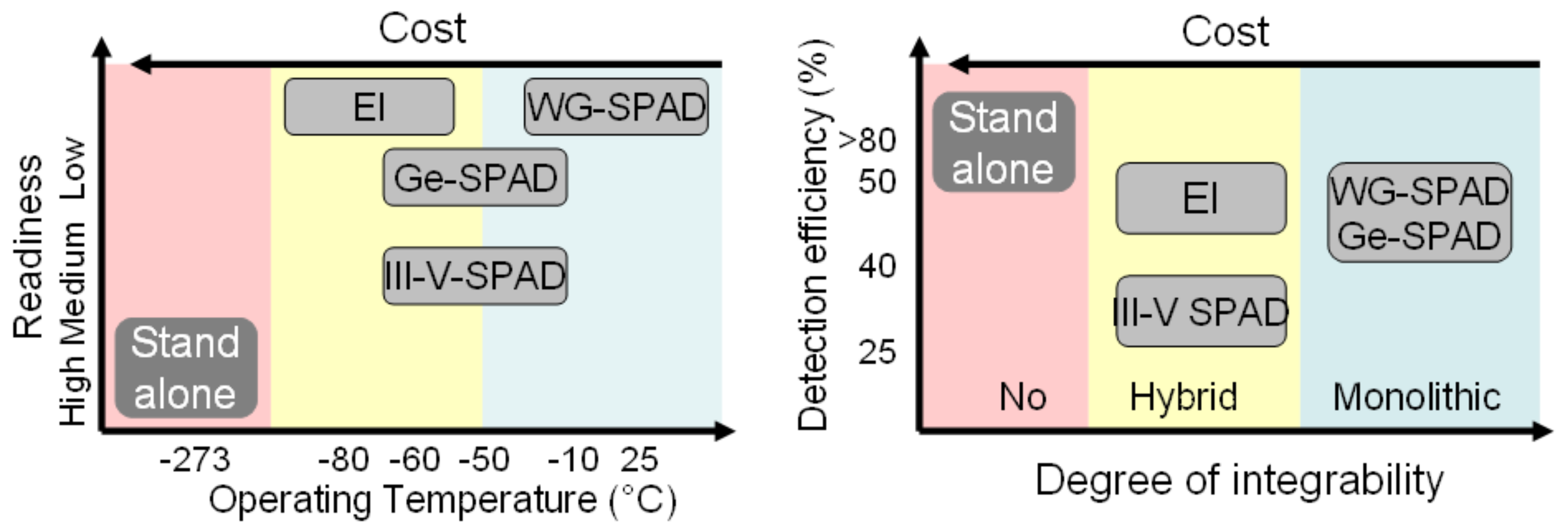
3.5. Technology Status Summary

Photonic integration is a well-consolidated trend in classical optical networks, which leads to a tangible decrease of cost, footprint, and energy consumption. This trend is also expected to positively impact QKD systems. Single or entangled photon sources based on III-V materials integrated on silicon or silicon nitride are an example of devices made possible by recent integrated photonics advances. Regarding single-photon detectors, none of the current solutions achieve the desired figures for cost, footprint, and energy efficiency altogether: III-V SPADs are the most immediate solution, but WG-SPADs monolithically integrated in silicon are more suitable for mass production and can operate close to room temperature. Two dimensional materials, such as graphene, may lead to further advances, such as true single-photon emitters at room temperature. Regarding quantum subsystems, QRNG is by far the device with the highest maturity and is the most ready to be commercialized. It is also used in classical cryptography systems. Photonic chip-based implementations have high potential for mass production and generation of high bit rates. Regarding technology maturity, quantum repeaters are still at the proof of concept stage, and it is unclear at the moment what a realistic market-ready timeframe could be.

So far, we have analyzed quantum systems from a technological viewpoint. Technology maturity is an important factor. However, it is not the only factor determining the large-scale deployment of commercial quantum systems. In the rest of this paper, we analyze in more detail application areas and market drivers.

4. QKD Applications

While QKD systems are based on a few core principles, the large number of implementation variants drastically influences the complexity and cost of each solution. Since the application domains for QKD are numerous and heterogeneous, it is important to understand which set of protocols, systems, and devices are preferable for the different use cases, along with their different requirements. This mapping will help to clarify the correlation between technologies (protocols, systems, devices) and potential markets, and will be used in the following to elaborate considerations about the strategy the community should pursue to pierce the industrial barrier.

Many discriminant factors may be considered for such a classification process, but we limit the discussion to three of them.

A first classification can be made in terms of the medium into which the light travels, distinguishing between guided (fiber, waveguide) and unguided (in air) systems. This medium has a direct impact on both protocols and devices, due the large differences of the light propagation laws in different media. For example, the propagation in guided media is affected by random polarization rotation, which prevents easy implementation of encoding of polarization information. The limiting factor in air is instead the coupling of light with the detector due to the very low level of detected power and the high variability of weather conditions.

A second classification parameter is the distance between the sender and receiver, leading to the coarse distinction between short-reach and long-reach communications. The distance limitation is defined here as the inherent limit of unamplified quantum transmission above which signal regeneration is required.

The third factor we propose is the cost, which may range from extremely low (e.g., quantum encryption in sensors or smartphones) to extremely high for military and space applications. This also relates to the used technology—QKD systems requiring cryogenic cooling are very costly, while cheaper solutions with lower performance may be based on integrated devices used for classical optical communications.

Table 2. Technology features versus different application domains.

Devices	Protocols	Medium	Cost	Distance	Application
Integrated	DV-QKD CV-QKD	In Air	Low	Short (1–10 m)	Internet of Things, Contactless payment
Bulky/Integrated Weak pulses	DV-QKD Decosy states MDI Pol. Enc.	In Air	Medium	High (2000–35000+ km)	Space Communications
Bulky/Integrated Weak pulses	DV-QKD Decoy states MDI Pol. Enc. CV-QKD	In Fiber	Medium	Medium (10–100 km)	Inter Database communications, Short reach meshed networks
Bulky Cryogenic Temp.	DV-QKD MDI One Time Pad	In Fiber In Air	High	Medium/high (10–1000 km)	Critical infrastructure management
Bulky/Integrated Weak pulses	DV-QKD CV-QKD	In Fiber	Medium	Medium	Wide area network

maps technology features (devices, protocols, propagation medium, cost, distance) versus different application domains.

4.1. Long-Range Fiber Communication

Including QKD encryption in existing optical metro and core networks is widely recognized as an important application scenario. This means reusing infrastructure designed for classical networks to enable QKD encryption along the telecom services. This is the reason why CV-QKD gives an advantage in respect to DV-QKD, due to better compatibility with commercial devices. However, the current limits in terms of security and reachable distance mean that CV-QKD is still not comparable to DV-QKD, meaning that both approaches are still relevant. For this use case, guided phase or spin-modulated DV-QKD with possible MDI, decoy states, and trusted nodes (where acceptable) could be the right choice, especially considering that some integration work has been already taken out [121,122]. However, the compatibility issues with the existing classical networks remain dramatic, and too few works exist in this area [52,123,124]. Most of the QKD systems are assumed to work over point-to-point nodes, without the chance of using optical amplification.

The situation is different for critical environment services or military applications, where due to the amount of resources invested it is possible to build dedicated QKD infrastructures, while also adopting high-efficiency cooled systems to increase the rate and distance. In some scenarios, even the one-time pad approach might be acceptable.

Leakage of data from critical infrastructure that may be vulnerable to cyber attacks is considered of utmost importance at the European level, and has been defined in a previous directive [125], which identifies energy, digital services, air transport, bank systems, water supply, and healthcare as critical services.

4.2. Aerospace Communication

In the aerospace segment, due to difficulties with physical access to devices, the sensitiveness of data transmitted, and also due to the huge amount of investment needed, QKD technologies appear to be a short-term solution to avoid cyber-attacks. QKD could be used to encrypt: (1) critical ground-to-space communication, (2) satellite-to-satellite links, and by combining the two, (3) ground-to-ground communication over satellite networks. Quantum systems may be employed in both low and medium earth orbit (LEO/MEO), where the relative proximity to the earth surface guarantees acceptable losses due to diffraction of light, while their high speed in respect to the ground represents the main drawback for pointing the laser. Applications could also involve geostationary earth orbit (GEO) networks, where instead there is huge distance from the ground to the satellite, but the link can be maintained continuatively [126]. In aerospace, DV-QKD is easier to adopt compared to CV-QKD due to the high variability of the atmospheric channel, the changing positions of objects, and the long distances, increasing the complexity of channel estimation. Polarization encoding is adopted in a straightforward manner, since the polarization state can travel unaffected by rotation in air. The high distances and the size of the equipment suggest the usage of bulky, high detection efficiency devices supported by low temperature operation. Further, the absence of a wired infrastructure between communicating devices in earth-to-satellite scenarios makes a possible network implementation based on point-to-point links without quantum switches and routers difficult to implement.

4.3. Internet of Things

Another relevant market segment is the internet of things (IoT), which interconnects a massive number of sensors, actuators, and humans, and exchanging data over the Internet. IoT aims to increases the quality of life by permeating the world with connected sensors and actuators, and enabling novel services. However, this can lead to security issues because those devices must be small, simple, and cheap, even when acquiring and communicating critical sensitive data. Even though securing those devices is an urgent problem, maintaining low cost and size is a priority, meaning that adopting QKD is only feasible with highly integrated solutions, such as silicon photonic devices, attenuated single-photon LEDs, and decoy techniques, in order to remove the constraints of using pure single-photon sources. Since the devices can be mobile and are spread over a wide area, guided communication is not an option, and in-air protocols are more likely to be used in this context together with polarization encoding. CV-QKD may be envisioned to reduce the costs, but the dynamic nature of the environment in short-reach in-air links, often in urban scenarios, may impair its performance, reducing the key rate to unacceptable values [127].

4.4. Data Center Infrastructure

Data centers store an unprecedented amount of data, including private sensitive information, government agency data, office data, and any other kind of critical information. Today, around 7500 databases are present worldwide [128]. This is the reason why database interconnection is of utmost importance. In cloud networks, databases are often physically located away from the place where the data are generated, and may adopt a distributed architecture for both efficiency reasons and security purposes. The common distances between data centers are of the order of tens of kilometers, perfectly in the range of DV-QKD or CV-QKD fiber communication. Moreover, such infrastructure may allow dedicated quantum communication infrastructure to be built. These databases probably represent the market segment that will be impacted first by QKD.

4.5. Quantum Applications Summary

Application areas with various performance and cost requirements have been analyzed. For long-range fiber communication, compatibility with classical switched optical networks is a must, as well as the use of cost-effective photonic integrated technologies. CV-QKD is more promising under this context [59] but it suffers from performance issues that may be mitigated using phase- or spin-modulated DV-QKD with decoy states. Since repeaters will not be available for a long time, trusted nodes will be used. Communication between data centers has less stringent distance requirements and could be the first application where QKD systems in fiber will be tested in the field. Similarly, the aerospace industry is less cost-sensitive than the fiber communication industry, meaning this field may be used as a test bench for technologies that will be engineered further before being moved to other areas. Cost and operation at ambient temperature are even more important for sensors used in the IoT, so we expect quantum technologies will be adopted in that area when integrated quantum devices are available for fiber communication.

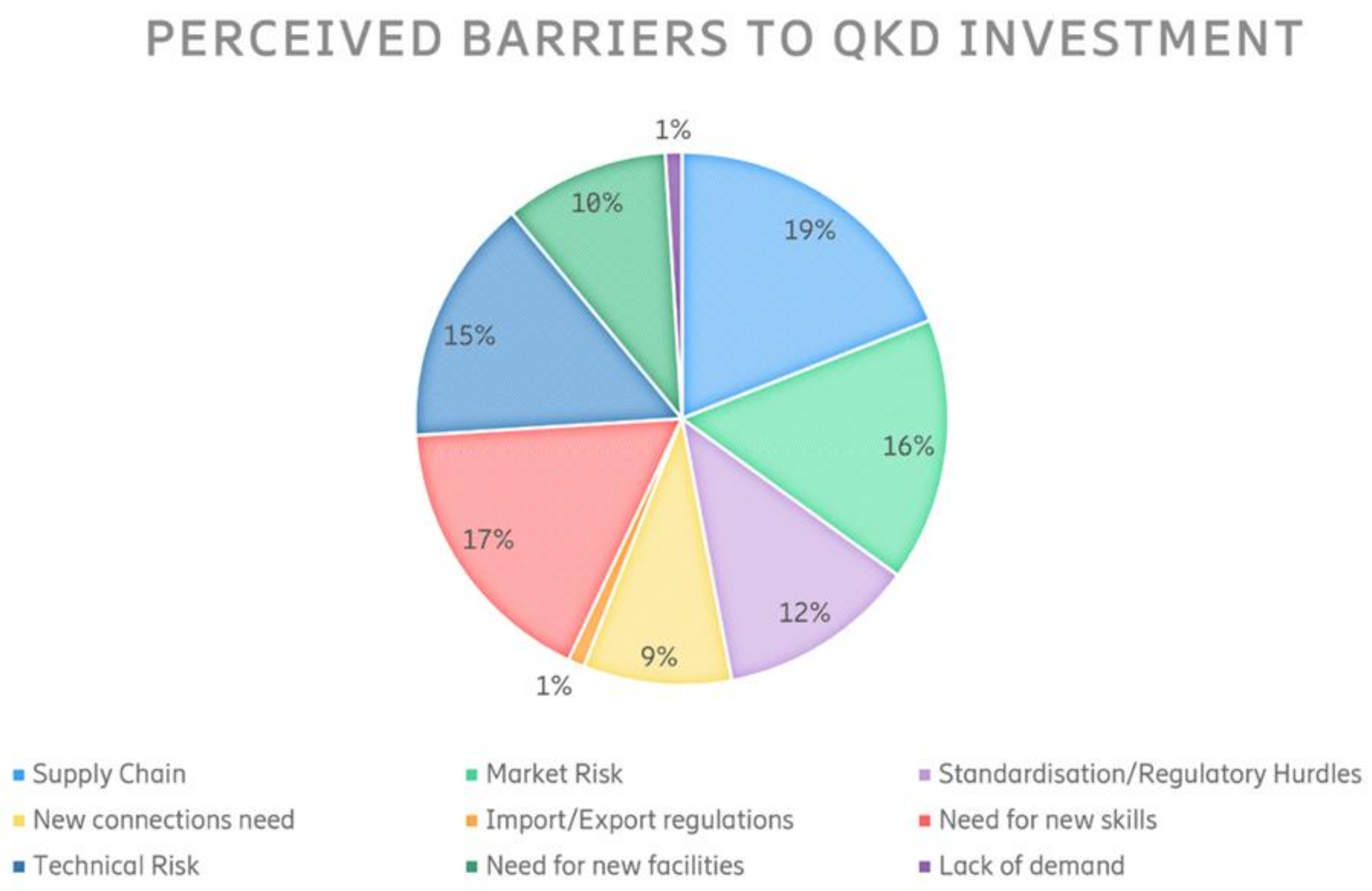
5. QKD Market Perspectives

Several studies forecast a rapid growth of QKD system sales, from several million euros currently to several billion euros by 2030. Despite these optimistic predictions, several challenges remain related to the creation of a wide market for QKD systems, moving them from laboratories to a real production environment. These primarily include access to appropriate economic and human resources, and the introduction of new cost-effective technologies that can ensure performance repeatability, reliability, manufacturability at a large scale. To overcome the first issue, innovation platforms could be the ideal tool for startups and spinoff companies to gain access, so as create new technologies, standards, and protocols and share their experiences. To face the second issue (i.e., the availability of technologies deployable on large scale), the integration of optical and electronic quantum devices is a necessary step. Recent advances in photonics integration offer new opportunities in this direction. For example, silicon photonics allows the realization of miniaturized Mach–Zehnder interferometers [129] with highly stable, temperature-controlled phase shift between the two interferometers arms. Other examples are single-photon sources based on quantum dots [130], single-photon detectors able to work at room temperature [131], high-speed QRNG [132], and on-chip receivers for continuous variable systems [132].

Applications, protocols, and software are other key ingredients that require further development. Other key ingredients are those constituting a flexible network protocol stack capable of dealing with a variety of services, network topologies, and technologies, without requiring the final user to have specific quantum skills. A deeper analysis of security features at the network level is also necessary. For example, “an advanced security analysis is required for new quantum communication protocols, including continuous-variable QKD with discrete modulation, protocols exploiting relativistic effects, or QKD protocols exploring different photonic degrees-of-freedom (frequency, time bins, polarization, paths, orbital angular momentum) [133]”.

An important challenge in a QKD network is extending, in a secure way, the distance between the two end points beyond the distance of a single QKD span, which using practical thermoelectric cooling is today limited to several hundred kilometers. In principle, quantum repeaters allow long-haul communication (up to thousands of kilometers), but the technology is far from being ready for the market. Examples of candidate technologies for quantum repeaters are the already mentioned quantum repeaters based on rare earth materials [134] and on highly entangled cluster states based on quantum dots [135]. Practical implementations of MDI-QKD [136] and twin-field QKD (TF-QKD) [137] may allow network deployments where intermediate nodes can be placed in untrusted locations in the future [133].

Besides those technological aspects, initial skepticism from network providers, stakeholders, venture capitalists, and the general public could be a non-negligible delay factor in the introduction of QKD technologies. Devices and systems based on quantum physics are often considered exotic technologies that are not economically attractive and not fully understood. Figure 3 [138] shows expected barriers acquired through surveys to companies in various market segments. QKD systems will have to demonstrate that they can compete with standard encryption algorithms and complement conventional networks, giving a plausible return of investment in the short and medium time periods. There is also a growing view that excessively stringent regulations may impede the setting up of new businesses. Regulation and standardization, however, are essential for QKD to succeed. QKD security indeed depends on the implementation of interoperable protocols with well understood and certified security properties.

Lastly, a barrier that cannot be neglected while considering the spreading of a technology is the cost. For most of the market segments, commercial QKD systems are seen as prohibitive and not competitive considering the maturity of the technology. This is true also for critical infrastructure, where the cost may be considered more marginal than security. Considering the analysis proposed in [139], they estimated that a small network with 5–10 nodes would cost more than 500,000 euro for equipment only, considering actual available technologies. For satellite systems, where the installation of fibers and switching or routing devices is not needed, the cost is expected to be higher than 500,000 euro. They envisioned a reduction to less than 200,000 euro by 2022 by reaching the expected volumes of production, while reducing this value below 50,000 euro may also enable QKD for smaller (Cubesat) satellites, which would open a new, larger market segment. In the telecommunications sector, the dominant cost is in the sources and detectors, which currently cost around 100,000 euro and is expected to decrease to less than 10,000 euro by 2022. However, it is estimated that most of the market share in the telecommunications sector will be dominated by QRNG systems, enabling many applications for IoT, for which the costs are already relatively low. For QRNGs, the cost can be thousands of euros for the most efficient ones, while for those scenarios where high performance is not required, the price is expected to decrease to tens of euros within a couple of years, approaching the cost level of the IoT sector. A reliable assessment of strengths and weaknesses of QKD systems requires a thorough understanding of both the QKD protocol itself and its practical implementation, as reflected in European Telecommunications Standards (ETSI) reference documents on security proofs [140] and module security specifications [141].

6. Industrial Roadmap

A roadmap towards the commercialization of all quantum technologies, including QKD, is reported in the Strategic Research Agenda [133] prepared by the European Quantum Flagship. A summary of the expected developments is as follows:

-

Within 3-years: standards and certification methodologies for QRNG and QKD; development of use cases and business models; cost-effective systems for inter-city and intra-city communications; protocols for the security of long-lived systems and secret sharing, exploiting quantum and classical cryptographic techniques; protocol execution over an elementary quantum repeater link using an integrated control plane and platform-independent software stack; improved device performance addressing parameter benchmarks of relevance for cryptography and network applications.

-

Within 6–10 years: Advanced QKD and QRNG systems for critical infrastructure, IoT, and 5G; trusted-node network functionality and interoperability for fiber, free-space, and satellite links; end-to-end security over trusted nodes and eventually repeaters between countries; integration of at least three physically distant quantum repeaters over telecom fiber, demonstrating key generation over more than 500 km; demonstrations of entanglement-based network application and satellite-based links; showcase of a network of physically distant processing nodes (e.g., in the quantum memory), with at least 20 qubits per node and programmable in platform-independent software.

Similar research and development phasing efforts were undertaken by individual countries such as the United Kingdom [142], which put an emphasis on a ten-fold cost reduction of quantum communications technologies within 15 years from now, and of course by countries with large investment capabilities, such as China and the United States. The U.S. high level strategy is illustrated in [143]. For quantum networking, exploring and using coherent or entangled multi-party quantum states is envisaging. An excellent analysis of the global scenario, including socio-economic and strategic implications for Europe, is provided in [144]. A short summary of the various initiatives covered in [145], is provided below:

-

A comprehensive public program for the deployment of a QKD infrastructure is being pursued by China, and comprises a ~2000 km Beijing–Shanghai quantum backbone, four metropolitan networks, a ~50km free air link, and a quantum satellite for intercontinental communications.

-

The government of South Korea is funding the development of a ~250 km quantum backbone connecting existing metropolitan quantum networks.

-

Australia is implementing a government quantum network for intra-governmental communications in Canberra.

-

In South Africa, a quantum communication security solution has been deployed in Durban’s municipal fiber-optic network.

-

In Japan, several industrial and public partners have jointly developed an extensive quantum network in Tokyo.

-

Besides China, satellite-based quantum communications are also currently being investigated in Japan, Canada, and the United States. In 2007m the European Space Agency published a review paper on its activity in this field, comprising a feasibility study for the placement of an entangled photon source on the International Space Station.

-

In the United States, a fiber-based QKD infrastructure has been in development since 2003, with a Defense Advanced Research Projects (DARPA) funded project, and several players, both public (Department of Commerce with NIST, Department of Energy with Los Alamos Labs) and private companies (mostly from the defense and aerospace sectors, e.g., Magiq, BBN Raytheon, Boeing, Batelle), are accumulating intellectual property and expertise, in some cases complemented by field deployments.

-

A real-world application of QKD was demonstrated in Austria in 2004. In 2007, in Switzerland the canton of Geneva transmitted ballot results using a QKD link.

-

A high point in European research towards practical application of quantum cryptography was achieved in 2004–2008 with the SECOQC FP6 project, which involved several academic as well as industrial partners. However, some European companies seem to have now reduced their engagement.

In light of the section on the application domain, we suggest which segments could be affected in the medium and short term. We consider not only the previously discussed technology aspects, but also the interest and investment capacity of the markets. The deployment in the short term is likely to be led by the absence of repeaters (limiting the link distance to tens of kilometers) with simple network topologies to avoid complex system coexistence. The space segment is expected to grow faster, considering the sensitiveness of data transferred and the amount of investment in the field. The higher reachable distance (achievable without repeaters), the unguided medium, and the simple network topology (without switching, routing, or amplifying) will further help. Inter-database connections are characterized typically by simple network topologies, short distances, and a low number of network nodes, providing a good opportunity for short-term impact. Other market segments may be found with similar characteristics, for example where short-reach optical networks exist, as in the radio access network (RAN), connecting mobile user equipment to base stations. Here, the low cost is an important requirement, however, integrated hardware is also required. Special critical ad-hoc infrastructure (e.g., links between security agencies or banks) may be deployed and realized soon. For large-scale wide area network (WAN) deployment, further effort concerning the integration of quantum systems in commercial networks is needed and efficient techniques to increase the distance are required.

7. Standardization of QKD Systems

Standardization is crucial for the industrialization of QKD systems in order to develop interoperable multi-vendor products and mitigate the risk of individual companies developing proprietary solutions that may never succeed. Considerable standardization efforts toward QKD systems have been undertaken by the standardization sector of the International Telecommunication Union (ITU), ETSI, and Internet Engineering Task Force (IETF).

At the standardization sector of ITU, referred as ITU-Telecommunications (ITU-T), a Focus Group on Quantum Information Technology for Networks (FG-QIT4N) was established in September 2019 as a collaborative platform for investigating quantum communication networks, with the main objectives of studying the evolution and applications of communication networks based on quantum technologies; the definition of terminology and use cases for quantum networks; and the preparation of technical background information to support related standardization work in ITU-T study groups. As a result, standardization work on QKD networks started with ITU-T Study Group 13. Besides an overview of networks supporting QKD [146], covered topics in the Y.QKDN draft recommendation series are functional requirements and architecture; business role-based models; quantum key management; control and management, including software defined networks (SDN) control; and quality of service (QoS) aspects.

At ETSI, an industry specification group (ISG) on quantum key distribution for users was established to enable digital keys to be shared privately without relying on computational complexity. The scope of the group encompasses the specification of QKD system interfaces, implementation of security requirements, and optical characterization of QKD systems and their components [141,144,147,148,149,150,151,152,153].

At IETF, the Quantum Internet Proposed Research Group (QIRG) was established to investigate and engineer the new communication and remote computation capabilities offered by quantum technologies. Cryptographic functions are within the groups scope, including quantum key distribution and quantum byzantine agreement, as well as routing schemes, dynamic resource allocation, connection establishment, interoperability, and design of application programming interfaces (APIs). The QIRG intends to understand the applications of quantum Internet, specifying its characteristics (e.g., the data rate) and addressing multi-party states and multi-party transfers (e.g., network coding) rather than simple, independent point-to-point transfers. The QIRG will define an architectural framework delineating network node roles and definitions to build a common vocabulary and serve as the first step toward a quantum network architecture.

8. Conclusions

In this document, we tried to give the reader a multi-view panorama of the protocols, devices, and industrial segments that could be influenced by quantum cryptography, the main exploitable application in the field of quantum communication.

We exposed our view of the actual scenario, summarizing the state of the art and exposing the main factors afflicting the process of industrialization following the European directives that are delineating the roadmap in the field. The high diversity of solutions characterizing quantum communications was highlighted, which must be properly matched with the wide number of market segments within the telecommunications world, each with their specific requirements. We expect that the industrialization process, unlike others technology trends such as artificial intelligence, machine learning, and IoT, which are transversally affecting all the market segments, will instead proceed in a sectorial manner. Firstly, aerospace networks and topologically small, critical in-fiber networks will be impacted; for these, a well-studied DV approach could be directly applied with current technology and the known practical limits could easily be overcome, either by investing in ad-hoc infrastructure with dedicated fibers if enough resources are available or by exploiting the properties of such fields where the integration would be simpler (e.g., exploiting point-to-point in-air links). We expect instead other segments to be impacted in a second tranche, requiring a more involved integration with complex devices (wide area networks) with higher distances requirements, or segments where small, low-cost chips are required (IoT), whereby the integration process will reach a mature state and the large-scale production will push down the costs. Altogether, we expect by this time that the CV approach will become robust enough to solve compatibility issues of the devices, and hopefully quantum repeaters will substitute the trust-based approach to reach arbitrary distances.