Approximate Solution to Fractional Order Models Using a New Fractional Analytical Scheme

Abstract

In the present work, a new fractional analytical scheme (NFAS) is developed to obtain the approximate results of fourth-order parabolic fractional partial differential equations (FPDEs). The fractional derivatives are considered in the Caputo sense. In this scheme, we show that a Taylor series destructs the recurrence relation and minimizes the heavy computational work. This approach presents the results in the sense of convergent series. In addition, we provide the convergence theorem that shows the authenticity of this scheme. The proposed strategy is very simple and straightforward for obtaining the series solution of the fractional models. We take some differential problems of fractional orders to present the robustness and effectiveness of this developed scheme. The significance of NFAS is also shown by graphical and tabular expressions.

1. Introduction

In latest decades, partial differential problems of fractional orders have been widely used in numerous branches of sciences such as that chemical engineering, metrology, optical fibres, optimal theory, viscoelasticity, Chemotaxis and many other nonlinear models [1,2,3,4]. There have been numerous definitions of the integral and derivative of fractional orders. Various researchers have considered the Riemann, Liouville, Hadamard, and Caputo definitions as the most significant ones [5,6,7,8]. 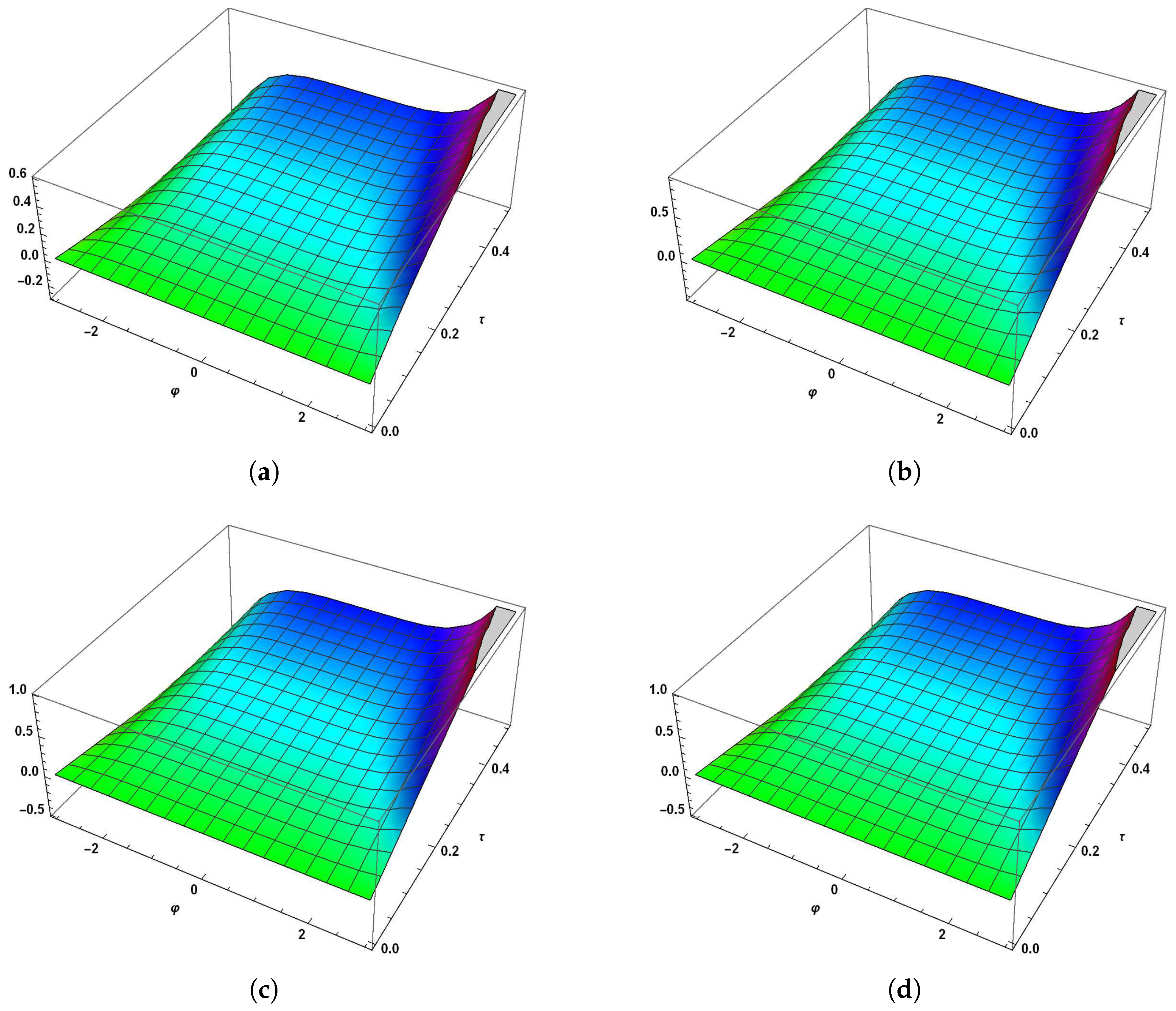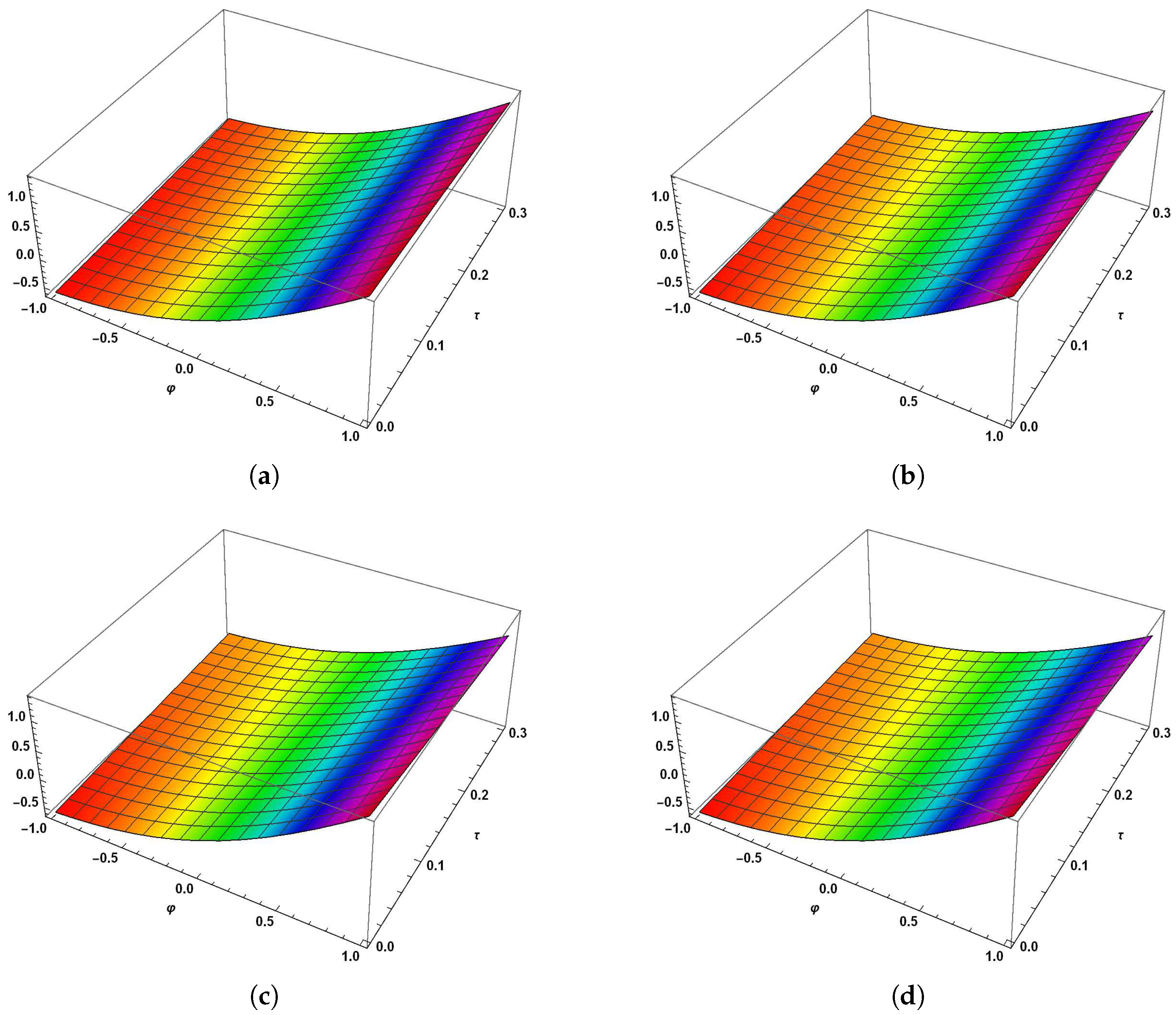In addition to this, numerous modern definitions of the fractional derivative have been presented, but the Caputo concept continues to be the most widely used, because it has several applications in real-world phenomena [9,10]. However, the investigation of the exact solutions of these problems still pose a challenging task in various physical phenomena.

In this work, we consider the fourth-order time-fractional parabolic PDEs of the form [11,12]

$$\begin{array}{c}\hfill \frac{{\partial }^{2\alpha }\vartheta }{\partial {\tau }^{2\alpha }}+\alpha (\phi ,\upsilon ,\eta )\frac{{\partial }^4\vartheta }{\partial {\phi }^4}+\beta (\phi ,\upsilon ,\eta )\frac{{\partial }^4\vartheta }{\partial {\upsilon }^4}+\gamma (\phi ,\upsilon ,\eta )\frac{{\partial }^4\vartheta }{\partial {\eta }^4}=g(\phi ,\upsilon ,\eta ,\tau ),\end{array}$$

(1)

where $\alpha ,\beta ,\gamma$ are variables subjected to the initial conditions

$$\begin{array}{cc}\hfill \vartheta (\phi ,\upsilon ,\eta ,0)& =f_1(\phi ,\upsilon ,\eta ),\frac{\partial \vartheta }{\partial \tau }(\phi ,\upsilon ,\eta ,0)=f_2(\phi ,\upsilon ,\eta ),\hfill \end{array}$$

(2)

and boundary conditions

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \vartheta (a,\upsilon ,\eta ,\tau )& =g_0(\upsilon ,\eta ,\tau ),\vartheta (b,\upsilon ,\eta ,\tau )=g_1(\upsilon ,\eta ,\tau ),\hfill \\ \hfill \vartheta (\phi ,a,\eta ,\tau )& =k_0(\phi ,\eta ,\tau ),\vartheta (\phi ,b,\eta ,\tau )=k_1(\phi ,\eta ,\tau ),\hfill \\ \hfill \vartheta (\phi ,\upsilon ,a,\tau )& =h_0(\phi ,\upsilon ,\tau ),\vartheta (\phi ,\upsilon ,b,\tau )=h_1(\phi ,\upsilon ,\tau ),\hfill \\ \hfill \frac{{\partial }^2\vartheta }{\partial {\phi }^2}(a,\upsilon ,\eta ,\tau )& =\overline{g_0}(\upsilon ,\eta ,\tau ),\frac{{\partial }^2\vartheta }{\partial {\phi }^2}(b,\upsilon ,\eta ,\tau )=\overline{g_1}(\upsilon ,\eta ,\tau ),\hfill \\ \hfill \frac{{\partial }^2\vartheta }{\partial {\upsilon }^2}(\phi ,a,\eta ,\tau )& =\overline{k_0}(\phi ,\eta ,\tau ),\frac{{\partial }^2\vartheta }{\partial {\upsilon }^2}(\phi ,b,\eta ,\tau )=\overline{k_1}(\phi ,\eta ,\tau ),\hfill \\ \hfill \frac{{\partial }^2\vartheta }{\partial {\eta }^2}(\phi ,\upsilon ,a,\tau )& =\overline{h_0}(\phi ,\upsilon ,\tau ),\frac{{\partial }^2\vartheta }{\partial {\eta }^2}(\phi ,\upsilon ,b,\tau )=\overline{h_1}(\phi ,\upsilon ,\tau ),\hfill \end{array}\end{array}$$

(3)

where $f_l,g_l,h_l,k_l,\overline{g_l},\overline{h_l},\overline{k_l},$ and $l=0$ present that the functions are continuous. The parabolic equation has gone through significant improvement since it was originally used in underwater acoustics, especially regarding improvements in accuracy and its application in the domain of time. The wide-angle parabolic equation was developed to considerably reduce the phase errors of the solutions to the parabolic equation, which resemble the solution to the wave equation. The time domain parabolic problem has been extended to include wide-angle diffraction, sediment dispersion, nonlinear propagation, density variations, and sediment attenuation. The fourth-order boundary value problems have much significance in various applications of real-life problems and are being considered for the modeling of slabs of bridge, flooring patterns, wings of aviation, and frame glasses [13]. Parabolic PDEs have great importance in the analysis of viscous fluid and inflexible flows, laser distortion, and layered stretching [14].

There are numerous methods that have been studied to solve some fractional PDEs. Kheyrinataj and Nazemi [15] proposed a scheme on the basis of a neural network adaptive structure and obtained the numerical solution to the fractional differential problems. Mamehrashi [16] presented the idea of Ritz approximate strategy to derive the results of fractional control equations. Arikoglu and Ozkol [17] implemented a differential transform scheme for some composite fractional oscillation problems. Liu et al. [18] presented a multi-AUV dynamic scheme based on interval information game theory and fractional-order differential problems. Li and Zhao [19] utilized a Haar wavelet operational matrix and obtained the computational solution of some differential problems of fractional orders. The solution to these fractional problems has been obtained by numerous approaches, such as the reduced differential transform method [20], the optimal control method [21], the trial equation scheme [22], the Homotopy analysis method [23], the Melnikov method [24], the Laplace transform [25], He’s variational method [26] and the Chebyshev–Tau approach [27]. Due to some drawbacks and limitations such as restriction of the variables, assumption theory, convolution theorem, and the Lagrange multipliers in the recurrence relation, we developed an efferent approach that can overcome these drawbacks and limitations.

In the current work, we introduce a new fractional analytical scheme for the approximate solution of fourth-order parabolic FPDEs. The significant feature is that this approach computes the iteration results very quickly and close to the exact solution of the proposed problems. The obtained results are verified through 3D graphical representations and the error distribution, thus presenting the behaviour of the proposed problems under various conditions. In our model, we consider the Caputo derivative due to its common use of fractional analysis in the literature. It is used because it has a memory effect, and the derivative of a constant function becomes zero. It is also widely recognized in derivatives that fractional operators do not have the same features as a classical derivative. This work is summarized as follows: In Section 2, we reveal a few definitions of fractional calculus. We develope the idea of NFAS and present the detail for how to apply this approach to the fourth order parabolic partial differential equations in Section 3. We discuss the convergence and stability analysis of NFAS in Section 4. We illustrate three numerical applications in Section 5 to check the performance of the NAD. We summarize the results in conclusion Section 6.

2. Concepts of Fractional Calculus

In the current segment, we provide the initial concepts and ideas of fractional calculus for the development of this study [28,29].

Definition 1. 

Let $\vartheta \left(\phi \right),\phi >0$ be a real function in space $C_{\mu }$ where $\mu \in \mathcal{R}$; then, there exists a real number $p>\mu$ such that $\vartheta \left(\tau \right)={\tau }^p{\vartheta }_1\left(\tau \right)$, where ${\vartheta }_1\left(t\right)\in C(0,\infty )$, and it can be considered in space $C_{\mu }^n$ only if ${\vartheta }^n\in C_{\mu }$, where $n\in N$.

Definition 2. 

The Riemann–Liouville fractional integral operator of order $\propto >0$ of a function $\vartheta \in C_{\mu },\mu >-1$ is expressed as

$$\begin{array}{c}\hfill j^{\alpha }\vartheta \left(\tau \right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^{\tau }{(\tau -s)}^{\alpha -1}\vartheta \left(s\right)ds;\alpha >0\\ \hfill j^0\vartheta \left(\tau \right)=\vartheta \left(\tau \right).\end{array}$$

Since numerous researchers have explained the various inequalities of Riemann–Liouville fractional integrals [21,22,23,24], we will explain only a few properties of the operator $j^{\alpha }$ as follows: For $\vartheta \in C_{\mu },\mu \ge -1,\propto ,\beta \ge 0$, and $\gamma \ge -1$,

$$\begin{array}{c}\hfill j^{\alpha }{j}^{\beta }\vartheta \left(\tau \right)=j^{\beta +\alpha }\vartheta \left(\tau \right),\\ \hfill j^{\alpha }{\tau }^{\gamma }=\frac{\Gamma (\gamma +1)}{\Gamma (\gamma +\alpha +1)}{\tau }^{\alpha +\gamma }.\end{array}$$

Definition 3. 

Let $\vartheta \left(\tau \right)$ be a function; then, the fractional derivative in the Caputo sense is expressed as [25]

$$\begin{array}{c}\hfill D^{\alpha }\vartheta \left(\tau \right)=j^{m-\alpha }{D}^m\vartheta \left(\tau \right)\end{array}$$

for $m-1<\alpha \le m,m\in N,\tau >0$, and $\vartheta \in C_{-1}^m$.

The Caputo fractional derivative has such a significant feature such that a fractional integral is considered for an ordinary derivative to calculate the fractional order derivative, although the Riemann–Liouville fractional integral operator is linear such that

$$\begin{array}{c}\hfill j^{\alpha }\left(\sum _{i-1}^n{c}_i{\vartheta }_i\left(\tau \right)\right)=\sum _{i=1}^n{c}_i{j}^{\alpha }{\vartheta }_i\left(\tau \right),\end{array}$$

where ${\left\{c_i\right\}}_{i=1}^n$ are constants.

3. Development of New Fractional Analytical Scheme (NFAS)

In this section, we provide the development of new fractional analytical scheme for the analytical results of time-fractional fourth-order parabolic partial differential problems. Let us consider the following PDE of the fractional order

$$\begin{array}{c}\hfill D_{\tau }^{2\alpha }\vartheta (\phi ,\tau )=F(D_{\tau }^{\alpha }\vartheta ,\vartheta ,D_{\phi }^{\alpha }\vartheta ,D_{\phi }^{2\alpha }\vartheta ,\cdots ),\end{array}$$

(4)

with the initial conditions

$$\begin{array}{c}\hfill \vartheta (\phi ,0)=h_0\left(\phi \right),D_{\tau }^{\alpha }\vartheta (\phi ,0)=h_1\left(\phi \right).\end{array}$$

(5)

By applying the fractional integral to Equation (4) from 0 to $\tau$, it yields

$$\begin{array}{c}\hfill D_{\tau }^{\alpha }\vartheta (\phi ,\tau )-D_{\tau }^{\alpha }\vartheta (\phi ,0)=I_{\tau }^{\alpha }F\left(\vartheta \right),\\ \hfill D_{\tau }^{\alpha }\vartheta (\phi ,\tau )-h_1\left(\phi \right)=I_{\tau }^{\alpha }F\left(\vartheta \right),\end{array}$$

$$\begin{array}{c}\hfill D_{\tau }^{\alpha }\vartheta (\phi ,\tau )=h_1\left(\phi \right)+I_{\tau }^{\alpha }F\left(\vartheta \right),\end{array}$$

(6)

where

$$\begin{array}{c}\hfill F\left(\vartheta \right)=F(D_{\tau }^{\alpha }\vartheta ,\vartheta ,D_{\phi }^{\alpha }\vartheta ,D_{\phi }^{2\alpha }\vartheta ,\cdots ).\end{array}$$

Again, implement the integration on both sides of Equation (6) to yield

$$\begin{array}{c}\hfill \vartheta (\phi ,\tau )-\vartheta (\phi ,0)=h_1\left(\phi \right)\frac{{\tau }^{\alpha }}{\Gamma (\alpha +1)}+I_{\tau }^{2\alpha }F\left(\vartheta \right),\\ \hfill \vartheta (\phi ,\tau )-h_0\left(\phi \right)=h_1\left(\phi \right)\frac{{\tau }^{\alpha }}{\Gamma (\alpha +1)}+I_{\tau }^{2\alpha }F\left(\vartheta \right),\end{array}$$

This implies that

$$\begin{array}{c}\hfill \vartheta (\phi ,\tau )=h_0\left(\phi \right)+h_1\left(\phi \right)\frac{{\tau }^{\alpha }}{\Gamma (\alpha +1)}+I_{\tau }^{2\alpha }F\left(\vartheta \right).\end{array}$$

(7)

The Taylor series can be expanded for $F\left(\vartheta \right)$ about $\tau =0$, and we get

$$\begin{array}{c}\hfill F\left(\vartheta \right)=\sum _{n=0}^{\infty }\frac{D_{\tau }^{n\alpha }F\left({\vartheta }_0\right)}{\Gamma (n\alpha +1)}{\tau }^{n\alpha }.\end{array}$$

(8)

We can write it as

$$\begin{array}{c}\hfill F\left(\vartheta \right)=F\left({\vartheta }_0\right)+\frac{D_{\tau }^{\alpha }F\left({\vartheta }_0\right)}{\Gamma (\alpha +1)}{\tau }^{\alpha }+\frac{D_{\tau }^{2\alpha }F\left({\vartheta }_0\right)}{\Gamma (2\alpha +1)}{\tau }^{2\alpha }+\frac{D_{\tau }^{3\alpha }F\left({\vartheta }_0\right)}{\Gamma (3\alpha +1)}{\tau }^{3\alpha }+\cdots +\frac{D_{\tau }^{n\alpha }F\left({\vartheta }_0\right)}{\Gamma (n\alpha +1)}{\tau }^{n\alpha }+\cdots .\end{array}$$

(9)

When we put Equation (9) into Equation (7), we obtain

$$\begin{array}{c}\vartheta (\phi ,\tau )=h_0\left(\phi \right)+h_1\left(\phi \right)\frac{{\tau }^{\alpha }}{\Gamma (\alpha +1)}+I_{\tau }^{2\alpha }\left[F\left({\vartheta }_0\right)+\frac{D_{\tau }^{\alpha }F\left({\vartheta }_0\right)}{\Gamma (\alpha +1)}{\tau }^{\alpha }+\frac{D_{\tau }^{2\alpha }F\left({\vartheta }_0\right)}{\Gamma (2\alpha +1)}{\tau }^{2\alpha }+\frac{D_{\tau }^{3\alpha }F\left({\vartheta }_0\right)}{\Gamma (3\alpha +1)}{\tau }^{3\alpha }+\cdots \right],\\ \vartheta (\phi ,\tau )=h_0\left(\phi \right)+h_1\left(\phi \right)\frac{{\tau }^{\alpha }}{\Gamma (\alpha +1)}+\frac{F\left({\vartheta }_0\right)}{\Gamma (2\alpha +1)}{\tau }^{2\alpha }+\frac{D_{\tau }^{\alpha }F\left({\vartheta }_0\right)}{\Gamma (3\alpha +1)}{\tau }^{3\alpha }+\frac{D_{\tau }^{2\alpha }F\left({\vartheta }_0\right)}{\Gamma (4\alpha +1)}{\tau }^{4\alpha }+\cdots ,\\ =a_0+a_1\frac{{\tau }^{\alpha }}{\Gamma (\alpha +1)}+a_2\frac{{\tau }^{2\alpha }}{\Gamma (2\alpha +1)}+a_3\frac{{\tau }^{3\alpha }}{\Gamma (3\alpha +1)}+a_4\frac{{\tau }^{\alpha }}{\Gamma (\alpha +1)}+\cdots .\end{array}$$

(10)

Here,

$$\begin{array}{cc}\hfill a_0=& h_0\left(\phi \right),\hfill \\ \hfill a_1=& h_1\left(\phi \right),\hfill \\ \hfill a_2=& F\left({\vartheta }_0\right),\hfill \\ \hfill a_3=& D_{\tau }^{\alpha }F\left({\vartheta }_0\right),\hfill \\ \hfill a_4=& D_{\tau }^{2\alpha }F\left({\vartheta }_0\right),\hfill \\ \hfill & ⋮\hfill \\ \hfill a_n=& F^{(n-2)\alpha }\left({\vartheta }_0\right),\hfill \end{array}$$

where n stands the particularly high derivative of $\vartheta$. The endorsement of Equation (10) is to proceed the Taylor series for $\vartheta$ about $\tau =0$. Thus,

$$\begin{array}{cc}\hfill a_0=& \vartheta (\phi ,0),\hfill \\ \hfill a_1=& D_{\tau }^{\alpha }\vartheta (\phi ,0),\hfill \\ \hfill a_2=& D_{\tau }^{2\alpha }\vartheta (\phi ,0),\hfill \\ \hfill a_3=& D_{\tau }^{3\alpha }\vartheta (\phi ,0),\hfill \\ \hfill a_4=& D_{\tau }^{4\alpha }\vartheta (\phi ,0),\hfill \\ \hfill & ⋮\hfill \\ \hfill a_n=& D_{\tau }^{n\alpha }\vartheta (\phi ,0).\hfill \end{array}$$

As a result, we easily obtain the desired mathematical results.

4. Convergence and Stability Analysis of NFAS

In this section, we discuss convergence and stability analysis for the fractional problems and show that our approach is valid and authentic throughout the manuscript.

4.1. Convergence Analysis

Consider the following PDE

$$\begin{array}{c}\hfill \vartheta (\phi ,\tau )=Q\left(\vartheta \right(\phi ,\tau \left)\right),\end{array}$$

(11)

where Q is a nonlinear operator. The following sequence gives the identical solution such that

$$\begin{array}{c}\hfill Q_n=\sum _{i=0}^n{\vartheta }_i=\sum _{i=0}^n{\rho }_i\frac{{(\Delta \tau )}^i}{i!}.\end{array}$$

(12)

Theorem 1. 

Let Q be an operator stating Hilbert space such that $\mathbb{H}\mapsto \mathbb{H}$ and ϑ represents the exact results of Equation (13). Then, the approximate results

$$\begin{array}{c}\hfill \sum _{i=0}^n{\vartheta }_i=\sum _{i=0}^n{\rho }_i\frac{{(\Delta \tau )}^i}{i!}\end{array}$$

yield to the exact solution ϑ when ∃ a $\rho (0\le \rho <1),∥{\vartheta }_{i+1}∥\le \rho ∥{\vartheta }_i∥\forall i\in \mathbb{N}\cup \left\{0\right\}$.

Proof. 

To show that ${\left\{Q_n\right\}}_{n=0}^{\infty }$ is a converged Cauchy sequence, we present the following:

$$\begin{array}{c}\hfill ∥Q_{n+1}-Q_n∥=∥{\vartheta }_{n+1}∥\le \rho ∥{\vartheta }_n∥\le {\rho }^2∥{\vartheta }_{n-1}∥\le \cdots \le {\rho }^n∥{\vartheta }_1∥\le {\rho }^{n+1}∥{\vartheta }_0∥.\end{array}$$

We start as $n,m\in \mathbb{N},$ and $n\ge m$; thus, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill ∥Q_n-Q_m∥& =∥\left(Q_n-Q_{n-1}\right)+\left(Q_{n-1}-Q_{n-2}\right)+\cdots +\left(Q_{m+1}-Q_m\right)∥\hfill \\ \hfill & \le ∥Q_n-Q_{n-1}∥+∥Q_{n-1}-Q_{n-2}∥+\cdots +∥Q_{m+1}-Q_m∥\hfill \\ \hfill & \le {\rho }^n∥{\vartheta }_0∥+{\rho }^{n-1}∥{\vartheta }_0∥+\cdots +{\rho }^{m+1}∥{\vartheta }_0∥\hfill \\ \hfill & \le \left({\rho }^{m+1}+{\rho }^{m+2}+\cdots +{\rho }^n\right)∥{\vartheta }_0∥={\rho }^{m+1}\frac{1-{\rho }^{n-m}}{1-\rho }∥{\vartheta }_0∥.\hfill \end{array}\end{array}$$

Hence, ${lim}_{n,m\to \infty }∥Q_n-Q_m∥=0$, i.e., ${\left\{Q_n\right\}}_{n=0}^{\infty }$ is a Cauchy sequence in the $\mathbb{H}$. Thus, ∃ a $Q\in \mathbb{H}$ s.$\tau {lim}_{n\to \infty }{Q}_n=Q$, where $Q=\vartheta$. □

Definition 4. 

We define for every $n\in \mathbb{N}\cup \left\{0\right\}$,

$$\begin{array}{c}\hfill {\rho }_n=\left\{\begin{array}{cc}{\displaystyle \frac{∥{\vartheta }_{n+1}∥}{∥{\vartheta }_n∥}}\hfill & ∥{\vartheta }_n∥\ne 0\hfill \\ 0\hfill & otherwise.\hfill \end{array}\right.\end{array}$$

Corollary 1. 

From Theorem 1,

$$\begin{array}{c}\hfill \sum _{i=0}^n{\vartheta }_i=\sum _{i=0}^n{\rho }_i\frac{{(\Delta \tau )}^i}{i!}\end{array}$$

is convergent to ϑ, where $0\le {\rho }_i<1$, and $i=0,1,2,3,\cdots$ [30,31].

4.2. Stability Analysis

Let us consider the differential problem in a Caputo fractional order sense such that

$$\begin{array}{c}\hfill D_{\alpha }^C\phi =f_1(\tau ,\phi ),\end{array}$$

(13)

where $\phi \in {\mathbb{R}}^n$ represents the state component, and $f_1:{\mathbb{R}}^{+}\times {\mathbb{R}}^n⟶{\mathbb{R}}^n$ is a continuing locally Lipschitz function that satisfies $f_1(\tau ,0)=0$. Since the initial condition is ${\phi }_0\in {\mathbb{R}}^n$, the solution of Equation (13) starting from $\phi \left({\tau }_0\right)$ at time $\tau ={\tau }_0$ is represented by $\phi (.)=\phi (.,\phi \left({\tau }_0\right))$.

Additionally, since f is contiguous and locally Lipschitz, the solution of the fractional differential problem defined by Equation (13) exists. The following definitions are very important for the study of the stability of fractional differential equations.

Definition 5. 

The trivial solution of Equation (13) is stable only if $q>0$, and there exists a $\xi =\xi \left(q\right)$ so that, considering any initial condition $\parallel \phi \left({\tau }_0\parallel <\delta \right.$, our results $\phi \left(\tau \right)$ of Equation (13) yield to the inequality $\parallel \phi \left(\tau \right)\parallel <ϵ$ with $\tau >{\tau }_0$. The trivial solution to the system $D_{\alpha }^c\phi =f(\tau ,\phi )$ is called asymptotically stable only if it is stable and, additionally, if ${lim}_{\tau \to +\infty }\phi \left(\tau \right)=0$.

Definition 6. 

The origin of the fractional differential equation defined by Equation (13) is called Mittag–Leffler stable only if the condition $∥\phi \left({\tau }_0\right)∥$ satisfies the following result:

$$\begin{array}{c}\hfill ∥\phi \left(\tau ,{\phi }_0\right)∥⩽{\left[m_1\left(∥\phi \left({\tau }_0\right)∥\right)E_{\alpha }\left(\lambda {\left(\tau -{\tau }_0\right)}^{\alpha }\right)\right]}^{\frac{1}{b_1}},\end{array}$$

where ${\mathrm{b}}_1>0$ and $m_1$ are locally Lipschitz on a domain ${\mathbb{R}}^{\mathrm{n}}$ that satisfies $m\left(0\right)=0$.

Definition 7. 

The Equation (13) is called globally continuous and asymptotically stable only if there is a function β so that for any condition, $∥\phi \left({\tau }_0\right)∥$ satisfies the following result:

$$\begin{array}{c}\hfill ∥\phi \left(\tau ,{\phi }_0\right)∥⩽\beta \left(∥\phi \left({\tau }_0\right)∥,\tau -{\tau }_0\right).\end{array}$$

Many authors have discussed the stability of fractional problems in various fractional orders. We suggested that the readers study a detail on stability from the following work: [32,33,34].

5. Numerical Applications

This section explains the authenticity of the NFAS by illustrating some numerical applications and by stating that this scheme is reliable and accurate for obtaining the solution to fractional problems. We provide the the different behaviours of the profile solutions of the proposed models to understand the physical nature of the presented scheme. We point out that the graphical results have strong resemblance among the approximate solution and the graphical solution of the exact results.

5.1. Example 1

Consider the following equation of the FPDEs in the one-dimensional form as the following:

$$\begin{array}{c}\hfill \frac{{\partial }^{2\alpha }\vartheta }{\partial {\tau }^{2\alpha }}+\left(\frac{1}{\phi }+\frac{{\phi }^4}{120}\right)\frac{{\partial }^4\vartheta }{\partial {\phi }^4}=0,\end{array}$$

(14)

with initial conditions

$$\begin{array}{c}\hfill \vartheta (\phi ,0)=0,{\vartheta }_{\tau }(\phi ,0)=1+\frac{{\phi }^5}{120}.\end{array}$$

(15)

By following the process of the NFAS, we obtain

$$\begin{array}{c}\hfill F\left(\vartheta \right)=-\left(\frac{1}{\phi }+\frac{{\phi }^4}{120}\right)\frac{{\partial }^4\vartheta }{\partial {\phi }^4}.\end{array}$$

(16)

Thus, we can obtain the following iterations

$$\begin{array}{c}\hfill a_0=h_0\left(\phi \right)=\vartheta (\phi ,0)=0,\end{array}$$

$$\begin{array}{c}\hfill a_1=h_1\left(\phi \right)={\vartheta }_{\tau }(\phi ,0)=1+\frac{{\phi }^5}{120},\end{array}$$

$$\begin{array}{c}\hfill a_2=-\left(\frac{1}{\phi }+\frac{{\phi }^4}{120}\right)\frac{{\partial }^4{a}_0}{\partial {\phi }^4}=0,\end{array}$$

$$\begin{array}{cc}\hfill a_3=& -\left(\frac{1}{\phi }+\frac{{\phi }^4}{120}\right)\frac{{\partial }^4{a}_1}{\partial {\phi }^4}=-\left(1+\frac{{\phi }^5}{120}\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill a_4=& -\left(\frac{1}{\phi }+\frac{{\phi }^4}{120}\right)\frac{{\partial }^4{a}_2}{\partial {\phi }^4}=0,\hfill \end{array}$$

$$\begin{array}{cc}\hfill a_5=& -\left(\frac{1}{\phi }+\frac{{\phi }^4}{120}\right)\frac{{\partial }^4{a}_3}{\partial {\phi }^4}=\left(1+\frac{{\phi }^5}{120}\right).\hfill \end{array}$$

Proceeding in a similar way, we obtain

$$\begin{array}{c}\hfill \vartheta (\phi ,\tau )=a_0+a_1\frac{{\tau }^{\alpha }}{\Gamma (\alpha +1)}+a_2\frac{{\tau }^{2\alpha }}{\Gamma (2\alpha +1)}+a_3\frac{{\tau }^{3\alpha }}{\Gamma (3\alpha +1)}+a_4\frac{{\tau }^{4\alpha }}{\Gamma (4\alpha +1)}+a_5\frac{{\tau }^{5\alpha }}{\Gamma (5\alpha +1)}+\cdots .\end{array}$$

(17)

By putting the values of $a_0,a_1,a_2,a_3,\cdots$, we obtain

$$\begin{array}{c}\hfill \vartheta (\phi ,\tau )=\left(1+\frac{{\phi }^5}{120}\right)(\tau -\frac{{\tau }^{3\alpha }}{\Gamma (3\alpha +1)}+\frac{{\tau }^{5\alpha }}{\Gamma (5\alpha +1)}+\cdots ).\end{array}$$

(18)

which leads to the exact solution such that

$$\begin{array}{c}\hfill \vartheta (\phi ,\tau )=\left(1+\frac{{\phi }^5}{120}\right)sin\tau .\end{array}$$

(19)

Example 1 shows the graphical representation of fourth-order parabolic PDEs in the two-dimensional form. Figure 1 is presented into two parts, where Figure 1a–c present the approximate results of $\vartheta (\phi ,\tau )$ for $0\le \phi \le 10$ and $0\le \tau \le 10$, and Figure 1d demonstrates the precise solution of $\vartheta (\phi ,\tau )$. This comparison of approximate solutions obtained by the NFAS with the exact solution has full agreement.

Table 1. The NFAS results for distinct parameters of $\alpha$ when $\tau =0.3$ for Example 1.

$\mathit{\phi }$	${\mathit{\vartheta }}_{\mathit{\alpha }=0.50}$	${\mathit{\vartheta }}_{\mathit{\alpha }=0.75}$	${\mathit{\vartheta }}_{\mathit{\alpha }=1}$	Exact Solution
0.10	0.190039	0.274522	0.29552	0.29552
0.15	0.190039	0.274522	0.29552	0.29552
0.20	0.190039	0.274523	0.29551	0.29551
0.25	0.190040	0.274524	0.295523	0.295523
0.30	0.190042	0.274528	0.295526	0.295526
0.35	0.190047	0.274534	0.295533	0.295533
0.40	0.190055	0.274545	0.295545	0.295545
0.45	0.0190068	0.274564	0.295566	0.295566
0.50	0.190088	0.274594	0.295597	0.295597

presents the NFAS results for distinct parameters of $\alpha$ and reveals a high accuracy towards the precise solution.

5.2. Example 2

Consider the following equation of the FPDEs in the two-dimensional form as the following:

$$\begin{array}{c}\hfill \frac{{\partial }^{2\alpha }\vartheta }{\partial {\tau }^{2\alpha }}+2\left(\frac{1}{{\phi }^2}+\frac{{\phi }^4}{6!}\right)\frac{{\partial }^4\vartheta }{\partial {\phi }^4}+2\left(\frac{1}{{\upsilon }^2}+\frac{{\upsilon }^4}{6!}\right)\frac{{\partial }^4\vartheta }{\partial {\upsilon }^4}=0,\end{array}$$

(20)

with initial conditions

$$\begin{array}{c}\hfill \vartheta (\phi ,\upsilon ,0)=0,{\vartheta }_{\tau }(\phi ,\upsilon ,0)=2+\frac{{\phi }^6}{6!}+\frac{{\upsilon }^6}{6!}.\end{array}$$

(21)

By following the process of the NFAS, we obtain

$$\begin{array}{c}\hfill F\left(\vartheta \right)=-2\left(\frac{1}{{\phi }^2}+\frac{{\phi }^4}{6!}\right)\frac{{\partial }^4\vartheta }{\partial {\phi }^4}-2\left(\frac{1}{{\upsilon }^2}+\frac{{\upsilon }^4}{6!}\right)\frac{{\partial }^4\vartheta }{\partial {\upsilon }^4}.\end{array}$$

(22)

Thus, we can obtain the following iterations

$$\begin{array}{c}\hfill a_0=h_0(\phi ,\upsilon )=0,\end{array}$$

$$\begin{array}{c}\hfill a_1=h_1(\phi ,\upsilon )=2+\frac{{\phi }^6}{6!}+\frac{{\upsilon }^6}{6!},\end{array}$$

$$\begin{array}{c}\hfill a_2=F\left({\vartheta }_0\right)=-2\left(\frac{1}{{\phi }^2}+\frac{{\phi }^4}{6!}\right)\frac{{\partial }^4{a}_0}{\partial {\phi }^4}-2\left(\frac{1}{{\upsilon }^2}+\frac{{\upsilon }^4}{6!}\right)\frac{{\partial }^4{a}_0}{\partial {\upsilon }^4}=0,\end{array}$$

$$\begin{array}{c}\hfill a_3=D_{\tau }^{\alpha }F\left({\vartheta }_0\right)=-2\left(\frac{1}{{\phi }^2}+\frac{{\phi }^4}{6!}\right)\frac{{\partial }^4{a}_1}{\partial {\phi }^4}-2\left(\frac{1}{{\upsilon }^2}+\frac{{\upsilon }^4}{6!}\right)\frac{{\partial }^4{a}_1}{\partial {\upsilon }^4}=-\left(2+\frac{{\phi }^6}{6!}+\frac{{\upsilon }^6}{6!}\right),\end{array}$$

$$\begin{array}{c}\hfill a_4=D_{\tau }^{2\alpha }F\left({\vartheta }_0\right)=-2\left(\frac{1}{{\phi }^2}+\frac{{\phi }^4}{6!}\right)\frac{{\partial }^4{a}_2}{\partial {\phi }^4}-2\left(\frac{1}{{\upsilon }^2}+\frac{{\upsilon }^4}{6!}\right)\frac{{\partial }^4{a}_2}{\partial {\upsilon }^4}=0,\end{array}$$

$$\begin{array}{c}\hfill a_5=D_{\tau }^{3\alpha }F\left({\vartheta }_0\right)=-2\left(\frac{1}{{\phi }^2}+\frac{{\phi }^4}{6!}\right)\frac{{\partial }^4{a}_3}{\partial {\phi }^4}-2\left(\frac{1}{{\upsilon }^2}+\frac{{\upsilon }^4}{6!}\right)\frac{{\partial }^4{a}_3}{\partial {\upsilon }^4}=\left(2+\frac{{\phi }^6}{6!}+\frac{{\upsilon }^6}{6!}\right),\end{array}$$

By proceeding in a similar way, we obtain

$$\begin{array}{c}\hfill \vartheta (\phi ,\upsilon ,\tau )=a_0+a_1\frac{{\tau }^{\alpha }}{\Gamma (\alpha +1)}+a_2\frac{{\tau }^{2\alpha }}{\Gamma (2\alpha +1)}+a_3\frac{{\tau }^{3\alpha }}{\Gamma (3\alpha +1)}+a_4\frac{{\tau }^{4\alpha }}{\Gamma (4\alpha +1)}+a_5\frac{{\tau }^{5\alpha }}{\Gamma (5\alpha +1)}+\cdots ,\end{array}$$

(23)

By putting the values of $a_0,a_1,a_2,a_3,\cdots$, we obtain

$$\begin{array}{c}\hfill \vartheta (\phi ,\upsilon ,\tau )=\left(2+\frac{{\phi }^6}{6!}+\frac{{\upsilon }^6}{6!}\right)(\tau -\frac{{\tau }^{3\alpha }}{\Gamma (3\alpha +1)}+\frac{{\tau }^{5\alpha }}{\Gamma (5\alpha +1)}+\cdots ),\end{array}$$

(24)

which leads to the exact solution such that

$$\begin{array}{c}\hfill \vartheta (\phi ,\upsilon ,\tau )=\left(2+\frac{{\phi }^6}{6!}+\frac{{\upsilon }^6}{6!}\right)sin\tau .\end{array}$$

(25)

Example 2 shows the graphical representation of fourth-order parabolic PDEs in the two-dimensional form. Figure 2 is presented into two parts, where Figure 2a–c present the approximate results of $\vartheta (\phi ,\upsilon ,\tau )$ for $0\le \phi \le 10$ and $0\le \tau \le 10$, and Figure 2d demonstrates the precise solution of $\vartheta (\phi ,\upsilon ,\tau )$. This comparison of approximate solutions obtained by the NFAS with the exact solution has full agreement.

Table 2. The NFAS results for distinct parameters of $\alpha$ when $\upsilon =0.5$ and $\tau =0.3$ for Example 2.

$\mathit{\phi }$	${\mathit{\vartheta }}_{\mathit{\alpha }=0.50}$	${\mathit{\vartheta }}_{\mathit{\alpha }=0.75}$	${\mathit{\vartheta }}_{\mathit{\alpha }=1}$	Exact Solution
0.10	0.380073	0.549038	0.591034	0.591034
0.15	0.380073	0.549038	0.591034	0.591034
0.20	0.380073	0.549038	0.591034	0.591034
0.25	0.380073	0.549038	0.591034	0.591034
0.30	0.380073	0.549038	0.591034	0.591034
0.35	0.380073	0.549039	0.591035	0.591035
0.40	0.380074	0.549040	0.591036	0.591036
0.45	0.380075	0.549041	0.591037	0.591037
0.50	0.380077	0.549044	0.591040	0.591040

presents the NFAS results for distinct parameters of $\alpha$ and reveals a high accuracy towards the precise solution.

5.3. Example 3

Consider the following equation of the FPDEs in the three-dimensional form as the following:

$$\begin{array}{c}\hfill \frac{{\partial }^2\vartheta }{\partial {\tau }^2}+\left(\frac{\upsilon +\eta }{2cos\phi }-1\right)\frac{{\partial }^4\vartheta }{\partial {\phi }^4}+\left(\frac{\phi +\eta }{2cos\upsilon }-1\right)\frac{{\partial }^4\vartheta }{\partial {\upsilon }^4}+\left(\frac{\upsilon +\phi }{2cos\eta }-1\right)\frac{{\partial }^4\vartheta }{\partial {\eta }^4}=0,\end{array}$$

(26)

with initial conditions

$$\begin{array}{c}\hfill \vartheta (\phi ,\upsilon ,\eta ,0)=\phi +\upsilon +\eta -\left(cos\phi +cos\upsilon +cos\eta \right),{\vartheta }_{\tau }(\phi ,\upsilon ,\eta ,0)=\left(cos\phi +cos\upsilon +cos\eta \right)-(\phi +\upsilon +\eta ).\end{array}$$

(27)

By following the process of the NFAS, we obtain

$$\begin{array}{c}\hfill F\left(\vartheta \right)=-\left(\frac{\upsilon +\eta }{2cos\phi }-1\right)\frac{{\partial }^4\vartheta }{\partial {\phi }^4}-\left(\frac{\phi +\eta }{2cos\upsilon }-1\right)\frac{{\partial }^4\vartheta }{\partial {\upsilon }^4}-\left(\frac{\upsilon +\phi }{2cos\eta }-1\right)\frac{{\partial }^4\vartheta }{\partial {\eta }^4},\end{array}$$

(28)

$$\begin{array}{c}\hfill a_0=h_0(\phi ,\upsilon ,\eta )=\vartheta (\phi ,\upsilon ,\eta ,0)=\phi +\upsilon +\eta -\left(cos\phi +cos\upsilon +cos\eta \right),\end{array}$$

$$\begin{array}{c}\hfill a_1=h_1(\phi ,\upsilon ,\eta )={\vartheta }_{\tau }(\phi ,\upsilon ,\eta ,0)=\left(cos\phi +cos\upsilon +cos\eta \right)-(\phi +\upsilon +\eta ),\end{array}$$

$$\begin{array}{cc}\hfill a_2=& \left(\phi +\upsilon +\eta -cos\phi -cos\upsilon -cos\eta \right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill a_3=& -\left(\phi +\upsilon +\eta -cos\phi -cos\upsilon -cos\eta \right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill a_4=& \left(\phi +\upsilon +\eta -cos\phi -cos\upsilon -cos\eta \right).\hfill \end{array}$$

By proceeding in a similar way, we obtain

$$\begin{array}{c}\hfill \vartheta (\phi ,\upsilon ,\eta ,\tau )=a_0+a_1\frac{{\tau }^{\alpha }}{\Gamma (\alpha +1)}+a_2\frac{{\tau }^{2\alpha }}{\Gamma (2\alpha +1)}+a_3\frac{{\tau }^{3\alpha }}{\Gamma (3\alpha +1)}+a_4\frac{{\tau }^{4\alpha }}{\Gamma (4\alpha +1)}+a_5\frac{{\tau }^{5\alpha }}{\Gamma (5\alpha +1)}+\cdots .\end{array}$$

(29)

By putting the values of $a_0,a_1,a_2,a_3,\cdots$, we obtain

$$\begin{array}{c}\hfill \vartheta (\phi ,\upsilon ,\eta ,\tau )=\left(\phi +\upsilon +\eta -cos\phi -cos\upsilon -cos\eta \right)(1-\tau +\frac{{\tau }^2}{2!}-\frac{{\tau }^3}{3!}+\frac{{\tau }^4}{4!}-\frac{{\tau }^5}{5!}+\cdots ),\end{array}$$

(30)

which leads to the exact solution such that

$$\begin{array}{c}\hfill \vartheta (\phi ,\upsilon ,\eta ,\tau )=\left(\phi +\upsilon +\eta -cos\phi -cos\upsilon -cos\eta \right)e^{-\tau }.\end{array}$$

(31)

Example 3 shows the graphical representation of fourth-order parabolic PDEs in the two-dimensional form. Figure 3 is presented into two parts, where Figure 3a–c present the approximate results of $\vartheta (\phi ,\upsilon ,\eta ,\tau )$ for $0\le \phi \le 10$ and $0\le \tau \le 10$, and Figure 3d demonstrates the precise solution of $\vartheta (\phi ,\upsilon ,\eta ,\tau )$. This comparison of approximate solutions obtained by the NFAS with the exact solution has full agreement.

Table 3. The NFAS results for distinct parameters of $\alpha$ when $\upsilon =1$, $\eta =1$, and $\tau =0.3$ for Example 3.

$\mathit{\phi }$	${\mathit{\vartheta }}_{\mathit{\alpha }=0.50}$	${\mathit{\vartheta }}_{\mathit{\alpha }=0.75}$	${\mathit{\vartheta }}_{\mathit{\alpha }=1}$	Exact Solution
0.10	−1.56817	−1.47581	−1.42272	−1.42272
0.15	−1.51193	−1.41958	−1.36648	−1.36648
0.20	−1.45323	−1.36087	−1.30778	−1.30778
0.25	−1.39208	−1.29972	−1.24662	−1.24662
0.30	−1.3285	−1.23614	−1.18305	−1.18305
0.35	−1.26254	−1.17018	−1.11708	−1.11708
0.40	−1.19422	−1.10187	−1.04877	−1.04877
0.45	−1.12361	−1.03125	−0.978158	−0.978158
0.50	−1.05075	−0.958389	−0.905293	−0.905293

presents the NFAS results for distinct parameters of $\alpha$ and reveals a high accuracy towards the precise solution.

6. Conclusions and Future Work

In this article, we obtained the analytical results of fourth-order parabolic fractional partial differential equations with variable coefficients via a new fractional analytical scheme. The proposed algorithm is independent of any type of restriction and assumptions. We evaluated the the approximate solution of $\vartheta (\phi ,\tau )$ at $\alpha =0.5$, $\alpha =0.75$, and $\alpha =1$ and compared it with the exact solution. We observe that the approximate solution of $\vartheta (\phi ,\tau )$ at $\alpha =1$ has a strong agreement with the exact solution, which shows the accuracy of our proposed scheme. The rate of convergence depends on the fractional order of the differential problem. Our graphical representation and Tables show that, as the fractional order increases, the approximate solution yields to the exact solution. This scheme requires only a short number of iterations to converge to the solution. Graphical visuals and error distributions were also presented to provide the physical nature of the fourth-order fractional parabolic partial differential equations at various fractional orders. This scheme ensures the accuracy of obtaining results with the exact solutions, which has the advantage of being a direct approach to the numerical problems. In future work, we aim to use this proposed strategy for the solution of various nonlinear differential problems such as reaction–diffusion equations, the fractional KdV-Burger’s equation, the Klein–Gordon equation, and the time-fractional Boussinesq equation in terms of the Atangana–Baleanu Caputo fractional derivative operator.