An Underactuated Bio-Inspired Helical Swimming Microrobot Using Fuzzy-PI Controller with Novel Error Detection Method for 5-DOF Micromanipulation
Abstract
:1. Introduction
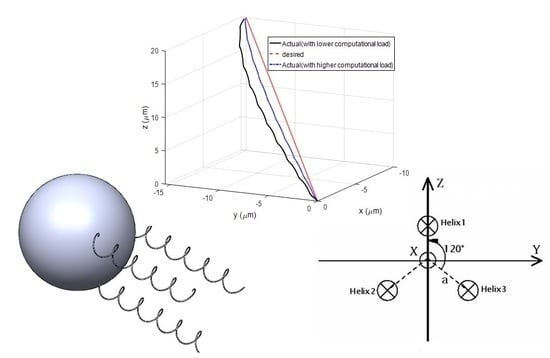
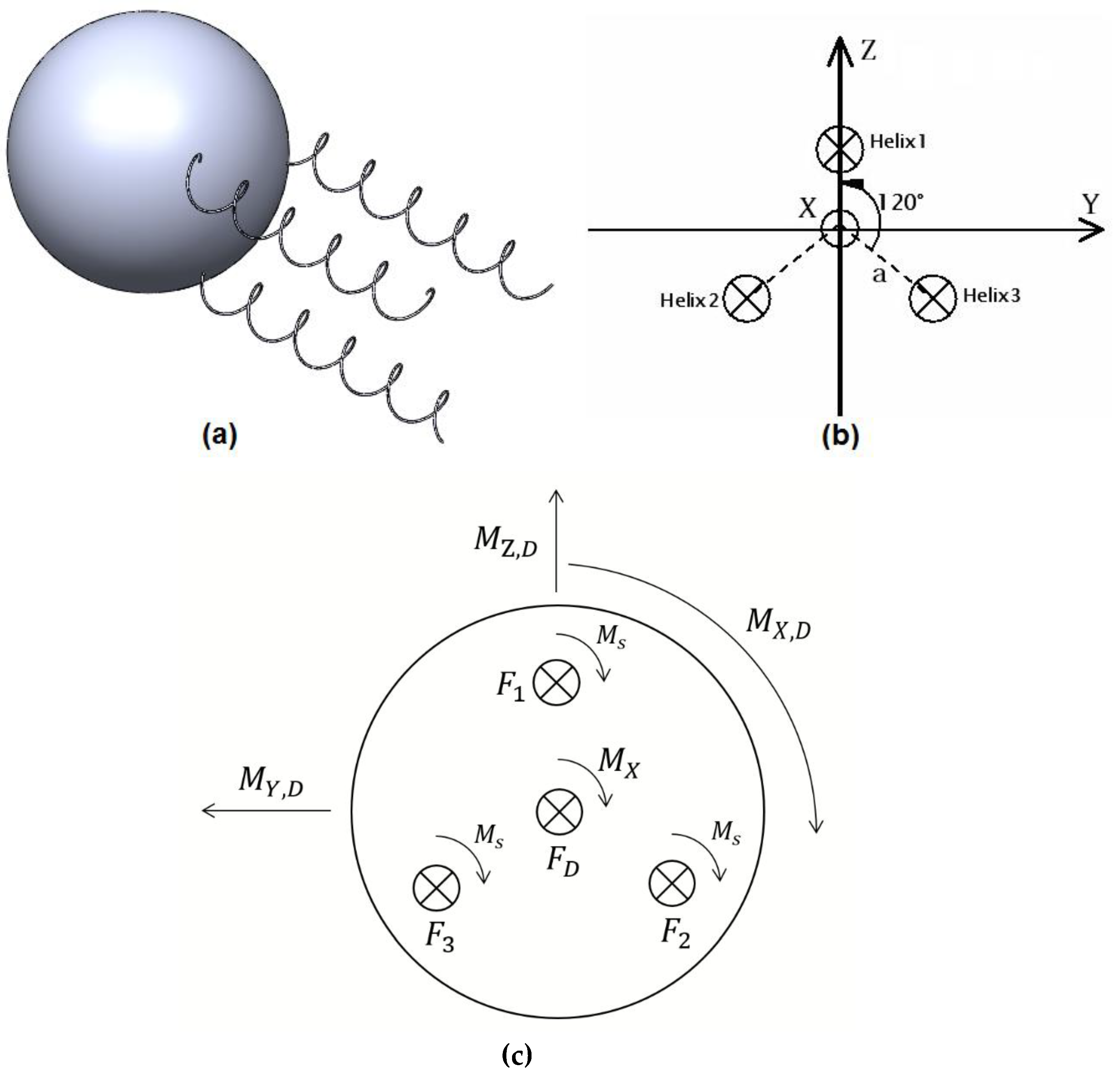
2. Dynamic Modelling
3. System Control
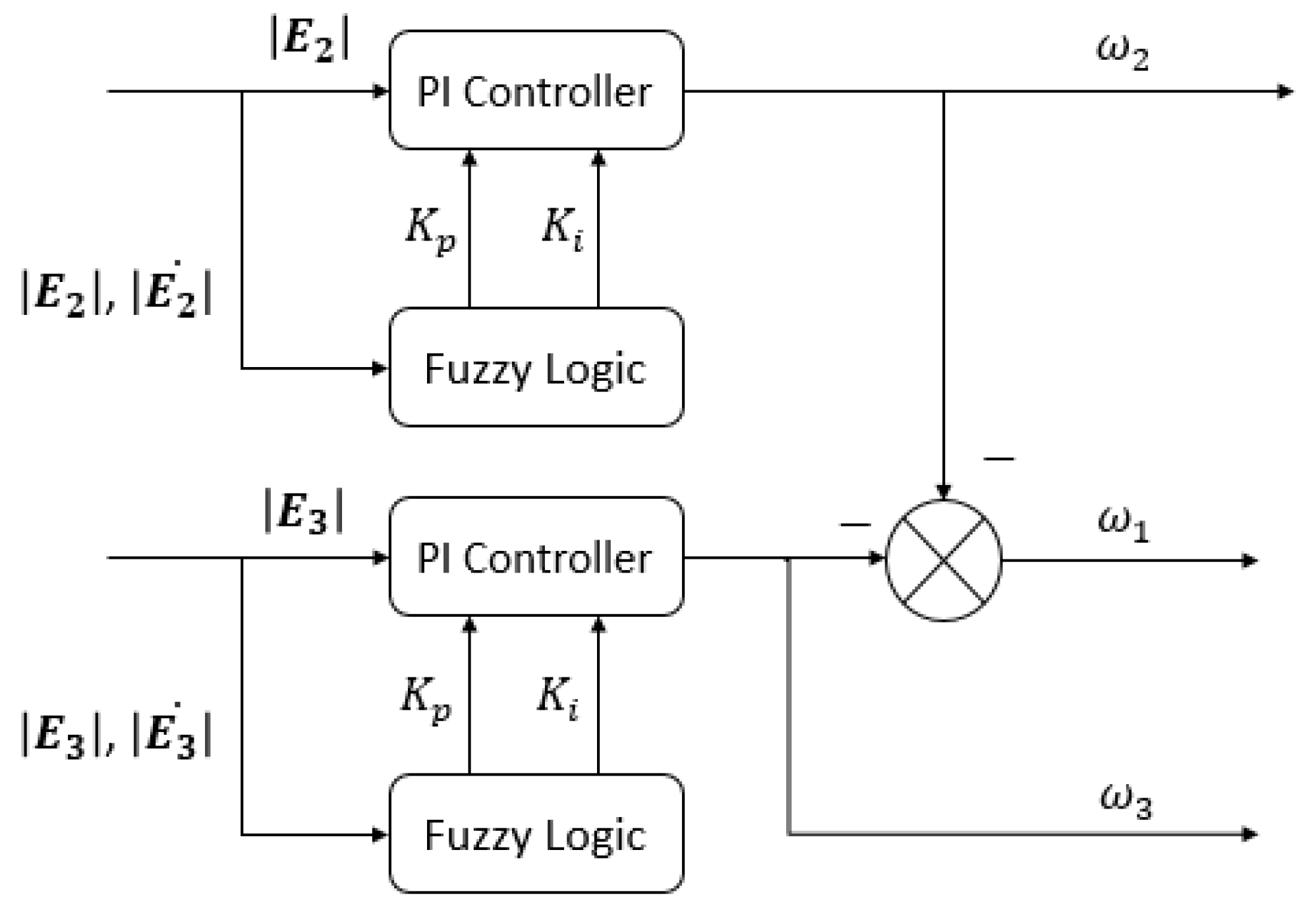
3.1. Error Definition
3.2. Fuzzy-PI Controller
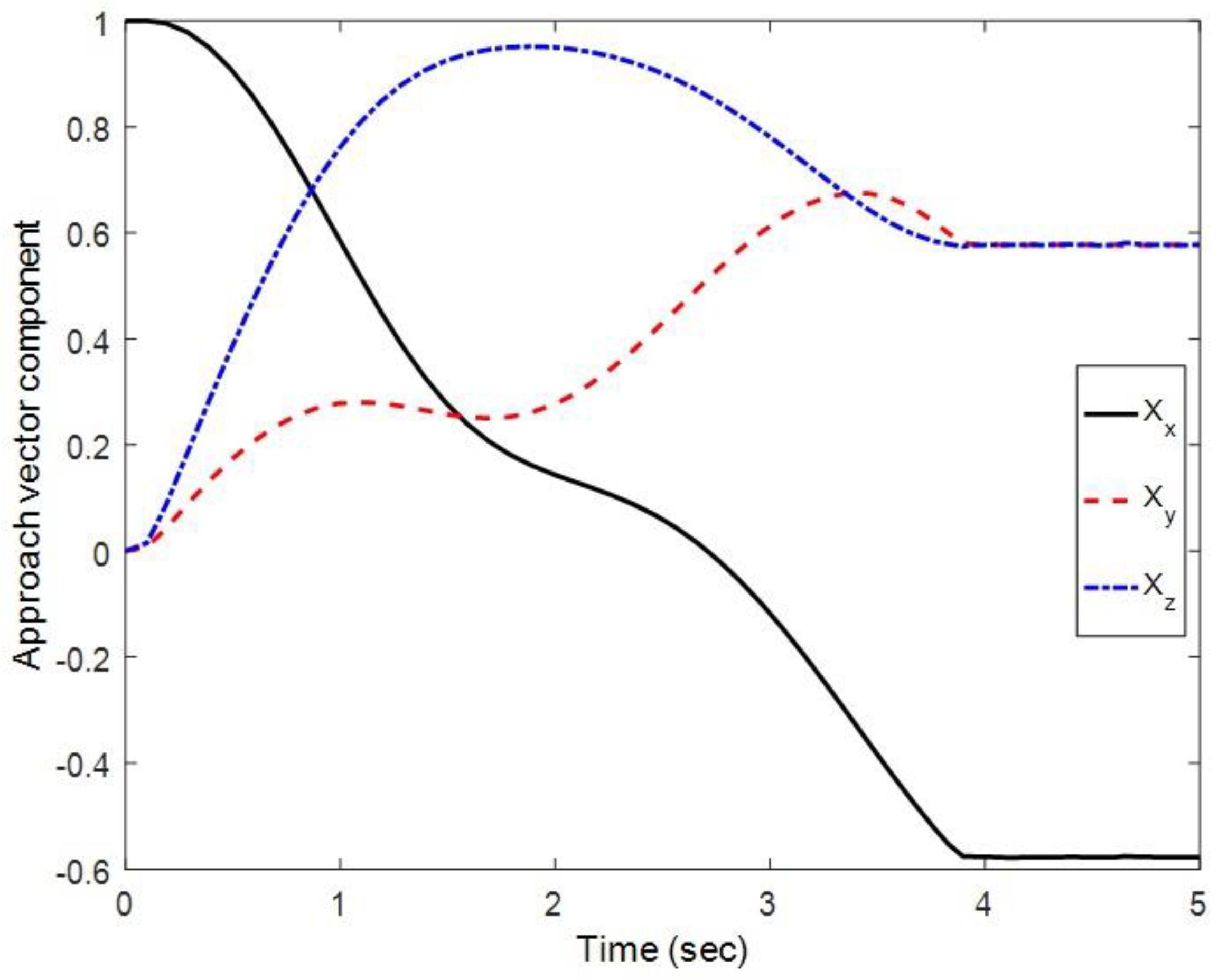
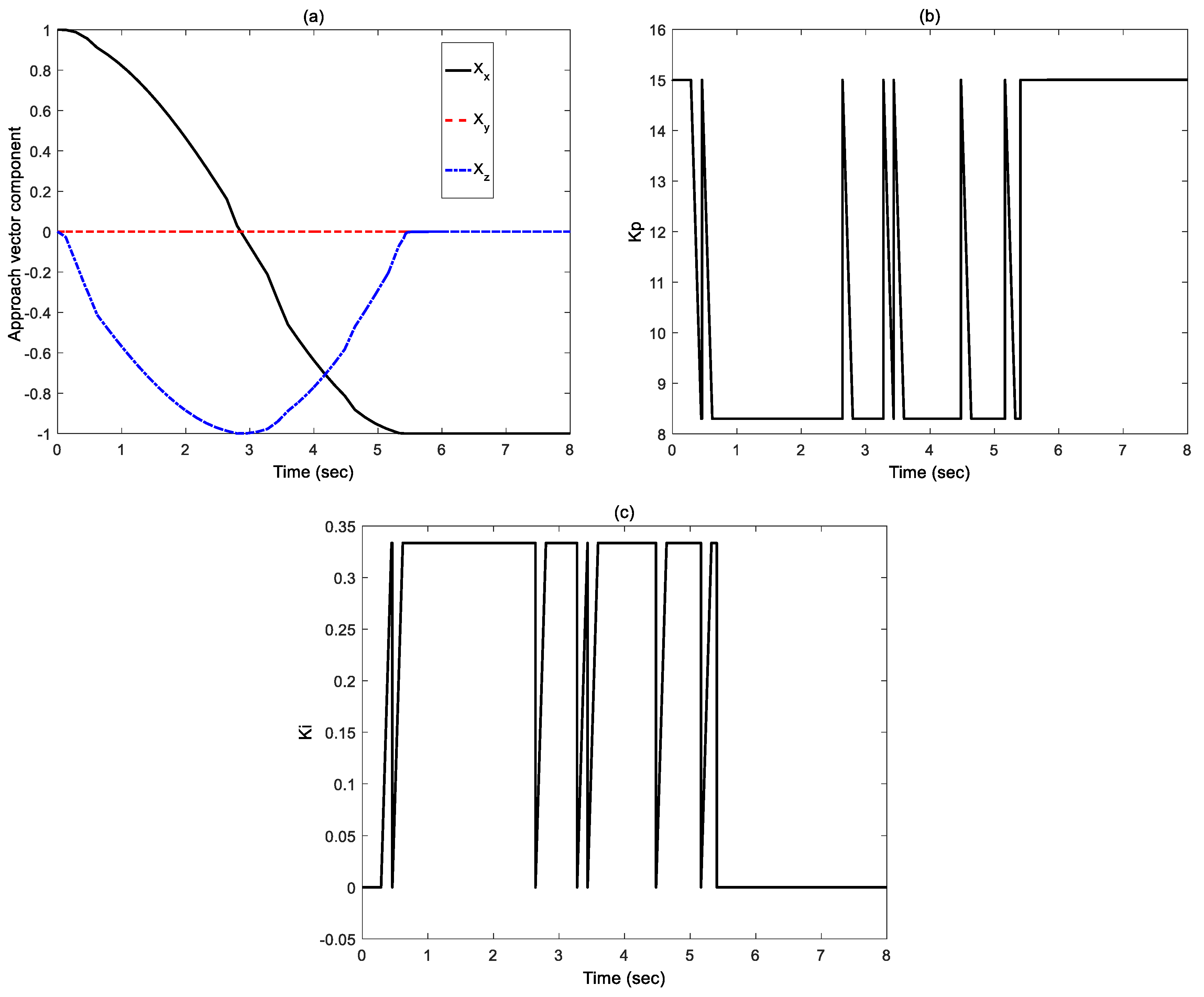
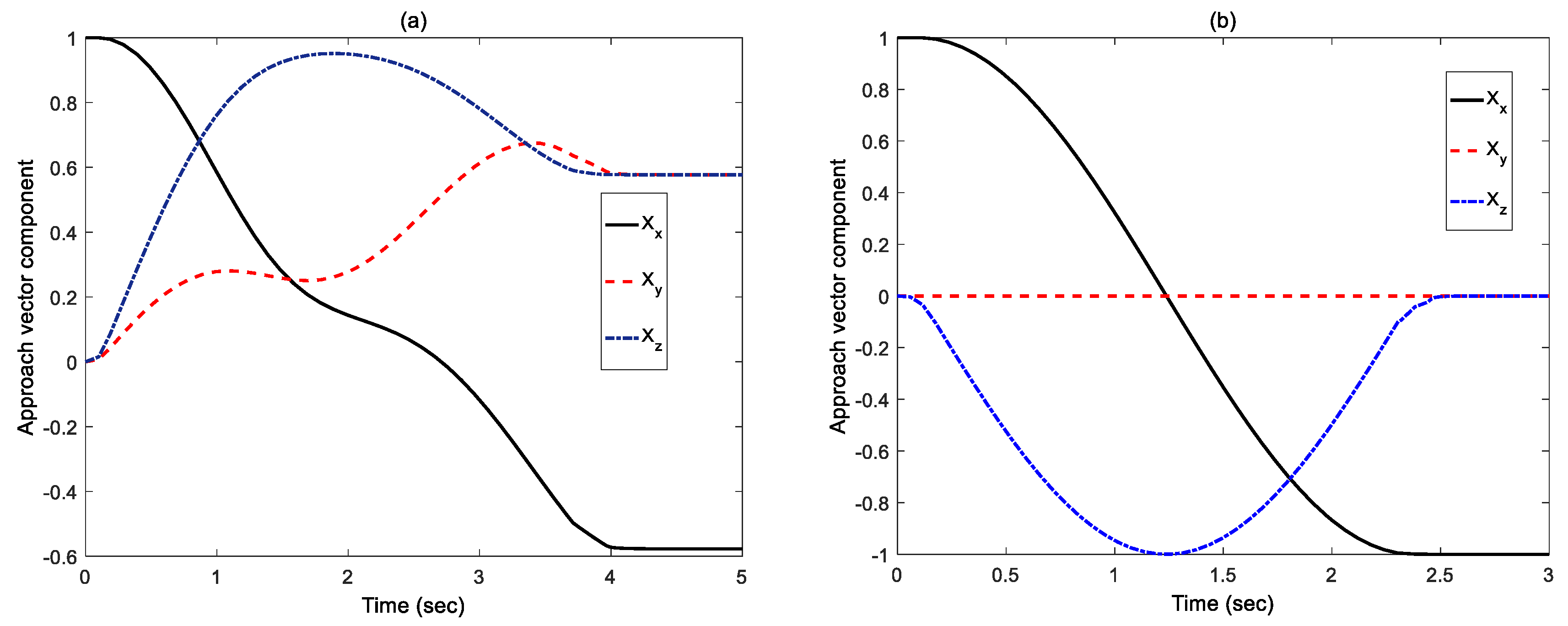
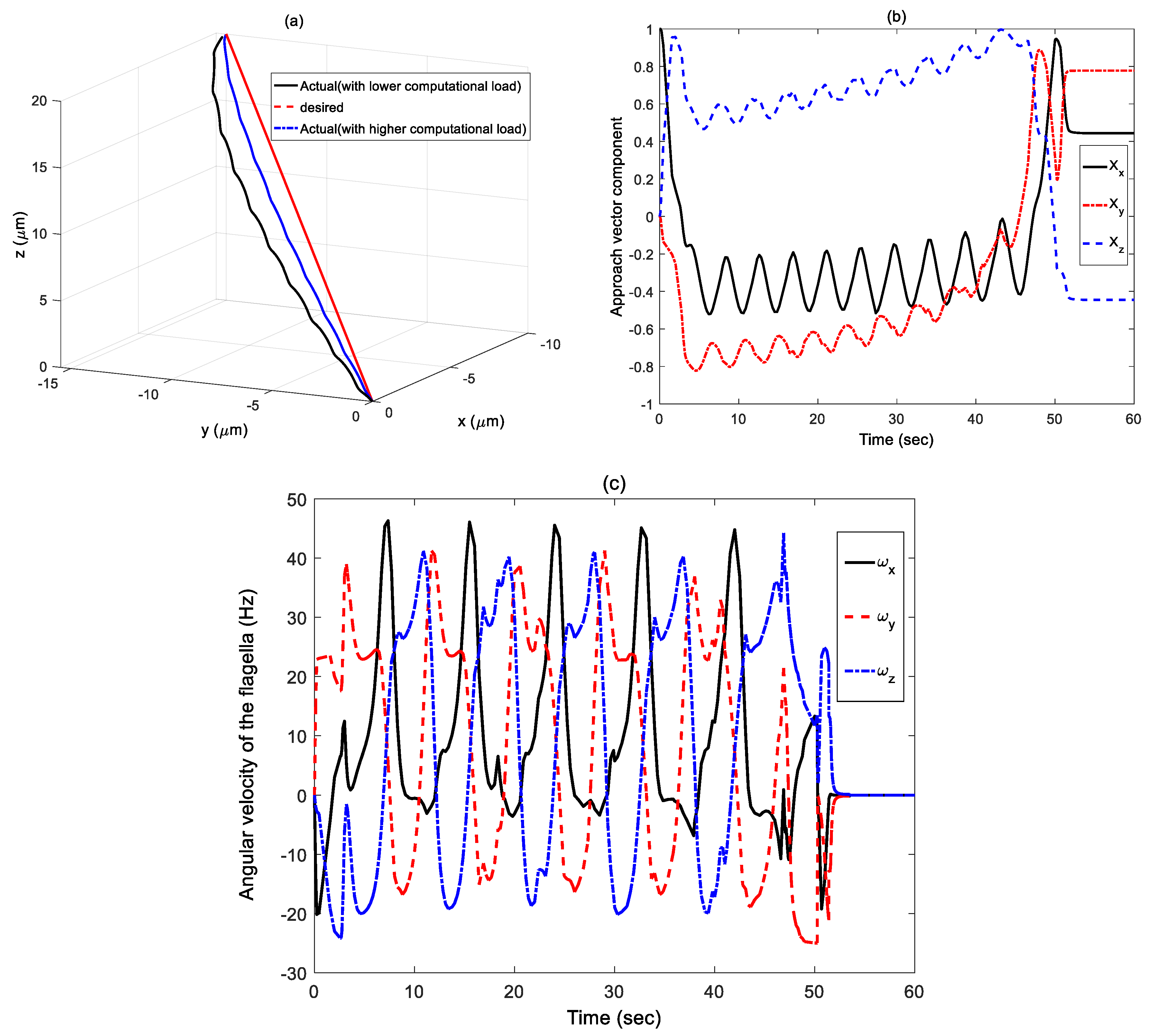
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Khalil, I.S.; Magdanz, V.; Sanchez, S.; Schmidt, O.G.; Abelmann, L.; Misra, S. Magnetic control of potential microrobotic drug delivery systems: Nanoparticles, magnetotactic bacteria and self-propelled microjets. In Proceedings of the 35th Annual International Conference of the IEEE, Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; pp. 5299–5302. [Google Scholar]
- Devlin, P.M. Brachytherapy: Applications and Techniques; Springer Publishing Company: New York, NY, USA, 2015. [Google Scholar]
- Trachoo, O.; Rivolta, M.N. Neural differentiation of human embryonic stem cells and their potential application in a therapy for sensorineural hearing loss. In Trends in Stem Cell Biology and Technology; Springer: New York, NY, USA, 2009; pp. 261–282. [Google Scholar]
- Nelson, B.J.; Kaliakatsos, I.K.; Abbott, J.J. Microrobots for minimally invasive medicine. Annu. Rev. Biomed. Eng. 2010, 12, 55–85. [Google Scholar] [CrossRef] [PubMed]
- Folio, D.; Ferreira, A. Two-dimensional robust magnetic resonance navigation of a ferromagnetic microrobot using pareto optimality. IEEE Trans. Robot. 2017, 33, 583–593. [Google Scholar] [CrossRef]
- Kummer, M.P.; Abbott, J.J.; Kratochvil, B.E.; Borer, R.; Sengul, A.; Nelson, B.J. Octomag: An electromagnetic system for 5-dof wireless micromanipulation. IEEE Trans. Robot. 2010, 26, 1006–1017. [Google Scholar] [CrossRef]
- Evans, A.A.; Lauga, E. Propulsion by passive filaments and active flagella near boundaries. Phys. Rev. E 2010, 82, 041915. [Google Scholar] [CrossRef] [PubMed]
- Abbott, J.J.; Peyer, K.E.; Dong, L.X.; Nelson, B.J. How should microrobots swim. In Robotics Research; Springer: New York, NY, USA, 2010; pp. 157–167. [Google Scholar]
- Floyd, S.; Pawashe, C.; Sitti, M. Microparticle manipulation using multiple untethered magnetic micro-robots on an electrostatic surface. In Proceedings of the IROS 2009. IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 528–533. [Google Scholar]
- Dijkink, R.; Van Der Dennen, J.; Ohl, C.; Prosperetti, A. The ‘acoustic scallop’: A bubble-powered actuator. J. Micromech. Microeng. 2006, 16, 1653. [Google Scholar] [CrossRef]
- Yang, L.; Wang, Q.; Vong, C.-I.; Zhang, L. A miniature flexible-link magnetic swimming robot with two vibration modes: Design, modeling and characterization. IEEE Robot. Autom. Lett. 2017, 2, 2024–2031. [Google Scholar] [CrossRef]
- Huang, C.; Lv, J.-A.; Tian, X.; Wang, Y.; Yu, Y.; Liu, J. Miniaturized swimming soft robot with complex movement actuated and controlled by remote light signals. Sci. Rep. 2015, 5, 17414. [Google Scholar] [CrossRef] [PubMed]
- Arcese, L.; Fruchard, M.; Ferreira, A. Endovascular magnetically guided robots: Navigation modeling and optimization. IEEE Trans. Biomed. Eng. 2012, 59, 977–987. [Google Scholar] [CrossRef] [PubMed]
- Nourmohammadi, H.; Keighobadi, J.; Bahrami, M. Design, dynamic modelling and control of a bio-inspired helical swimming microrobot with three-dimensional manoeuvring. Trans. Inst. Meas. Control. 2016, 39, 1037–1046. [Google Scholar] [CrossRef]
- Tabak, A.F.; Yesilyurt, S. Experiment-based kinematic validation of numeric modeling and simulated control of an untethered biomimetic microrobot in channel. In Proceedings of the 12th IEEE International Workshop on Advanced Motion Control (AMC), Sarajevo, Bosnia-Herzegovina, 25–27 March 2012; pp. 1–6. [Google Scholar]
- Flynn, A.M.; Tavrow, L.S.; Bart, S.F.; Brooks, R.A.; Ehrlich, D.J.; Udayakumar, K.R.; Cross, L.E. Piezoelectric micromotors for microrobots. J. Microelectromech. Syst. 1992, 1, 44–51. [Google Scholar] [CrossRef]
- Tadokoro, S.; Murakami, T.; Fuji, S.; Kanno, R.; Hattori, M.; Takamori, T.; Oguro, K. An elliptic friction drive element using an icpf actuator. IEEE Control. Syst. 1997, 17, 60–68. [Google Scholar] [CrossRef]
- Magdanz, V.; Sanchez, S.; Schmidt, O.G. Development of a sperm-flagella driven micro-bio-robot. Adv. Mater. 2013, 25, 6581–6588. [Google Scholar] [CrossRef] [PubMed]
- Belharet, K.; Folio, D.; Ferreira, A. Three-dimensional controlled motion of a microrobot using magnetic gradients. Adv. Robot. 2011, 25, 1069–1083. [Google Scholar] [CrossRef]
- Marino, H.; Bergeles, C.; Nelson, B.J. Robust electromagnetic control of microrobots under force and localization uncertainties. IEEE Trans. Autom. Sci. Eng. 2014, 11, 310–316. [Google Scholar] [CrossRef] [Green Version]
- Arcese, L.; Fruchard, M.; Ferreira, A. Adaptive controller and observer for a magnetic microrobot. IEEE Trans. Robot. 2013, 29, 1060–1067. [Google Scholar] [CrossRef]
- Rovetta, A.; Wen, X. Fuzzy logic in robot grasping control. In Proceedings of the IROS’91, IEEE/RSJ International Workshop on Intelligent Robots and Systems ‘91: Intelligence for Mechanical Systems, Osaka, Japan, 3–5 November 1991; pp. 1632–1637. [Google Scholar]
- Katbab, A. Fuzzy logic and controller design-a review. In Proceedings of the Southeastcon’95: Visualize the Future, Raleigh, NC, USA, 26–29 March 1995; pp. 443–449. [Google Scholar]
- Yoo, B.K.; Ham, W.C. Adaptive control of robot manipulator using fuzzy compensator. IEEE Trans. Fuzzy Syst. 2000, 8, 186–199. [Google Scholar]
- Al-Hadithi, B.M.; Matia, F.; Jimenez, A. Robust fuzzy control for a mobile robot. In Proceedings of the World, Automation Congress (WAC 2008), Hawaii, HI, USA, 28 September–2 October 2008; pp. 1–6. [Google Scholar]
- Paliwal, S.; Chopra, V.; Singla, S.K. Stabilization of mobile inverted pendulum using fuzzy pid controllers. In Proceedings of the 7th India International Conference on Power Electronics (IICPE), Patiala, India, 17–19 November 2016; pp. 1–4. [Google Scholar]
- Li, H.; Huang, Y.; Lu, J. Reactive power compensation and dc link voltage control using fuzzy-pi on grid-connected pv system with d-statcom. In Proceedings of the Power and Energy Engineering Conference (APPEEC), 2016 IEEE PES Asia-Pacific, Xi’an, China, 25–28 October 2016; pp. 1240–1244. [Google Scholar]
- Korba, P.; Babuska, R.; Verbruggen, H.B.; Frank, P.M. Fuzzy gain scheduling: Controller and observer design based on Lyapunov method and convex optimization. IEEE Trans. Fuzzy Syst. 2003, 11, 285–298. [Google Scholar] [CrossRef]
- Palm, R.; Driankov, D. Design of a fuzzy gain scheduler using sliding mode control principles. Fuzzy Sets Syst. 2001, 121, 13–23. [Google Scholar] [CrossRef]
- Nguyen, K.-D.; Dankowicz, H. Adaptive control of underactuated robots with unmodeled dynamics. Robot. Auton. Syst. 2015, 64, 84–99. [Google Scholar] [CrossRef]
- Korkmaz, S. A review of active structural control: Challenges for engineering informatics. Comput. Struct. 2011, 89, 2113–2132. [Google Scholar] [CrossRef]
- Chwang, A.; Wu, T.Y. A note on the helical movement of micro-organisms. Proc. R. Soc. Lond. B Biol. Sci. 1971, 178, 327–346. [Google Scholar] [CrossRef] [PubMed]
- Yuan, H. Control of Nonholonomic Systems; University of Central Florida: Orlando, FL, USA, 2009. [Google Scholar]
- De Carli, A.; Liguori, P.; Marroni, A. A fuzzy-pi control strategy. Control. Eng. Pract. 1994, 2, 147–153. [Google Scholar] [CrossRef]
- Ullrich, F.; Bergeles, C.; Pokki, J.; Ergeneman, O.; Erni, S.; Chatzipirpiridis, G.; Pané, S.; Framme, C.; Nelson, B.J. Mobility experiments with microrobots for minimally invasive intraocular surgerymicrorobot experiments for intraocular surgery. Investig. Ophthalmol. Vis. Sci. 2013, 54, 2853–2863. [Google Scholar] [CrossRef] [PubMed]
| ZO | PS | PM | PB | ||
|---|---|---|---|---|---|
| NB | BB | B | B | M | |
| NM | BB | B | M | M | |
| NS | B | M | S | SS | |
| ZO | M | S | SS | SS | |
| PS | S | S | SS | SS | |
| PM | BB | SS | SS | SSS | |
| PB | BB | SS | SS | SSS | |
| ZO | PS | PM | PB | ||
|---|---|---|---|---|---|
| NB | NM | NM | ZO | ZO | |
| NM | NM | NS | ZO | ZO | |
| NS | NS | ZO | PS | PS | |
| ZO | ZO | PS | PS | PM | |
| PS | PS | PS | PM | PM | |
| PM | PS | PM | PB | PB | |
| PB | PM | PB | PB | PB | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pourmand, M.J.; Taghvaei, S.; Vatankhah, R.; Arefi, M.M. An Underactuated Bio-Inspired Helical Swimming Microrobot Using Fuzzy-PI Controller with Novel Error Detection Method for 5-DOF Micromanipulation. Designs 2018, 2, 18. https://doi.org/10.3390/designs2020018
Pourmand MJ, Taghvaei S, Vatankhah R, Arefi MM. An Underactuated Bio-Inspired Helical Swimming Microrobot Using Fuzzy-PI Controller with Novel Error Detection Method for 5-DOF Micromanipulation. Designs. 2018; 2(2):18. https://doi.org/10.3390/designs2020018
Chicago/Turabian StylePourmand, Mohammad Javad, Sajjad Taghvaei, Ramin Vatankhah, and Mohammad Mehdi Arefi. 2018. "An Underactuated Bio-Inspired Helical Swimming Microrobot Using Fuzzy-PI Controller with Novel Error Detection Method for 5-DOF Micromanipulation" Designs 2, no. 2: 18. https://doi.org/10.3390/designs2020018
APA StylePourmand, M. J., Taghvaei, S., Vatankhah, R., & Arefi, M. M. (2018). An Underactuated Bio-Inspired Helical Swimming Microrobot Using Fuzzy-PI Controller with Novel Error Detection Method for 5-DOF Micromanipulation. Designs, 2(2), 18. https://doi.org/10.3390/designs2020018