The BKT Universality Class in the Presence of Correlated Disorder
Abstract
:1. Introduction
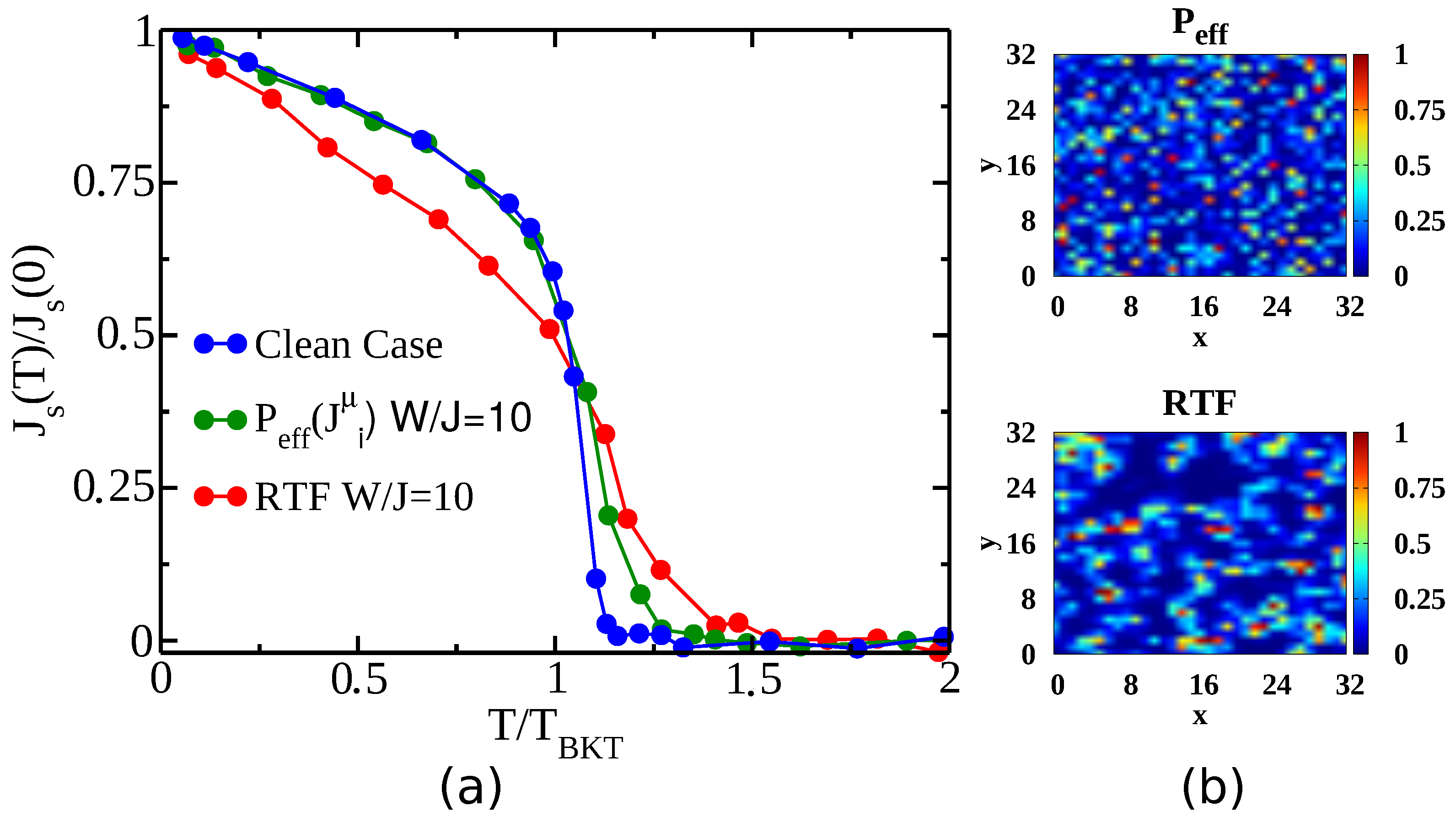
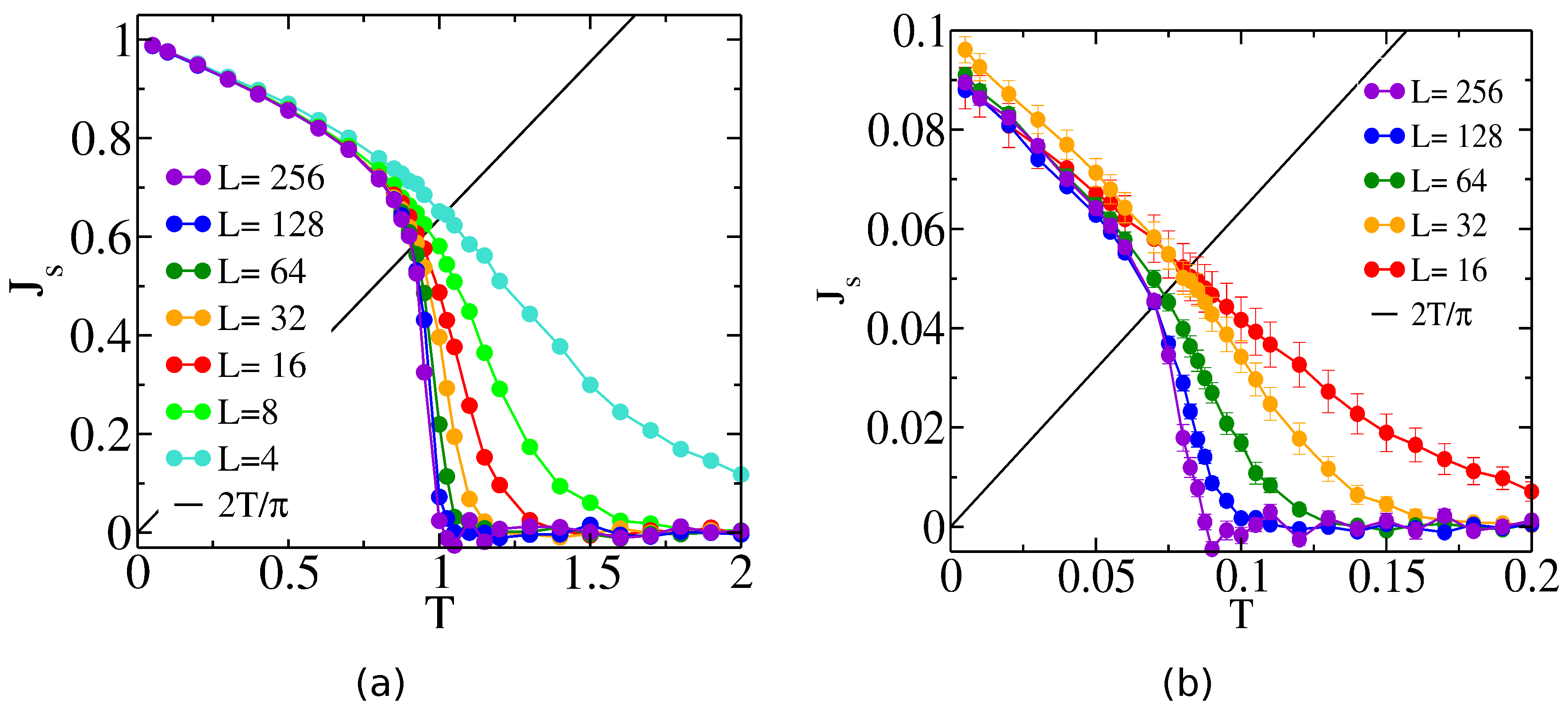
2. Results
2.1. Scaling from
2.2. Scaling from
3. Methods
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Berezinsky, V.L. Destruction of long-range order in one-dimensional and two-dimensional systems possessing a continuous symmetry group. JETP 1972, 34, 610. [Google Scholar]
- Kosterlitz, J.M.; Thouless, D.J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C 1973, 6, 1181. [Google Scholar] [CrossRef]
- Kosterlitz, J.M. The critical properties of the two-dimensional xy model. J. Phys. C 1974, 7, 1046. [Google Scholar] [CrossRef]
- José, J.V. 40 Years of Berezinskii-Kosterlitz-Thouless Theory; World Scientific: Singapore, 2013. [Google Scholar]
- McQueeney, D.; Agnolet, G.; Reppy, J.D. Surface superfluidity in dilute 4He-3He mixtures. Phys. Rev. Lett. 1984, 52, 1325. [Google Scholar] [CrossRef]
- Hadzibabic, Z.; Krüger, P.; Cheneau, M.; Battelier, B.; Dalibard, J. Berezinskii-Kosterlitz-Thouless crossover in a trapped atomic gas. Nature 2006, 44, 1118. [Google Scholar] [CrossRef] [PubMed]
- Murthy, P.A.; Boettcher, I.; Bayha, L.; Holzmann, M.; Kedar, D.; Neidig, M.; Ries, M.G.; Wenz, A.N.; Zürn, G.; Jochim, S. Observation of the Berezinskii-Kosterlitz-Thouless phase transition in an ultracold Fermi gas. Phys. Rev. Lett. 2015, 115, 010401. [Google Scholar] [CrossRef] [PubMed]
- Epstein, K.; Goldman, A.M.; Kadin, A.M. Vortex-antivortex pair dissociation in two-dimensional superconductors. Phys. Rev. Lett 1981, 47, 534. [Google Scholar] [CrossRef]
- Kadin, A.M.; Epstein, K.; Goldman, A.M. Renormalization and the Kosterlitz-Thouless transition in a two-dimensional superconductor. Phys. Rev. B 1983, 27, 6691. [Google Scholar] [CrossRef]
- Fiory, A.T.; Hebard, A.F.; Glaberson, W.I. Superconducting phase transitions in indium/indium-oxide thin-film composites. Phys. Rev. B 1983, 28, 5075. [Google Scholar] [CrossRef]
- Turneaure, S.J.; Lemberger, T.R.; Graybeal, J.M. Effect of thermal phase fluctuations on the superfluid density of two-dimensional superconducting films. Phys. Rev. Lett. 2000, 84, 987. [Google Scholar] [CrossRef] [PubMed]
- Crane, R.W.; Armitage, N.P.; Johansson, A.; Sambandamurthy, G.; Shahar, D.; Gruner, G. Fluctuations, dissipation, and nonuniversal superfluid jumps in two-dimensional superconductors. Phys. Rev. B 2007, 75, 094506. [Google Scholar] [CrossRef]
- Liu, W.; Kim, M.; Sambandamurthy, G.; Armitage, N.P. Dynamical study of phase fluctuations and their critical slowing down in amorphous superconducting films. Phys. Rev. B 2011, 84, 024511. [Google Scholar] [CrossRef]
- Mondal, M.; Kumar, S.; Chand, M.; Kamlapure, A.; Saraswat, G.; Seibold, G.; Benfatto, L.; Raychaudhuri, P. Role of the vortex-core energy on the Berezinskii-Kosterlitz-Thouless transition in thin films of NbN. Phys. Rev. Lett. 2011, 107, 217003. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.H.; Nelson, J.; Goldman, A.M. Suppression of the Berezinskii-Kosterlitz-Thouless transition in 2D superconductors by macroscopic quantum tunneling. Phys. Rev. Lett. 2012, 109, 017002. [Google Scholar] [CrossRef] [PubMed]
- Misra, S.; Urban, L.; Kim, M.; Sambandamurthy, G.; Yazdani, A. Measurements of the magnetic-field-tuned conductivity of disordered two-dimensional Mo43Ge57 and InOx superconducting films: Evidence for a universal minimum superfluid response. Phys. Rev. Lett 2013, 110, 037002. [Google Scholar] [CrossRef] [PubMed]
- Kamlapure, A.; Mondal, M.; Chand, M.; Mishra, A.; Jesudasan, J.; Bagwe, V.; Benfatto, L.; Tripathi, V.; Raychaudhuri, P. Measurement of magnetic penetration depth and superconducting energy gap in very thin epitaxial NbN films. Appl. Phys. Lett. 2010, 96, 072509. [Google Scholar] [CrossRef]
- Corson, J.; Mallozzi, R.; Orenstein, J.; Eckstein, J.N.; Bozovic, I. Vanishing of phase coherence in underdoped Bi2Sr2CaCu2O8+δ. Nature 1999, 398, 221. [Google Scholar] [CrossRef]
- Broun, D.M.; Huttema, W.A.; Turner, P.J.; Ozcan, S.; Morgan, B.; Liang, R.; Hardy, W.N.; Bonn, D.A. Superfluid density in a highly underdoped YBa2Cu3O6+y superconductor. Phys. Rev. Lett. 2007, 99, 237003. [Google Scholar] [CrossRef] [PubMed]
- Hetel, I.; Lemberger, T.R.; Randeria, M. Quantum critical behaviour in the superfluid density of strongly underdoped ultrathin copper oxide films. Nat. Phys. 2007, 3, 700. [Google Scholar] [CrossRef]
- Yong, J.; Hinton, M.J.; McCray, A.; Randeria, M.; Naamneh, M.; Kanigel, A.; Lemberger, T.R. Evidence of two-dimensional quantum critical behavior in the superfluid density of extremely underdoped Bi2Sr2CaCu2O8+x. Phys. Rev. B 2012, 85, 180507. [Google Scholar] [CrossRef]
- Baity, P.G.; Shi, X.; Shi, Z.; Benfatto, L.; Popović, D. Effective two-dimensional thickness for the Berezinskii-Kosterlitz-Thouless-like transition in a highly underdoped La2−xSrxCuO4. Phys. Rev. B 2016, 93, 024519. [Google Scholar] [CrossRef]
- Bert, J.A.; Nowack, K.C.; Kalisky, B.; Noad, H.; Kirtley, J.R.; Bell, C.; Sato, H.K.; Hosoda, M.; Hikita, Y.; Hwang, H.Y.; et al. Gate-tuned superfluid density at the superconducting LaAlO3/SrTiO3 interface. Phys. Rev. B 2012, 86, 060503. [Google Scholar] [CrossRef]
- Daptary, G.N.; Kumar, S.; Kumar, P.; Dogra, A.; Mohanta, N.; Taraphder, A.; Bid, A. Correlated non-Gaussian phase fluctuations in LaAlO3/SrTiO3 heterointerfaces. Phys. Rev. B 2016, 94, 085104. [Google Scholar] [CrossRef]
- Saito, Y.; Kasahara, Y.; Ye, J.; Iwasa, Y.; Nojima, T. Metallic ground state in an ion-gated two-dimensional superconductor. Science 2015, 350, 409. [Google Scholar] [CrossRef] [PubMed]
- Benfatto, L.; Castellani, C.; Giamarchi, T. Berezinskii-Kosterlitz-Thouless Transition within the Sine-Gordon Approach: The Role of the Vortex-Core Energy. In 40 Years of Berezinskii-Kosterlitz-Thouless Theory; José, J.V., Ed.; World Scientific: Singapore, 2013. [Google Scholar]
- Benfatto, L.; Castellani, C.; Giamarchi, T. Kosterlitz-thouless behavior in layered superconductors: The role of the vortex core energy. Phys. Rev. Lett. 2007, 98, 117008. [Google Scholar] [CrossRef] [PubMed]
- Ghosal, A.; Randeria, M.; Trivedi, N. Inhomogeneous pairing in highly disordered s-wave superconductors. Phys. Rev. B 2001, 65, 014501. [Google Scholar] [CrossRef]
- Dubi, Y.; Meir, Y.; Avishai, Y. Nature of the superconductor-insulator transition in disordered superconductors. Nature 2007, 449, 876. [Google Scholar]
- Ioffe, L.B.; Mezard, M. Disorder-driven quantum phase transitions in superconductors and magnets. Phys. Rev. Lett. 2010, 105, 037001. [Google Scholar] [CrossRef] [PubMed]
- Bouadim, K.; Loh, Y.L.; Randeria, M.; Trivedi, N. Single-and two-particle energy gaps across the disorder-driven superconductor–insulator transition. Nat. Phys. 2011, 7, 884. [Google Scholar] [CrossRef]
- Seibold, G.; Benfatto, L.; Castellani, C.; Lorenzana, J. Superfluid density and phase relaxation in superconductors with strong disorder. Phys. Rev. Lett. 2012, 108, 207004. [Google Scholar] [CrossRef] [PubMed]
- Lemarie, G.; Kamlapure, A.; Bucheli, D.; Benfatto, L.; Lorenzana, J.; Seibold, G.; Ganguli, S.C.; Raychaudhuri, P.; Castellani, C. Universal scaling of the order-parameter distribution in strongly disordered superconductors. Phys. Rev. B 2013, 87, 184509. [Google Scholar] [CrossRef]
- Maccari, I.; Benfatto, L.; Castellani, C. Broadening of the Berezinskii-Kosterlitz-Thouless transition by correlated disorder. Phys. Rev. B 2017, 96, 060508. [Google Scholar] [CrossRef]
- Cea, T.; Bucheli, D.; Seibold, G.; Benfatto, L.; Lorenzana, J.; Castellani, C. Optical excitation of phase modes in strongly disordered superconductors. Phys. Rev. B 2014, 89, 174506. [Google Scholar] [CrossRef]
- Ma, M.; Lee, P.A. Localized superconductors. Phys. Rev. B 1985, 32, 5658. [Google Scholar] [CrossRef]
- Nelson, D.R.; Kosterlitz, J.M. Universal jump in the superfluid density of two-dimensional superfluids. Phys. Rev. Lett. 1977, 19, 1201. [Google Scholar] [CrossRef]
- Harris, A.B. Effect of random defects on the critical behaviour of Ising models. J. Phys. C 1974, 7, 1671. [Google Scholar] [CrossRef]
- Hasenbusch, M. The two-dimensional XY model at the transition temperature: A high-precision Monte Carlo study. J. Phys. Gen. A Math. 2005, 38, 5869. [Google Scholar] [CrossRef]
- Schultka, N.; Manousakis, E. Finite-size scaling in two-dimensional superfluids. Phys. Rev. B 1994, 49, 12071. [Google Scholar] [CrossRef]
- Sandvick, A.W. Computational studies of quantum spin systems. AIP Conf. Proc. 2010, 1297, 135. [Google Scholar]
- Weber, H.; Minnhagen, P. Monte Carlo determination of the critical temperature for the two-dimensional XY model. Phys. Rev. B 1988, 37, 5986. [Google Scholar] [CrossRef]
- Fisher, M.E.; Barber, M.N. Scaling theory for finite-size effects in the critical region. Phys. Rev. Lett. 1972, 28, 1516. [Google Scholar] [CrossRef]
- Mondal, M.; Kamlapure, A.; Chand, M.; Saraswat, G.; Kumar, S.; Jesudasan, J.; Benfatto, L.; Tripathi, V.; Raychaudhuri, P. Phase fluctuations in a strongly disordered s-wave NbN superconductor close to the metal-insulator transition. Phys. Rev. Lett. 2011, 106, 047001. [Google Scholar] [CrossRef] [PubMed]
- Halperin, B.I.; Nelson, D.R. Resistive transition in superconducting films. J. Low Temp. Phys. 1979, 36, 599. [Google Scholar] [CrossRef]
- Benfatto, L.; Castellani, C.; Giamarchi, T. Broadening of the Berezinskii-Kosterlitz-Thouless superconducting transition by inhomogeneity and finite-size effects. Phys. Rev. B 2009, 80, 214506. [Google Scholar] [CrossRef]
- Caprara, S.; Grilli, M.; Benfatto, L.; Castellani, C. Effective medium theory for superconducting layers: A systematic analysis including space correlation effects. Phys. Rev. B 2011, 84, 014514. [Google Scholar] [CrossRef]
- Singh, G.; Jouan, A.; Benfatto, L.; Couedo, F.; Kumar, P.; Dogra, A.; Budhani, R.; Caprara, S.; Grilli, M.; Lesne, E.; et al. Competition between electron pairing and phase coherence in superconducting interfaces. arXiv, 2017; arXiv:1704.03365. [Google Scholar]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maccari, I.; Benfatto, L.; Castellani, C. The BKT Universality Class in the Presence of Correlated Disorder. Condens. Matter 2018, 3, 8. https://doi.org/10.3390/condmat3010008
Maccari I, Benfatto L, Castellani C. The BKT Universality Class in the Presence of Correlated Disorder. Condensed Matter. 2018; 3(1):8. https://doi.org/10.3390/condmat3010008
Chicago/Turabian StyleMaccari, Ilaria, Lara Benfatto, and Claudio Castellani. 2018. "The BKT Universality Class in the Presence of Correlated Disorder" Condensed Matter 3, no. 1: 8. https://doi.org/10.3390/condmat3010008



