Garbled Quantum Computation
Abstract
:1. Introduction
1.1. Our Contribution
- In Section 3, we present a protocol for secure two-party quantum computation that we refer to as QYao. This protocol involves two parties with asymmetric roles that wish to securely compute any given unitary on a joint quantum input. Similar to the classical protocol of [22], in QYao, an honest-but-curious (formally defined for the quantum setting in [21]) client capable of preparing only random single qubit and performing constant depth classical computation “garbles” the entire unitary. The fully-malicious server/evaluator receives instructions from the garbler and inserts their input either using a (classical) oblivious transfer (OT) or by a quantum input insertion scheme secure against the honest-but-curious garbler. The evaluator performs the computation, extracts its own output qubits and returns the remaining output qubits to the garbler. After the garbler verifies the computation, the encryption keys of the evaluator output qubits are released. Unlike the classical setting, our proposed QYao protocol is interactive, but importantly, only classical online communication is required. The gain we have, on the other hand, is the boosted security since apart from the initial input exchange where classical OT is needed, the rest of the protocol is unconditionally secure. If one could replace the classical OT’s in our QYao protocol with new primitives, such as the unconditionally secure relativistic primitives [23], the security would be extended to fully unconditional. In Section 4, we prove the security of the protocol in the ideal real-world paradigm using a simulation-based technique.
- In Section 5, we follow the classical approach of [24] and make our QYao protocol non-interactive by using the classical hardware primitive “one-time memory” (OTM), which is essentially a non-interactive oblivious transfer. Using OTM, the need for initial OT calls, in our QYao protocol, is also removed, leading to a one-time universal compiler for any given quantum computation. Such one-time quantum programs can be executed only once, where the input can be chosen at any time. The one-time programs have a wide range of applications ranging from program obfuscation, software protection to temporary transfer of cryptographic ability [24]. Classically, the challenge in lifting the Yao protocol for two-party computation to a one-time program is addressing the issue of a malicious adversary. However, our QYao protocol is already secure against a malicious evaluator without any extra primitive or added overhead. Our quantum one-time program is therefore a straightforward translation of QYao. The same technique is applicable to essentially any cryptographic protocols developed in the measurement-based model that require offline quantum preparation and online classical communications. In any such MBQC computation, there are exponentially many branches of computation (this expansion is the result of the non-deterministic nature of the intermediate single-qubits measurement that occurs during the computation); however, we prove that a single OTM (of constant size) per computation qubit suffices to make the QYao non-interactive. This is due to the fact that in any constant degree graph-state (the underlying entanglement resources for an MBQC computation), the flow of information acts locally. We prove that this is the case for the required entangled recourse in the verifiable UBQC introduced in [25] that is the basis of our QYao protocol. Hence, each classical message between parties, in the interactive case, depends only on the constant number of previous messages, and this allows us to remove this interaction using a simple constant-size OTM.
1.2. Related Works
2. Preliminaries
2.1. Verifiable Universal Blind Quantum Computation
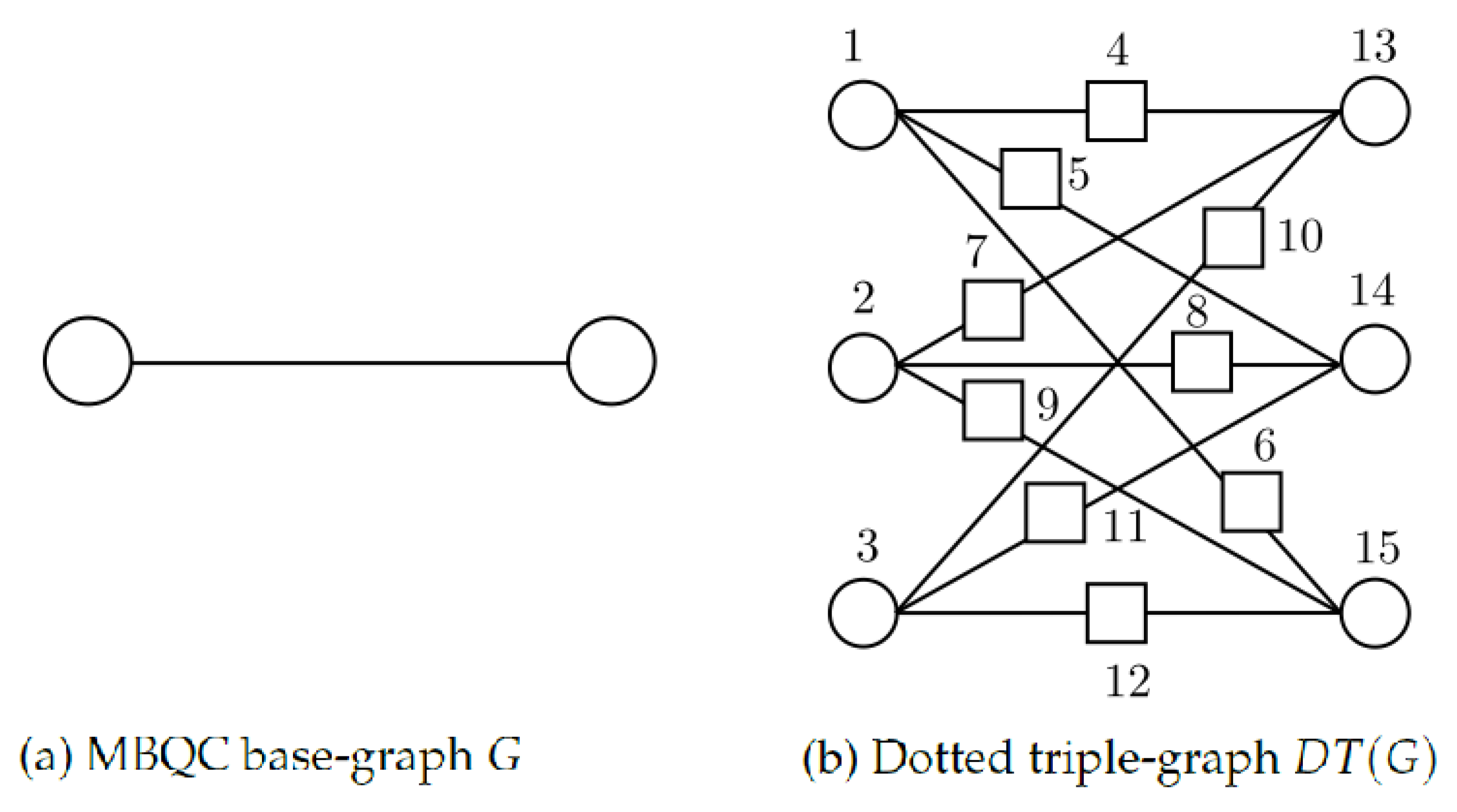
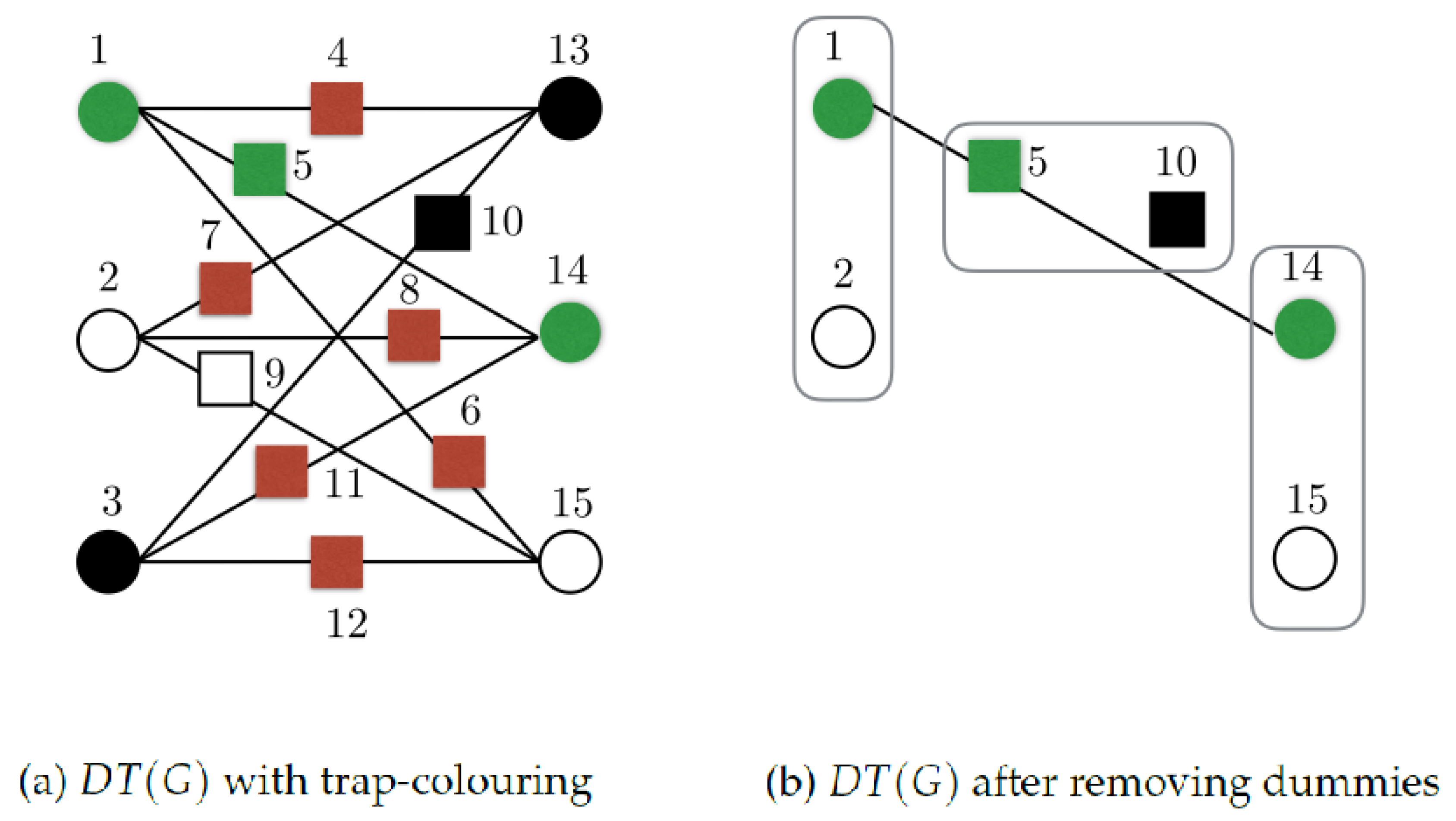
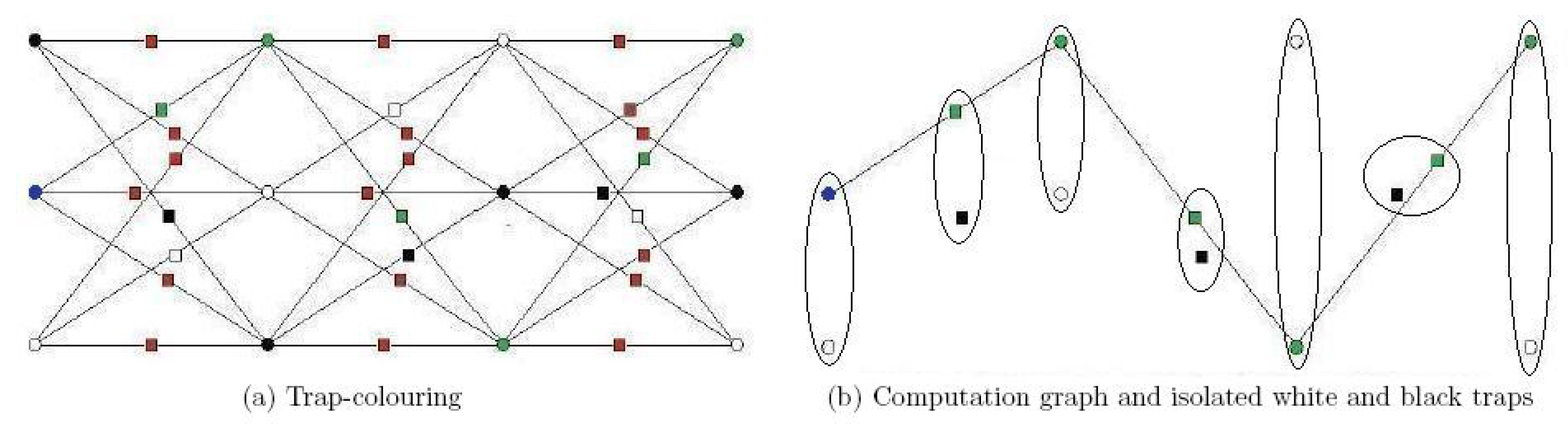
- We are given a base-graph G that has vertices and edges .
- For each vertex , we define a set of three new vertices . These are called primary vertices.
- Corresponding to each edge of the base-graph that connects the base vertices and , we introduce a set of nine edges that connect each of the vertices in the set with each of the vertices in the set .
- We replace every edge in the resulted graph with a new vertex connected to the two vertices originally joined by that edge. The new vertices added in this step are called added vertices. This is the dotted triple-graph .
- (i)
- Primary vertices are coloured in one of the three colours, white or black (for traps) and green (for computation). There is an exception for input base-locations (see Step (v)).
- (ii)
- Added vertices are coloured in one of the four colours white, black, green or red.
- (iii)
- In each primary set , there is exactly one vertex of each colour.
- (iv)
- Colouring the primary vertices fixes the colours of the added vertices: added vertices that connect primary vertices of different colour are red; added vertices that connect primary vertices of the same colour get that colour.
- (v)
- For input base-locations, instead of green, we have a blue vertex (but all other rules, including how to connect with the other vertices, apply in the same way as if it were green).
| Protocol 1 Verifiable universal blind quantum computation using the dotted triple graph (with fault-tolerant encoding); taken from [25]. |
| We assume that a standard labelling of the vertices of the dotted triple-graph , is known to both the client and the server. The number of qubits is at most where c is the maximum degree of the base graph G. • Client’s resources – Client is given a base graph G. The corresponding dotted graph state is generated by graph that is obtained from G by replacing every edge with a new vertex connected to the two vertices originally joined by that edge. – Client is given an MBQC measurement pattern which: Applied on the dotted graph state performs the desired computation, in a fault-tolerant way, that can detect or correct errors fewer than . – Client generates the dotted triple-graph , and selects a trap-colouring according to Definition 1 which is done by choosing independently the colours for each set . – Client for all red vertices will send dummy qubits and thus performs break operation. – Client chooses the green graph to perform the computation. – Client for the white graph sends dummy qubits for all added qubits and thus generates white isolated qubits at each primary vertex set . Similarly for the black graph the client sends dummy qubits for the primary qubits and thus generates black isolated qubits at each added vertex set . – The dummy qubits position set D is chosen as defined above (fixed by the trap-colouring). – A binary string of length at most represents the measurement outcomes. It is initially set to all zero’s. – A sequence of measurement angles, with , consistent with . We define to be the measurement angle in MBQC, when corrections due to previous measurement outcomes are taken into account (the function depends on the specific base-graph and its flow, see e.g., [3]). We also set for all of the trap and dummy qubits. The Client chooses a measurement order on the dotted base-graph that is consistent with the flow of the computation (this is known to Server). The measurements within each set of graph are ordered randomly. – random variables with value taken uniformly at random from A. – random variables and random variable with values taken uniformly at random from . – A fixed function that for each non-output qubit i computes the angle of the measurement of qubit i to be sent to the Server. • Initial Step – Client’s move: Client sets all of the values in to be 0 and prepares the input qubits as – Server’s move: Server receives single qubits and entangles them according to . – Continues to Protocol 2 |
| Protocol 2 Continuing from Protocol 1: VUBQC with DT(G). |
| • Step – Client’s move: Client computes the angle and sends it to the Server. – Server’s move: Server measures qubit i with angle and sends the Client the result . – Client’s move: Client sets the value of in to be . • Final Step: – Server’s move: Server returns the last layer of qubits (output layer) to the Client. • Verification – After obtaining the output qubits from the Server, the Client measures the output trap qubits with angle to obtain . – Client accepts if for all of the white (primary) and black (added) trap qubits i. |
2.2. Two-Party Quantum Protocols
- 1.
- input spaces and memory spaces and
- 2.
- n-tuple of quantum operations and such that and similarly for .
- 3.
- n-tuple of oracle operations where each oracle is a global operation for that step,
- 1.
- operations where ,
- 2.
- sequence of bits determining if the simulator calls the ideal functionality at step i ( calls the ideal functionality).
3. Secure Two-Party Quantum Computation
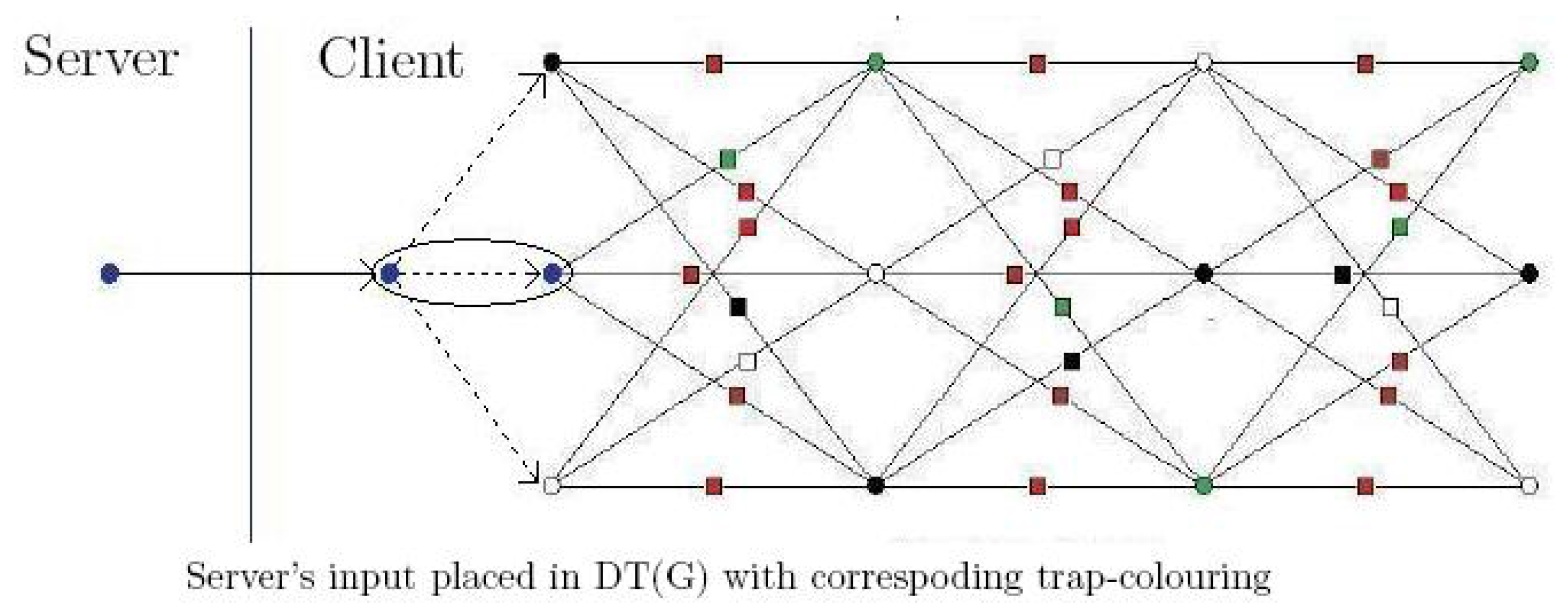
3.1. Server’s Input Injection
3.2. Server’s Output Extraction
3.3. The QYao Protocol
| Protocol 3 Server’s input injection |
| Setting: • The server has input that corresponds to specific positions of the input layer of the base-graph. For each i qubit, server chooses pair of secret bits . Instructions:
Outcome: • The server receives a DT(G), where the quantum input is the joint input of the client and server and the related measurement angles instructions perform the desired unitary operation, if the client is honest. |
| Protocol 4 Server’s output extraction. |
| Setting: • The server has the state at the corresponding positions of their output base-locations of the DT(G). For each i qubit, server chooses pair of secret bits . Instructions:
Outcome: • The server obtains the computation qubits of their output base-locations unpadded . |
| Protocol 5 Secure 2PQC-QYao. |
Input:
Output:
The protocol
|
4. Proof of the Privacy of the QYao Protocol
4.1. Client’s Simulators
- The simulator runs the protocol with fixed but random input , to obtain .
- The simulator obtains the fixed state and the isometry , which are both independent of the input.
- The simulated view is then defined to be:
- By , we define the padding of the server’s and client’s output, respectively. In more detail, these keys are functions of the trap-colouring (trap positions) of the last layer, the rotations , the secret parameters r’s and measurement results b’s of the previous two layers. We collectively denote the rest, i.e., all of the other secret keys, as .
- We also assume that the classical measurement outcomes b’s are in the Hilbert space of the client, while being classical and public, could be copied to the server’s Hilbert space as well (adding this copy does not affect the client’s simulators and complicates the notation). Moreover, classical results corresponding to trap measurements are denoted , while other results are simply denoted b. The trap measurements outcomes (in the honest run) are , where is one of the secret parameters included in .
- The final layer (unmeasured) qubits are separated into: (i) output qubits (those of the server and the client; and it includes the purification of their inputs), (ii) dummy qubits collectively denoted for server/client unmeasured dummies and (iii) trap qubits denoted as . The dummies and trap qubits are in the tensor product with the rest (in the honest run).
- The Hilbert spaces containing the output qubits (and the related purification of honest run) are denoted , while the remaining qubits are .
- For brevity, we denote and use the analogous notation for other states.
- The simulator obtains from the client the choice of secret keys (that can be viewed as part of the client’s input).
- The simulator sets . For the other measurement outcomes b, the simulator chooses randomly a bit value (to ensure that the b’s obtained are indistinguishable from the real honest protocol, the simulator can run the full protocol with some random input . Since in the honest run, the values of b’s do not depend on (are not correlated to) the input, the outcomes that the simulator returns would be indistinguishable from those of a run with the correct input. Finally, speciousness ensures that this state is also close to the real protocol).
- The simulator, using the previous steps, constructs the state .
- The simulator uses the state from Lemma 1 for the i-th step, which is a fixed state (independent of the input).
- The simulator calls the ideal functionality and receives the state .
- The simulator uses the keys and the state received from the ideal functionality and constructs .
- The simulator obtains the operator from the definition of specious and constructs the isometry acting from .
- The simulated view is then:
4.2. Server’s Simulators
- The simulator prepares multiple Bell states , sends the one qubit of each pair to the server and instructs them to entangle the qubits as it would in the normal protocol.
- The simulator for each qubit chooses randomly an angle and instructs the server to measure in this angle.
- The simulator obtains from the server’s (malicious) strategy the parameter (see Equation (6)).
- With probability , the simulator returns an abort. Otherwise, it performs the remaining steps.
- The simulator calls the ideal functionality and obtains the state , where is the deviated input that the corrupted server inputs.
- The simulator encrypts the outcome using , and sends the output qubits of the server back in the state:
- The simulator returns the keys to the server.
5. Non-Interactive QYao
| Protocol 6 Preparation of OTMs for non-interactive QYao. |
Description of OTM’s: We will use an (at most) one out of K OTM, where . Note, that the first layer does not need an OTM, since (i) we give the angle directly (does not depend on anything) and (ii) there is no trap in the previous layer and thus no need to give a flag. Moreover, for the last layer, while the qubits are not measured (and thus there is no corresponding angle ) we will use an OTM to obtain the last flags (that correspond to testing traps in the previous layers).
|
| Protocol 7 Non-interactive QYao. |
| Assumptions Client and server want to jointly compute a unitary as in Protocol 5. The client has N OTM’s that are 1-out-of-K, i.e., one OTM per qubit, with sufficient entries to store a pair of measurement angle and flag bit-string (of length at least ), for each extended influence past of the qubit. Protocol
|
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| UBQC | Universal blind quantum computation |
| MBQC | Measurement-based quantum computation |
| VBQC | Verifiable blind quantum computation |
| QYao | Quantum “Yao” protocol |
| OT | Oblivious transfer |
| OTM | One-time memory |
| DT(G) | Dotted triple graph |
| 2PQC | Secure two-party quantum computation |
Appendix A. Measurement-Based Quantum Computation
Appendix B. On Specious Adversaries Definitions
Appendix B.1. Restricting to Classical Inputs
Appendix B.2. About the Secret Random Parameters
Appendix B.3. Regarding Secure SWAP No-Go Theorem
Appendix C. Examples
Appendix C.1. Example for Protocol 5
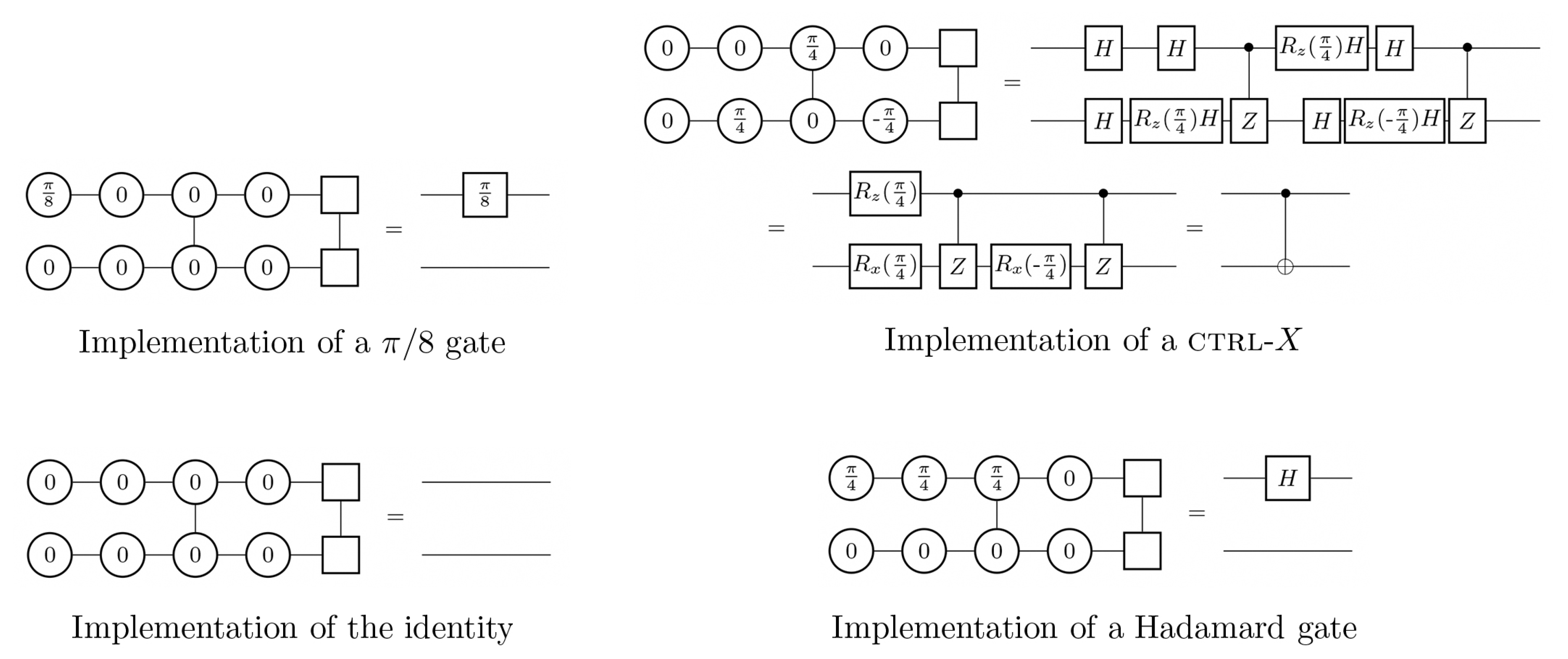
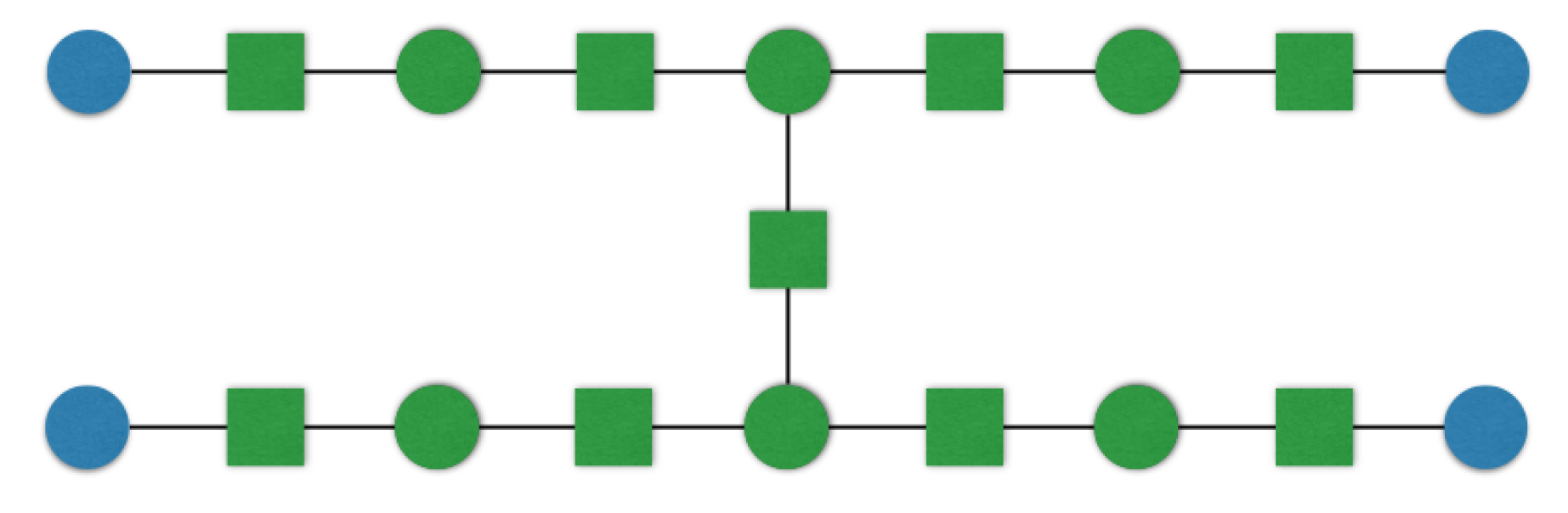
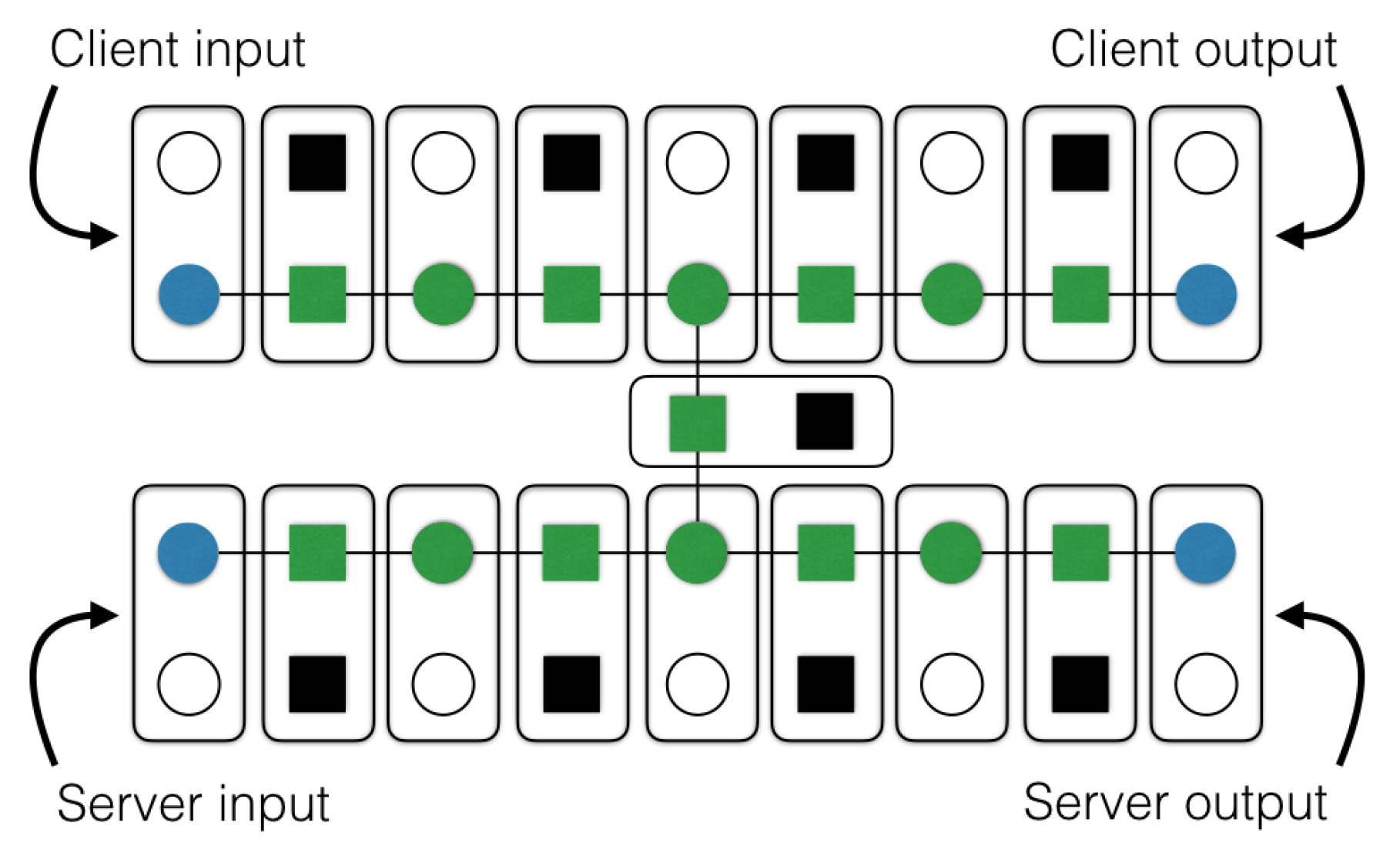
Appendix C.2. Example for Protocol 7
| Qubit | Influence-past | Extended influence-past | Non-trivial flag dependence |
| 13 | ∅ | ||
| 14 | |||
| 15 | ∅ |
Appendix D. Proof of Commuting
References
- Childs, A. Secure assisted quantum computation. Quant. Inf. Compt. 2005, 5, 456. [Google Scholar]
- Arrighi, P.; Salvail, L. Blind Quantum Computation. Int. J. Quant. Inf. 2006, 4, 883–898. [Google Scholar] [CrossRef]
- Broadbent, A.; Fitzsimons, J.; Kashefi, E. Universal blind quantum computation. In Proceedings of the 50th Annual Symposium on Foundations of Computer Science, Atlanta, GA, USA, 25–27 October 2009; pp. 517–526. [Google Scholar]
- Aharonov, D.; Ben-Or, M.; Eban, E. Interactive Proofs for Quantum Computations. Proceedings of Innovations in Computer Science 2010, Beijing, China, 5–7 January 2010; pp. 453–469. [Google Scholar]
- Reichardt, B.W.; Unger, R.F.; Vazirani, U. Classical command of quantum systems. Nature 2013, 496, 456–460. [Google Scholar] [CrossRef] [PubMed]
- Broadbent, A.; Gutoski, G.; Stebila, D. Quantum One-Time Programs. In Advances in Cryptology—CRYPTO 2013; Canetti, R., Garay, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume Voume 8043, pp. 344–360. [Google Scholar]
- Raussendorf, R.; Briegel, H.J. A One-Way Quantum Computer. Phys. Rev. Lett. 2001, 86, 5188–5191. [Google Scholar] [CrossRef] [PubMed]
- Nickerson, N.H.; Fitzsimons, J.F.; Benjamin, S.C. Freely scalable quantum technologies using cells of 5-to-50 qubits with very lossy and noisy photonic links. Phys. Rev. X 2014, 4, 041041. [Google Scholar] [CrossRef]
- Barz, S.; Kashefi, E.; Broadbent, A.; Fitzsimons, J.F.; Zeilinger, A.; Walther, P. Demonstration of blind quantum computing. Science 2012, 335, 303. [Google Scholar] [CrossRef] [PubMed]
- Fitzsimons, J.F.; Kashefi, E. Unconditionally verifiable blind computation. arXiv 2012. [Google Scholar]
- Kapourniotis, T.; Kashefi, E.; Datta, A. Blindness and Verification of Quantum Computation with One Pure Qubit. In Proceedings of the 9th Conference on the Theory of Quantum Computation, Communication and Cryptography (TQC 2014), Singapore, 21–23 May 2014; pp. 176–204. [Google Scholar]
- Gheorghiu, A.; Kashefi, E.; Wallden, P. Robustness and device independence of verifiable blind quantum computing. New J. Phys. 2015, 17, 083040. [Google Scholar] [CrossRef]
- Kapourniotis, T.; Dunjko, V.; Kashefi, E. On optimising quantum communication in verifiable quantum computing, 2015. In Proceedings of the 15th Asian Quantum Information Science Conference (AQISC 2015), Seoul, Korea, 25–28 August 2015; pp. 23–25. [Google Scholar]
- Dunjko, V.; Fitzsimons, J.F.; Portmann, C.; Renner, R. Composable Security of Delegated Quantum Computation. In Advances in Cryptology; Springer: Kaoshiung, Taiwan, 2014. [Google Scholar]
- McKague, M. Interactive proofs for BQP via self-tested graph states. arXiv 2013. [Google Scholar]
- Broadbent, A. How to verify a quantum computation. arXiv 2015. [Google Scholar]
- Gheorghiu, A.; Wallden, P.; Kashefi, E. Rigidity of quantum steering and one-sided device-independent verifiable quantum computation. New J. Phys. 2017, 19, 023043. [Google Scholar] [CrossRef]
- Dupuis, F.; Nielsen, J.B.; Salvail, L. Actively secure two-party evaluation of any quantum operation. In Advances in Cryptology—CRYPTO 2012; Springer: Santa Barbara, CA, USA, 2012; pp. 794–811. [Google Scholar]
- Dunjko, V.; Kashefi, E. Blind quantum computing with two almost identical states. arXiv 2016. [Google Scholar]
- Maurer, U.; Renner, R. Abstract cryptography. In Innovations in Computer Science; Citeseer: Beijing, China, 2011. [Google Scholar]
- Dupuis, F.; Nielsen, J.B.; Salvail, L. Secure two-party quantum evaluation of unitaries against specious adversaries. In Advances in Cryptology—CRYPTO 2010; Springer: Santa Barbara, CA, USA, 2010; pp. 685–706. [Google Scholar]
- Yao, A. How to generate and exchange secrets. In Proceedings of the 27th Annual Symposium on Foundations of Computer Science, Toronto, ON, Canada, 27–29 October 1986; pp. 162–167. [Google Scholar]
- Kent, A. Unconditionally secure bit commitment. Phys. Rev. Lett. 1999, 83, 1447. [Google Scholar] [CrossRef]
- Goldwasser, S.; Kalai, Y.T.; Rothblum, G.N. One-time programs. In Advances in Cryptology—CRYPTO 2008; Springer: Santa Barbara, CA, USA, 2008; pp. 39–56. [Google Scholar]
- Kashefi, E.; Wallden, P. Optimised resource construction for verifiable quantum computation. J. Phys. A Math. Theor. 2017, 50, 145306. [Google Scholar] [CrossRef]
- Bennett, C.; Brassard, G.; Ekert, A. Quantum cryptography. In Progress in Atomic physics Neutrinos and Gravitation, Proceedings of the XXVIIth Rencontre de Moriond, Les Arcs, Savoie, France, 25 January–1 February 1992; Atlantica Séguier Frontières: Biarritz, France, 1992; p. 371. [Google Scholar]
- Broadbent, A.; Schaffner, C. Quantum cryptography beyond quantum key distribution. Des. Codes Cryptogr. 2016, 78, 351–382. [Google Scholar] [CrossRef]
- Alagic, G.; Fefferman, B. On quantum obfuscation. arXiv 2016. [Google Scholar]
- Hayashi, M.; Morimae, T. Verifiable measurement-only blind quantum computing with stabilizer testing. arXiv 2015. [Google Scholar]
- Dulek, Y.; Schaffner, C.; Speelman, F. Quantum homomorphic encryption for polynomial-sized circuits. arXiv 2016. [Google Scholar]
- Kashefi, E.; Pappa, A. Blind multiparty quantum computing. 2016; in preparation. [Google Scholar]
- Abraham, I.; Dolev, D.; Gonen, R.; Halpern, J. Distributed Computing Meets Game Theory: Robust Mechanisms for Rational Secret Sharing and Multiparty Computation. In Proceedings of the Twenty-fifth Annual ACM Symposium on Principles of Distributed Computing, Denver, CO, USA, 23–26 July 2006; pp. 53–62. [Google Scholar]
- Kol, G.; Naor, M. Cryptography and game theory: Designing protocols for exchanging information. In Theory of Cryptography; Springer: New York, NY, USA, 2008; pp. 320–339. [Google Scholar]
- Eisert, J.; Wilkens, M.; Lewenstein, M. Quantum Games and Quantum Strategies. Phys. Rev. Lett. 1999, 83, 3077–3080. [Google Scholar] [CrossRef]
- Pappa, A.; Kumar, N.; Lawson, T.; Santha, M.; Zhang, S.; Diamanti, E.; Kerenidis, I. Nonlocality and Conflicting Interest Games. Phys. Rev. Lett. 2015, 114, 020401. [Google Scholar] [CrossRef] [PubMed]
- Childs, A.M.; Leung, D.W.; Nielsen, M.A. Unified derivations of measurement-based schemes for quantum computation. Phys. Rev. A 2005, 71, 032318. [Google Scholar] [CrossRef]
- Danos, V.; Kashefi, E.; Panangaden, P. The Measurement Calculus. J. ACM 2007, 54, 8. [Google Scholar] [CrossRef]
- Hein, M.; Eisert, J.; Briegel, H.J. Multiparty entanglement in graph states. Phys. Rev. A 2004, 69, 062311. [Google Scholar] [CrossRef]
- Naor, M.; Pinkas, B. Oblivious transfer and polynomial evaluation. In Proceedings of the Thirty-First Annual ACM Symposium on Theory of computing, Atlanta, GA, USA, 1–4 May 1999; pp. 245–254. [Google Scholar]
- Gennaro, R.; Gentry, C.; Parno, B. Non-interactive verifiable computing: Outsourcing computation to untrusted workers. In Advances in Cryptology—CRYPTO 2010; Springer: Santa Barbara, CA, USA, 2010; pp. 465–482. [Google Scholar]
- Danos, V.; Kashefi, E. Determinism in the one-way model. Phys. Rev. A 2006, 74, 052310. [Google Scholar] [CrossRef]
- Browne, D.E.; Kashefi, E.; Mhalla, M.; Perdrix, S. Generalized flow and determinism in measurement-based quantum computation. New J. Phys. 2007, 9, 250. [Google Scholar] [CrossRef]
- Goldreich, O.; Micali, S.; Wigderson, A. How to Play ANY Mental Game. In Proceedings of the Nineteenth Annual ACM Symposium on Theory of Computing, New York, NY, USA, 25–27 May 1987; pp. 218–229. [Google Scholar]
- Kashefi, E.; Music, L.; Wallden, P. The Quantum Cut-and-Choose Technique and Quantum Two-Party Computation. arXiv 2017. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kashefi, E.; Wallden, P. Garbled Quantum Computation. Cryptography 2017, 1, 6. https://doi.org/10.3390/cryptography1010006
Kashefi E, Wallden P. Garbled Quantum Computation. Cryptography. 2017; 1(1):6. https://doi.org/10.3390/cryptography1010006
Chicago/Turabian StyleKashefi, Elham, and Petros Wallden. 2017. "Garbled Quantum Computation" Cryptography 1, no. 1: 6. https://doi.org/10.3390/cryptography1010006
APA StyleKashefi, E., & Wallden, P. (2017). Garbled Quantum Computation. Cryptography, 1(1), 6. https://doi.org/10.3390/cryptography1010006





