VIIRS Day/Night Band—Correcting Striping and Nonuniformity over a Very Large Dynamic Range
Abstract
:1. Introduction
1.1. VIIRS Design
1.2. On-Orbit DNB Calibration Process
1.2.1. Original DNB Calibration Process
1.2.2. DNB RSB Automatic Calibration Process
2. Materials and Methods
2.1. Source of Data
2.2. Hardware
2.3. Software Language and Libraries
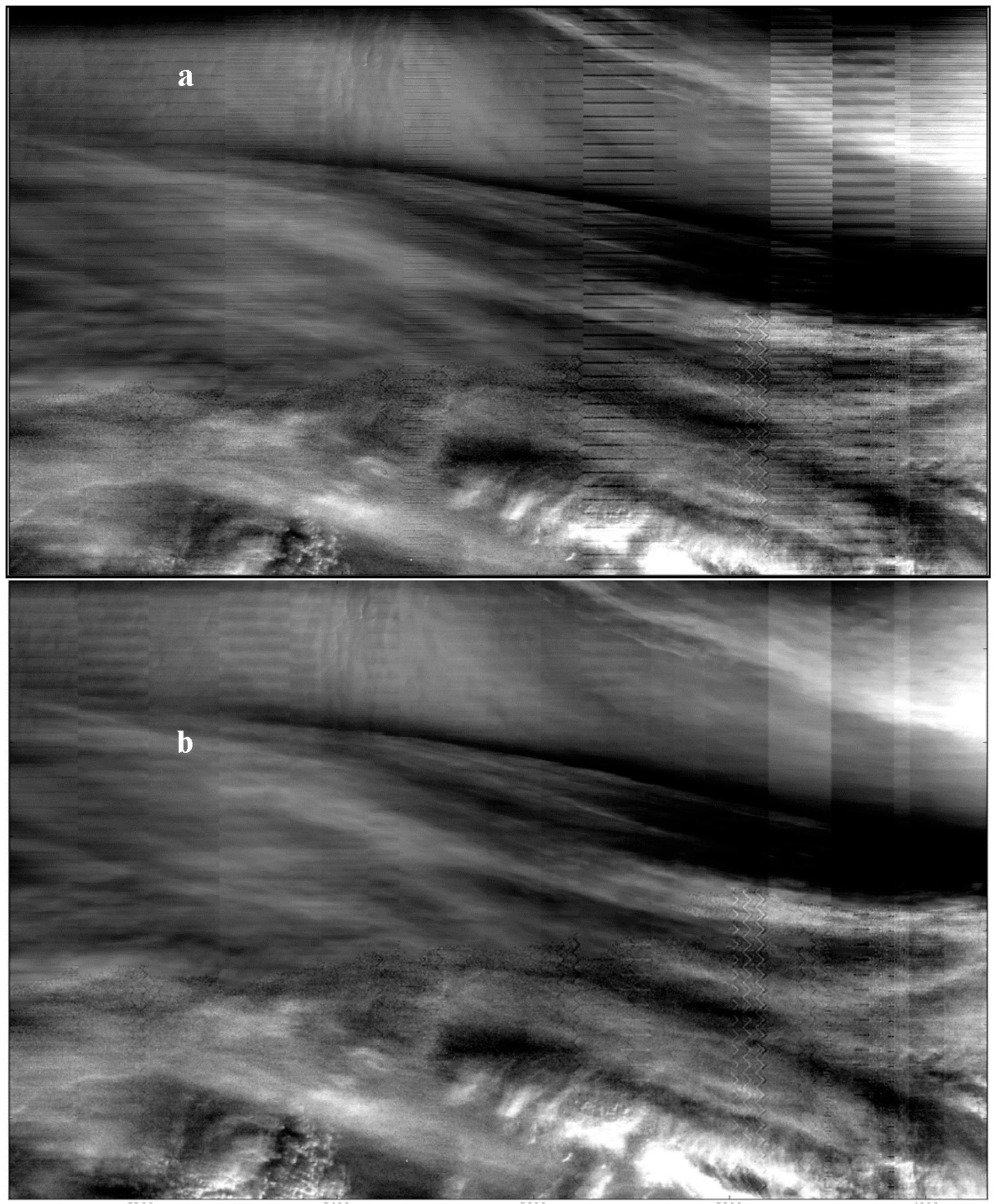
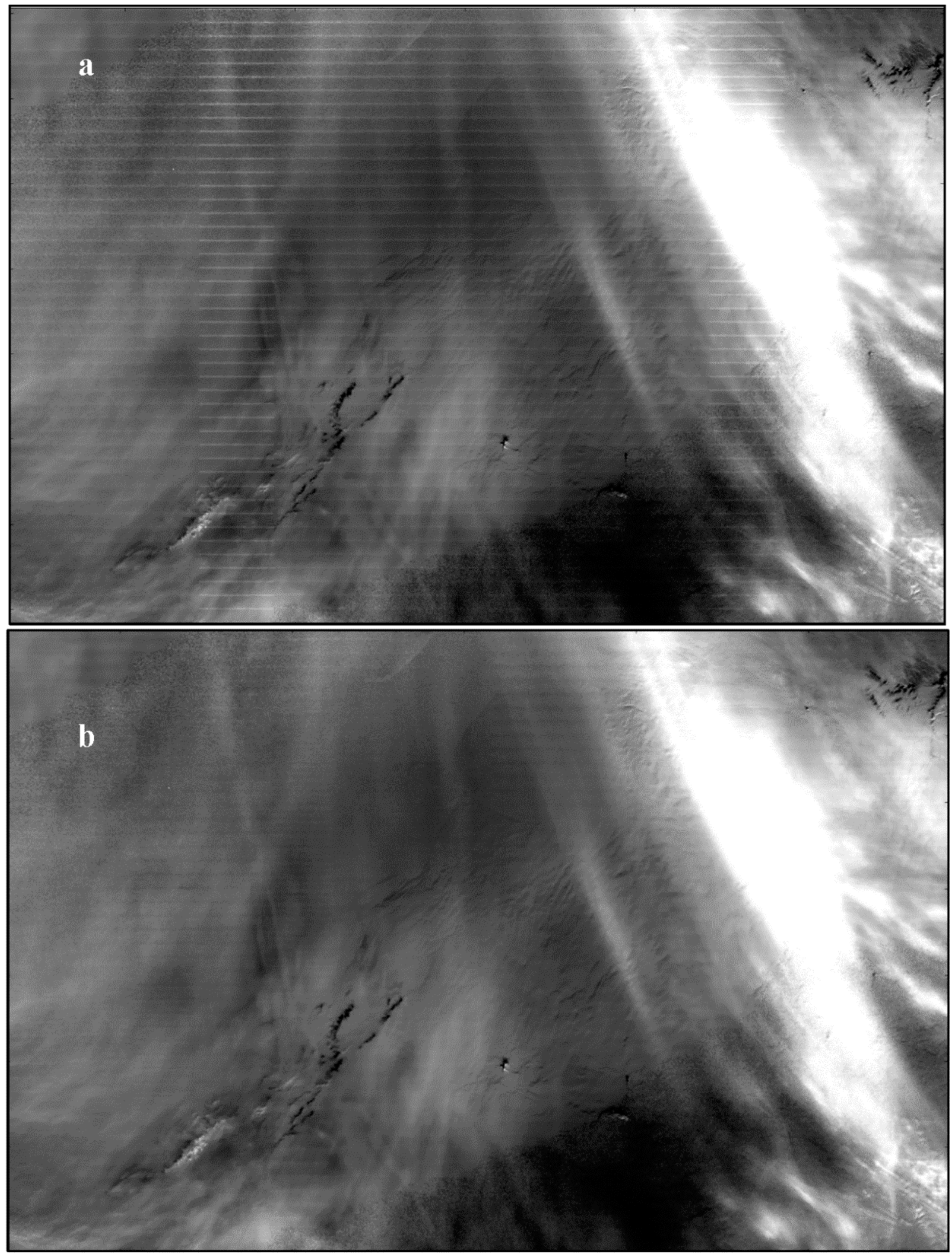
2.4. Histogram Matching Method Destriping Algorithm Description
- Offset correction for night scenes similar to what is described in the On-Orbit DNB Calibration section above.
- Gain correction for moonlit scenes using the Moment Matching (MM) technique.
- Complete correction over the entire dynamic range using the Histogram Matching Method (HMM).
2.5. Investigative Methodology
- We conducted a thorough survey of DNB imagery to discover all conditions where striping occurs. We have collected data from many days taken over the span of the S-NPP mission, and viewed all images taken over a 24-h period, including daytime and nighttime. We specifically chose dates near the phases of the moon—new moon, first quarter, full moon, last quarter and some between these.
- In order to observe features in twilight imagery striping we used the Near Constant Contrast algorithm to produce imagery from DNB radiance that minimizes the contrast due to changes in twilight illumination. This algorithm divides the DNB radiance by a factor that is dependent on the computed direct or indirect solar and lunar irradiance. The solar and lunar illumination levels are estimated in the twilight region using a fit to the twilight radiances during new moon [29]. The NCC images here are not from the official version, but use a similar technique to minimize twilight contrast. These NCC images were plotted on a gray scale for evaluation.
- Along with the radiance plots, we evaluated the associated geolocation to understand the solar or lunar illumination conditions associated with a particular striping artifact. This provides clues as to the root cause of the artifact.
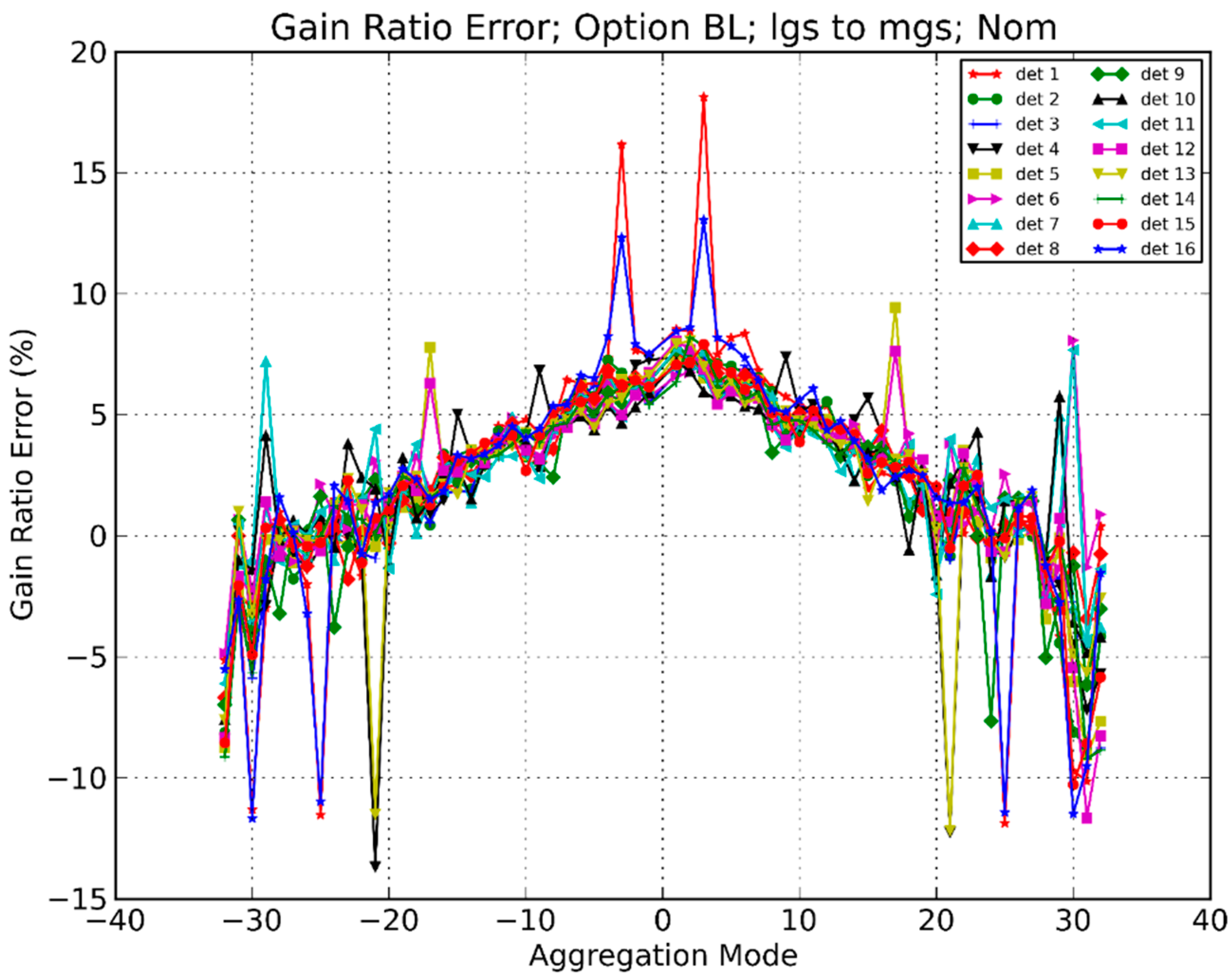
- We collected and analyzed several days of on-board calibrator data, and in some cases calibrated the counts into radiances using nominal linear calibration coefficients. We produced plots of this cal sector data as a function of time, ASN and/or detector number. In some cases we simulated the calibration process by computing gain ratios and offsets. The on-board calibrator data reveals uncertainties in the calibration process that can lead to striping.
- We applied the HMM algorithms to SDR data where striping was found and compared the uncorrected images with the corrected images plotted over the same radiance range. We thus evaluated the performance of the destriping algorithm. We also plotted the correction tables used because the detector-to-detector variation seen in the plots are a characterization of the level of striping produced by the DNB.
3. Results
3.1. Survey of DNB Imagery
3.1.1. Observations for Daytime Scenes
3.1.2. Observations for Twilight Scenes
3.1.3. Observations for Nighttime Scenes
3.2. Evaluating Causes of Striping and Nonuniformities
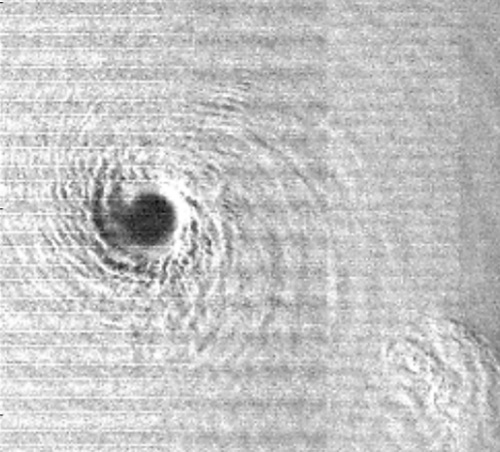
3.2.1. Stray Light in the Cross-Calibration
3.2.2. Residual Uncorrected Stray Light in the Earth-View
- The correction uses “dark” new moon scenes to characterize the background stray light, but in reality these scenes are not completely dark, since they contain variable amounts of nightglow. The nightglow is estimated from areas where there is no stray light, but since nightglow is not uniform over the scene [31] this variation leads to over/under-correction.
- The correction look-up tables are constructed as a function of solar zenith angle. In reality, stray light intensity is also a function of solar azimuth angle, and this changes seasonally over the year. This azimuthal dependence is handled empirically; via monthly updates of look-up tables but for times between these synoptic updates the changes in actual stray light cause over/under-correction. This can be somewhat alleviated by taking advantage of the year-to-year 9-days shift in the lunar cycle and using tables created from the previous years. This assumes, however, that the stray light does not change long-term from year to year for other reasons.
- The stray light cannot be characterized for scenes with twilight illumination, so correction in these areas are estimated either through extrapolation [22] or by setting it to a constant based on the solar zenith angle [10]. Neither of these estimates are perfect, and so this results in residual over/under-correction.
- Changes in offset between the time the correction tables are made and when they are applied can cause additional striping due to drifts in offset described previously. This is because there is striping in the signal used to estimate airglow, and these offset errors become a part of the correction tables. When the offsets drift, their effect remains in the tables and it creates additional striping in the stray light corrected scene.
3.2.3. Electronic Effects—Hysteresis and Crosstalk
3.2.4. Detector Nonlinearity
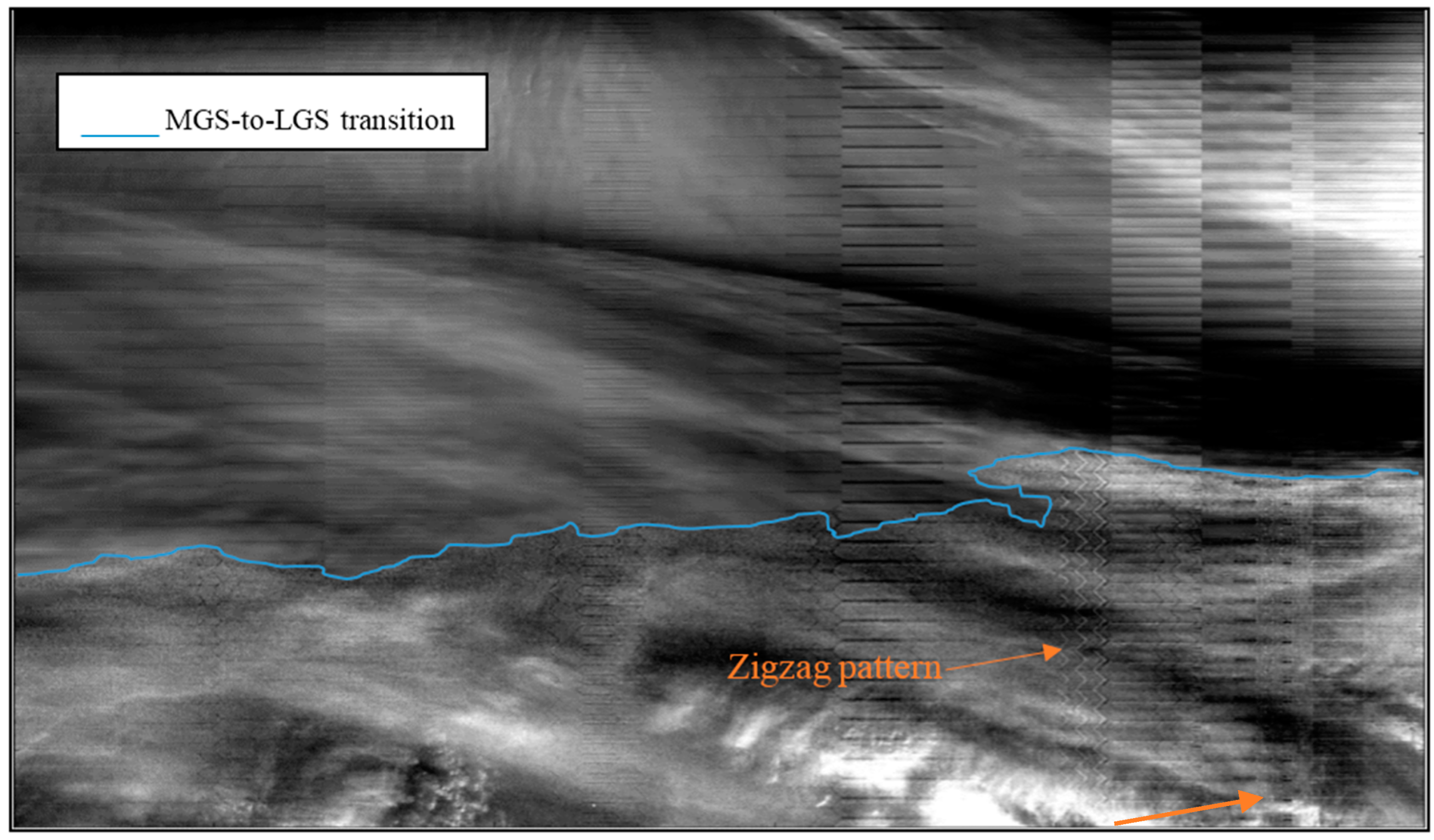
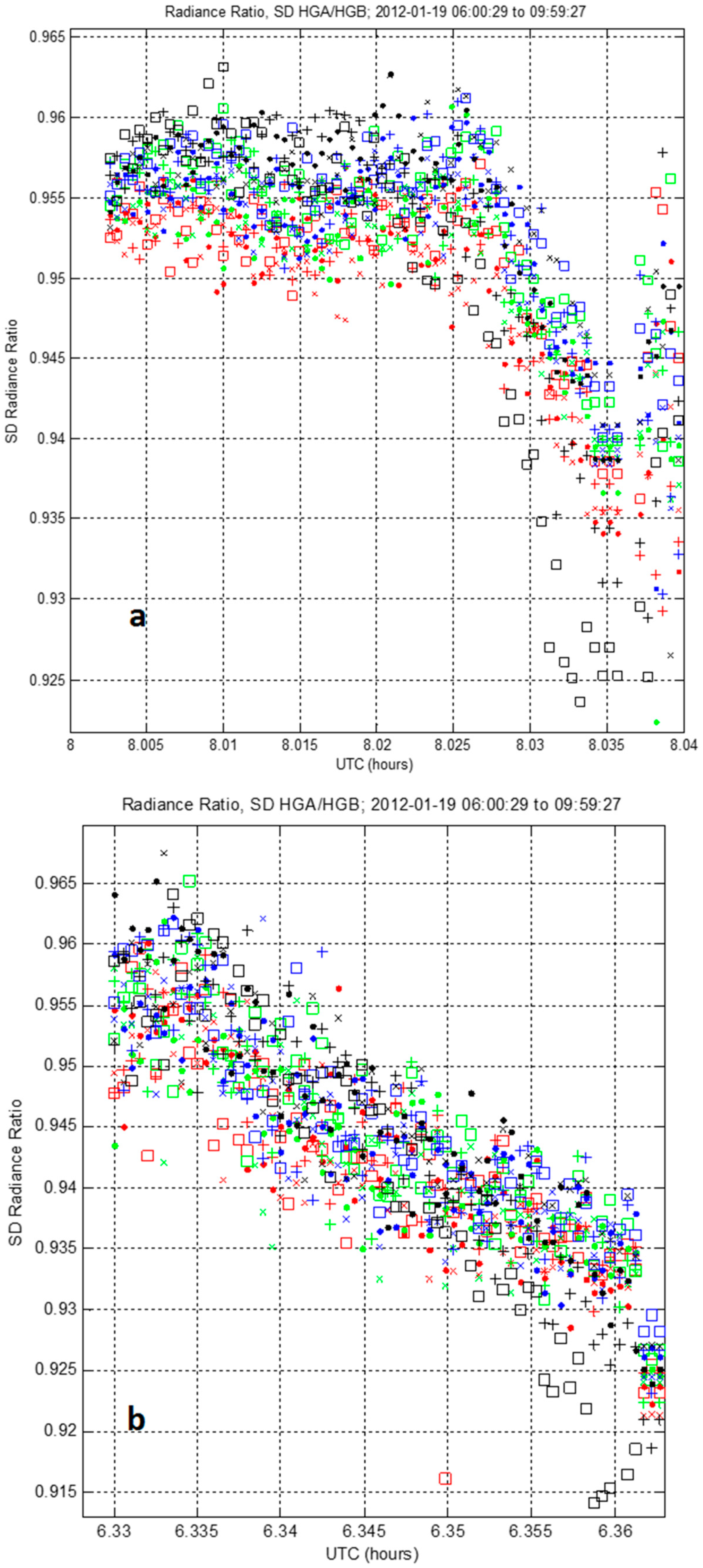
3.2.5. Half-Angle Mirror Side Differences
3.3. Histogram Matching Method Results
4. Discussion
4.1. Changing the DNB Calibration Process to Reduce Striping
4.2. Histogram Matching Method Computational Considerations
- Collecting the ensemble of pixel radiances, filtering the ensemble, producing histograms, and computing correction tables from the histograms.
- Applying the correction tables to the DNB radiances.
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ASN | Aggregation Sequence Number |
| BB | Black Body |
| CLASS | Comprehensive Large Array-data Stewardship System |
| DNB | Day/Night Band |
| HAM | Half-Angle Mirror |
| HGA | High-Gain A |
| HGB | High-Gain B |
| HGS | High-Gain Stage |
| HMM | Histogram Matching Method |
| IDPS | Interface Data Processing Segment |
| LGS | Low-Gain Stage |
| MGS | Mid-Gain Stage |
| MM | Moment Matching |
| MODIS | Moderate-Resolution Imaging Spectroradiometer |
| NCC | Near-Constant Contrast |
| RVS | Response Versus Scan |
| RSB | Reflective Solar Band |
| SD | Solar Diffuser |
| SDR | Senor Data Record |
| SIPS | Science Investigator-led Processing System |
| S-NPP | Suomi National Polar-orbiting Partnership |
| SV | Space View |
| VCST | VIIRS Science Support Team |
| VIIRS | Visible Infrared Imaging Radiometer Suite |
References
- Liao, L.B.; Weiss, S.; Mills, S.; Hauss, B. Suomi NPP VIIRS day and night band on-orbit performance. J. Geophys. Res. Atmos. 2013, 118, 12705–12718. [Google Scholar] [CrossRef]
- Miller, S.D.; Straka, W., III; Mills, S.P.; Elvidge, C.D.; Lee, T.F.; Solbrig, J.; Walther, A.; Heidinger, A.K.; Weiss, S.C. Illuminating the capabilities of the Suomi NPP VIIRS Day/Night Band. Remote Sens. 2013, 5, 6717–6766. [Google Scholar] [CrossRef]
- Miller, S.D.; Mills, S.P.; Elvidge, C.D.; Lindsey, D.T.; Lee, T.F.; Hawkins, J.D. Suomi satellite brings to light a unique frontier of nighttime environmental sensing capabilities. Proc. Natl. Acad. Sci. USA 2012, 109, 15706–15711. [Google Scholar] [CrossRef] [PubMed]
- Baugh, K.; Hsu, F.C.; Elvidge, C.; Zhizhin, M. Nighttime Lights Compositing Using the VIIRS Day-Night Band: Preliminary Results. Proc. Asia Pac. Adv. Netw. 2013, 35, 70–86. [Google Scholar] [CrossRef]
- Mills, S.; Miller, S. VIIRS Day-Night Band (DNB) calibration methods for improved uniformity. Proc. SPIE 2014, 9218. [Google Scholar] [CrossRef]
- Miller, S.D.; Turk, F.J.; Lee, T.F.; Hawkins, J.D.; Velden, C.S.; Schmidt, C.C.; Prins, E.M.; Haddock, S.H. The origin of sensors: Evolutionary considerations for next-generation satellite programs. American meteorological society. In Proceedings of the 14th Conference on Satellite Meteorology and Oceanography, Atlanta, GA, USA, 28–30 January 2006.
- Baker, N. Instrument overview. In Joint Polar Satellite System (JPSS) VIIRS Radiometric Calibration Algorithm Theoretical Basis Document ATBD, rev. C; Goddard Space Flight Center: Greenbelt, MD, USA, 2013; pp. 12–24. [Google Scholar]
- Baker, N. Day-night band FPA and Interface Electronics. In Joint Polar Satellite System (JPSS) VIIRS Radiometric Calibration Algorithm Theoretical Basis Document ATBD, rev. C; Goddard Space Flight Center: Greenbelt, MD, USA, 2013; pp. 25–29. [Google Scholar]
- Miller, S.W.; Jamilkowski, M.; Grant, K. Joint Polar Satellite System (JPSS) Common Ground System (CGS) Architectural Overview and Tenets. Available online: http://www.jpss.noaa.gov/AMS_2014/Presentations/31_JPSS_CGS_Overview_and_Architectural_Tenets.pdf (accessed 1 Dec 2015).
- Lee, S.; Chiang, K.F.; Xiong, X.; Sun, C.; Samuel, A. The S-S-NPP VIIRS Day-Night Band On-Orbit Calibration/Characterization and Current State of SDR Products. Remote Sens. 2014, 6, 12427–12446. [Google Scholar] [CrossRef]
- Baker, N. Day-night band calibration. In Joint Polar Satellite System (JPSS) VIIRS Radiometric Calibration Algorithm Theoretical Basis Document ATBD, rev. C; Goddard Space Flight Center: Greenbelt, MD, USA, 2013; pp. 102–109. [Google Scholar]
- Mills, S.; Jacobson, E.; Jaron, J.; McCarthy, J.; Ohnuki, T.; Plonski, M.; Searcy, D.; Weiss, S. Calibration of the VIIRS Day/Night Band (DNB). In Proceedings of the 6th Annual Symposium on Future National Operational Environmental Satellite Systems-NPOESS and GOES-R, Atlanta, GA, USA, 17–21 January 2010.
- Geis, J.; Florio, C.; Moyer, D.; Rausch, K.; de Luccia, F. VIIRS day-night band gain and offset determination and performance. Proc. SPIE 2012, 8510, 8510–8512. [Google Scholar]
- Baker, N. Solar Diffuser Calibration Multi-Orbit Aggregation. Joint Polar Satellite System (JPSS) VIIRS Radiometric Calibration Algorithm Theoretical Basis Document ATBD, rev. C; Goddard Space Flight Center: Greenbelt, MD, USA, 2013; p. 145. [Google Scholar]
- Rausch, K.; Houchin, S.; Cardema, J.; Moy, G.; Haas, E.; de Luccia, F.J. Automated calibration of the Suomi National Polar-Orbiting Partnership (S-NPP) Visible Infrared Imaging Radiometer Suite (VIIRS) reflective solar bands. J. Geophys. Res. Atmos. 2013, 118, 13434–13442. [Google Scholar] [CrossRef]
- Mills, S. VIIRS DNB Stray Light Anomaly Analysis (DR4623); NOAA internal document # ND3475506; NOAA: Silver Spring, MD, USA, 2012.
- Lee, S.; McIntire, J.; Oudrari, H.; Schwarting, T.; Xiong, X. A New Method for Suomi-NPP VIIRS Day–Night Band On-Orbit Radiometric Calibration. IEEE Trans. Geosci. Remote Sens. 2014. [Google Scholar] [CrossRef]
- Lee, S. VIIRS F1 Day Night Band Offset Determination: VROP702 vs. Pitch Maneuver; NOAA Internal document, NICST_REPORT_POST_12_011; NOAA: Silver Spring, MD, USA, 2012.
- Mills, S. VIIRS DNB Cross-Stage Gain Calibration Using Earthshine on Solar Diffuser; NOAA internal document # ND3475507; NOAA: Silver Spring, MD, USA, 2012.
- Haas, E. RSBAutoCal Status and Path Forward, STAR JPSS Annual Science Team Meeting, 26 August 2015. Available online: http://www.star.nesdis.noaa.gov/star/documents/meetings/2015JPSSAnnual/ (accessed on 23 November 2015).
- Baker, N. Description of theoretical basis for Reflective Solar Band (RSB) Automatic calibration (RSBAutocal) algorithm. In Joint Polar Satellite System (JPSS) VIIRS Radiometric Calibration Algorithm Theoretical Basis Document ATBD, rev. C; Goddard Space Flight Center: Greenbelt, MD, USA, 2013; pp. 154–161. [Google Scholar]
- Mills, S.; Weiss, S.; Liang, C. VIIRS day/night band (DNB) stray light characterization and correction. Proc. SPIE 2013, 8866. [Google Scholar] [CrossRef]
- NOAA Comprehensive Large Array-Data Stewardship System. Available online: www.class.ngdc.noaa.gov/saa/products/welcome (accessed on 1 December 2015).
- Community Satellite Processing Package. Available online: http://cimss.ssec.wisc.edu/cspp/ (accessed on 1 December 2015).
- Gumley, L. CSPP polar-orbiting satellite software and products. In Proceedings of the 2015 CSPP/IMAPP Users’ Group Meeting, Darmstadt, Germany, 14–16 April 2015.
- Bouali, M.; Ladjal, S. Toward Optimal Destriping of MODIS Data Using a Unidirectional Variational Model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2924–2935. [Google Scholar] [CrossRef]
- Mills, S. VIIRS Day-Night Band destriping methods for improved uniformity. GSICS Q. 2015, 9. [Google Scholar] [CrossRef]
- Horn, B.K.P.; Woodham, R.J. Destriping Landsat MSS images by histogram modification. Comput. Gr. Image Process. 1979, 10, 69–83. [Google Scholar] [CrossRef]
- Liang, C.K.; Mills, S.; Hauss, B.I.; Miller, S.D. Improved VIIRS Day/Night Band Imagery with Near-Constant Contrast. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6964–6971. [Google Scholar] [CrossRef]
- Bhatt, R.; Doelling, D.R.; Wu, A.; Xiong, X.; Scarino, B.R.; O’Haney, C.; Gopalan, A. Initial Stability Assessment of S-NPP VIIRS Reflective Solar Band Calibration Using Invariant Desert and Deep Convective Cloud Targets. Remote Sens. 2014, 6, 2809–2826. [Google Scholar] [CrossRef]
- Cao, C.; de Luccia, F.J.; Xiong, X.; Wolfe, R.; Weng, F. Early on-orbit performance of the visible infrared imaging radiometer suite onboard the Suomi national polar-orbiting Partnership (S-NPP) satellite. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1142–1156. [Google Scholar] [CrossRef]
- Velden, C.; Harper, B.; Wells, F.; Beven, J.L., II; Zehr, R.; Olander, T.; Mayfield, M.; Guard, C.; Lander, M.; Edson, R.; et al. The Dvorak Tropical Cyclone Intensity Estimation Technique, A Satellite-Based Method that Has Endured for over 30 Years. BAMS 2006. [Google Scholar] [CrossRef]
- Mills, S.; Liang, C. VIIRS DNB Cross-Stage Calibration Coefficient Ratio Change in 1 Month; NOAA internal document # ND3475514; NOAA: Silver Spring, MD, USA, 2012.
- Mills, S.; Liang, C. Comparison of DNB Inter-Stage Gain Ratios; NOAA internal document # ND3475668; NOAA: Silver Spring, MD, USA, 2012.
- Liao, L.; Weiss, S.; Liang, C. DNB performance. In Proceedings of 2013 Suomi NPP SDR Science and Products Review, College Park, MD, USA, 18–20 December 2013.
- McCarthy, J.K.; Jacobson, E.J.; Kilduff, T.M.; Estes, R.W.; Levine, P.A.; Mills, S.; Elvidge, C.; Miller, S.D. On the potential to enhance the spatial resolution of the day-night band (DNB) channel of the visible and infrared imaging radiometer suite (VIIRS) for the second joint polar satellite system (JPSS-2) and beyond. Proc. SPIE 2013, 8866. [Google Scholar] [CrossRef]
- Mills, S. JPSS-1 VIIRS DNB, prelaunch tests & performance. In Proceedings of 2015 STAR JPSS Annual Science Team Meeting, College Park, MD, USA, 24–28 August 2015.
- Miller, S.D.; Straka, W.C., 3rd; Yue, J.; Smith, S.M.; Alexander, M.J.; Hoffmann, L.; Setvák, M.; Partain, P.T. Upper atmospheric gravity wave details revealed in nightglow satellite imagery. Proc. Nat. Acad. Sci. USA 2015, 112. [Google Scholar] [CrossRef] [PubMed]


















© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mills, S.; Miller, S. VIIRS Day/Night Band—Correcting Striping and Nonuniformity over a Very Large Dynamic Range. J. Imaging 2016, 2, 9. https://doi.org/10.3390/jimaging2010009
Mills S, Miller S. VIIRS Day/Night Band—Correcting Striping and Nonuniformity over a Very Large Dynamic Range. Journal of Imaging. 2016; 2(1):9. https://doi.org/10.3390/jimaging2010009
Chicago/Turabian StyleMills, Stephen, and Steven Miller. 2016. "VIIRS Day/Night Band—Correcting Striping and Nonuniformity over a Very Large Dynamic Range" Journal of Imaging 2, no. 1: 9. https://doi.org/10.3390/jimaging2010009