Experimental Analysis of the Influence of the Sliding-Gate Valve on Submerged Entry Nozzle Outlet Jets
Abstract
:1. Introduction
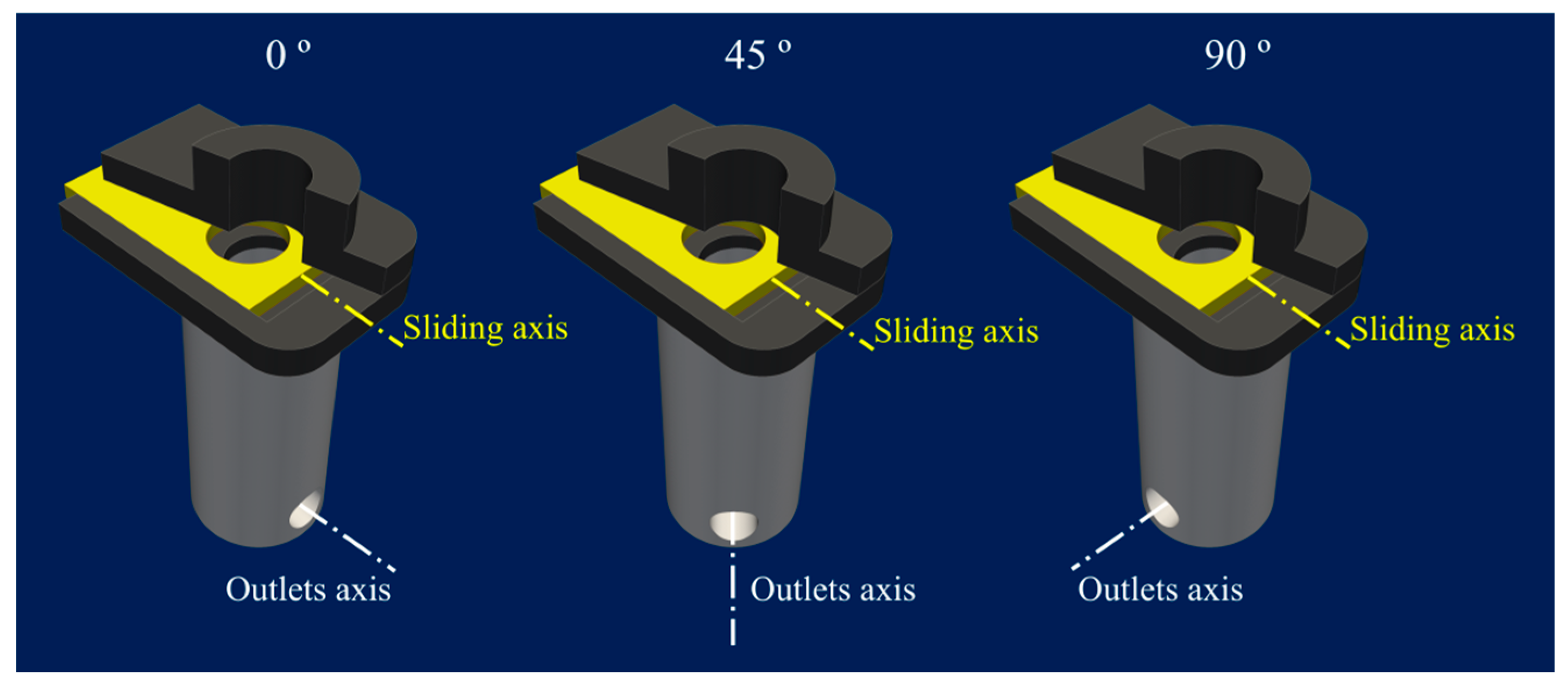
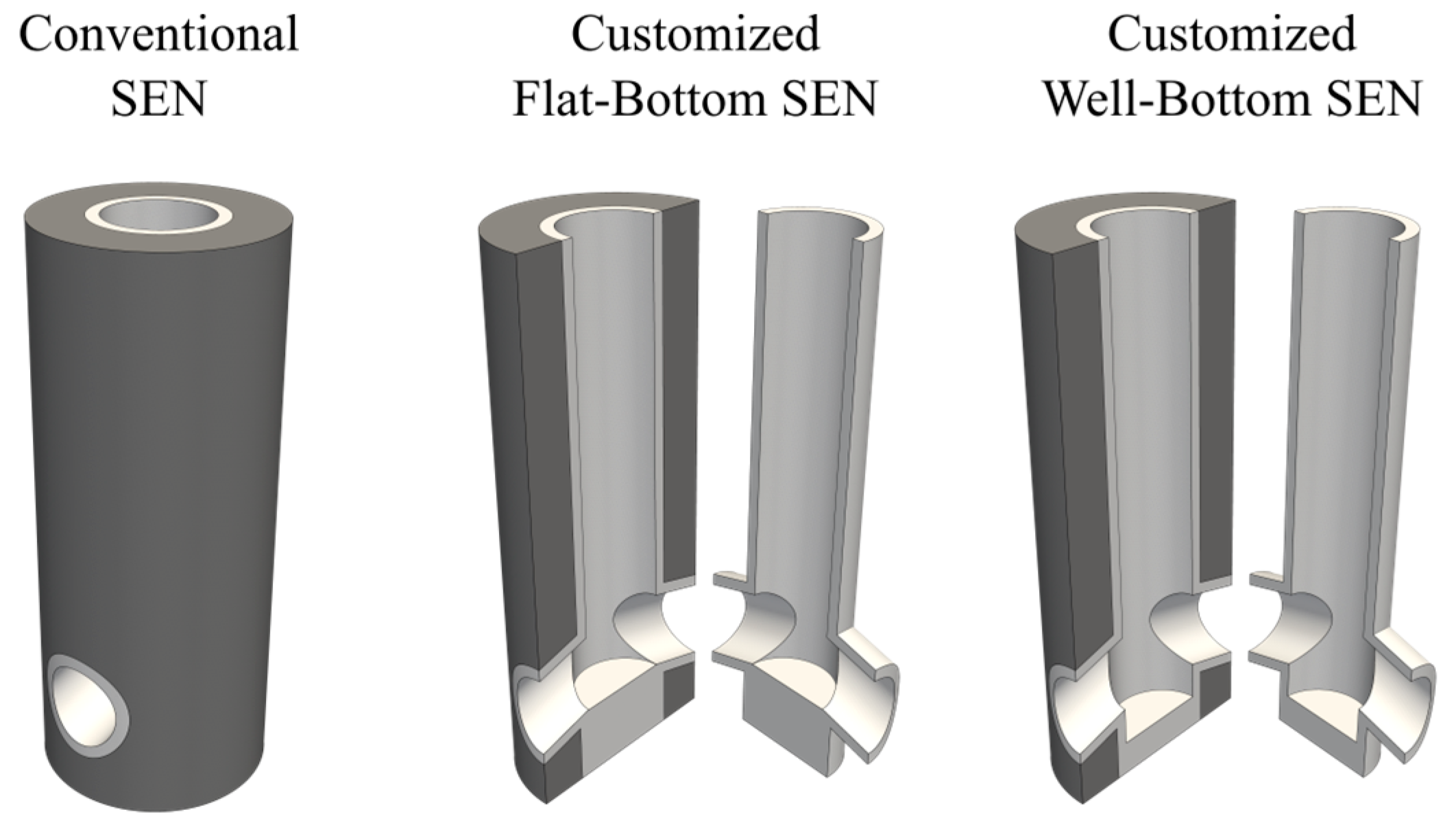
2. The CCC Process and the SEN Designs Studied in This Work
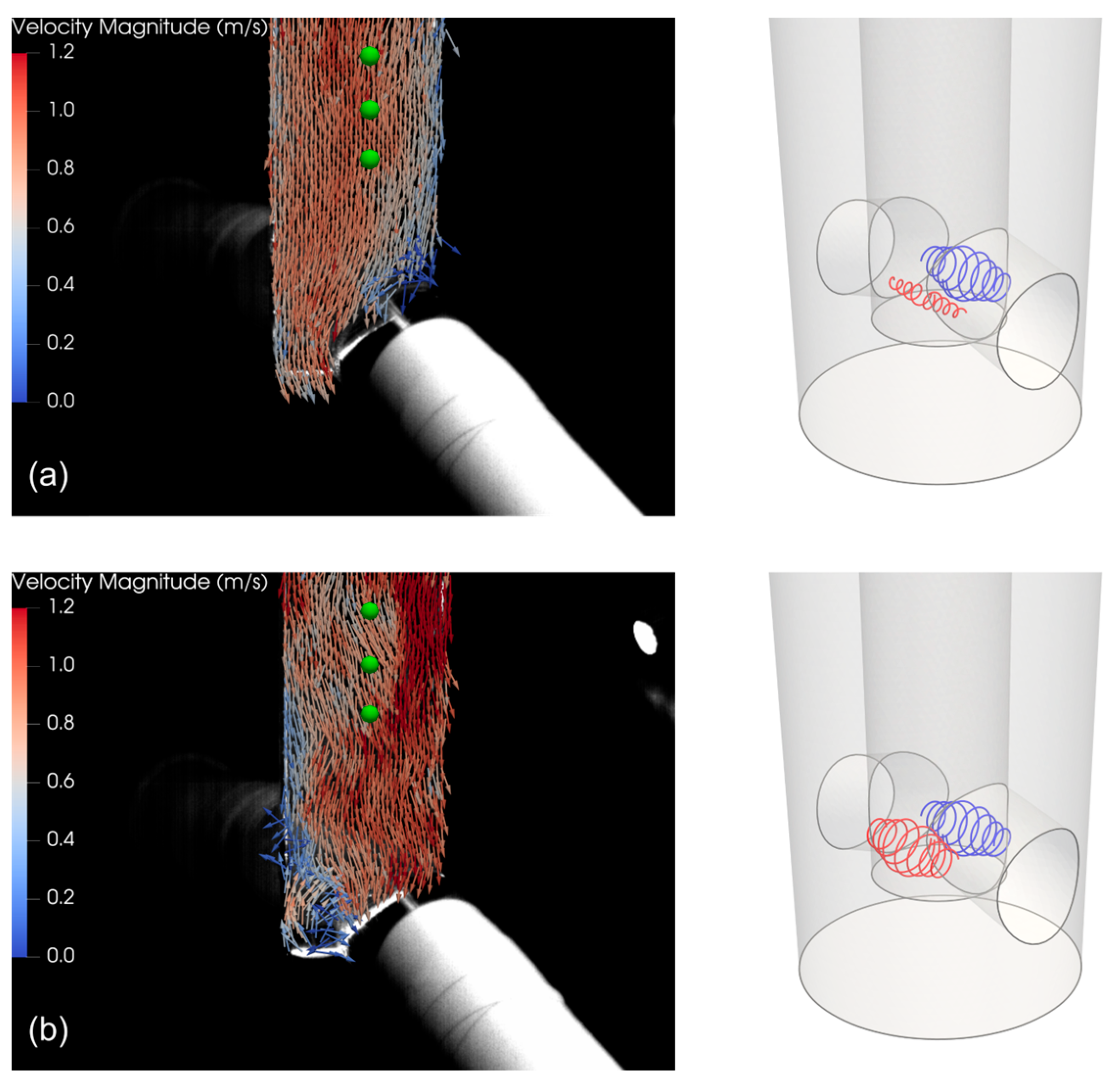
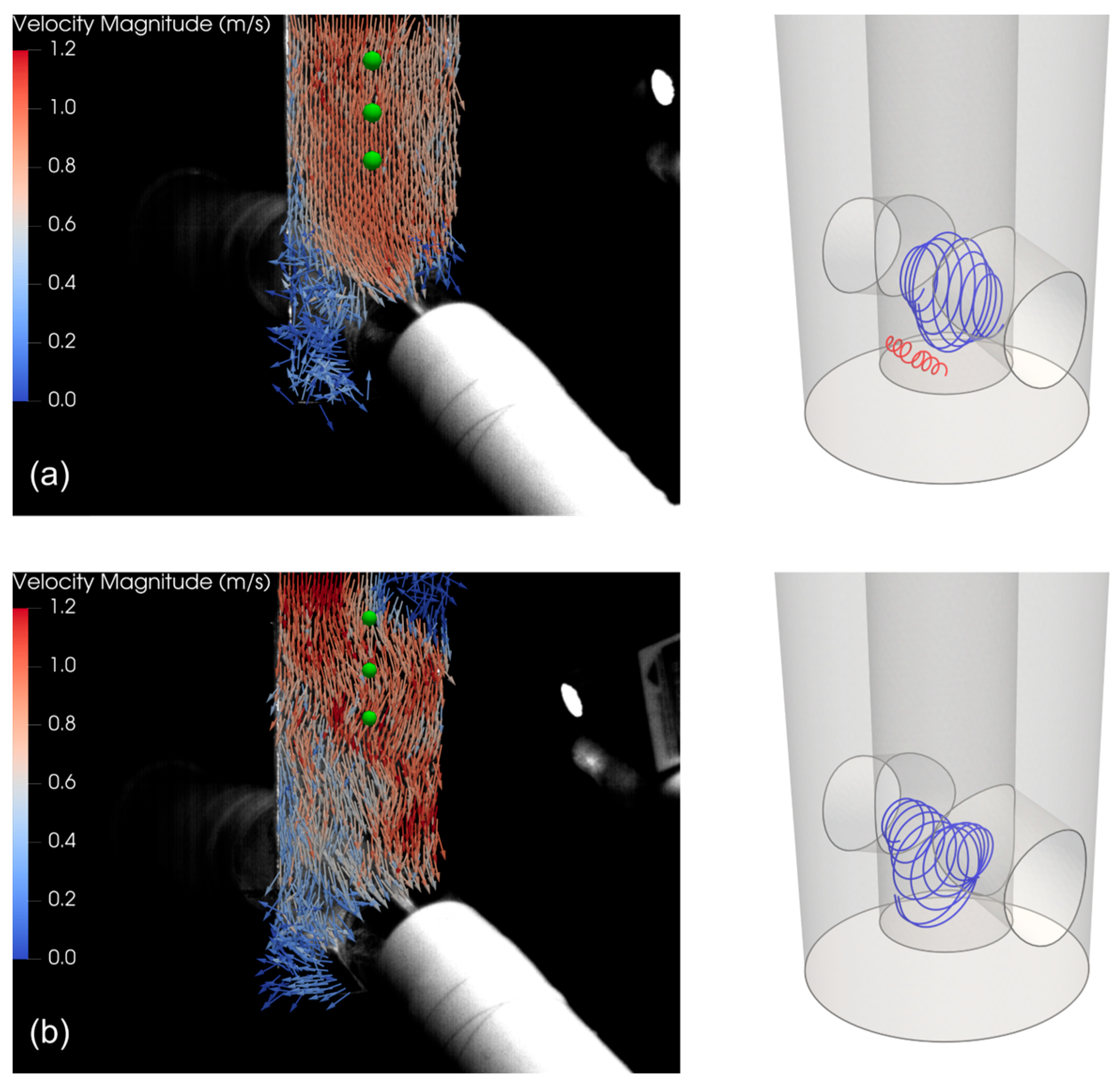
3. Transient Behavior of the Fluid Velocities Field inside the SEN’s Bore
4. Transient Behavior of the SEN Outlet Jets
4.1. Adjustments Made to the SEN
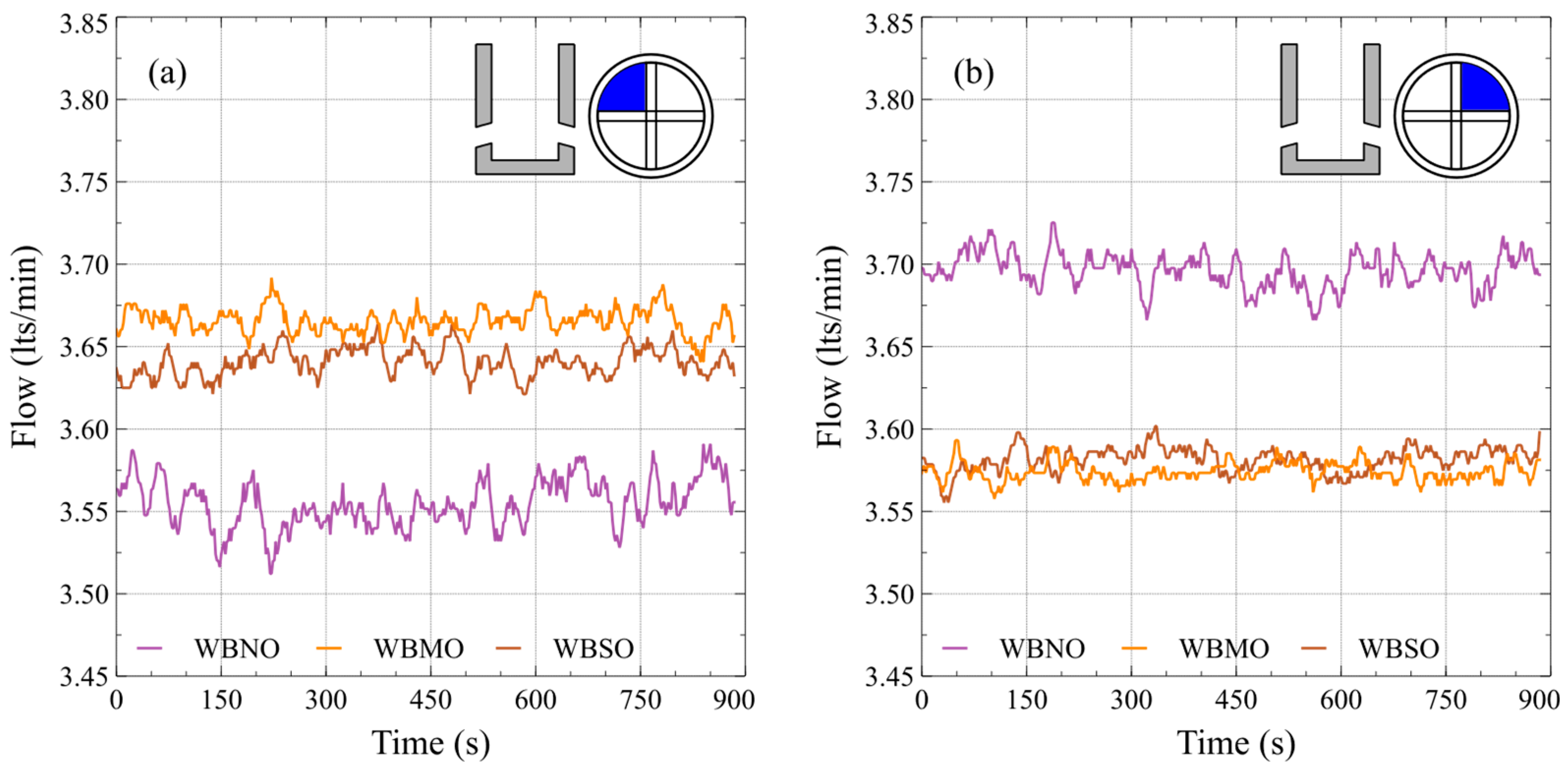
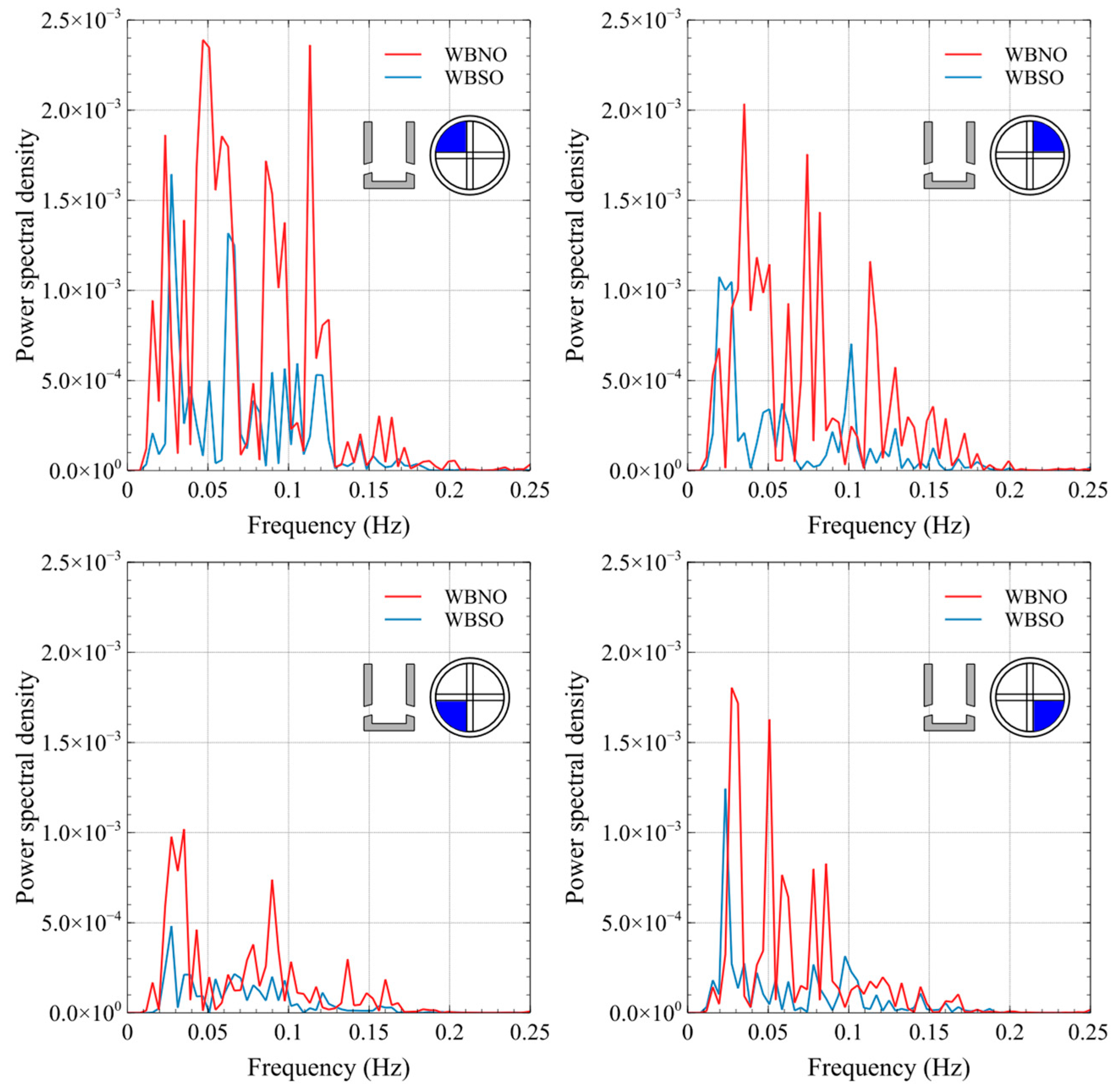
4.2. Analysis of the Flowmeters Signals
- The strength of the fluctuations in the lower quadrants increases, while for the SW it does not change;
- The strength of the fluctuations in the NE quadrant reduces significantly while periodic fluctuations considerably increase in the NW quadrant.
- The strength of the fluctuations in all the quadrants reduces, but it is much more noticeable in the southern quadrants;
- The strength of periodic fluctuations with specific frequencies increases, which is much more noticeable in the NE and SE quadrants.
4.3. Analysis of the Conic Couplers Effect
5. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| CCC | Conventional continuous casting |
| CO2 | Carbon dioxide |
| ESP | Endless strip production |
| FB | Flat-bottom SEN |
| FBMO | Flat-bottom SEN with moderate obstruction |
| FBNO | Flat-bottom SEN with no obstruction |
| FBSO | Flat-bottom SEN with severe obstruction |
| NE | Northeast |
| NW | Northwest |
| PIV | Particle image velocimetry |
| PLA | Polylactic acid |
| PSD | Power spectral density |
| PVC | Polyvinyl chloride |
| SE | Southeast |
| SEN | Submerged entry nozzle |
| SGV | Sliding-gate valve |
| SPH | Smoothed particle hydrodynamics |
| SR | Stopper rod |
| SW | Southwest |
| TSC | Thin slab caster |
| WB | Well-bottom SEN |
| WBMO | Well-bottom SEN with moderate obstruction |
| WBNO | Well-bottom SEN with no obstruction |
| WBSO | Well-bottom SEN with severe obstruction |
References
- Birat, J.-P. Society, Materials, and the Environment: The Case of Steel. Metals 2020, 10, 331. [Google Scholar] [CrossRef]
- Holappa, L. A General Vision for Reduction of Energy Consumption and CO2 Emissions from the Steel Industry. Metals 2020, 10, 1117. [Google Scholar] [CrossRef]
- Holappa, L. Challenges and Prospects of Steelmaking towards the Year 2050. Metals 2021, 11, 1978. [Google Scholar] [CrossRef]
- Raabe, D. The Materials Science behind Sustainable Metals and Alloys. Chem. Rev. 2023, 123, 2436–2608. [Google Scholar] [CrossRef]
- Mousa, E.; Wang, C.; Riesbeck, J.; Larsson, M. Biomass Applications in Iron and Steel Industry: An Overview of Challenges and Opportunities. Renew. Sustain. Energy Rev. 2016, 65, 1247–1266. [Google Scholar] [CrossRef]
- Cemernek, D.; Cemernek, S.; Gursch, H.; Pandeshwar, A.; Leitner, T.; Berger, M.; Klösch, G.; Kern, R. Machine Learning in Continuous Casting of Steel: A State-of-the-Art Survey. J. Intell. Manuf. 2022, 33, 1561–1579. [Google Scholar] [CrossRef]
- Merten, D.C.; Hütt, M.-T.; Uygun, Y. Effect of Slab Width on Choice of Appropriate Casting Speed in Steel Production. J. Iron Steel Res. Int. 2022, 29, 71–79. [Google Scholar] [CrossRef]
- Guthrie, R.I.L.; Isac, M.M. Continuous Casting Practices for Steel: Past, Present and Future. Metals 2022, 12, 862. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, L. Transient Fluid Flow Phenomena during Continuous Casting: Part I—Cast Start. ISIJ Int. 2010, 50, 1777–1782. [Google Scholar] [CrossRef]
- Zhang, Q.-Y.; Wang, X.-H. Numerical Simulation of Influence of Casting Speed Variation on Surface Fluctuation of Molten Steel in Mold. J. Iron Steel Res. Int. 2010, 17, 15–19. [Google Scholar] [CrossRef]
- Kubo, N.; Kubota, J.; Ishii, T. Simulation of Sliding Nozzle Gate Movements for Steel Continuous Casting. ISIJ Int. 2001, 41, 1221–1228. [Google Scholar] [CrossRef]
- Kalter, R.; Tummers, M.J.; Wefers Bettink, J.B.; Righolt, B.W.; Kenjereš, S.; Kleijn, C.R. Aspect Ratio Effects on Fluid Flow Fluctuations in Rectangular Cavities. Metall. Mater. Trans. B 2014, 45, 2186–2193. [Google Scholar] [CrossRef]
- Du, F.; Li, T.; Zeng, Y.; Zhang, K. Influence of Nozzle Design on Flow Characteristic in the Continuous Casting Machinery. Coatings 2022, 12, 631. [Google Scholar] [CrossRef]
- Sambasivam, R. Clogging Resistant Submerged Entry Nozzle Design through Mathematical Modelling. Ironmak. Steelmak. 2006, 33, 439–453. [Google Scholar] [CrossRef]
- Chaudhary, R.; Lee, G.-G.; Thomas, B.G.; Kim, S.-H. Transient Mold Fluid Flow with Well- and Mountain-Bottom Nozzles in Continuous Casting of Steel. Metall. Mater. Trans. B 2008, 39, 870–884. [Google Scholar] [CrossRef]
- Chatterjee, D. CFD Model Study of a New Four-Port Submerged Entry Nozzle for Decreasing the Turbulence in Slab Casting Mold. ISRN Metall. 2013, 2013, 981597. [Google Scholar] [CrossRef]
- Srinivas, P.S.; Singh, A.; Korath, J.M.; Jana, A.K. A Water-Model Experimental Study of Vortex Characteristics Due to Nozzle Clogging in Slab Caster Mould. Ironmak. Steelmak. 2017, 44, 473–485. [Google Scholar] [CrossRef]
- Cho, S.-M.; Thomas, B.G. Electromagnetic Forces in Continuous Casting of Steel Slabs. Metals 2019, 9, 471. [Google Scholar] [CrossRef]
- Bao, Y.; Li, Z.; Zhang, L.; Wu, J.; Ma, D.; Jia, F. Asymmetric Flow Control in a Slab Mold through a New Type of Electromagnetic Field Arrangement. Processes 2021, 9, 1988. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, L.; Bao, Y.; Ma, D.; Wang, E. Influence of the Vertical Pole Parameters on Molten Steel Flow and Meniscus Behavior in a FAC-EMBr Controlled Mold. Metall. Mater. Trans. B 2022, 53, 938–953. [Google Scholar] [CrossRef]
- Schurmann, D.; Glavinić, I.; Willers, B.; Timmel, K.; Eckert, S. Impact of the Electromagnetic Brake Position on the Flow Structure in a Slab Continuous Casting Mold: An Experimental Parameter Study. Metall. Mater. Trans. B 2020, 51, 61–78. [Google Scholar] [CrossRef]
- Kharicha, A.; Vakhrushev, A.; Karimi-Sibaki, E.; Wu, M.; Ludwig, A. Reverse Flows and Flattening of a Submerged Jet under the Action of a Transverse Magnetic Field. Phys. Rev. Fluids 2021, 6, 123701. [Google Scholar] [CrossRef]
- Vakhrushev, A.; Kharicha, A.; Karimi-Sibaki, E.; Wu, M.; Ludwig, A.; Nitzl, G.; Tang, Y.; Hackl, G.; Watzinger, J.; Eckert, S. Generation of Reverse Meniscus Flow by Applying an Electromagnetic Brake. Metall. Mater. Trans. B 2021, 52, 3193–3207. [Google Scholar] [CrossRef]
- Zhang, X.-W.; Jin, X.-L.; Wang, Y.; Deng, K.; Ren, Z.-M. Comparison of Standard k-ε Model and RSM on Three Dimensional Turbulent Flow in the SEN of Slab Continuous Caster Controlled by Slide Gate. ISIJ Int. 2011, 51, 581–587. [Google Scholar] [CrossRef]
- Gursoy, K.A.; Yavuz, M.M. Effect of Flow Rate Controllers and Their Opening Levels on Liquid Steel Flow in Continuous Casting Mold. ISIJ Int. 2016, 56, 554–563. [Google Scholar] [CrossRef]
- Thumfart, M.; Hackl, G.; Fellner, W. Water Model Experiments on the Influence of Phase Distribution in the Submerged Entry Nozzle Considering Varying Operating Conditions. Steel Res. Int. 2022, 93, 2100824. [Google Scholar] [CrossRef]
- Bai, H.; Thomas, B.G. Turbulent Flow of Liquid Steel and Argon Bubbles in Slide-Gate Tundish Nozzles: Part II. Effect of Operation Conditions and Nozzle Design. Metall. Mater. Trans. B 2001, 32, 269–284. [Google Scholar] [CrossRef]
- Bai, H.; Thomas, B.G. Turbulent Flow of Liquid Steel and Argon Bubbles in Slide-Gate Tundish Nozzles: Part I. Model Development and Validation. Metall. Mater. Trans. B 2001, 32, 253–267. [Google Scholar] [CrossRef]
- Szekely, J.; Yadoya, R.T. The Physical and Mathematical Modeling of the Flow Field in the Mold Region in Continuous Casting Systems: Part I. Model Studies with Aqueous Systems. Metall. Trans. 1972, 3, 2673–2680. [Google Scholar] [CrossRef]
- Li, G.; Tu, L.; Wang, Q.; Zhang, X.; He, S. Fluid Flow in Continuous Casting Mold for Ultra-Wide Slab. Materials 2023, 16, 1135. [Google Scholar] [CrossRef]
- Mahapatra, R.B.; Brimacombe, J.K.; Samarasekera, I.V.; Walker, N.; Paterson, E.A.; Young, J.D. Mold Behavior and Its Influence on Quality in the Continuous Casting of Steel Slabs: Part I. Industrial Trials, Mold Temperature Measurements, and Mathematical Modeling. Metall. Trans. B 1991, 22, 861–874. [Google Scholar] [CrossRef]
- Shen, J.L.; Chen, D.F.; Xie, X.; Zhang, L.L.; Dong, Z.H.; Long, M.J.; Ruan, X.B. Influences of SEN Structures on Flow Characters, Temperature Field and Shell Distribution in 420 Mm Continuous Casting Mould. Ironmak. Steelmak. 2013, 40, 263–275. [Google Scholar] [CrossRef]
- Cai, C.; Shen, M.; Ji, K.; Zhang, Z.; Liu, Y. Research on the Influence of the Inner Wall Structure of the Continuous Casting Submerged Nozzle on the Stream of Molten Steel. Trans. Indian Inst. Met. 2022, 75, 613–624. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, S.; Cai, K.; Li, J.; Wan, X.; Thomas, B.G. Investigation of Fluid Flow and Steel Cleanliness in the Continuous Casting Strand. Metall. Mater. Trans. B 2007, 38, 63–83. [Google Scholar] [CrossRef]
- Najjar, F.M.; Thomas, B.G.; Hershey, D.E. Numerical Study of Steady Turbulent Flow through Bifurcated Nozzles in Continuous Casting. Metall. Mater. Trans. B 1995, 26, 749–765. [Google Scholar] [CrossRef]
- Gupta, D.; Lahiri, A.K. Water Modelling Study of the Jet Characteristics in a Continuous Casting Mould. Steel Res. Int. 1992, 63, 201–204. [Google Scholar] [CrossRef]
- Zhang, X.-G.; Zhang, W.-X.; Jin, J.-Z.; Evans, J.W. Flow of Steel in Mold Region During Continuous Casting. J. Iron Steel Res. Int. 2007, 14, 30–35. [Google Scholar] [CrossRef]
- Mohammadi-Ghaleni, M.; Asle Zaeem, M.; Smith, J.D.; O’Malley, R. Computational Fluid Dynamics Study of Molten Steel Flow Patterns and Particle–Wall Interactions Inside a Slide-Gate Nozzle by a Hybrid Turbulent Model. Metall. Mater. Trans. B 2016, 47, 3056–3065. [Google Scholar] [CrossRef]
- Lu, H.; Li, B.; Li, J.; Zhong, Y.; Ren, Z.; Lei, Z. Numerical Simulation of In-Mold Electromagnetic Stirring on Slide Gate Caused Bias Flow and Solidification in Slab Continuous Casting. ISIJ Int. 2021, 61, 1860–1871. [Google Scholar] [CrossRef]
- Yang, H.; Olia, H.; Thomas, B.G. Modeling Air Aspiration in Steel Continuous Casting Slide-Gate Nozzles. Metals 2021, 11, 116. [Google Scholar] [CrossRef]
- Chen, K.K.; Rowley, C.W.; Stone, H.A. Vortex Breakdown, Linear Global Instability and Sensitivity of Pipe Bifurcation Flows. J. Fluid Mech. 2017, 815, 257–294. [Google Scholar] [CrossRef]
- Chen, K.K.; Rowley, C.W.; Stone, H.A. Vortex Dynamics in a Pipe T-Junction: Recirculation and Sensitivity. Phys. Fluids 2015, 27, 034107. [Google Scholar] [CrossRef]
- Real, C.; Miranda, R.; Vilchis, C.; Barron, M.; Hoyos, L.; Gonzalez, J. Transient Internal Flow Characterization of a Bifurcated Submerged Entry Nozzle. ISIJ Int. 2006, 46, 1183–1191. [Google Scholar] [CrossRef]
- Real-Ramirez, C.A.; Carvajal-Mariscal, I.; Sanchez-Silva, F.; Cervantes-de-la-Torre, F.; Diaz-Montes, J.; Gonzalez-Trejo, J. Three-Dimensional Flow Behavior Inside the Submerged Entry Nozzle. Metall. Mater. Trans. B 2018, 49, 1644–1657. [Google Scholar] [CrossRef]
- Gonzalez-Trejo, J.; Real-Ramirez, C.A.; Miranda-Tello, J.R.; Gabbasov, R.; Carvajal-Mariscal, I.; Sanchez-Silva, F.; Cervantes-de-la-Torre, F. Influence of the Submerged Entry Nozzle’s Bottom Well on the Characteristics of Its Exit Jets. Metals 2021, 11, 398. [Google Scholar] [CrossRef]
- Gonzalez-Trejo, J.; Real-Ramirez, C.A.; Carvajal-Mariscal, I.; Sanchez-Silva, F.; Cervantes-De-La-Torre, F.; Miranda-Tello, R.; Gabbasov, R. Hydrodynamic Analysis of the Flow inside the Submerged Entry Nozzle. Math. Probl. Eng. 2020, 2020, 6267472. [Google Scholar] [CrossRef]
- Javurek, M.; Wincor, R. Bubbly Mold Flow in Continuous Casting: Comparison of Numerical Flow Simulations with Water Model Measurements. Steel Res. Int. 2020, 91, 2000415. [Google Scholar] [CrossRef]
- American Water Works Association. ANSI/AWWA C701-15: Cold-Water Meters—Turbine Type, for Customer Service; American Water Works Association: Denver, CO, USA, 2015. [Google Scholar]
- Real-Ramirez, C.A.; Carvajal-Mariscal, I.; Gonzalez-Trejo, J.; Miranda-Tello, R.; Gabbasov, R.; Sanchez-Silva, F.; Cervantes-de-la-Torre, F. Visualization and Measurement of Turbulent Flow inside a SEN and off the Ports. Rev. Mex. Fis. 2021, 67, 1–10. [Google Scholar] [CrossRef]
- Hérault, A.; Bilotta, G.; Dalrymple, R.A. SPH on GPU with CUDA. J. Hydraul. Res. 2010, 48, 74–79. [Google Scholar] [CrossRef]
- Gabbasov, R.; González-Trejo, J.; Real-Ramírez, C.A.; Molina, M.M.; la Torre, F.C. Evaluation of GPUSPH Code for Simulations of Fluid Injection Through Submerged Entry Nozzle. In Proceedings of the 10th International Conference on Supercomputing in Mexico, Monterrey, Mexico, 25–29 March 2019; Springer International Publishing: Cham, Switzerland, 2019; pp. 218–226. [Google Scholar]




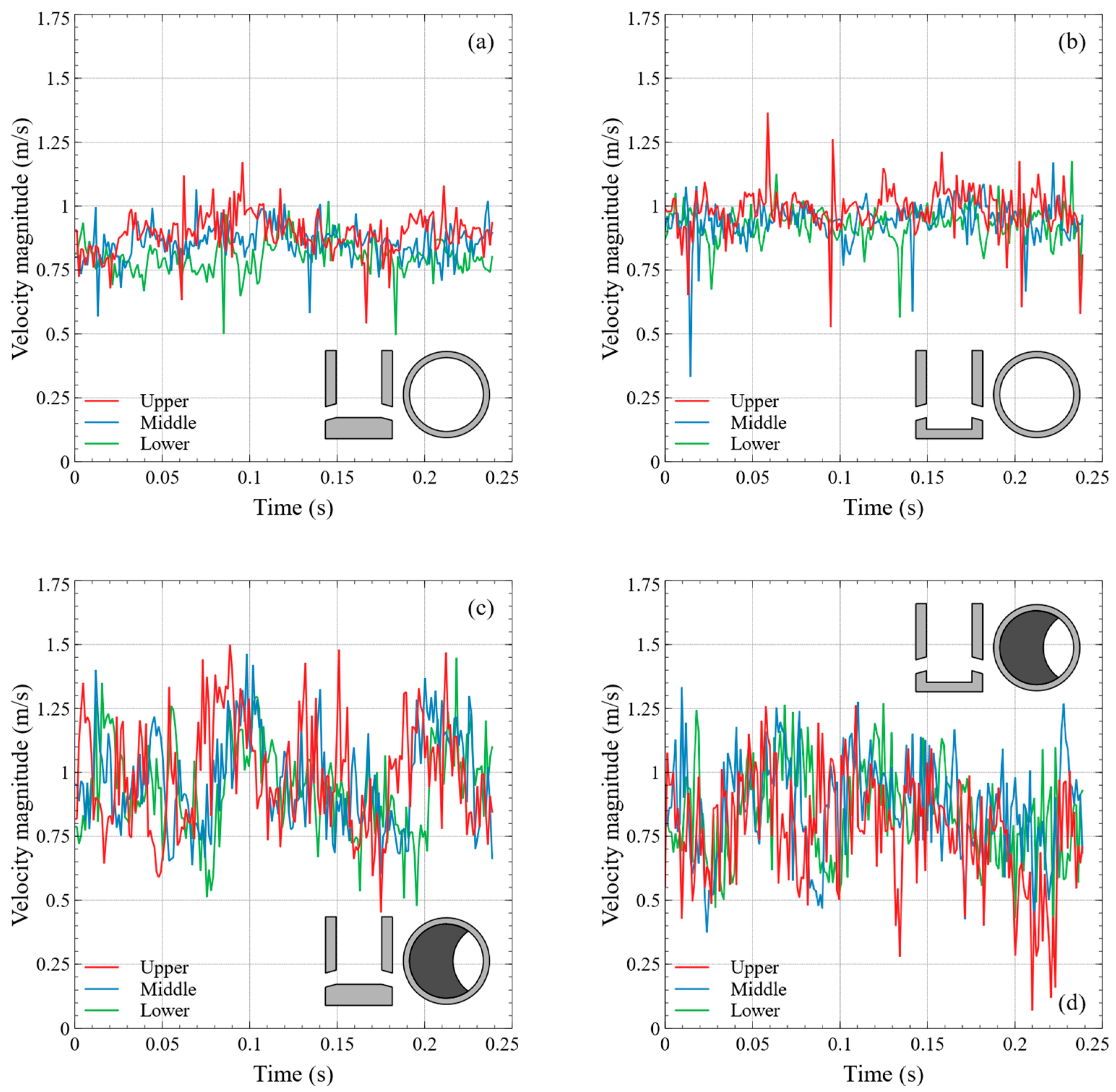
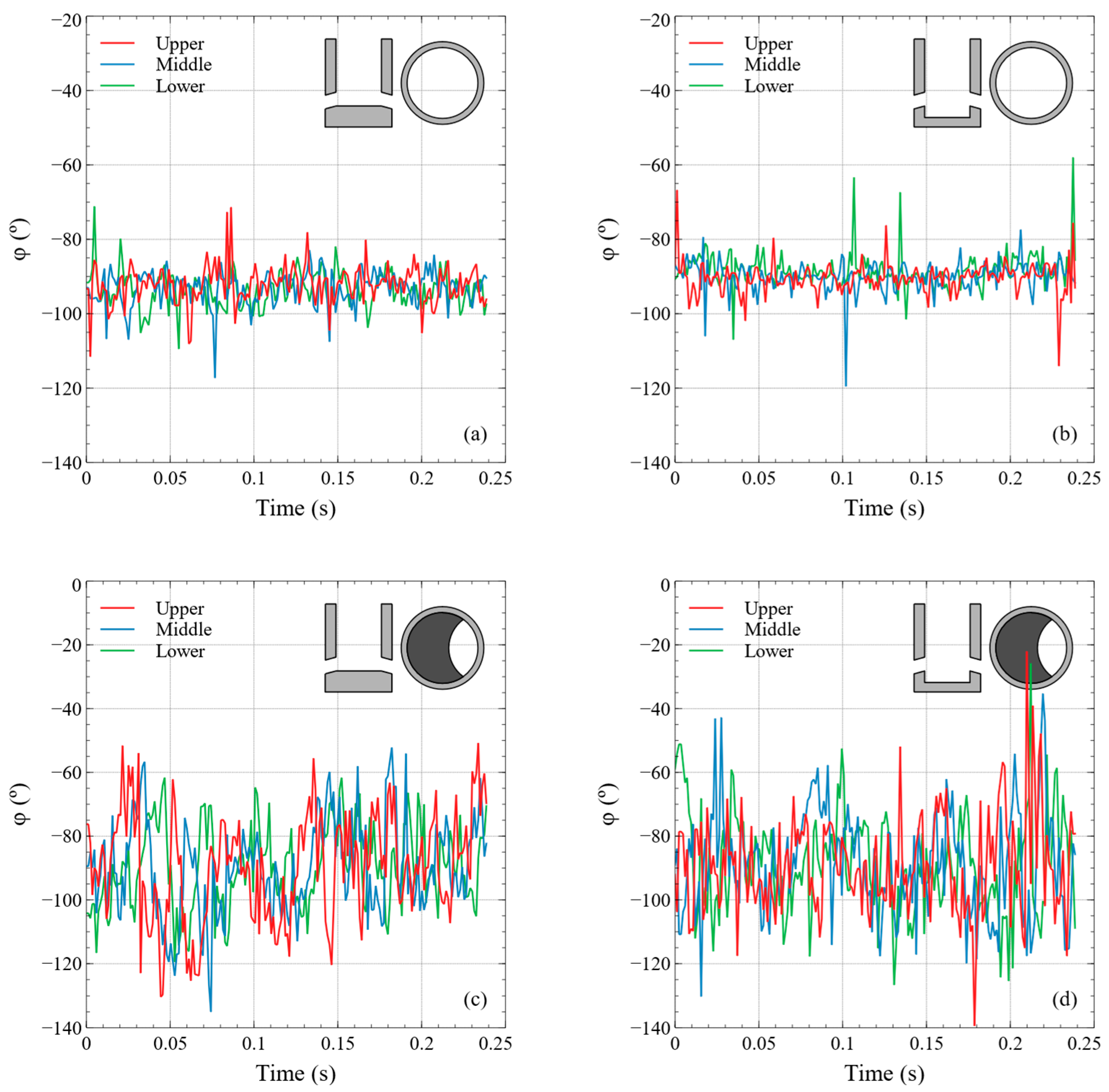







| Property | Measure Location | SEN Configuration | |||
|---|---|---|---|---|---|
| FBNO | WBNO | FBSO | WBSO | ||
| (m/s) | Upper | 0.8933 | 0.9890 | 0.9841 | 0.7739 |
| Middle | 0.8603 | 0.9706 | 0.9427 | 0.8660 | |
| Lower | 0.8027 | 0.9407 | 0.9283 | 0.8384 | |
| (m/s) | Upper | 0.0797 | 0.2126 | 0.0934 | 0.2190 |
| Middle | 0.0691 | 0.1830 | 0.0794 | 0.1923 | |
| Lower | 0.0672 | 0.1757 | 0.0664 | 0.1847 | |
| (°) | Upper | −92.1871 | −89.5019 | −90.4573 | −89.0357 |
| Middle | −93.1295 | −90.0346 | −90.0301 | −88.7205 | |
| Lower | −93.5627 | −89.7711 | −88.2866 | −88.7562 | |
| (°) | Upper | 4.9855 | 4.1513 | 16.6630 | 15.1172 |
| Middle | 4.5028 | 3.9837 | 14.9233 | 16.1136 | |
| Lower | 4.7685 | 4.6367 | 12.8194 | 15.6815 | |
| Quadrant | Statistic (L/min) | SEN Configuration | |||||
|---|---|---|---|---|---|---|---|
| FBNO | FBMO | FBSO | WBNO | WBMO | WBSO | ||
| NW | 3.602 | 3.557 | 3.565 | 3.555 | 3.666 | 3.641 | |
| 3.617 | 3.576 | 3.589 | 3.591 | 3.692 | 3.664 | ||
| 3.586 | 3.541 | 3.539 | 3.512 | 3.640 | 3.621 | ||
| SW | 3.844 | 3.857 | 3.861 | 3.876 | 3.895 | 3.917 | |
| 3.857 | 3.874 | 3.877 | 3.891 | 3.913 | 3.931 | ||
| 3.833 | 3.839 | 3.846 | 3.859 | 3.881 | 3.896 | ||
| SE | 3.854 | 3.859 | 3.863 | 3.873 | 3.865 | 3.861 | |
| 3.865 | 3.874 | 3.880 | 3.899 | 3.881 | 3.877 | ||
| 3.841 | 3.843 | 3.846 | 3.848 | 3.850 | 3.846 | ||
| NE | 3.700 | 3.727 | 3.711 | 3.696 | 3.574 | 3.581 | |
| 3.731 | 3.741 | 3.723 | 3.725 | 3.593 | 3.602 | ||
| 3.672 | 3.698 | 3.696 | 3.666 | 3.558 | 3.555 | ||
| Statistic (%) | SEN Configuration | |||||
|---|---|---|---|---|---|---|
| FBNO | FBMO | FBSO | WBNO | WBMO | WBSO | |
| 4.1 | 5.7 | 5.2 | 6.1 | 3.8 | 3.1 | |
| 0.8 | 0.9 | 0.9 | 1.0 | 1.6 | 2.2 | |
| 7.6 | 9.4 | 9.5 | 10.8 | 7.5 | 8.6 | |
| 5.2 | 4.8 | 5.0 | 6.4 | 9.1 | 9.0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzalez-Trejo, J.; Miranda-Tello, R.; Gabbasov, R.; Real-Ramirez, C.A.; Cervantes-de-la-Torre, F. Experimental Analysis of the Influence of the Sliding-Gate Valve on Submerged Entry Nozzle Outlet Jets. Fluids 2024, 9, 30. https://doi.org/10.3390/fluids9010030
Gonzalez-Trejo J, Miranda-Tello R, Gabbasov R, Real-Ramirez CA, Cervantes-de-la-Torre F. Experimental Analysis of the Influence of the Sliding-Gate Valve on Submerged Entry Nozzle Outlet Jets. Fluids. 2024; 9(1):30. https://doi.org/10.3390/fluids9010030
Chicago/Turabian StyleGonzalez-Trejo, Jesus, Raul Miranda-Tello, Ruslan Gabbasov, Cesar A. Real-Ramirez, and Francisco Cervantes-de-la-Torre. 2024. "Experimental Analysis of the Influence of the Sliding-Gate Valve on Submerged Entry Nozzle Outlet Jets" Fluids 9, no. 1: 30. https://doi.org/10.3390/fluids9010030
APA StyleGonzalez-Trejo, J., Miranda-Tello, R., Gabbasov, R., Real-Ramirez, C. A., & Cervantes-de-la-Torre, F. (2024). Experimental Analysis of the Influence of the Sliding-Gate Valve on Submerged Entry Nozzle Outlet Jets. Fluids, 9(1), 30. https://doi.org/10.3390/fluids9010030






