Computational Fluid Dynamics Modeling of Concrete Flows in Drilled Shafts
Abstract
:1. Introduction

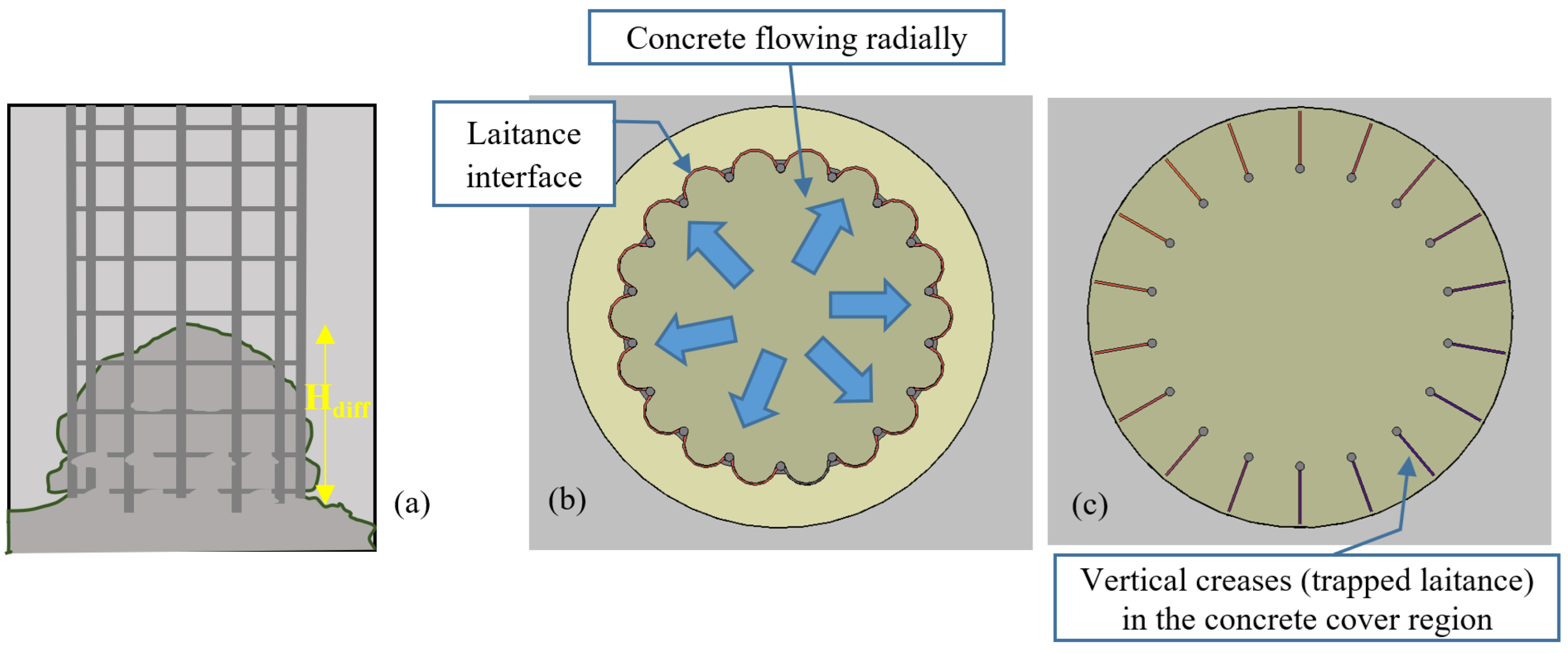
2. Governing Equations
2.1. Incompressible Navier-Stokes Equations
2.2. The Volume of Fluid Method
2.3. Surface Tension
2.4. Constitutive Model
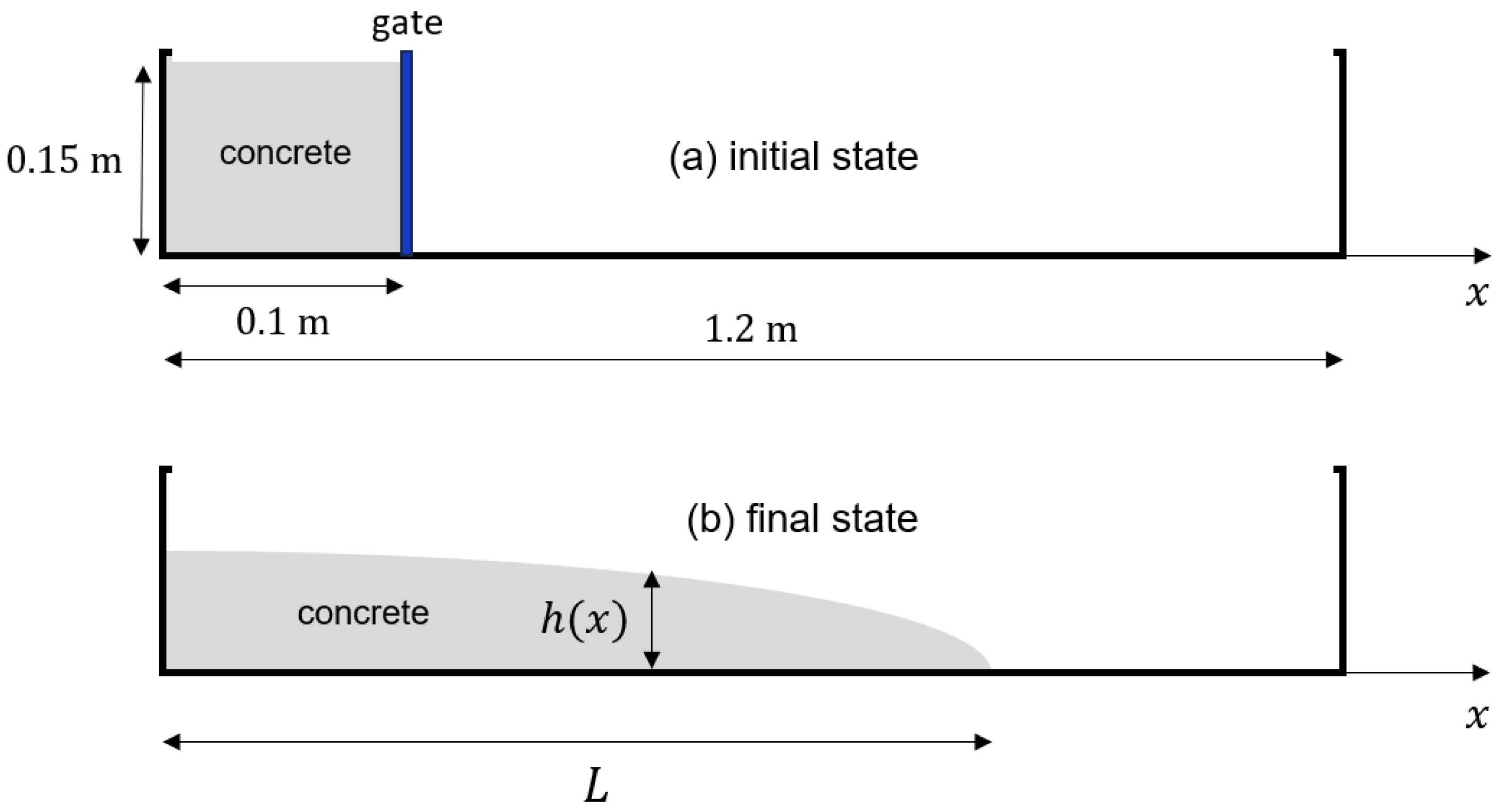
3. Computational Setup
3.1. Model Geometries
3.2. Boundary Conditions
3.3. Computational Grids
3.4. Material Properties
3.5. Numerical Methods and Computations
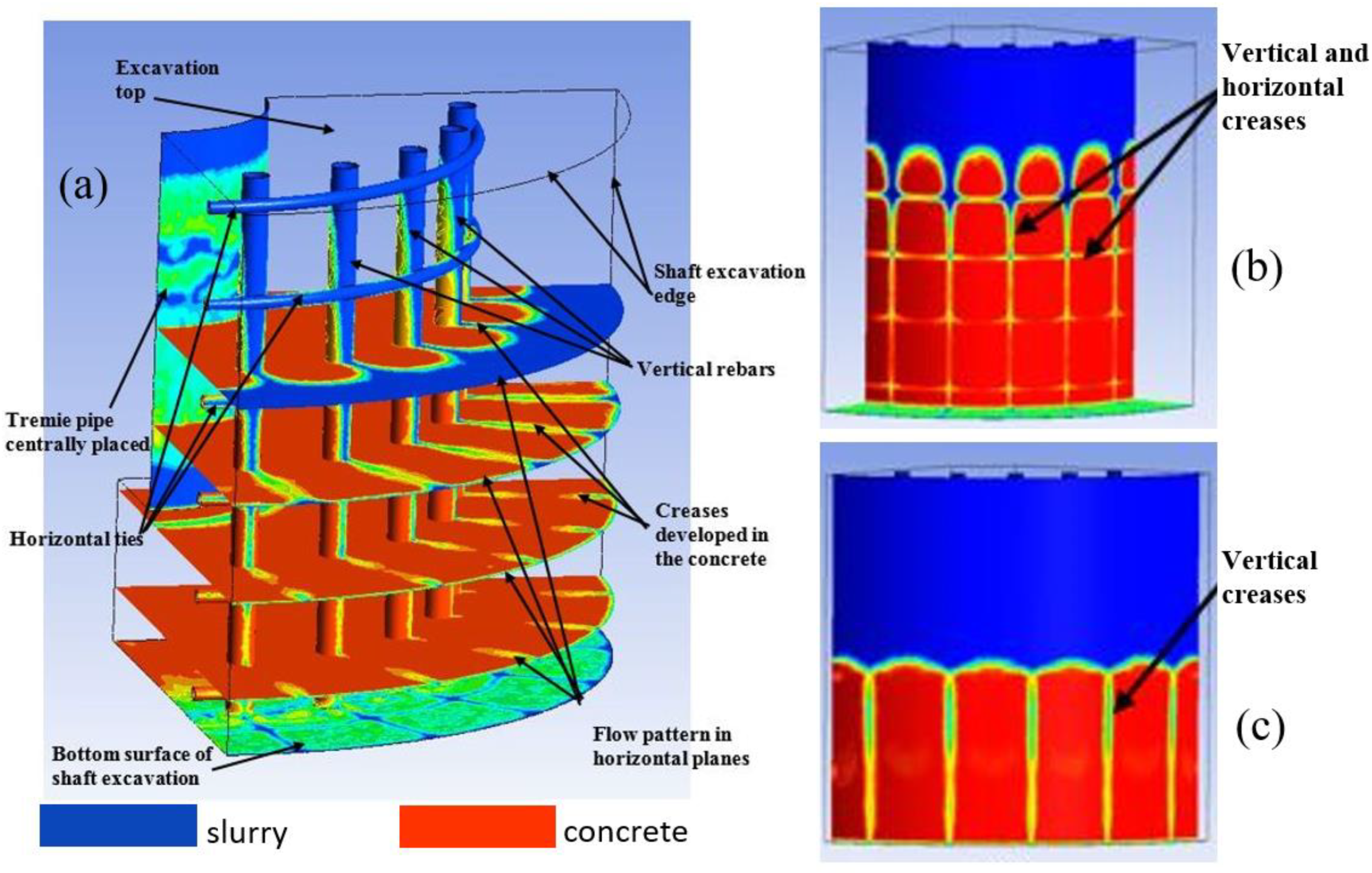
4. Results
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Concrete Rheology



References
- Brown, D.; Turner, J.; Castelli, R. Drilled Shafts: Construction Procedures and LRFD Design Methods; FHWA NHI-10-016, NHI COURSE NO. 132014 GEOTECHNICAL ENGINEERING CIRCULAR NO. 10; U.S. Department of Transportation Federal Highway Administration: Washington, DC, USA, 2010.
- Mullins, A.G.; Ashmawy, K.A. Factors Affecting Anomaly Formation in Drilled Shafts-Final Report; FDOT Report; University of South Florida: Tampa, FL, USA, 2005. [Google Scholar]
- Deese, G.; Mullins, G. Factors Affecting Concrete Flow in Drilled Shaft Construction. In Proceedings of the ADSC GEO3, GEO Construction Quality Assurance/Quality Control Conference, Dallas/Fort Worth, TX, USA, 6–9 November 2005; Bruce, D.A., Cadden, A.W., Eds.; 2005; pp. 144–155. [Google Scholar]
- Bowen, J. The Effects of Drilling Slurry on Reinforcement in Drilled Shaft Construction. Master’s Thesis, University of South Florida, Tampa, FL, USA, 2013. [Google Scholar]
- Beckhaus, K. (Ed.) EFFC/DFI Best Practice Guide to Tremie Concrete for Deep Foundations, 1st ed.; Deep Foundations Institute: Hawthorne, NJ, USA, 2016. [Google Scholar]
- Mullins, A.G. Development of Self Consolidating Mix Designs for Drilled Shafts; FDOT Report; University of South Florida: Tampa, FL, USA, 2005. [Google Scholar]
- Mullins, A.G.; Zayed, A.; Mobley, S.; Costello, K.; Jeyaraj, J.A.; Mee, T. Evaluation of Self Consolidating Concrete and Class IV Concrete Flow in Frilled Shafts; FDOT Report BDV 25-977-25; University of South Florida: Tampa, FL, USA, 2019. [Google Scholar]
- Gram, A.; Silfwerbrand, J. Numerical simulation of fresh SCC flow: Applications. Mater Struct. 2011, 44, 805–813. [Google Scholar] [CrossRef]
- Vasilic, K.; Gram, A.; Wallevik, J.E. Numerical Simulation of Fresh Concrete Flow: Insight and Challenges. RILEM Tech. Lett. 2019, 4, 57–66. [Google Scholar] [CrossRef]
- Roussel, N.; Gram, A. (Eds.) Simulation of Fresh Concrete Flow: State of the Art Report of the RILEM Technical Committee 222-SCF; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar]
- Vasilic, K.; Schmidt, W.; Kühne, H.C.; Haamkens, F.; Mechtcherine, V.; Roussel, N. Flow of fresh concrete through reinforced elements: Experimental validation of the porous analogy numerical method. Cem. Concr. Res. 2016, 88, 1–6. [Google Scholar] [CrossRef]
- ACI 237R-07, Emerging Technology Series, “Self-Consolidating Concrete”. Available online: https://rosap.ntl.bts.gov/view/dot/25610/dot_25610_DS1.pdf (accessed on 27 December 2023).
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A Continuum Method for Modeling Surface Tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Carreau, P.J. Rheological Equations from Molecular Network Theories. Trans. Soc. Rheol. 1972, 16, 99–127. [Google Scholar] [CrossRef]
- Planchard, D.C.; CSWP. SolidWorks 2015 Tutorial with Video Instruction; SDC Publications: Mission, KS, USA, 2014. [Google Scholar]
- Banfill, P.F.G. Rheology of Fresh Cement and Concrete. In Rheology Reviews; British Society of Rheology: England, UK, 2006; pp. 61–130. [Google Scholar]
- West, R.; Ryde, D.; Astle, M.; Bayer, W. CRC Chemistry and Physics Handbook, 70th ed.; CRC Press, Inc.: Boca Raton, FL, USA, 1989. [Google Scholar]
- Ansys Inc. “ANSYS Release Notes 18.2” August 2017, Ansys, Inc. Southpointe, 2600 ANSYS Drive, Canonburg, PA 15317. Available online: https://www.luis.uni-hannover.de/fileadmin/software-lizenzen/Ueberlassung/ANSYS18.2_ReleaseNotes.pdf (accessed on 27 December 2023).
- Jeyaraj, J.A. Numerical Modeling of Concrete Flow in Drilled Shaft. Doctoral Dissertation, University of South Florida, Tampa, FL, USA, 2018; 124p. [Google Scholar]
- Engler Faleiros, D.; van den Bos, W.; Botto, L.; Scarano, F. TU Delft COVID-app: A Tool to Democratize CFD Simulations for SARS-CoV-2 Infection Risk Analysi. Sci. Total Environ. 2022, 826, 154143. [Google Scholar] [CrossRef] [PubMed]



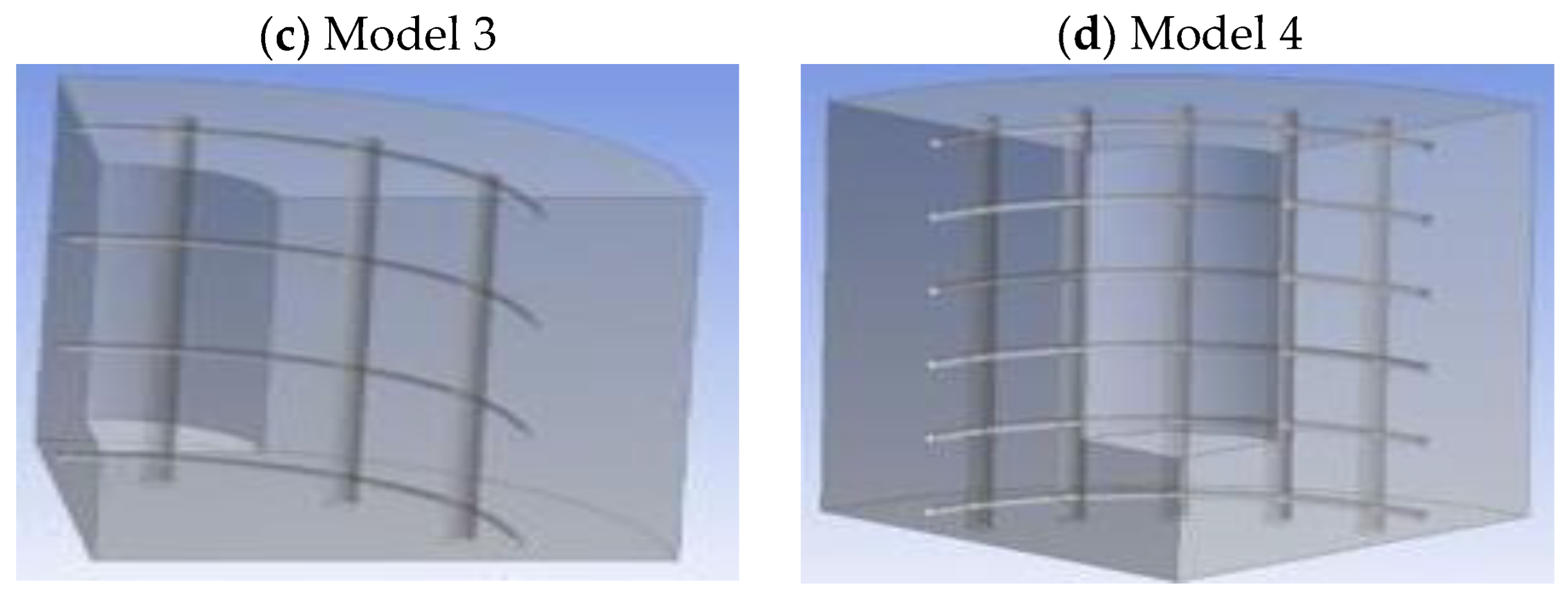

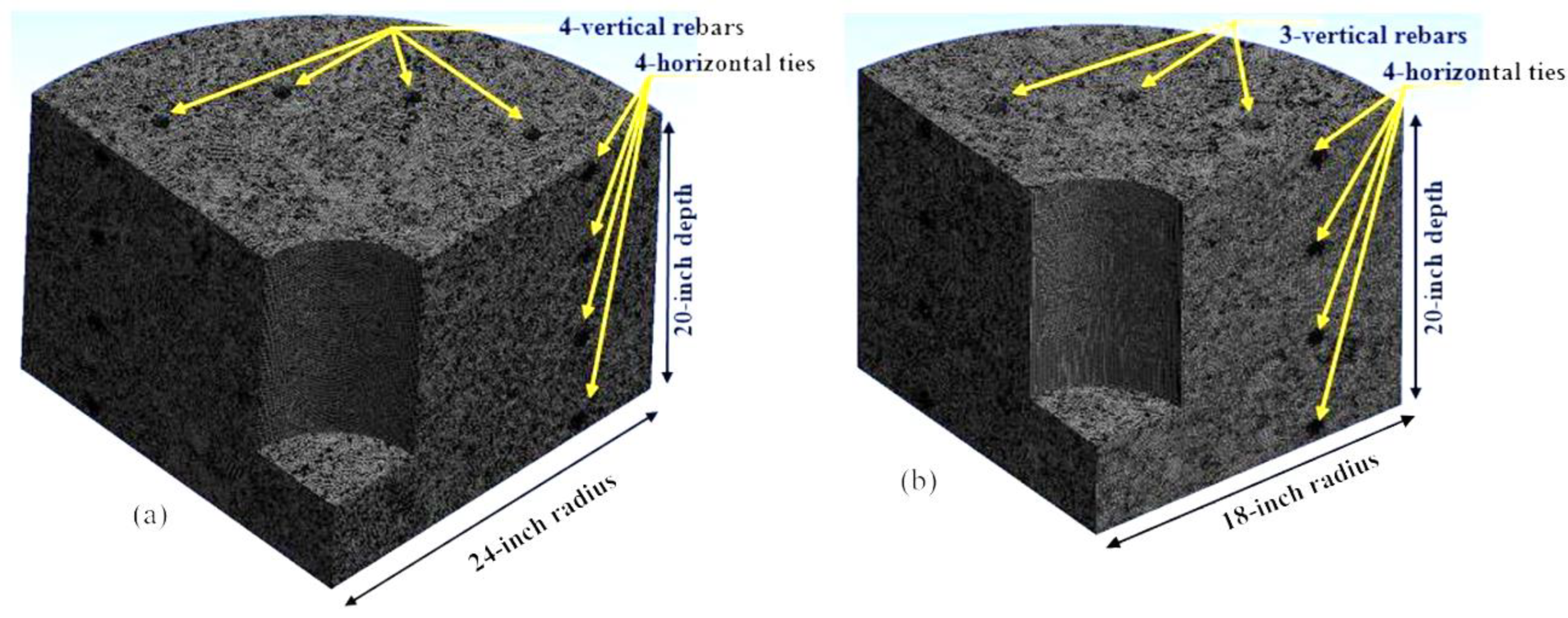


| Model | Shaft Size (Diameter) (in) | Tremie Size (Diameter) (in) | Vertical Rebars, Number and Spacing | Horizontal Ties, Number and Spacing | Cage Spacing (in) |
|---|---|---|---|---|---|
| 1 | 48 | 12 | 4 rebars at 7-inch spacing | 4 ties at 6-inch spacing | 9.2 |
| 2 | 48 | 12 | 8 rebars at 3.5-inch spacing | 6 ties at 3.5-inch spacing | 4.95 |
| 3 | 36 | 10 | 3 rebars at 6.3-inch spacing | 4 ties at 6-inch spacing | 8.7 |
| 4 | 36 | 10 | 5 rebars at 3.8-inch spacing | 6 ties at 3.5-inch spacing | 5.2 |
| Model | Mesh Size | Number of Grid Cells | Number of Grid Nodes | |
|---|---|---|---|---|
| Min. (in) | Max. (in) | |||
| 1 | 0.033 | 0.12 | 1,188,233 | 6,366,030 |
| 2 | 0.035 | 0.13 | 1,176,169 | 6,317,274 |
| 3 | 0.03 | 0.11 | 994,014 | 5,326,261 |
| 4 | 0.03 | 0.11 | 1,069,758 | 5,718,755 |
| Fluid | Density (kg/m3) | s) | |
|---|---|---|---|
| LVC | 2300 | 250 | 25 |
| NC | 2400 | 2500 | 100 |
| Slurry | 1150 | 0.5 | |
| Model | Inlet vel. (ft/s) | Outlet vel. (ft/s) | Cage Spacing (in) | Hdiff (in) with NC | Hdiff (in) with LVC |
|---|---|---|---|---|---|
| 1 | 17.7 | 1.15 | 9 | 4.0 | 0.75 |
| 2 | 17.7 | 1.15 | 5 | 10.75 | 1.0 |
| 3 | 25.6 | 2.07 | 9 | 4.50 | 0.75 |
| 4 | 25.6 | 2.07 | 5 | 12.50 | 1.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeyaraj, J.A.; Perez, A.; Zayed, A.; Mullins, A.G.; Tejada-Martinez, A.E. Computational Fluid Dynamics Modeling of Concrete Flows in Drilled Shafts. Fluids 2024, 9, 13. https://doi.org/10.3390/fluids9010013
Jeyaraj JA, Perez A, Zayed A, Mullins AG, Tejada-Martinez AE. Computational Fluid Dynamics Modeling of Concrete Flows in Drilled Shafts. Fluids. 2024; 9(1):13. https://doi.org/10.3390/fluids9010013
Chicago/Turabian StyleJeyaraj, Jesudoss Aservitham, Anthony Perez, Abla Zayed, Austin Gray Mullins, and Andres E. Tejada-Martinez. 2024. "Computational Fluid Dynamics Modeling of Concrete Flows in Drilled Shafts" Fluids 9, no. 1: 13. https://doi.org/10.3390/fluids9010013




