Trapped Solitary Waves in a Periodic External Force: A Numerical Investigation Using the Whitham Equation and the Sponge Layer Method
Abstract
:1. Introduction
2. Mathematical Formulation
3. Numerical Method
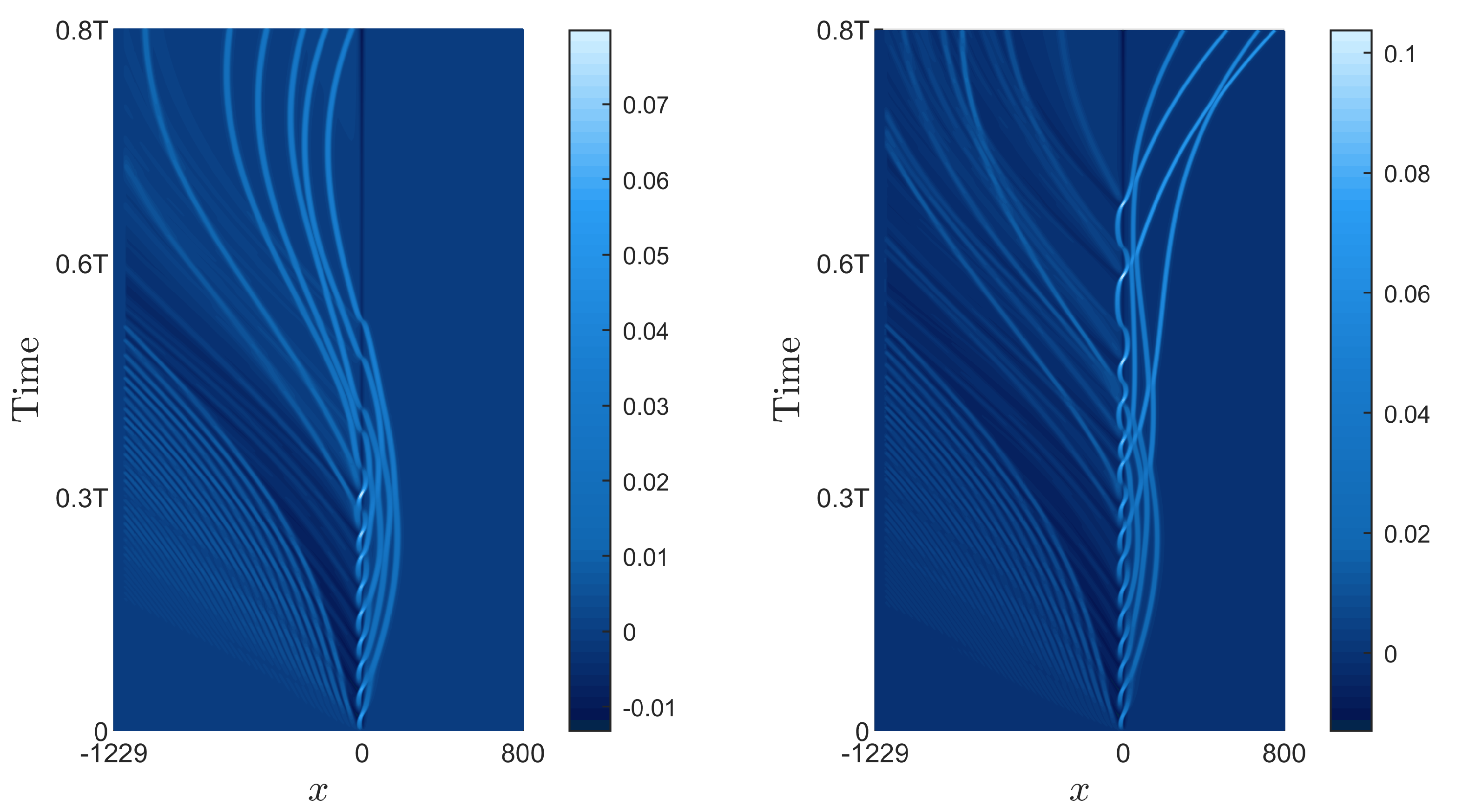
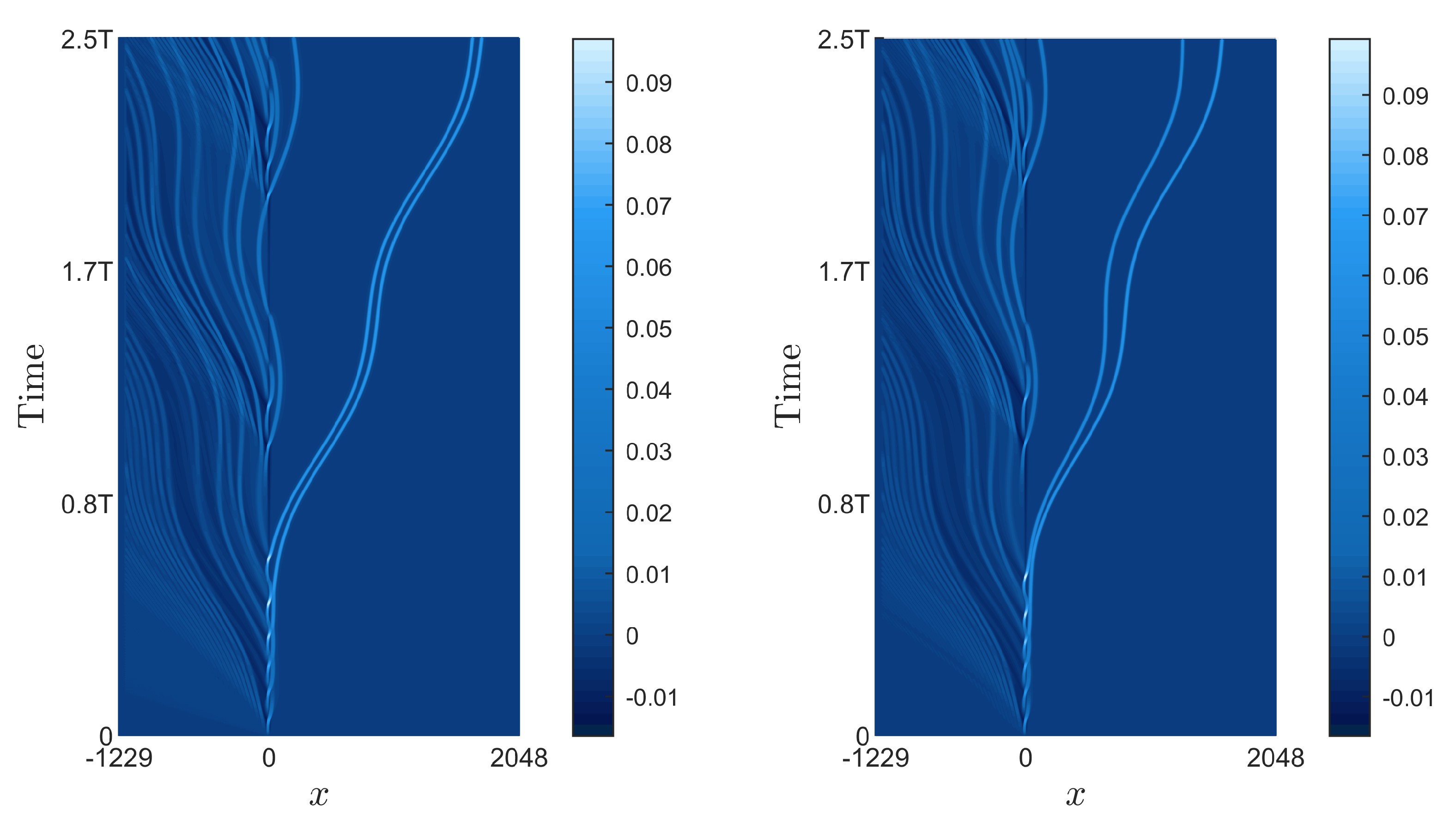
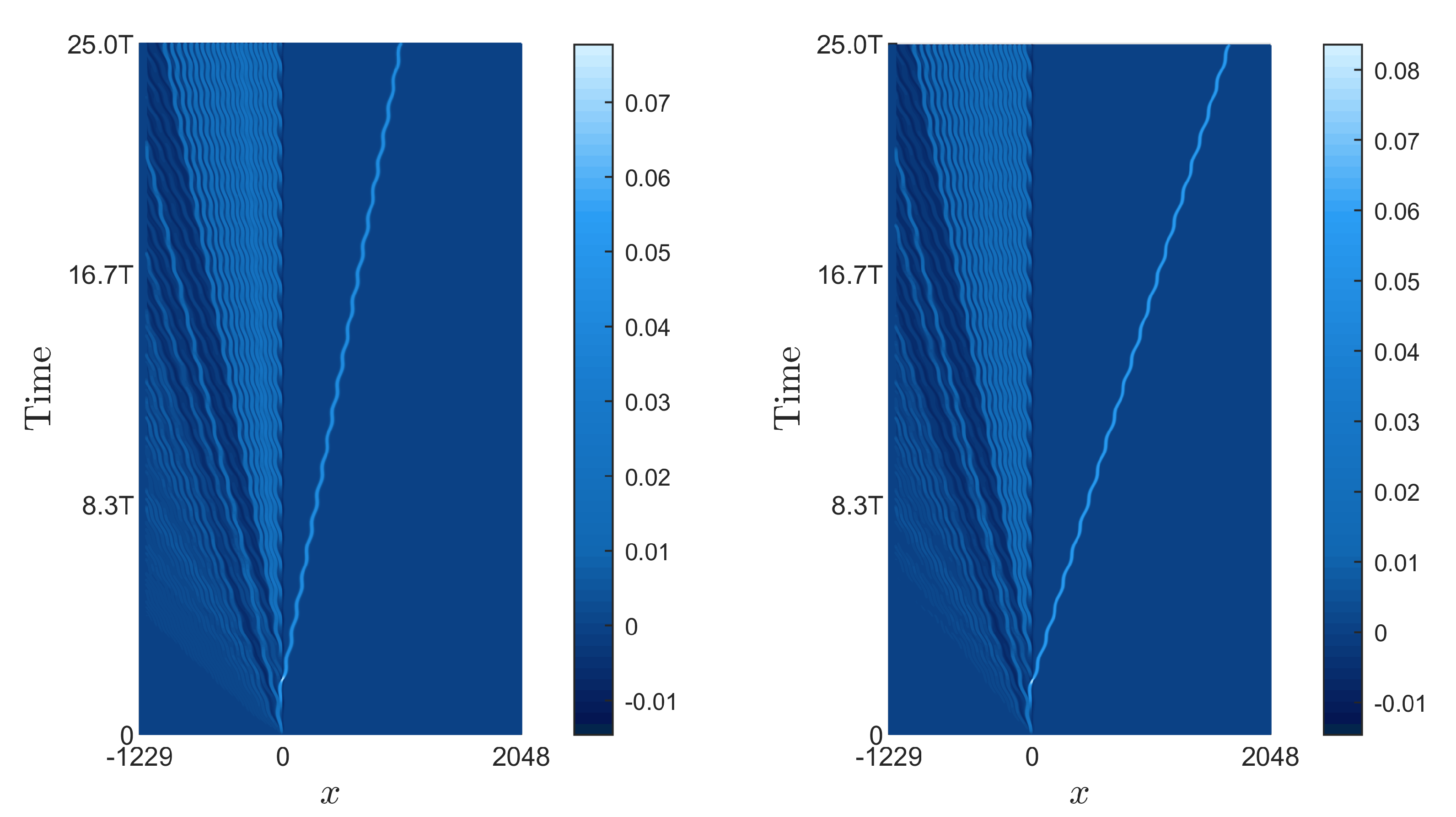
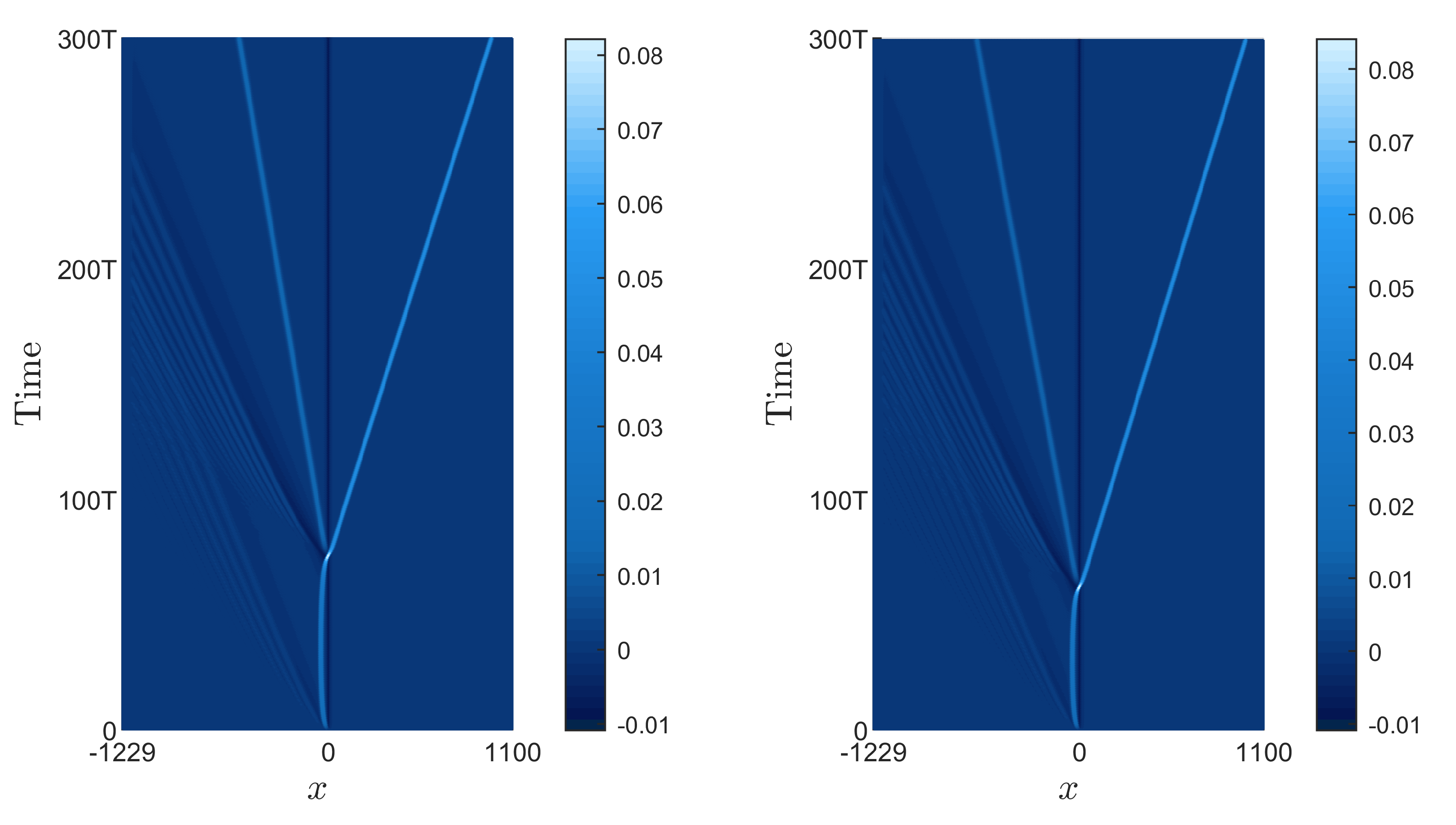
4. Results and Discussions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
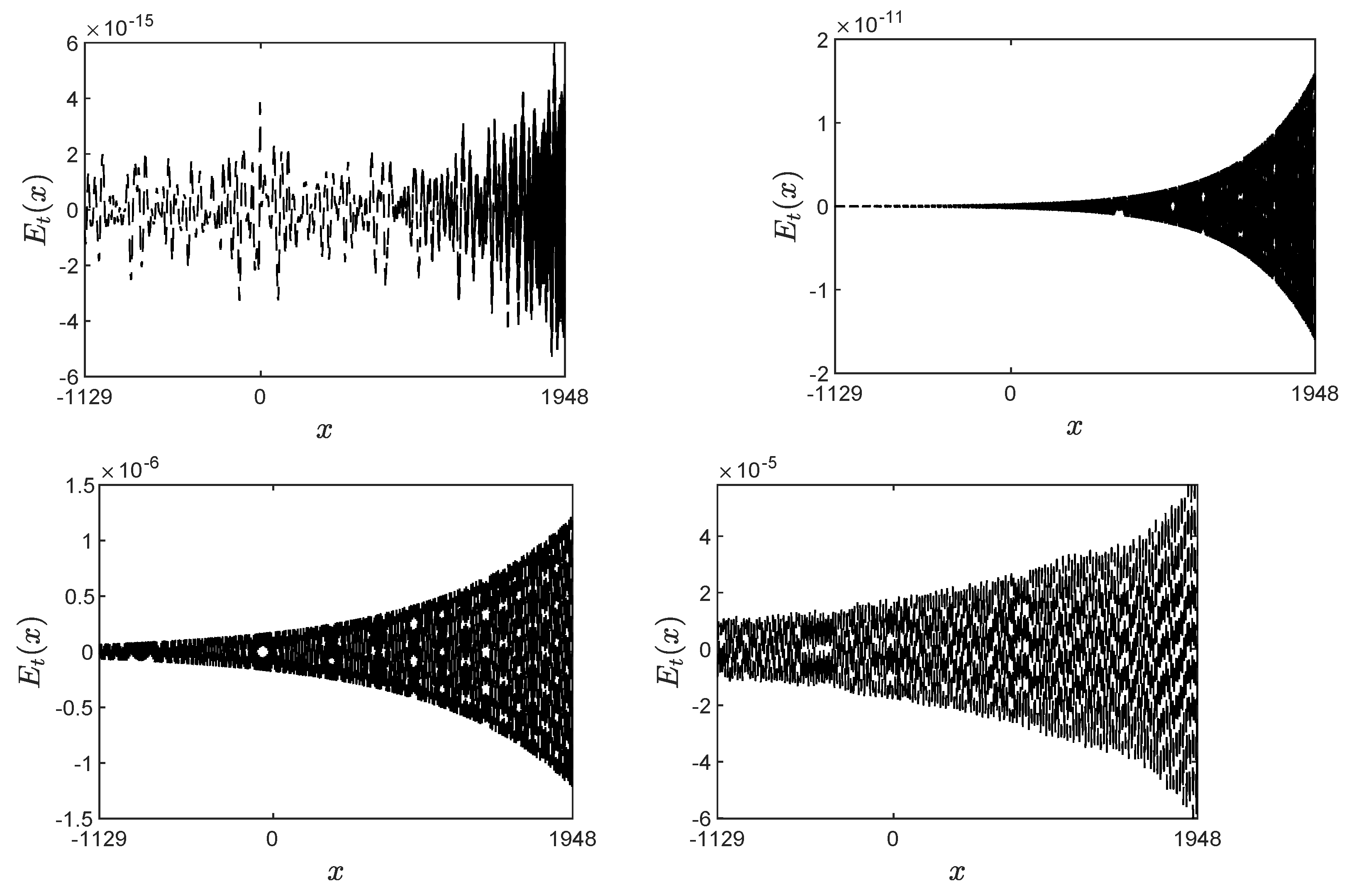
Appendix A. The Sponge Layer Effect
References
- Craik, A.D.D. The Origins of water Wave Theory. Annu. Rev. Fluid Mech. 2004, 36, 1–28. [Google Scholar] [CrossRef]
- Zabusky, N.J.; Kruskal, M.D. Interaction of solitons in a collisionless plasma and the recurrence of initial states. Phys. Rev. Lett. 1965, x15, 240. [Google Scholar] [CrossRef] [Green Version]
- Manukure, S.; Booker, T. A short overview of solitons and applications. Partial. Differ. Equations Appl. Math. 2021, 4, 100140. [Google Scholar] [CrossRef]
- Joseph, A. Investigating Seafloors and Oceans: From mud Volcanoes to Giant Squid; Elsevierl: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Baines, P. Topographic Effects in Stratified Flows; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Johnson, R.S. Models for the formation of a critical layer in water wave propagation. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2012, 370, 1638–1660. [Google Scholar] [CrossRef] [PubMed]
- Ermakov, A.; Stepanyants, Y. Soliton interaction with external forcing within the Korteweg-de Vries equation. Chaos 2019, 29, 013117. [Google Scholar] [CrossRef] [Green Version]
- Flamarion, M.V.; Ribeiro, R., Jr. Solitary water wave interactions for the Forced Korteweg-de Vries equation. Comp. Appl. Math. 2021, 40, 312. [Google Scholar] [CrossRef]
- Grimshaw, R.; Malewoong, M. Transcritical flow over two obstacles: Forced Korteweg-de Vries framework. J. Fluid Mech. 2016, 809, 918–940. [Google Scholar] [CrossRef]
- Grimshaw, R.; Malewoong, M. Transcritical flow over obstacles and holes: Forced Korteweg-de Vries framework. J. Fluid Mech. 2019, 881, 660–678. [Google Scholar] [CrossRef]
- Grimshaw, R.; Pelinovsky, E.; Tian, X. Interaction of a soliton with an external force. Physica D 1994, 77, 405–433. [Google Scholar] [CrossRef]
- Grimshaw, R.; Pelinovsky, E.; Sakov, P. Interaction of a soliton with an external force moving with variable speed. Stud. Appl. Math. 1996, 142, 433–464. [Google Scholar]
- Kim, H.; Choi, H. A study of wave trapping between two obstacles in the forced Korteweg-de Vries equation. J. Eng. Math. 2018, 108, 197–208. [Google Scholar] [CrossRef]
- Lee, S.; Whang, S. Trapped supercritical waves for the forced KdV equation with two bumps. Appl. Math. Model. 2015, 39, 2649–2660. [Google Scholar] [CrossRef]
- Lee, S. Dynamics of trapped solitons for the forced KdV equation. Symmetry 2018, 10, 129. [Google Scholar] [CrossRef] [Green Version]
- Malomed, B.A. Emission of radiation by a KdV soliton in a periodic forcing. Phys. Lett. A 1993, 172, 373–377. [Google Scholar] [CrossRef]
- Flamarion, M.V. Generation of trapped depression solitons in gravity-capillary flows over an obstacle. Comp. Appl. Math. 2022, 41, 31. [Google Scholar] [CrossRef]
- Flamarion, M.V.; Ribeiro, R., Jr. Gravity-capillary flows over obstacles for the fifth-order forced Korteweg-de Vries equation. J. Eng. Math. 2021, 129, 1–17. [Google Scholar] [CrossRef]
- Flamarion, M.V.; Pelinovsky, E. Solitary wave interactions with an external periodic force: The extended Korteweg-de Vries framework. Mathematics 2022, 10, 4538. [Google Scholar] [CrossRef]
- Flamarion, M.V.; Pelinovsky, E. Soliton interactions with an external forcing: The modified Korteweg–de Vries framework. Chaos Solitons Fractals 2022, 165, 112889. [Google Scholar] [CrossRef]
- Grimshaw, R.; Pelinovsky, E. Interaction of a soliton with an external force in the extended Korteweg-de Vries equation. Int. J. Bifurcat. Chaos 2002, 12, 2409–2419. [Google Scholar] [CrossRef]
- Pelinovsky, E. Autoresonance Processes under Interaction of Solitary Waves with the External Fields. Int. J. Fluid Mech. Res. 2002, 30, 493–501. [Google Scholar] [CrossRef]
- Whitham, G.B. Linear and Nonlinear Waves; John Wiley & Sons Inc: New York, NY, USA, 1974. [Google Scholar]
- Whitham, G.B. Variational methods and applications to water waves. Phil. Trans. R. Soc. A 1967, 229, 6–25. [Google Scholar]
- Ehrnström, M.; Kalisch, H. Traveling waves for the Whitham equation. Differ. Integral Equ. 2009, 22, 1193–1210. [Google Scholar] [CrossRef]
- Ehrnström, M.; Wahlén, E. On Whitham’s conjecture of a highest cusped wave for a nonlocal dispersive equation. Ann. L’Institut Henri Poincaré C 2019, 36, 769–799. [Google Scholar]
- Hur, V.M.; Pandey, A.K. Modulational instability in a full-dispersion shallow water model. Stud. Appl. Math. 2019, 142, 3–47. [Google Scholar] [CrossRef] [Green Version]
- Sanford, N.; Kodama, K.; Clauss, G.F.; Onorato, M. Stability of traveling wave solutions to the Whitham equation. Phys. Lett. A 2014, 378, 2100–2107. [Google Scholar] [CrossRef]
- Klein, C.; Linares, F.; Pilod, D.; Saut, J.C. On Whitham and Related Equations. Stud. Appl. Math. 2018, 140, 133–177. [Google Scholar] [CrossRef] [Green Version]
- Carter, J.D.; Kalisch, H.; Kharif, C.; Abid, M. The cubic vortical Whitham equation. arXiv 2021, arXiv:2110.02072v1. [Google Scholar] [CrossRef]
- Grimshaw, R.; Malomed, B.A.; Tian, X. Dynamics of a KdV soliton due to periodic forcing. Phys. Lett. A 1993, 179, 291–298. [Google Scholar] [CrossRef]
- Flamarion, M.V. Trapped waves generated by an accelerated moving disturbance for the Whitham equation. Partial. Differ. Equ. Appl. Math. 2022, 5, 100356. [Google Scholar] [CrossRef]
- Grimshaw, R.; Pelinovsky, E.; Talipova, T.; Kurkina, O. Internal solitary waves: Propagation, deformation and disintegration. Nonlin Processes. Geophys. 2010, 17, 633–649. [Google Scholar] [CrossRef] [Green Version]
- Chen, M. Equations for bi-directional waves over an uneven bottom. Math. Comput. Simul. 2003, 62, 3–9. [Google Scholar] [CrossRef]
- Aceves-Sánchez, P.; Minzoni, A.A.; Panayotaros, P. Numerical study of a nonlocal model for water- waves with variable depth. Wave Motion. 2013, 50, 80–93. [Google Scholar] [CrossRef]
- Vargas-Magaña, R.M.; Marchant, T.R.; Smyth, N.F. Numerical and analytical study of undular bores governed by the full water wave equations and bidirectional Whitham-Boussinesq equations. Phys. Fluids 2021, 33, 067105. [Google Scholar] [CrossRef]
- Carter, J.D. Bidirectional Whitham equations as models of waves on shallow water. Wave Motion 2018, 82, 5161. [Google Scholar] [CrossRef]
- Flamarion, M.V.; Milewski, P.A.; Nachbin, A. Rotational waves generated by current-topography interaction. Stud. Appl. Math. 2019, 142, 433–464. [Google Scholar] [CrossRef]
- Milewski, P.A. The Forced Korteweg-de Vries equation as a model for waves generated by topography. CUBO Math. J. 2004, 6, 33–51. [Google Scholar]
- Trefethen, L.N. Spectral Methods in MATLAB; SIAM: Philadelphia, PA, USA, 2001. [Google Scholar]
- Alias, A.; Ismail, N.N.A.N.; Harun, F.N. Pseudospecteral method with linear damping effect and de-aliasing technique in solving nonlinear PDEs. J. Physics Conf. Ser. 2019, 1366, 012009. [Google Scholar] [CrossRef] [Green Version]

| N | Equation | ||
|---|---|---|---|
| fKdV | |||
| Whitham | |||
| fKdV | |||
| Whitham | |||
| fKdV | |||
| Whitham |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Flamarion, M.V.; Ribeiro-Jr, R.; Vianna, D.L.S.S.; Sato, A.M. Trapped Solitary Waves in a Periodic External Force: A Numerical Investigation Using the Whitham Equation and the Sponge Layer Method. Fluids 2023, 8, 223. https://doi.org/10.3390/fluids8080223
Flamarion MV, Ribeiro-Jr R, Vianna DLSS, Sato AM. Trapped Solitary Waves in a Periodic External Force: A Numerical Investigation Using the Whitham Equation and the Sponge Layer Method. Fluids. 2023; 8(8):223. https://doi.org/10.3390/fluids8080223
Chicago/Turabian StyleFlamarion, Marcelo V., Roberto Ribeiro-Jr, Diogo L. S. S. Vianna, and Alex M. Sato. 2023. "Trapped Solitary Waves in a Periodic External Force: A Numerical Investigation Using the Whitham Equation and the Sponge Layer Method" Fluids 8, no. 8: 223. https://doi.org/10.3390/fluids8080223





