Comprehensive Perturbation Approach to Nonlinear Viscous Gravity–Capillary Surface Waves at Arbitrary Wavelengths in Finite Depth
Abstract
:1. Introduction
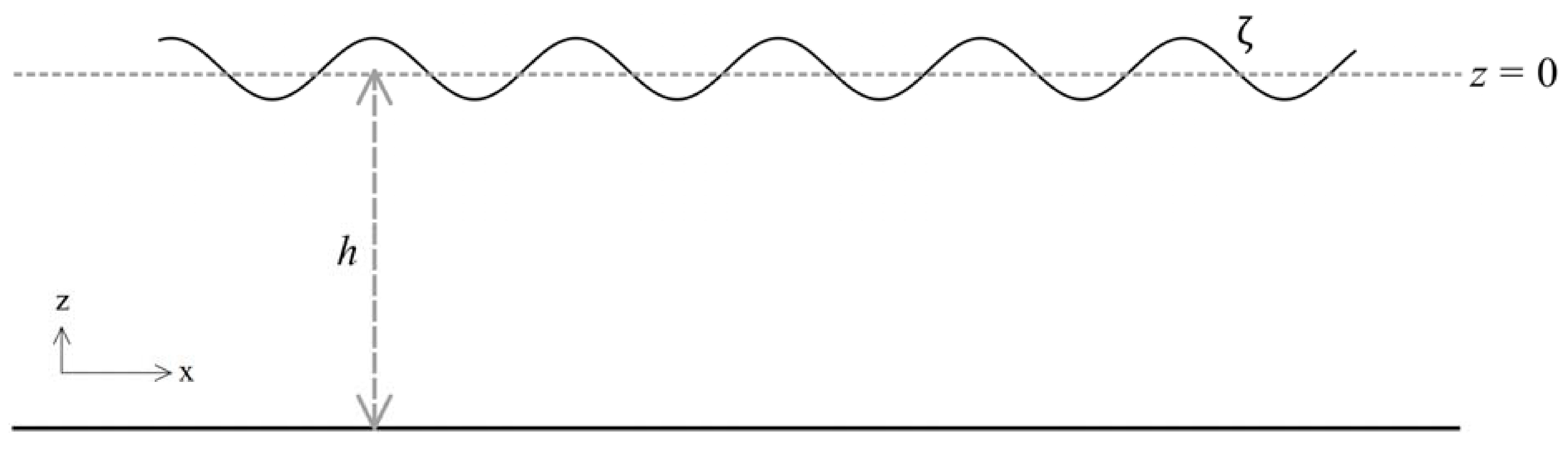
2. Formulation of the Problem
3. First-Order Solutions
4. Second-Order Solutions
5. Surface-Wave Equation
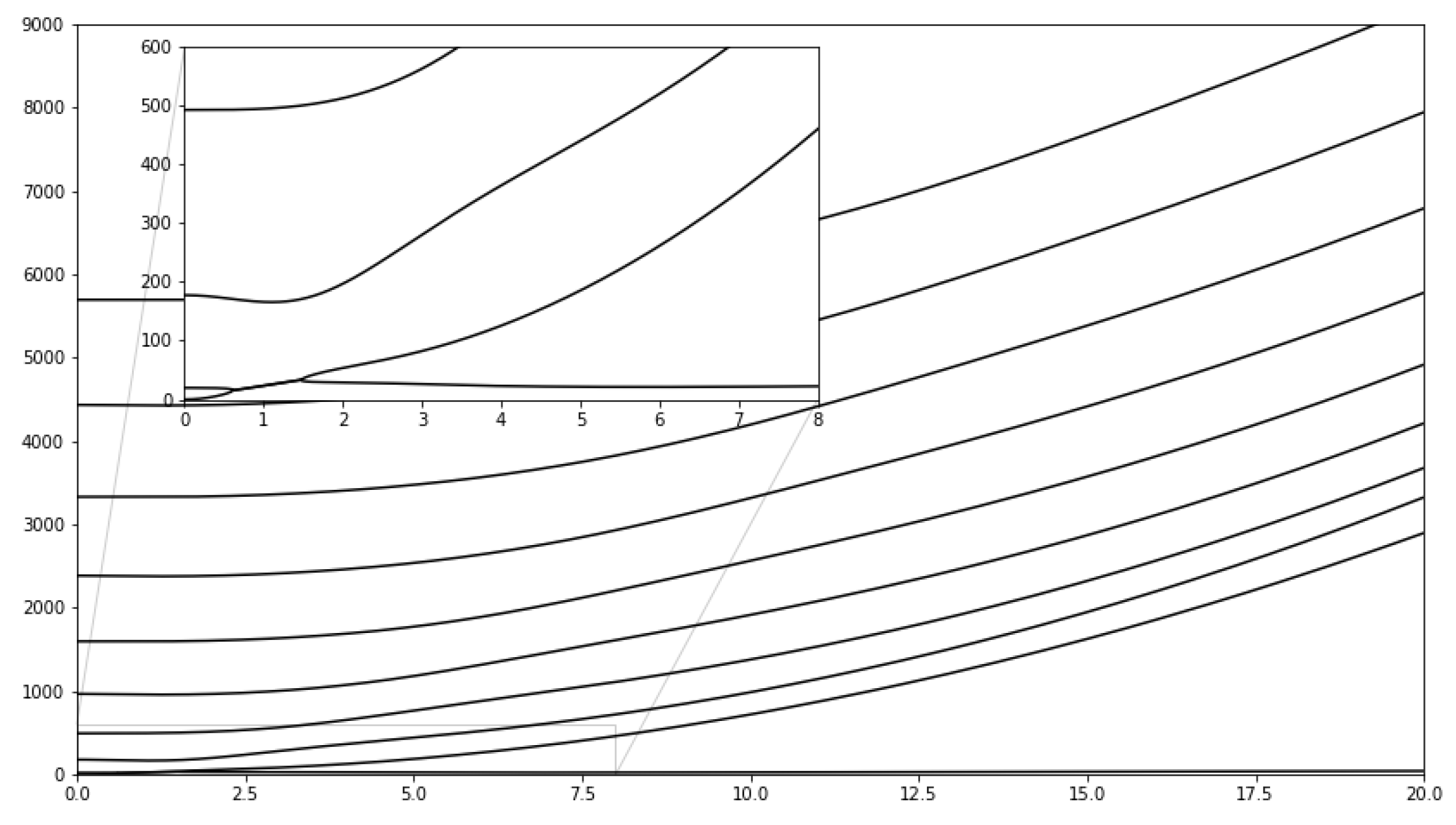
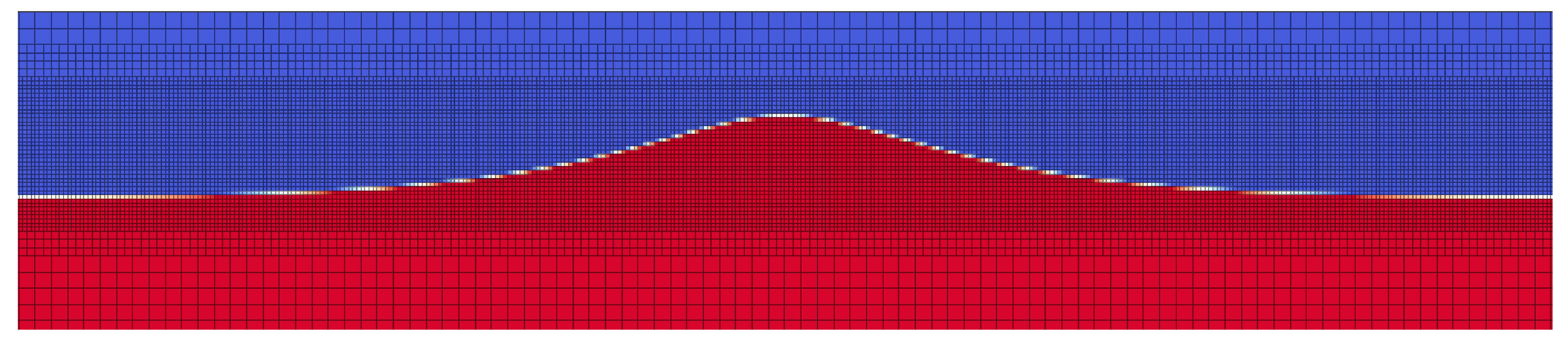
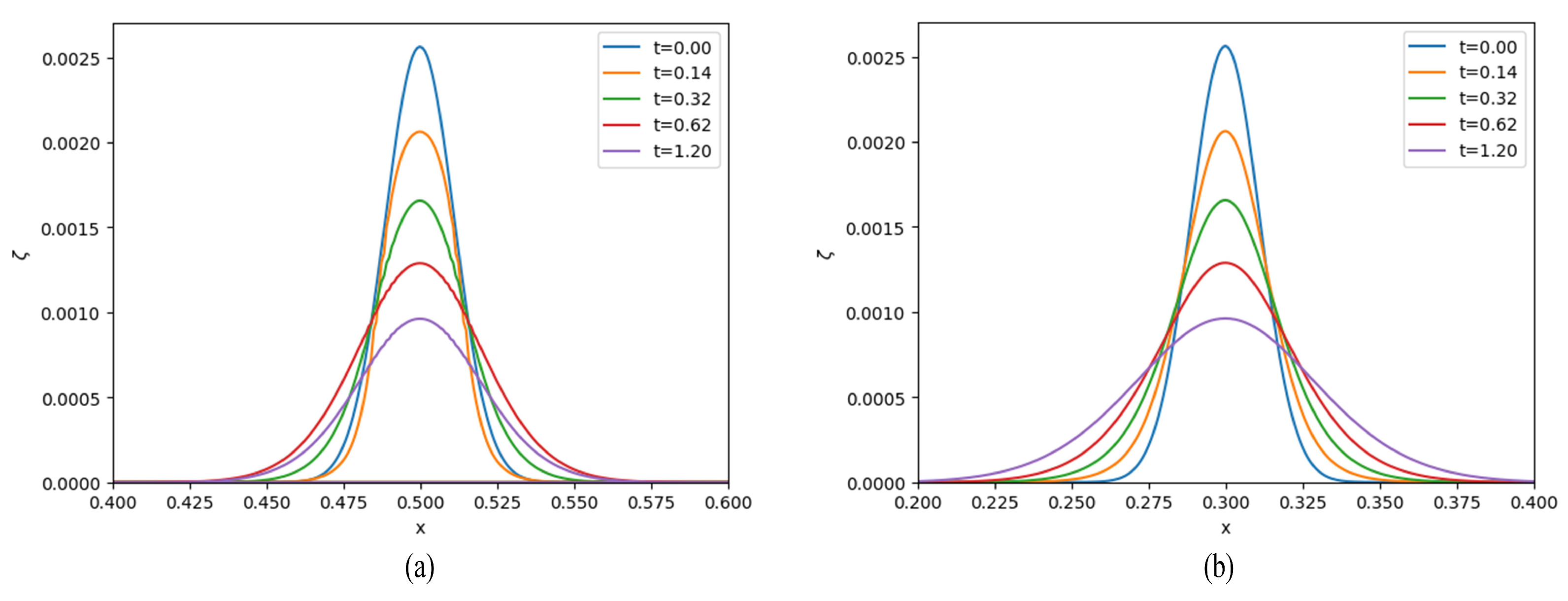
6. Numerical Results
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Matsuno, Y. Nonlinear evolutions of surface gravity waves on fluid of finite depth. Phys. Rev. Lett. 1992, 69, 609. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Artiles, W.; Nachbin, A. Nonlinear evolution of surface gravity waves over highly variable depth. Phys. Rev. Lett. 2004, 93, 234501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Z.; Milewski, P.A. Dynamics of gravity–capillary solitary waves in deep water. J. Fluid Mech. 2012, 708, 480–501. [Google Scholar] [CrossRef] [Green Version]
- Belibassakis, K.; Touboul, J. A nonlinear coupled-mode model for waves propagating in vertically sheared currents in variable bathymetry—Collinear waves and currents. Fluids 2019, 4, 61. [Google Scholar] [CrossRef] [Green Version]
- Gao, T.; Milewski, P.; Wang, Z. Capillary–gravity solitary waves on water of finite depth interacting with a linear shear current. Stud. Appl. Math. 2021, 147, 1036–1057. [Google Scholar] [CrossRef]
- Li, Y. A Mathematical Model for Nonlinear Gravity–Capillary Waves in a Large Temporal-Spatial Domain. In Porceedings of the EGU General Assembly 2023, Vienna, Austria, 24–28 April 2023; 2023. EGU23-13972. [Google Scholar]
- Ambrose, D.; Bona, J.; Nicholls, D. Well-Posedness of a Model for Water Waves with Viscosity. DIscrete Continous Dyn. Syst. Ser. B 2012, 17, 4. [Google Scholar] [CrossRef]
- Kurkina, O.; Kurkin, A.; Pelinovsky, E.; Stepanyants, Y.; Talipova, T. Nonlinear Models of Finite Amplitude Interfacial Waves in Shallow Two-Layer Fluid. In Applied Wave Mathematics II: Selected Topics in Solids, Fluids, and Mathematical Methods and Complexity; Springer: Cham, Switzerland, 2019; pp. 61–87. [Google Scholar]
- Liu, J.; Hayatdavoodi, M.; Ertekin, R.C. A Comparative Study on Generation and Propagation of Nonlinear Waves in Shallow Waters. J. Mar. Sci. Eng. 2023, 11, 917. [Google Scholar] [CrossRef]
- Giamagas, G.; Zonta, F.; Roccon, A.; Soldati, A. Propagation of capillary waves in two-layer oil–water turbulent flow. J. Fluid Mech. 2023, 960, A5. [Google Scholar] [CrossRef]
- Mao, Y.; Hoefer, M.A. Experimental investigations of linear and nonlinear periodic travelling waves in a viscous fluid conduit. J. Fluid Mech. 2023, 954, A14. [Google Scholar] [CrossRef]
- Clamond, D.; Dutykh, D. Accurate fast computation of steady two-dimensional surface gravity waves in arbitrary depth. J. Fluid Mech. 2018, 844, 491–518. [Google Scholar] [CrossRef] [Green Version]
- Khatskevich, V.L. On the asymptotics of the motion of a nonlinear viscous fluid. Sib. Math. J. 2017, 58, 329–337. [Google Scholar] [CrossRef]
- Jiang, S.C.; Liu, C.F.; Sun, L. Numerical comparison for focused wave propagation between the fully nonlinear potential flow and the viscous fluid flow models. China Ocean. Eng. 2020, 34, 279–288. [Google Scholar] [CrossRef]
- Harrison, W. The influence of viscosity and capillarity on waves of finite amplitude. Proc. Lond. Math. Soc. 1909, 2, 107–121. [Google Scholar] [CrossRef]
- Dias, F.; Kharif, C. Nonlinear gravity and capillary–gravity waves. Annu. Rev. Fluid Mech. 1999, 31, 301–346. [Google Scholar] [CrossRef] [Green Version]
- Hunt, J.N. Interfacial waves of finite amplitude. La Houille Blanche 1961, 4, 515–531. [Google Scholar] [CrossRef] [Green Version]
- Tsuji, Y.; Nagata, Y. Stokes’ expansion of internal deep water waves to the fifth order. J. Oceanogr. Soc. Jpn. 1973, 29, 61–69. [Google Scholar]
- Trulsen, K.; Kliakhandler, I.; Dysthe, K.B.; Velarde, M.G. On weakly nonlinear modulation of waves on deep water. Phys. Fluids 2000, 12, 2432–2437. [Google Scholar] [CrossRef] [Green Version]
- Stiassnie, M. Note on the modified nonlinear Schrödinger equation for deep water waves. Wave Motion 1984, 6, 431–433. [Google Scholar] [CrossRef]
- Sulem, C.; Sulem, P.L. The Nonlinear SchröDinger Equation: Self-Focusing and Wave Collapse; Springer Science & Business Media: New York, NY, USA, 2007; Volume 139. [Google Scholar]
- Dysthe, K.B. Note on a modification to the nonlinear Schrödinger equation for application to deep water waves. Proc. R. Soc. Lond. Math. Phys. Sci. 1979, 369, 105–114. [Google Scholar]
- Lamb, H. Hydrodynamics; Dover Publications: New York, NY, USA, 1945; p. 445. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics: Landau and Lifshitz: Course of Theoretical Physics; Elsevier: Amsterdam, The Netherlands, 2013; Volume 6. [Google Scholar]
- Robertson, S.; Rousseaux, G. Viscous dissipation of surface waves and its relevance to analogue gravity experiments. arXiv 2017, arXiv:1706.05255. [Google Scholar]
- Dias, F.; Dyachenko, A.I.; Zakharov, V.E. Theory of weakly damped free-surface flows: A new formulation based on potential flow solutions. Phys. Lett. 2008, 372, 1297–1302. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.M.; Hwung, H.H.; Yang, R.Y. On the study of second-order wave theory and its convergence for a two-fluid system. Math. Probl. Eng. 2013, 2013, 253401. [Google Scholar] [CrossRef] [Green Version]
- Longuet-Higgins, M.S. Mass transport in water waves. Philos. Trans. R. Soc. Lond. Ser. Math. Phys. Sci. 1953, 245, 535–581. [Google Scholar]
- Longuet-Higgins, M. Mass transport in the boundary layer at a free oscillating surface. J. Fluid Mech. 1960, 8, 293–306. [Google Scholar] [CrossRef]
- Debnath, L.; Basu, K. Nonlinear water waves and nonlinear evolution equations with applications. In Solitons; Springer: New York, NY, USA, 2022; p. 1. [Google Scholar]
- Vitanov, N.K.; Ivanova, T.I. Solitary wave solutions of several nonlinear PDEs modeling shallow water waves. arXiv 2017, arXiv:1709.05320. [Google Scholar]
- Barannyk, L.L.; Papageorgiou, D.T. Fully nonlinear gravity–capillary solitary waves in a two-fluid system of finite depth. J. Eng. Math. 2002, 42, 321–339. [Google Scholar] [CrossRef]
- Ghahraman, A.; Bene, G. Bifurcation Analysis and Propagation Conditions of Free-Surface Waves in Incompressible Viscous Fluids of Finite Depth. Fluids 2023, 8, 173. [Google Scholar] [CrossRef]
- Le Meur, H.V. Derivation of a viscous Boussinesq system for surface water waves. Asymptot. Anal. 2015, 94, 309–345. [Google Scholar] [CrossRef]
- Armaroli, A.; Eeltink, D.; Brunetti, M.; Kasparian, J. Viscous damping of gravity–capillary waves: Dispersion relations and nonlinear corrections. Phys. Rev. Fluids 2018, 3, 124803. [Google Scholar] [CrossRef] [Green Version]
- Ammar, N.; Ali, H.A. Mathematical Modelling for Peristaltic Flow of Sutterby Fluid Through Tube under the Effect of Endoscope. Iraqi J. Sci. 2023, 2368–2381. [Google Scholar] [CrossRef]
- Nazeer, M.; Alqarni, M.Z.; Hussain, F.; Saleem, S. Computational analysis of multiphase flow of non-Newtonian fluid through inclined channel: Heat transfer analysis with perturbation method. Comput. Part. Mech. 2023, 10, 1371–1381. [Google Scholar]
- Rafiq, M.; Abbas, Z.; Hasnain, J. Theoretical exploration of thermal transportation with Lorentz force for fourth-grade fluid model obeying peristaltic mechanism. Arab. J. Sci. Eng. 2021, 46, 12391–12404. [Google Scholar] [CrossRef]
- Abbas, Z.; Rafiq, M.; Hasnain, J.; Umer, H. Impacts of lorentz force and chemical reaction on peristaltic transport of Jeffrey fluid in a penetrable channel with injection/suction at walls. Alex. Eng. J. 2021, 60, 1113–1122. [Google Scholar] [CrossRef]
- Abbas, Z.; Rafiq, M.; Hasnain, J.; Javed, T. Peristaltic transport of a Casson fluid in a non-uniform inclined tube with Rosseland approximation and wall properties. Arab. J. Sci. Eng. 2021, 46, 1997–2007. [Google Scholar] [CrossRef]
- Jian, Y.; Zhu, Q.; Zhang, J.; Wang, Y. Third order approximation to capillary gravity short crested waves with uniform currents. Appl. Math. Model. 2009, 33, 2035–2053. [Google Scholar] [CrossRef]
- Farsoiya, P.K.; Mayya, Y.; Dasgupta, R. Axisymmetric viscous interfacial oscillations–theory and simulations. J. Fluid Mech. 2017, 826, 797–818. [Google Scholar] [CrossRef]
- Boujelbene, M.; Hadimani, B.; Choudhari, R.; Sanil, P.; Gudekote, M.; Vaidya, H.; Prasad, K.V.; Fadhl, B.M.; Makhdoum, B.M.; Ijaz Khan, M.; et al. Impact of Variable Slip and Wall Properties on Peristaltic Flow of Eyring—Powell Fluid Through Inclined Channel: Artificial Intelligence Based Perturbation Technique. Fractals 2023, 31, 2340140. [Google Scholar] [CrossRef]
- Hunt, J.N. The viscous damping of gravity waves in shallow water. La Houille Blanche 1964, 6, 685–691. [Google Scholar] [CrossRef] [Green Version]
- Dubrovin, B. Dispersion Relations for Nonlinear Waves and the Schottky Problem; Springer: Berlin/Heidelberg, Germany, 2012; pp. 86–98. [Google Scholar]

| Authors | Finite Depth | Viscosity | Surface Tension | Exact Dispersion Relation | Method |
|---|---|---|---|---|---|
| Harrison [15] | X | ✓ | ✓ | X | Perturbation expansion |
| Dias and Kharif [16] | X | X | X | ✓ | – |
| Hunt [17] | ✓ | X | X | X | Levi–Civita’s method |
| Tsuji and Nagata [18] | X | X | ✓ | X | Perturbation expansion |
| Matsuno [1] | ✓ | X | X | X | Principles of complex functions and a methodical perturbation theory |
| Dysthe [22] | X | X | X | X | Perturbation expansion |
| Dias, Dyachenko and Zakharov [26] | X | ✓ | X | X | Helmholtz decomposition |
| Le Meur [34] | ✓ | ✓ | ✓ | ✓ | Boussinesq approximation |
| Armaroli [35] | X | ✓ | ✓ | ✓ | – |
| Ghahraman and Bene [33] | ✓ | ✓ | ✓ | ✓ | Linear approximation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghahraman, A.; Bene, G. Comprehensive Perturbation Approach to Nonlinear Viscous Gravity–Capillary Surface Waves at Arbitrary Wavelengths in Finite Depth. Fluids 2023, 8, 218. https://doi.org/10.3390/fluids8080218
Ghahraman A, Bene G. Comprehensive Perturbation Approach to Nonlinear Viscous Gravity–Capillary Surface Waves at Arbitrary Wavelengths in Finite Depth. Fluids. 2023; 8(8):218. https://doi.org/10.3390/fluids8080218
Chicago/Turabian StyleGhahraman, Arash, and Gyula Bene. 2023. "Comprehensive Perturbation Approach to Nonlinear Viscous Gravity–Capillary Surface Waves at Arbitrary Wavelengths in Finite Depth" Fluids 8, no. 8: 218. https://doi.org/10.3390/fluids8080218




