Frequency Specificity of Liquid-Fountain Swinging with Mist Generation: Effects of Ultrasonic Irradiation Angle
Abstract
:1. Introduction
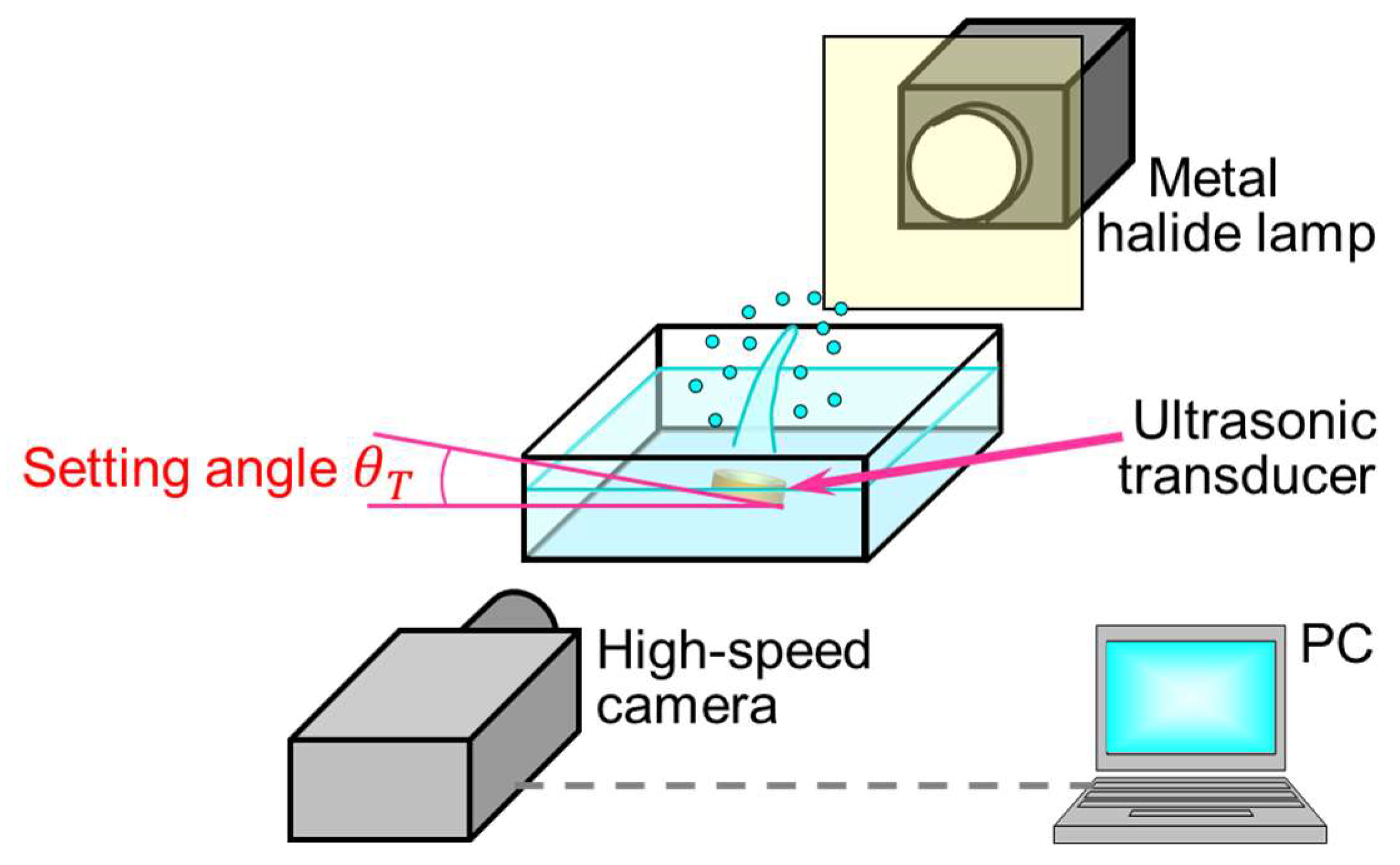
2. Experimental
2.1. High-Speed Visualization and Image Analysis
2.2. Time-Series Data Analysis
3. Results and Discussion
3.1. Structure of Liquid Fountain with Mist
3.2. Axial Growth and Breakup Dynamics of Liquid Fountain
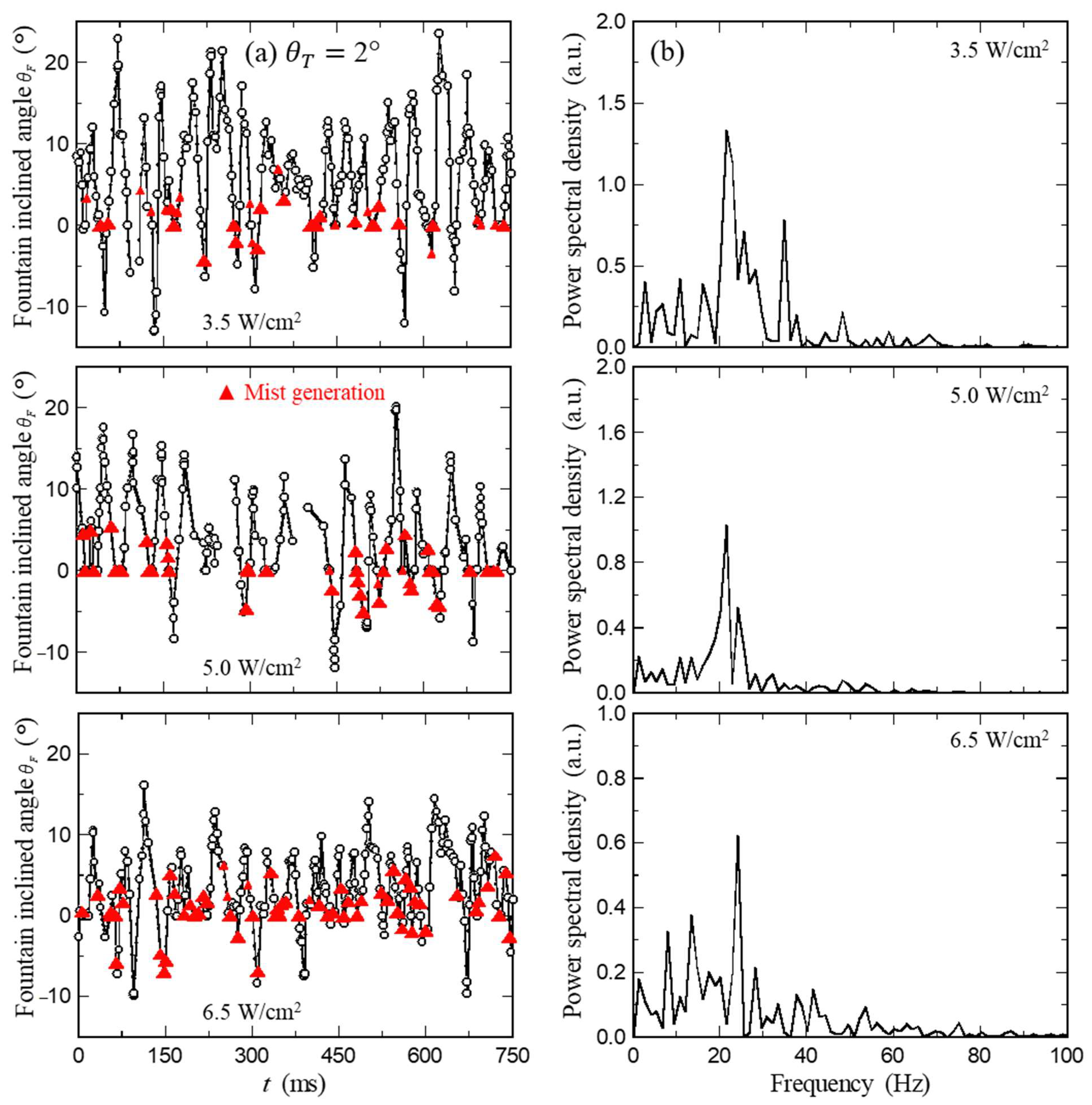
3.3. Time-Dependent Characteristics of Fountain Swinging
3.4. Model-Evaluated Periodicity of Fountain Swinging
- ⊳
- The total mass moment of the fountain consisting of Bodies 1 and 2, the geometries of which are respectively a cone of the base radius and the height , and a cylinder of the radius and the height :
- ⊳
- The total mass itself of the fountain:
- ⊳
- The apparent center of mass for the fountain as a whole () as well as the fountain length itself () combined as
4. Concluding Remarks
- (1)
- A slight tilt in irradiation of ultrasound should be advantageous in both operational and mist-generating performances. The acoustic liquid fountain will become improved in its operability/stability by avoiding the disruption of oscillation rhythm of the fountain from vertically interacting tip-separated drops;
- (2)
- The atomization, or mist generation, is mostly—almost exclusively—triggered and enhanced as the laterally swinging fountain comes across the direction of irradiation, more specifically, with its inclined angle being shifted from positive to negative in the 0° ± 5° range. The degree of occurrence of mist generation and the amount of identifiable mist generated would decrease, associated with reductions in both the growth rate and breakup frequency of the fountain on the tilt;
- (3)
- In line with such axial extents of growth and breakup of the fountain, both taking maximum values at the transducer installation angle of 2°, its optimum value should be recommended to be slightly tilted 2° from the viewpoint of stability of the UsA fountain and not to exceed 5° from that of effective mist generation;
- (4)
- A mechanistic view of the UsA process is provided in terms of the swinging periodicity of liquid fountain with mist generated intermittently, in particular, if the ultrasound is irradiated on the tilt—under the influence of gravity. The periodicity of both the axial and lateral oscillations has been quantified—the latter in particular being model-predicted based on a simple planar pendulum concept proposed, partly confirmed via FFT-evaluated dominant frequency.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Compound Pendulum Modeling
- (1)
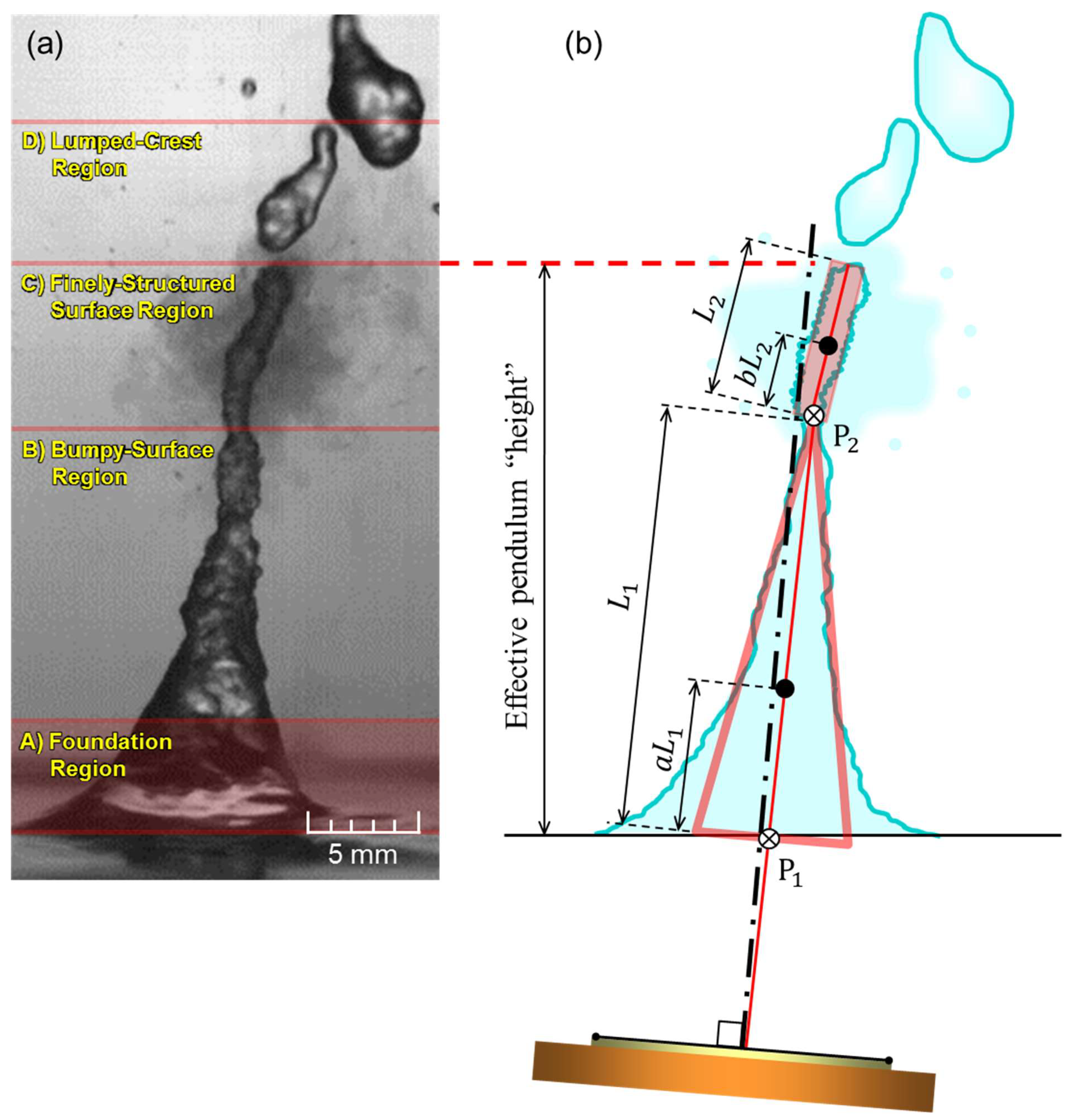
- The fountain, while altering its local shape dynamically, consists of two parts during the growth-and-breakup period, on average, simplified in geometry by a “cone” and cigar-shape or more simply a “cylinder.” The former involves the FR and BSR, the latter the FSSR which accompanies mist spreading (Figure 2);
- (2)
- (3)
- When the tilting is increased beyond 4 or 5°, this single entity will experience its bending at the “connecting” region between the cone and the cylinder (Figure 3);
- (4)
- Under the most probable complex situation, the fountain will behave as a two-body entity which exhibits two “separate” swinging motions with two pivotal regions—one near the base of the FR and the other around the connecting region—resembling the so-called “double compound” pendulum [40].
- (5)
- The waveform of fountain-swinging, exhibited in Figure 5b, particularly demonstrates the periodicity of the fountain’s lateral dynamics with a peculiar nature of asymmetricity on the positive side of the angle . This experimental trend of skewness signifies its frequency would be twice as high as an assumed symmetric (i.e., regular sinusoidal—given by the red, dashed smooth) waveform (cf. [41,42]);
- (6)
- The axial growth−breakup time-series data, on the other hand, with frequencies as high as 5–8 times that of the lateral will lead to the assumed representation of time-invariant fountain height throughout the oscillations.
- (7)
- The “tension-like” force(s) required to sustain the pendulum straight in the direction of its axis on the equilibrium position—specified by a prescribed angle—should be the acoustic strength, or acoustic radiation pressure/force(s) (denoted by ), which could be balanced by the gravitational contribution () where is the apparent mass of the pendulum (i.e., fountain) as a whole;
- (8)
- The fountain, modeled by a dual-compound pendulum, is assigned to have the lower body of cone-shape of mass (Body 1, spanning the FR and BSR) and the upper body of cylindrical-shape of mass (Body 2, spanning the FSSR);
- (9)
- The two bodies thus simplified geometrically will rotate about their specific pivotal locations—Bodies 1 and 2 around Pivots 1 and 2, respectively—where Pivot 2 serves as the joint connecting the two bodies.

References
- Dong, Z.; Yao, C.; Zhang, X.; Xu, J.; Chen, G.; Zhao, Y.; Yuan, Q. A high-power ultrasonic microreactor and its application in gas–liquid mass transfer intensification. Lab Chip 2015, 15, 1145–1152. [Google Scholar] [CrossRef] [PubMed]
- Tamidi, A.M.; Lau, K.K.; Khalit, S.H. A review of recent development in numerical simulation of ultrasonic-assisted gas-liquid mass transfer process. Comput. Chem. Eng. 2021, 155, 107498. [Google Scholar] [CrossRef]
- Mahamuni, N.N.; Adewuyi, Y.G. Advanced oxidation processes (AOPs) involving ultrasound for waste water treatment: A review with emphasis on cost estimation. Ultrason. Sonochem. 2010, 17, 990–1003. [Google Scholar] [CrossRef] [PubMed]
- Kunde, G.B.; Sehgal, B. Application of sol-gel assisted ultrasound-induced atomization in the mesostructuring of nickel aluminate UF membranes. Microporous Mesoporous Mater. 2021, 325, 111299. [Google Scholar] [CrossRef]
- Tay, W.H.; Lau, K.K.; Shariff, A.M. High frequency ultrasonic-assisted CO2 absorption in a high pressure water batch system. Ultrason. Sonochem. 2016, 33, 190–196. [Google Scholar] [CrossRef] [PubMed]
- Tay, W.H.; Lau, K.K.; Shariff, A.M. High performance promoter-free CO2 absorption using potassium carbonate solution in an ultrasonic irradiation system. J. CO2 Util. 2017, 21, 383–394. [Google Scholar] [CrossRef]
- Wei, J.; Gu, J.; Guo, J.; Li, W.; Wang, C.; Zhang, J. Simultaneous removal of nitrogen oxides and sulfur dioxide using ultrasonically atomized hydrogen peroxide. Environ. Sci. Pollut. Res. 2019, 26, 22351–22361. [Google Scholar] [CrossRef]
- Marjanian, M.M.; Shahhosseini, S.; Ansari, A. Investigation of the ultrasound assisted CO2 absorption using different absorbents. Process Saf. Environ. Prot. 2021, 149, 277–288. [Google Scholar] [CrossRef]
- Dalmoro, A.; Barba, A.A.; d’Amore, M. Analysis of Size Correlations for Microdroplets Produced by Ultrasonic Atomization. Sci. World J. 2013, 2013, 482910. [Google Scholar] [CrossRef]
- Kaur, J.; Singh, R.R.; Khan, E.; Kumar, A.; Joshi, A. Piperine-Loaded PLGA Nanoparticles as Cancer Drug Carriers. ACS Appl. Nano Mater. 2021, 4, 14197–14207. [Google Scholar] [CrossRef]
- Nii, S.; Oka, N. Size-selective separation of submicron particles in suspensions with ultrasonic atomization. Ultrason. Sonochem. 2014, 21, 2032–2036. [Google Scholar] [CrossRef]
- Kim, H.; Lee, J.; Won, Y.-Y. A simple derivation of the critical condition for the ultrasonic atomization of polymer solutions. Ultrasonics 2015, 61, 20–24. [Google Scholar] [CrossRef]
- Hinman, J.G.; Hinman, J.J.; Janicek, B.E.; Huang, P.Y.; Suslick, K.S.; Murphy, C.J. Ultrasonic Nebulization for TEM Sample Preparation on Single-Layer Graphene Grids. Nano Lett. 2019, 19, 1938–1943. [Google Scholar] [CrossRef]
- Kirpalani, D.M.; Suzuki, K. Ethanol enrichment from ethanol–water mixtures using high frequency ultrasonic atomization. Ultrason. Sonochem. 2011, 18, 1012–1017. [Google Scholar] [CrossRef]
- Mai, N.L.; Koo, Y.-M.; Ha, S.H. Separation characteristics of hydrophilic ionic liquids from ionic liquids-water solution by ultrasonic atomization. Ultrason. Sonochem. 2019, 53, 187–191. [Google Scholar] [CrossRef]
- Matsuura, K.; Kobayashi, M.; Hirotsune, M.; Sato, M.; Sasaki, H.; Shimizu, K. New separation technique under normal temperature and pressure using an ultrasonic atomization. Jpn. Soc. Chem. Eng. Symp. Ser. 1995, 46, 44–49. [Google Scholar]
- Sato, M.; Matsuura, K.; Fujii, T. Ethanol separation from ethanol-water solution by ultrasonic atomization and its proposed mechanism based on parametric decay instability of capillary wave. J. Chem. Phys. 2001, 114, 2382–2386. [Google Scholar] [CrossRef]
- Wang, X.; Mori, Y.; Tsuchiya, K. Periodicity in ultrasonic atomization involving beads-fountain oscillations and mist generation: Effects of driving frequency. Ultrason. Sonochem. 2022, 86, 105997. [Google Scholar] [CrossRef]
- Tsuchiya, K.; Hayashi, H.; Fujiwara, K.; Matsuura, K. Visual analysis of ultrasonic atomization and its associated phenomena. Earozoru Kenkyu 2011, 26, 11–17. [Google Scholar] [CrossRef]
- Kobara, H.; Tamiya, M.; Wakisaka, A.; Fukazu, T.; Matsuura, K. Relationship between the size of mist droplets and ethanol condensation efficiency at ultrasonic atomization on ethanol–water mixtures. AIChE J. 2010, 56, 810–814. [Google Scholar] [CrossRef]
- Kudo, T.; Sekiguchi, K.; Sankoda, K.; Namiki, N.; Nii, S. Effect of ultrasonic frequency on size distributions of nanosized mist generated by ultrasonic atomization. Ultrason. Sonochem. 2017, 37, 16–22. [Google Scholar] [CrossRef]
- Kooij, S.; Astefanei, A.; Corthals, G.L.; Bonn, D. Size distributions of droplets produced by ultrasonic nebulizers. Sci. Rep. 2019, 9, 6128. [Google Scholar] [CrossRef]
- Panão, M. Ultrasonic Atomization: New Spray Characterization Approaches. Fluids 2022, 7, 29. [Google Scholar] [CrossRef]
- Xu, Z.; Yasuda, K.; Liu, X. Simulation of the formation and characteristics of ultrasonic fountain. Ultrason. Sonochem. 2016, 32, 241–246. [Google Scholar] [CrossRef]
- Kim, G.; Cheng, S.; Hong, L.; Kim, J.-T.; Li, K.C.; Chamorro, L.P. On the acoustic fountain types and flow induced with focused ultrasound. J. Fluid Mech. 2021, 909, R2. [Google Scholar] [CrossRef]
- Aikawa, T.; Kudo, N. Relation between thresholds of free radical generation and atomization under ultrasound exposure. Jpn. J. Appl. Phys. 2021, 60, SDDD13. [Google Scholar] [CrossRef]
- Orisaki, M.; Kajishima, T. Numerical analysis of water surface rising caused by underwater ultrasonic wave. Trans. JSME 2022, 88, 21-00377. [Google Scholar] [CrossRef]
- Simon, J.C.; Sapozhnikov, O.A.; Khokhlova, V.A.; Crum, L.A.; Bailey, M.R. Ultrasonic atomization of liquids in drop-chain acoustic fountains. J. Fluid Mech. 2015, 766, 129–146. [Google Scholar] [CrossRef] [PubMed]
- Kawase, Y.; Masuya, T.; Yasuda, K.; Nakamura, M. Effect of Flow Mode of Carrier Gas on Performance of Ultrasonic Atomization. J. Chem. Eng. Jpn. 2006, 39, 842–845. [Google Scholar] [CrossRef]
- Yasuda, K.; Honma, H.; Xu, Z.; Asakura, Y.; Koda, S. Ultrasonic Atomization Amount for Different Frequencies. Jpn. J. Appl. Phys. 2011, 50, 07HE23. [Google Scholar] [CrossRef]
- Percival, D.B.; Walden, A.T. Wavelet Methods for Time Series Analysis; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
- Lee, J.; Yasui, K.; Tuziuti, T.; Kozuka, T.; Towata, A.; Iida, Y. Spatial Distribution Enhancement of Sonoluminescence Activity by Altering Sonication and Solution Conditions. J. Phys. Chem. B 2008, 112, 15333–15341. [Google Scholar] [CrossRef]
- Lee, J.; Ashokkumar, M.; Yasui, K.; Tuziuti, T.; Kozuka, T.; Towata, A.; Iida, Y. Development and optimization of acoustic bubble structures at high frequencies. Ultrason. Sonochem. 2011, 18, 92–98. [Google Scholar] [CrossRef]
- Son, Y.; Lim, M.; Ashokkumar, M.; Khim, J. Geometric Optimization of Sonoreactors for the Enhancement of Sonochemical Activity. J. Phys. Chem. C 2011, 115, 4096–4103. [Google Scholar] [CrossRef]
- Fujita, K.; Tsuchiya, K. Cavitating Bubble inside Liquid Fountain of Beads Associated with Ultrasonic Atomization. In Proceedings of the 8th International Conference on Multiphase Flow 2013 (ICMF2013), Jeju, Korea, 26–31 May 2013. Paper 863. [Google Scholar]
- Tsuchiya, K.; Fan, L.-S. Prediction of the wake size of a single gas bubble in liquid and/or liquid–solid media—The pendulum model. Chem. Eng. Sci. 1988, 43, 2893–2897. [Google Scholar] [CrossRef]
- Fan, L.-S.; Tsuchiya, K. Bubble Wake Dynamics in Liquids and Liquid–Solid Suspensions; Butterworth–Heinemann: Stoneham, MA, USA, 1990. [Google Scholar]
- Liu, F.; Ghigliotti, G.; Feng, J.J.; Chen, C.-H. Numerical simulations of self-propelled jumping upon drop coalescence on non-wetting surfaces. J. Fluid Mech. 2014, 752, 39–65. [Google Scholar] [CrossRef]
- Sankaranarayanan, K.; Shan, X.; Kevrekidis, I.G.; Sundaresan, S. Analysis of drag and virtual mass forces in bubbly suspensions using an implicit formulation of the lattice Boltzmann method. J. Fluid Mech. 2002, 452, 61–96. [Google Scholar] [CrossRef]
- Huat, O.J.; Ghista, D.N.; Beng, N.K.; John, T.C.C. Optimal stride frequency computed from the double-compound pendulum of the leg, and verified experimentally as the preferred stride frequency of jogging. Int. J. Comput. Appl. Technol. 2004, 21, 46–51. [Google Scholar] [CrossRef]
- Alexander, R.M. Principles of Animal Locomotion; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar] [CrossRef]
- Van Bijlert, P.A.; van Soest, A.J.K.; Schulp, A.S. Natural Frequency Method: Estimating the preferred walking speed of Tyrannosaurus rex based on tail natural frequency. R. Soc. Open Sci. 2021, 8, 201441. [Google Scholar] [CrossRef]





| Input Power (W/cm2) | (mm) | (mm) | (mm) | (mm) | (kg) | (kg) | (kg m2) | (kg m2) | Pred [Equation (4)] (Hz) | Exp (FFT) Main Freq. (Hz) |
|---|---|---|---|---|---|---|---|---|---|---|
| 3.5 @2° | 10.8 | 4.8 | 2.9 | 0.8 | 0.95 | 0.96 | 2.4 | 0.31 | 19.1–21.5 | 21 |
| 5.0 @2° | 16.6 | 5.2 | 3.5 | 1.0 | 2.10 | 1.60 | 7.7 | 0.81 | 16.2–17.9 | 21 |
| 5.0 @5° | 14.7 | 6.2 | 3.1 | 0.7 | 1.50 | 0.95 | 4.3 | 0.23 | 18.4–19.0 | 18 |
| 6.5 @2° | 18.5 | 8.2 | 3.0 | 1.0 | 1.70 | 2.60 | 4.6 | 1.30 | 13.4–17.3 | 24 |
| Liquid fountain (W/cm2) | (mm) | (Hz) | (Hz) | (m/s) | ||||||
| 3.5 @2° | 2.9 | 21.5 | 10.7 | 0.16 | 1030 | 0.39 | 0.79 | 2.07 | 1.30 | 1.84 |
| 5.0 @2° | 3.5 | 17.9 | 9.0 | 0.14 | 1130 | 0.44 | 0.87 | 2.27 | 1.50 | 2.12 |
| 5.0 @5° | 3.1 | 19.0 | 9.5 | 0.15 | 1060 | 0.39 | 0.77 | 2.14 | 1.33 | 1.88 |
| 6.5 @2° | 3.0 | 17.3 | 8.7 | 0.16 | 1040 | 0.34 | 0.67 | 2.10 | 1.22 | 1.72 |
| Beads fountain (MHz) | (mm) | (kHz) | (kHz) | (m/s) | ||||||
| 1.0 | 1.47 | 0.13 | 0.38 | 0.21 | 114 | 0.92 | 2.68 | 1.28 | 1.22 | 2.09 |
| 2.0 | 0.74 | 0.36 | 1.08 | 0.29 | 81 | 0.91 | 2.72 | 0.91 | 0.86 | 1.49 |
| 3.0 | 0.49 | 0.66 | 1.99 | 0.36 | 66 | 0.90 | 2.70 | 0.74 | 0.70 | 1.21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Tsuchiya, K. Frequency Specificity of Liquid-Fountain Swinging with Mist Generation: Effects of Ultrasonic Irradiation Angle. Fluids 2022, 7, 306. https://doi.org/10.3390/fluids7090306
Wang X, Tsuchiya K. Frequency Specificity of Liquid-Fountain Swinging with Mist Generation: Effects of Ultrasonic Irradiation Angle. Fluids. 2022; 7(9):306. https://doi.org/10.3390/fluids7090306
Chicago/Turabian StyleWang, Xiaolu, and Katsumi Tsuchiya. 2022. "Frequency Specificity of Liquid-Fountain Swinging with Mist Generation: Effects of Ultrasonic Irradiation Angle" Fluids 7, no. 9: 306. https://doi.org/10.3390/fluids7090306






