On the Wake Dynamics of an Oscillating Cylinder via Proper Orthogonal Decomposition
Abstract
:1. Introduction
2. Material and Methods
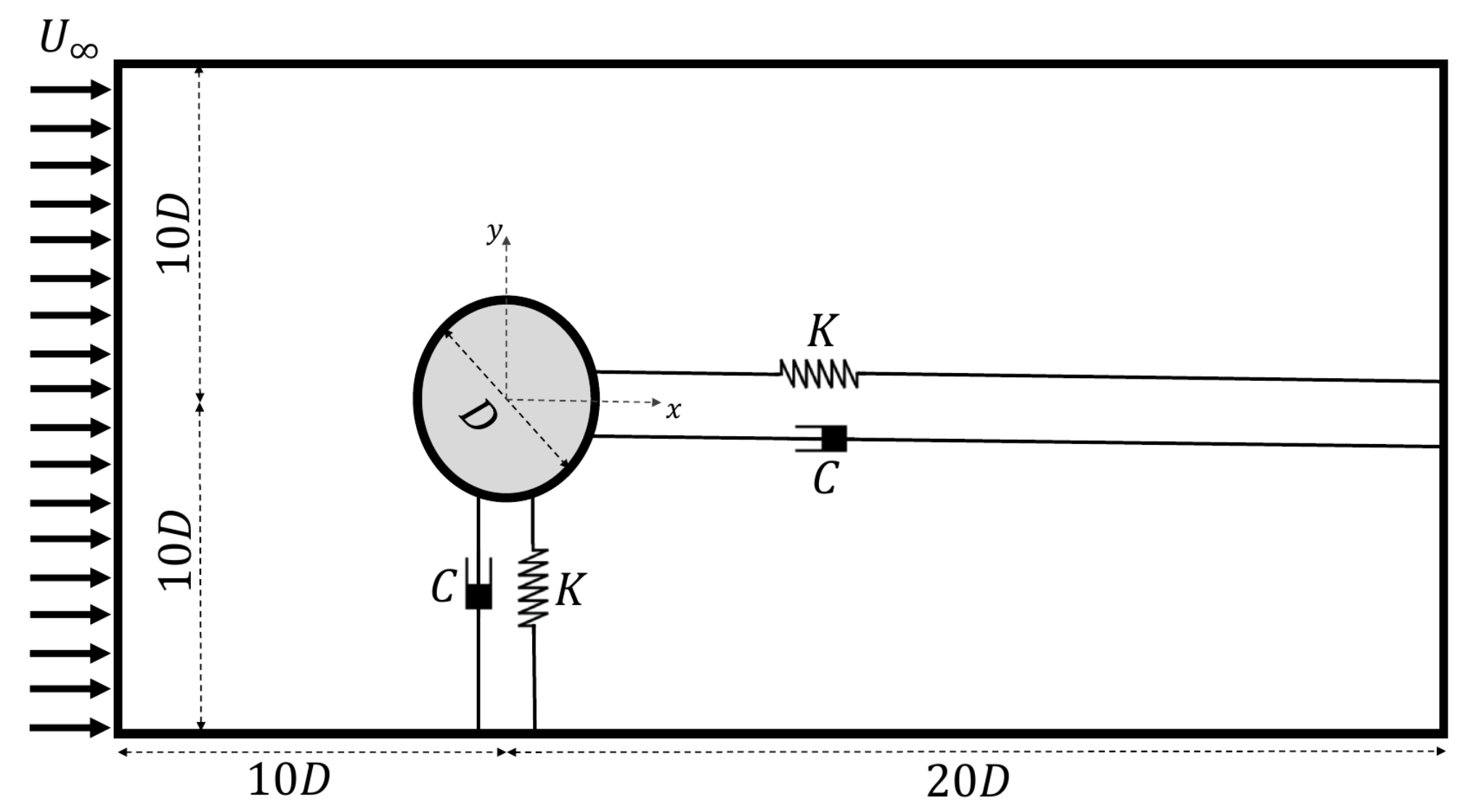
2.1. Definition of the Case
2.2. Summary of the Numerical Implementation
2.3. Proper Orthogonal Decomposition (POD)
| Algorithm 1: Proper orthogonal decomposition. |
 |
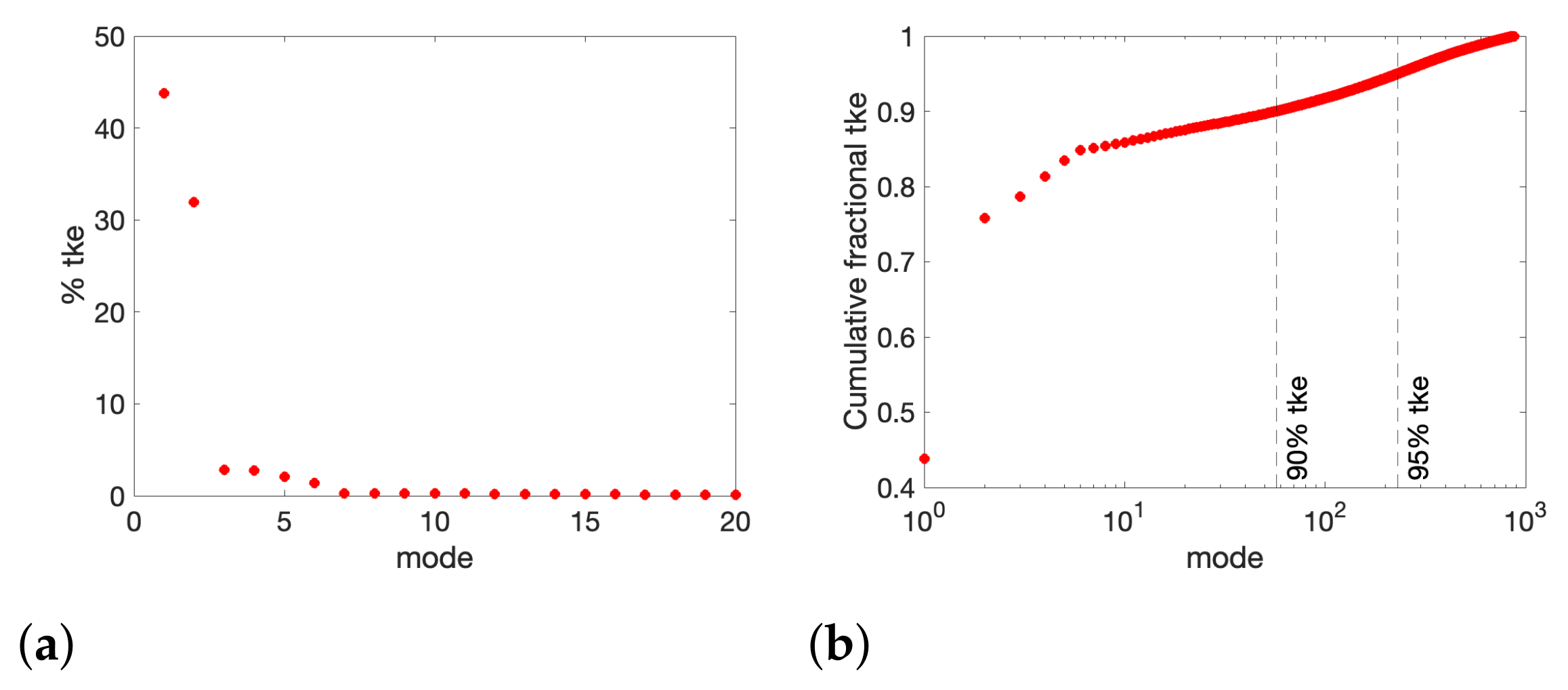
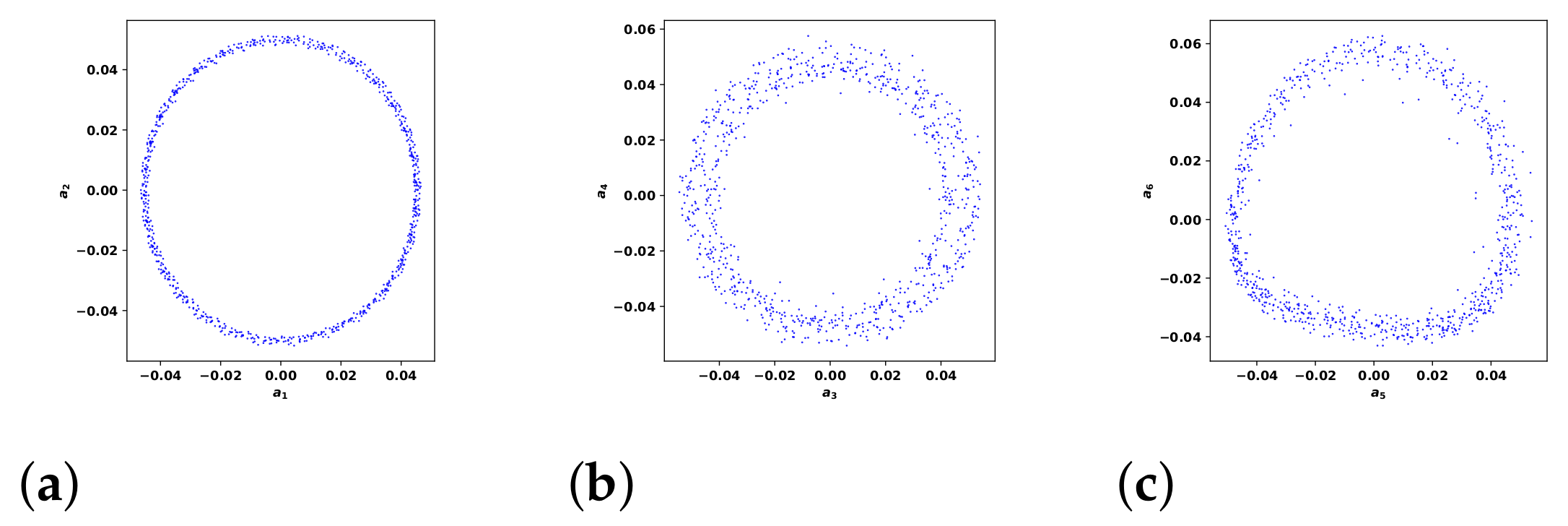
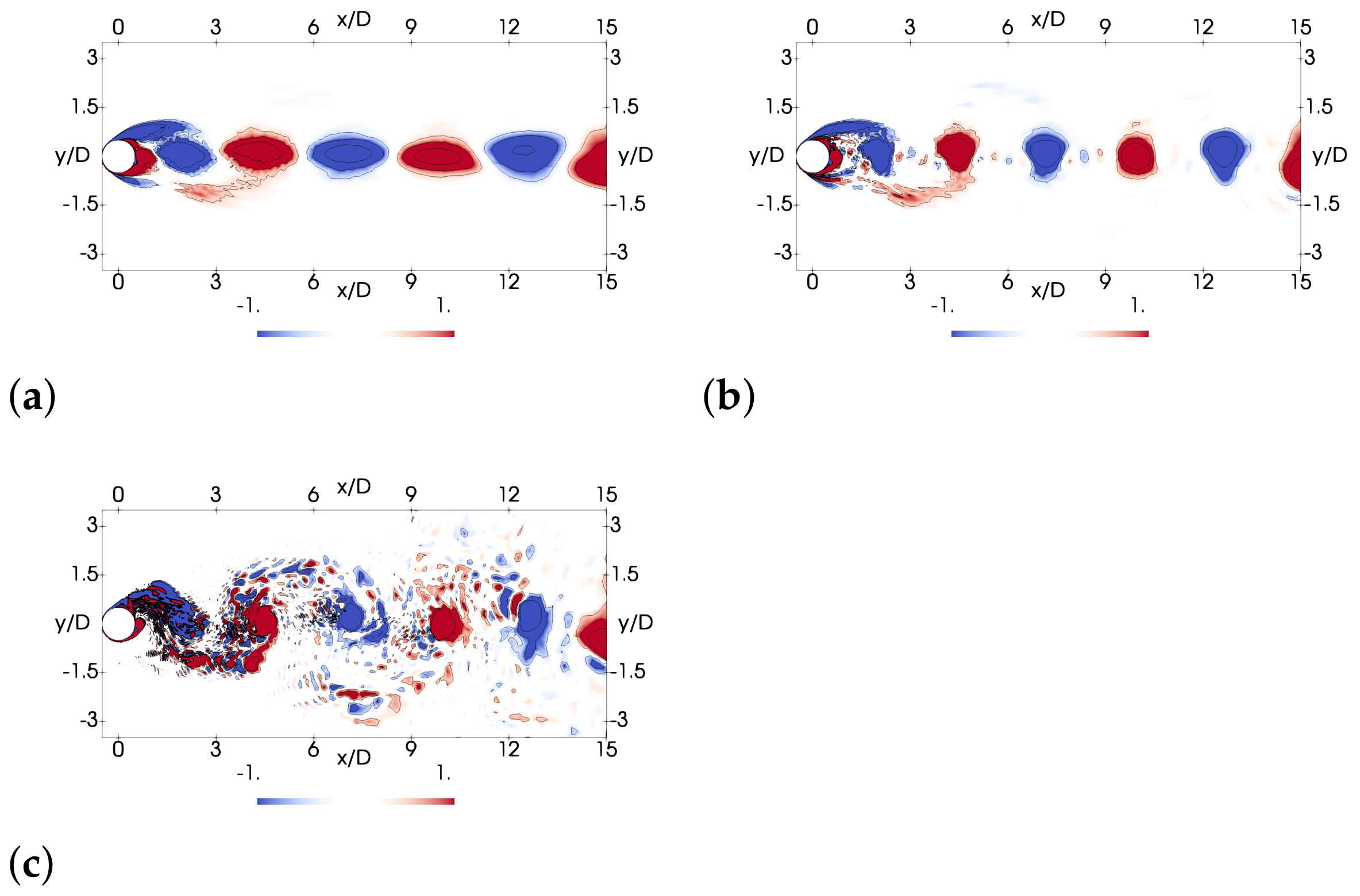
3. Results
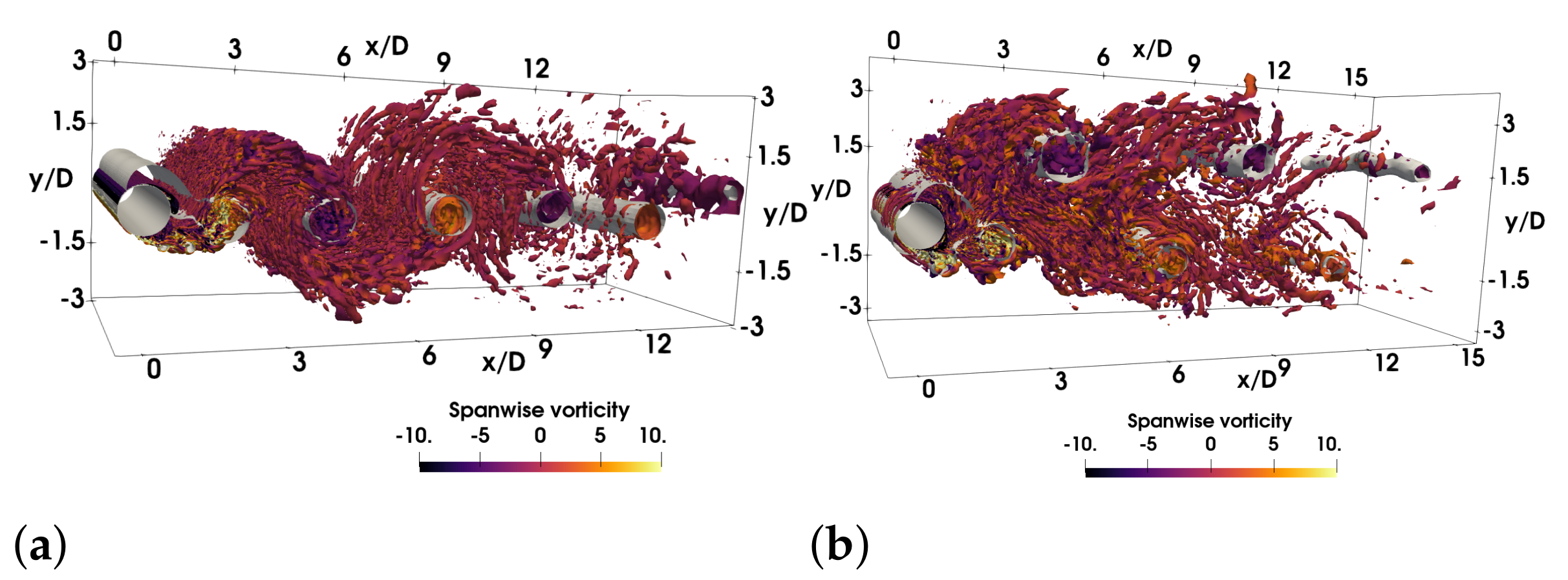
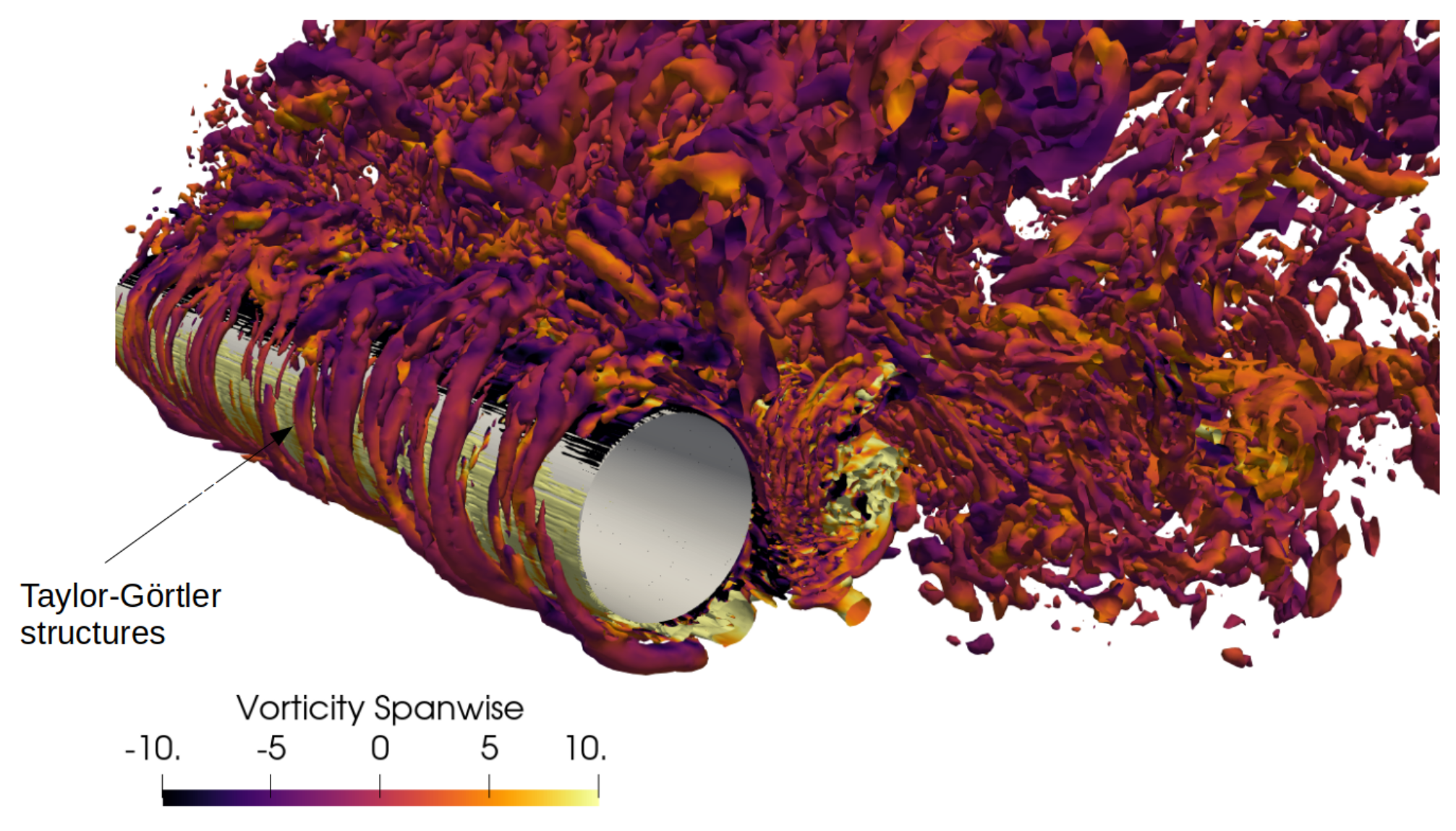
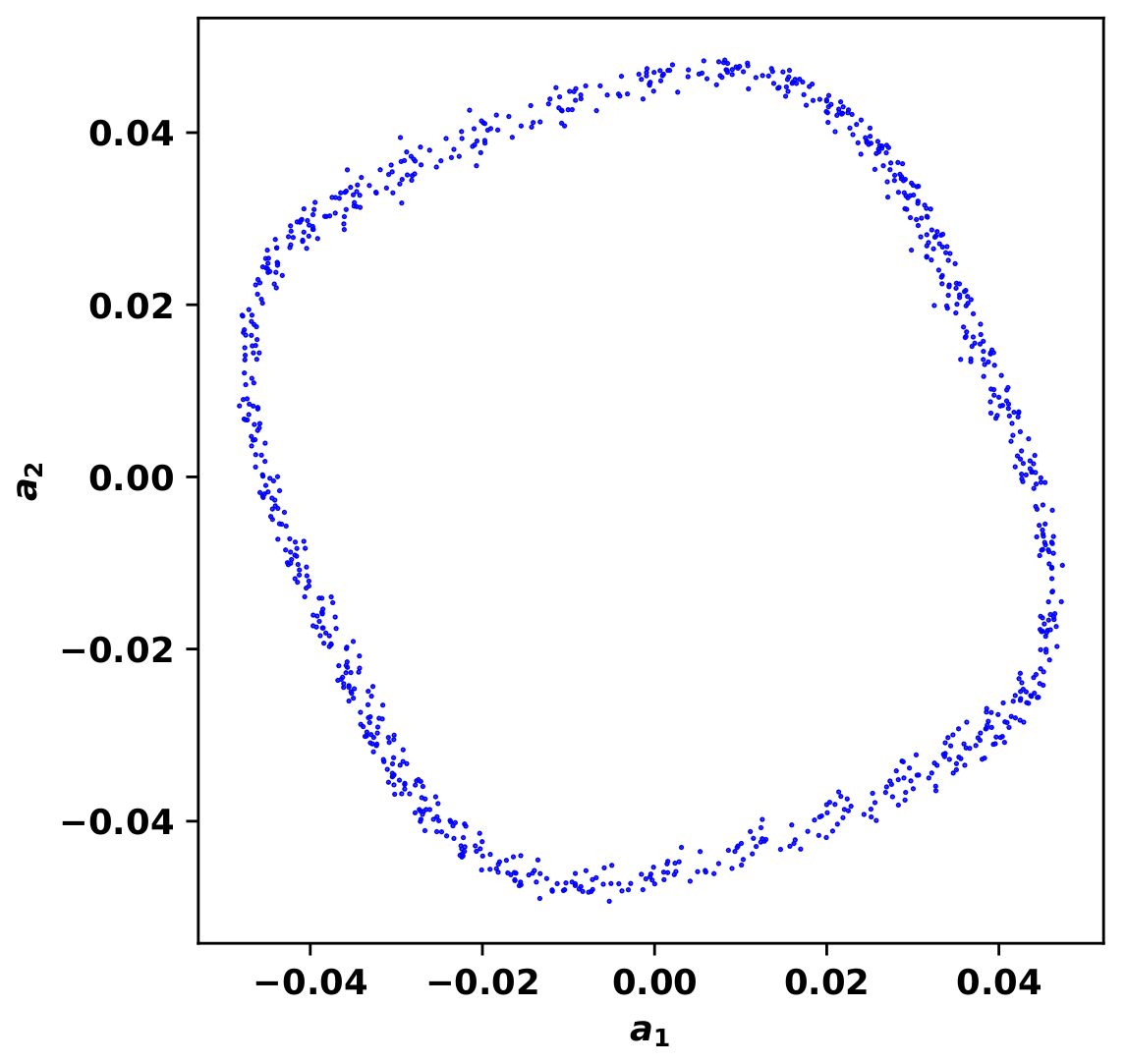
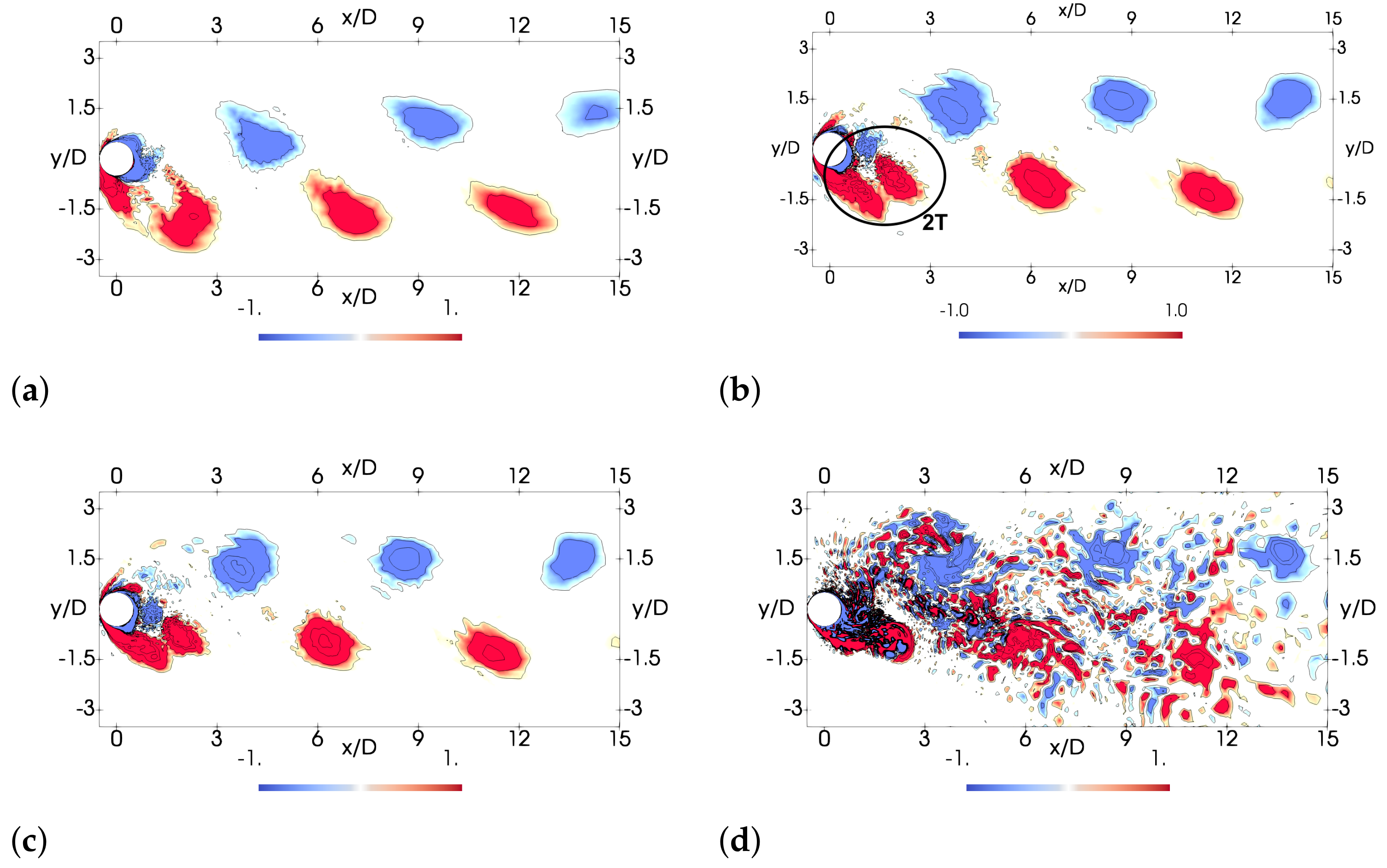
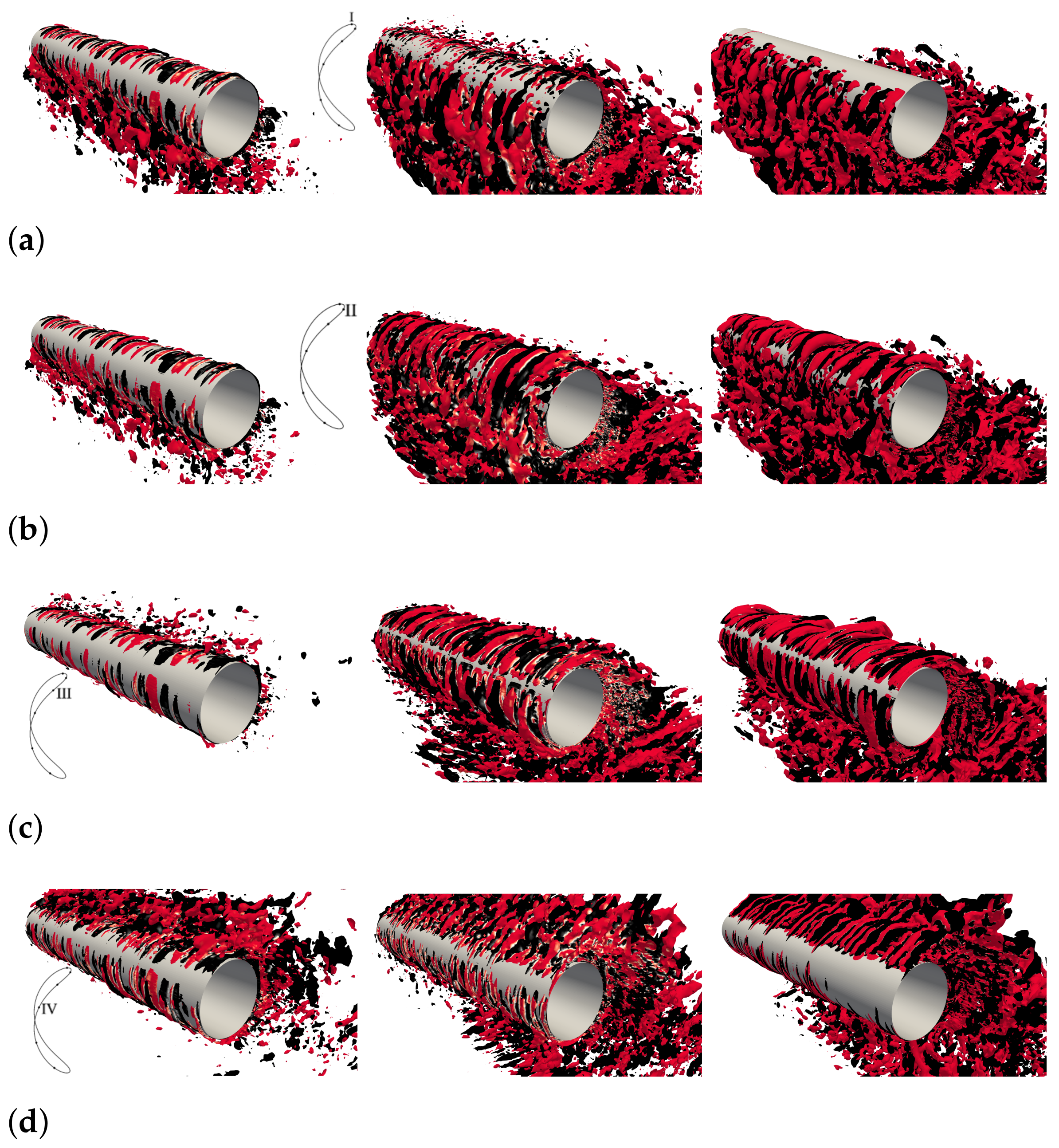
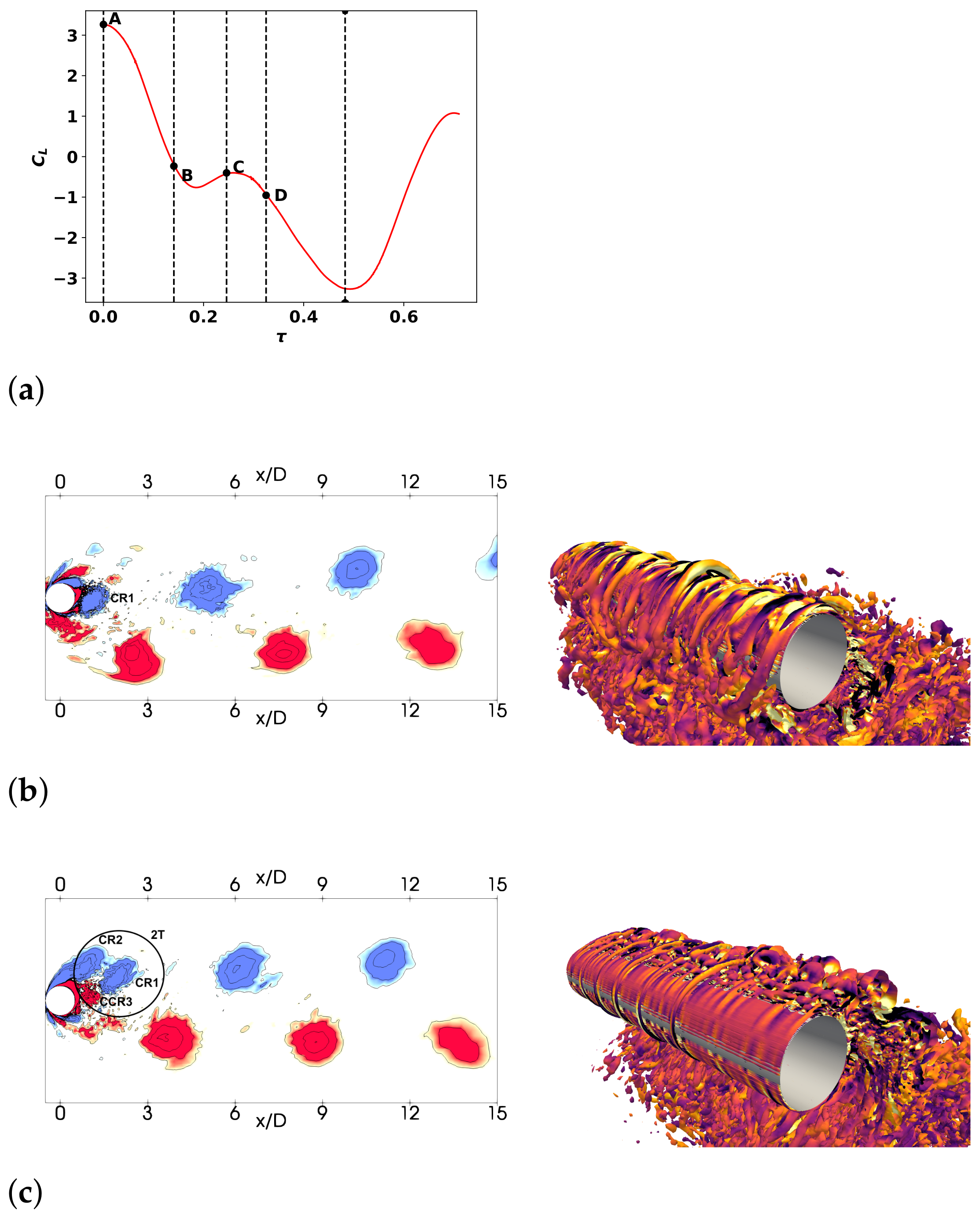
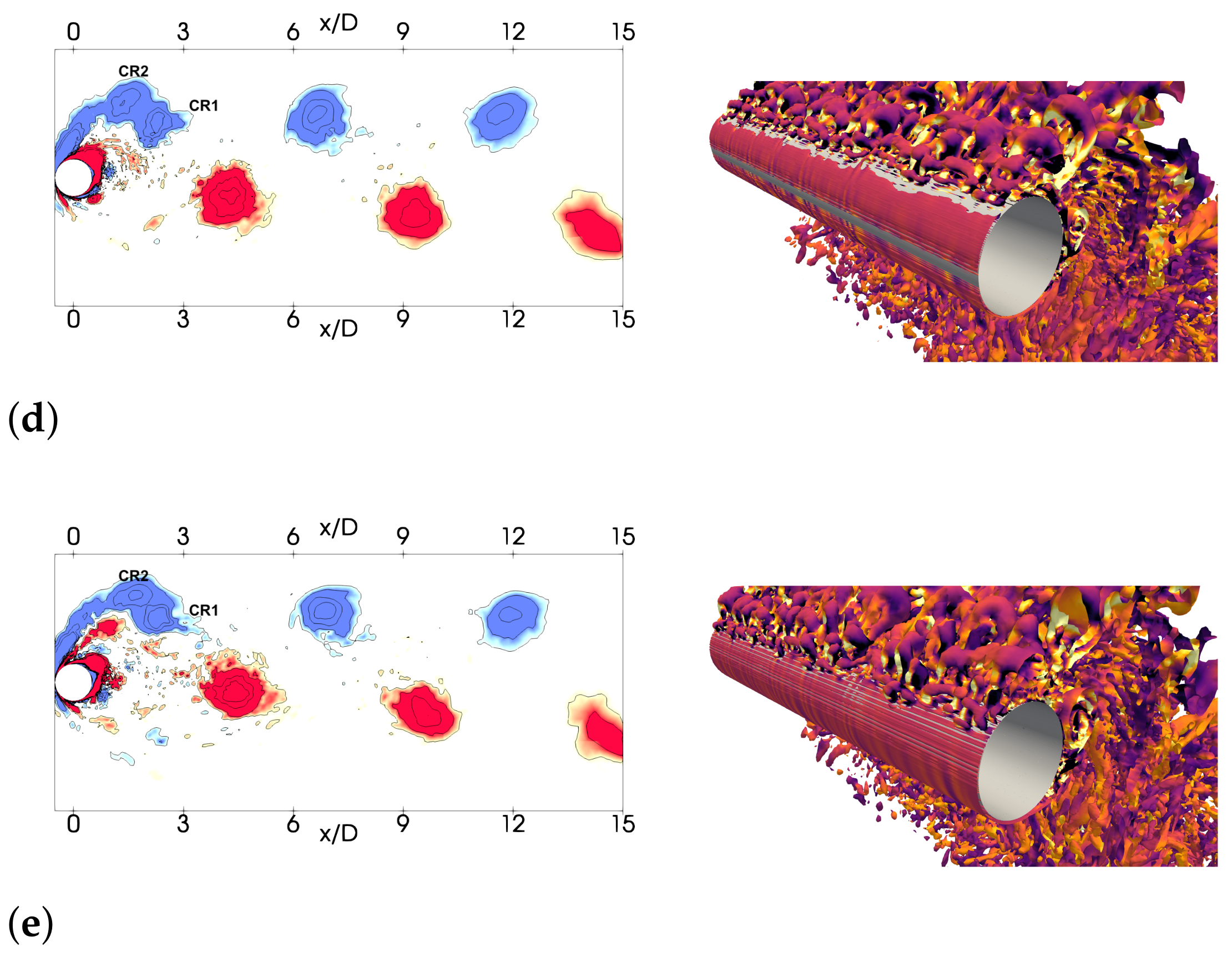
3.1. Flow Field Salient Features
3.2. Initial Branch,
3.3. Super-Upper Branch
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | movement amplitude |
| temporal coefficients | |
| c | damping |
| drag coefficient | |
| D | cylinder diameter |
| spatial and temporal field | |
| f | frequency |
| natural frequency of the cylinder | |
| k | structural stiffness |
| L | cylinder length |
| m | mass of the cylinder |
| mass ratio | |
| M | number of spatial points |
| N | number of modes |
| Reynolds number | |
| S | singular values (energy of the modes) |
| Strouhal number | |
| t | time |
| U | left singular vectors (POD modes) |
| freestream velocity | |
| reduced velocity | |
| V | right singular vectors (temporal coefficients) |
| ith singular vector | |
| X | spatial coordinates |
| Y | snapshot matrix |
| Greeks | |
| fluid density | |
| spatial modes | |
| ith spatial mode | |
| damping ratio | |
| kinematic viscosity | |
| Subscripts | |
| T | transposed |
| vortex-shedding | |
| x | stream-wise |
| y | cross-stream |
| Acronyms | |
| ALE | arbitrary Lagrangian–Eulerian |
| CCR | counter-clockwise-rotating |
| CR | clockwise-rotating |
| DoF | degrees of freedom |
| FE | finite element |
| FSI | fluid structure interaction |
| LES | large-eddy simulations |
| PIV | particle image velocimetry |
| POD | proper orthogonal decomposition |
| ROM | reduced-order model |
| SGS | sub-grid scale |
| SPOD | spectral proper orthogonal decomposition |
| SVD | single-value decomposition |
| TG | Taylor–Görtler |
| tke | turbulent kinetic energy |
| VIV | vortex-induced vibrations |
References
- Williamson, C.; Govardhan, R. Vortex-Induced Vibrations. Annu. Rev. Fluid Mech. 2004, 36, 413–455. [Google Scholar] [CrossRef]
- Modarres-Sadeghi, Y.; Mukundan, H.; Dahl, J.M.; Hover, F.S.; Triantafyllou, M.S. The effect of higher harmonic forces on fatigue life of marine risers. J. Sound Vib. 2010, 329, 43–55. [Google Scholar] [CrossRef]
- Akaydın, H.D.; Elvin, N.; Andreopoulos, Y. Wake of a cylinder: A paradigm for energy harvesting with piezoelectric materials. Exp Fluids 2010, 49, 291–304. [Google Scholar] [CrossRef]
- Mehmood, A.; Abdelkefi, A.; Hajj, M.R.; Nayfeh, A.H.; Akhtar, I.; Nuhait, A.O. Piezoelectric energy harvesting from vortex-induced vibrations of circular cylinder. J. Sound Vib. 2013, 332, 4656–4667. [Google Scholar] [CrossRef]
- Xu-Xu, J.; Barrero-Gil, A.; Velazquez, A. Dual mass system for enhancing energy extraction from Vortex-Induced Vibrations of a circular cylinder. Int. J. Mar. Energy 2016, 16, 250–261. [Google Scholar] [CrossRef]
- Bernitsas, M.M.; Raghavan, K.; Ben-Simon, Y.; Garcia, E.M.H. VIVACE (Vortex Induced Vibration Aquatic Clean Energy): A New Concept in Generation of Clean and Renewable Energy From Fluid Flow. J. Offshore Mech. Arct. Eng. 2008, 130, 041101. [Google Scholar] [CrossRef]
- Ding, L.; Zhang, L.; Bernitsas, M.M.; Chang, C.C. Numerical simulation and experimental validation for energy harvesting of single-cylinder VIVACE converter with passive turbulence control. Renew. Energy 2016, 85, 1246–1259. [Google Scholar] [CrossRef]
- Grouthier, C.; Michelin, S.; Bourguet, R.; Modarres-Sadeghi, Y.; de Langre, E. On the efficiency of energy harvesting using vortex-induced vibrations of cables. J. Fluids Struct. 2014, 49, 427–440. [Google Scholar] [CrossRef]
- Sarpkaya, T. Vortex-Induced Oscillations: A Selective Review. J. Appl. Mech. 1979, 46, 241–258. [Google Scholar] [CrossRef]
- Bearman, P.W. Vortex Shedding from Oscillating Bluff Bodies. Annu. Rev. Fluid Mech. 1984, 16, 195–222. [Google Scholar] [CrossRef]
- Sarpkaya, T. A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 2004, 19, 389–447. [Google Scholar] [CrossRef]
- Wiliamson, C.H.; Govardhan, R. Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 2004, 28, 477–539. [Google Scholar]
- Williamson, C.H.K.; Govardhan, R. A brief review of recent results in vortex-induced vibrations. J. Wind Eng. Ind. Aerodyn. 2008, 96, 713–735. [Google Scholar] [CrossRef]
- Triantafyllou, M.S.; Bourguet, R.; Dahl, J.; Modarres-Sadeghi, Y. Vortex-Induced Vibrations. In Springer Handbook of Ocean Engineering; Dhanak, M.R., Xiros, N.I., Eds.; Springer Handbooks; Springer International Publishing: Cham, Switzerland, 2016; pp. 819–850. [Google Scholar] [CrossRef]
- Williamson, C.H.K.; Roshko, A. Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 1988, 2, 355–381. [Google Scholar] [CrossRef]
- Pastrana, D.; Cajas, J.; Lehmkuhl, O.; Rodríguez, I.; Houzeaux, G. Large-eddy simulations of the vortex-induced vibration of a low mass ratio two-degree-of-freedom circular cylinder at subcritical Reynolds numbers. Comput. Fluids 2018, 173, 118–132. [Google Scholar] [CrossRef]
- Jauvtis, N.; Williamson, C. The effect of two degrees of freedom on vortex-induced vibration at low mass and damping. J. Fluid Mech. 2004, 509, 23–62. [Google Scholar] [CrossRef]
- Dahl, J.; Hover, F.; Triantafyllou, M.; Dong, S.; Karniadakis, G.E. Resonant vibrations of bluff bodies cause multivortex shedding and high frequency forces. Phys. Rev. Lett. 2007, 99, 144503. [Google Scholar] [CrossRef]
- Gsell, S.; Bourguet, R.; Braza, M. Two-degree-of-freedom vortex-induced vibrations of a circular cylinder at Re = 3900. J. Fluids Struct. 2016, 67, 156–172. [Google Scholar] [CrossRef]
- Pastrana, D.; Rodriguez, I.; Cajas, J.; Lehmkuhl, O.; Houzeaux, G. On the formation of Taylor-Görtler structures in the vortex induced vibration phenomenon. Int. J. Heat Fluid Flow 2020, 83, 108573. [Google Scholar] [CrossRef]
- Lumley, J.L. Rational Approach to Relations between Motions of Differing Scales in Turbulent Flows. Phys. Fluids 1981, 10, 1405. [Google Scholar] [CrossRef]
- Yondo, R.; Andrés, E.; Valero, E. A review on design of experiments and surrogate models in aircraft real-time and many-query aerodynamic analyses. Prog. Aerosp. Sci. 2018, 96, 23–61. [Google Scholar] [CrossRef]
- Ma, X.; Karamanos, G.S.; Karniadakis, G. Dynamics and low-dimensionality of a turbulent near wake. J. Fluid Mech. 2000, 410, 29–65. [Google Scholar] [CrossRef]
- Perrin, R.; Braza, M.; Cid, E.; Cazin, S.; Barthet, A.; Sevrain, A.; Mockett, C.; Thiele, F. Obtaining phase averaged turbulence properties in the near wake of a circular cylinder at high Reynolds number using POD. Exp. Fluids 2007, 43, 341–355. [Google Scholar] [CrossRef]
- Bergmann, M.; Cordier, L. Optimal control of the cylinder wake in the laminar regime by trust-region methods and POD reduced-order models. J. Comput. Phys. 2008, 227, 7813–7840. [Google Scholar] [CrossRef]
- Wang, H.; Cao, H.; Zhou, Y. POD analysis of a finite-length cylinder near wake. Exp. Fluids 2014, 55, 1–15. [Google Scholar] [CrossRef]
- Dhanwani, M.A.; Sarkar, A.; Patnaik, B. Lumped parameter models of vortex induced vibration with application to the design of aquatic energy harvester. J. Fluids Struct. 2013, 43, 302–324. [Google Scholar] [CrossRef]
- Srinivasan, S.; Narasimhamurthy, V.; Patnaik, B. Reduced order modeling of two degree-of-freedom vortex induced vibrations of a circular cylinder. J. Wind Eng. Ind. Aerodyn. 2018, 175, 342–351. [Google Scholar] [CrossRef]
- Liberge, E.; Hamdouni, A. Reduced order modelling method via proper orthogonal decomposition (POD) for flow around an oscillating cylinder. J. Fluids Struct. 2010, 26, 292–311. [Google Scholar] [CrossRef]
- Huera-Huarte, F.J.; Vernet, A. Vortex modes in the wake of an oscillating long flexible cylinder combining POD and fuzzy clustering. Exp. Fluids 2010, 48, 999–1013. [Google Scholar] [CrossRef]
- Riches, G.; Martinuzzi, R.; Morton, C. Proper orthogonal decomposition analysis of a circular cylinder undergoing vortex-induced vibrations. Phys. Fluids 2018, 30, 105103. [Google Scholar] [CrossRef]
- O’Neill, C.M.; Riches, G.; Morton, C. Wake dynamics and heuristic modelling in the desynchronization region of 1-DOF VIV. Int. J. Heat Fluid Flow 2021, 88, 108729. [Google Scholar] [CrossRef]
- Janocha, M.J.; Ong, M.C.; Yin, G. Large eddy simulations and modal decomposition analysis of flow past a cylinder subject to flow-induced vibration. Phys. Fluids 2022, 34, 045119. [Google Scholar] [CrossRef]
- Schubert, Y.; Sieber, M.; Oberleithner, K.; Martinuzzi, R. Towards robust data-driven reduced-order modelling for turbulent flows: Application to vortex-induced vibrations. Theor. Comput. Fluid Dyn. 2022, 36, 517–543. [Google Scholar] [CrossRef]
- Zhang, M.; Zheng, Z.C. Relations of POD modes and Lyapunov exponents to the nonlinear dynamic states in flow over oscillating tandem cylinders. Phys. Fluids 2018, 30, 123602. [Google Scholar] [CrossRef]
- Mella, D.; Brevis, W.; Susmel, L. Spanwise wake development of a bottom-fixed cylinder subjected to vortex-induced vibrations. Ocean Eng. 2020, 218, 108280. [Google Scholar] [CrossRef]
- Lehmkuhl, O.; Houzeaux, G.; Owen, H.; Chrysokentis, G.; Rodriguez, I. A low-dissipation finite element scheme for scale resolving simulations of turbulent flows. J. Comput. Phys. 2019, 390, 51–65. [Google Scholar] [CrossRef]
- Rodriguez, I.; Lehmkuhl, O.; Soria, M. On the effects of the free-stream turbulence on the heat transfer from a sphere. Int. J. Heat Mass Transf. 2021, 164, 120579. [Google Scholar] [CrossRef]
- Rodriguez, I.; Lehmkuhl, O. On the Characteristics of the Super-Critical Wake behind a Circular Cylinder. Fluids 2021, 6, 396. [Google Scholar] [CrossRef]
- Capuano, F.; Coppola, G.; Rández, L.; de Luca, L. Explicit Runge-Kutta schemes for incompressible flow with improved energy-conservation properties. J. Comput. Phys. 2017, 328, 86–94. [Google Scholar] [CrossRef]
- Trias, F.X.; Lehmkuhl, O. A self-adaptive strategy for the time integration of Navier-Stokes equations. Numer. Heat Transfer. Part B 2011, 60, 116–134. [Google Scholar] [CrossRef]
- Vreman, A.W. The filtering analog of the variational multiscale method in large-eddy simulation. Phys. Fluids 2003, 15, L61. [Google Scholar] [CrossRef]
- Cajas, J.; Houzeaux, G.; Vázquez, M.; García, M.; Casoni, E.; Calmet, H.; Artigues, A.; Borrell, R.; Lehmkuhl, O.; Pastrana, D.; et al. Fluid-Structure Interaction Based on HPC Multicode Coupling. SIAM J. Sci. Comput. 2018, 40, C677–C703. [Google Scholar] [CrossRef]
- Holmes, P.J.; Lumley, J.L.; Berkooz, G.; Mattingly, J.C.; Wittenberg, R.W. Low-dimensional models of coherent structures in turbulence. Phys. Rep. 1997, 287, 337–384. [Google Scholar] [CrossRef]
- Liang, Y.C.; Lee, H.P.; Lim, S.P.; Lin, W.Z.; Lee, K.H.; Wu, C.G. Proper orthogonal decomposition and its applications—Part I: Theory. J. Sound Vib. 2002, 252, 527–544. [Google Scholar] [CrossRef]
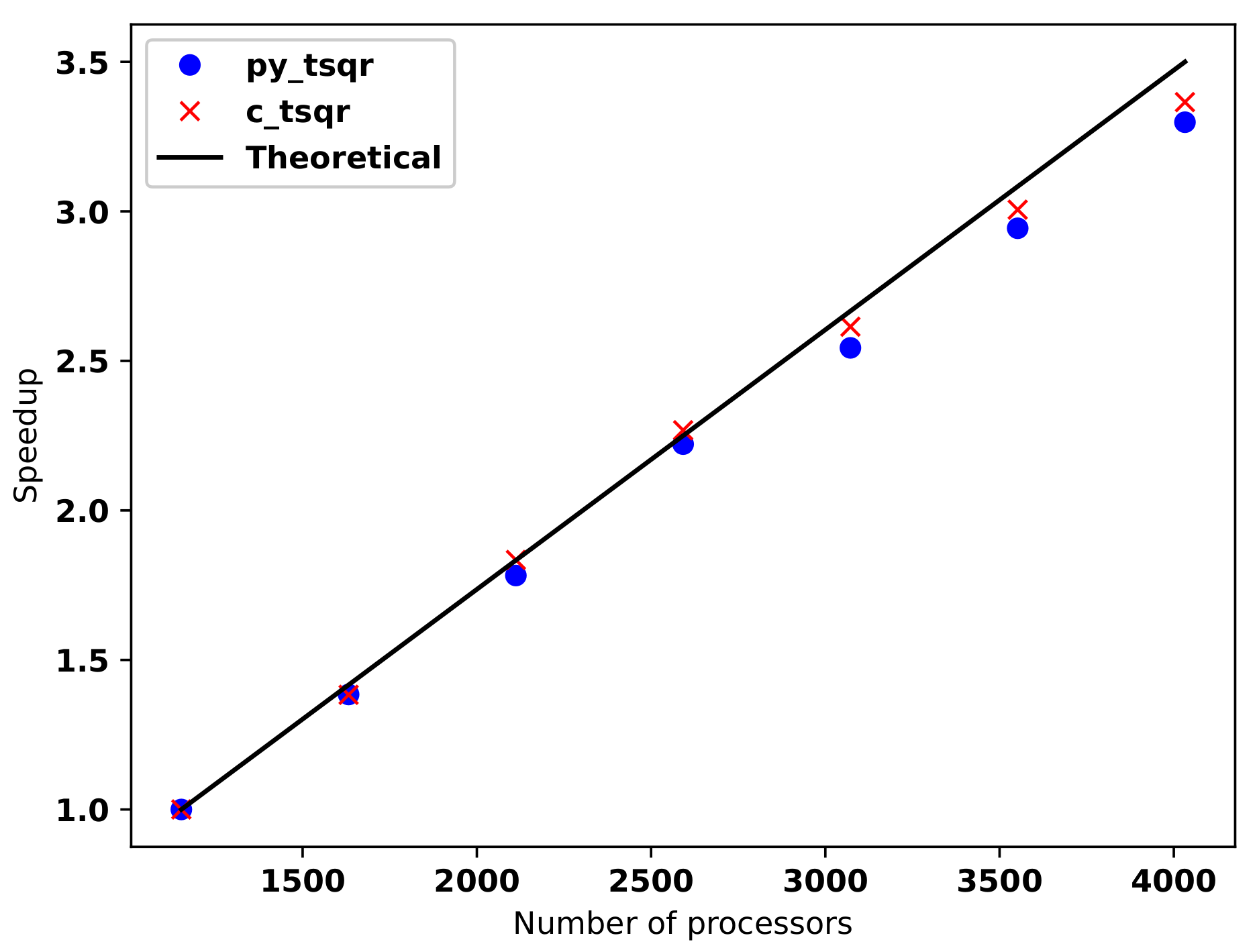
- Demmel, J.; Grigori, L.; Hoemmen, M.; Langou, J. Communication-optimal Parallel and Sequential QR and LU Factorizations. SIAM J. Sci. Comput. 2012, 34, A206–A239. [Google Scholar] [CrossRef]
- Norberg, C. LDV measurements in the near wake of a circular cylinder. In Proceedings of the ASME Conference on Advances in the Understanding of Bluff Body Wakes and Vortex Induced Vibration, Washington, DC, USA, 21–25 June 1998. [Google Scholar]
- Aljure, D.; Lehmkhul, O.; Rodríguez, I.; Oliva, A. Three dimensionality in the wake of the flow around a circular cylinder at Reynolds number 5000. Comput. Fluids 2017, 147, 102–118. [Google Scholar] [CrossRef]
- Ziada, S.; Rockwell, D. Generation of higher harmonics in a self-oscillating mixing layer-wedge system. AIAA J. 1982, 20, 196–202. [Google Scholar] [CrossRef]
- Rodríguez, I.; Lehmkuhl, O.; Pastrana, D.; Cajas, J.C.; Houzeaux, G. Wakes and Instabilities of Static and Freely Vibrating Cylinders. In ERCOFTAC Workshop Direct and Large Eddy Simulation; García-Villalba, M., Kuerten, H., Salvetti, M.V., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 49–59. [Google Scholar]


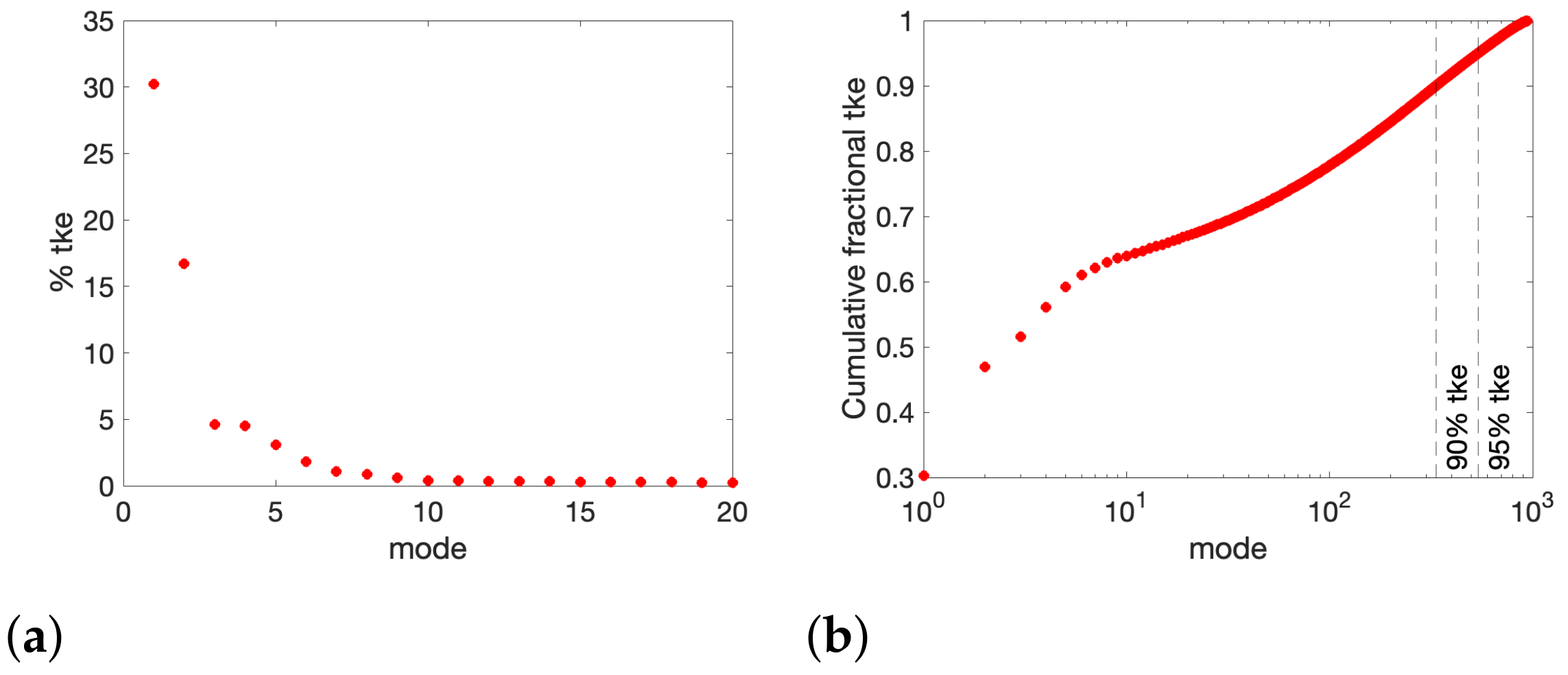
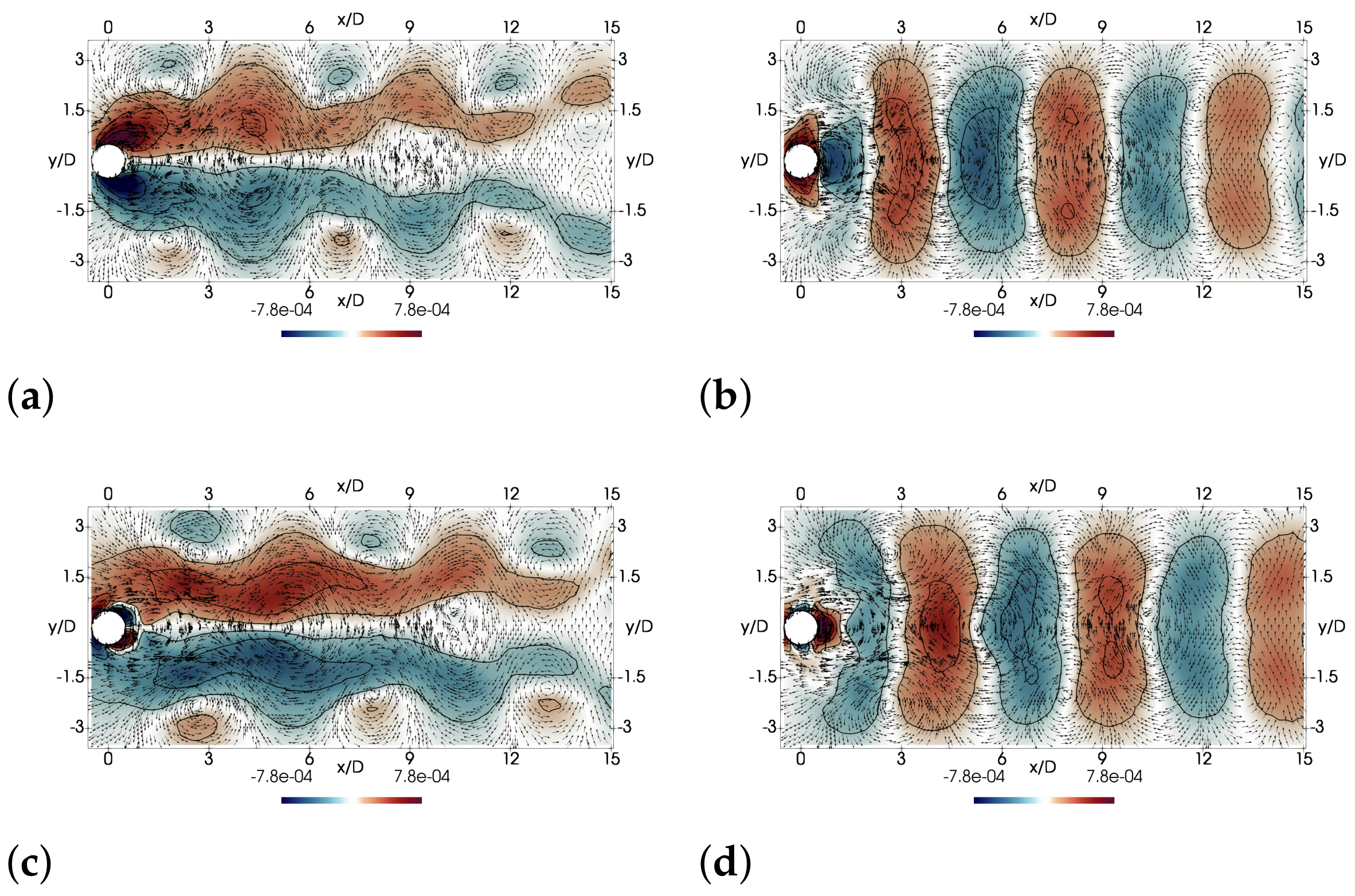
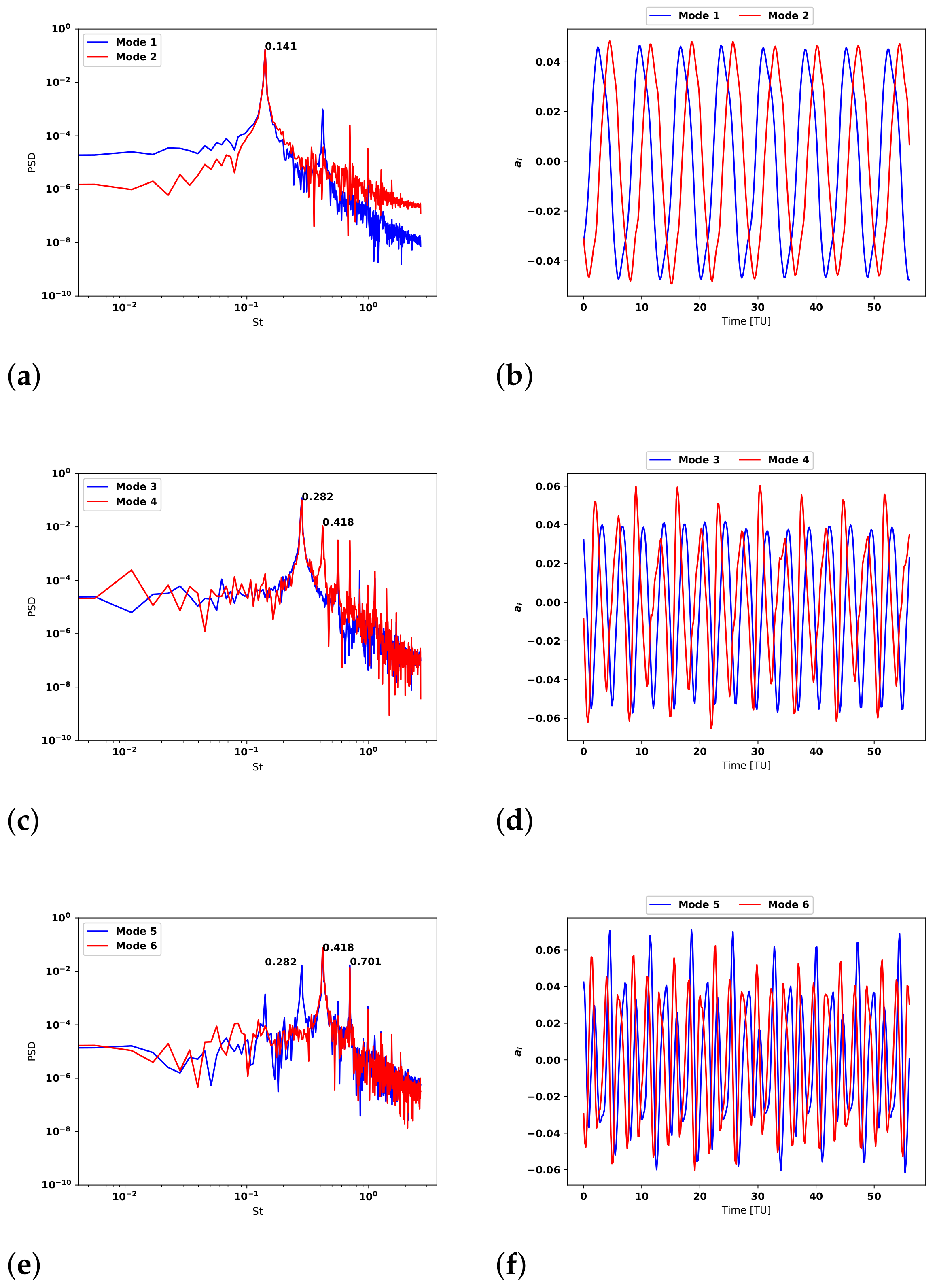

| N | |||
|---|---|---|---|
| 3.0 | 880 | 0.165 | 0.0054 |
| 5.5 | 944 | 0.139 | 0.0036 |
| 3.0 | 1.709 | 0.165 | 0.166 | 0.331 | 0.186 | 0.091 |
| 5.5 | 3.235 | 0.141 | 0.141 | 0.282 | 1.200 | 0.322 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eiximeno, B.; Miró, A.; Cajas, J.C.; Lehmkuhl, O.; Rodriguez, I. On the Wake Dynamics of an Oscillating Cylinder via Proper Orthogonal Decomposition. Fluids 2022, 7, 292. https://doi.org/10.3390/fluids7090292
Eiximeno B, Miró A, Cajas JC, Lehmkuhl O, Rodriguez I. On the Wake Dynamics of an Oscillating Cylinder via Proper Orthogonal Decomposition. Fluids. 2022; 7(9):292. https://doi.org/10.3390/fluids7090292
Chicago/Turabian StyleEiximeno, Benet, Arnau Miró, Juan Carlos Cajas, Oriol Lehmkuhl, and Ivette Rodriguez. 2022. "On the Wake Dynamics of an Oscillating Cylinder via Proper Orthogonal Decomposition" Fluids 7, no. 9: 292. https://doi.org/10.3390/fluids7090292





