Numerical Characterization of the Flow Dynamics and COP Estimation of a Binary Fluid Ejector Ground Source Heat Pump Cooling System
Abstract
:1. Introduction
2. Refrigeration COP Calculation
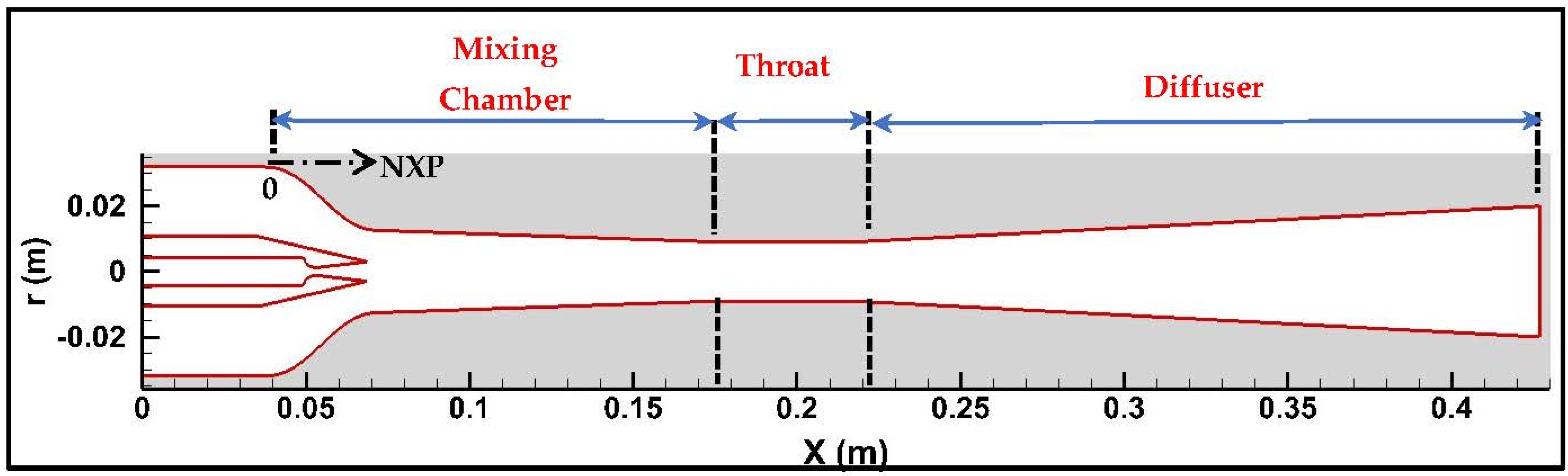
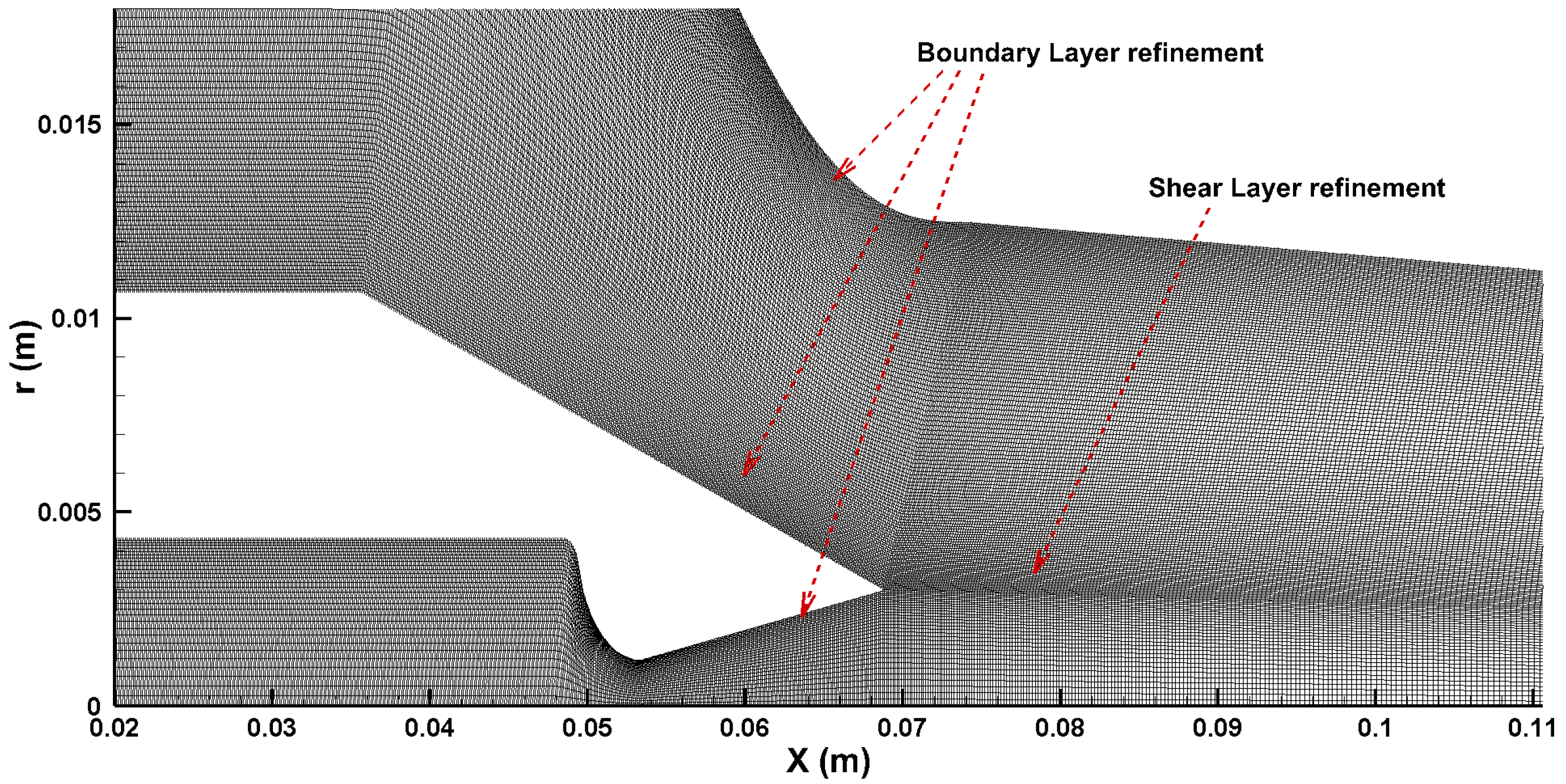
3. Ejector Geometry and CFD Simulations
4. Results and Discussion
4.1. Binary Fluid Pair Assay and Ranking
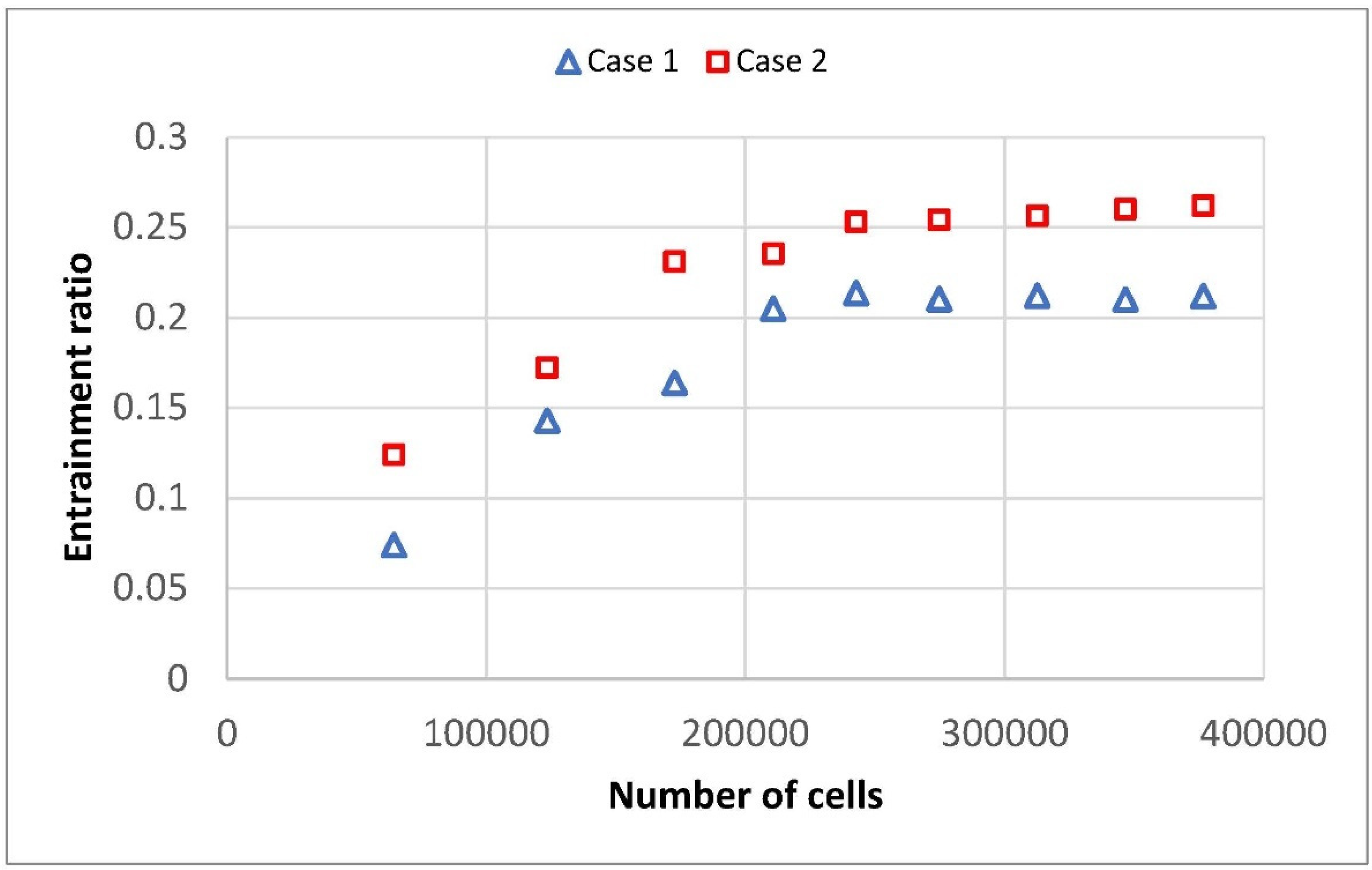
4.2. Entrainement Ratio Using Single Fluid Ejector
4.3. CFD Simulations for Selected Binary Fluid Candidates
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Acronyms | |
| BFE GSHP | Binary Fluid Ejector Ground Source Heat Pump |
| COP | Coefficient of Performance |
| CFD | Computational Fluid Dynamics |
| CR | Compression Ratio |
| TKE | Turbulent Kinetic Energy |
| MS | Mixing section |
| TS | Throat section |
| DS | Diffuser section |
| M1 | Molecular mass of the primary fluid |
| M2 | Molecular mass of the secondary fluid |
| Symbols | |
| TBoil | Boiler Saturation Temperature |
| TEvap | Evaporator Saturation Temperature |
| TCond | Condenser Saturation Temperature |
| QS,Evap | Refrigeration capacity |
| QP,Boil | Heat load for Boiler |
| QP,Cond | Heat rejection from Condenser |
| Enthalpy of vaporization in the Evaporator (secondary fluid) | |
| Enthalpy of vaporization in the Boiler (primary fluid) | |
| Average specific heat capacity of primary fluid | |
| Average specific heat capacity of secondary fluid | |
| Mass entrainment ratio |
References
- El Hassan, M.; Gubanov, A.; May, W.; Martinuzzi, R. Numerical investigation of the flow dynamics of a supersonic fluid ejector. In Proceedings of the International Conference on Heat Transfer and Fluid Flow, Prague, Czech Republic, 11–12 August 2014. [Google Scholar]
- El Hassan, M.; Bukharin, N. Numerical investigation of the flow dynamics inside single fluid and binary fluid ejectors. J. Phys. Conf. Ser. 2019, 1276, 012012. [Google Scholar] [CrossRef]
- Chunnanond, K.; Aphornratana, S. An Experimental investigation of a steam ejector refrigerator: The analysis of the pressure profile along the ejector. Appl. Therm. Eng. 2004, 27, 311–322. [Google Scholar] [CrossRef]
- Buyadgie, D.I.; Nichenko, S.V.; Buyadgie, O.D. Novel ejector cooling technologies using binary fluids. In Proceedings of the 9th International Conference on Sustainable Energy Technologies, Shanghai, China, 24–27 August 2010. [Google Scholar]
- Eames, I.W.; Ablwaifa, A.E.; Petrenko, V. Results of an experimental study of an advanced jet-pump refrigerator operating with R245fa. Appl. Therm. Eng. 2007, 27, 2833–2840. [Google Scholar] [CrossRef]
- Sankarlal, T.; Mani, A. Experimental investigations on ejector refrigeration system with ammonia. Renew. Energy 2007, 32, 1403–1413. [Google Scholar] [CrossRef]
- Varga, S.; Lebre, P.S.; Oliveira, A.C. Readdressing working fluid selection with a view to designing a variable geometry ejector. Int. J. Low-Carbon Technol. 2015, 10, 205–215. [Google Scholar] [CrossRef] [Green Version]
- El Zohbi, B.; Bukharin, N.; Assoum, H.H.; Abed-Meraim, K.; Sakout, A.; El Hassan, M. Investigation of the effects of the jet nozzle geometry and location on the performance of supersonic fluid ejectors. Energy Rep. 2022, 8, 228–233. [Google Scholar] [CrossRef]
- Eames, I.W.; Aphornratana, S.; Haider, H. A theoretical and experimental study of a small-scale steam jet refrigerator. Int. J. Regrigeration 1995, 18, 378–386. [Google Scholar] [CrossRef]
- Eames, I.W. A new prescription for the design of supersonic jet pumps: The constant rate of momentum change method. Appl. Therm. Eng. 2002, 22, 121–131. [Google Scholar] [CrossRef]
- Chunnanond, K.; Aphornratana, S. Ejectors: Applications in refrigeration technology. Renew. Sustain. Energy Rev. 2004, 8, 129–155. [Google Scholar] [CrossRef]
- Chang, Y.J.; Chen, Y.M. Enhancement of a steam-jet refrigerator using a novel application of the petal nozzle. Exp. Therm. Fluid Sci. 2000, 22, 203–211. [Google Scholar] [CrossRef]
- El Hassan, M.; Assoum, H.H.; Bukharin, N.; Abed-Meraim, K.; Sakout, A. Investigation of thermo-physical fluid properties effect on binary fluid ejector performance. Energy Rep. 2020, 6, 287–292. [Google Scholar] [CrossRef]
- Xiao, J.; Wu, Q.; Chen, L.; Ke, W.; Wu, C.; Yang, X.; Yu, L.; Jiang, H. Assessment of Different CFD Modeling and Solving Approaches for a Supersonic Steam Ejector Simulation. Atmosphere 2022, 13, 144. [Google Scholar] [CrossRef]
- Han, Y.; Wang, X.; Sun, H.; Zhang, G.; Guo, L.; Tu, J. CFD simulation on the boundary layer separation in the steam ejector and its influence on the pumping performance. Energy 2019, 167, 469–483. [Google Scholar] [CrossRef]
- Buyadgie, D.; Buyadgie, O.; Artemenko, S.V.; Chamchine, A.; Drakhnia, O. Conceptual design of binary/multicomponent fluid ejector refrigeration systems. Int. J. Low-Carbon Technol. 2012, 7, 120–127. [Google Scholar] [CrossRef] [Green Version]
- Buyadgie, O.; Drakhnia, O.; Miyazaki, T. The analysis of binary fluid ejector assisted solar desalination system. In Proceedings of the 17th International Refrigeration and Air Conditioning Conference. Purdue University, West Lafayette, IN, USA, 9–12 July 2018. [Google Scholar]
- Liu, X.; Munk, J. Field Test and Evaluation of Residential Ground Source Heat Pump Systems Using Emerging Ground Coupling Technologies. In Proceedings of the 11th International Energy Agency Heat Pump Conference, Montréal, QC, Canada, 11–12 May 2014. [Google Scholar]
- El Hassan, M. Numerical Investigation of the Flow Dynamics Inside Supersonic Fluid Ejector. Arab. J. Sci. Eng. 2019, 45, 909–919. [Google Scholar] [CrossRef]
- Bartosiewicz, Y.; Aidoun, Z.; Desevaux, P.; Mercadier, Y. Numerical and experimental investigations on supersonic ejectors. Int. J. Heat Fluid Flow 2005, 26, 56–70. [Google Scholar] [CrossRef]
- El Hassan, M.; Meslem, A. Time-resolved stereoscopic particle image velocimetry investigation of the entrainment in the near field of circular and daisy-shaped orifice jets. Phys. Fluids 2010, 22, 035107. [Google Scholar] [CrossRef]


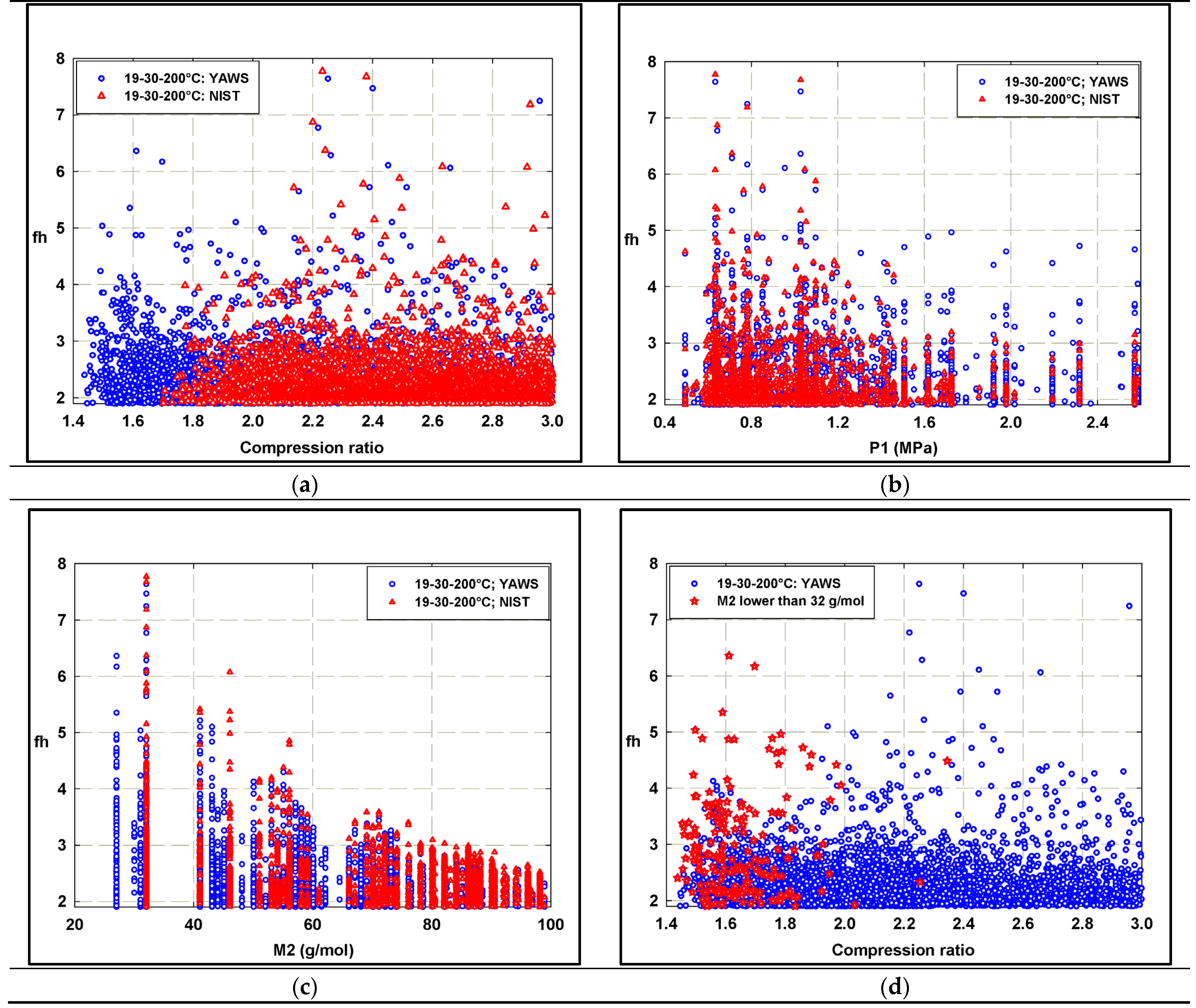

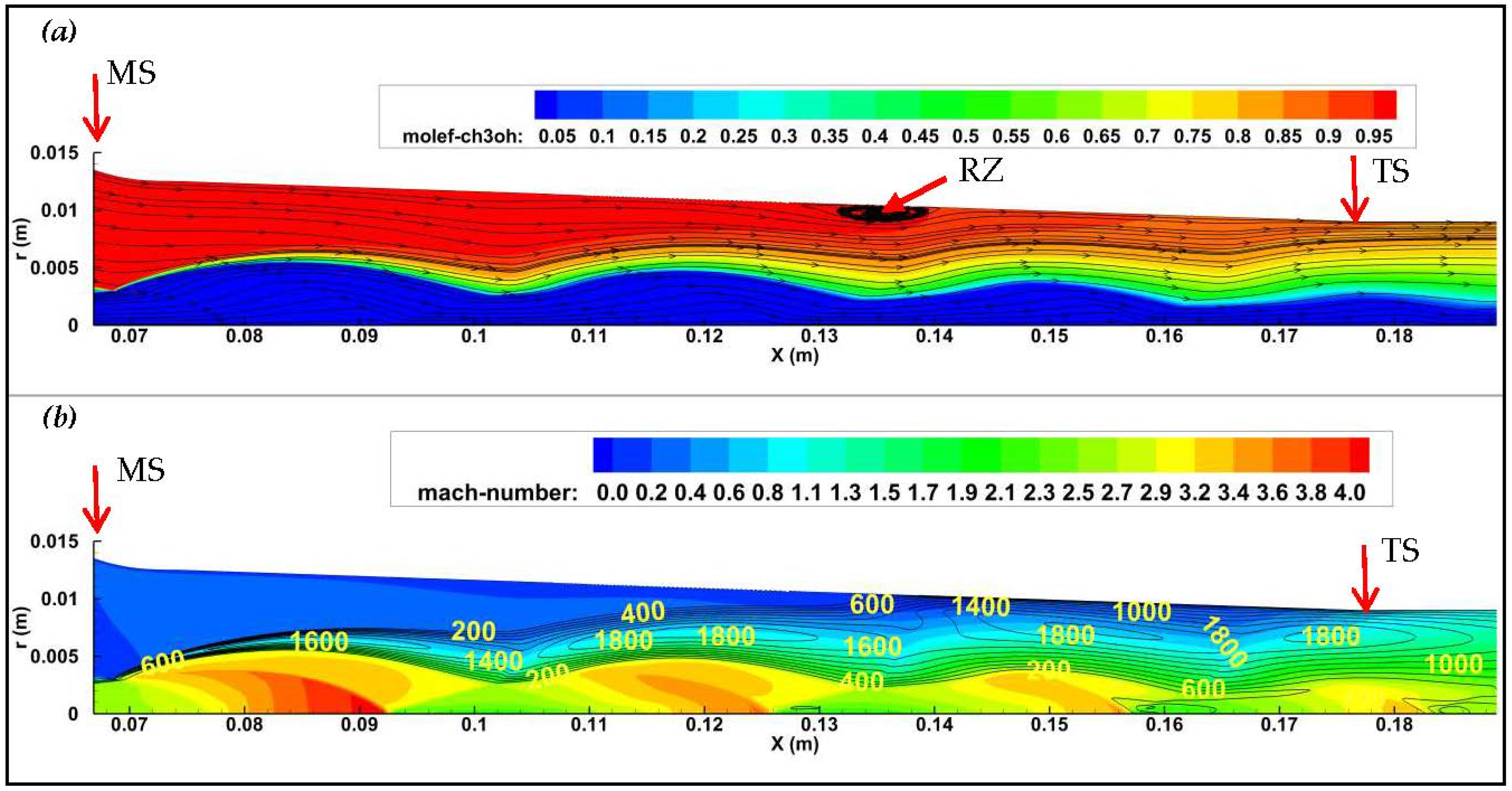
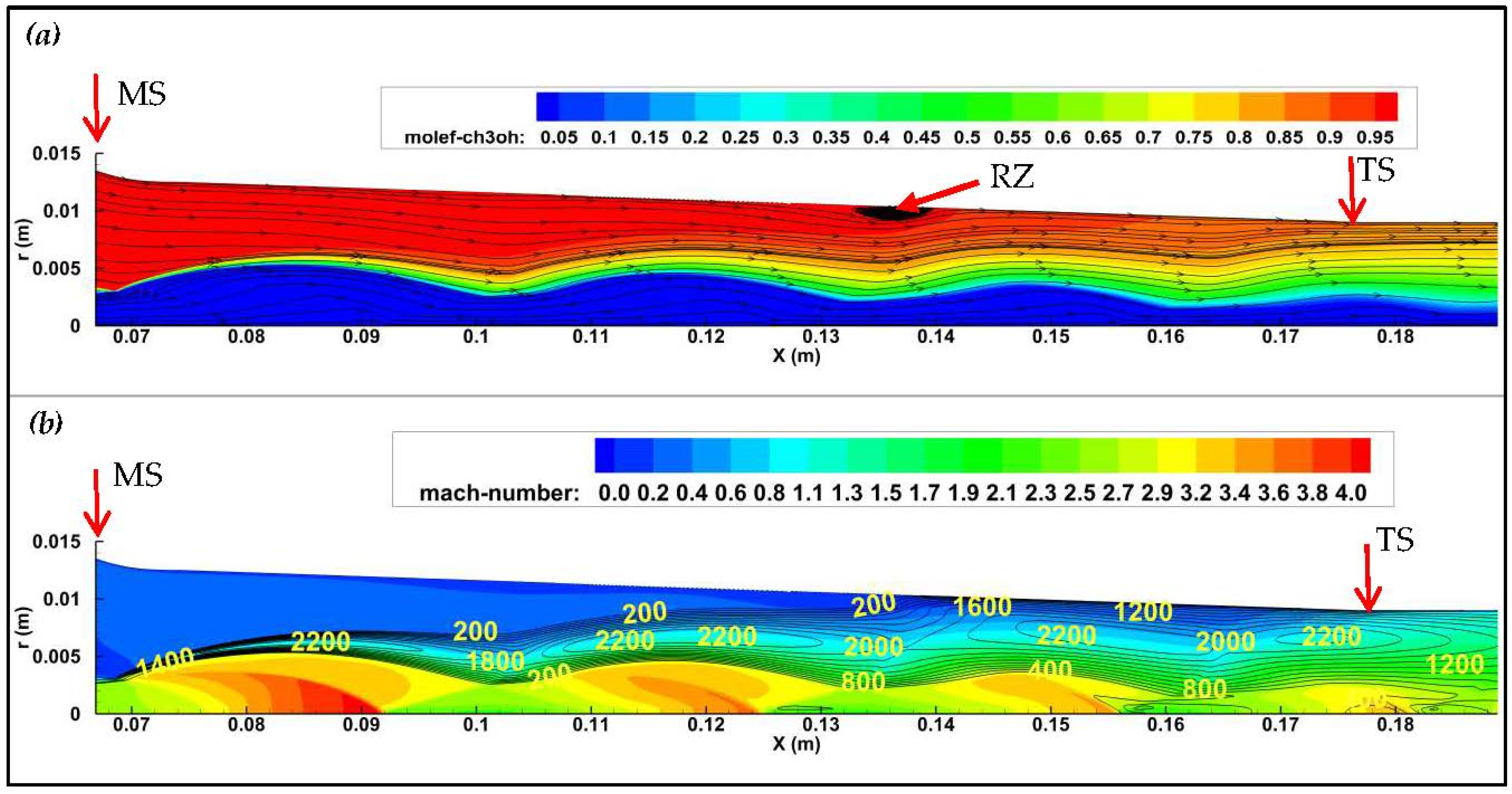
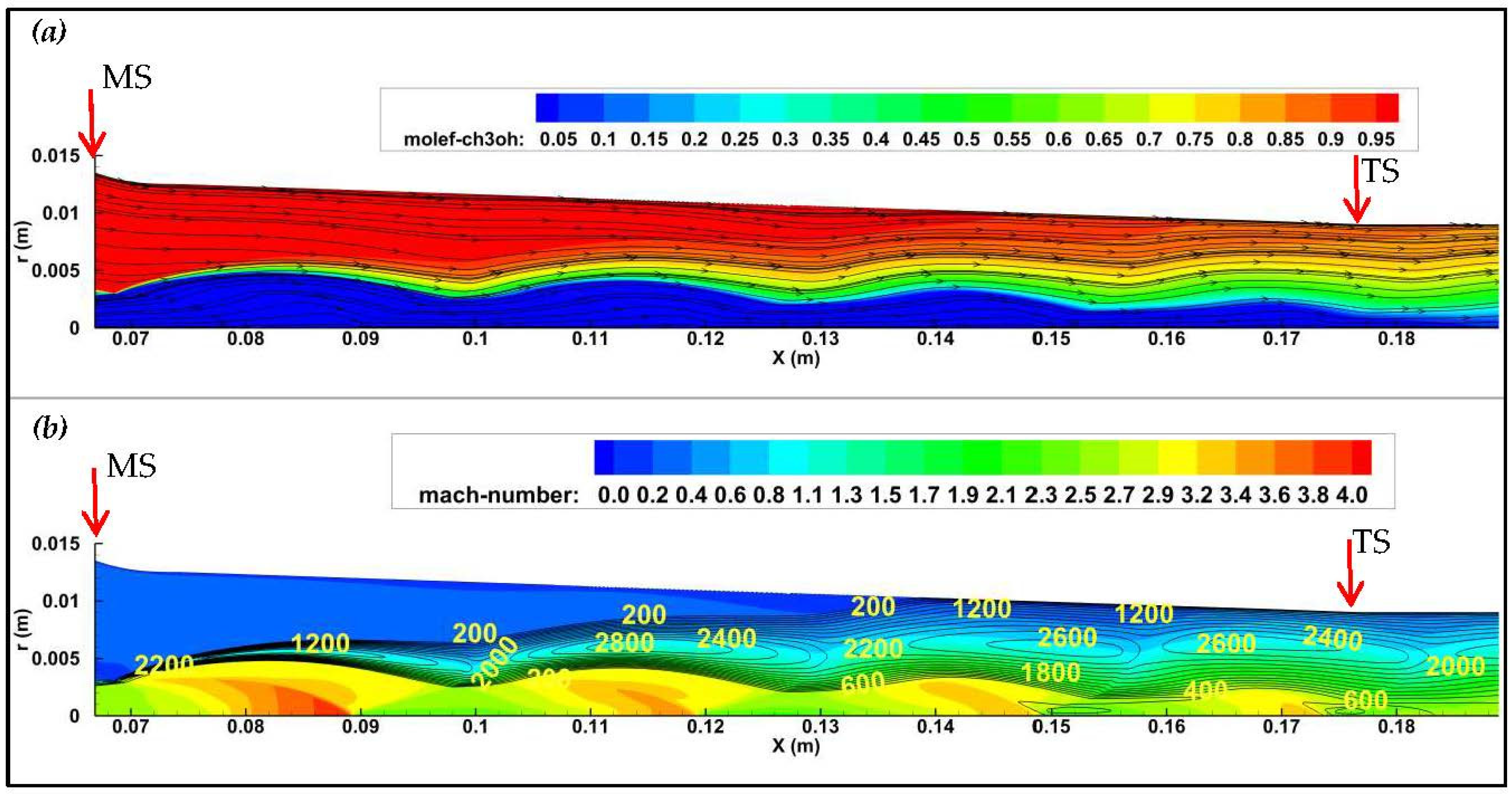
| Primary Fluid | Secondary Fluid | M1 (g/mol) | M2 (g/mol) | M1/M2 | PBoil (Mpa) | PEvap (Kpa) | PCond (Kpa) | CR | fh |
|---|---|---|---|---|---|---|---|---|---|
| difluorodiiodomethane | methanol | 304.00 | 32.04 | 9.49 | 1.03 | 12.31 | 29.10 | 2.36 | 7.68 |
| bromofluoroiodomethane | methanol | 238.83 | 32.04 | 7.45 | 0.80 | 12.31 | 27.00 | 2.19 | 6.37 |
| bromotrichloromethane | methanol | 198.00 | 32.04 | 6.18 | 0.83 | 12.31 | 28.00 | 2.27 | 4.92 |
| Chloroiodomethane | acetonitrile | 176.38 | 41.05 | 4.30 | 0.87 | 8.91 | 17.70 | 1.99 | 2.90 |
| ethylene, 1,1-dibromo | acetonitrile | 185.85 | 41.05 | 4.53 | 1.02 | 8.91 | 17.50 | 1.96 | 2.80 |
| 2-chloropropenoyl fluoride | methanol | 108.50 | 32.04 | 3.39 | 1.20 | 12.31 | 29.00 | 2.36 | 2.47 |
| 3-methylthiophene | methanol | 98.17 | 32.04 | 3.06 | 0.70 | 12.31 | 25.50 | 2.07 | 2.34 |
| methanedithiol | methanol | 80.17 | 32.04 | 2.50 | 1.20 | 12.31 | 29.00 | 2.36 | 2.12 |
| 1-methoxycyclopentene | methanol | 98.14 | 32.04 | 3.06 | 0.77 | 12.31 | 25.20 | 2.05 | 1.97 |
| Primary Fluid | Secondary Fluid | M1 (g/mol) | M2 (g/mol) | M1/M2 | PEvap (KPa) | PCond (KPa) | PBoil (MPa) | TBoil (°C) | CR | (g/s) | (g/s) | ER | fh | COP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Difluorodiiodomethane | methanol | 304.00 | 32.04 | 9.50 | 12.31 | 29.10 | 1.03 | 200 | 2.36 | 25 | 5.2 | 0.21 | 7.68 | 1.60 |
| Bromofluoroiodomethane | methanol | 238.83 | 32.04 | 7.45 | 12.31 | 27.00 | 1.00 | 220 | 2.19 | 21.1 | 5.6 | 0.26 | 6.37 | 1.69 |
| Bromotrichloromethane | methanol | 198.00 | 32.04 | 6.19 | 12.31 | 28.00 | 0.83 | 210 | 2.27 | 16.2 | 5.9 | 0.36 | 4.92 | 1.79 |
| Chloroiodomethane | acetonitrile | 176.38 | 41.05 | 4.30 | 8.90 | 17.70 | 0.70 | 180 | 1.99 | 13.3 | 4.5 | 0.34 | 3.00 | 1.02 |
| ethylene, 1,1-dibromo | acetonitrile | 185.85 | 41.05 | 4.53 | 8.90 | 17.50 | 0.70 | 170 | 1.97 | 13.7 | 4.4 | 0.32 | 2.80 | 0.90 |
| 2-chloropropenoyl fluoride | methanol | 108.50 | 32.04 | 3.39 | 12.31 | 29.00 | 1.20 | 200 | 2.36 | 17.5 | 6.4 | 0.37 | 2.36 | 0.86 |
| 3-methylthiophene | methanol | 98.17 | 32.04 | 3.06 | 12.31 | 25.50 | 0.80 | 204 | 2.07 | 10.8 | 6.3 | 0.58 | 2.34 | 1.37 |
| Methanedithiol | methanol | 80.17 | 32.04 | 2.50 | 12.31 | 29.00 | 1.20 | 200 | 2.36 | 13.3 | 7.05 | 0.53 | 2.02 | 1.07 |
| 1-methoxycyclopentene | methanol | 98.14 | 32.00 | 3.07 | 12.31 | 25.20 | 0.77 | 200 | 2.05 | 10.6 | 6.53 | 0.62 | 1.97 | 1.21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Hassan, M. Numerical Characterization of the Flow Dynamics and COP Estimation of a Binary Fluid Ejector Ground Source Heat Pump Cooling System. Fluids 2022, 7, 250. https://doi.org/10.3390/fluids7070250
El Hassan M. Numerical Characterization of the Flow Dynamics and COP Estimation of a Binary Fluid Ejector Ground Source Heat Pump Cooling System. Fluids. 2022; 7(7):250. https://doi.org/10.3390/fluids7070250
Chicago/Turabian StyleEl Hassan, Mouhammad. 2022. "Numerical Characterization of the Flow Dynamics and COP Estimation of a Binary Fluid Ejector Ground Source Heat Pump Cooling System" Fluids 7, no. 7: 250. https://doi.org/10.3390/fluids7070250






