Multidimensional Vibro-Acoustical Diagnostics of Cavitation: Theory and Illustration on a Kaplan Turbine
Abstract
:1. Introduction
2. The Multidimensional Approach
- It adds a spatial dimension in the description of the cavitation processes by using many spatially distributed sensors—typically, on all guide-vane trunnions or levers, and on the turbine shaft. This makes the cavitation-intensity estimates unbiased.
- It also adds a time dimension to the description by following variations of cavitation within a revolution, thus assessing and interpreting data dependence on the instantaneous angular position of the runner.
- By checking all the individual spatial and temporal samples at all relevant operation points, it deals with a full set of individual spatial/temporal/operational resolution cells of the quantifiers of the cavitation processes.
- It does not transform the acquired signals into spectra or other globalising formats in which data on individual cavitation processes are smoothed or in which partly or fully disappear. Instead, it preserves and displays full individual data on the cavitation mechanisms generated by the rotor-stator interaction in their natural form. To do so, sufficiently broad-band and fast sensors (acoustic emission sensors or fast accelerometers) are used to pick up all or most components of cavitation-generated noise and to assess them correctly, where the signal and data processing is started by squaring the outputs of (linear) vibro-acoustical sensors; this makes the quantities stemming from independent cavitation mechanisms additive. Using these squares as estimates of the random instantaneous local cavitation intensity, it calculates – synchronised with runner rotation – averages of the squares over revolutions, and delivers estimates of the deterministic description of the cavitation intensity specific to each spatial/temporal/operational cell. This approaches the maximum of the interpretable data on cavitation that can be achieved vibro-acoustically.
3. Tested Case
- the prototype; and on three turbine models both in accordance with the common procedure (visual detection of cavitation and sigma-break curves) and vibro-acoustically:
- the model of the existing turbine, tested on the prototype;
- the model with an improved runner;
- the model with both the runner and the guide vanes improved.

4. Measurement Method

4.1. Data Acquisition

4.2. Parameters Setting
4.3. Additivity of Mechanisms
- In almost all cavitation cases, and especially in the erosive ones, signal samples taken at the same values of , Θ, and Φ but in different revolutions are independent and thus uncorrelated:<x(,Θ,Φ,n1) x(,Θ,Φ,n2)> ≡ 0, <y(,Φ,n1) y(,Φ,n2)> ≡ 0, for n1 ≠ n2.
- Even if coming at the same moment, within the same revolution, the cavitation components that are developed in different VB patterns of rotor-stator interaction are independent and thus uncorrelated. Indeed, since stemming from independent inflow wakes, they have an independent fine structure of cavitation pulses.
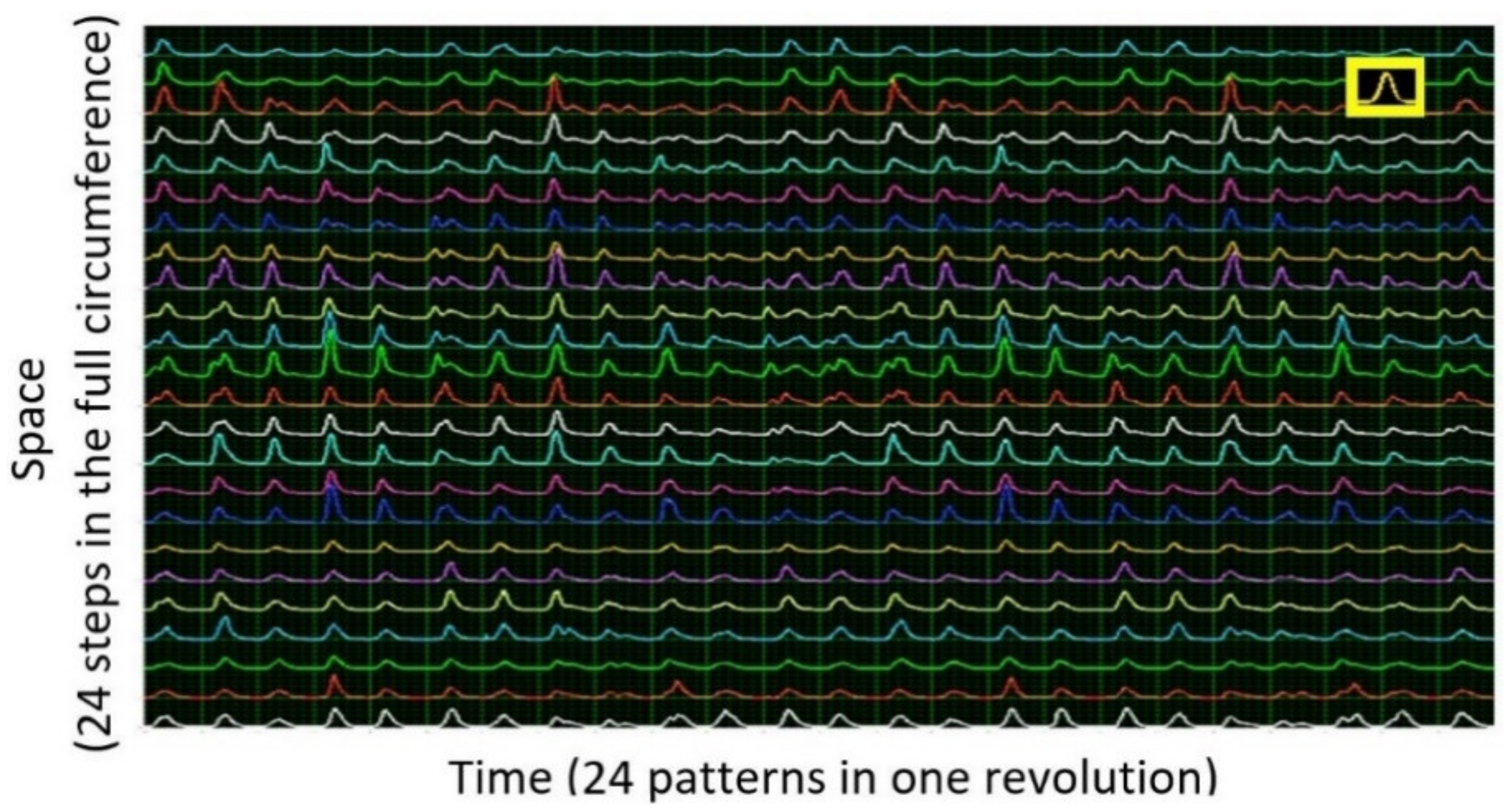
4.4. Further Data Formats
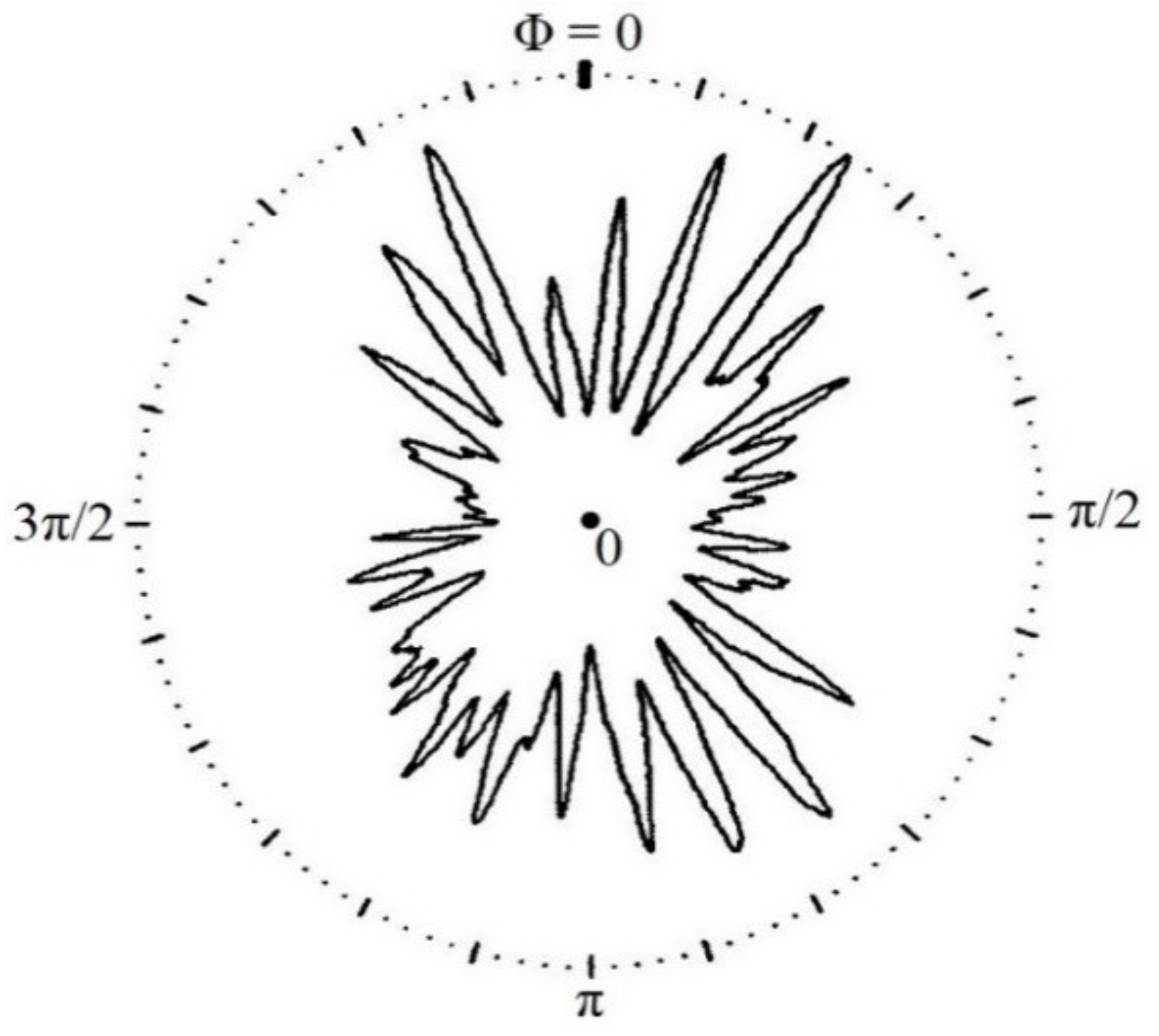
4.5. Quantification of Cavitation Mechanisms
4.6. Calibration for Erosion
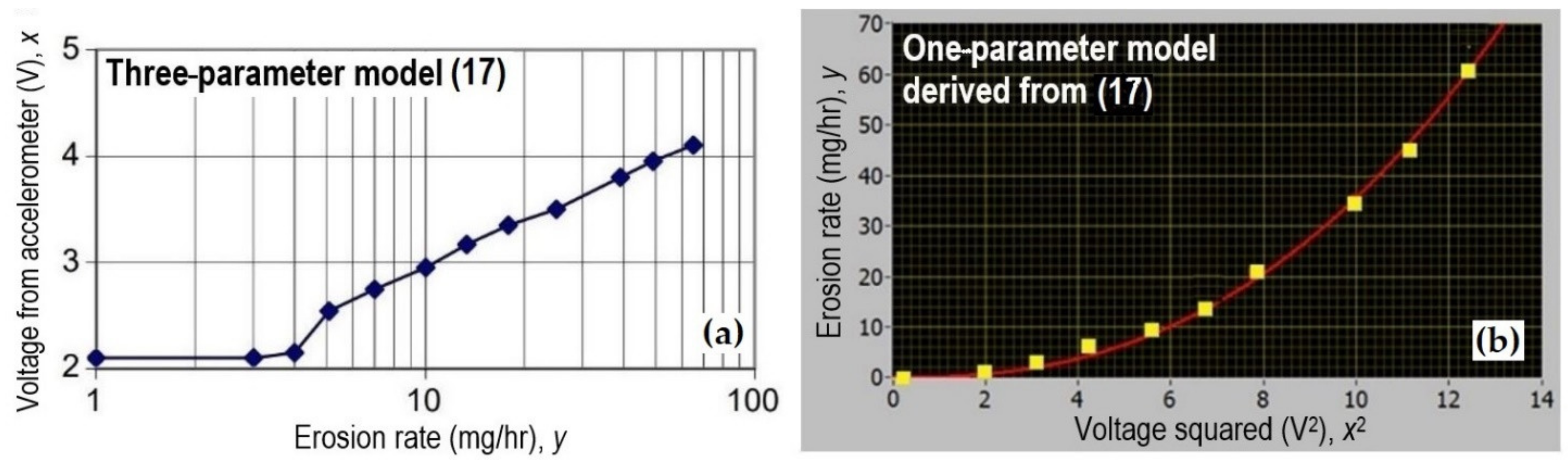
- If only one cavitation mechanism is found in the turbine under consideration, the task is resolved: erosion is caused by it and the quantification of that mechanism results in the quantification of the erosion.
- If different cavitation mechanisms appear in different load intervals, and the turbine operation is limited to one of these intervals or is predominantly performed in it, the task is resolved.
- In other cases, the data on the influence of the stay and guide vanes, or cavitation-intensity differences in different locations behind the spiral casing, together with an insight from model tests, might help to determine the mechanisms which are responsible for erosion.
4.7. Comments on the Method
5. Case Analysis
5.1. Recognising Turbine Parts
5.2. Introductory Turbine Characteristics
- Basicturbine cavitation characteristics: Separately estimated cavitation intensity caused by each guide-vane/runner-blade pair
- Runnercavitation characteristic: Cavitation intensity related to each runner blade (averaged over all guide vanes)
- Distributorcavitation characteristic: Influence of each guide vane including other turbine elements upstream of the runner (averaged over all runner blades)
- Globalcavitation characteristic: Global cavitation intensity in a turbine (averaged over everything).
5.3. Classification of Cavitation-Intensity Data
5.4. Influence of Runner Blade vs. Guide Vane Correlation
5.5. Stationary and Rotating Cavitation Mechanisms
5.6. Necessary Number of Sensors
6. Cavitation on Prototype: Diagnostic Results
- (1)
- The two cavitation mechanisms are successfully recognised vibro-acoustically.
- (2)
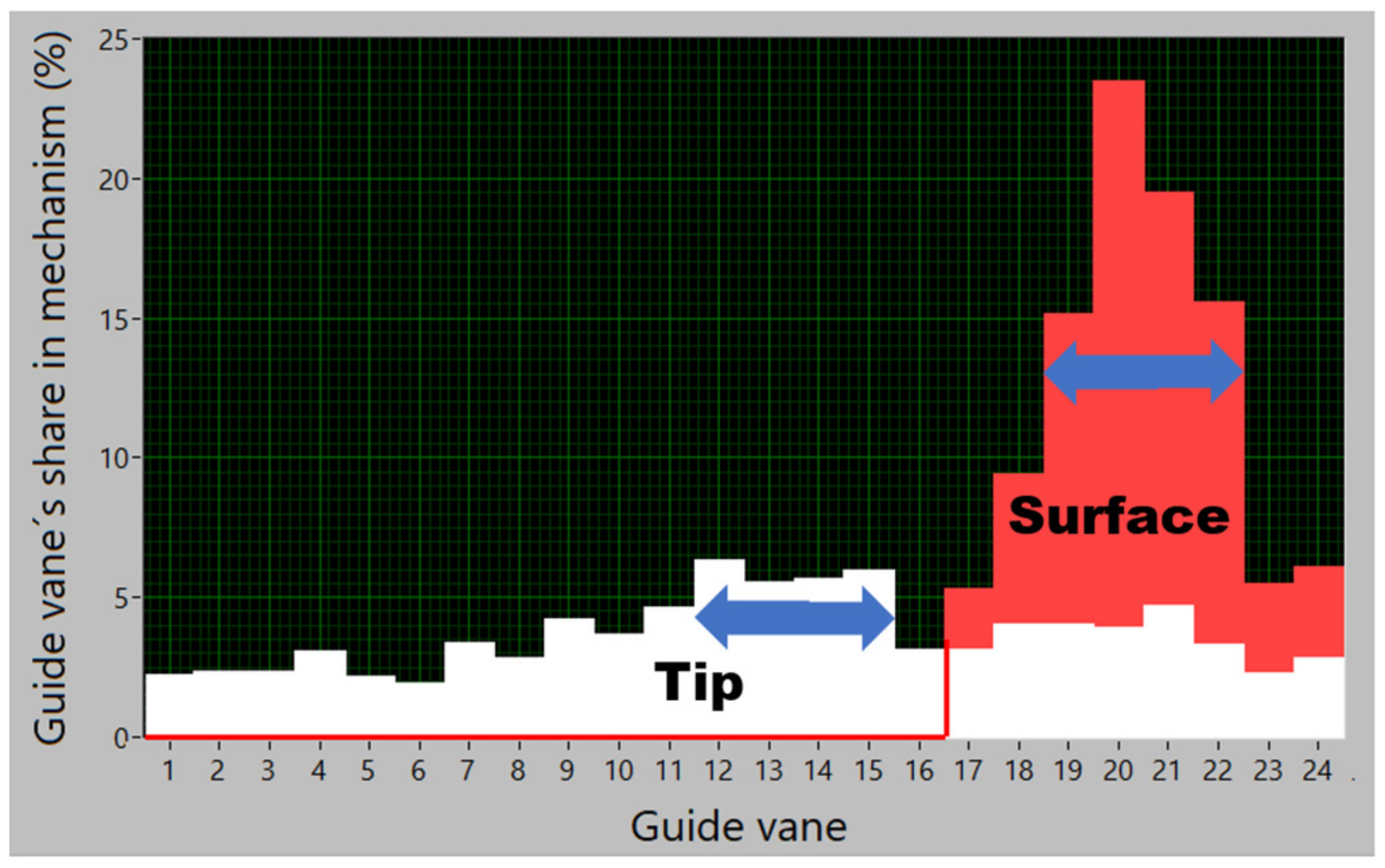
- Their locations with respect to the surrounding turbine parts are determined:Each of the 24 independent patches of the tip cavitation group is stationary in the still space; each one is fixed to the respective guide vane.The patches of the surface cavitation group, which occur on all the four runner blades, are stationary in the rotating frame of reference; they rotate with the respective blade.
- (3)
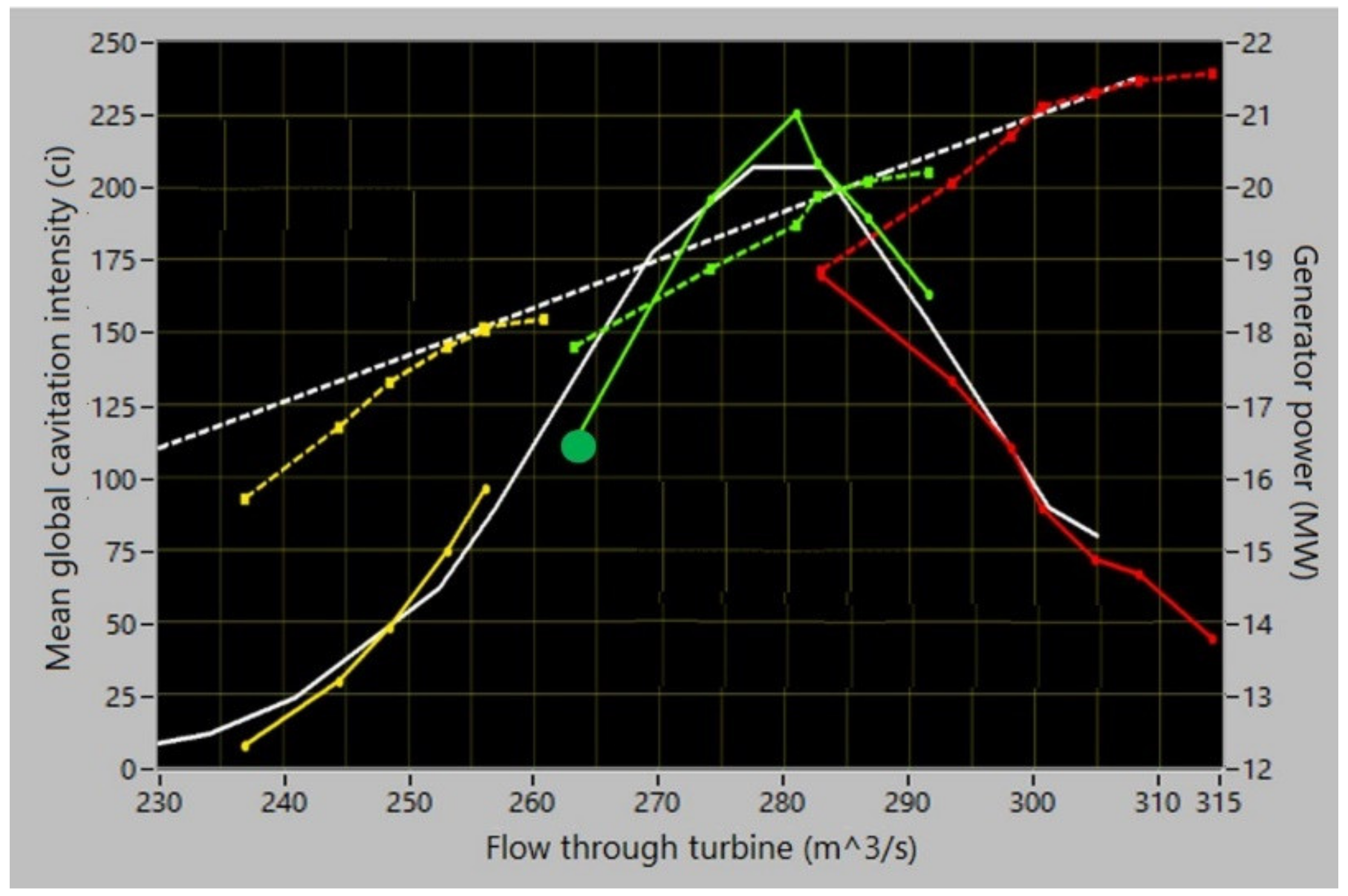
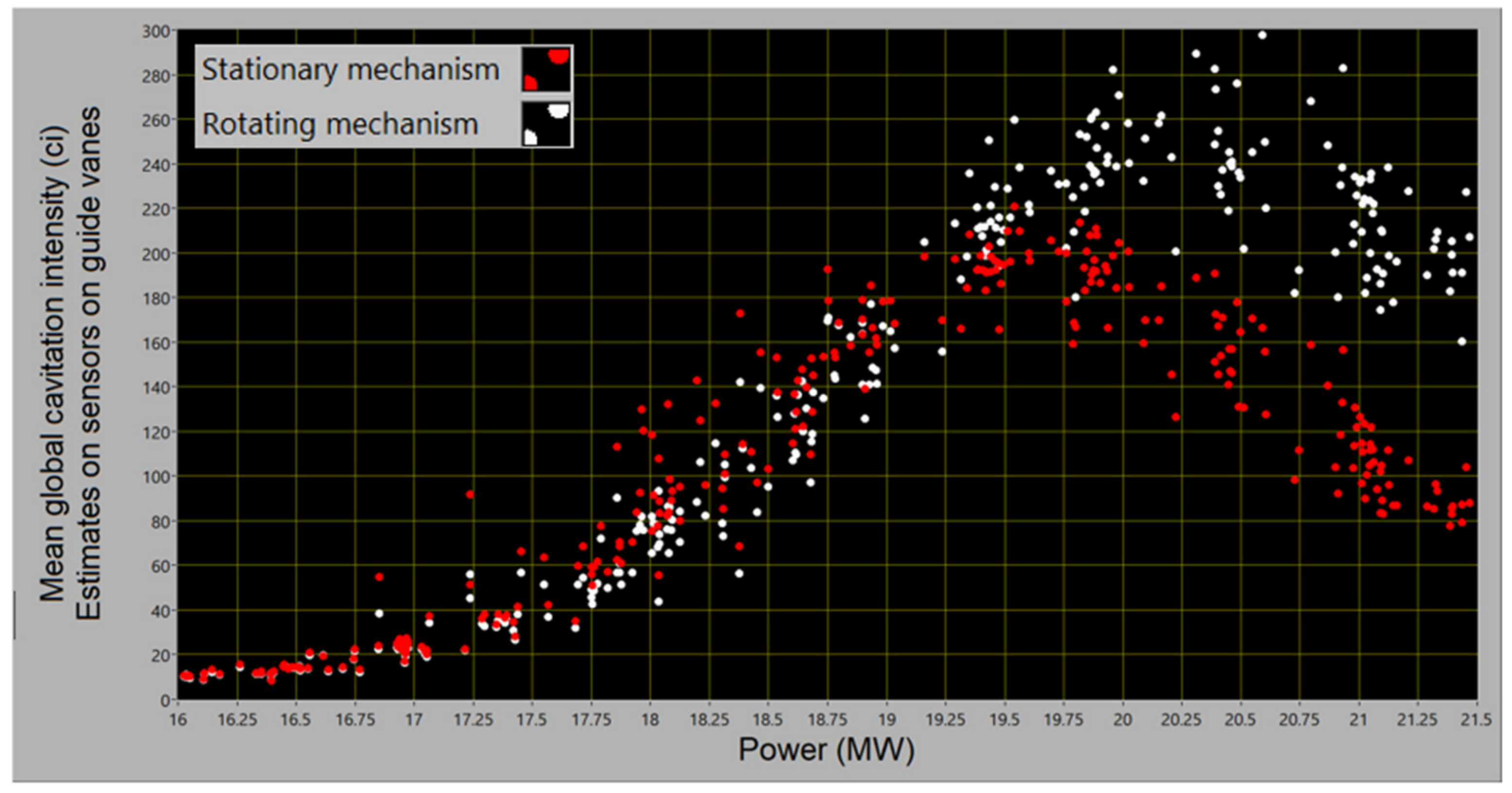
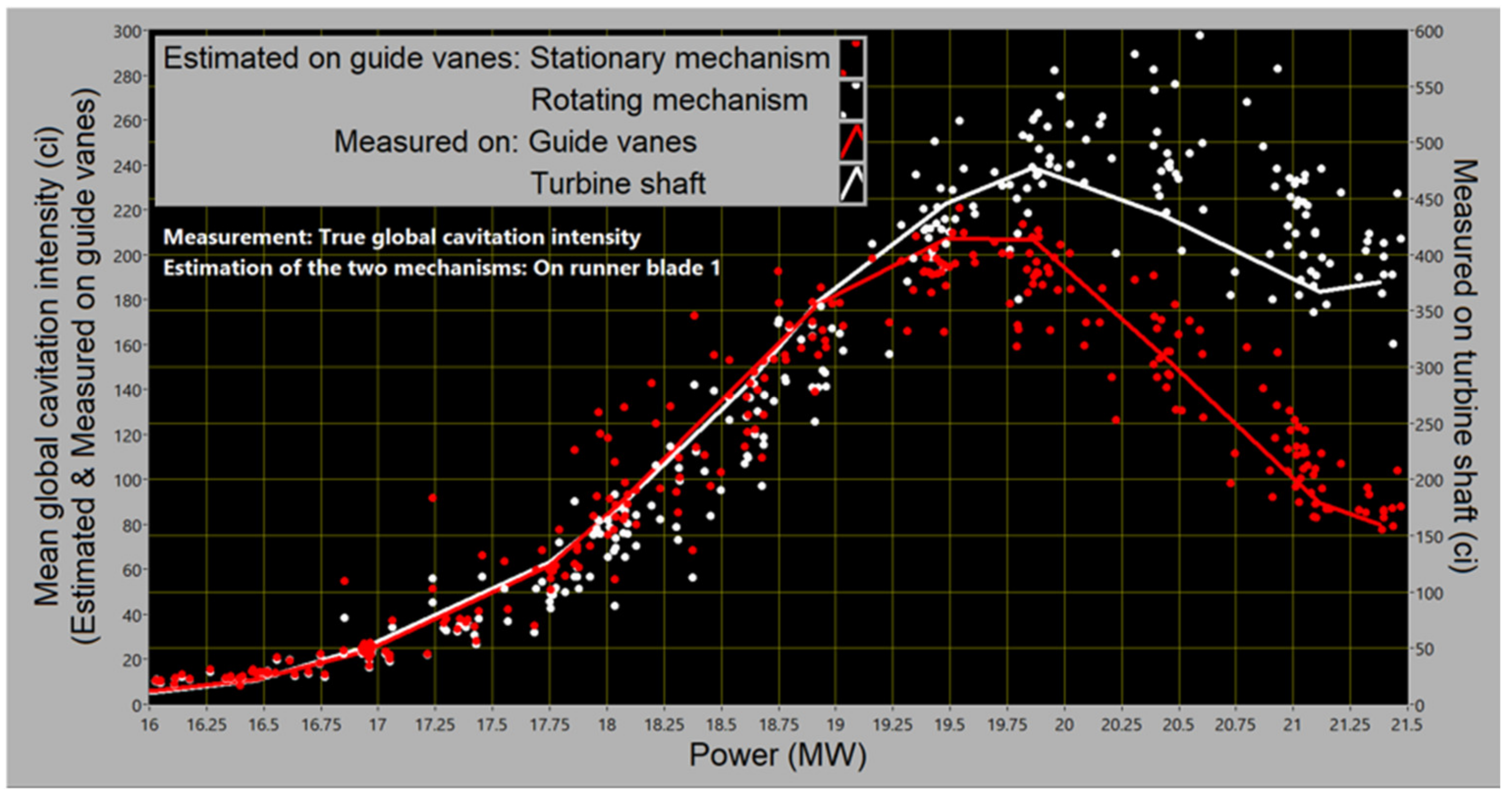
- The simplest quantification of the cavitation intensity, through the global mean value, i.e., at each operation point, by one value for each of the two groups of mechanisms and for their cumulative effect equal to the sum of the values for the two groups, is shown in Figure 17.

- These results can be used for operation optimisation, directly or transformed via (18)/(19) with the sum over m = 1 and 2 for the two groups, into relative predictions of the erosion rate.Three levels of cavitation description can be followed:- direct, via cavitation intensities;- via the non-normalised prediction of the erosion rate based on the km-values made equal to the k from (16), and unspecified Cm’s, also assumed equal;- performing calibration of Cm’s while assuming km’s as in (16), this being organised as steady tracking of the cavitation intensity between two visual inspections and comparing the accumulated cavitation intensity transformed into the erosion rate with direct estimation of the metal loss due to each of the two groups of mechanisms;- performing three or more calibrations such as this and also assessing the km-values.
- (4)
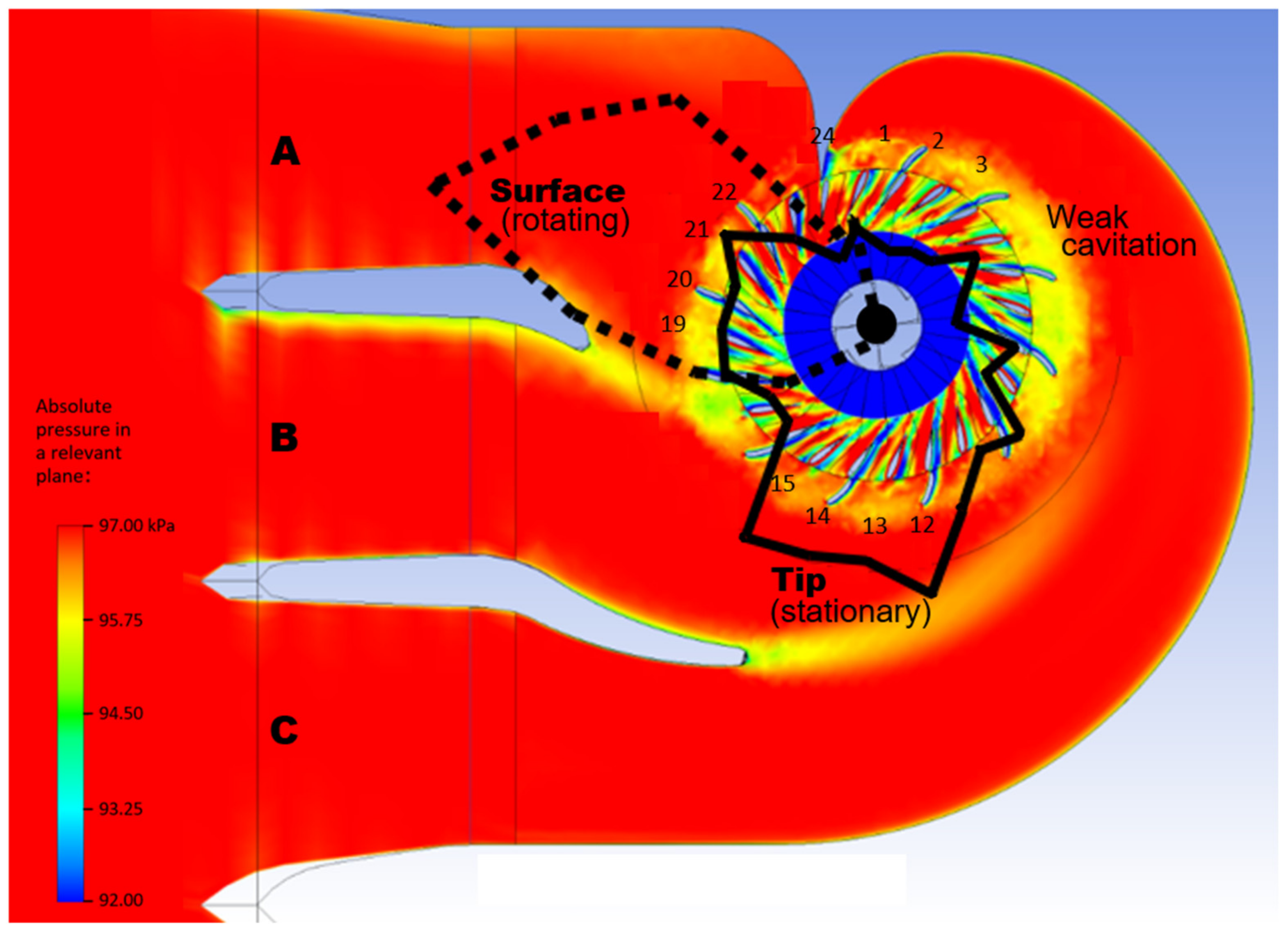
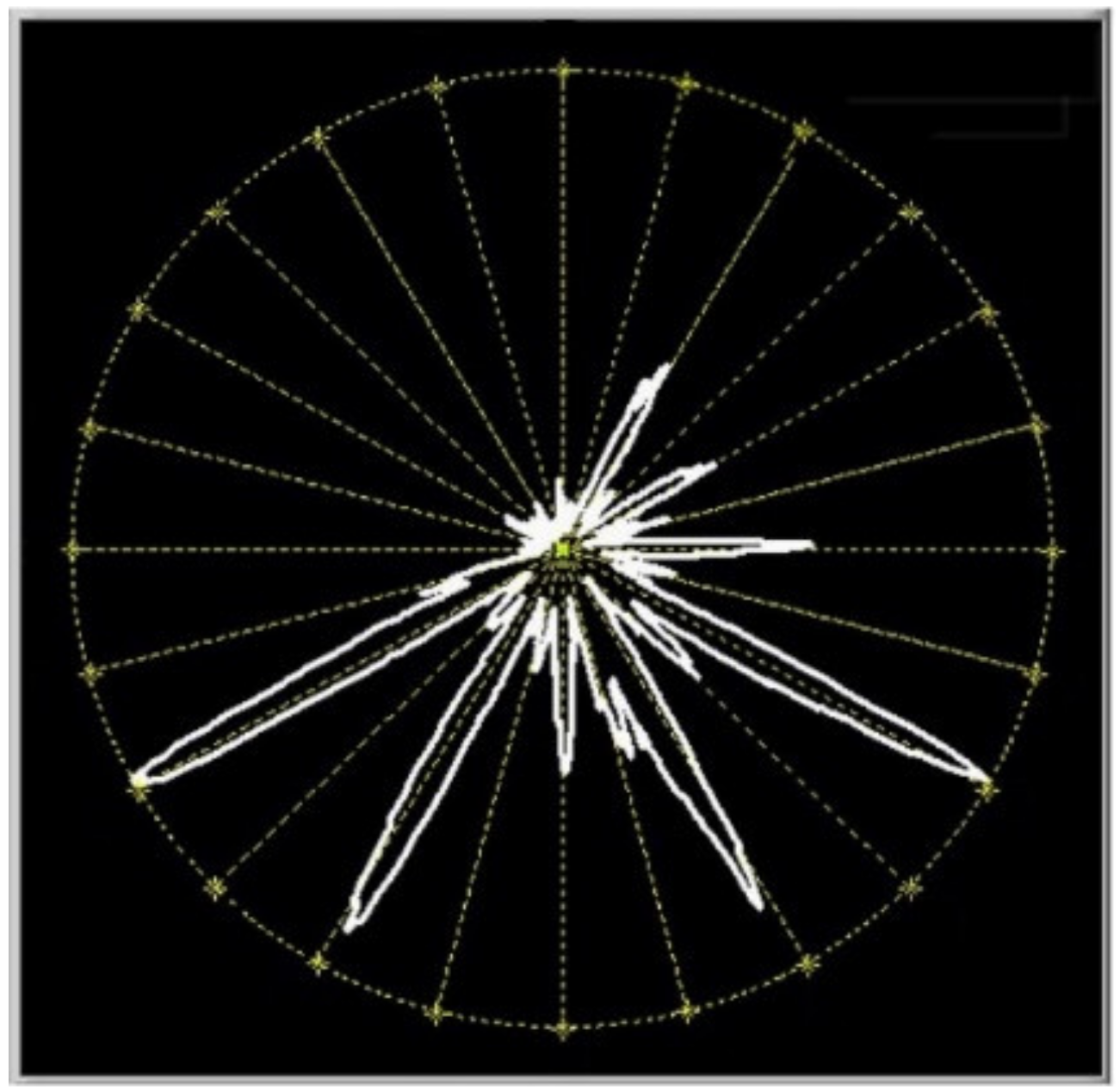
- A situation with the rotor-stator interaction as specified in Figure 18 and Figure 19 is found. This gives insights in the causes of cavitation.The intake channel C causes no problems.The strongest tip cavitation occurs in channel B; weaker tip cavitation occurs behind all the guide vanes.The surface cavitation is caused by the flow disturbances stemming from the inflow through channel A.
- (5)
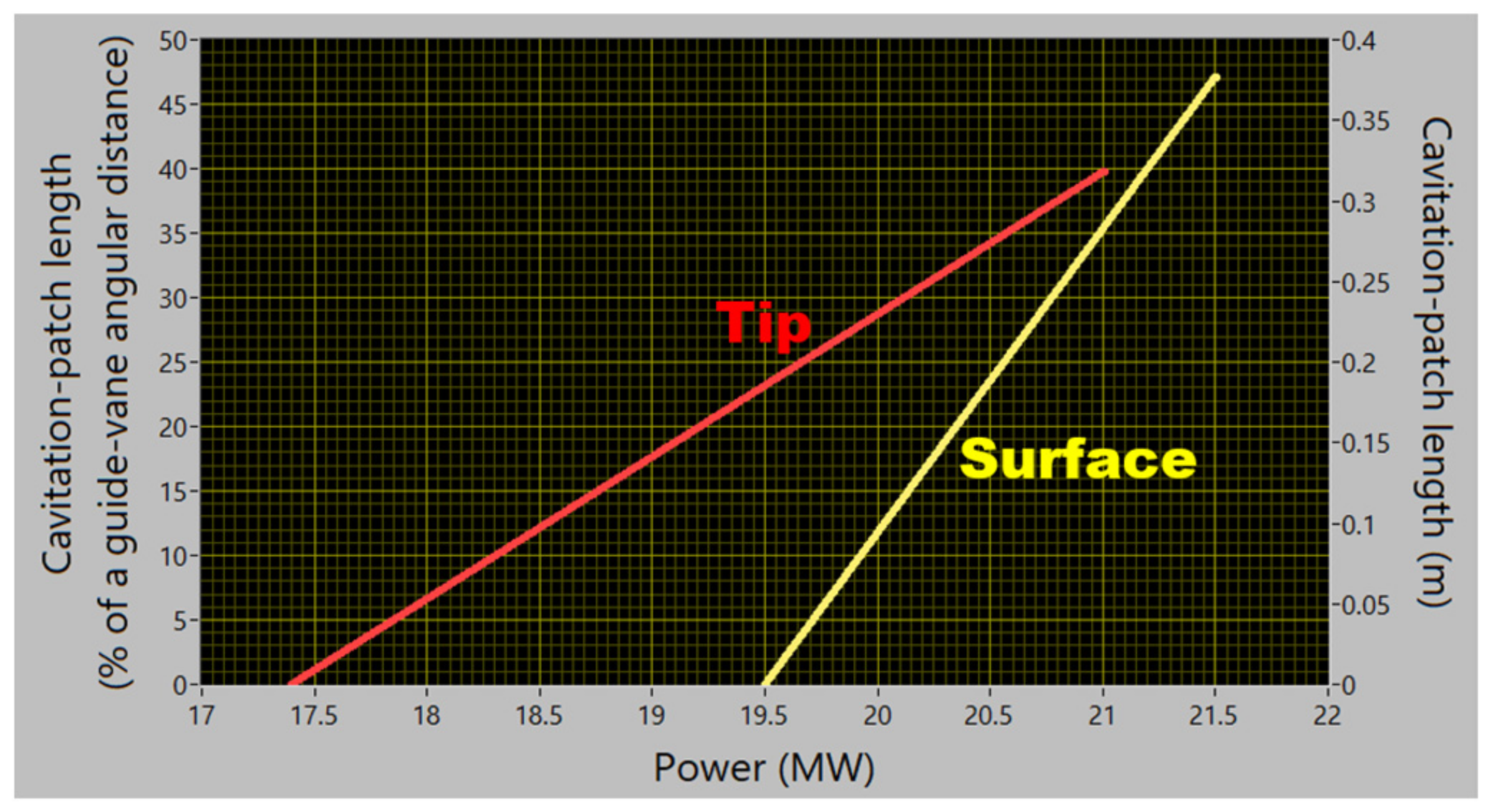
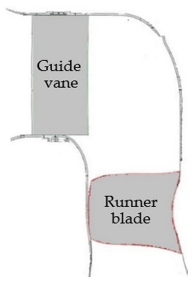
- The average size of the cavitation patches is also vibro-acoustically assessed (Figure 20). When the mechanisms are fully developed, the patches occupy up to a half of the distance between the neighbouring guide vanes. The size of the surface cavitation rises with the increasing load twice as fast as that of the tip cavitation.
- (6)
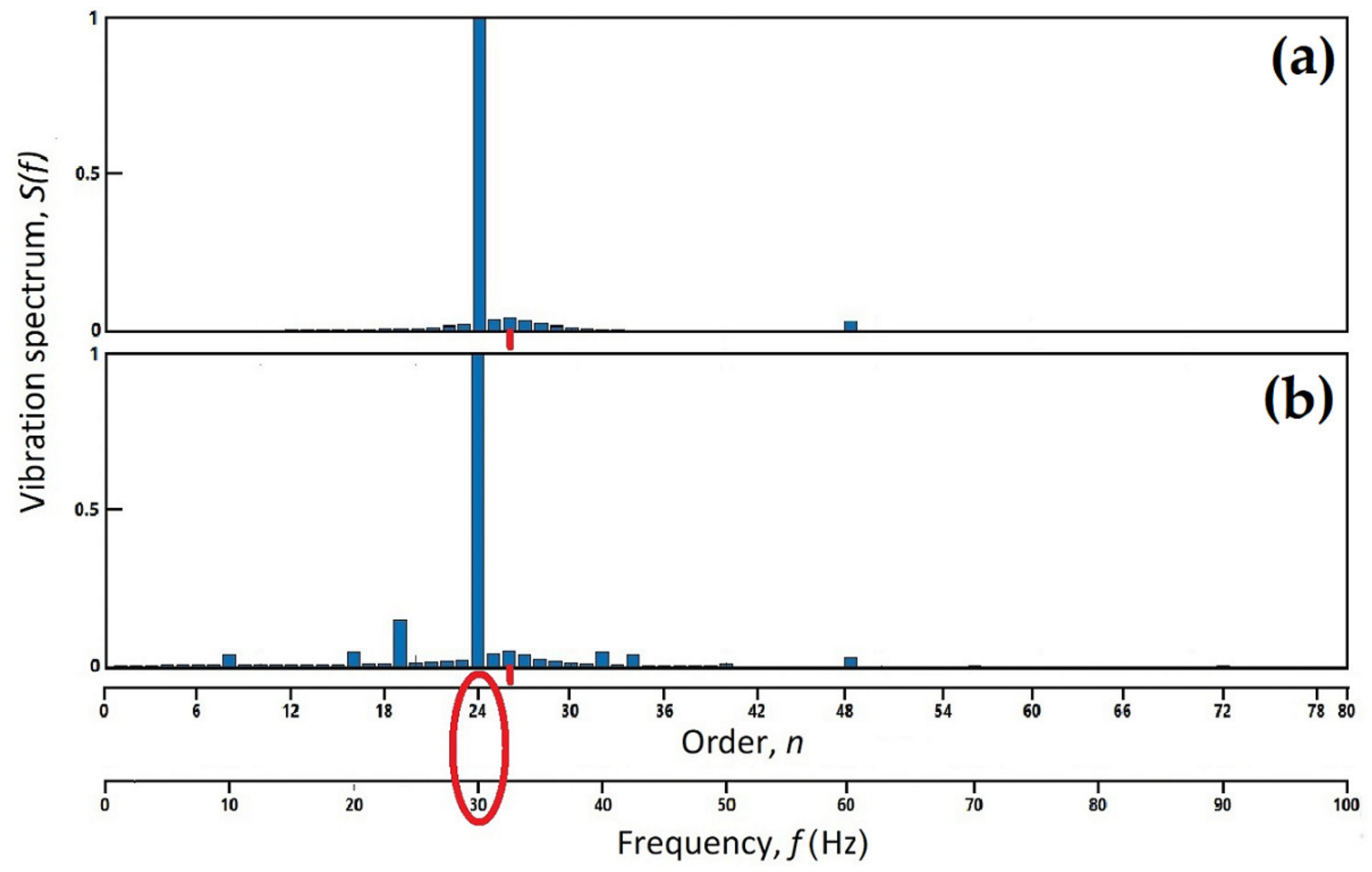
- The method also reveals systematic differences in cavitation behind the guide vanes that have stay vanes in front of themselves and those that stand alone, as well as deviations in the general time periodicity of the cavitation mechanisms (Figure 21).
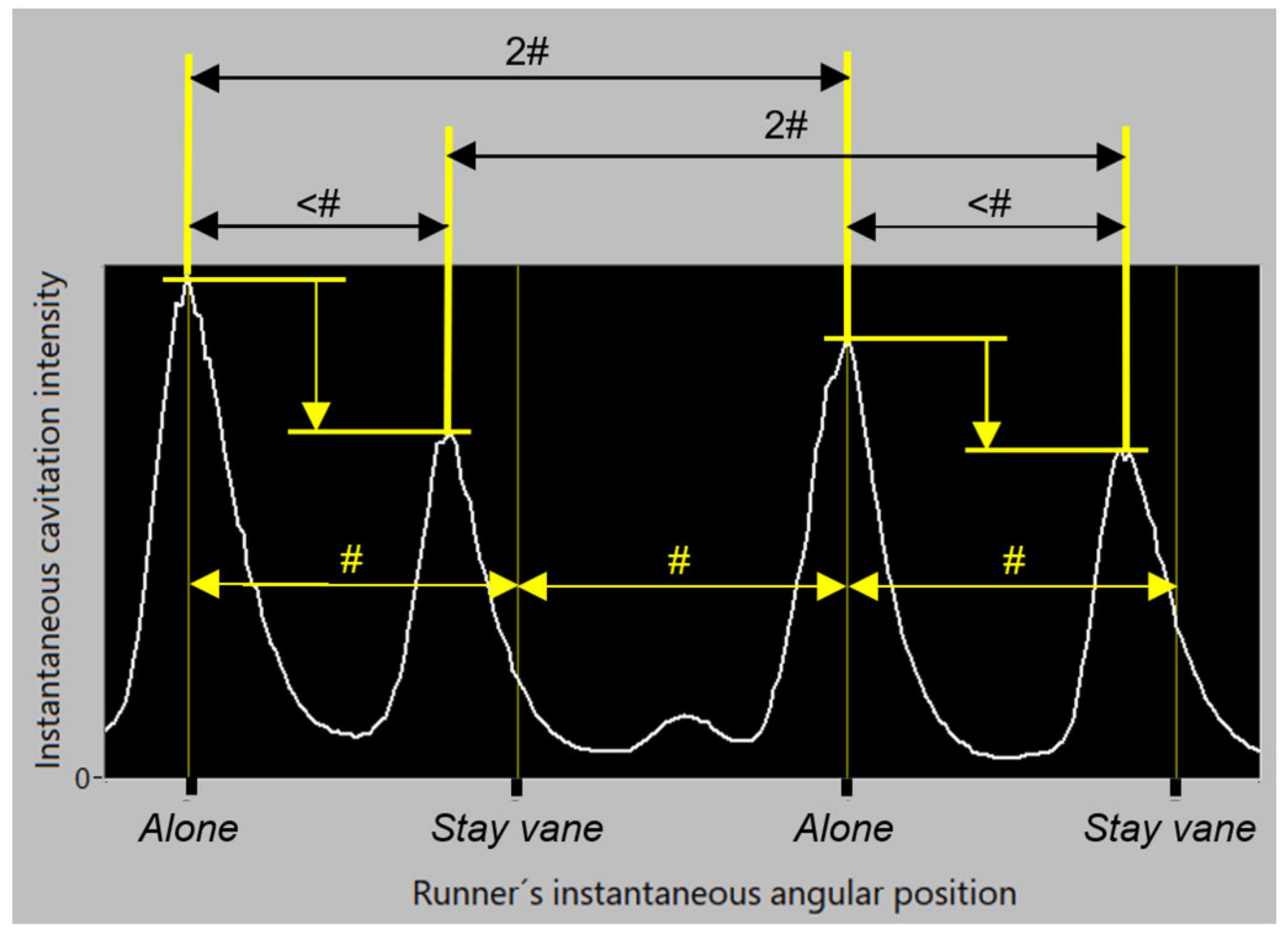
- (7)
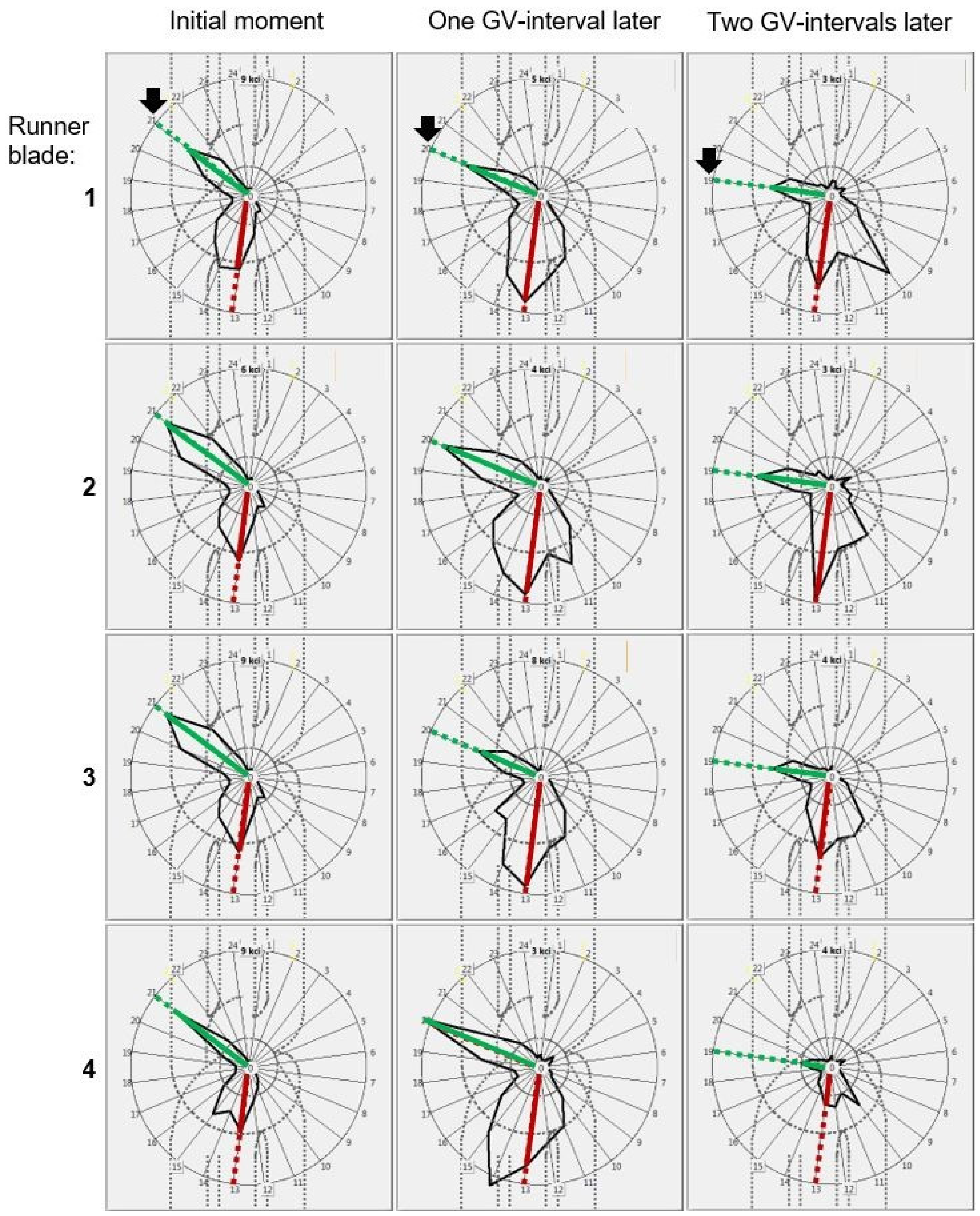
- The four runner blades do not have equal cavitation quality. Some of this can be seen in Figure 22. If necessary, these data can be analysed further.

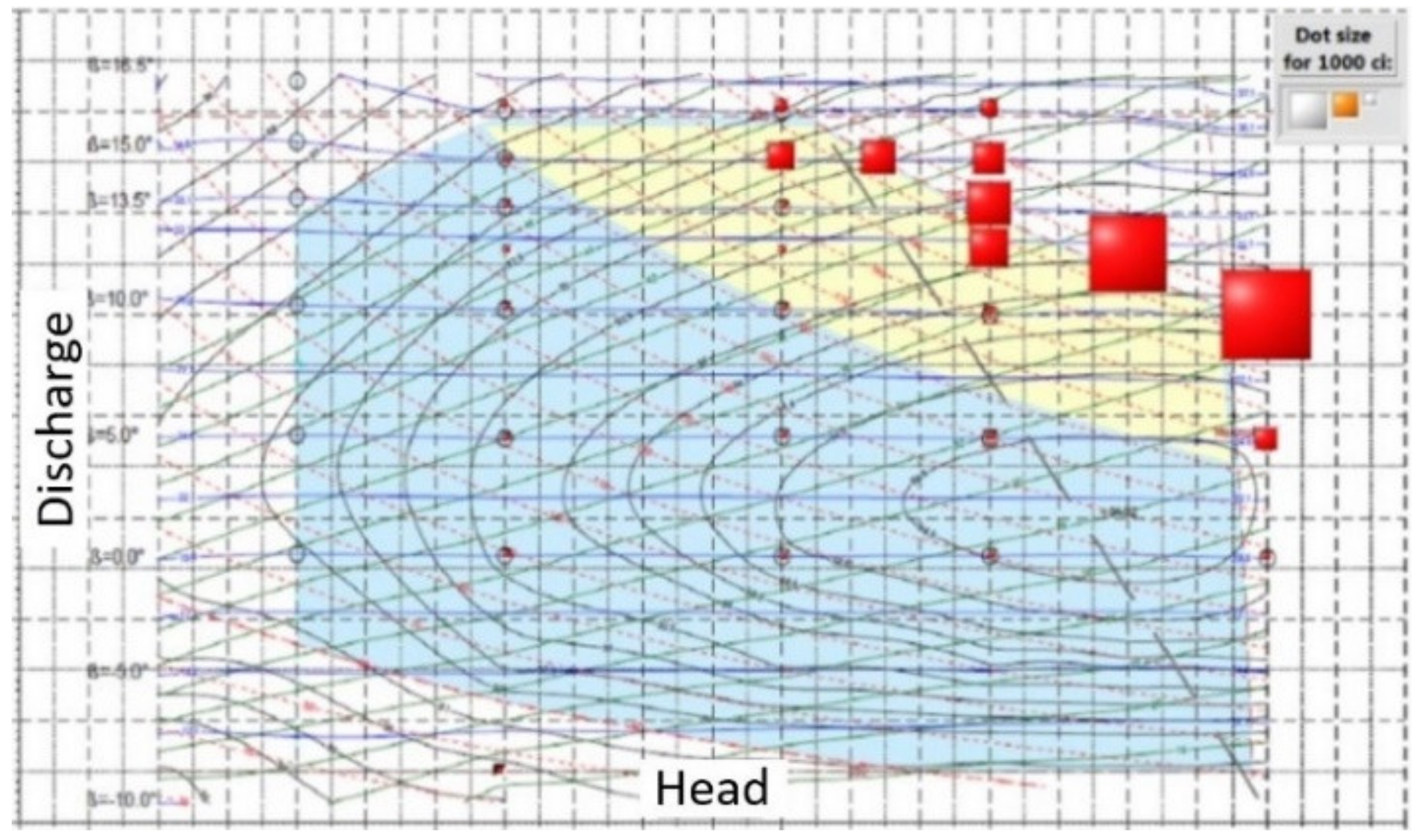
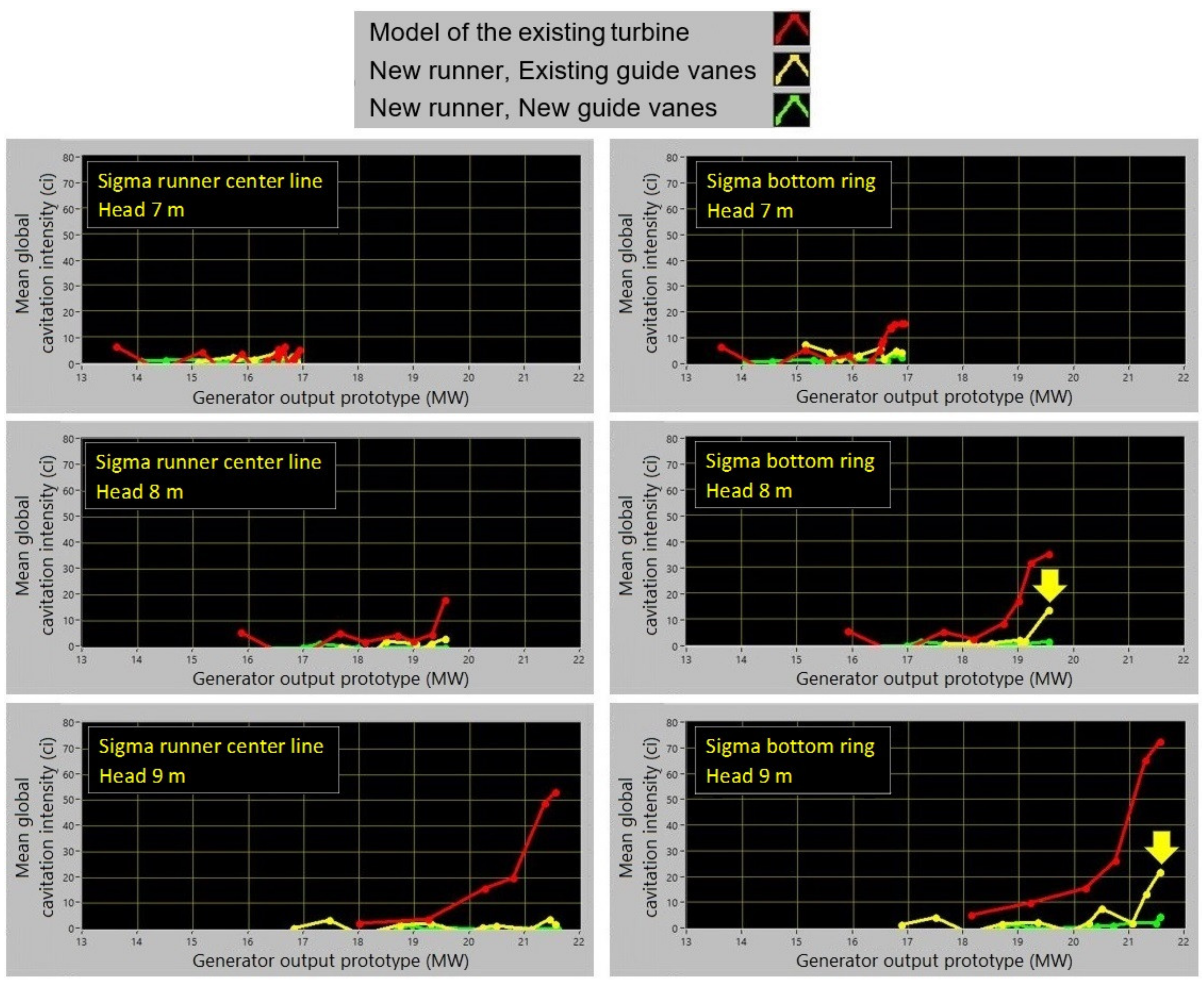
7. Cavitation on Models: Comparison of Three Turbine Versions
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| B | number of runner blades (-) |
| Bx() | Bx(,Θ) assumed equal in all sensors (ci) |
| Bx(,Θ) | non-cavitation background in the sensor on the guide vane at Θ, at the operation point (ci) |
| By() | non-cavitation background in the sensor on the turbine shaft, at the operation point (ci) |
| c | adjustment constant for the turbine-shaft channel (-) |
| C, Cm | turbine-specific constants in the erosion model (16)/(19) |
| ci | ad hoc cavitation-intensity unit |
| E, Em | erosion rate in the erosion model (16)/(19) (kg per 10000 h or alike) |
| I() | mean global cavitation intensity assessed by the sensors on the guide vanes at the operation point (ci) |
| Im() | m-th cavitation mechanism in I() or cJ() (ci) |
| Irot () | rotating mechanism in I() or cJ() (ci) |
| Ista () | stationary mechanism in I() or cJ() (ci) |
| Is(,Θ) | spatial dependence of the mean cavitation intensity (ci) |
| It(,Φ) | temporal dependence of the spatially mean cavitation intensity (ci) |
| Itr(,Φ) | temporal dependence of the rotating cavitation mechanism, resulting from a synthetic sensor focused on the rotating mechanism (ci) |
| I(,Θ,Φ) | spatial and temporal dependence of cavitation intensity assessed by the sensors on the guide vanes at the operation point (ci) |
| Ir(,Θ,Φ) | spatial and temporal dependence of cavitation intensity of the rotating cavitation mechanism at the operation point (ci) |
| rot() | total intensity of the rotating mechanism at the operation point (ci) |
| sta() | total intensity of the stationary mechanism at the operation point (ci) |
| rot(,Φ) | temporal dependence of the total intensity of the rotating mechanism at the operation point (ci) |
| sta(,Φ) | temporal dependence of the total intensity of the stationary mechanism at the operation point (ci) |
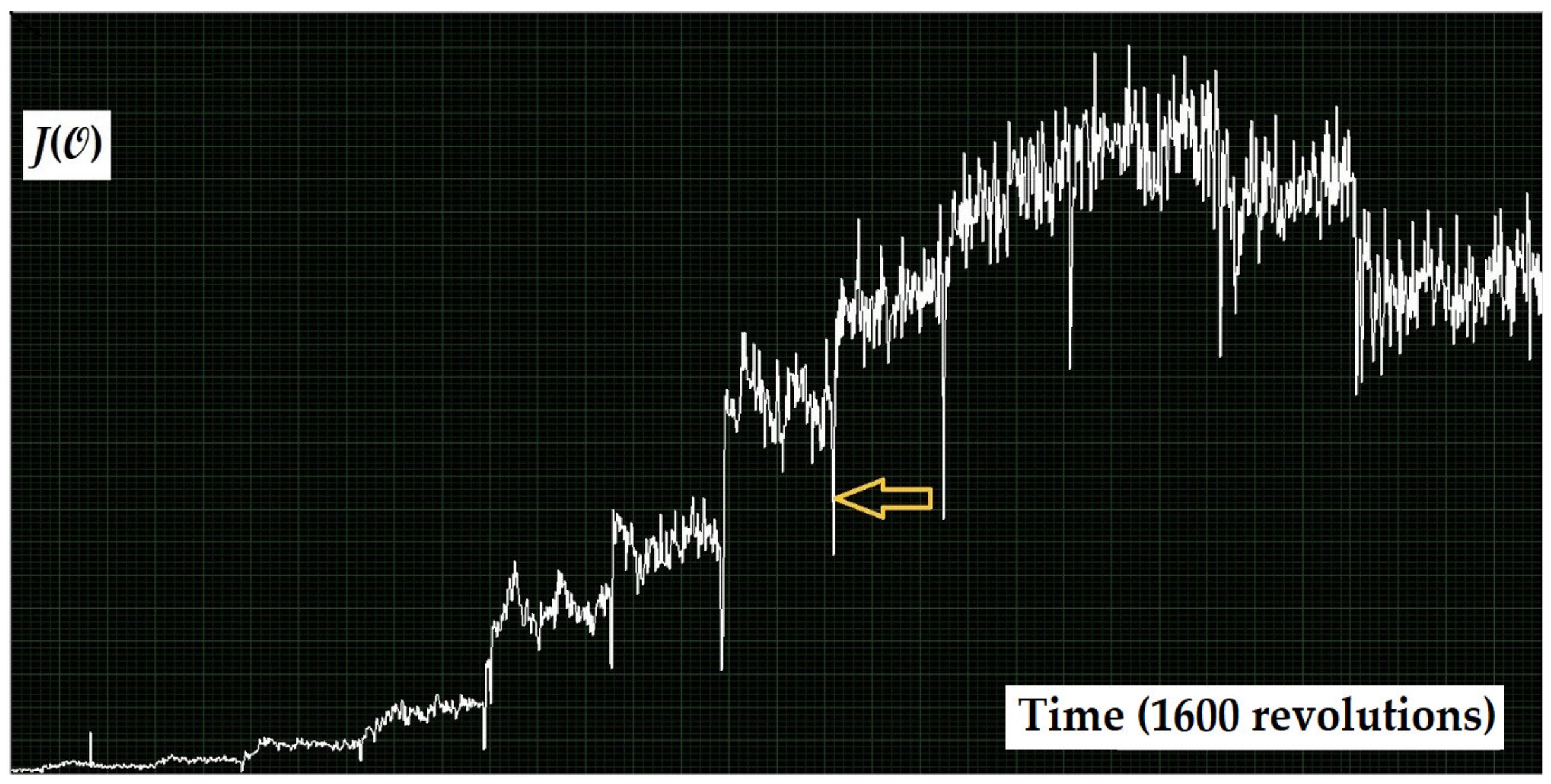
| J() | mean global cavitation intensity assessed by the sensor on the turbine shaft at the operation point (ci) |
| J(,Φ) | temporal dependence of cavitation intensity assessed by the sensor on the turbine shaft at the operation point (ci) |
| k, km | exponent in the erosion model (16)/(19) (-) |
| K | number of temporal samples taken within an angular pattern of cavitation intensity (-) |
| m | cavitation-mechanism number (-) |
| M | number of temporal samples taken within one revolution (-) |
| n | revolution number (-) |
| N | number of revolutions included in the result (-) |
| turbine operation point (set of quantities used to quantify the operation) | |
| b | safely non-cavitation operation point |
| o | operation point at which c is estimated |
| v | guide-vane number (-) |
| V | number of guide vanes (-) |
| x(,Θ,Φ,n) | output of the sensor on the guide vane lying at Θ with the runner in the revolution n in the position Φ at the operation point (e.g., for accelerometer m/s2) |
| y(,Φ,n) | output of the sensor on the turbine shaft with the runner in the revolution n in the position Φ at the operation point (e.g., for accelerometer m/s2) |
| Θ | angular position of the guide vane equipped with the sensors (spatial coordinate, discrete) (rad) |
| Θv | value of Θ for the guide vane v (rad) |
| Φ | instantaneous angular position of the runner (temporal coordinate, continuous) (rad) |
| sum over the cavitation mechanisms m | |
| sum over the guide vanes v behind which the rotating mechanism occurs (or dominates) | |
| sum over the guide vanes v behind which the stationary mechanism occurs (or dominates) | |
| <·> | averaging over the statistical ensamble |
| <·>n | averaging over N revolutions n |
| <·>Θ | averaging over Θ ∈ [0,2π) |
| <·>Φ | averaging over Φ ∈ [0,2π) |
| * | denotes erosive cavitation mechanism and sum over erosive mechanisms |
Appendix 1. Details of Prototype Diagnosis



Appendix 2. Suitable Input Circuitry
Appendix 3. On Cavitation-Generated Vibration
| Number of guide vanes causing cavitation Number of runner blades with cavitation | 1 1 | 1 All | All 1 | All All |
| Number of cavitation events per revolution in the total intensity Vibration amplitude is proportional to thus, for V = 24, B = 4, to Basic vibration frequency = revolution frequency multiplied by thus, for V = 24, B = 4, by | 1 1 1 1 1 | B B 4 B 4 | V V 24 V 24 | V V2 576 V 24 |
References
- Rayleigh, L. On the pressure developed in the liquid during the collapse of a spherical cavity. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1917, 34, 94–98. [Google Scholar] [CrossRef]
- Brennen, C.E. Cavitation and Bubble Dynamics; Oxford Press: Oxford, UK, 1995. [Google Scholar]
- Pearsall, I.S. Acoustic detection of cavitation. In Proceedings of the Symposium on Vibrations in Hydraulic Pumps and Turbines, Manchester, England, 14–16 September 1966; Volume 181, pp. 1–8. [Google Scholar]
- Varga, J.J.; Sebestyen, G.; Fay, A. Detection of cavitation by acoustic and vibration-measurement methods. La Houille Blanche 1969, 24, 137–149. [Google Scholar] [CrossRef] [Green Version]
- Abbot, P.A.; Gedney, C.J.; Greeley, D.L. Cavitation monitoring of two axial-flow-hydroturbines using novel acoustic and vibration methods. In Proceedings of the 13th IAHR Symposium, Montreal, QC, Canada, 2–5 September 1986; Volume 1. Paper 23. [Google Scholar]
- Abbot, P.A. Cavitation detection measurements on Francis and Kaplan hydroturbines. In Proceedings of the International Symposium on Cavitation Noise and Erosion in Fluid Systems, ASME, New York, NY, USA, 10–15 December 1989; FED-88. pp. 55–61. [Google Scholar]
- Bourdon, P.; Simoneau, R.; Lavagne, P. A vibratory approach to the detection of erosive cavitation. In Proceedings of the International Symposium on Cavitation Noise and Erosion in Fluid Systems, San Francisco, CA, USA, 10–15 December 1989; FED-Vol. 88. pp. 103–109. [Google Scholar]
- Bajic, B.; Keller, A. Spectrum normalization method in vibroacoustical diagnostic measurements of hydroturbine cavitation. J. Fluids Eng. 1996, 118, 756–761. [Google Scholar] [CrossRef]
- Farhat, M.; Bourdon, P.; Lavigne, P. Some Hydro Quebec experiences on the vibratory approach for cavitation monitoring. In Proceedings of the Conference Modelling, Testing & Monitoring for Hydro Powerplants, Lausanne, Switzerland, 8–11 July 1996; pp. 151–161. [Google Scholar]
- Bajic, B. Vibroacoustical diagnosis of hydroturbine cavitation: Some measurement and analysis methods. In Proceedings of the Conference Modelling, Testing & Monitoring for Hydro Powerplants, Lausanne, Switzerland, 8–11 July 1996; pp. 169–178. [Google Scholar]
- Bajic, B. Inflow decomposition: A vibroacoustical technique to reveal details of hydroturbine cavitation. In Proceedings of the Conference Hydropower into the Next Century, Portoroz, Slovenia, 15–17 September 1997; pp. 185–196. [Google Scholar]
- Bajic, B. Multidimensional diagnostics of turbine cavitation. J. Fluids Eng. 2002, 124, 943–950. [Google Scholar] [CrossRef]
- Escaler, X.; Egusquiza, E.; Mebarki, T.; Avellan, F.; Farhat, M. Field assessment of cavitation detection methods in hydropower plants. In Proceedings of the 21st IAHR Symposium on Hydraulic Machinery and Systems, Lausanne, Switzerland, 9–12 September 2002. [Google Scholar]
- Bajic, B. Multidimensional monitors for hydroelectric power plants. In Proceedings of the Hydro 2002 Conference, Kiris, Turkey, 4–7 November 2002. [Google Scholar]
- Bajic, B. Methods for vibroacoustic diagnostic of turbine cavitation. J. Hydraul. Res. 2003, 41, 87–96. [Google Scholar] [CrossRef]
- Escaler, X.; Egusquiza, E.; Farhat, M.; Avellan, F. Vibration cavitation detection using onboard measurements. In Proceedings of the Fifth International Symposium on Cavitation, Osaka, Japan, 1–4 November 2003. [Google Scholar]
- Escaler, X.; Egusquiza, E.; Farhat, M.; Avellan, F. Cavitation erosion prediction in hydro turbines from onboard vibrations. In Proceedings of the 22nd IAHR Symposium on Hydraulic Machinery and Systems, Stockholm, Sweden, 29 June–2 July 2004. [Google Scholar]
- Escaler, X.; Egusquiza, E.; Farhat, M.; Avellan, F.; Coussirat, M. Detection of cavitation in hydraulic turbines. Mech. Syst. Signal Process. 2006, 20, 983–1007. [Google Scholar] [CrossRef] [Green Version]
- Pastushenko, V. Kavitation in Wasserturbinen—Entwicklung eines Monitoringsystems. Ph.D. Thesis, Munich Technical University, München, Germany, 2006. [Google Scholar]
- Bajic, B. Grand Coulee G-20 Multidimensional Cavitation Test - Comparison of Three Cavitation Monitoring Techniques; Report Korto GC082103, 2008, Volume 1. Available online: http://www.korto.com/downloads/reports/Korto_Grand_Coulee_G-20_Cavitation_Report_Korto_GC082103-Vol_1.pdf (accessed on 13 February 2022).
- Bajic, B. Grand Coulee G-20 Multidimensional Cavitation Test - Comparison of Three Cavitation Monitoring Techniques; Report Korto GC082103, 2008, Volume 2. Available online: http://www.korto.com/downloads/reports/Korto_Grand_Coulee_G-20_Cavitation_Report_Korto_GC082103-Vol_2.pdf (accessed on 13 February 2022).
- Bajic, B. Multidimensional and simple techniques for cavitation diagnostics and monitoring. Powertec Russ. CIS, 21 September 2010; 50–63. Available online: https://issuu.com/rogtecmagazine/docs/powertec_issue2_lowres(accessed on 13 February 2022).
- Schmidt, H.; Kirschner, O.; Riedelbauch, S.; Necker, J.; Kopf, E.; Rieg, M.; Arantes, G.; Wessiak, M.; Mayrhuber, J. Influence of the vibroacoustic sensor position on cavitation detection in a Kaplan turbine. In Proceedings of the 27th IAHR Symposium on Hydraulic Machinery and Systems, Montreal, Canada, 22–26 September 2014; IOP Conf. Series: Earth and Environmental Science. 2014; Volume 22, p. 052006. [Google Scholar]
- Germann, J. Cavitation Detection Technology for Optimizing Hydraulic Turbine Operation and Maintenance. U.S. Bureau of Reclamation Report ST-2015-2944-01. 2017. Available online: https://www.usbr.gov/research/projects/detail.cfm?id=2944 (accessed on 13 February 2022).
- Valentin, D.; Presas, A.; Egusquiza, M.; Valero, C.; Egusquiza, E. Transmission of high frequency vibrations in rotating systems. Application to cavitation detection in hydraulic turbines. Appl. Sci. 2018, 8, 451. [Google Scholar] [CrossRef] [Green Version]
- Valentin, D.; Presas, A.; Valero, C.; Egusquiza, M.; Egusquiza, E. Detection of hydraulic phenomena in Francis turbines with different sensors. Sensors 2019, 19, 4053. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Presas, A.; Luo, Y.; Valentin, D.; Egusquiza, M.; Wang, Z.; Valero, C.; Egusquiza, E. Detection of erosive cavitation on hydraulic turbines through demodulation analysis. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2019; Volume 240, p. 062048. Available online: https://iopscience.iop.org/article/10.1088/1755-1315/240/6/062048 (accessed on 13 February 2022).
- Mortensen, J. Cavitation Detection—Method Development to Detect Damaging Cavitation. U.S. Bureau of Reclamation Report ST-2017-1708-01. 2017. Available online: https://usbr.gov/tsc/techreferences/hydraulics_lab/pubs/HL/HL-2017-10.pdf (accessed on 13 February 2022).
- Luo, X.-W.; Ji, B.; Tsujimoto, Y. A review of cavitation in hydraulic machinery. J. Hydrodyn. 2016, 28, 335–358. [Google Scholar] [CrossRef]
- Jones, R.K.; March, P.A. Application of Acoustic Emissions for Real-Time Monitoring of Cavitation; Report No. WR28-4-900-234; Tennessee Valley Authority: Norris, TN, USA, 1989. [Google Scholar]
- Derakhshan, O.; Houghton, J.R.; Jones, R.K.; March, P.A. Cavitation Monitoring of Hydroturbines with True-RMS Acoustic Emission Measurement; ASTM Special Publication 1077; American Society for Testing and Materials: Philadelphia, PA, USA, 1990. [Google Scholar]
- Wolff, P.J.; Jones, R.K.; March, P. Evaluation of Results from Acoustic Emissions-Based Cavitation Monitor, Grand Coulee Unit G-24: Cavitation Monitoring System Comparison Tests; Grand Coulee Project Final Report; WolffWare Ltd.: Noriss, TN, USA, 2005; Available online: http://www.wolffwareltd.com/downloads/Grand%20Coulee%20Cavitation%20Report.pdf (accessed on 13 February 2022).


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bajic, B.; Weissenberger, S.; Keller, M. Multidimensional Vibro-Acoustical Diagnostics of Cavitation: Theory and Illustration on a Kaplan Turbine. Fluids 2022, 7, 193. https://doi.org/10.3390/fluids7060193
Bajic B, Weissenberger S, Keller M. Multidimensional Vibro-Acoustical Diagnostics of Cavitation: Theory and Illustration on a Kaplan Turbine. Fluids. 2022; 7(6):193. https://doi.org/10.3390/fluids7060193
Chicago/Turabian StyleBajic, Branko, Simon Weissenberger, and Markus Keller. 2022. "Multidimensional Vibro-Acoustical Diagnostics of Cavitation: Theory and Illustration on a Kaplan Turbine" Fluids 7, no. 6: 193. https://doi.org/10.3390/fluids7060193