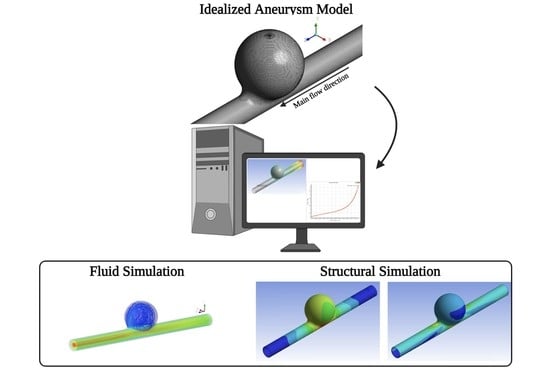
Fluid Flow and Structural Numerical Analysis of a Cerebral Aneurysm Model
Abstract
:1. Introduction
2. Problem Description
2.1. Fluid Flow Simulations
2.1.1. Geometrical Domain and Mesh
2.1.2. Boundary Conditions and Solver
2.1.3. Model Validation
2.2. Structural Simulations
3. Results
3.1. Fluid Flow Analysis
3.1.1. Flow Patterns
3.1.2. Pressure
3.2. Structural Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Johnston, S.C.; Higashida, R.T.; Barrow, D.L.; Caplan, L.R.; Dion, J.E.; Hademenos, G.; Hopkins, L.N.; Molyneux, A.; Rosenwasser, R.H.; Vinuela, F.; et al. Recommendations for the endovascular treatment of intracranial aneurysms: A statement for healthcare professionals from the Committee on Cerebrovascular Imaging of the American Heart Association Council on Cardiovascular Radiology. Stroke 2002, 33, 2536–2544. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schievink, W.I. Intracranial Aneurysms. N. Engl. J. Med. 1997, 336, 28–40. [Google Scholar] [CrossRef] [PubMed]
- Thompson, B.G.; Brown, R.D., Jr.; Amin-Hanjani, S.; Broderick, J.P.; Crokroft, K.M.; Connolly, E.S., Jr.; Duckwiler, G.R.; Harris, C.C.; Howard, V.J.; Johnston, S.C.C.; et al. Guidelines for the Management of Patients With Unruptured Intracranial Aneurysms: A Guideline for Healthcare Professionals From the American Heart Association/American Stroke Association. Stroke 2015, 46, 2368–2400. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Amenta, P.S.; Yadla, S.; Campbell, P.G.; Maltenfort, M.G.; Dey, S.; Ghosh, S.; Ali, M.S.; Jallo, J.I.; Tjoumakaris, S.I.; Gonzalez, L.F.; et al. Analysis of nonmodifiable risk factors for intracranial aneurysm rupture in a large, retrospective cohort. Neurosurgery 2012, 70, 693–701. [Google Scholar] [CrossRef] [PubMed]
- Lasheras, J.C. The Biomechanics of Arterial Aneurysms. Annu. Rev. Fluid Mech. 2007, 39, 293–319. [Google Scholar] [CrossRef] [Green Version]
- Tromp, G.; Weinsheimer, S.; Ronkainen, A.; Kuivaniemi, H. Molecular basis and genetic predisposition to intracranial aneurysm. Ann. Med. 2014, 46, 597–606. [Google Scholar] [CrossRef] [Green Version]
- Baratchi, S.; Khoshmanesh, K.; Woodman, O.L.; Potocnik, S.; Peter, K.; McIntyre, P. Molecular Sensors of Blood Flow in Endothelial Cells. Trends Mol. Med. 2017, 23, 850–868. [Google Scholar] [CrossRef]
- Hoskins, P.R.; Lawford, P.V.; Doyle, B.J. Cardiovascular Biomechanics; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Cebral, J.R.; Raschi, M. Suggested connections between risk factors of intracranial aneurysms: A review. Ann. Biomed. Eng. 2013, 41, 1366–1383. [Google Scholar] [CrossRef]
- Gasser, T.C.; Ogden, R.W.; Holzapfel, G.A. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J. R. Soc. Interface 2006, 3, 15–35. [Google Scholar] [CrossRef]
- Victor, A.; Ribeiro, J.; Araújo, F.F. Study of PDMS characterization and its applications in biomedicine: A review. J. Mech. Eng. Biomech. 2019, 4, 1–9. [Google Scholar] [CrossRef]
- Ariati, R.; Sales, F.; Souza, A.; Lima, R.A.; Ribeiro, J. Polydimethylsiloxane Composites Characterization and Its Applications: A Review. Polymers 2021, 13, 4258. [Google Scholar] [CrossRef] [PubMed]
- Roloff, C.; Stucht, D.; Beuing, O.; Berg, P. Comparison of intracranial aneurysm flow quantification techniques: Standard PIV vs. stereoscopic PIV vs. tomographic PIV vs. phase-contrast MRI vs. CFD. J. Neurointerv. Surg. 2019, 11, 275–282. [Google Scholar] [CrossRef] [PubMed]
- Doutel, E.; Viriato, N.; Carneiro, J.; Campos, J.B.L.M.; Miranda, J.M. Geometrical effects in the hemodynamics of stenotic and non-stenotic left coronary arteries—numerical and in vitro approaches. Int. J. Numer. Method. Biomed. Eng. 2019, 35, e3207. [Google Scholar] [CrossRef] [PubMed]
- Souza, A.; Souza, M.S.; Pinho, D.; Agujetas, R.; Ferrera, C.; Lima, R.; Puga, H.; Ribeiro, J. 3D manufacturing of intracranial aneurysm biomodels for flow visualizations: Low cost fabrication processes. Mech. Res. Commun. 2020, 107, 103535. [Google Scholar] [CrossRef]
- Querzoli, G.; Fortini, S.; Espa, S.; Costantini, M.; Sorgini, F. Fluid dynamics of aortic root dilation in Marfan syndrome. J. Biomech. 2014, 47, 3120–3128. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Querzoli, G.; Fortini, S.; Espa, S.; Melchionna, S. A laboratory model of the aortic root flow including the coronary arteries. Exp. Fluids 2016, 57, 1–9. [Google Scholar] [CrossRef]
- Tupin, S.; Saqr, K.M.; Ohta, M. Effects of wall compliance on multiharmonic pulsatile flow in idealized cerebral aneurysm models: Comparative PIV experiments. Exp. Fluids 2020, 61, 1–11. [Google Scholar] [CrossRef]
- Rodrigues, R.O.; Pinho, D.; Bento, D.; Lima, R.; Ribeiro, J. Wall expansion assessment of an intracranial aneurysm model by a 3D Digital Image Correlation System. Measurement 2016, 88, 262–270. [Google Scholar] [CrossRef] [Green Version]
- Carvalho, V.; Maia, I.; Souza, A.; Ribeiro, J.; Costa, P.; Puga, H.; Teixeira, S.; Lima, R.A. In vitro stenotic arteries to perform blood analogues flow visualizations and measurements: A Review. Open Biomed. Eng. J. 2020, 14, 87–102. [Google Scholar] [CrossRef]
- Carvalho, V.; Gonçalves, I.; Lage, T.; Rodrigues, R.O.; Minas, G.; Teixeira, S.F.C.F.; Moita, A.S.; Hori, T.; Kaji, H.; Lima, R.A. 3D printing techniques and their applications to organ-on-a-chip platforms: A systematic review. Sensors 2021, 21, 3304. [Google Scholar] [CrossRef]
- Souza, R.R.; Gonçalves, I.M.; Rodrigues, R.O.; Minas, G.; Miranda, J.M.; Moreira, A.L.N.; Lima, R.; Coutinho, G.; Pereira, J.E.; Moita, A.S. Recent advances on the thermal properties and applications of nanofluids: From nanomedicine to renewable energies. Appl. Therm. Eng. 2022, 201, 117725. [Google Scholar] [CrossRef]
- Sadek, S.H.; Rubio, M.; Lima, R.; Vega, E.J. Blood particulate analogue fluids: A review. Materials 2021, 14, 2451. [Google Scholar] [CrossRef] [PubMed]
- Pinho, D.; Carvalho, V.; Gonçalves, I.M.; Teixeira, S.; Lima, R. Visualization and measurements of blood cells flowing in microfluidic systems and blood rheology: A personalized medicine perspective. J. Pers. Med. 2020, 10, 249. [Google Scholar] [CrossRef] [PubMed]
- Faustino, V.; Rodrigues, R.O.; Pinho, D.; Costa, E.; Santos-Silva, A.; Miranda, V.; Amaral, J.S.; Lima, R. A microfluidic deformability assessment of pathological red blood cells flowing in a hyperbolic converging microchannel. Micromachines 2019, 10, 645. [Google Scholar] [CrossRef] [Green Version]
- Pinho, D.; Muñoz-Sánchez, B.N.; Anes, C.F.; Vega, E.J.; Lima, R. Flexible PDMS microparticles to mimic RBCs in blood particulate analogue fluids. Mech. Res. Commun. 2019, 100, 18–20. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues, R.O.; Lima, R.; Gomes, H.T.; Silva, A.M.T. Polymer microfluidic devices: An overview of fabrication methods. U. Porto J. Eng. 2015, 1, 67–79. [Google Scholar] [CrossRef] [Green Version]
- Miranda, I.; Souza, A.; Sousa, P.; Ribeiro, J.; Castanheira, E.M.S.; Lima, R.; Minas, G. Properties and Applications of PDMS for Biomedical Engineering: A Review. J. Funct. Biomater. 2022, 13, 2. [Google Scholar] [CrossRef]
- Saalfeld, S.; Voß, S.; Beuing, O.; Preim, B.; Berg, P. Flow-splitting-based computation of outlet boundary conditions for improved cerebrovascular simulation in multiple intracranial aneurysms. Int. J. Comput. Assist. Radiol. Surg. 2019, 14, 1805–1813. [Google Scholar] [CrossRef]
- Hoi, Y.; Meng, H.; Woodward, S.H.; Bendok, B.R.; Hanel, R.A.; Guterman, L.R.; Hopkins, L.N. Effects of arterial geometry on aneurysm growth: Three-dimensional computational fluid dynamics study. J. Neurosurg. 2004, 101, 676–681. [Google Scholar] [CrossRef]
- Carvalho, V.; Pinho, D.; Lima, R.A.; Teixeira, J.C.; Teixeira, S. Blood Flow Modeling in Coronary Arteries: A Review. Fluids 2021, 6, 53. [Google Scholar] [CrossRef]
- Carvalho, V.; Arcipreste, B.; Soares, D.; Ribas, L.; Rodrigues, N.; Teixeira, S.F.C.F.; Teixeira, J.C. Numerical modeling of the wave soldering process and experimental validation. J. Electron. Packag.—ASME 2021, 144, 011011. [Google Scholar] [CrossRef]
- Carvalho, V.; Carneiro, F.; Ferreira, A.C.; Gama, V.; Teixeira, J.C.; Teixeira, S. Numerical study of the unsteady flow in simplified and realistic iliac bifurcation models. Fluids 2021, 6, 284. [Google Scholar] [CrossRef]
- Carvalho, V.; Rodrigues, N.; Lima, R.A.; Teixeira, S.F.C.F. Modeling blood pulsatile turbulent flow in stenotic coronary arteries. Int. J. Biol. Biomed. Eng. 2020, 14, 1998–4510. [Google Scholar] [CrossRef]
- Shimogonya, Y.; Ishikawa, T.; Imai, Y.; Matsuki, N.; Yamaguchi, T. Can temporal fluctuation in spatial wall shear stress gradient initiate a cerebral aneurysm? A proposed novel hemodynamic index, the gradient oscillatory number (GON). J. Biomech. 2009, 42, 550–554. [Google Scholar] [CrossRef]
- Rashad, S.; Sugiyama, S.; Niizuma, K.; Sato, K.; Endo, H.; Omodaka, S.; Matsumoto, Y.; Fujimura, M.; Tominaga, T. Impact of bifurcation angle and inflow coefficient on the rupture risk of bifurcation type basilar artery tip aneurysms. J. Neurosurg. 2018, 128, 723–730. [Google Scholar] [CrossRef]
- Saqr, K.M.; Rashad, S.; Tupin, S.; Niizuma, K.; Hassan, T.; Tominaga, T.; Ohta, M. What does computational fluid dynamics tell us about intracranial aneurysms? A meta-analysis and critical review. J. Cereb. Blood Flow Metab. 2019, 40, 1021–1039. [Google Scholar] [CrossRef]
- Hassan, T.; Ezura, M.; Timofeev, E.V.; Tominaga, T.; Saito, T. Computational Simulation of Therapeutic Parent Artery Occlusion to Treat Giant Vertebrobasilar Aneurysm. AJNR Am. J. Neuroradiol. 2004, 25, 63–68. [Google Scholar]
- Usmani, A.Y.; Patel, S. Hemodynamics of a cerebral aneurysm under rest and exercise conditions. Int. J. Energy Clean Environ. 2018, 19, 119–136. [Google Scholar] [CrossRef]
- Li, Y.; Verrelli, D.I.; Yang, W.; Qian, Y.; Chong, W. A pilot validation of CFD model results against PIV observations of haemodynamics in intracranial aneurysms treated with flow-diverting stents. J. Biomech. 2019, 100, 109590. [Google Scholar] [CrossRef]
- Janiga, G.; Daróczy, L.; Berg, P.; Thévenin, D.; Skalej, M.; Beuing, O. An automatic CFD-based flow diverter optimization principle for patient-specific intracranial aneurysms. J. Biomech. 2015, 48, 3846–3852. [Google Scholar] [CrossRef]
- Carvalho, V.; Rodrigues, N.; Lima, R.A.; Teixeira, S. Numerical simulation of blood pulsatile flow in stenotic coronary arteries: The effect of turbulence modeling and non-Newtonian assumptions. In Proceedings of the International Conference on Applied Mathematics & Computer Science, Chania, Greece, 19–22 July 2020; pp. 112–116. [Google Scholar]
- Appanaboyina, S.; Mut, F.; Löhner, R.; Putman, C.M.; Cebral, J.R. Computational fluid dynamics of stented intracranial aneurysms using adaptive embedded unstructured grids. Int. J. Numer. Methods Fluids 2008, 57, 475–493. [Google Scholar] [CrossRef]
- Xiang, J.; Natarajan, S.K.; Tremmel, M.; Ma, D.; Mocco, J.; Hopkins, L.N.; Siddiqui, A.H.; Levy, E.I.; Meng, H. Hemodynamic-morphologic discriminants for intracranial aneurysm rupture. Stroke 2011, 42, 144–152. [Google Scholar] [CrossRef] [Green Version]
- Dolan, J.M.; Kolega, J.; Meng, H. High wall shear stress and spatial gradients in vascular pathology: A review. Ann. Biomed. Eng. 2013, 41, 1411–1427. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.S.J.; Haga, J.H.; Chien, S. Molecular basis of the effects of shear stress on vascular endothelial cells. J. Biomech. 2005, 38, 1949–1971. [Google Scholar] [CrossRef]
- Rashad, S.; Han, X.; Saqr, K.; Tupin, S.; Ohta, M.; Niizuma, K.; Tominaga, T. Epigenetic response of endothelial cells to different wall shear stress magnitudes: A report of new mechano-miRNAs. J. Cell. Physiol. 2020, 235, 7827–7839. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Sugawara, M.; Tanaka, G.; Ohta, M.; Liu, H.; Yamaguchi, R. Effect of elasticity on wall shear stress inside cerebral aneurysm at anterior cerebral artery. Technol. Heal. Care. 2016, 24, 349–357. [Google Scholar] [CrossRef] [PubMed]
- Mooney, M. A theory of large elastic deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Lawrence, K.L. ANSYS Workbench Tutorial Release 14; SDC Publications: Mission, KS, USA, 2012. [Google Scholar]
- Chen, X.; Liu, Y. Finite Element Modeling and Simulation with ANSYS Workbench; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Parlea, L.; Fahrig, R.; Holdsworth, D.W.; Lownie, S.P. An Analysis of the Geometry of Saccular Intracranial Aneurysms. AJNR Am. J. Neuroradiol 1999, 20, 1079–1089. [Google Scholar]
- Bird, R.B.; Armstrong, R.C.; Hassager, O. Dynamic of Polymeric Liquids; John Willey & Sons: New York, NY, USA, 1987; Volume 1. [Google Scholar]
- Çengel, Y.A.; Ghajar, A.J. Heat and Mass Transfer, 4th ed.; Mc. Graw Hill: New York, NY, USA, 2012. [Google Scholar]
- Cardoso, C.; Fernandes, C.S.; Lima, R.; Ribeiro, J. Biomechanical analysis of PDMS channels using different hyperelastic numerical constitutive models. Mech. Res. Commun. 2018, 90, 26–33. [Google Scholar] [CrossRef] [Green Version]

















| Re | (ΔP/L)Equation (3) (Pa/m) | (ΔP/L)numerical (Pa/m) | Relative Error (%) |
|---|---|---|---|
| 100 | 716.11 | 713.79 | 0.33 |
| 500 | 3580.54 | 3575.83 | 0.13 |
| 1000 | 7161.08 | 7364.60 | 2.84 |
| Re | ΔPCarreau (Pa) | ΔPNewtonian (Pa) | ΔPratio |
|---|---|---|---|
| 100 | 46.73 | 37.64 | 1.24 |
| 500 | 290.41 | 274.81 | 1.06 |
| 1000 | 726.12 | 704.84 | 1.03 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Souza, M.S.; Souza, A.; Carvalho, V.; Teixeira, S.; Fernandes, C.S.; Lima, R.; Ribeiro, J. Fluid Flow and Structural Numerical Analysis of a Cerebral Aneurysm Model. Fluids 2022, 7, 100. https://doi.org/10.3390/fluids7030100
Souza MS, Souza A, Carvalho V, Teixeira S, Fernandes CS, Lima R, Ribeiro J. Fluid Flow and Structural Numerical Analysis of a Cerebral Aneurysm Model. Fluids. 2022; 7(3):100. https://doi.org/10.3390/fluids7030100
Chicago/Turabian StyleSouza, Maria Sabrina, Andrews Souza, Violeta Carvalho, Senhorinha Teixeira, Carla S. Fernandes, Rui Lima, and João Ribeiro. 2022. "Fluid Flow and Structural Numerical Analysis of a Cerebral Aneurysm Model" Fluids 7, no. 3: 100. https://doi.org/10.3390/fluids7030100
APA StyleSouza, M. S., Souza, A., Carvalho, V., Teixeira, S., Fernandes, C. S., Lima, R., & Ribeiro, J. (2022). Fluid Flow and Structural Numerical Analysis of a Cerebral Aneurysm Model. Fluids, 7(3), 100. https://doi.org/10.3390/fluids7030100