Experimental and Computational Studies of Peristaltic Flow in a Duodenal Model
Abstract
:1. Introduction
2. Materials and Methods
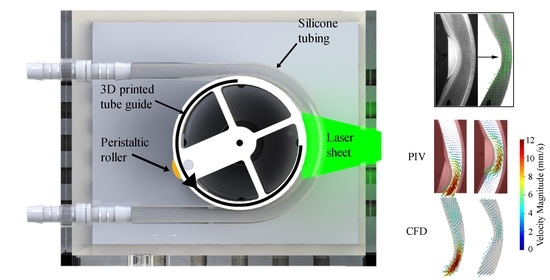
2.1. Model Construction
2.2. PIV Analysis
2.3. Tube Deformation Imaging
2.4. Computational Model
3. Results
3.1. Tube Deformation Patterns
3.2. PIV Results
3.3. Repeatability of Contraction Patterns
3.4. PIV—CFD Comparison
3.5. CFD Simulations of Different Fluids
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hall, J. Guyton and Hall Textbook of Medical Physiology; Guyton Physiology Series; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Cronin, C.G.; Delappe, E.; Lohan, D.G.; Roche, C.; Murphy, J.M. Normal small bowel wall characteristics on MR enterography. Eur. J. Radiol. 2010, 75, 207–211. [Google Scholar] [CrossRef] [PubMed]
- Lacy, B.E.; Mearin, F.; Chang, L.; Chey, W.D.; Lembo, A.J.; Simren, M.; Spiller, R. Bowel disorders. Gastroenterology 2016, 150, 1393–1407. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- El-Salhy, M. Recent developments in the pathophysiology of irritable bowel syndrome. World J. Gastroenterol. WJG 2015, 21, 7621. [Google Scholar] [CrossRef] [PubMed]
- Faulk, D.L.; Anuras, S.; Christensen, J. Chronic intestinal pseudoobstruction. Gastroenterology 1978, 74, 922–931. [Google Scholar] [CrossRef]
- Barr, J.; White, R.R. Motility Disorders of the Stomach and Small Intestine. In Shackelford’s Surgery of the Alimentary Tract, 2 Volume Set, 8th ed.; Yeo, C.J., Ed.; Elsevier: Philadelphia, PA, USA, 2019; pp. 755–763. [Google Scholar]
- Kozu, H.; Kobayashi, I.; Neves, M.A.; Nakajima, M.; Uemura, K.; Sato, S.; Ichikawa, S. PIV and CFD studies on analyzing intragastric flow phenomena induced by peristalsis using a human gastric flow simulator. Food Funct. 2014, 5, 1839–1847. [Google Scholar] [CrossRef] [PubMed]
- Nahar, S.; Jeelani, S.A.; Windhab, E.J. Peristaltic flow characterization of a shear thinning fluid through an elastic tube by UVP. Appl. Rheol. 2012, 22, 43941. [Google Scholar]
- Hari, B.; Bakalis, S.; Fryer, P. Computational modelling and simulation of the human duodenum. In Proceedings of the Excerpt from the Proceedings of the COMSOL Conference, Milan, Italy, 10–12 October 2012. [Google Scholar]
- Love, R.; Lentle, R.; Asvarujanon, P.; Hemar, Y.; Stafford, K. An expanded finite element model of the intestinal mixing of digesta. Food Dig. 2013, 4, 26–35. [Google Scholar] [CrossRef]
- De Loubens, C.; Lentle, R.G.; Love, R.J.; Hulls, C.; Janssen, P.W. Fluid mechanical consequences of pendular activity, segmentation and pyloric outflow in the proximal duodenum of the rat and the guinea pig. J. R. Soc. Interface 2013, 10, 20130027. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sinnott, M.D.; Cleary, P.W.; Harrison, S.M. Peristaltic transport of a particulate suspension in the small intestine. Appl. Math. Model. 2017, 44, 143–159. [Google Scholar] [CrossRef]
- Trusov, P.; Zaitseva, N.V.; Kamaltdinov, M. A Multiphase Flow in the Antroduodenal Portion of the Gastrointestinal Tract: A Mathematical Model. Comput. Math. Methods Med. 2016, 2016, 5164029. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Palmada, N.; Cater, J.E.; Cheng, L.K.; Suresh, V. Modelling Flow and Mixing in the Proximal Small Intestine. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montréal, QC, Canada, 20–24 July 2020; pp. 2496–2499. [Google Scholar]
- Froehlich, J.M.; Patak, M.A.; von Weymarn, C.; Juli, C.F.; Zollikofer, C.L.; Wentz, K.U. Small bowel motility assessment with magnetic resonance imaging. J. Magn. Reson. Imaging 2005, 21, 370–375. [Google Scholar] [CrossRef] [PubMed]
- Cheng, N.S. Formula for the viscosity of a glycerol-water mixture. Ind. Eng. Chem. Res. 2008, 47, 3285–3288. [Google Scholar] [CrossRef]
- Thielicke, W.; Stamhuis, E.J. PIVlab – Towards User-friendly, Affordable and Accurate Digital Particle Image Velocimetry in MATLAB. J. Open Res. Softw. 2014, 2, e30. [Google Scholar] [CrossRef] [Green Version]
- Juretić, F. cfMesh User Guide v. 1.1; Creative Fields, Ltd.: Zagreb, Croatia, 2015. [Google Scholar]
- Holzmann, T. Mathematics, Numerics, Derivations and OpenFOAM (R), Holzmann CFD; Holzmann CFD: Augsburg, Germany, 2019. [Google Scholar]
- Palmada, N.; Cater, J.E.; Cheng, L.K.; Suresh, V. Data from Experimental and Computational Studies of Peristaltic Flow in a Duodenal Model; University of Auckland: Auckland, New Zealand, 2022. [Google Scholar] [CrossRef]











| Location | Pressure | Velocity |
|---|---|---|
| Inlet and Outlet | totalPressure | pressureInletOutletVelocity |
| Wall | zeroGradient | movingWallVelocity |
| nOuterCorrectors | 500 | |
| nCorrectors | 2 | |
| nNonOrthogonalCorrectors | 1 | |
| correctPhi | yes | |
| residualControl | U-tolerance | 1 |
| p-tolerance | 1 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palmada, N.; Cater, J.E.; Cheng, L.K.; Suresh, V. Experimental and Computational Studies of Peristaltic Flow in a Duodenal Model. Fluids 2022, 7, 40. https://doi.org/10.3390/fluids7010040
Palmada N, Cater JE, Cheng LK, Suresh V. Experimental and Computational Studies of Peristaltic Flow in a Duodenal Model. Fluids. 2022; 7(1):40. https://doi.org/10.3390/fluids7010040
Chicago/Turabian StylePalmada, Nadun, John E. Cater, Leo K. Cheng, and Vinod Suresh. 2022. "Experimental and Computational Studies of Peristaltic Flow in a Duodenal Model" Fluids 7, no. 1: 40. https://doi.org/10.3390/fluids7010040