Development of an Analytical Wall Function for Bypass Transition
Abstract
:1. Introduction
2. Transition and Turbulence Models
2.1. k − ω Turbulence Model
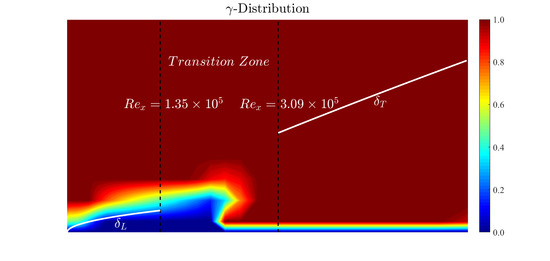
2.2. Algebraic Transition Model
3. Analytical Wall Function
3.1. Eddy Viscosity of the Near-Wall Cell P
3.2. Wall Shear Stress at Face s (South) of the Near-Wall Cell P
3.3. k-Equation of the Near-Wall Cell P
3.4. ω-Equation of the Near-Wall Cell P
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Acknowledgments
Conflicts of Interest
References
- Balonishnikov, A.M. Simplified description of small-scale turbulence. Tech. Phys. 2003, 48, 1407–1412. [Google Scholar] [CrossRef]
- Ershkov, S. About existence of stationary points for the Arnold–Beltrami–Childress (ABC) flow. Appl. Math. Comput. 2016, 276, 379–383. [Google Scholar] [CrossRef] [Green Version]
- Pacciani, R.; Marconcini, M.; Fadai-Ghotbi, A.; Lardeau, S.; Leschziner, M.A. Calculation of high-lift cascades in low pressure turbine conditions using a three-equation model. J. Turbomach. 2011, 133, 031016. [Google Scholar] [CrossRef]
- Pacciani, R.; Marconcini, M.; Arnone, A.; Bertini, F. Predicting high-lift low-pressure turbine cascades flow using transition-sensitive turbulence closures. J. Turbomach. 2013, 136, 051007. [Google Scholar] [CrossRef]
- Patankar, S.V.; Spalding, D.B. Heat and Mass Transfer in Boundary Layers; Morgan-Grampian Press: London, UK, 1967. [Google Scholar]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Hanjalić, K.; Launder, B. Modelling Turbulence in Engineering and the Environment: Second-Moment Routes to Closure; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Saric, S.; Basara, B.; Suga, K.; Gomboc, S. Analytical wall-function strategy for the modelling of turbulent heat transfer in the automotive CFD applications. SAE Tech. Paper 2019. [Google Scholar] [CrossRef]
- Craft, T.J.; Gerasimov, A.V.; Iacovides, H.; Launder, B.E. Progress in the generalization of wall-function treatments. Int. J. Heat Fluid Flow 2002, 23, 148–160. [Google Scholar] [CrossRef]
- Craft, T.J.; Gerasimov, A.V.; Iacovides, H.; Kidger, J.W.; Launder, B.E. The negatively buoyant turbulent wall jet: Performance of alternative options in RANS modelling. Int. J. Heat Fluid Flow 2004, 25, 809–823. [Google Scholar] [CrossRef]
- Suga, K.; Craft, T.J.; Iacovides, H. An analytical wall-function for turbulent flows and heat transfer over rough walls. Int. J. Heat Fluid Flow 2006, 27, 852–866. [Google Scholar] [CrossRef]
- Suga, K. Computation of high Prandtl number turbulent thermal fields by the analytical wall-function. Int. J. Heat Mass Transf. 2007, 50, 4967–4974. [Google Scholar] [CrossRef]
- Suga, K.; Nishiguchi, S. Computation of turbulent flows over porous/fluid interfaces. Fluid Dyn. Res. 2009, 41, 012401. [Google Scholar] [CrossRef]
- Suga, K.; Kubo, M. Modelling turbulent high Schmidt number mass transfer across undeformable gas–liquid interfaces. Int. J. Heat Mass Transf. 2010, 53, 2989–2995. [Google Scholar] [CrossRef]
- Suga, K.; Ishibashi, Y.; Kuwata, Y. An analytical wall-function for recirculating and impinging turbulent heat transfer. Int. J. Heat Fluid Flow 2013, 41, 45–54. [Google Scholar] [CrossRef]
- Amano, R.S.; Arakawa, H.; Suga, K. Turbulent heat transfer in a two-pass cooling channel by several wall turbulence models. Int. J. Heat Mass Transf. 2014, 77, 406–418. [Google Scholar] [CrossRef]
- Omranian, A.; Craft, T.J.; Iacovides, H. The computation of buoyant flows in differentially heated inclined cavities. Int. J. Heat Mass Transf. 2014, 77, 1–16. [Google Scholar] [CrossRef]
- Wang, X.; Craft, T.J.; Iacovides, H. An analytical wall function for 2-D shock wave/turbulent boundary layer interactions. In Proceedings of the 3rd World Congress on Mechanical, Chemical, and Material Engineering (MCM’17), Rome, Italy, 9–10 June 2017; pp. 7–10. [Google Scholar] [CrossRef]
- Chedevergne, F. Analytical wall function including roughness corrections. Int. J. Heat Fluid Flow 2018, 73, 258–269. [Google Scholar] [CrossRef] [Green Version]
- Aupoix, B. Improved heat transfer predictions on rough surfaces. Int. J. Heat Fluid Flow 2015, 56, 160–171. [Google Scholar] [CrossRef]
- Aupoix, B. Roughness corrections for the k–ω shear stress transport model: Status and proposals. J. Fluids Eng. 2015, 137, 021202. [Google Scholar] [CrossRef]
- Suga, K. Amendments to the extended analytical wall function for turbulent high Prandtl number flows. In Turbulence, Heat and Mass Transfer; Hanjalić, K., Nagano, Y., Jakirlić, S., Eds.; Begell House Inc.: Danbury, CT, USA, 2006; Volume 5. [Google Scholar]
- Fu, S.; Wang, L. RANS modeling of high-speed aerodynamic flow transition with consideration of stability theory. Prog. Aerosp. Sci. 2013, 58, 36–59. [Google Scholar] [CrossRef]
- Durbin, P.A. Perspectives on the phenomenology and modeling of boundary layer transition. Flow Turbul. Combust. 2017, 99, 1–23. [Google Scholar] [CrossRef]
- Durbin, P.A. Some recent developments in turbulence closure modeling. Annu. Rev. Fluid Mech. 2018, 50, 77–103. [Google Scholar] [CrossRef]
- Dick, E.; Kubacki, S. Transition models for turbomachinery boundary layer flows: A review. Int. J. Turbomach. Propuls. Power 2017, 2, 4. [Google Scholar] [CrossRef] [Green Version]
- Langtry, R.B.; Menter, F.R. Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes. AIAA J. 2009, 47, 2894–2906. [Google Scholar] [CrossRef]
- Juntasaro, E.; Ngiamsoongnirn, K. A new physics-based γ-kL transition model. Int. J. Comput. Fluid Dyn. 2014, 28, 204–218. [Google Scholar] [CrossRef]
- Juntasaro, E.; Narejo, A.A. A γ-kL Transition model for transitional flow with pressure gradient effects. Eng. J. 2017, 21, 279–304. [Google Scholar] [CrossRef]
- Xu, J.K.; Bai, J.Q.; Qiao, L.; Zhang, Y.; Fu, Z.Y. Fully local formulation of a transition closure model for transitional flow simulations. AIAA J. 2016, 54, 3015–3023. [Google Scholar] [CrossRef]
- Xu, J.K.; Bai, J.Q.; Fu, Z.Y.; Qiao, L.; Zhang, Y.; Xu, J.L. Parallel compatible transition closure model for high-speed transitional Flow. AIAA J. 2017, 55, 3040–3050. [Google Scholar] [CrossRef]
- Lodefier, K.; Merci, B.; De Langhe, C.; Dick, E. Transition modelling with the k-Ω turbulence model and an intermittency transport equation. J. Therm. Sci. 2004, 13, 220–225. [Google Scholar] [CrossRef]
- Wang, L.; Fu, S. Development of an intermittency equation for the modeling of the supersonic/hypersonic boundary layer flow transition. Flow, Turbul. Combust. 2011, 87, 165–187. [Google Scholar] [CrossRef]
- Durbin, P.A. An intermittency model for bypass transition. Int. J. Heat Fluid Flow 2012, 36, 1–6. [Google Scholar] [CrossRef]
- Ge, X.; Arolla, S.; Durbin, P. A Bypass transition model based on the intermittency function. Flow Turbul. Combust. 2014, 93, 37–61. [Google Scholar] [CrossRef]
- Menter, F.R.; Smirnov, P.E.; Liu, T.; Avancha, R. A one-equation local correlation-based transition model. Flow Turbul. Combust. 2015, 95, 583–619. [Google Scholar] [CrossRef]
- Juntasaro, E.; Ngiamsoongnirn, K.; Thawornsathit, P.; Durbin, P. Development of an intermittency transport equation for modeling bypass, natural and separation-induced transition. J. Turbul. 2021, 22, 562–595. [Google Scholar] [CrossRef]
- Mayle, R.E.; Schulz, A. Heat transfer committee and turbomachinery committee best paper of 1996 award: The path to predicting bypass transition. J. Turbomach. 1997, 119, 405–411. [Google Scholar] [CrossRef]
- Walters, D.K.; Leylek, J.H. A new model for boundary layer transition using a single-point RANS approach. J. Turbomach. 2004, 126, 193–202. [Google Scholar] [CrossRef]
- Walters, D.K.; Cokljat, D. A three-equation eddy-viscosity model for Reynolds-Averaged Navier–Stokes simulations of transitional flow. J. Fluids Eng. 2008, 130, 121401. [Google Scholar] [CrossRef]
- Medina, H.; Beechook, A.; Fadhila, H.; Aleksandrova, S.; Benjamin, S. A novel laminar kinetic energy model for the prediction of pretransitional velocity fluctuations and boundary layer transition. Int. J. Heat Fluid Flow 2018, 69, 150–163. [Google Scholar] [CrossRef]
- Lopez, M.; Walters, D.K. Prediction of transitional and fully turbulent flow using an alternative to the laminar kinetic energy approach. J. Turbul. 2016, 17, 253–273. [Google Scholar] [CrossRef]
- Kubacki, S.; Dick, E. An algebraic model for bypass transition in turbomachinery boundary layer flows. Int. J. Heat Fluid Flow 2016, 58, 68–83. [Google Scholar] [CrossRef]
- Kubacki, S.; Dick, E. An algebraic intermittency model for bypass, separation-induced and wake-induced transition. Int. J. Heat Fluid Flow 2016, 62, 344–361. [Google Scholar] [CrossRef]
- Sandhu, J.P.S.; Ghosh, S. A local correlation-based zero-equation transition model. Comput Fluids 2021, 214, 104758. [Google Scholar] [CrossRef]
- Wilcox, D.C. Formulation of the k-ω turbulence model revisited. AIAA J. 2008, 46, 2823–2838. [Google Scholar] [CrossRef] [Green Version]
- Suga, K. Analytical wall-functions of turbulence for complex surface flow phenomena. Comput. Fluid Dyn. Heat Transf. Emerg. Top. 2010, 41, 331–380. [Google Scholar] [CrossRef]
- ERCOFTAC Classic Collection Database. Coupland (1990). Available online: http://cfd.mace.manchester.ac.uk/ercoftac (accessed on 1 May 2005).







| Test Case | Viscosity Ratio | |||
|---|---|---|---|---|
| T3A | 5.4 | 3.6 | 12 | 6.1 × 105 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Juntasaro, E.; Ngiamsoongnirn, K.; Thawornsathit, P.; Suga, K. Development of an Analytical Wall Function for Bypass Transition. Fluids 2021, 6, 328. https://doi.org/10.3390/fluids6090328
Juntasaro E, Ngiamsoongnirn K, Thawornsathit P, Suga K. Development of an Analytical Wall Function for Bypass Transition. Fluids. 2021; 6(9):328. https://doi.org/10.3390/fluids6090328
Chicago/Turabian StyleJuntasaro, Ekachai, Kiattisak Ngiamsoongnirn, Phongsakorn Thawornsathit, and Kazuhiko Suga. 2021. "Development of an Analytical Wall Function for Bypass Transition" Fluids 6, no. 9: 328. https://doi.org/10.3390/fluids6090328