Numerical Simulation and Linearized Theory of Vortex Waves in a Viscoelastic, Polymeric Fluid
Abstract
:1. Introduction
2. Vorticity Generation in a Viscoelastic Fluid
3. Linearized Equations for Vortex Waves
4. Numerical Methods
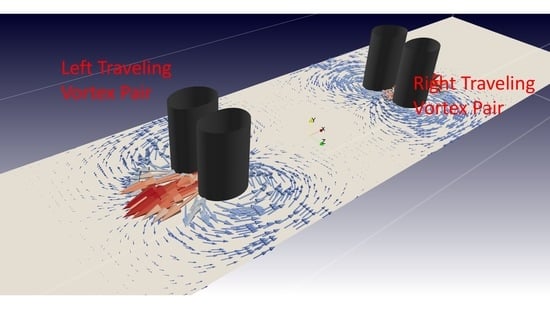
5. Flow Visualization and Kinematics
6. Linearized Wave Equation and the Undamped Solution
6.1. Linearized Wave Equation
6.2. Analytical Solution for Undamped Waves
7. Viscous Effects
7.1. Temporal Evolution of the Vorticity Magnitude from Numerical Simulations
7.2. One-Dimensional Analytical Solution of the Linearized Wave Equation with Viscosity
7.3. Two-Dimensional Analytical Solution of the Linearized Wave Equation with Viscosity
8. Vortex Wave Speed
8.1. Effect of Wave Amplitude on Wave Speed
8.2. Effect of the Initial Elastic Stress on Wave Speed
8.3. Effect of the Maximum Polymer Extensional Length on Wave Speed
9. Summary and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of the Initial Time Rate of Change of the Vorticity
Appendix B. Table of Symbols
| Symbol | Definition | Units |
|---|---|---|
| Coordinates: the vortex waves travel in the x-direction, z is perpendicular to this direction, and y is the vertical direction (see Figure 1) | Dimensional | |
| Scripted coordinates corresponding to | Dimensional | |
| Lengths of the computational domain in the , , and directions. is the half-height of the computational domain in the y-direction | Dimensional | |
| Coordinates x,y,z made dimensionless using | Dimensionless | |
| Computational domain lengths made dimensionless using . Note that this definition leads to . | Dimensionless | |
| Time | Dimensional | |
| Velocity and components of the velocity | Dimensional | |
| Vorticity and components of the vorticity | Dimensional | |
| Polymer conformation tensor and its components | Dimensionless. The conformation tensor is made dimensionless using the rest length of the polymer molecule | |
| Fluid pressure | Dimensional | |
| Average or mean value of the velocity (e.g., time or ensemble averaged) and its perturbation | Dimensional | |
| Average or mean value of the vorticity (e.g., time or ensemble averaged) and its perturbation | Dimensional | |
| Average or mean value of the conformation tensor (e.g., time or ensemble averaged) and its perturbation | Dimensional | |
| Average or mean value of the pressure (e.g., time or ensemble averaged) and its perturbation | Dimensional | |
| Solution viscosity | Dimensional | |
| Polymer relaxation time | Dimensional | |
| Ratio of the solvent to the solution viscosity | Dimensionless | |
| Stress parameter. | Dimensional | |
| Maximum possible extensional length made dimensionless using the polymer rest length | Dimensionless | |
| Vortex wave speed. See definition directly following Equation (21). | Dimensional | |
| Length associated with the region in which the fluid tension experiences a deficit. The region is a square with length on each side. See Figure 1B. | Dimensional | |
In the simulations and theory, . See Figure 1B. | Dimensionless | |
| The transition time a/C. Before this time, the vortex wave expands without translating. Translation occurs when | Dimensional | |
| Dimensionless transition time, . | Dimensionless | |
| Dimensionless time. = . | Dimensionless | |
| Dimensionless vortex wave speed.. | Dimensionless | |
| Initial value of the component of the conformation tensor, which is directly proportional to the fluid tension in the fluid. | Dimensionless | |
| The Peterlin function. where . | Dimensionless | |
| Amplitude of the polymer conformation deficit, which is proportional to the stress deficit. | Dimensionless | |
| Amplitude parameter given by . When , the vortex wave can be considered linear. | Dimensionless | |
| Component of the vorticity in the vertical (y) direction. | Dimensional | |
| Dimensionless vertical vorticity where . | Dimensionless | |
| translational time scale for a vortex wave | Dimensional | |
| d | distance traveled by a vortex wave in time | Dimensional |
| Q | amplitude of the source of the vortex wave | Dimensional |
Appendix C. Analytical Solution of the One-Dimensional Damped, Linearized Vorticity Equation
Appendix D. Analytical Solution of the Two-Dimensional Damped, Linearized Vorticity Equation
References
- Handler, R.A.; Blaisten-Barojas, E.; Ligrani, P.M.; Dong, P.; Paige, M. Vortex generation in a finitely extensible nonlinear elastic Peterlin fluid initially at rest. Eng. Rep. 2020, 2, e12135. [Google Scholar] [CrossRef] [Green Version]
- Pan, L.; Morozov, A.; Wagner, C.; Arratia, P.E. Nonlinear Elastic Instability in Channel Flows at Low Reynolds Numbers. Phys. Rev. Lett. 2013, 110, 174502. [Google Scholar] [CrossRef]
- Qin, B.; Arratia, P.E. Characterizing elastic turbulence in channel flows at low Reynolds number. Phys. Rev. Fluids 2017, 2, 083302. [Google Scholar] [CrossRef]
- Kim, K.; Adrian, R.J.; Balachandar, S.; Sureshkumar, R. Dynamics of Hairpin Vortices and Polymer-Induced Turbulent Drag Reduction. Phys. Rev. Lett. 2008, 100, 134504. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.; Sureshkumar, R. Spatiotemporal evolution of hairpin eddies, Reynolds stress, and polymer torque in polymer drag-reduced turbulent channel flows. Phys. Rev. E 2013, 87, 063002. [Google Scholar] [CrossRef] [Green Version]
- Min, T.; Yoo, J.Y.; Choi, H.; Joseph, D.D. Drag reduction by polymer additives in a turbulent channel flow. J. Fluid Mech. 2003, 486, 213–238. [Google Scholar] [CrossRef] [Green Version]
- Toms, B.A. Some observations on the flow of linear polymer solutions straight tubes at large Reynolds numbers. In Proceedings of the International Congress on Rheology; North Holland: Amsterdam, The Netherlands, 1948; Volume 2, pp. 135–141. [Google Scholar]
- Samantha, G.; Housiadis, K.D.; Handler, R.A.; Beris, A.N. Effects of viscoelasticity on the probability density functions in turbulent channel flow. Phys. Fluids 2009, 21, 115106. [Google Scholar] [CrossRef]
- White, C.M.; Mungal, M.G. Mechanics and prediction of turulent drag reduction with polymer additives. Annu. Rev. Fluid Mech. 2008, 40, 235–256. [Google Scholar] [CrossRef]
- Lumley, J.L. Drag reduction by additives. Annu. Rev. Fluid Mech. 1969, 1, 367–384. [Google Scholar] [CrossRef]
- Sureshkumar, R.; Beris, A.N.; Handler, R.A. Direct numerical simulation of the turbulent channel flow of a polymer solution. Phys. Fluids 1997, 9, 743–755. [Google Scholar] [CrossRef]
- Dimitropoulos, C.D.; Sureshkumar, R.; Beris, A.N. Direct numerical simulation of viscoelastic turbulent channel flow exhibiting drag reduction: Effect of the variation of rheological parameters. J. Non-Newton. Fluid Mech. 1998, 79, 433–468. [Google Scholar] [CrossRef]
- Dimitropoulos, C.D.; Sureshkumar, R.; Beris, A.N.; Handler, R.A. Budgets of Reynolds stress, kinetic energy and streamwise enstrophy in viscoelastic turbulent channel flow. Phys. Fluids 2001, 13, 1016–1027. [Google Scholar] [CrossRef]
- Housiadas, K.; Beris, A.N.; Handler, R.A. Viscoelastic effects on higher order statistics and on coherent structures in turbulent channel flow. Phys. Fluids 2005, 17, 35106. [Google Scholar] [CrossRef]
- Handler, R.A.; Housiadas, K.; Beris, A.N. Karhunen–Loeve representations of turbulent channel flows using the method of snapshots. Int. J. Numer. Methods Fluids 2006, 52, 1339–1360. [Google Scholar] [CrossRef]
- Virk, P.S. Drag reduction fundamentals. AIChE J. 1975, 21, 625–656. [Google Scholar] [CrossRef]
- De Gennes, P. Towards a scaling theory of drag reduction. Physica A 1986, 140, 9–25. [Google Scholar] [CrossRef]
- Manz, A.; Harrison, D.J.; Verpoorte, E.; Widmer, H.M. Planar chips technology for miniaturization of separation systems: A developing perspective in chemical monitoring. Adv. Chromatogr. 1993, 33, 1–66. [Google Scholar]
- Reyes, D.R.; Iossifidis, D.; Auroux, P.A.; Manz, A. Micro total analysis systems. Introduction, theory, and technology. Anal. Chem. 2002, 74, 2623–2636. [Google Scholar]
- Vijayendran, R.A.; Motsegood, K.M.; Beebe, D.J.; Leckband, D.E. Evaluation of a three-dimensional micromixer in a surface-based biosensor. Langmuir 2003, 19, 1824–1828. [Google Scholar] [CrossRef]
- Ho, C.M.; Tai, Y.C. Micro-electro-mechanical-systems (MEMS). Annu. Rev. Fluid Mech. 1998, 30, 579–612. [Google Scholar] [CrossRef] [Green Version]
- Verpoorte, E.; De Rooij, N.F. Microfluidics meets MEMS. Proc. IEEE 2003, 91, 930–953. [Google Scholar] [CrossRef] [Green Version]
- Wiggins, S.; Ottino, J.M. Foundations of chaotic mixing. Philos. Trans. R. Soc. A 2004, 362, 937–970. [Google Scholar] [CrossRef]
- Eckart, C. An analysis of the stirring and mixing processes in incompressible fluids. J. Mar. Res. 1948, 7, 265–275. [Google Scholar]
- Aref, H.; Balachandar, S. Chaotic advection in a Stokes flow. Phys. Fluids 1986, 29, 3515. [Google Scholar] [CrossRef]
- Ottino, J.M. The Kinematics of Mixing: Stretching, Chaos, and Transport; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Stremler, M.A.; Haselton, F.R.; Aref, H. Designing for chaos: Applications of chaotic advection at the microscale. Philos. Trans. R. Soc. A 2004, 362, 1019–1036. [Google Scholar] [CrossRef] [PubMed]
- Bringer, M.R.; Gerdts, C.J.; Song, H.; Tice, J.D.; Ismagilov, R.F. Microfluidic systems for chemical kinetics that rely on chaotic mixing in droplets. Philos. Trans. R. Soc. A 2004, 362, 1087–1104. [Google Scholar] [CrossRef] [Green Version]
- Bottausci, F.; Mezic, I.; Meinhart, C.D.; C. Cardonne, C. Mixing in the shear superposition micromixer: Three dimensional analysis. Philos. Trans. R. Soc. A 2004, 362, 1001–1008. [Google Scholar] [CrossRef] [PubMed]
- Campbell, C.J.; Grzybowski, B.A. Microfluidic Mixers: From Microfabricated to Self-Assembled Devices. Philos. Trans. R. Soc. A 2004, 362, 1069–1086. [Google Scholar] [CrossRef] [PubMed]
- Darhuber, A.A.; Chen, J.Z.; Davis, J.M.; Troian, S.M. A study of mixing in thermocapillary flows on micropatterned surfaces. Philos. Trans. R. Soc. A 2004, 362, 1037–1058. [Google Scholar] [CrossRef] [PubMed]
- Mensing, G.A.; Pearce, T.M.; Graham, M.D.; Beebe, D.J. An externally driven magnetic microstirrer. Philos. Trans. R. Soc. A 2004, 362, 1059–1068. [Google Scholar] [CrossRef] [PubMed]
- Stroock, A.D.; McGraw, G.J. Investigation of the staggered herringbone mixer with a simple analytical model. Philos. Trans. R. Soc. A 2004, 362, 971–986. [Google Scholar] [CrossRef] [PubMed]
- Tabeling, P.; Chabert, M.; Dodge, A.; Jullien, C.; Okkels, F. Chaotic mixing in cross-channel micromixers. Philos. Trans. R. Soc. A 2004, 362, 987–1000. [Google Scholar] [CrossRef] [PubMed]
- Stroock, A.; Dertinger, S.K.W.; Ajdari, A.; Mezić, I.; Stone, H.A.; Whitesides, G.M. Chaotic Mixer for Microchannels. Science 2002, 295, 647–651. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ottino, J.M. Mixing, chaotic advection and turbulence. Annu. Rev. Fluid Mech. 1990, 22, 207–253. [Google Scholar] [CrossRef]
- Aref, H. Stirring by chaotic advection. J. Fluid Mech. 1984, 143, 1–23. [Google Scholar] [CrossRef]
- Chou, H.-P.; Unger, M.A.; Quake, S.R. A Microfabricated Rotary Pump. Biomed. Microdevices 2001, 3, 323–330. [Google Scholar] [CrossRef]
- Sudarsan, A.P.; Ugaz, V.M. Multivortex micromixing. Proc. Natl. Acad. Sci. USA 2006, 103, 7228–7233. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xia, S.; Wan, Y.M.; Shu, C.; Chew, Y.T. Chaotic micromixers using two-layer crossing channels to exhibit fast mixing at low Reynolds numbers. Lab. Chip 2005, 5, 748–755. [Google Scholar] [CrossRef]
- Nguyen, N.; Wu, Z. Micromixers—A review. J. Micromech. Microeng. 2005, 15, R1–R16. [Google Scholar] [CrossRef]
- Bau, H.H.; Zhong, J.; Yi, M. A minute magnetohydrodynamic (MHD) mixer. Sens. Actuators B 2001, 79, 207–215. [Google Scholar] [CrossRef] [Green Version]
- Mao, H.; Yang, T.; Cremer, P.S. A microfluidic device with a linear temperature gradient for parallel and combinatorial measurements. J. Am. Chem. Soc. 2002, 124, 4432–4435. [Google Scholar] [CrossRef] [PubMed]
- Tsai, J.H.; Lin, L. Active microfluidic mixer and gas bubble filter driven by thermal bubble pump. Sens. Actuators A 2002, 97–98, 665–671. [Google Scholar] [CrossRef]
- Liu, R.H.; Yang, J.; Pindera, M.Z.; Athavale, M.; Grodzinski, P. Bubble-induced acoustic micromixing. Lab. Chip 2002, 2, 151–157. [Google Scholar] [CrossRef]
- Liu, R.H.; Lenigk, R.; Druyor-Sanchez, R.L.; Yang, J.; Grodzinski, P. Hybridization Enhancement Using Cavitation Microstreaming. Anal. Chem. 2003, 75, 1911–1917. [Google Scholar] [CrossRef] [PubMed]
- Yaralioglu, G.G.; Wygant, I.O.; Marentis, T.C.; Khuri-Yakub, B.T. Ultrasonic mixing in microfluidic channels using integrated transducers. Anal. Chem. 2004, 76, 3694–3698. [Google Scholar] [CrossRef]
- Squires, T.M.; Quake, S.R. Microfluidics: Fluid physics at the nanoliter scale. Rev. Mod. Phys. 2005, 77, 977–1025. [Google Scholar] [CrossRef] [Green Version]
- Stone, H.A.; Stroock, A.D.; Ajdari, A. Engineering flows in small devices: Microfluidics toward a Lab-on-a-Chip. Annu. Rev. Fluid Mech. 2004, 36, 381–411. [Google Scholar] [CrossRef] [Green Version]
- Pearson, J.R.A. Instability in Non-Newtonian Flow. Annu. Rev. Fluid Mech. 1976, 8, 163–181. [Google Scholar] [CrossRef]
- Petrie, C.J.S.; Denn, M.M. Instabilities in polymer processing. AIChE J. 1976, 22, 209–236. [Google Scholar] [CrossRef]
- Larson, R.G. Instabilities in viscoelastic flows. Rheol. Acta 1992, 31, 213–263. [Google Scholar] [CrossRef]
- McKinley, G.; Pakdel, P.; Öztekin, A. Rheological and geometric scaling of purely elastic flow instabilities. J. Non-Newton. Fluid Mech. 1996, 67, 19–47. [Google Scholar] [CrossRef]
- Baumert, B.M.; Muller, S.J. Flow visualization of the elastic Taylor-Couette instability in Boger fluids. Rheol. Acta 1995, 34, 147–159. [Google Scholar] [CrossRef]
- Graham, M. Effect of axial flow on viscoelastic Taylor–Couette instability. J. Fluid Mech. 1998, 360, 341–374. [Google Scholar] [CrossRef]
- Pakdel, P.; McKinley, G. Elastic Instability and Curved Streamlines. Phys. Rev. Lett. 1996, 77, 2459–2462. [Google Scholar] [CrossRef]
- Phan-Thien, N. Coaxial-disk flow of an Oldroyd-B fluid: Exact solution and stability. J. Non-Newton. Fluid Mech. 1983, 13, 325–340. [Google Scholar] [CrossRef]
- Phan-Thien, N. Cone-and-plate flow of the Oldroyd-B fluid is unstable. J. Non-Newton. Fluid Mech. 1985, 17, 37–44. [Google Scholar] [CrossRef]
- McKinley, G.H.; Byars, J.A.; Brown, R.A.; Armstrong, R.C. Observations on the elastic instability in cone-and-plate and parallel-plate flows of a polyisobutylene Boger fluid. J. Non-Newton. Fluid Mech. 1991, 40, 201–229. [Google Scholar] [CrossRef]
- McKinley, G.; Öztekin, A.; Byars, J.A.; Brown, R.A. Self-similar spiral instabilities in elastic flows between a cone and a plate. J. Fluid Mech. 1995, 285, 123–164. [Google Scholar] [CrossRef]
- Byars, J.A.; Öztekin, A.; Brown, R.A.; McKinley, G. Spiral instabilities in the flow of highly elastic fluids between rotating parallel disks. J. Fluid Mech. 1994, 271, 173–218. [Google Scholar] [CrossRef]
- McKinley, G.H.; Armstrong, R.C.; Brown, R.A. The wake instability in viscoelastic flow past confined circular cylinders. Philos. Trans. R. Soc. A 1993, 344, 265–304. [Google Scholar]
- Graham, M.D. Iterfacial hoop stress and instability of viscoelastic free surface flows. Phys. Fluids 2003, 15, 1702–1710. [Google Scholar] [CrossRef] [Green Version]
- Kumar, K.A.; Graham, M.D. Bckling instabilities in models of viscoelastic free surface flows. J. Non-Newton. Fluid Mech. 2000, 89, 337–351. [Google Scholar] [CrossRef]
- Ligrani, P.M.; Copeland, D.; Ren, C.; Su, M.; Suzuki, M. Het transfer enhancements from elastic turbulence using sucrose-based polymer solutions. AIAA J. Thermophys. Heat Transf. 2018, 32, 51–60. [Google Scholar] [CrossRef] [Green Version]
- Ligrani, P.M.; Su, M.; Pippert, A.; Handler, R.A. Thermal Transport of Viscoelastic Fluids Within Rotating Couette Flows. J. Thermophys. Heat Transf. 2020, 34, 121–133. [Google Scholar] [CrossRef]
- Bird, R.B.; Curtiss, C.F.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids Kinetic Theory, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1987; Volume 2. [Google Scholar]
- Tanner, R.I. Engineering Rheology; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Ghosh, I.; McKinley, G.; Brown, R.A.; Armstrongb, R.C. Deficiencies of FENE dumbbell models in describing the rapid stretching of dilute polymer solutions. J. Rheol. 2001, 45, 721–758. [Google Scholar] [CrossRef] [Green Version]
- Morse, P.M.; Ingard, K.U. Theoretical Acoustics; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Vajipeyajula, B.; Khambampati, T.; Handler, R.A. Dynamics of a single buoyant plume in a FENE-P fluid. Phys. Fluids 2017, 29, 091701. [Google Scholar] [CrossRef]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods in Fluid Dynamics; Springer: Berlin, Germany, 1998. [Google Scholar]
- Kim, J.; Moin, P.; Moser, R. Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 1987, 177, 133–166. [Google Scholar] [CrossRef] [Green Version]
- Swearingen, J.D.; Crouch, J.D.; Handler, R.A. Dynamics and stability of a vortex ring impacting a solid boundary. J. Fluid Mech. 1995, 297, 1–28. [Google Scholar] [CrossRef]
- McCormack, P.D.; Crane, L. Physical Fluid Dynamics; Academic Press: New York, NY, USA, 1973. [Google Scholar]
- Richter, D.; Iaccarino, G.; Shaqfeh, E.S.G. Simulations of three-dimensional viscoelastic flows past a circular cylinder at moderate Reynolds numbers. J. Fluid Mech. 2010, 651, 415–442. [Google Scholar] [CrossRef] [Green Version]
- Buckingham, M.J. Causality, Stokes’ wave equation, and acoustic pulse propagation in a viscous fluid. Phys. Rev. E 2005, 72, 026610. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gaunaurd, G.C.; Everstine, G.C. Viscosity Effects on the Propagation of Acoustic Transients. J. Vib. Acoust. 2001, 124, 19–25. [Google Scholar] [CrossRef]
- Sousa, P.C.; Pinho, F.T.; Alves, M.A. Purely-elastic flow instabilities and elastic turbulence in microfluidic cross-slot devices. Soft Matter 2018, 14, 1344–1354. [Google Scholar] [CrossRef] [PubMed] [Green Version]










Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Handler, R.A.; Buckingham, M.J. Numerical Simulation and Linearized Theory of Vortex Waves in a Viscoelastic, Polymeric Fluid. Fluids 2021, 6, 325. https://doi.org/10.3390/fluids6090325
Handler RA, Buckingham MJ. Numerical Simulation and Linearized Theory of Vortex Waves in a Viscoelastic, Polymeric Fluid. Fluids. 2021; 6(9):325. https://doi.org/10.3390/fluids6090325
Chicago/Turabian StyleHandler, Robert A., and Michael J. Buckingham. 2021. "Numerical Simulation and Linearized Theory of Vortex Waves in a Viscoelastic, Polymeric Fluid" Fluids 6, no. 9: 325. https://doi.org/10.3390/fluids6090325