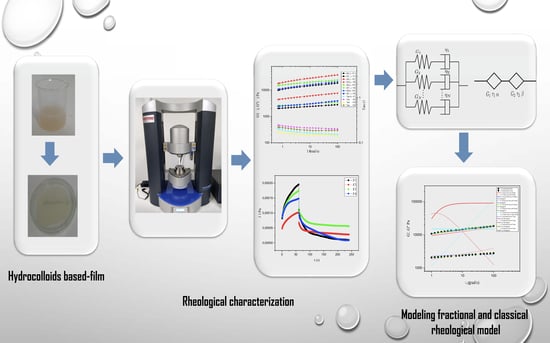
Characterization and Modeling of the Viscoelastic Behavior of Hydrocolloid-Based Films Using Classical and Fractional Rheological Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material
2.2. Film Preparation
2.3. Viscoelastic Tests
2.3.1. Dynamic Rheological Tests
2.3.2. Creep and Recovery Tests
3. Rheological Model
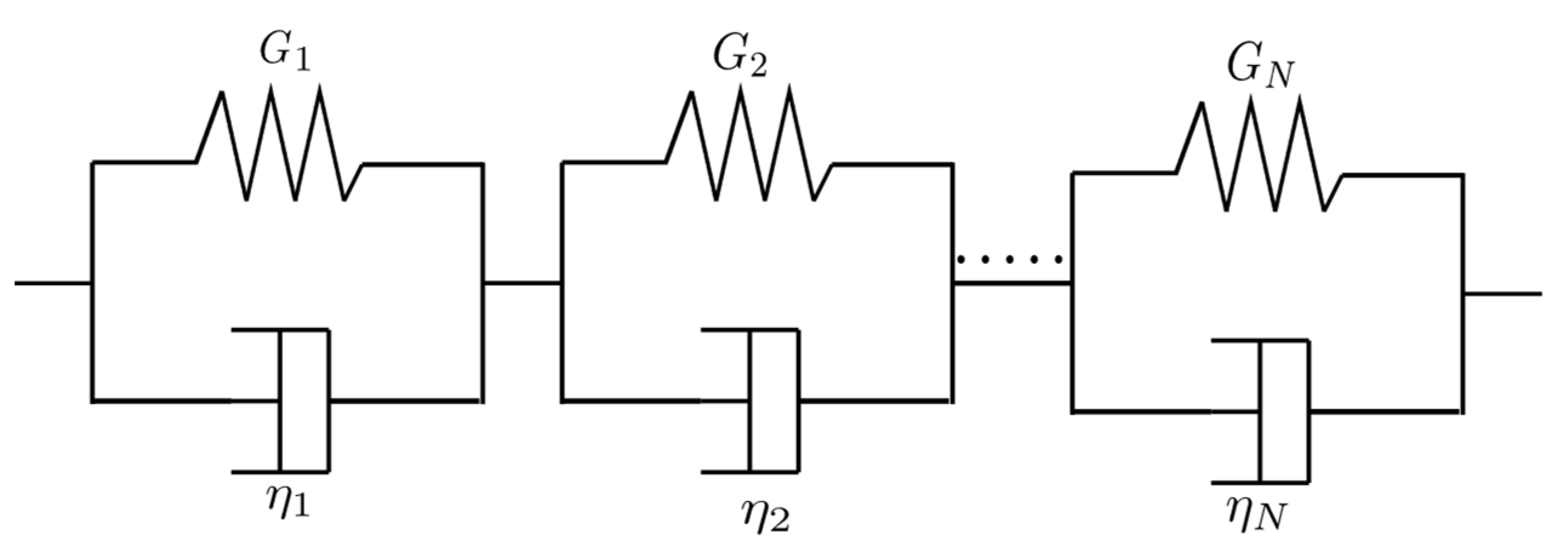
3.1. The Generalized Maxwell Model
3.2. The Fractional Maxwell Model
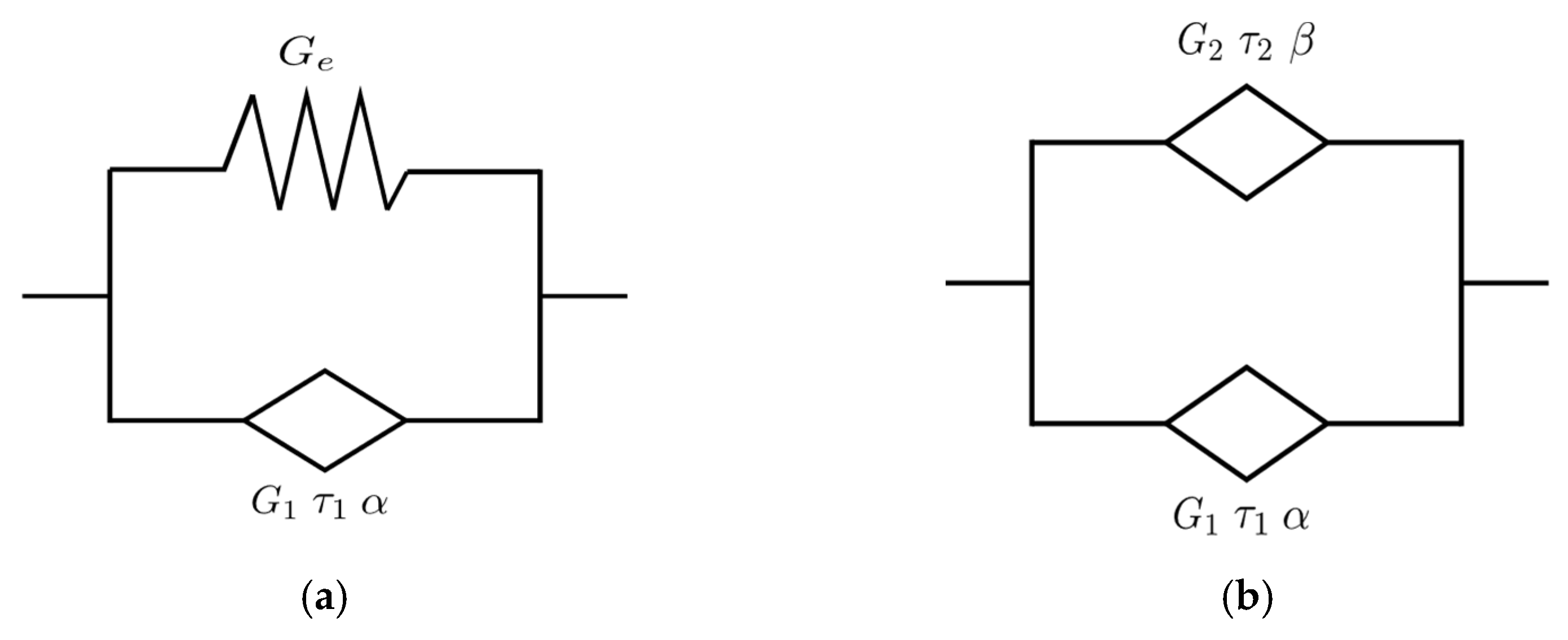
3.3. The Generalized Kelvin Model
3.4. The Fractional Kelvin Model
4. Vortex Search Algorithm (VSA)
- Initial Solution: The VSA works with the vector radius ( where t is the iteration counter) that generates a hyperellipsoid in a d-dimensional space. To center the hyperellipsoid in the solution space, let us define its center as , where:and and are the minimum and maximum bounds of the solution variables x.
- Candidate Solutions: To generate a set of candidate solutions (where subscript i is associated with the i-th individual in the population) a Gaussian distribution is used as follows:where is a vector of random variables, is a current center of the hyperellipsoid in the iteration t, and is a matrix of covariances. Here, we simplified this matrix with identical variances in diagonal null covariance, as recommended in [37]:where , with being an identity matrix with appropriate dimensions. Note that for initializing the radius vector ( with ), the VSA approach recommends assigning it as . Note that the vector radius is important in the VSA algorithm, since it governs the random vector of variables as , where generates a vector of random variables between and with dimension .
- Bounding the Candidate Solutions: Note that a Gaussian distribution can generate a set of solutions outside of the solution’s space bounds, which implies that a bounding procedure is always required, as presented below:where is a random number between 0 and 1.
- Selection of the new center: To advance through the solution space, it is necessary to select the new center of the hyperellipsoid as a function of the best solution attained in the population, i.e., must be selected as the individual in such that it produces the minimum (maximum) solution of the current population, which implies that = . Observe that the selection of the new center implies that all individuals in the current population have been evaluated in the objective function or in its equivalent [44] to determine the direction of exploration and exploitation of the solution space.
- The Radius Step-Down Process: To decrease the radius of the hyperellipsoid centered at use the incomplete inverse gamma function [42]; notwithstanding, here we propose an alternative decreasing method using an exponential function as follows [39]:where a is a constant parameter that governs the reduction speed of the radius of the hyperellipsoid that represents the solution space;
- Stopping criteria: The VSA algorithm stops its search process in the solution space when each of the following conditions is reached:
- If all the iterations have been made, i.e., ;
- If during k consecutive iterations the best fitness function has not been modified, with kmax being the maximum consecutive iterations without improvement, i.e., .
5. Optimization Problem
6. Results and Discussion
6.1. Viscoelastic Behavior
6.2. Validation of the Viscoelastic Rheological Model
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hasan, M.; Rusman, R.; Khaldun, I.; Ardana, L.; Mudatsir, M.; Fansuri, H. Active Edible Sugar Palm Starch-Chitosan Films Carrying Extra Virgin Olive Oil: Barrier, Thermo-Mechanical, Antioxidant, and Antimicrobial Properties. Int. J. Biol. Macromol. 2020, 163, 766–775. [Google Scholar] [CrossRef] [PubMed]
- León, P.G.; Chillo, S.; Conte, A.; Gerschenson, L.N.; Del Nobile, M.A.; Rojas, A.M. Rheological Characterization of Deacylated/Acylated Gellan Films Carrying l-(+)-Ascorbic Acid. Food Hydrocoll. 2009, 23, 1660–1669. [Google Scholar] [CrossRef]
- Skendi, A.; Biliaderis, C.G.; Lazaridou, A.; Izydorczyk, M.S. Structure and Rheological Properties of Water Soluble β-Glucans from Oat Cultivars of Avena Sativa and Avena Bysantina. J. Cereal Sci. 2003, 38, 15–31. [Google Scholar] [CrossRef]
- Mali, S.; Grossmann, M.V.E.; García, M.A.; Martino, M.N.; Zaritzky, N.E. Mechanical and Thermal Properties of Yam Starch Films. Food Hydrocoll. 2005, 19, 157–164. [Google Scholar] [CrossRef]
- Suhag, R.; Kumar, N.; Petkoska, A.T.; Upadhyay, A. Film Formation and Deposition Methods of Edible Coating on Food Products: A Review. Food Res. Int. 2020, 136, 109582. [Google Scholar] [CrossRef]
- Coutinho, D.F.; Sant, S.V.; Shin, H.; Oliveira, J.T.; Gomes, M.E.; Neves, N.M.; Khademhosseini, A.; Reis, R.L. Modified Gellan Gum Hydrogels with Tunable Physical and Mechanical Properties. Biomaterials 2010, 31, 7494–7502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goyal, R.; Tripathi, S.K.; Tyagi, S.; Ram, K.R.; Ansari, K.M.; Shukla, Y.; Chowdhuri, D.K.; Kumar, P.; Gupta, K.C. Gellan Gum Blended PEI Nanocomposites as Gene Delivery Agents: Evidences from in Vitro and in Vivo Studies. Eur. J. Pharm. Biopharm. 2011, 79, 3–14. [Google Scholar] [CrossRef] [PubMed]
- De Filpo, G.; Palermo, A.M.; Munno, R.; Molinaro, L.; Formoso, P.; Nicoletta, F.P. Gellan Gum/Titanium Dioxide Nanoparticle Hybrid Hydrogels for the Cleaning and Disinfection of Parchment. Int. Biodeterior. Biodegrad. 2015, 103, 51–58. [Google Scholar] [CrossRef]
- Vilela, J.A.P.; de Assis Perrechil, F.; Picone, C.S.F.; Sato, A.C.K.; da Cunha, R.L. Preparation, Characterization and in Vitro Digestibility of Gellan and Chitosan–Gellan Microgels. Carbohydr. Polym. 2015, 117, 54–62. [Google Scholar] [CrossRef]
- Rukmanikrishnan, B.; Ismail, F.R.M.; Manoharan, R.K.; Kim, S.S.; Lee, J. Blends of Gellan Gum/Xanthan Gum/Zinc Oxide Based Nanocomposites for Packaging Application: Rheological and Antimicrobial Properties. Int. J. Biol. Macromol. 2020, 148, 1182–1189. [Google Scholar] [CrossRef]
- Fouda, M.M.G.; El-Aassar, M.R.; El Fawal, G.F.; Hafez, E.E.; Masry, S.H.D.; Abdel-Megeed, A. K-Carrageenan/Poly Vinyl Pyrollidone/Polyethylene Glycol/Silver Nanoparticles Film for Biomedical Application. Int. J. Biol. Macromol. 2015, 74, 179–184. [Google Scholar] [CrossRef] [PubMed]
- Ganesan, A.R.; Munisamy, S.; Bhat, R. Effect of Potassium Hydroxide on Rheological and Thermo-Mechanical Properties of Semi-Refined Carrageenan (SRC) Films. Food Biosci. 2018, 26, 104–112. [Google Scholar] [CrossRef]
- Bui, V.T.N.T.; Nguyen, B.T.; Nicolai, T.; Renou, F. Mixed Iota and Kappa Carrageenan Gels in the Presence of Both Calcium and Potassium Ions. Carbohydr. Polym. 2019, 223, 115107. [Google Scholar] [CrossRef]
- Phan The, D.; Debeaufort, F.; Voilley, A.; Luu, D. Biopolymer Interactions Affect the Functional Properties of Edible Films Based on Agar, Cassava Starch and Arabinoxylan Blends. J. Food Eng. 2009, 90, 548–558. [Google Scholar] [CrossRef]
- Silva-Weiss, A.; Bifani, V.; Ihl, M.; Sobral, P.J.A.; Gómez-Guillén, M.C. Polyphenol-Rich Extract from Murta Leaves on Rheological Properties of Film-Forming Solutions Based on Different Hydrocolloid Blends. J. Food Eng. 2014, 140, 28–38. [Google Scholar] [CrossRef] [Green Version]
- Dogan, H.; Kokini, J.L. Rheological Properties of Foods. In Handbook Food Engineering, 2nd ed.; Heldman, D., Lund, D., Eds.; CRC Press: Boca Raton, FL, USA, 2007; pp. 1–124. [Google Scholar]
- Del Nobile, M.A.; Chillo, S.; Mentana, A.; Baiano, A. Use of the Generalized Maxwell Model for Describing the Stress Relaxation Behavior of Solid-like Foods. J. Food Eng. 2007, 78, 978–983. [Google Scholar] [CrossRef]
- Lu, H.; Ma, D.; Wang, J.; Yu, J. Research on Mechanical Behavior of Viscoelastic Food Material in the Mode of Compressed Chewing. Math. Probl. Eng. 2015, 2015, 581424. [Google Scholar] [CrossRef] [Green Version]
- Mahiuddin, M.; Khan, M.I.H.; Pham, N.D.; Karim, M.A. Development of Fractional Viscoelastic Model for Characterizing Viscoelastic Properties of Food Material during Drying. Food Biosci. 2018, 23, 45–53. [Google Scholar] [CrossRef] [Green Version]
- Mahiuddin, M.; Godhani, D.; Feng, L.; Liu, F.; Langrish, T.; Karim, M.A. Application of Caputo Fractional Rheological Model to Determine the Viscoelastic and Mechanical Properties of Fruit and Vegetables. Postharvest Biol. Technol. 2020, 163, 111147. [Google Scholar] [CrossRef]
- Di Paola, M.; Pirrotta, A.; Valenza, A. Visco-Elastic Behavior through Fractional Calculus: An Easier Method for Best Fitting Experimental Results. Mech. Mater. 2011, 43, 799–806. [Google Scholar] [CrossRef] [Green Version]
- Drăgănescu, G.E. Application of a Variational Iteration Method to Linear and Nonlinear Viscoelastic Models with Fractional Derivatives. J. Math. Phys. 2006, 47, 082902. [Google Scholar] [CrossRef]
- Kontou, E.; Katsourinis, S. Application of a Fractional Model for Simulation of the Viscoelastic Functions of Polymers. J. Appl. Polym. Sci. 2016, 133, 43505. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, W. A Fractional-Order Model on New Experiments of Linear Viscoelastic Creep of Hami Melon. Comput. Math. Appl. 2013, 66, 677–681. [Google Scholar] [CrossRef]
- Jaishankar, A.; McKinley, G.H. A Fractional K-BKZ Constitutive Formulation for Describing the Nonlinear Rheology of Multiscale Complex Fluids. J. Rheol. 2014, 58, 1751–1788. [Google Scholar] [CrossRef] [Green Version]
- Ma, L.; Barbosa-Cánovas, G.V. Simulating viscoelastic properties of selected food gums and gum mixtures using a fractional derivative model. J. Texture Stud. 1996, 27, 307–325. [Google Scholar] [CrossRef]
- Arikoglu, A. A New Fractional Derivative Model for Linearly Viscoelastic Materials and Parameter Identification via Genetic Algorithms. Rheol. Acta 2014, 53, 219–233. [Google Scholar] [CrossRef]
- Ciniello, A.P.D.; Bavastri, C.A.; Pereira, J.T. Identifying Mechanical Properties of Viscoelastic Materials in Time Domain Using the Fractional Zener Model. Lat. Am. J. Solids Struct. 2017, 14, 131–152. [Google Scholar] [CrossRef] [Green Version]
- Amabili, M.; Balasubramanian, P.; Breslavsky, I. Anisotropic Fractional Viscoelastic Constitutive Models for Human Descending Thoracic Aortas. J. Mech. Behav. Biomed. Mater. 2019, 99, 186–197. [Google Scholar] [CrossRef] [PubMed]
- Palacio-Torralba, J.; Hammer, S.; Good, D.W.; Alan McNeill, S.; Stewart, G.D.; Reuben, R.L.; Chen, Y. Quantitative Diagnostics of Soft Tissue through Viscoelastic Characterization Using Time-Based Instrumented Palpation. J. Mech. Behav. Biomed. Mater. 2015, 41, 149–160. [Google Scholar] [CrossRef] [Green Version]
- Müller, S.; Kästner, M.; Brummund, J.; Ulbricht, V. On the Numerical Handling of Fractional Viscoelastic Material Models in a FE Analysis. Comput. Mech. 2013, 51, 999–1012. [Google Scholar] [CrossRef]
- Palomares-Ruiz, J.E.; Rodriguez-Madrigal, M.; Lugo, J.G.C.; Rodriguez-Soto, A.A. Fractional Viscoelastic Models Applied to Biomechanical Constitutive Equations. Rev. Mex. Fis. 2015, 61, 261–267. [Google Scholar]
- Yin, B.; Hu, X.; Song, K. Evaluation of Classic and Fractional Models as Constitutive Relations for Carbon Black–Filled Rubber. J. Elastomers Plast. 2018, 50, 463–477. [Google Scholar] [CrossRef]
- Zhang, H.; Li, S.; Zhang, Z.; Luo, H.; Wang, Y. A Five-Parameter Fractional Derivative Temperature Spectrum Model for Polymeric Damping Materials. Polym. Test. 2020, 89, 106654. [Google Scholar] [CrossRef]
- Faber, T.J.; Jaishankar, A.; McKinley, G.H. Describing the Firmness, Springiness and Rubberiness of Food Gels Using Fractional Calculus. Part I: Theoretical Framework. Food Hydrocoll. 2017, 62, 311–324. [Google Scholar] [CrossRef]
- Schiessel, H.; Metzler, R.; Blumen, A.; Nonnenmacher, T.F. Generalized Viscoelastic Models: Their Fractional Equations with Solutions. J. Phys. A Math. Gen. 1995, 28, 6567–6584. [Google Scholar] [CrossRef]
- Doğan, B.; Ölmez, T. A New Metaheuristic for Numerical Function Optimization: Vortex Search Algorithm. Inf. Sci. 2015, 293, 125–145. [Google Scholar] [CrossRef]
- Figueroa-García, J.C.; Duarte-González, M.; Jaramillo-Isaza, S.; Orjuela-Cañon, A.D.; Díaz-Gutierrez, Y. (Eds.) Applied Computer Sciences in Engineering. In Proceedings of the 6th Workshop on Engineering Applications, WEA 2019, Santa Marta, Colombia, 16–18 October 2019; Communications in Computer and Information Science. Springer International Publishing: Cham, Switzerland, 2019; Volume 1052, ISBN 978-3-030-31018-9. [Google Scholar]
- Montoya, O.D.; Gil-Gonzalez, W.; Grisales-Norena, L.F. Vortex Search Algorithm for Optimal Power Flow Analysis in DC Resistive Networks With CPLs. IEEE Trans. Circuits Syst. II 2020, 67, 1439–1443. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Orozco-Henao, C. Vortex Search and Chu-Beasley Genetic Algorithms for Optimal Location and Sizing of Distributed Generators in Distribution Networks: A Novel Hybrid Approach. Eng. Sci. Technol. Int. J. 2020, 23, 1351–1363. [Google Scholar] [CrossRef]
- Gil-González, W.; Montoya, O.D.; Rajagopalan, A.; Grisales-Noreña, L.F.; Hernández, J.C. Optimal Selection and Location of Fixed-Step Capacitor Banks in Distribution Networks Using a Discrete Version of the Vortex Search Algorithm. Energies 2020, 13, 4914. [Google Scholar] [CrossRef]
- Dogan, B. A Modified Vortex Search Algorithm for Numerical Function Optimization. IJAIA 2016, 7, 37–54. [Google Scholar] [CrossRef]
- Li, P.; Zhao, Y. A Quantum-Inspired Vortex Search Algorithm with Application to Function Optimization. Nat. Comput. 2019, 18, 647–674. [Google Scholar] [CrossRef]
- Doğan, B.; Ölmez, T. Vortex Search Algorithm for the Analog Active Filter Component Selection Problem. AEU Int. J. Electron. Commun. 2015, 69, 1243–1253. [Google Scholar] [CrossRef]
- Lee, K.Y.; Kim, Y.-R.; Park, K.H.; Lee, H.G. Rheological and Gelation Properties of Rice Starch Modified with 4-α-Glucanotransferase. Int. J. Biol. Macromol. 2008, 42, 298–304. [Google Scholar] [CrossRef] [PubMed]
- González Cuello, R.E.; Urbina, N.A.; Morón Alcázar, L. Caracterización Viscoelástica de Biopelículas Obtenidas a Base de Mezclas Binarias. Inf. Tecnológica 2015, 26, 71–76. [Google Scholar] [CrossRef]
- Núñez-Santiago, M.C.; Tecante, A.; Garnier, C.; Doublier, J.L. Rheology and Microstructure of κ-Carrageenan under Different Conformations Induced by Several Concentrations of Potassium Ion. Food Hydrocoll. 2011, 25, 32–41. [Google Scholar] [CrossRef]
- Thrimawithana, T.R.; Young, S.; Dunstan, D.E.; Alany, R.G. Texture and Rheological Characterization of Kappa and Iota Carrageenan in the Presence of Counter Ions. Carbohydr. Polym. 2010, 82, 69–77. [Google Scholar] [CrossRef]
- Meng, Y.C.; Hong, L.B.; Jin, J.Q. A Study on the Gelation Properties and Rheological Behavior of Gellan Gum. AMM 2013, 284–287, 20–24. [Google Scholar] [CrossRef]
- MacArtain, P.; Jacquier, J.C.; Dawson, K.A. Physical Characteristics of Calcium Induced κ-Carrageenan Networks. Carbohydr. Polym. 2003, 53, 395–400. [Google Scholar] [CrossRef]
- Watase, M.; Nishinari, K. Effect of Potassium Ions on the Rheological and Thermal Properties of Gellan Gum Gels. Food Hydrocoll. 1993, 7, 449–456. [Google Scholar] [CrossRef]
- De Vries, A.; Wesseling, A.; van der Linden, E.; Scholten, E. Protein Oleogels from Heat-Set Whey Protein Aggregates. J. Colloid Interface Sci. 2017, 486, 75–83. [Google Scholar] [CrossRef]
- Bonfanti, A.; Kaplan, J.L.; Charras, G.; Kabla, A. Fractional Viscoelastic Models for Power-Law Materials. Soft Matter 2020, 16, 6002–6020. [Google Scholar] [CrossRef] [PubMed]

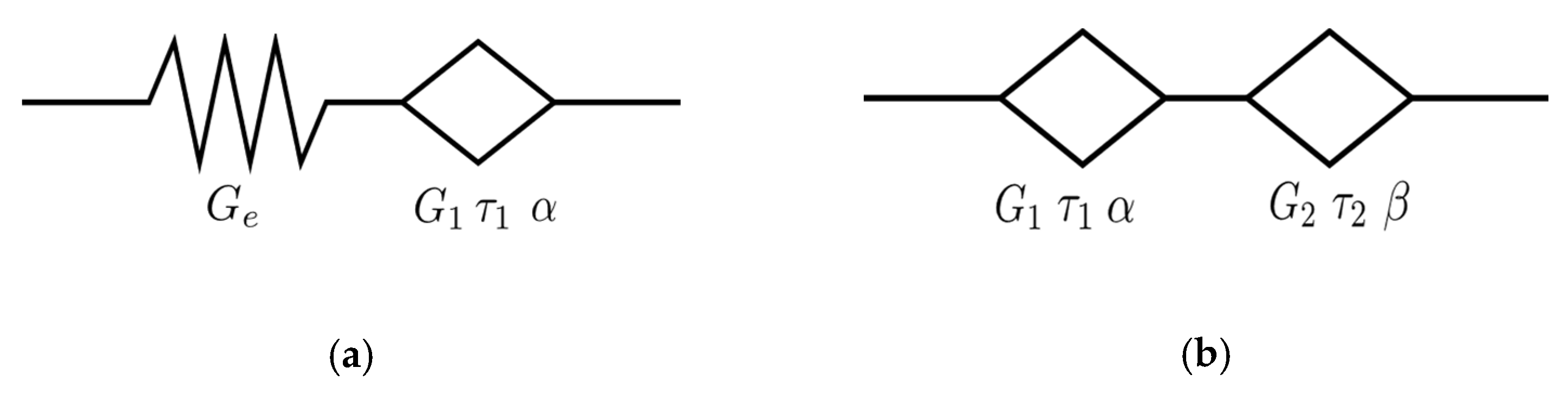
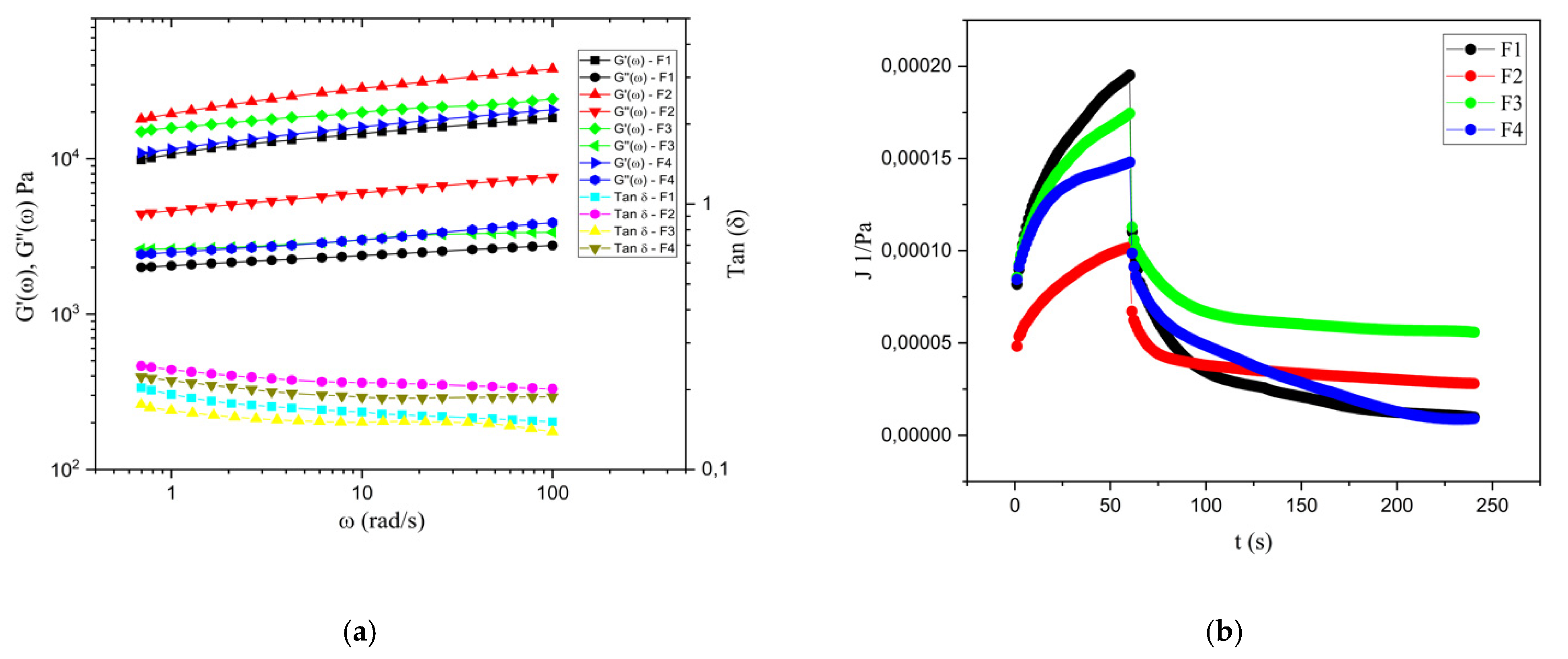
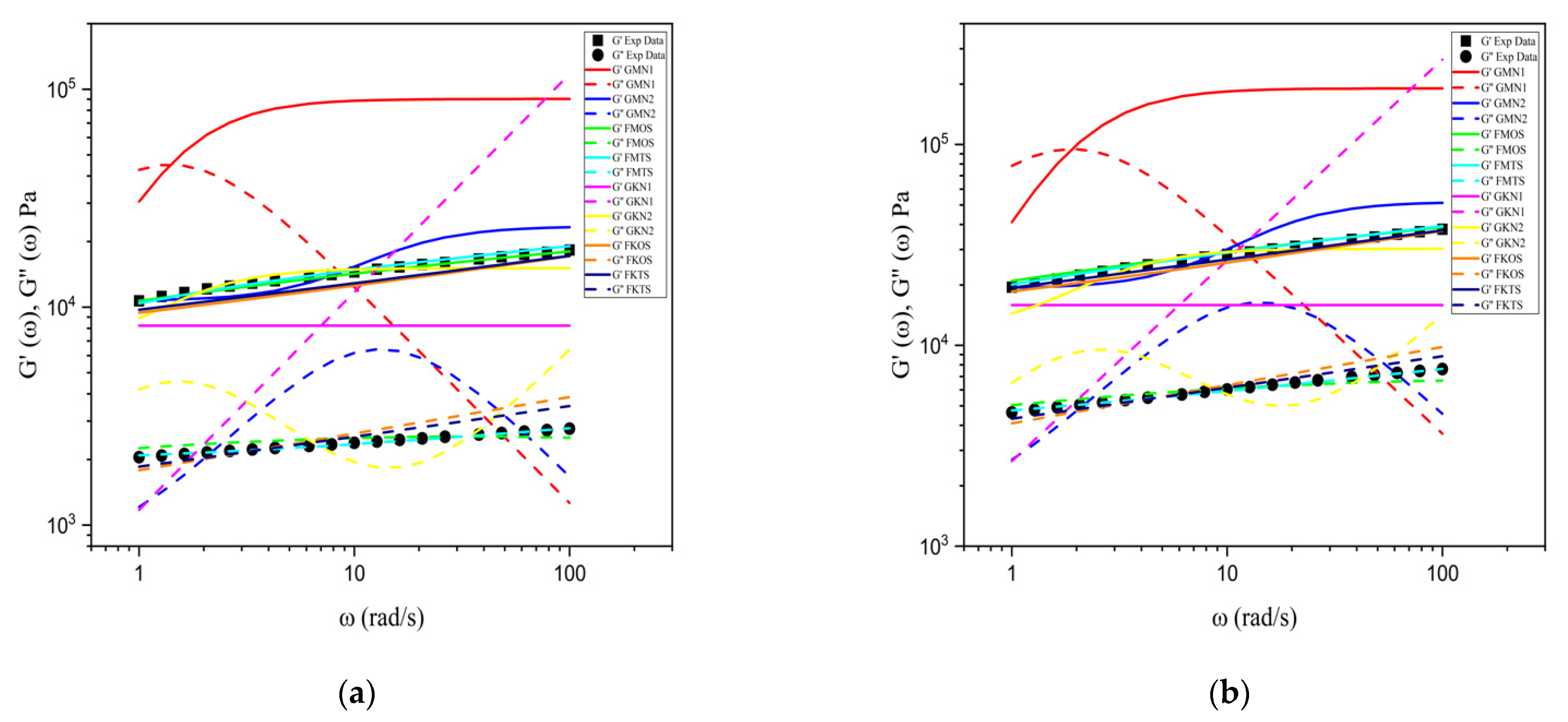



| Sample Code | Gellan Gum (%) | Carrageenan (%) | Potassium Citrate (%) | Calcium Chloride (%) |
|---|---|---|---|---|
| F1 | 0.25 | 1.35 | 0.2 | 0.4 |
| F2 | 0.25 | 1.35 | 0.4 | 0.2 |
| F3 | 0.4 | 1.2 | 0.2 | 0.4 |
| F4 | 0.4 | 1.2 | 0.4 | 0.2 |
| Rheological Model | F1 | F2 | F3 | F4 |
|---|---|---|---|---|
| Generalized Maxwell N = 1 | 52.751 | 55.906 | 52.974 | 57.504 |
| Generalized Maxwell N = 2 | 4.853 | 5.044 | 5.624 | 5.487 |
| Fractional Maxwell with one spring-pot | 0.343 | 0.222 | 0.605 | 0.122 |
| Fractional Maxwell with two spring-pot | 0.031 | 0.033 | 0.087 | 0.044 |
| Generalized Kelvin N = 1 | 32.151 | 34.272 | 46.119 | 26.171 |
| Generalized Kelvin N = 2 | 4.390 | 3.882 | 3.856 | 2.751 |
| Fractional Kelvin with one spring-pot | 1.623 | 0.828 | 3.288 | 0.371 |
| Fractional Kelvin with two spring-pot | 1.117 | 0.413 | 2.240 | 0.141 |
| Rheological Model | F1 | F2 | F3 | F4 |
|---|---|---|---|---|
| Generalized Maxwell N = 1 | / | / | / | / |
| Generalized Maxwell N = 2 | 0.79 | 0.83 | 0.15 | 0.58 |
| Fractional Maxwell with one spring-pot | 0.90 | 0.95 | 0.98 | 0.98 |
| Fractional Maxwell with two spring-pot | 0.99 | 0.99 | 0.98 | 0.98 |
| Generalized Kelvin N = 1 | / | / | / | / |
| Generalized Kelvin N = 2 | 0.21 | 0.12 | 0.71 | 0.07 |
| Fractional Kelvin with one spring-pot | 0.65 | 0.76 | 0.60 | 0.88 |
| Fractional Kelvin with two spring-pot | 0.72 | 0.85 | 0.71 | 0.95 |
| Sample Code | ||||
|---|---|---|---|---|
| F1 | 8487.75 | 139.65 | 0.57 | 0.09 |
| F2 | 11171.42 | 557.46 | 0.56 | 0.12 |
| F3 | 13335.38 | 41.03 | 0.42 | 0.08 |
| F4 | 5145.16 | 1537.85 | 0.89 | 0.12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramirez-Brewer, D.; Montoya, O.D.; Useche Vivero, J.; García-Zapateiro, L. Characterization and Modeling of the Viscoelastic Behavior of Hydrocolloid-Based Films Using Classical and Fractional Rheological Models. Fluids 2021, 6, 418. https://doi.org/10.3390/fluids6110418
Ramirez-Brewer D, Montoya OD, Useche Vivero J, García-Zapateiro L. Characterization and Modeling of the Viscoelastic Behavior of Hydrocolloid-Based Films Using Classical and Fractional Rheological Models. Fluids. 2021; 6(11):418. https://doi.org/10.3390/fluids6110418
Chicago/Turabian StyleRamirez-Brewer, David, Oscar Danilo Montoya, Jairo Useche Vivero, and Luis García-Zapateiro. 2021. "Characterization and Modeling of the Viscoelastic Behavior of Hydrocolloid-Based Films Using Classical and Fractional Rheological Models" Fluids 6, no. 11: 418. https://doi.org/10.3390/fluids6110418