Low-Speed DSMC Simulations of Hotwire Anemometers at High-Altitude Conditions
Abstract
:1. Introduction
2. Numerical Simulation Methodology
2.1. Statistical Scatter
- Select entire time series of heat transfer data (t, Nu) as initial window of data
- Normalize the time t in the window of data to have a range between 0 and 1 ()
- Calculate the average Nu in the data window ()
- Express Nu values as a percent change from the window average:
- Perform a linear regression analysis of the normalized data (, Nu)
- Compare the slope of the linear fit to the tolerance value of 1:
- (a)
- If : remove first data point (where ) from the current window of data and repeat steps 2–6
- (b)
- If : current window is the estimated steady-state section of data and the process ends
2.2. Boundary Conditions
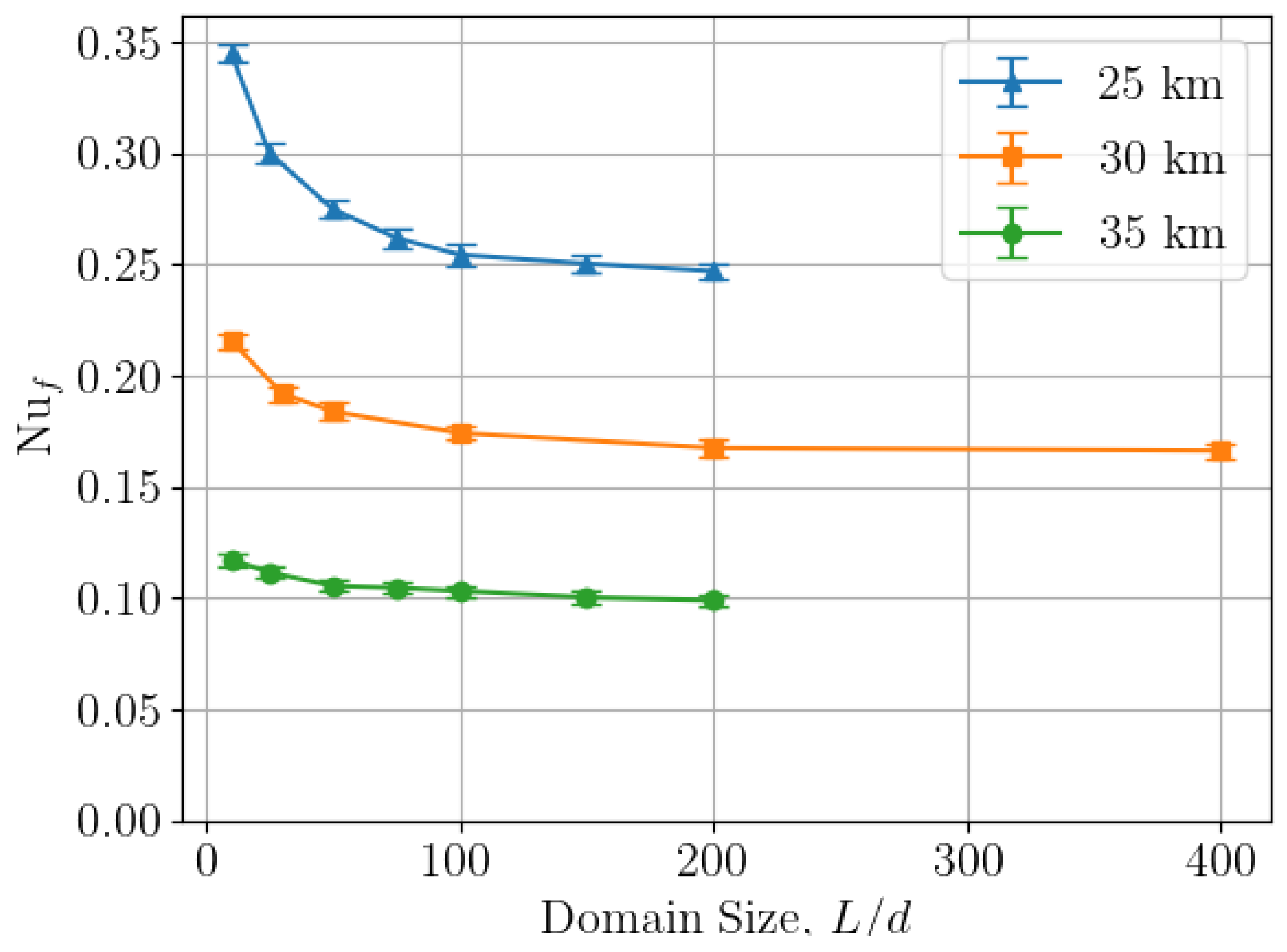
2.3. Domain Size
3. Results and Discussion
3.1. Simulating the Transition Regime
3.2. Dependence on Gas Mixture
3.3. Dependence on Accommodation Coefficient
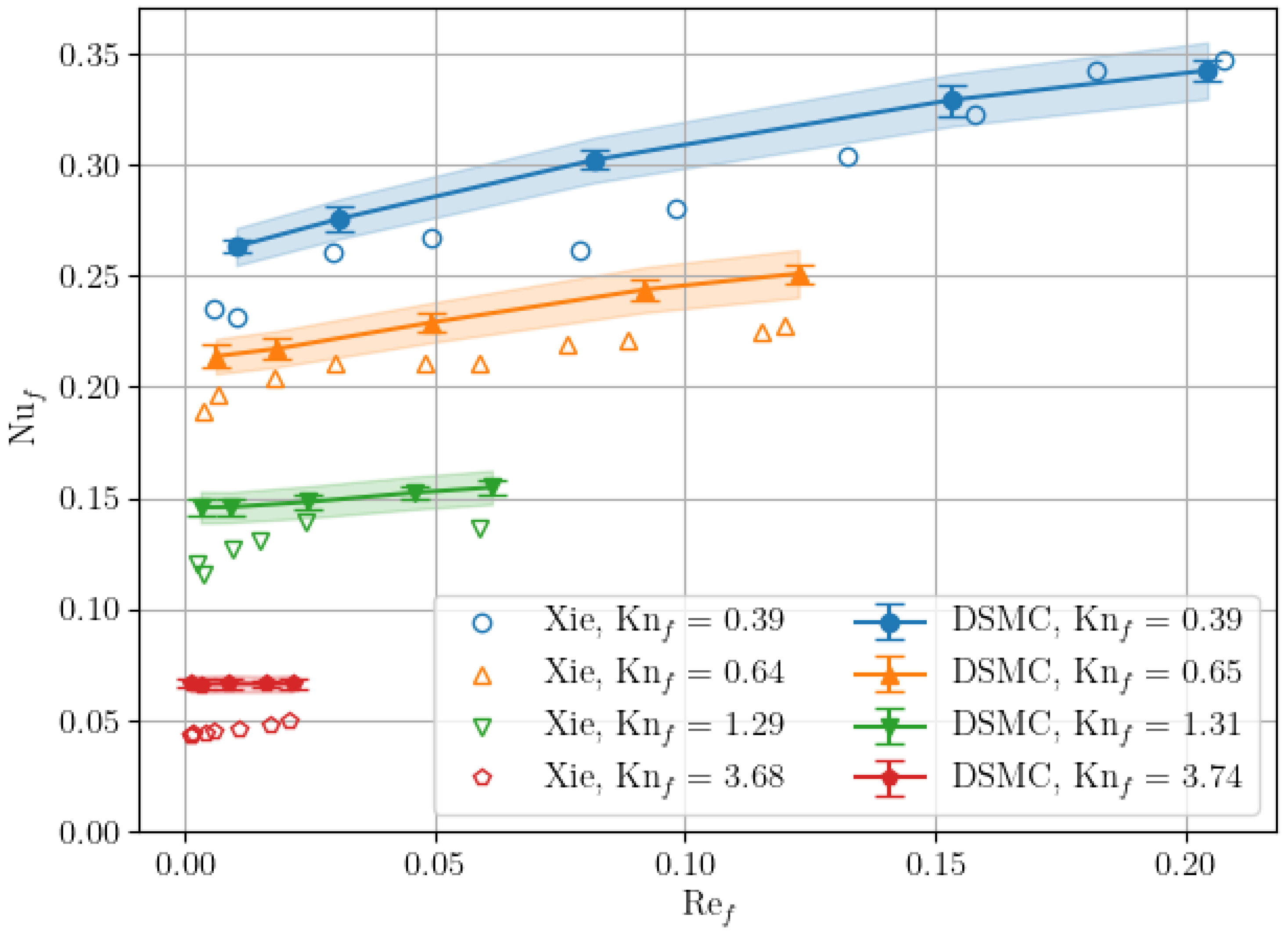
3.4. Comparison with Experimental Data
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- King, L.V., XII. On the convection of heat from small cylinders in a stream of fluid: Determination of the convection constants of small platinum wires with applications to hot-wire anemometry. Philos. Trans. R. Soc. London. Ser. A Contain. Pap. A Math. Phys. Character 1914, 214, 373–432. [Google Scholar] [CrossRef] [Green Version]
- Collis, D.C.; Williams, M.J. Two-dimensional convection from heated wires at low Reynolds numbers. J. Fluid Mech. 1959, 6, 357. [Google Scholar] [CrossRef]
- Levey, H.C. Heat transfer in slip flow at low Reynolds number. J. Fluid Mech. 1959, 6, 385. [Google Scholar] [CrossRef]
- Kassoy, D.R. Heat Transfer from Circular Cylinders at Low Reynolds Numbers. I. Theory for Variable Property Flow. Phys. Fluids 1967, 10, 938. [Google Scholar] [CrossRef]
- Andrews, G.; Bradley, D.; Hundy, G. Hot wire anemometer calibration for measurements of small gas velocities. Int. J. Heat Mass Transf. 1972, 15, 1765–1786. [Google Scholar] [CrossRef]
- Xie, F.; Li, Y.; Liu, Z.; Wang, X.; Wang, L. A forced convection heat transfer correlation of rarefied gases cross-flowing over a circular cylinder. Exp. Therm. Fluid Sci. 2017, 80, 327–336. [Google Scholar] [CrossRef]
- Xie, F.; Li, Y.; Wang, X.; Wang, Y.; Lei, G.; Xing, K. Numerical study on flow and heat transfer characteristics of low pressure gas in slip flow regime. Int. J. Therm. Sci. 2018, 124, 131–145. [Google Scholar] [CrossRef]
- Deissler, R. An analysis of second-order slip flow and temperature-jump boundary conditions for rarefied gases. Int. J. Heat Mass Transf. 1964, 7, 681–694. [Google Scholar] [CrossRef]
- Karniadakis, G.E. Numerical simulation of forced convection heat transfer from a cylinder in crossflow. Int. J. Heat Mass Transf. 1988, 31, 107–118. [Google Scholar] [CrossRef]
- Lange, C.; Durst, F.; Breuer, M. Momentum and heat transfer from cylinders in laminar crossflow at 10−4 ⩽ Re ⩽ 200. Int. J. Heat Mass Transf. 1998, 41, 3409–3430. [Google Scholar] [CrossRef]
- Bharti, R.P.; Chhabra, R.P.; Eswaran, V. A numerical study of the steady forced convection heat transfer from an unconfined circular cylinder. Heat Mass Transf. 2006, 43, 639–648. [Google Scholar] [CrossRef]
- Çelenligil, M.C. Heat transfer simulation of rarefied laminar flow past a circular cylinder. In AIP Conference Proceedings; AIP: Melville, NY, USA, 2016. [Google Scholar] [CrossRef]
- Bird, G. Molecular Gas Dynamics and the Direct Simulation of Gas Flows; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Plimpton, S.J.; Moore, S.G.; Borner, A.; Stagg, A.K.; Koehler, T.P.; Torczynski, J.R.; Gallis, M.A. Direct simulation Monte Carlo on petaflop supercomputers and beyond. Phys. Fluids 2019, 31, 086101. [Google Scholar] [CrossRef]
- U.S. Standard Atmosphere. Technical Report NASA-TM-X-74335; National Aeronautics and Space Administration: Washington, DC, USA, 1976. [Google Scholar]
- Pilinski, M.D.; Argrow, B.M.; Palo, S.E. Drag Coefficients of Satellites with Concave Geometries: Comparing Models and Observations. J. Spacecr. Rocket. 2011, 48, 312–325. [Google Scholar] [CrossRef]
- Sohn, I.; Li, Z.; Levin, D.A.; Modest, M.F. Coupled DSMC-PMC Radiation Simulations of a Hypersonic Reentry. J. Thermophys. Heat Transf. 2012, 26, 22–35. [Google Scholar] [CrossRef]
- Liou, W.; Fang, Y. Heat transfer in microchannel devices using DSMC. J. Microelectromech. Syst. 2001, 10, 274–279. [Google Scholar] [CrossRef]
- Cai, C.; Boyd, I.D.; Fan, J.; Candler, G.V. Direct Simulation Methods for Low-Speed Microchannel Flows. J. Thermophys. Heat Transf. 2000, 14, 368–378. [Google Scholar] [CrossRef]
- Fang, Y.; Liou, W.W. Computations of the Flow and Heat Transfer in Microdevices Using DSMC With Implicit Boundary Conditions. J. Heat Transf. 2001, 124, 338–345. [Google Scholar] [CrossRef]
- Fan, J.; Shen, C. Statistical Simulation of Low-Speed Rarefied Gas Flows. J. Comput. Phys. 2001, 167, 393–412. [Google Scholar] [CrossRef] [Green Version]
- Sun, Q. Development of an information preservation method for subsonic, micro-scale gas flows. In AIP Conference Proceedings; AIP: Melville, NY, USA, 2001. [Google Scholar] [CrossRef] [Green Version]
- Mahdavi, A.M.; Le, N.T.P.; Roohi, E.; White, C. Thermal Rarefied Gas Flow Investigations Through Micro-/Nano-Backward-Facing Step: Comparison of DSMC and CFD Subject to Hybrid Slip and Jump Boundary Conditions. Numer. Heat Transf. Part A Appl. 2014, 66, 733–755. [Google Scholar] [CrossRef] [Green Version]
- Amiri-Jaghargh, A.; Roohi, E.; Niazmand, H.; Stefanov, S. DSMC Simulation of Low Knudsen Micro/Nanoflows Using Small Number of Particles per Cells. J. Heat Transf. 2013, 135. [Google Scholar] [CrossRef]
- Stern, E.; Nompelis, I.; Schwartzentruber, T.E.; Candler, G.V. Microscale Simulations of Porous TPS Materials: Application to Permeability. In Proceedings of the 11th AIAA/ASME Joint Thermophysics and Heat Transfer Conference, Atlanta, GA, USA, 16–20 June 2014; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2014. [Google Scholar] [CrossRef]
- Plotnikov, M.Y. Hydrogen Dissociation in Rarefied Gas Flow Through a Wire Obstacle. J. Appl. Mech. Tech. Phys. 2018, 59, 794–800. [Google Scholar] [CrossRef]
- Stern, E.C.; Poovathingal, S.; Nompelis, I.; Schwartzentruber, T.E.; Candler, G.V. Nonequilibrium flow through porous thermal protection materials, Part I: Numerical methods. J. Comput. Phys. 2019, 380, 408–426. [Google Scholar] [CrossRef]
- Poovathingal, S.; Stern, E.C.; Nompelis, I.; Schwartzentruber, T.E.; Candler, G.V. Nonequilibrium flow through porous thermal protection materials, Part II: Oxidation and pyrolysis. J. Comput. Phys. 2019, 380, 427–441. [Google Scholar] [CrossRef]
- Çelenligil, M.C. Numerical Simulation of Rarefied Laminar Flow Past a Circular Cylinder; AIP Publishing LLC: Melville, NY, USA, 2014. [Google Scholar] [CrossRef]
- Gu, X.J.; Barber, R.W.; John, B.; Emerson, D.R. Non-equilibrium effects on flow past a circular cylinder in the slip and early transition regime. J. Fluid Mech. 2018, 860, 654–681. [Google Scholar] [CrossRef] [Green Version]
- Tseng, K.; Kuo, T.; Lin, S.; Su, C.; Wu, J. Simulations of subsonic vortex-shedding flow past a 2D vertical plate in the near-continuum regime by the parallelized DSMC code. Comput. Phys. Commun. 2012, 183, 1596–1608. [Google Scholar] [CrossRef]
- Ikegawa, M.; Kobayashi, J. Development of a Rarefield Gas Flow Simulator Using the Direct-Simulation Monte Carlo Method: 2-D Flow Analysis with the Pressure Conditions Given at the Upstream and Downstream Boundaries. JSME Int. J. 1990, 33, 463–467. [Google Scholar] [CrossRef] [Green Version]
- Nance, R.P.; Hash, D.B.; Hassan, H.A. Role of Boundary Conditions in Monte Carlo Simulation of Microelectromechanical Systems. J. Thermophys. Heat Transf. 1998, 12, 447–449. [Google Scholar] [CrossRef]
- Piekos, E.; Breuer, K. DSMC modeling of micromechanical devices. In Proceedings of the 30th Thermophysics Conference, San Diego, CA, USA, 19–22 June 1995; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1995. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Faghri, M. Effects of Rarefaction and Compressibility of Gaseous Flow in Microchannel Using DSMC. Numer. Heat Transf. Part A Appl. 2000, 38, 153–168. [Google Scholar] [CrossRef]
- Shah, N.; Gavasane, A.; Agrawal, A.; Bhandarkar, U. Comparison of Various Pressure Based Boundary Conditions for Three-Dimensional Subsonic DSMC Simulation. J. Fluids Eng. 2017, 140. [Google Scholar] [CrossRef]
- Amdur, I.; Guildner, L.A. Thermal Accommodation Coefficients on Gas-covered Tungsten, Nickel and Platinum1. J. Am. Chem. Soc. 1957, 79, 311–315. [Google Scholar] [CrossRef]
- Goodman, F. Thermal accommodation. Prog. Surf. Sci. 1974, 5, 261–375. [Google Scholar] [CrossRef]
- Chen, S.; Saxena, S. Interface heat transfer and thermal accommodation coefficients: Heated tungsten wire in nitrogen environment. Int. J. Heat Mass Transf. 1974, 17, 185–196. [Google Scholar] [CrossRef]








| Gas Species | , m | , K | ||||
|---|---|---|---|---|---|---|
| Nitrogen, N | 4.07 | 0.74 | 273.15 | 1.6 | 2 | 0.2 |
| Oxygen, O | 3.96 | 0.77 | 273.15 | 1.4 | 2 | 0.2 |
| Altitude, km | Kn | Re |
|---|---|---|
| 25 | 0.50 | 0.0190 |
| 30 | 1.08 | 0.0130 |
| 35 | 2.33 | 0.0039 |
| Kn | |
|---|---|
| 0.39 | 3.4% |
| 0.65 | 4.0% |
| 1.31 | 4.8% |
| 3.74 | 5.7% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roseman, C.A.; Argrow, B.M. Low-Speed DSMC Simulations of Hotwire Anemometers at High-Altitude Conditions. Fluids 2021, 6, 20. https://doi.org/10.3390/fluids6010020
Roseman CA, Argrow BM. Low-Speed DSMC Simulations of Hotwire Anemometers at High-Altitude Conditions. Fluids. 2021; 6(1):20. https://doi.org/10.3390/fluids6010020
Chicago/Turabian StyleRoseman, Christopher A., and Brian M. Argrow. 2021. "Low-Speed DSMC Simulations of Hotwire Anemometers at High-Altitude Conditions" Fluids 6, no. 1: 20. https://doi.org/10.3390/fluids6010020





