Hydrodynamic Responses of a 6 MW Spar-Type Floating Offshore Wind Turbine in Regular Waves and Uniform Current
Abstract
:1. Introduction
2. Theoretical Description
2.1. Definition and Governing Equation
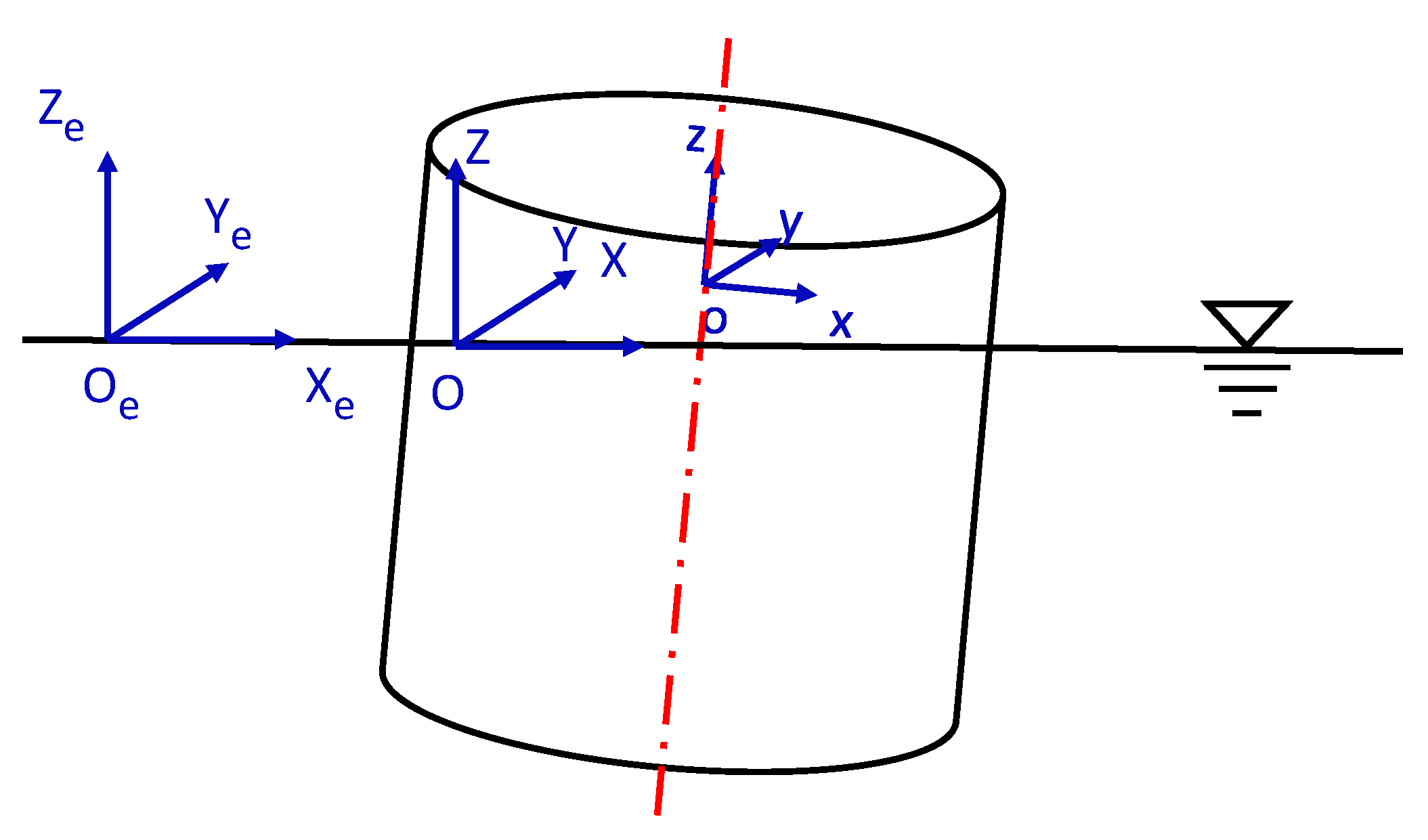
2.2. Formulation in a Body-Fixed Coordinate System
3. Numerical Model
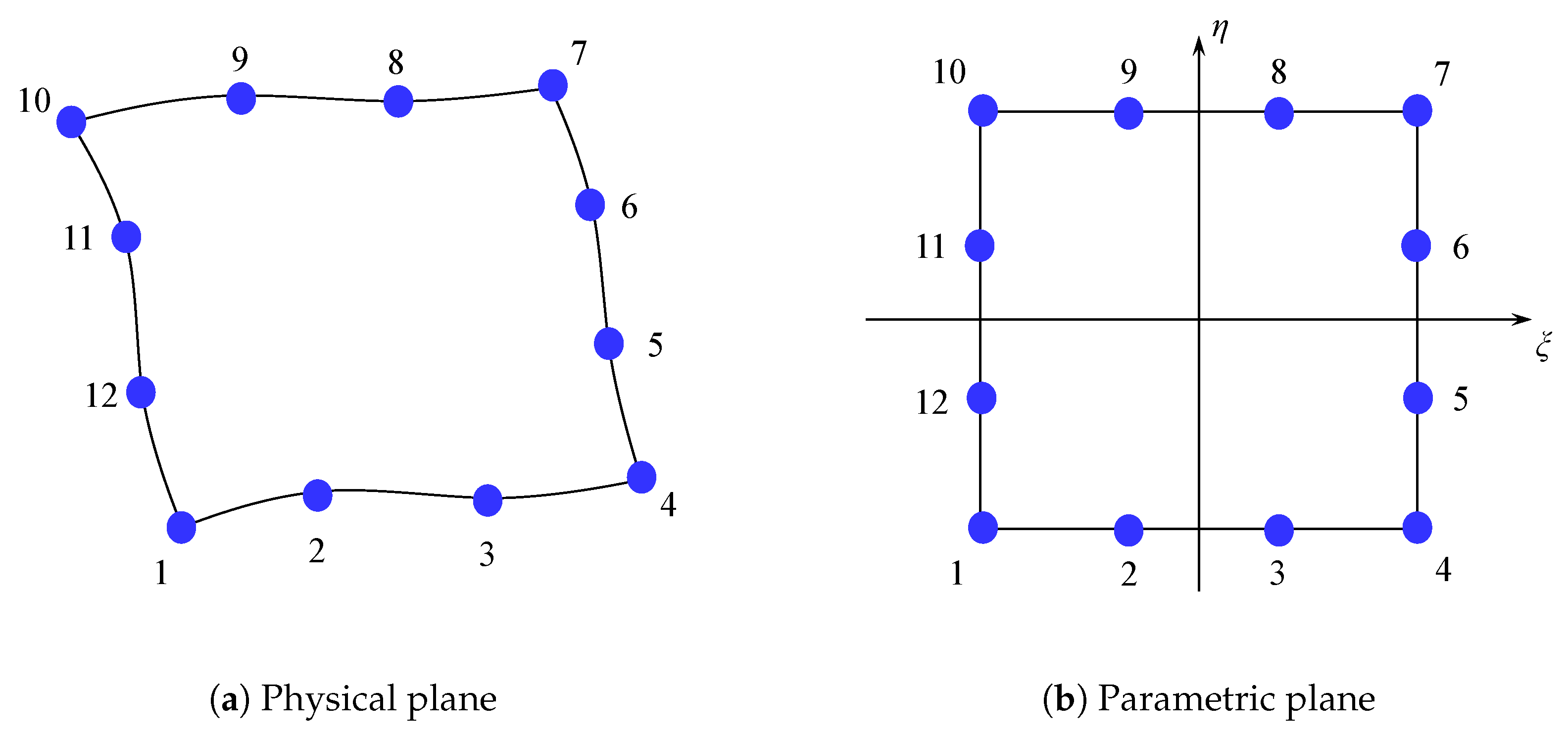
3.1. Cubic Elements and Calculation of Spatial Derivatives
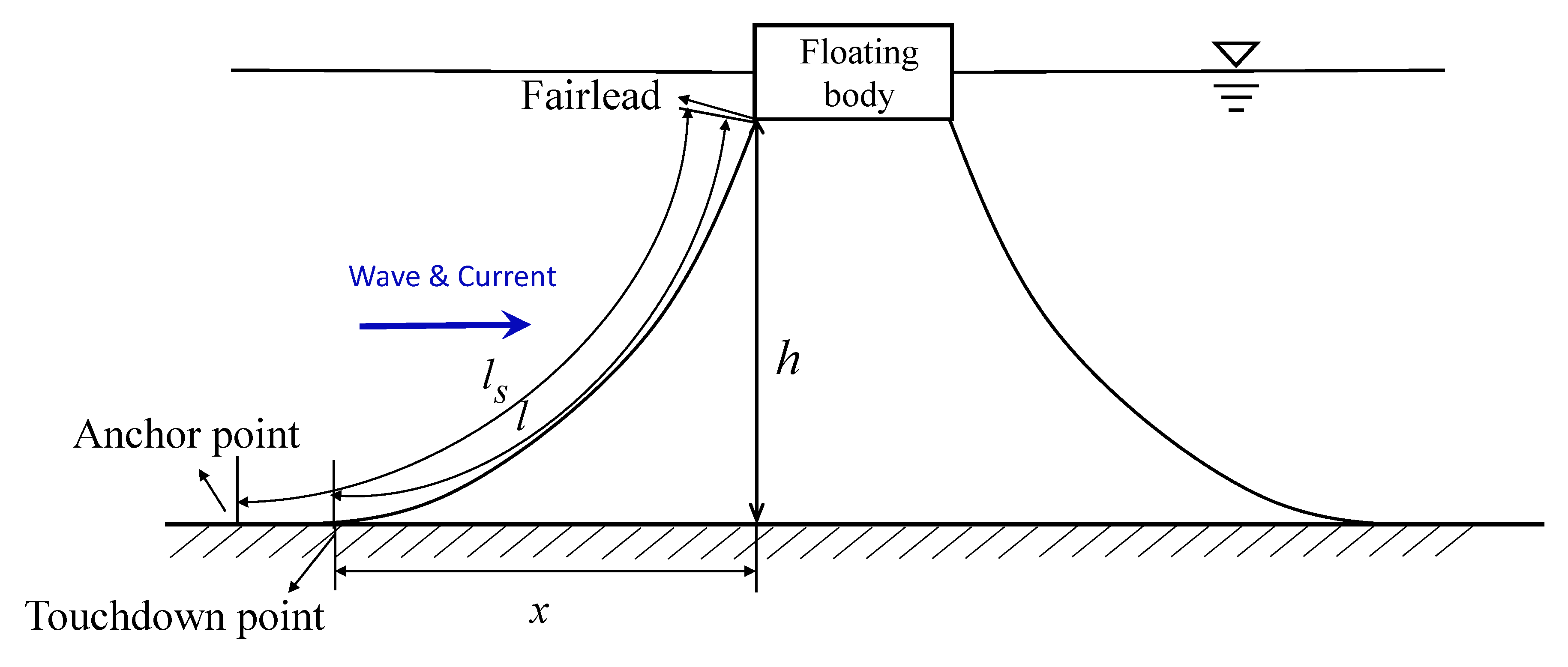
3.2. Catenary Mooring Line Model
3.3. Viscous Drag Loads
3.4. Potential-Flow Induced Forces/Moments
3.5. Time Integration of Free-Surface Boundary Conditions
3.6. Low-Pass Filter Close to the Waterline
4. Verification Cases
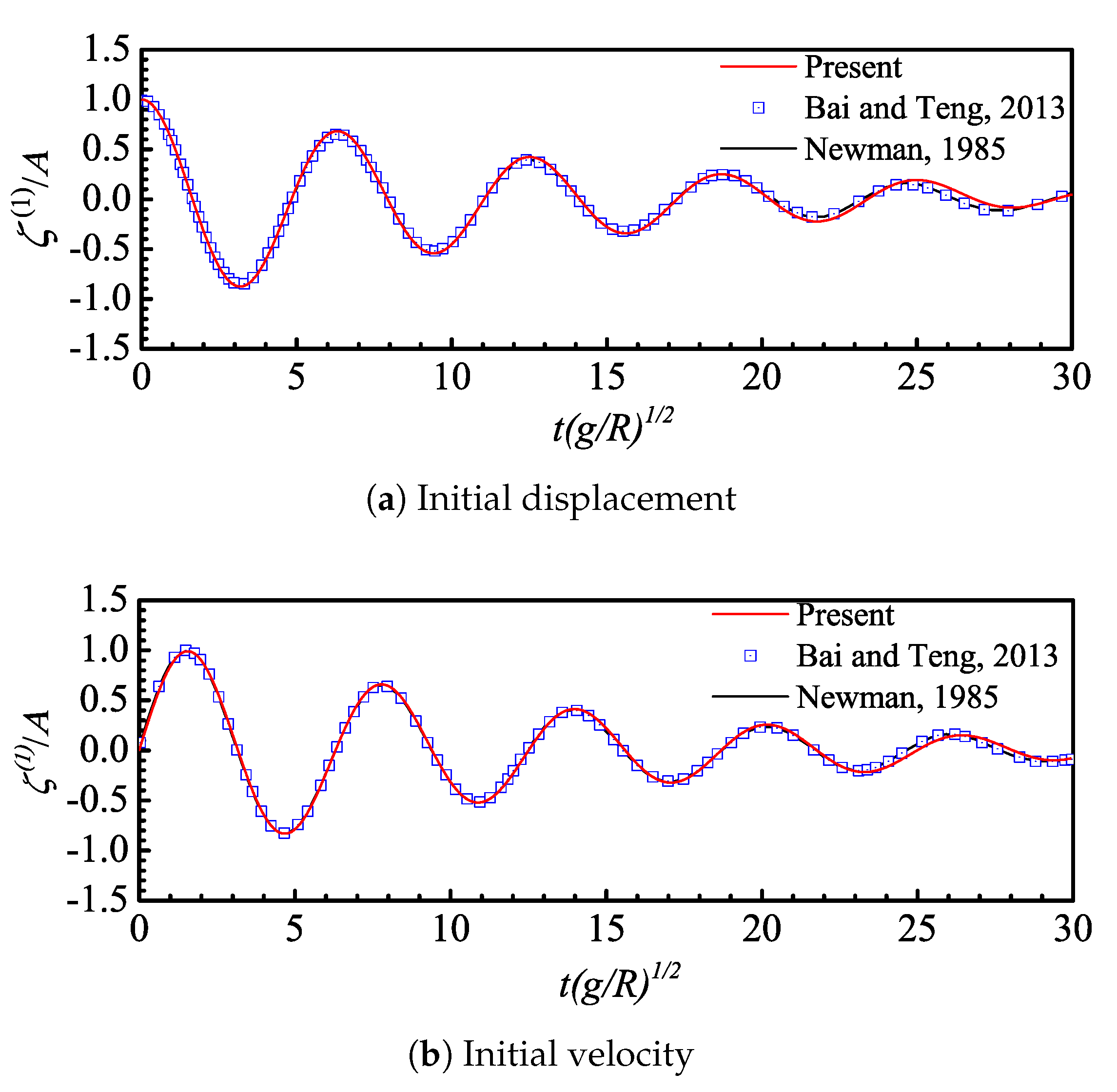
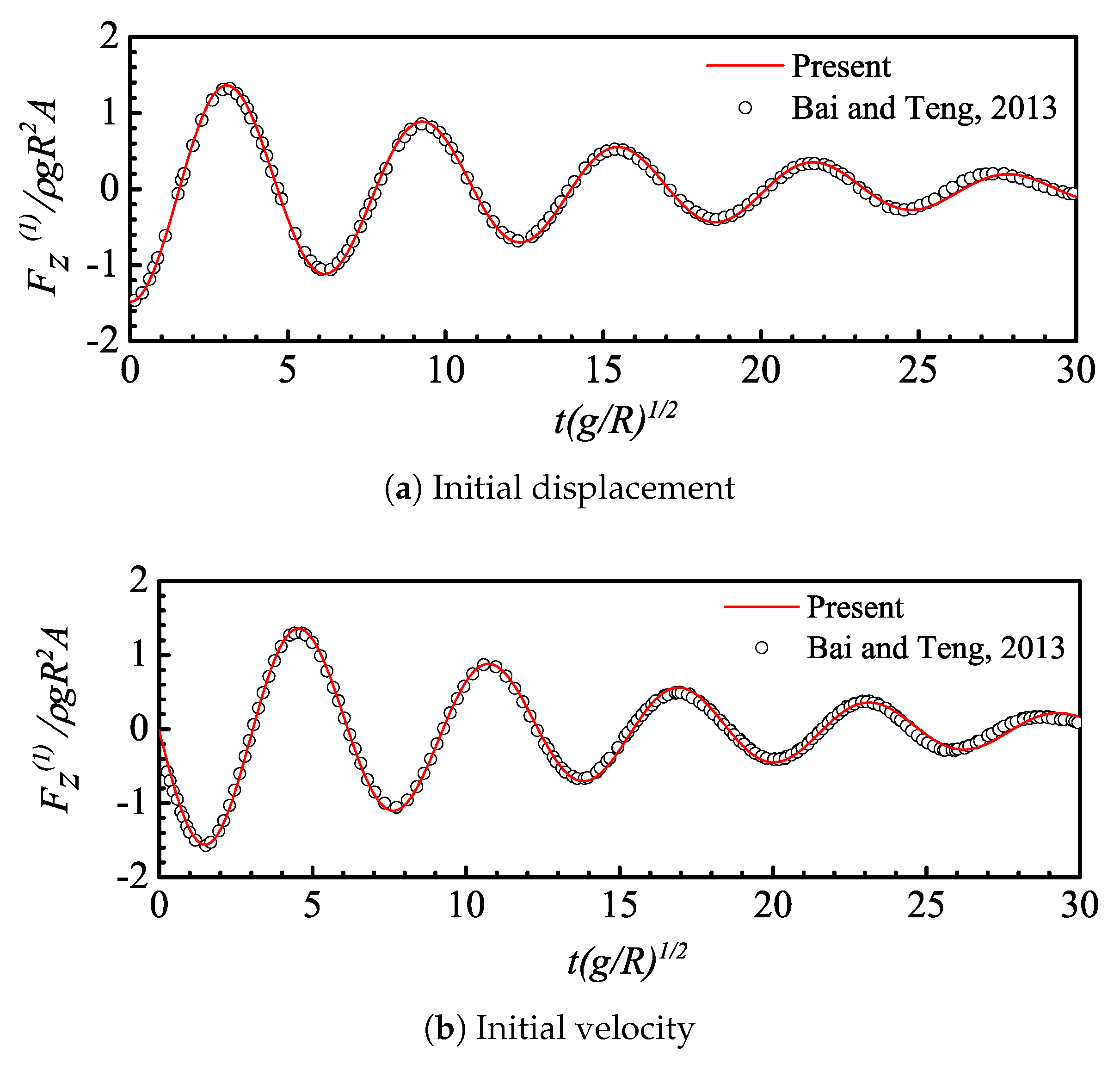
4.1. Free Decay of a Truncated Vertical Cylinder
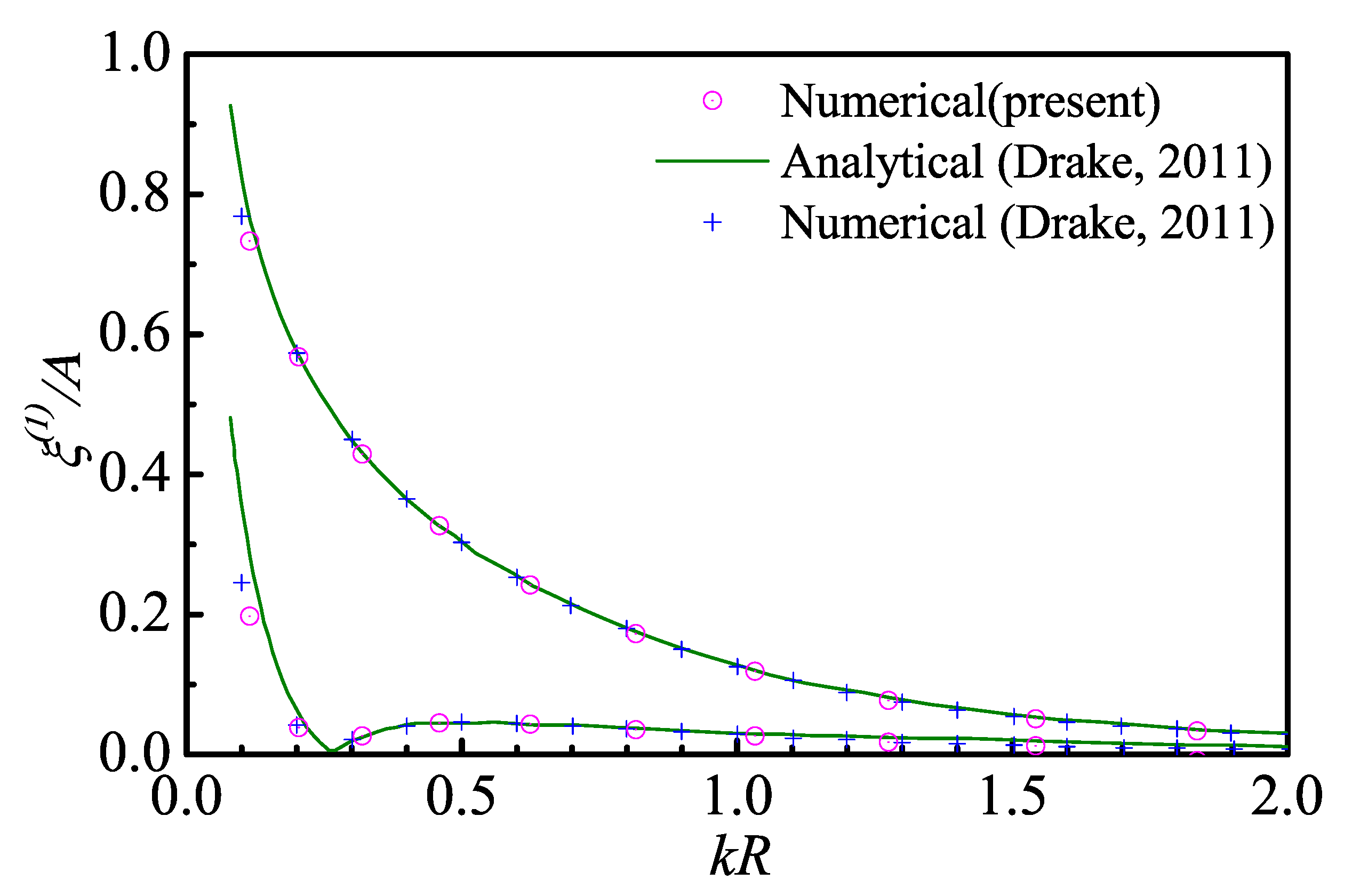
4.2. Deep Draught Spar in Regular Waves
4.3. Freely Floating Vertical Cylinder with a Small Forward Speed
5. Numerical Studies on a 6 MW Spar-Type FOWT
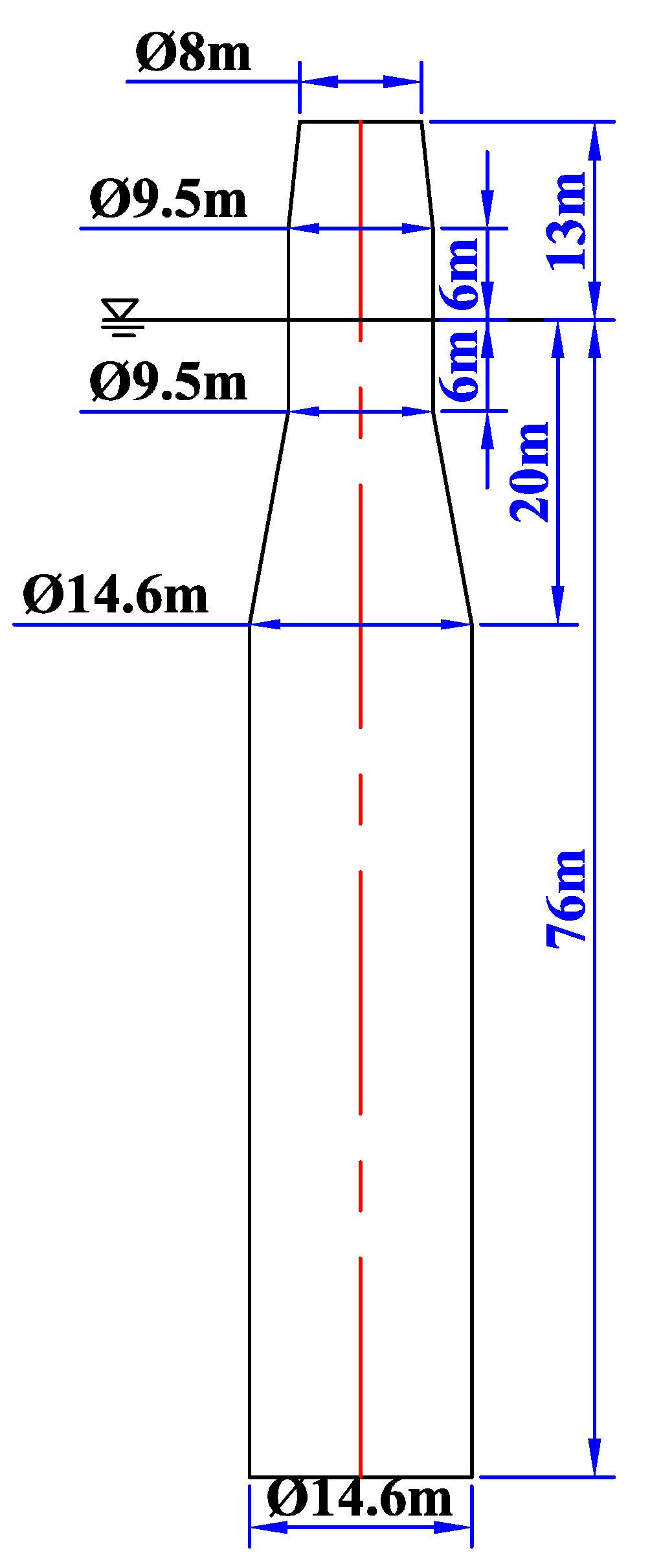
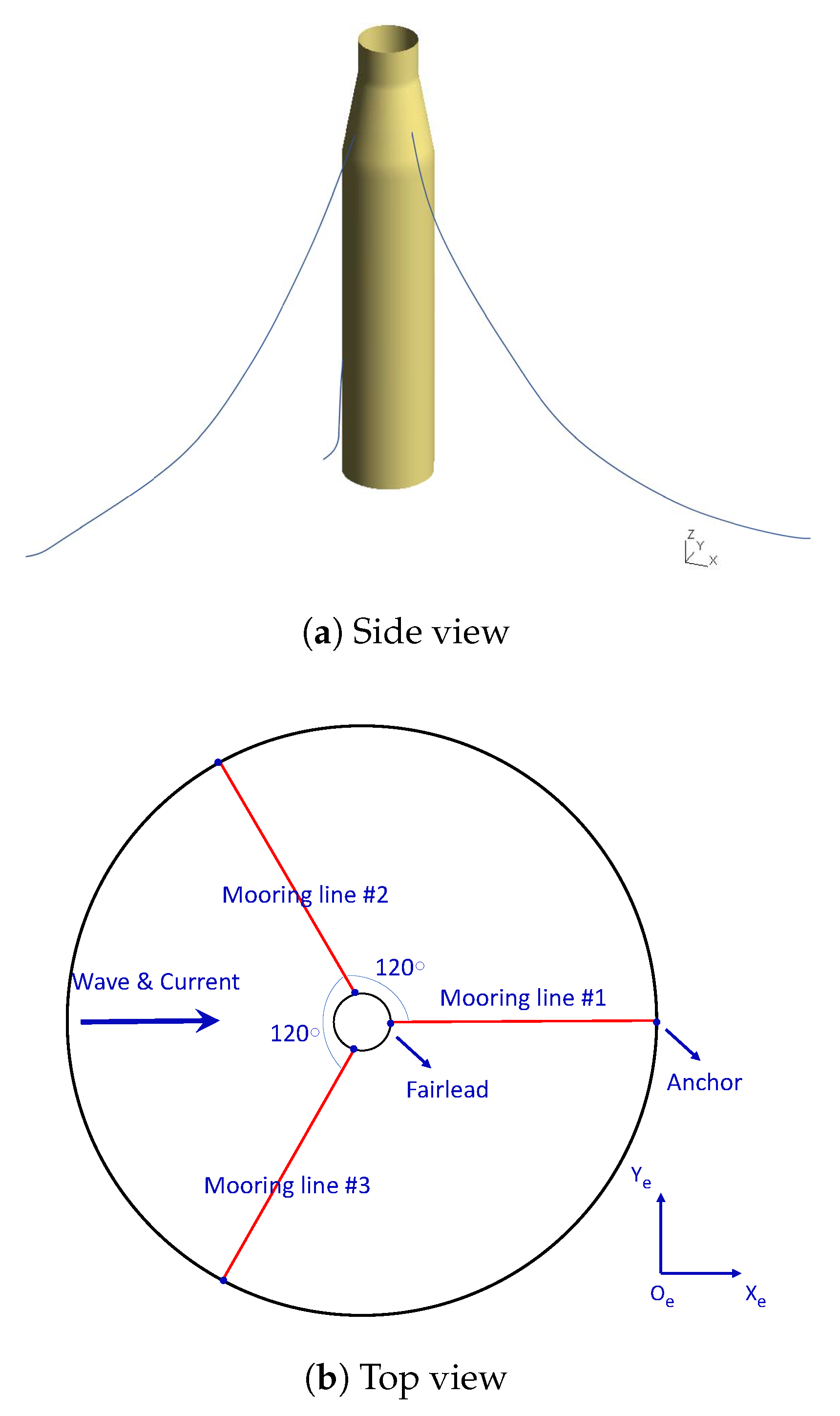
5.1. Model Description of the 6 MW Spar-Type FOWT
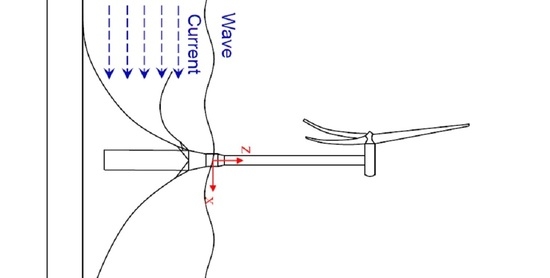
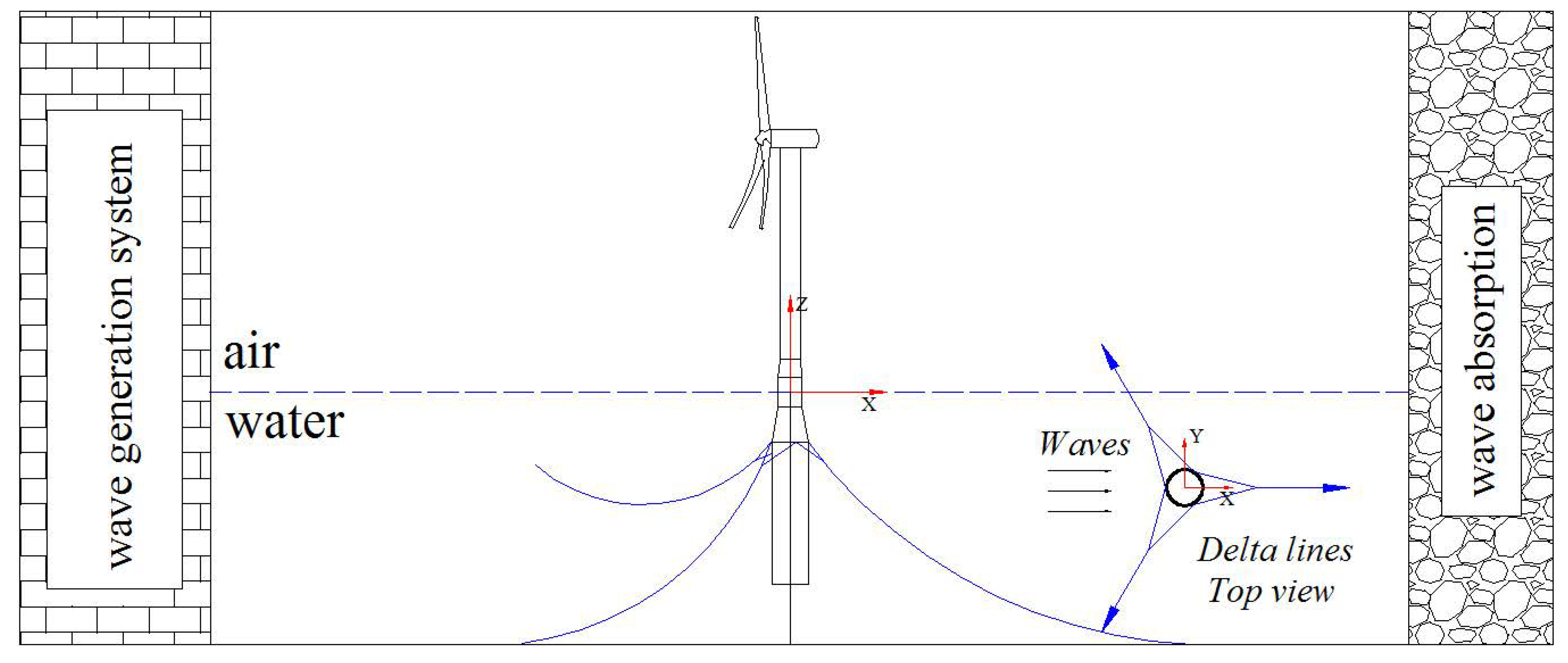
5.2. Experiment Setup
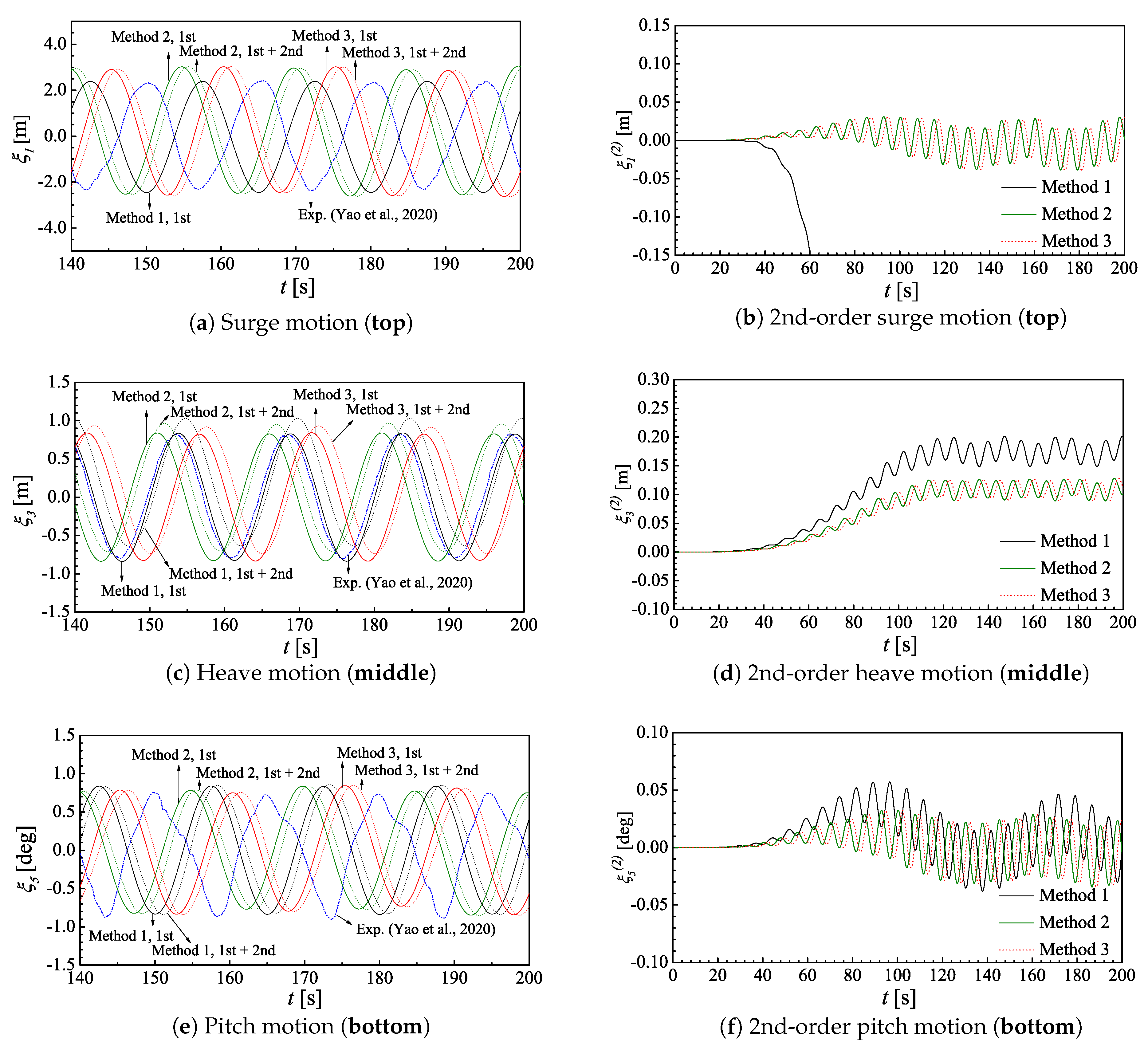
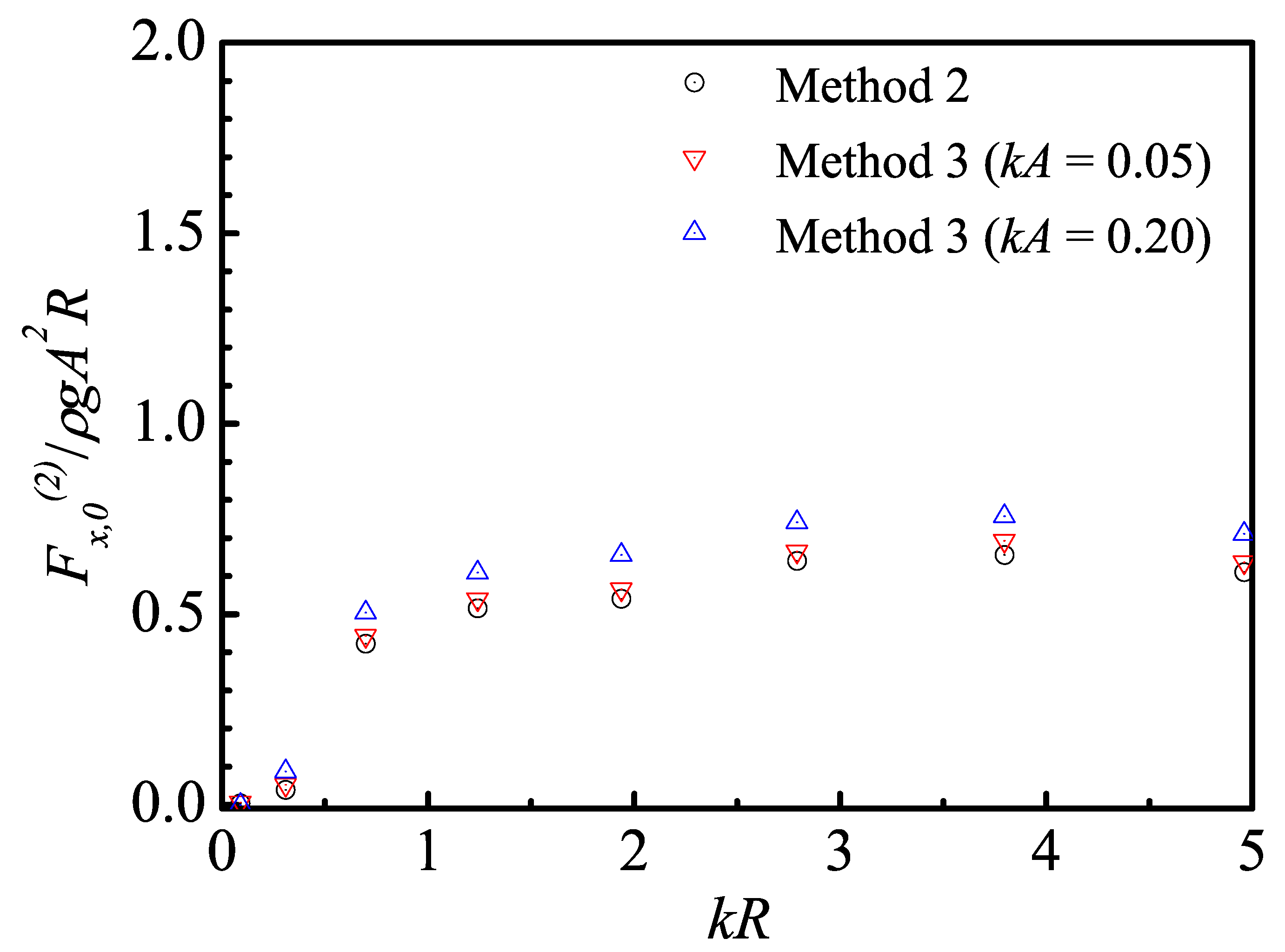
5.3. Validation against Model Test in a Regular Wave
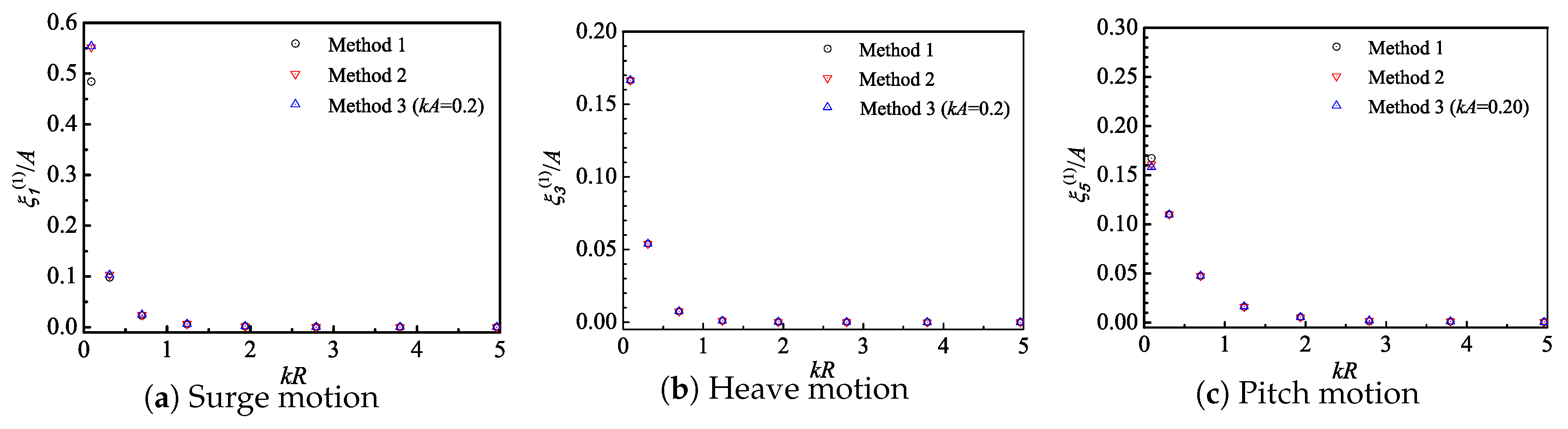
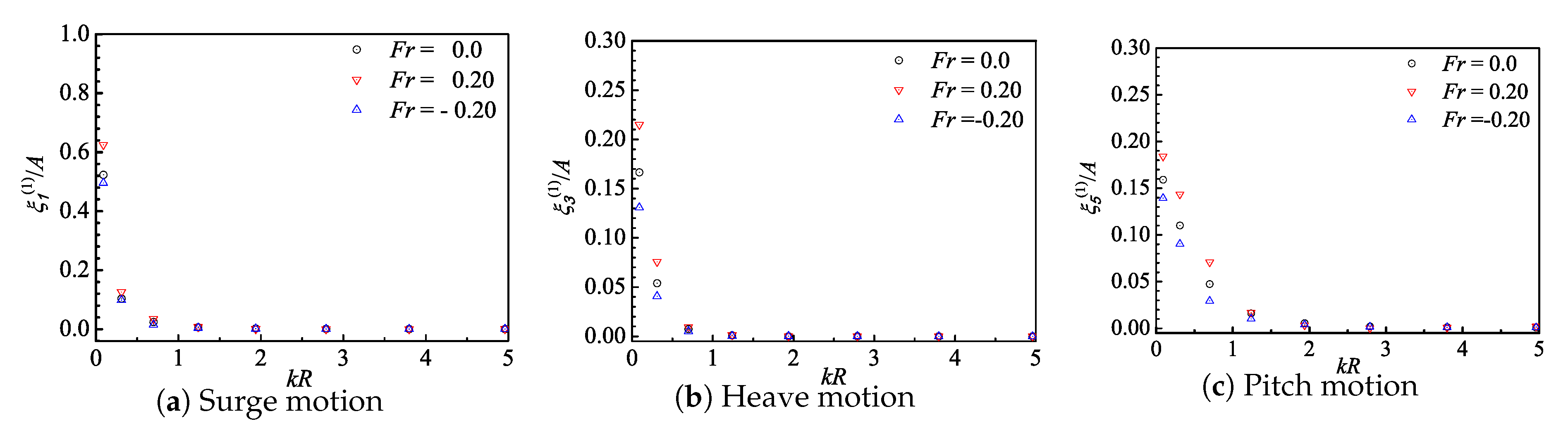
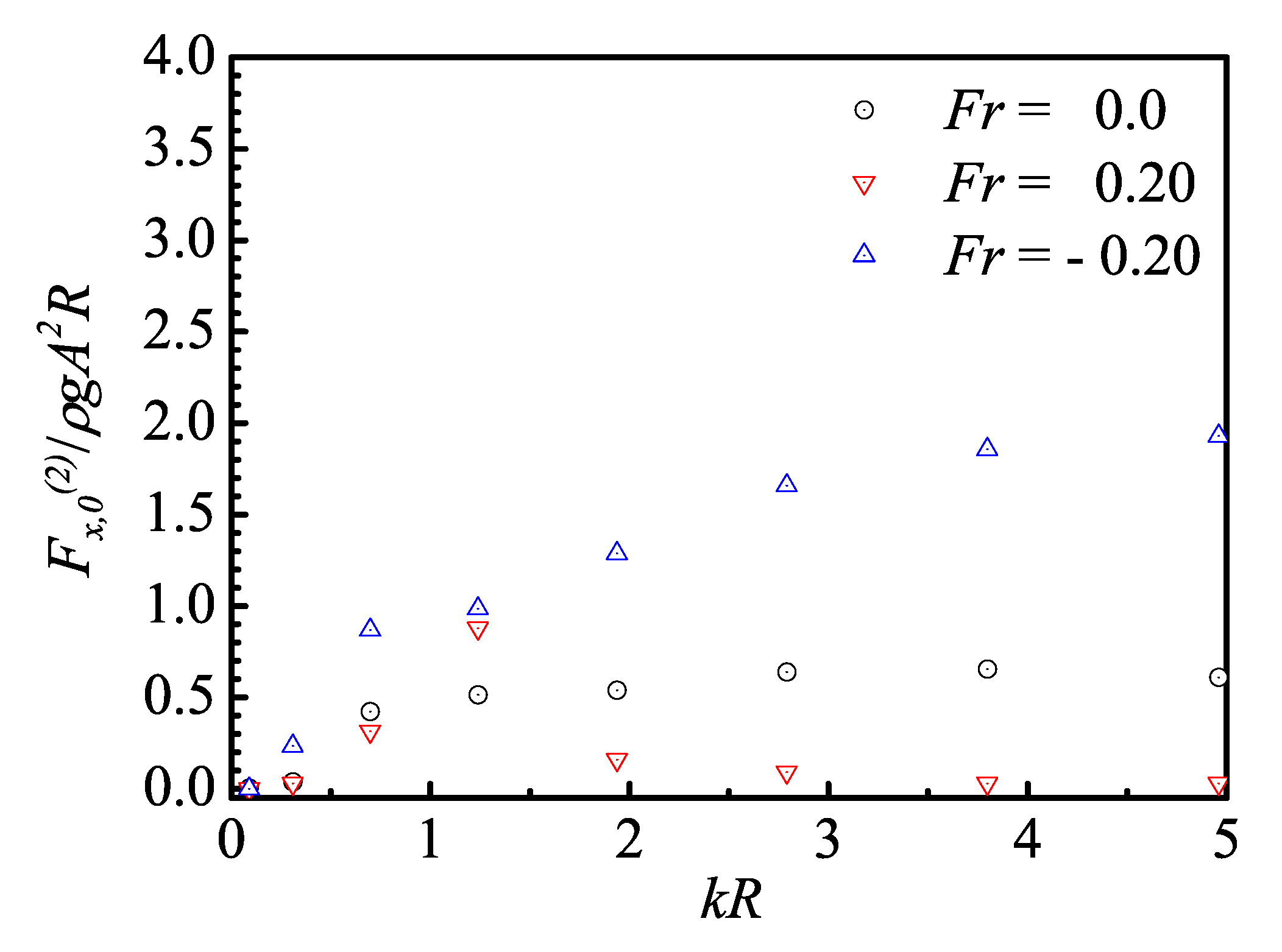
5.4. Current Effect
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Fulton, G.; Malcolm, D.; Moroz, E. Design of a semi-submersible platform for a 5MW wind turbine. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006; p. 997. [Google Scholar]
- Butterfield, S.; Musial, W.; Jonkman, J.; Sclavounos, P. Engineering Challenges for Floating Offshore Wind Turbines; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2007.
- Robertson, A.N.; Jonkman, J.M.; Goupee, A.J.; Coulling, A.J.; Prowell, I.; Browning, J.; Masciola, M.D.; Molta, P. Summary of conclusions and recommendations drawn from the DeepCwind scaled floating offshore wind system test campaign. Int. Conf. Offshore Mech. Arct. Eng. Am. Soc. Mech. Eng. 2013, 55423, V008T09A053. [Google Scholar]
- Coulling, A.J.; Goupee, A.J.; Robertson, A.N.; Jonkman, J.M.; Dagher, H.J. Validation of a FAST semi-submersible floating wind turbine numerical model with DeepCwind test data. J. Renew. Sustain. Energy 2013, 5, 023116. [Google Scholar] [CrossRef]
- Browning, J.; Jonkman, J.; Robertson, A.; Goupee, A. Calibration and validation of a spar-type floating offshore wind turbine model using the FAST dynamic simulation tool. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2014; Volume 555, p. 012015. [Google Scholar]
- Driscoll, F.; Jonkman, J.; Robertson, A.; Sirnivas, S.; Skaare, B.; Nielsen, F.G. Validation of a FAST model of the statoil-hywind demo floating wind turbine. Energy Procedia 2016, 94, 3–19. [Google Scholar] [CrossRef] [Green Version]
- Utsonomiya, T.; Sato, T.; Matsukuma, H.; Yago, K. Experimental validation for motion of a spar- type floating offshorewind turbine using 1/22.5 scale model. In International Conference on Ocean, Offshore and Arctic Engineering (OMAE2020) International Conference on Ocean, Offshore and Arctic Engineering; American Society of Mechanical Engineers: New York, NY, USA, 2009. [Google Scholar]
- Robertson, A.; Jonkman, J.; Masciola, M.; Song, H.; Goupee, A.; Coulling, A.; Luan, C. Definition of the Semisubmersible Floating System for Phase II of OC4; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2014.
- Benitz, M.A.; Schmidt, D.P.; Lackner, M.A.; Stewart, G.M.; Jonkman, J.; Robertson, A. Validation of hydrodynamic load models using CFD for the OC4-DeepCwind semisubmersible. In International Conference on Offshore Mechanics and Arctic Engineering; American Society of Mechanical Engineers: New York, NY, USA, 2015; Volume 56574, p. V009T09A037. [Google Scholar]
- Robertson, A.N.; Jonkman, J.M. Loads analysis of several offshore floating wind turbine concepts. In Proceedings of the Twenty-First, International Offshore and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011. [Google Scholar]
- Goupee, A.J.; Koo, B.; Lambrakos, K.; Kimball, R. Model tests for three floating wind turbine concepts. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 30 April–3 May 2012. [Google Scholar]
- Jonkman, J. Definition of the Floating System for Phase IV of OC3; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2010.
- Tomasicchio, G.R.; Armenio, E.; D’Alessandro, F.; Fonseca, N.; Mavrakos, S.A.; Penchev, V.; Jensen, P. Design of a 3D physical and numerical experiment on floating off-shore wind turbines. Coast. Eng. Proc. 2012, 1, 67. [Google Scholar] [CrossRef]
- Tomasicchio, G.R.; D’Alessandro, F.; Avossa, A.M.; Riefolo, L.; Musci, E.; Ricciardelli, F.; Vicinanza, D. Experimental modelling of the dynamic behaviour of a spar buoy wind turbine. Renew. Energy 2018, 127, 412–432. [Google Scholar] [CrossRef]
- Shin, H. Model test of the OC3-Hywind floating offshore wind turbine. In Proceedings of the Twenty-first International Offshore and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011. [Google Scholar]
- Ogilvie, T.F. Second-order hydrodynamic effects on ocean platforms. In Proceedings of the International Workshop on Ship and Platform Motions, Berkeley, CA, USA, 26–28 October 1983; pp. 205–265. [Google Scholar]
- Newman, J. The second-order wave force on a vertical cylinder. J. Fluid Mech. 1996, 320, 417–443. [Google Scholar] [CrossRef]
- Roald, L.; Jonkman, J.; Robertson, A.; Chokani, N. The effect of second-order hydrodynamics on floating offshore wind turbines. Energy Procedia 2013, 35, 253–264. [Google Scholar] [CrossRef] [Green Version]
- Meng, L.; He, Y.; Zhou, T.; Zhao, Y.; Liu, Y. Research on Dynamic Response Characteristics of 6MW Spar-Type Floating Offshore Wind Turbine. J. Shanghai Jiaotong Univ. (Sci.) 2018, 23, 505–514. [Google Scholar] [CrossRef]
- Coulling, A.J.; Goupee, A.J.; Robertson, A.N.; Jonkman, J.M. Importance of second-order difference-frequency wave-diffraction forces in the validation of a fast semi-submersible floating wind turbine model. In International Conference on Offshore Mechanics and Arctic Engineering; American Society of Mechanical Engineers: New York, NY, USA, 2013; Volume 55423, p. V008T09A019. [Google Scholar]
- Gueydon, S.; Duarte, T.; Jonkman, J. Comparison of second-order loads on a semisubmersible floating wind turbine. In International Conference on Offshore Mechanics and Arctic Engineering; American Society of Mechanical Engineers: New York, NY, USA, 2014; Volume 45530, p. V09AT09A024. [Google Scholar]
- Zhang, L.; Shi, W.; Karimirad, M.; Michailides, C.; Jiang, Z. Second-order hydrodynamic effects on the response of three semisubmersible floating offshore wind turbines. Ocean Eng. 2020, 207, 107371. [Google Scholar] [CrossRef]
- Bae, Y.; Kim, M. Rotor-floater-tether coupled dynamics including second-order sum–frequency wave loads for a mono-column-TLP-type FOWT (floating offshore wind turbine). Ocean Eng. 2013, 61, 109–122. [Google Scholar] [CrossRef]
- Gueydon, S.; Jonkman, J. Update on the Comparison of Second-Order Loads on a Tension Leg Platform for Wind Turbines; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2016.
- Li, Y.; Tang, Y.; Zhu, Q.; Qu, X.; Wang, B.; Zhang, R. Effects of second-order wave forces and aerodynamic forces on dynamic responses of a TLP-type floating offshore wind turbine considering the set-down motion. J. Renew. Sustain. Energy 2017, 9, 063302. [Google Scholar] [CrossRef]
- Jonkman, J.M. Dynamics Modeling and Loads Analysis of an Offshore Floating Wind Turbine; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2007.
- Bayati, I.; Jonkman, J.; Robertson, A.; Platt, A. The effects of second-order hydrodynamics on a semisubmersible floating offshore wind turbine. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2014; Volume 524, pp. 1–10. [Google Scholar]
- Wolfram, J. On alternative approaches to linearization and Morison’s equation for wave forces. Proc. R. Soc. Lond. A 1999, 157, 2957–2974. [Google Scholar] [CrossRef]
- Shao, Y.; You, J.; Glomnes, E.B. Stochastic linearization and its application in motion analysis of cylindrical floating structure with bilge boxes. In Proceedings of the 35th International Conference on Ocean, Offshore and Arctic Engineering, Busan, Korea, 19–24 June 2016. [Google Scholar]
- Lin, Y.; El Chahal, G.; Shao, Y. Caisson Breakwater for LNG & Bulk Terminals: A Study on Limiting Wave Conditions for Caisson Installation. In Proceedings of the 39th International Conference on Ocean, Offshore and Arctic Engineering (OMAE2020), Fort Lauderdale, FL, USA, 28 June–3 July 2020. [Google Scholar]
- Shao, Y.; Faltinsen, O.M. Use of body-fixed coordinate system in analysis of weakly nonlinear wave–body problems. Appl. Ocean Res. 2010, 32, 20–33. [Google Scholar] [CrossRef]
- Bai, W.; Teng, B. Simulation of second-order wave interaction with fixed and floating structures in time domain. Ocean Eng. 2013, 74, 168–177. [Google Scholar] [CrossRef]
- Duan, W.; Chen, J.; Zhao, B. Second-order Taylor expansion boundary element method for the second-order wave radiation problem. Appl. Ocean Res. 2015, 52, 12–26. [Google Scholar] [CrossRef]
- Shao, Y.; Faltinsen, O. Numerical Study on the Second-Order Radiation/Diffraction of Floating Bodies with/without Forward Speed. In Proceedings of the 25th International Workshop on Water Waves and Floating Bodies (IWWWFB 2010), Harbin, China, 9–12 May 2010. [Google Scholar]
- Shao, Y.L.; Faltinsen, O.M. Second-order diffraction and radiation of a floating body with small forward speed. J. Offshore Mech. Arct. Eng. 2013, 135, 011301. [Google Scholar] [CrossRef]
- Shao, Y.; Faltinsen, O.M. A numerical study of the second-order wave excitation of ship springing by a higher-order boundary element method. Int. J. Nav. Archit. Ocean Eng. 2014, 4, 1000–1013. [Google Scholar] [CrossRef] [Green Version]
- Teng, B.; Jin, R.; Cong, L. A twice expansion analysis method in the time-domain for wave action on a floater translating with a large amplitude. Ocean Eng. 2016, 118, 138–151. [Google Scholar] [CrossRef]
- Shao, Y. On a new explicit time-integration method for advection equation and its application in hydrodynamics. In Proceedings of the 35th International Workshop on Water Waves and Floating Bodies (IWWWFB 2020), Seoul, Korea, 24–28 August 2020. [Google Scholar]
- Faltinsen, O.M.; Timokha, A.N. Sloshing; Cambridge University Press: Cambridge, UK, 2009; Volume 577. [Google Scholar]
- Shao, Y. Numerical Potential-Flow Studies on Weakly-Nonlinear Wave-Body Interactions with/without Small Forward Speeds. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2010. [Google Scholar]
- Feng, A.; Kang, H.S.; Zhao, B.; Jiang, Z. Two-Dimensional Numerical Modelling of a Moored Floating Body under Sloping Seabed Conditions. J. Mar. Sci. Eng. 2020, 8, 389. [Google Scholar] [CrossRef]
- Faltinsen, O.M. Sea Loads on Ships and Offshore Structures; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Kring, D. Time Domain Ship Motions by a Three-Dimensional Rankine Panel Method. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1994. [Google Scholar]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Newman, J.N. Transient axisymmetric motion of a floating cylinder. J. Fluid Mech. 1985, 157, 17–33. [Google Scholar] [CrossRef]
- Drake, K.R. An analytical approximation for the horizontal drift force acting on a deep draught spar in regular waves. Ocean Eng. 2011, 38, 810–814. [Google Scholar] [CrossRef]
- Malenica, S.; Clark, P.J.; Molin, B. Wave and current forces on a vertical cylinder free to surge and sway. Appl. Ocean Res. 1995, 17, 79–90. [Google Scholar] [CrossRef]
- Yao, T.C.; Zhao, Y.S.; He, Y.P.; Shao, Y.L.; Han, Z.L.; Duan, L. CFD-based Analysis of a 6MW Spar-type Floating Wind Turbine with Focus on Nonlinear Wave Loads. In Proceedings of the 30th International Ocean and Polar Engineering Conference, Shanghai, China, 11–16 October 2020. [Google Scholar]
- Geuzaine, C.; Remacle, J.-F. R. Gmsh: A 3D finite element mesh generator with built-in pre-and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]




| Water depth [m] | 100 |
| Draft [m] | 76 |
| Mass [t] | 11,137 |
| Displacement [m3] | 11,420 |
| Center of gravity [m] | −49 |
| Moment of inertia(roll, pitch) [kg m2] | 4.20 × |
| Number of mooring lines | 3 |
| Angle between mooring lines [deg] | 120 |
| Unstretched mooring line length [m] | 400 |
| Radius of fairleads to centerline [m] | 8 |
| Radius of anchors to centerline [m] | 393.5 |
| Depth of fairleads [m] | 21 |
| Depth of anchors [m] | 100 |
| Extensional stiffness(EA) [N/m] | 8.0 × |
| Mass per unit length [kg m−1] | 370 |
| Water Depth [m] | Wave Height [m] | Wave Period [s] | Wave Length [m] | |
|---|---|---|---|---|
| Full scale | 100 | 10 | 15 | 338 |
| Model scale (1:65.3) | 1.53 | 0.153 | 1.856 | 5.171 |
| Cases | Case Setup |
|---|---|
| Method 1 | Ramp periods = 8T |
| Method 2 | Catenary mooring |
| Method 3 | Catenary mooring + Viscous drag |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Z.; Chen, J.; Liang, H.; Zhao, Y.; Shao, Y. Hydrodynamic Responses of a 6 MW Spar-Type Floating Offshore Wind Turbine in Regular Waves and Uniform Current. Fluids 2020, 5, 187. https://doi.org/10.3390/fluids5040187
Zheng Z, Chen J, Liang H, Zhao Y, Shao Y. Hydrodynamic Responses of a 6 MW Spar-Type Floating Offshore Wind Turbine in Regular Waves and Uniform Current. Fluids. 2020; 5(4):187. https://doi.org/10.3390/fluids5040187
Chicago/Turabian StyleZheng, Zhiping, Jikang Chen, Hui Liang, Yongsheng Zhao, and Yanlin Shao. 2020. "Hydrodynamic Responses of a 6 MW Spar-Type Floating Offshore Wind Turbine in Regular Waves and Uniform Current" Fluids 5, no. 4: 187. https://doi.org/10.3390/fluids5040187