Numerical Simulation of Fountain Formation due to Normal and Inclined Twin-Jet Impingement on Ground
Abstract
:1. Introduction
2. Numerical Method and Validation
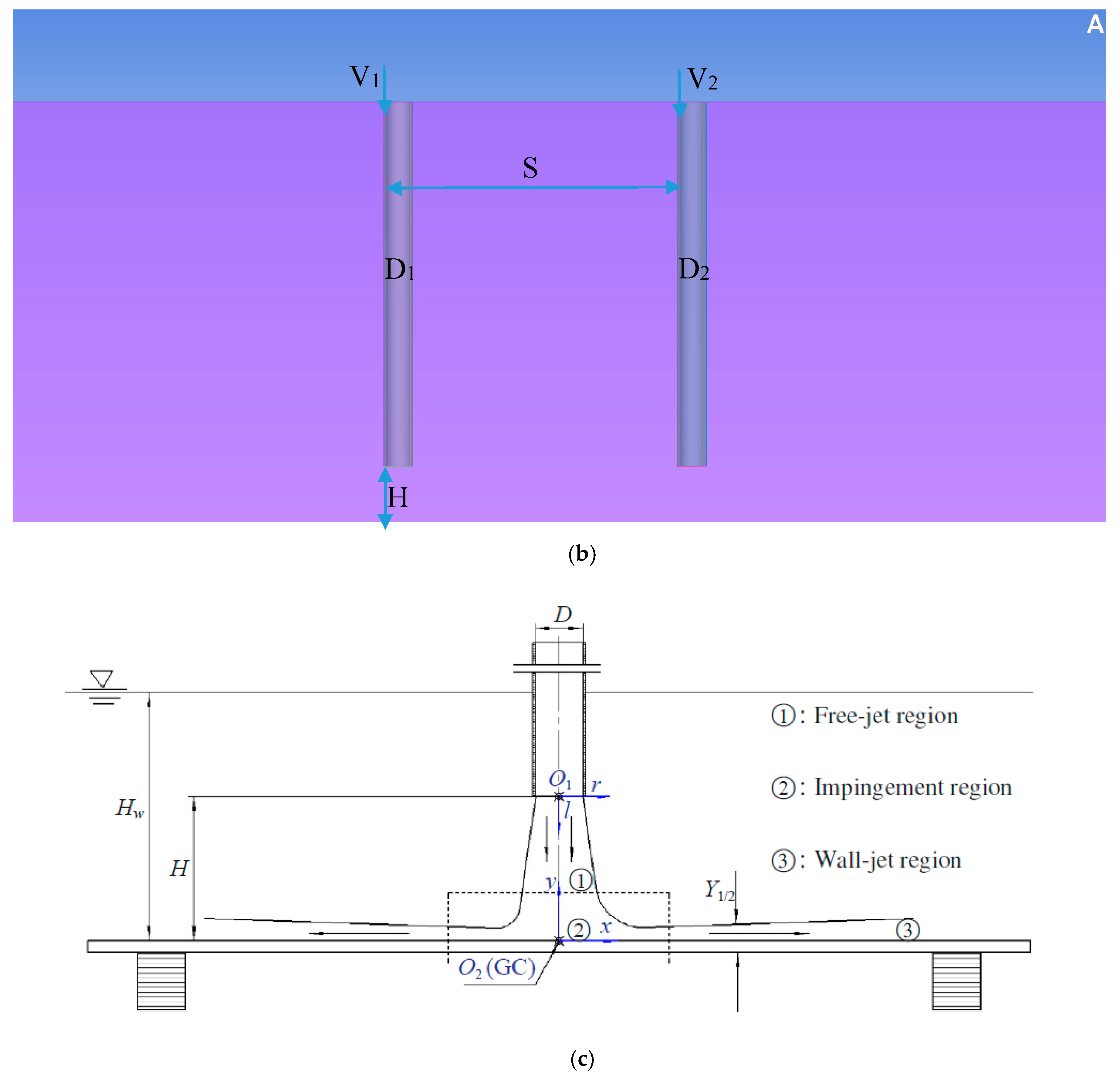
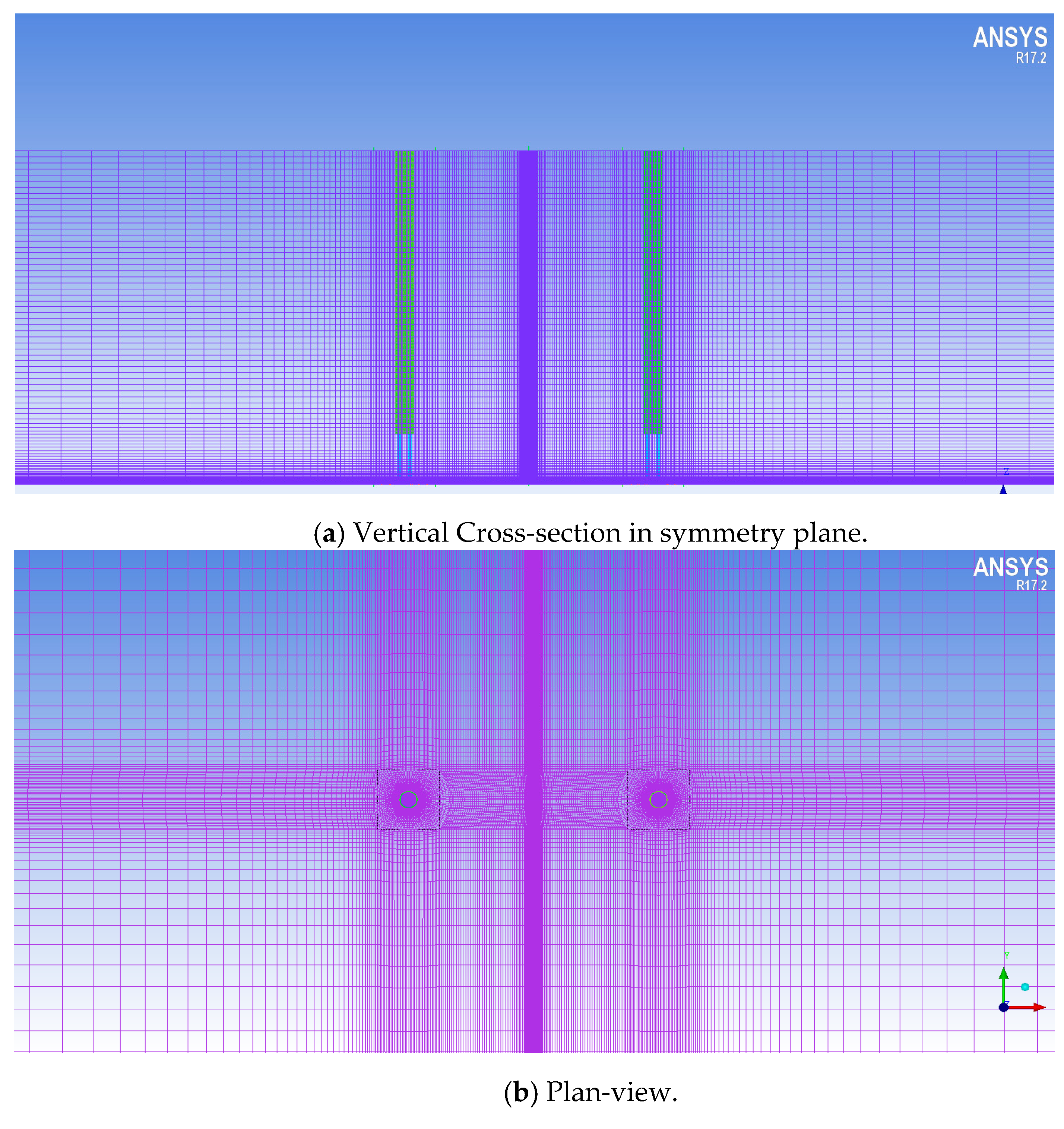
2.1. Physical Model
2.2. Governing Equations and Numerical Method
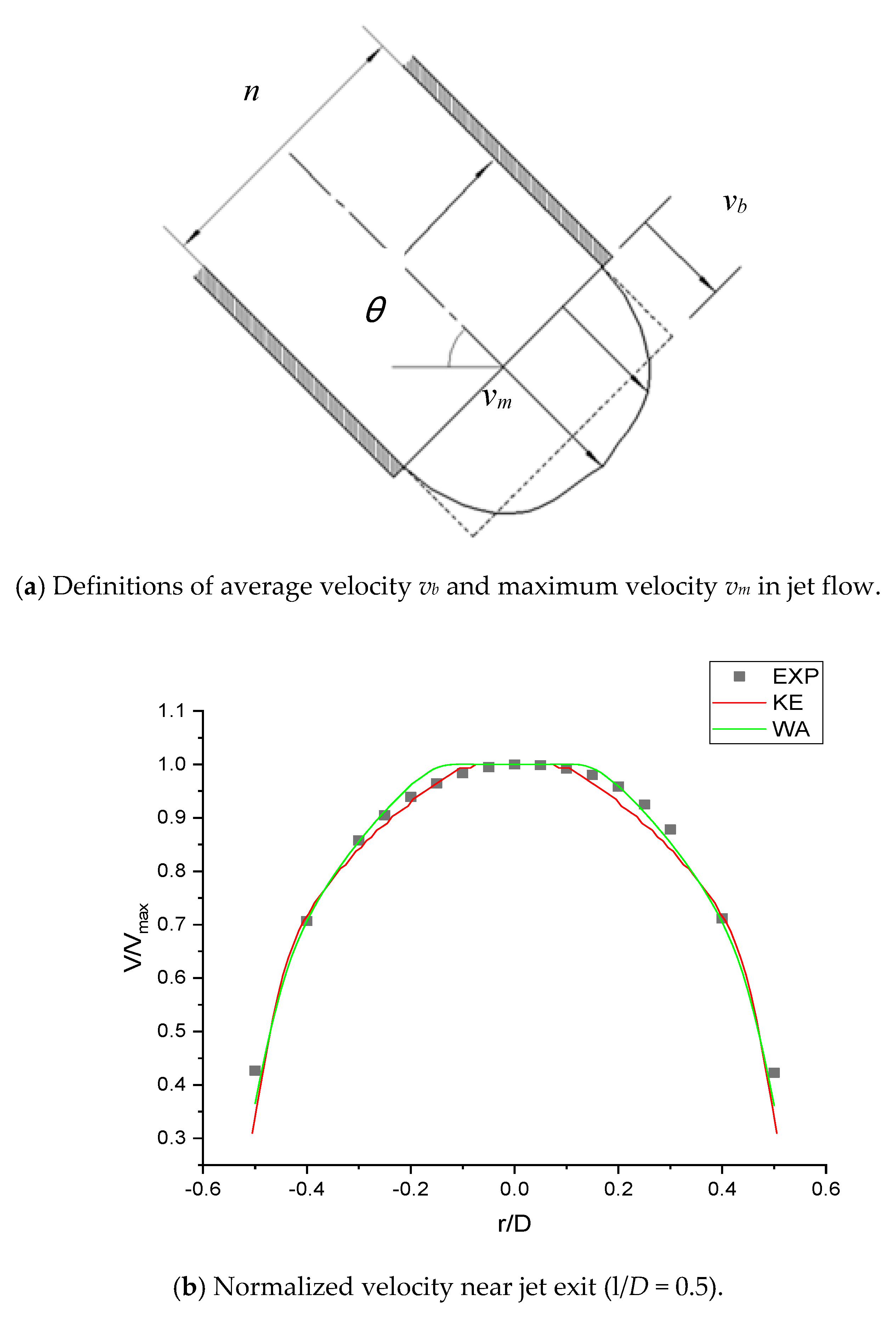
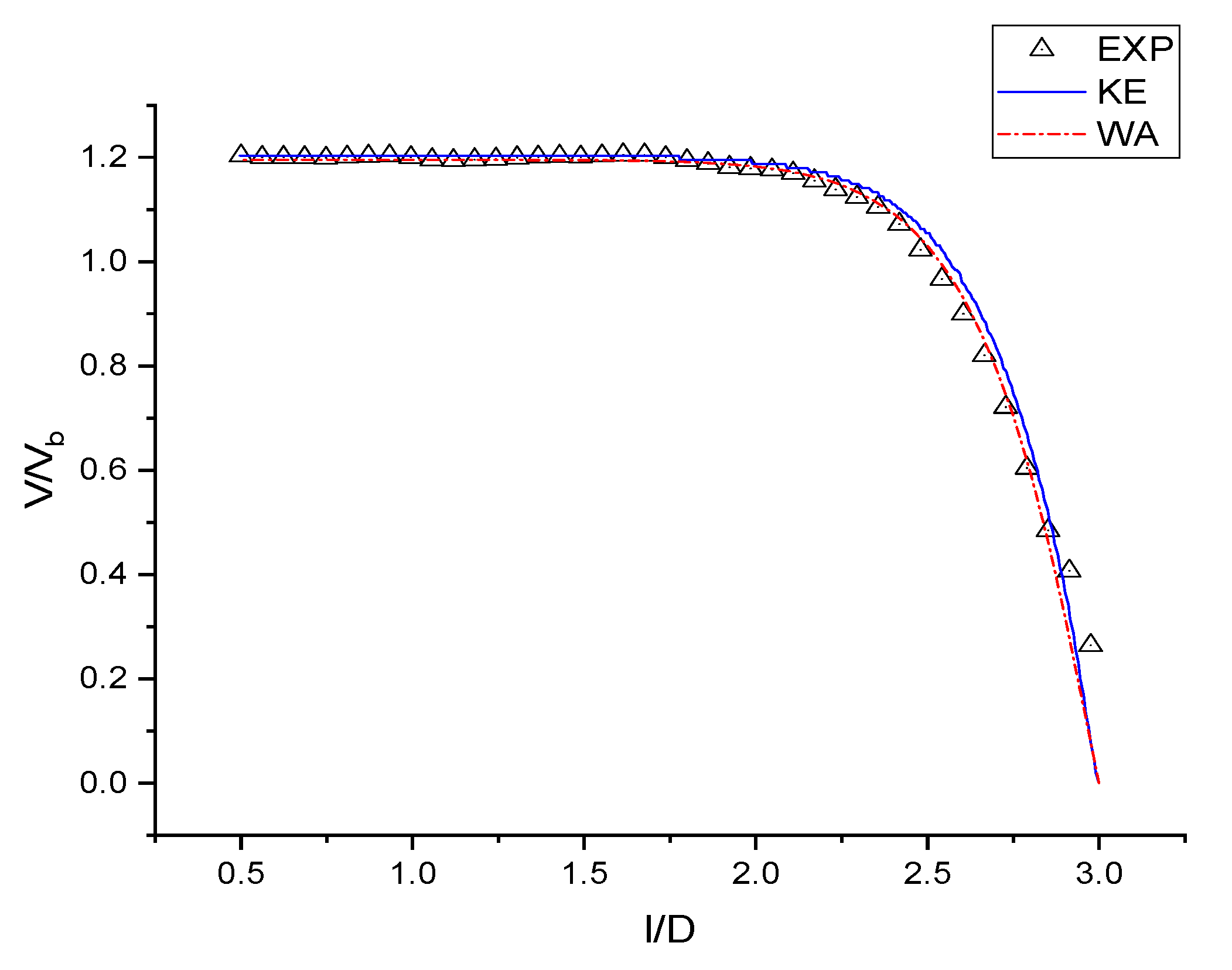
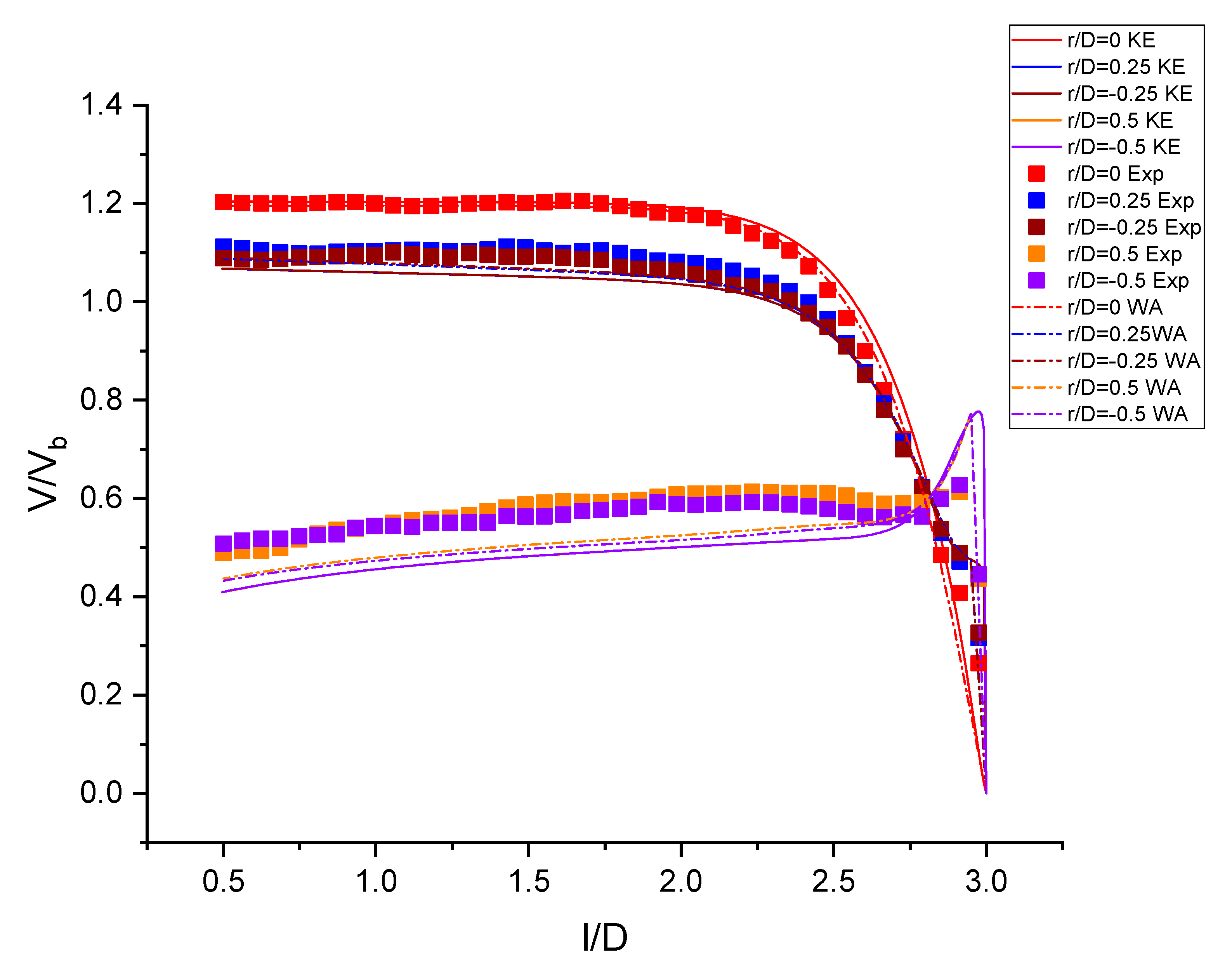
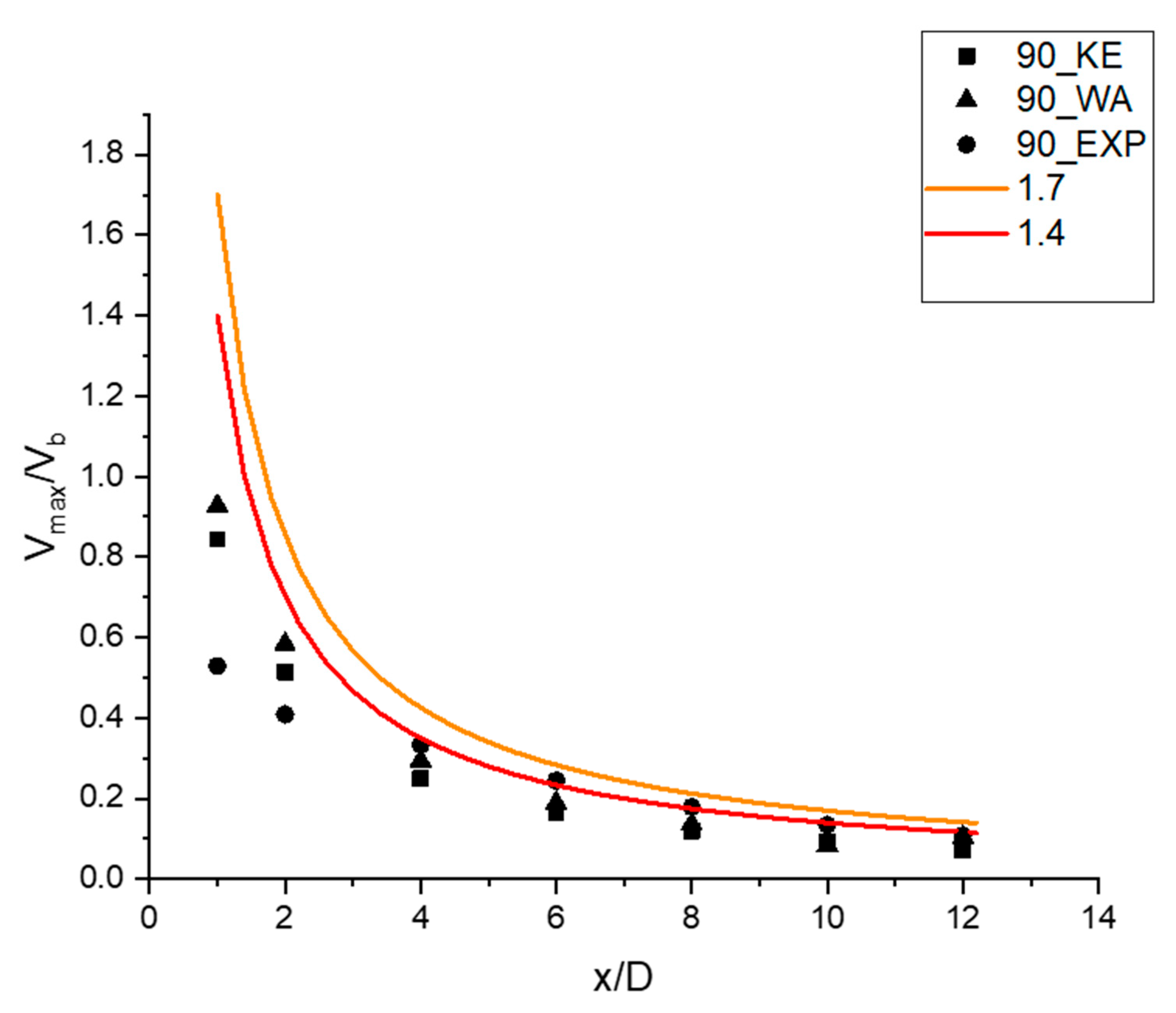
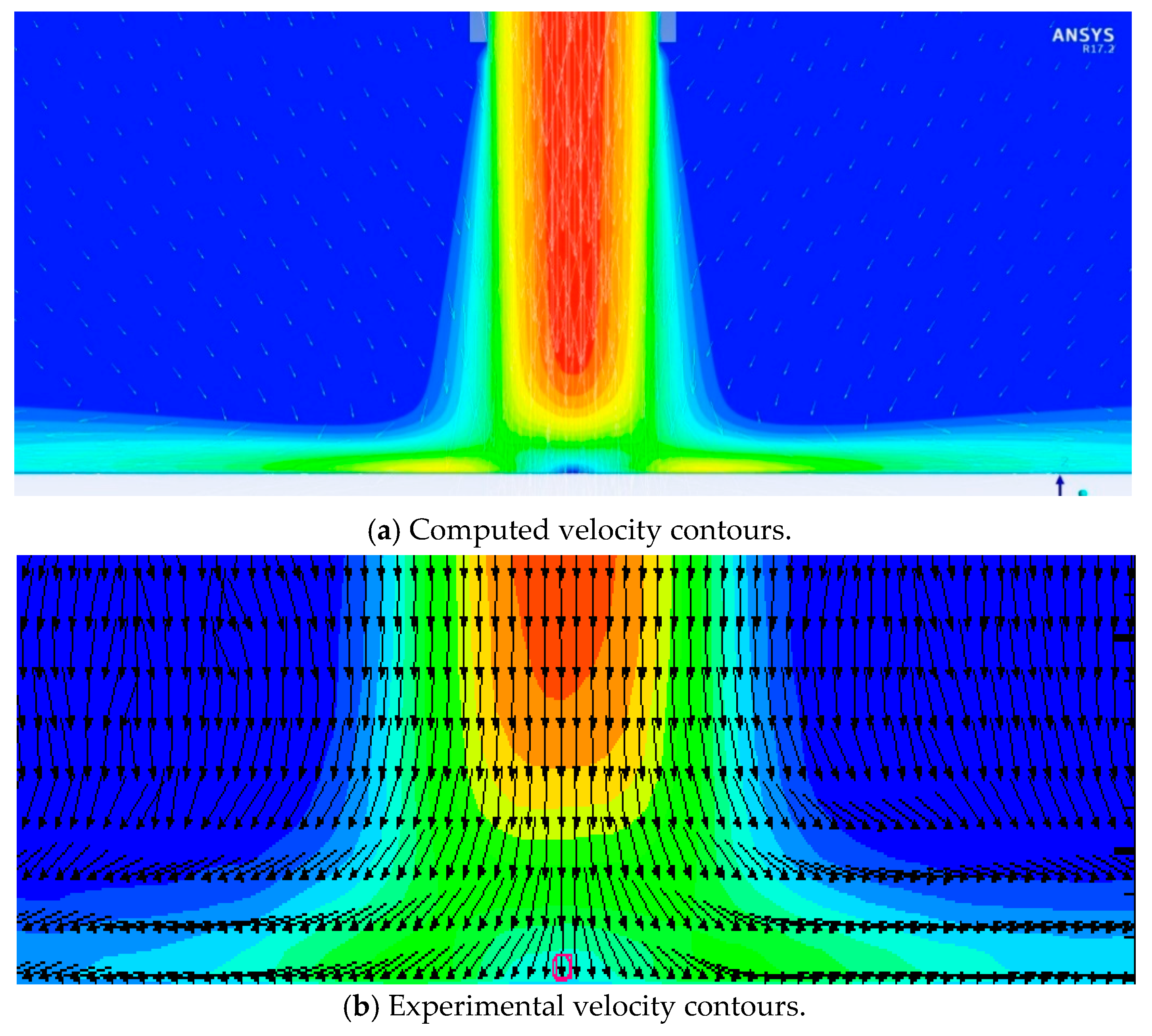
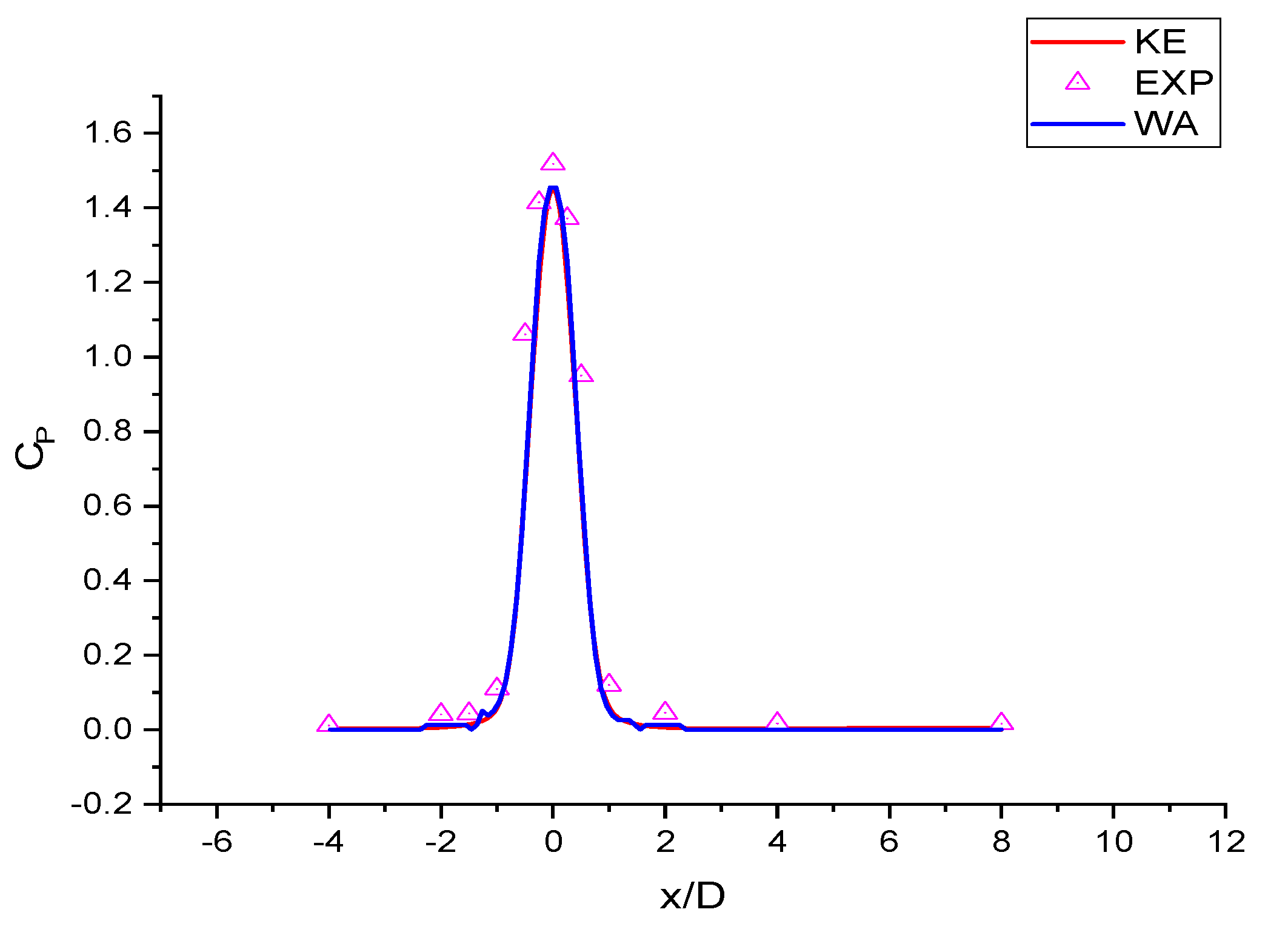
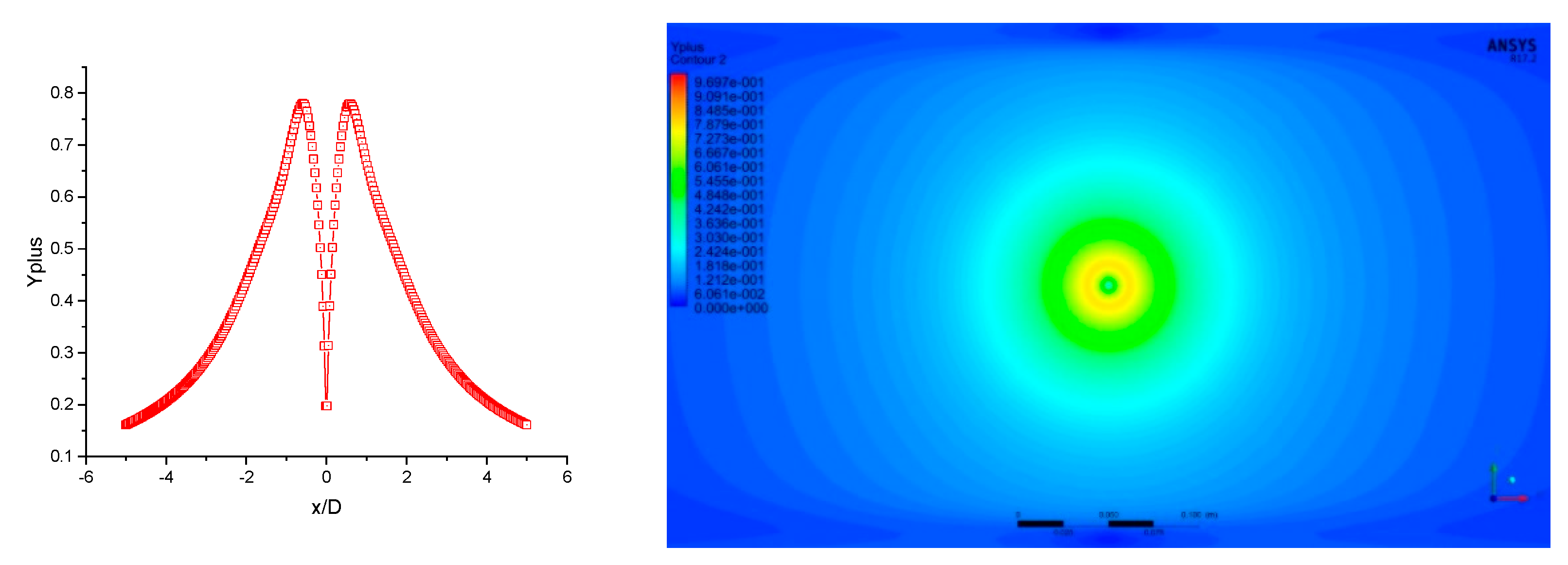
2.3. Validation with Experiment of Single Jet Impingement
3. Results and Discussion
3.1. Flow Conditions to Form a Straight Fountain
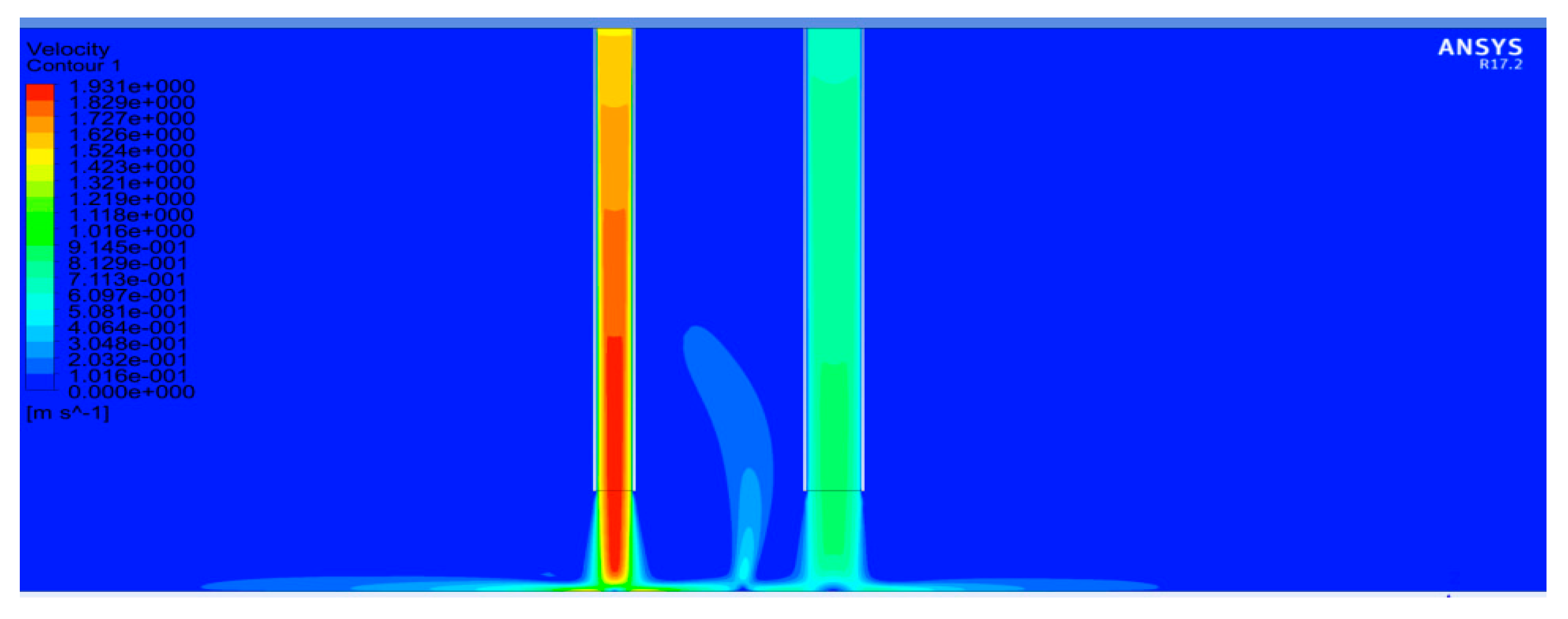
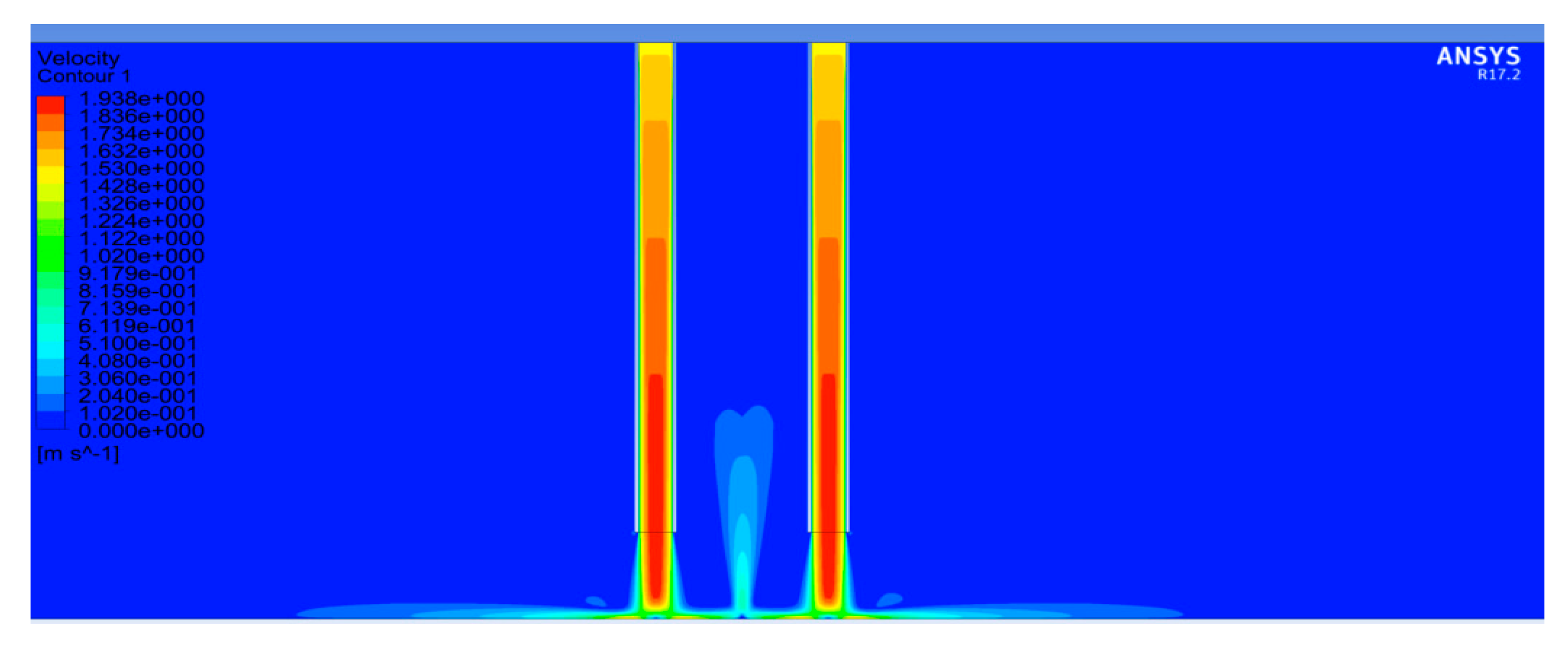
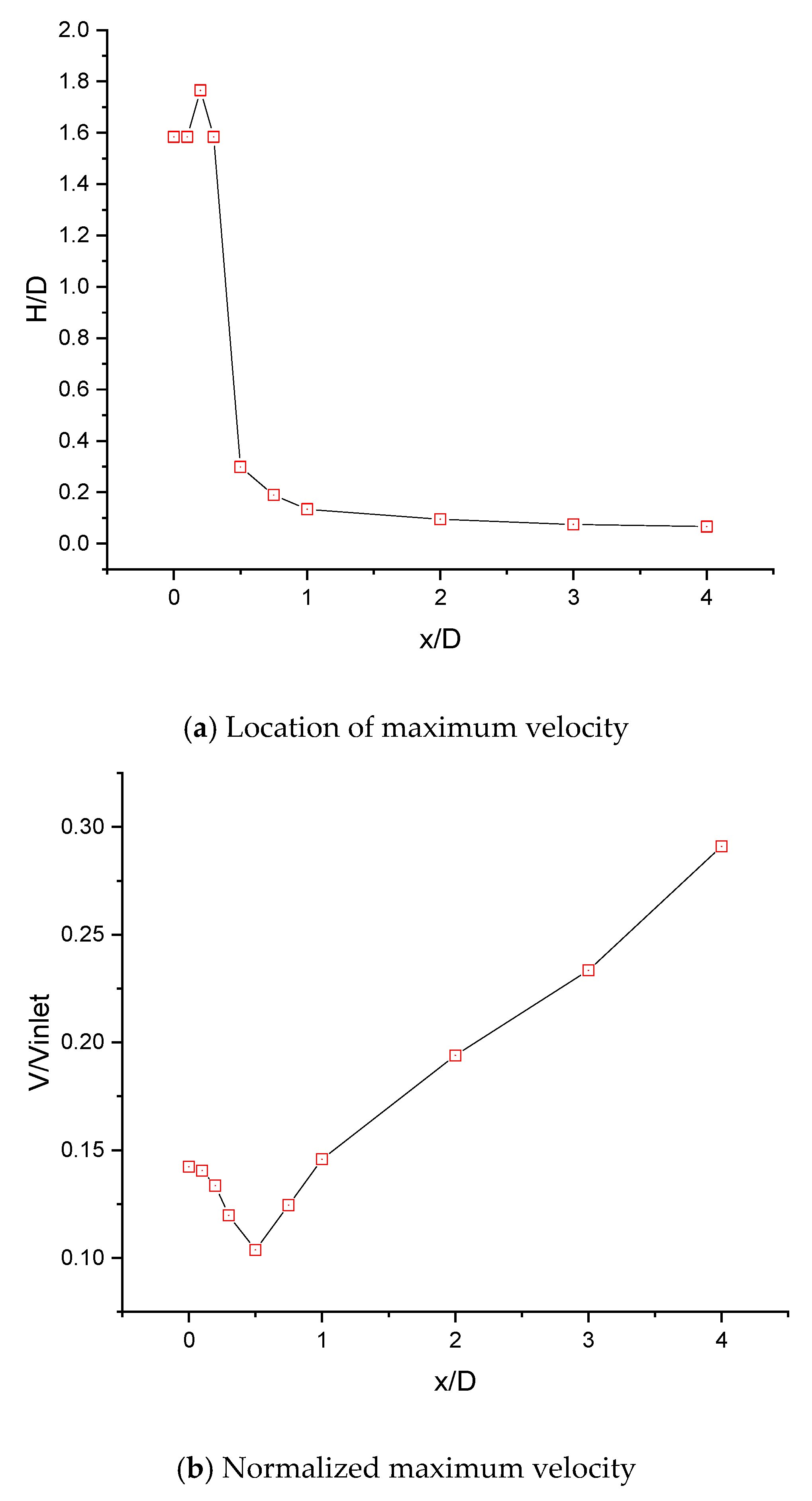
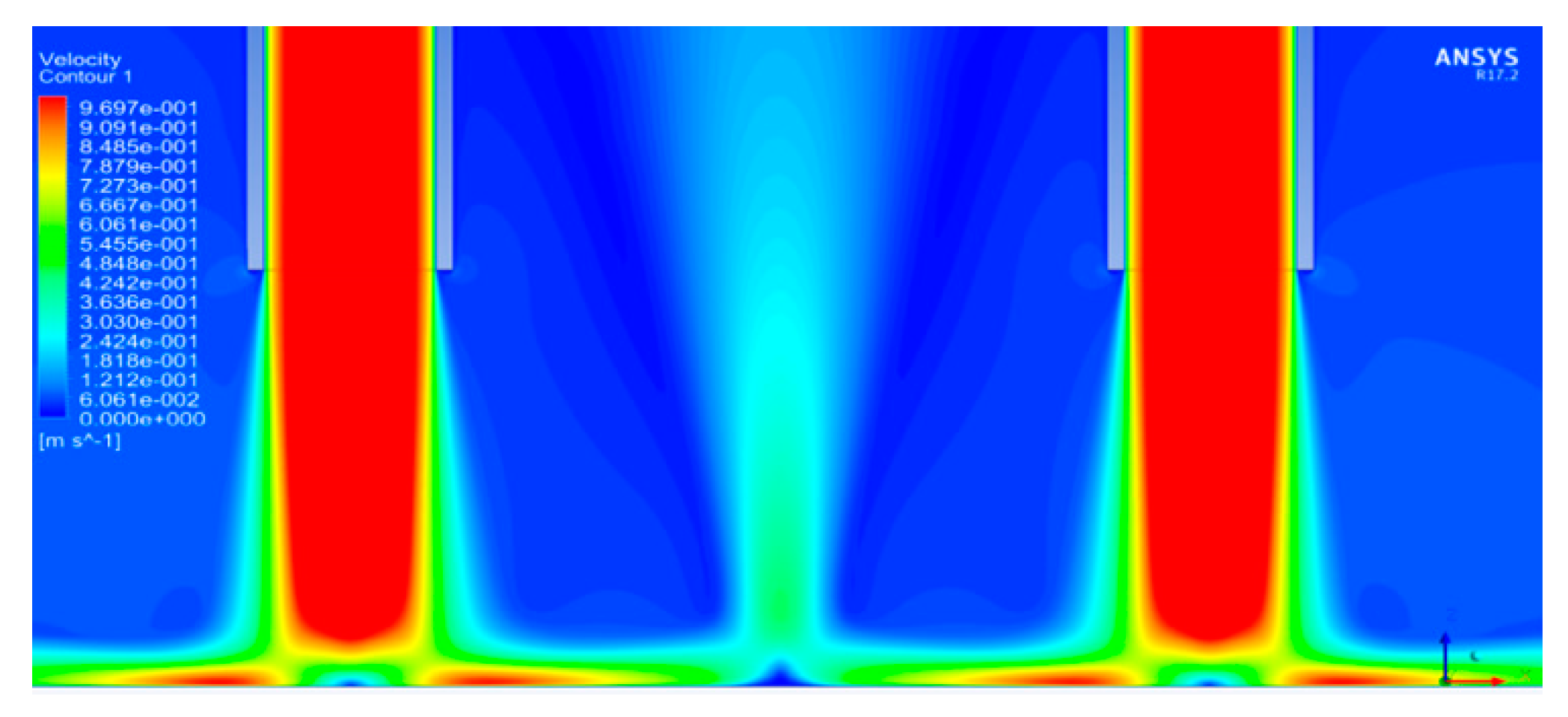
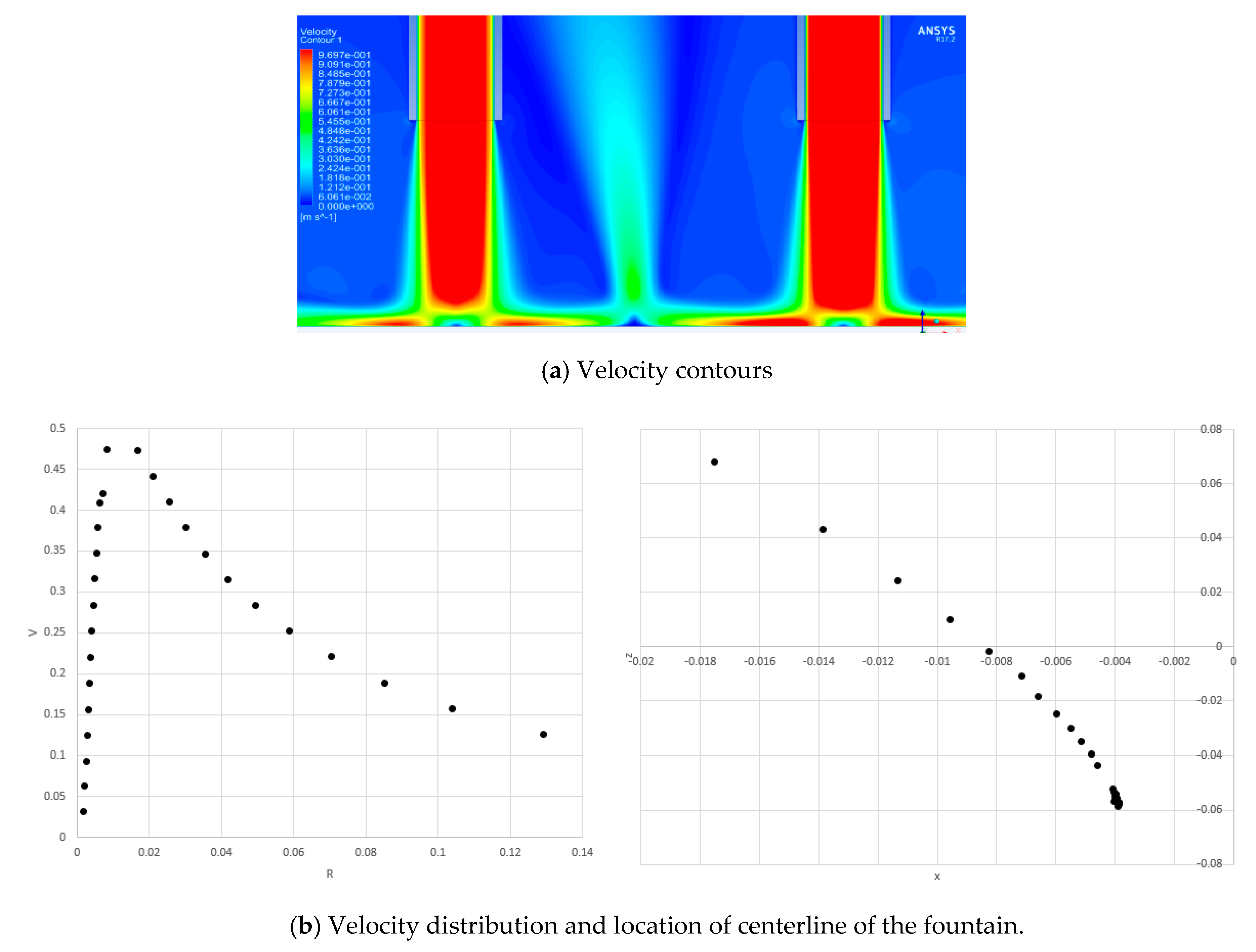
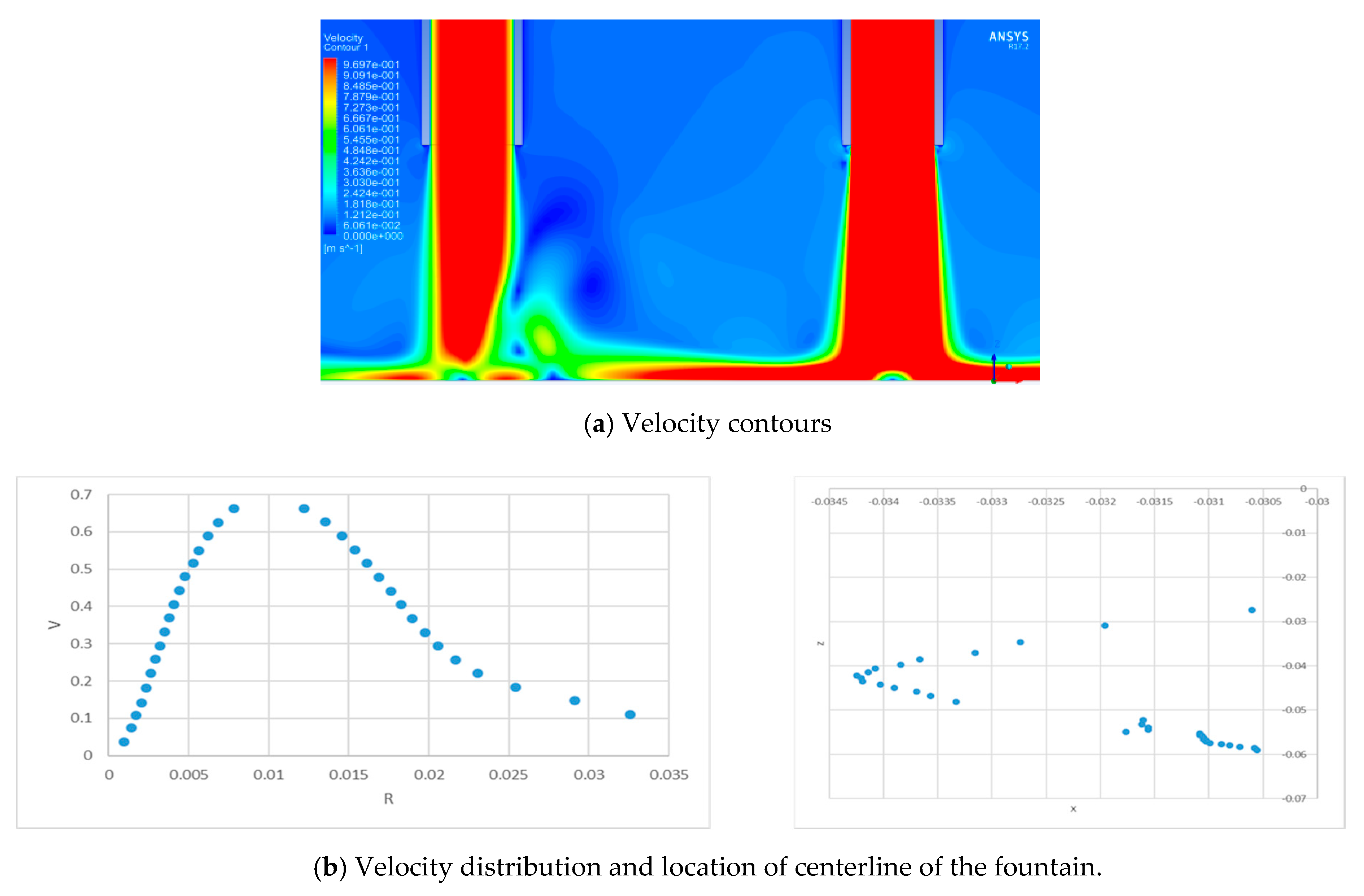
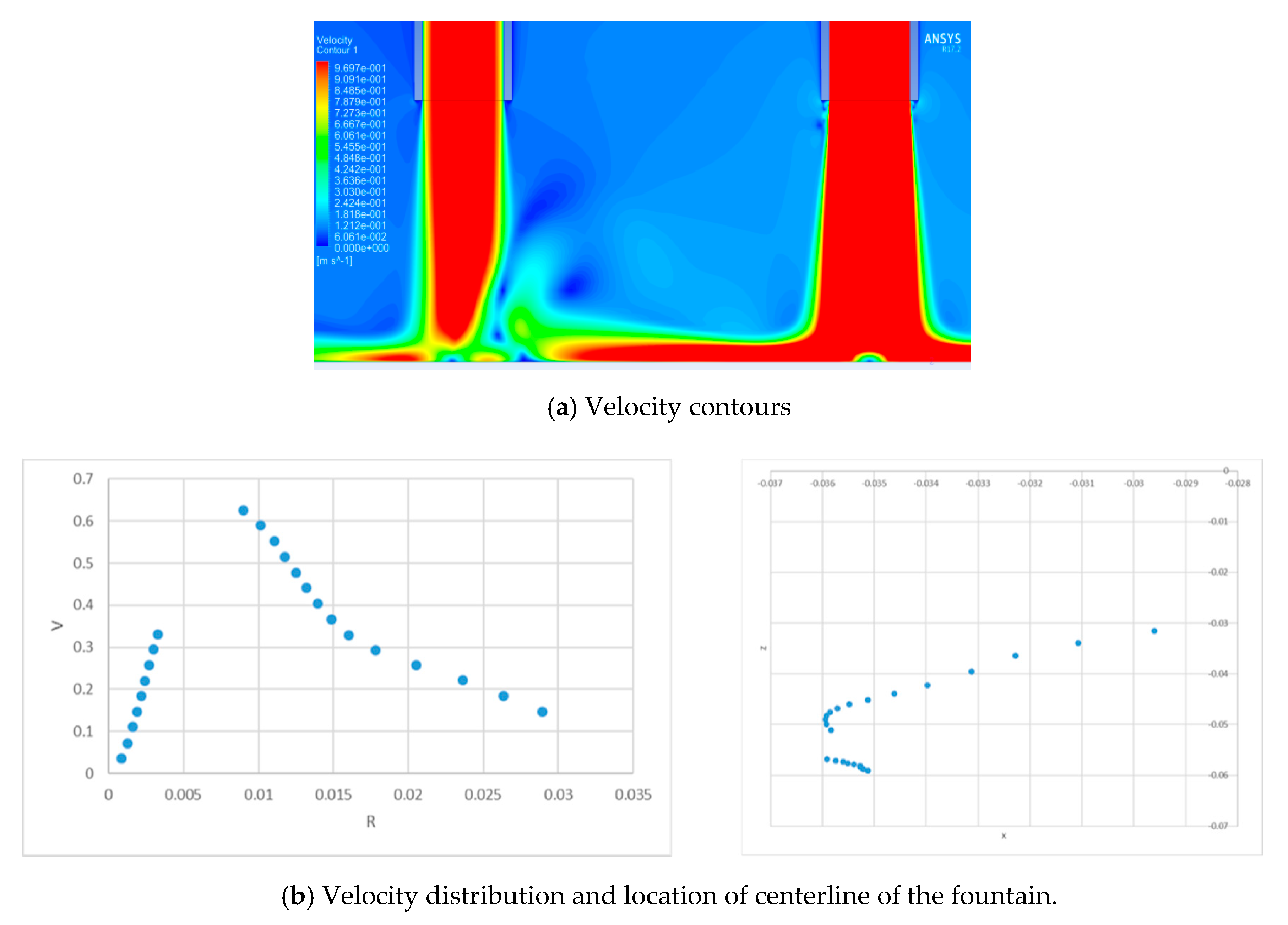
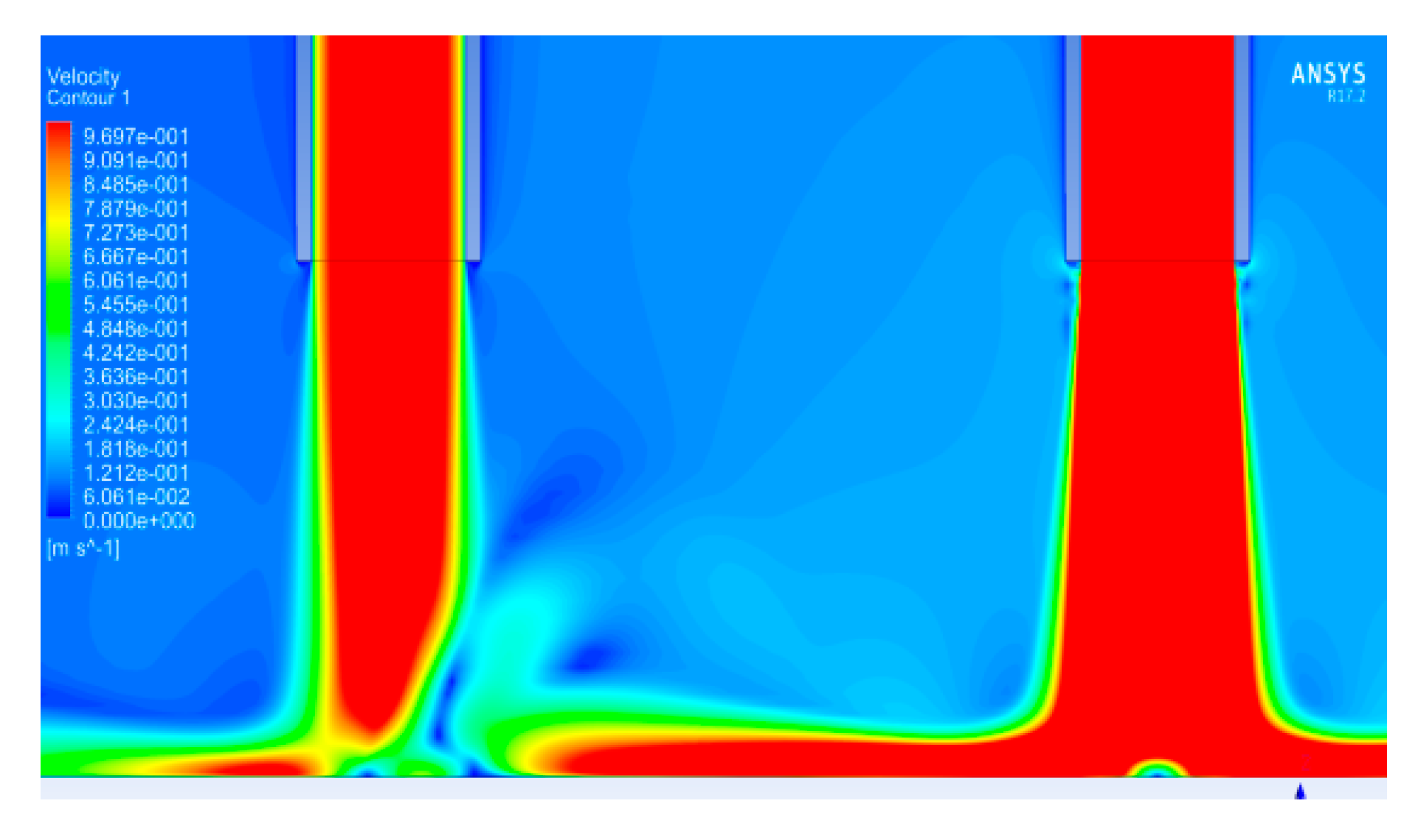
3.2. Straight Up-Wash Fountain
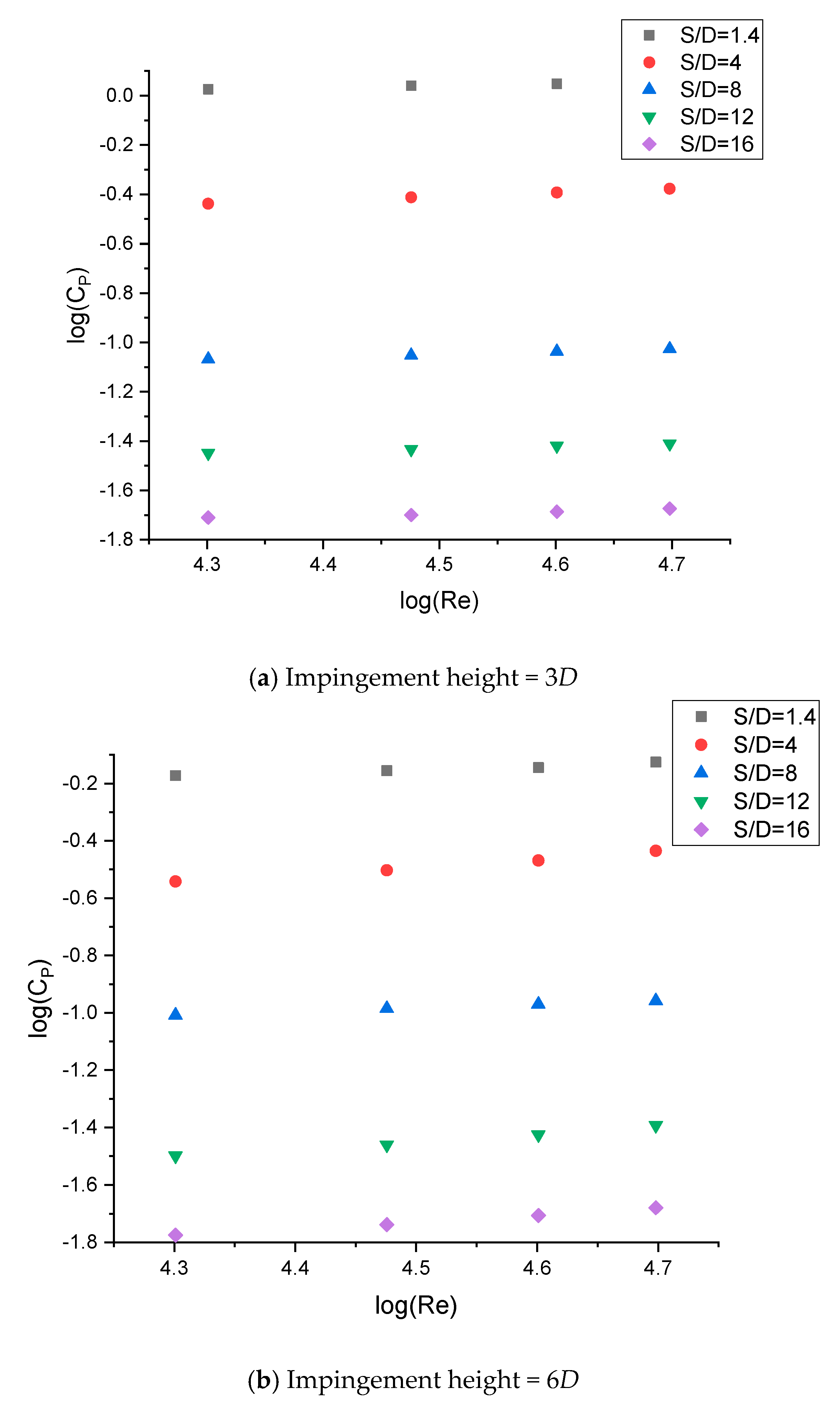
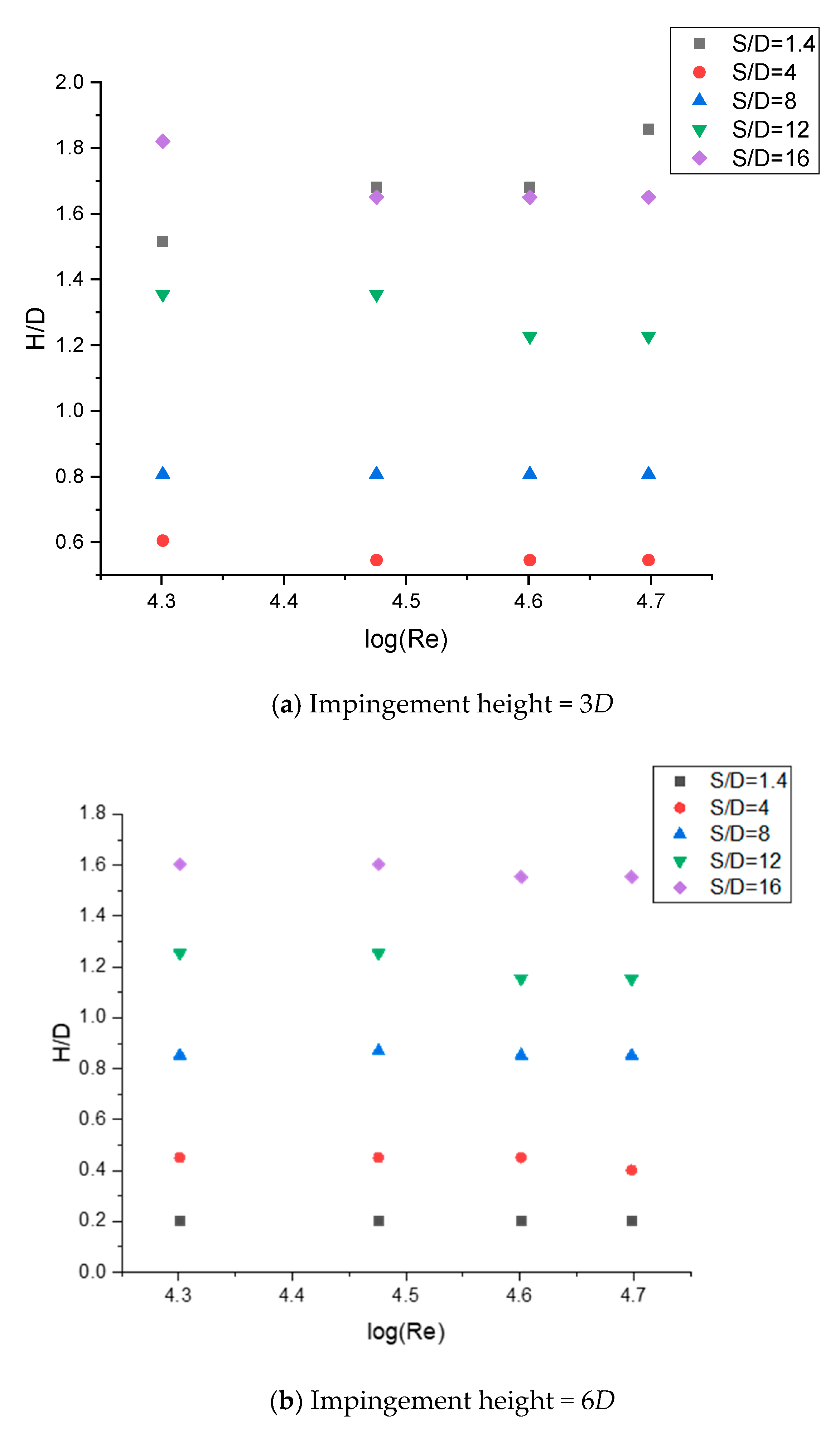
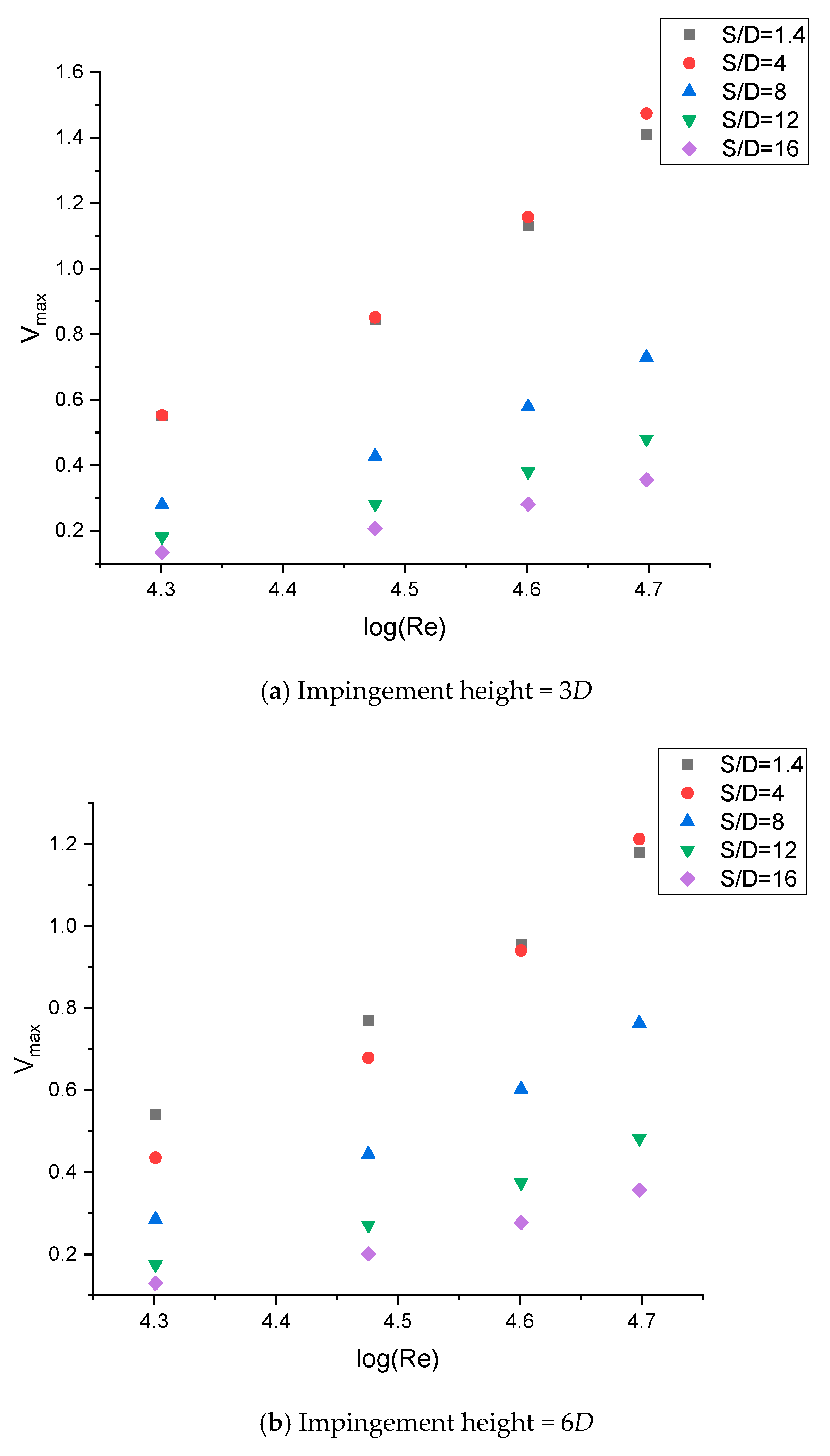
3.3. Straight Fountain Formation under Various Flow Conditions
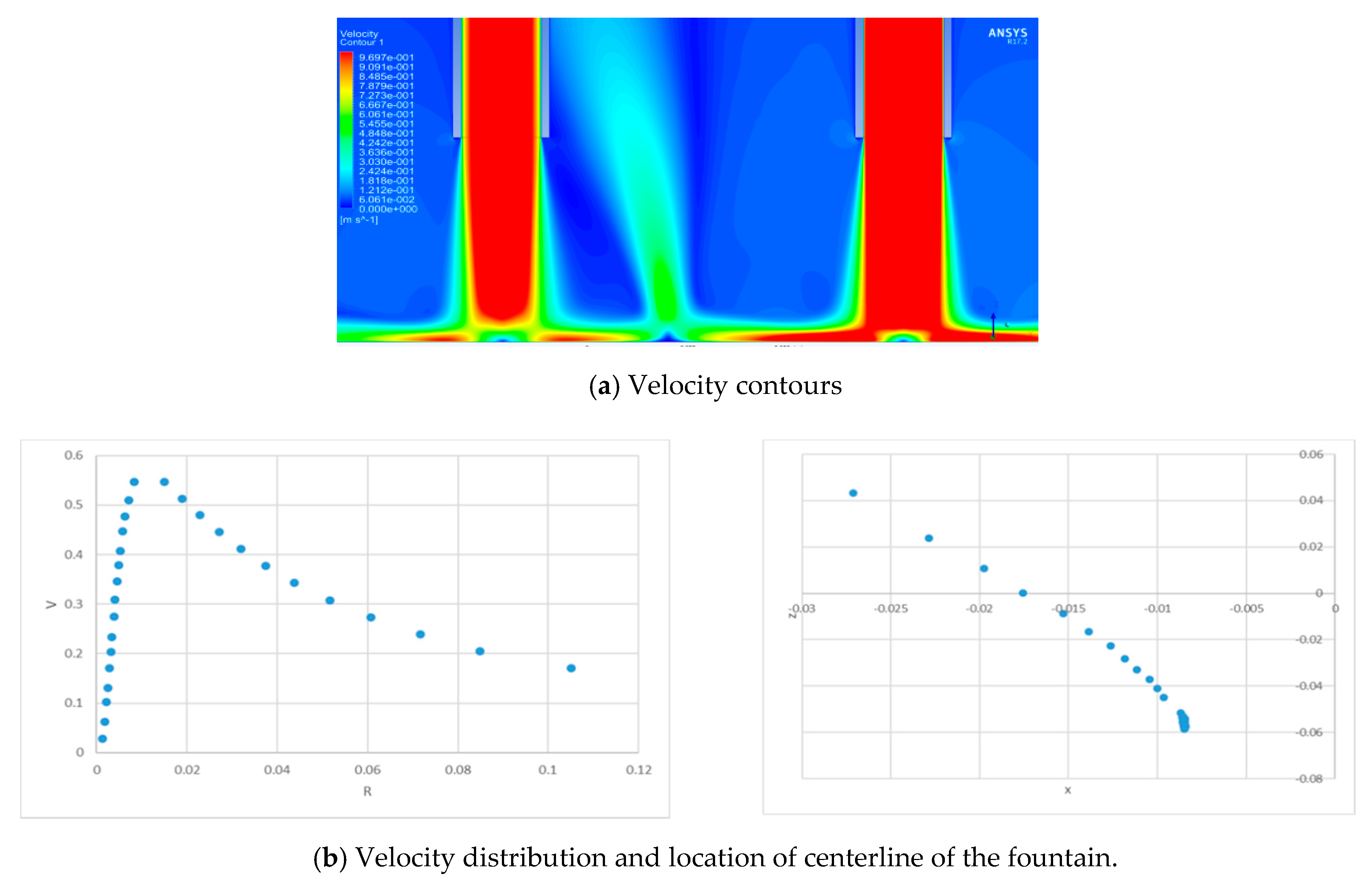
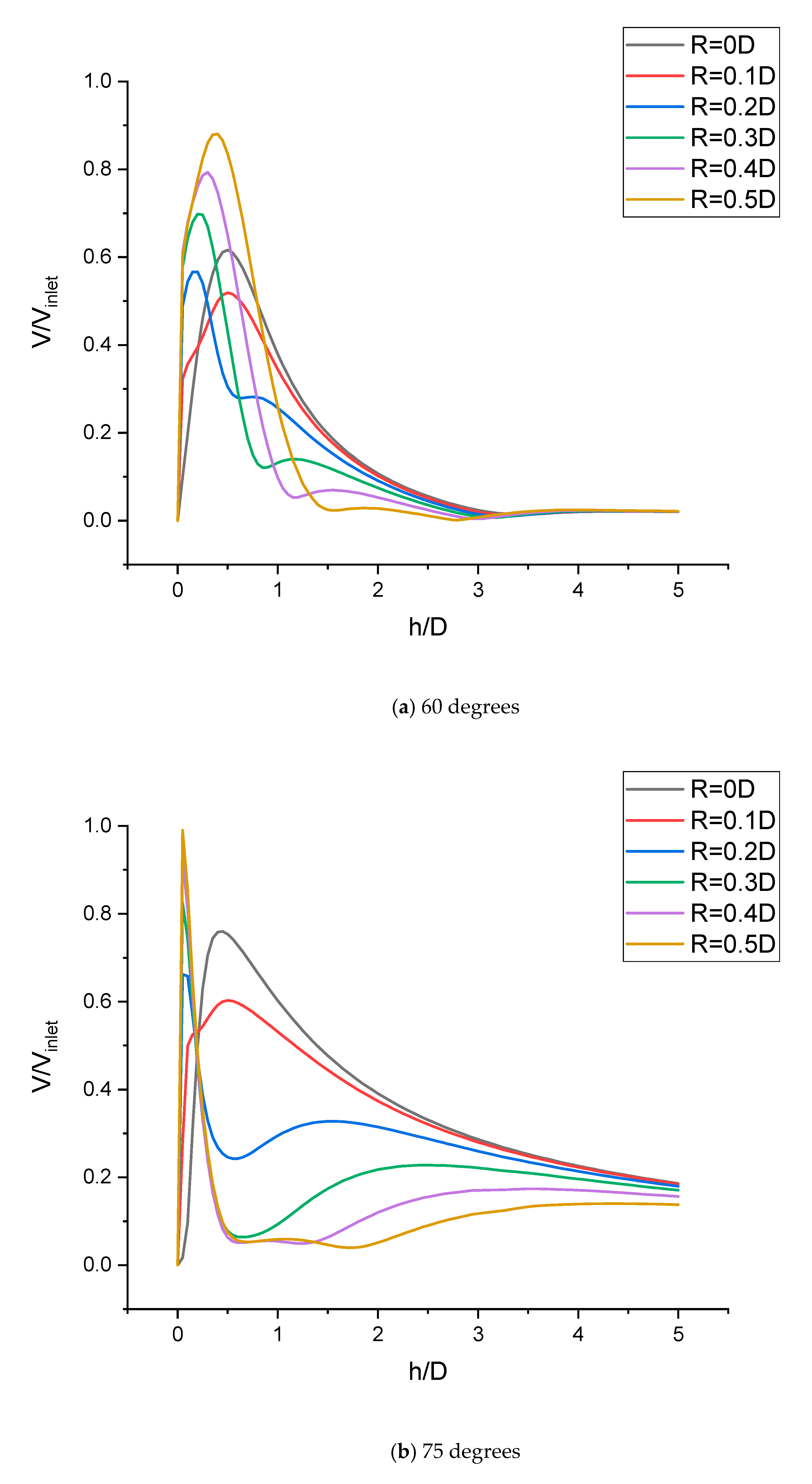
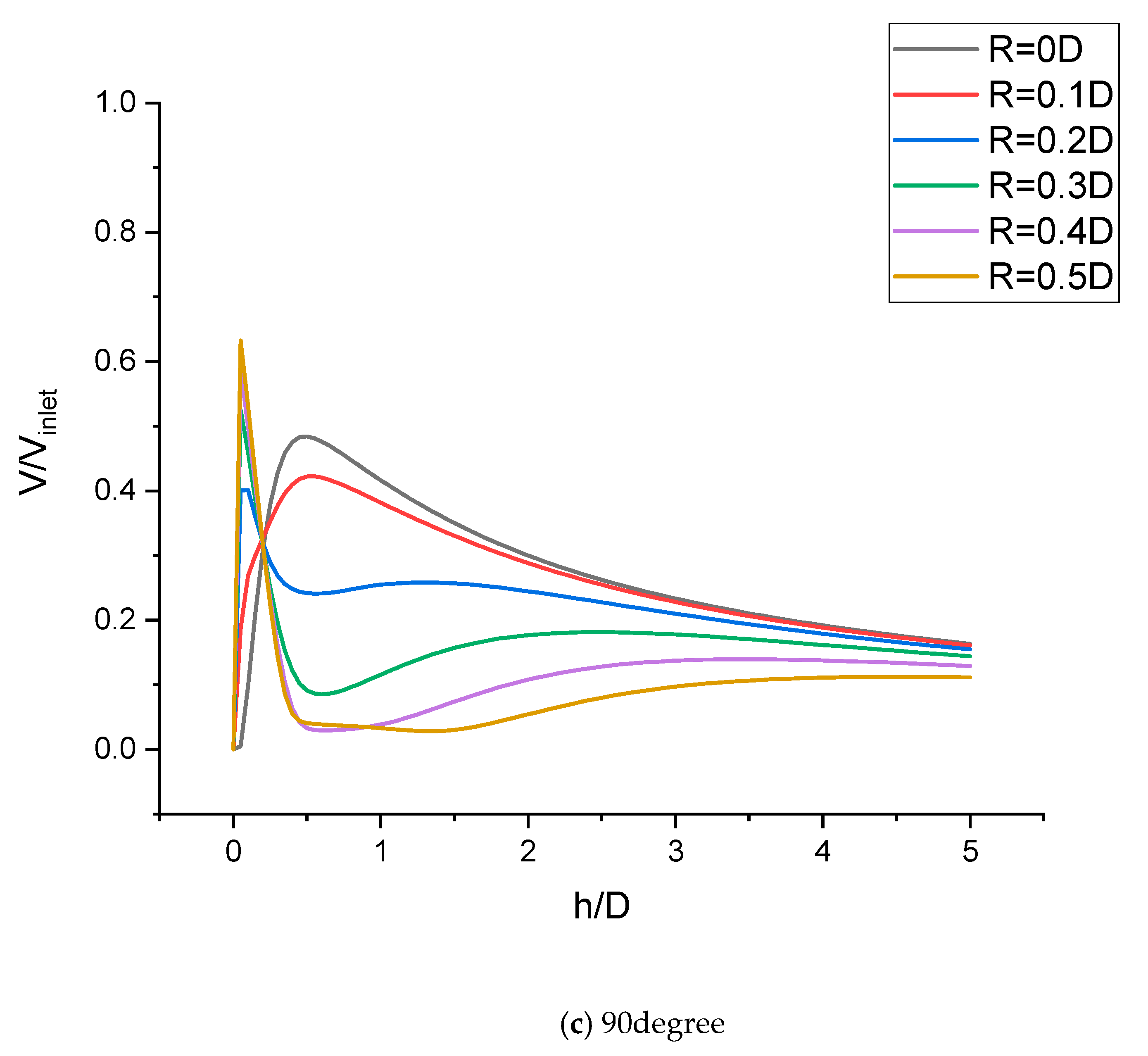
3.4. Inclined Fountain Formation
3.5. Fountain Formed by Inclined Jets
4. Conclusions
- 1
- Numerical results from both k-ε and Wray-Agarwal turbulence model show good agreement with experimental data for single jet impingement.
- 2
- For the fountain formed by two round jets, if Reynolds number of the two jets at the inlet is identical and exits of jets are located at same horizontal level, the fountain formed in this condition is straight and upwards.
- 3
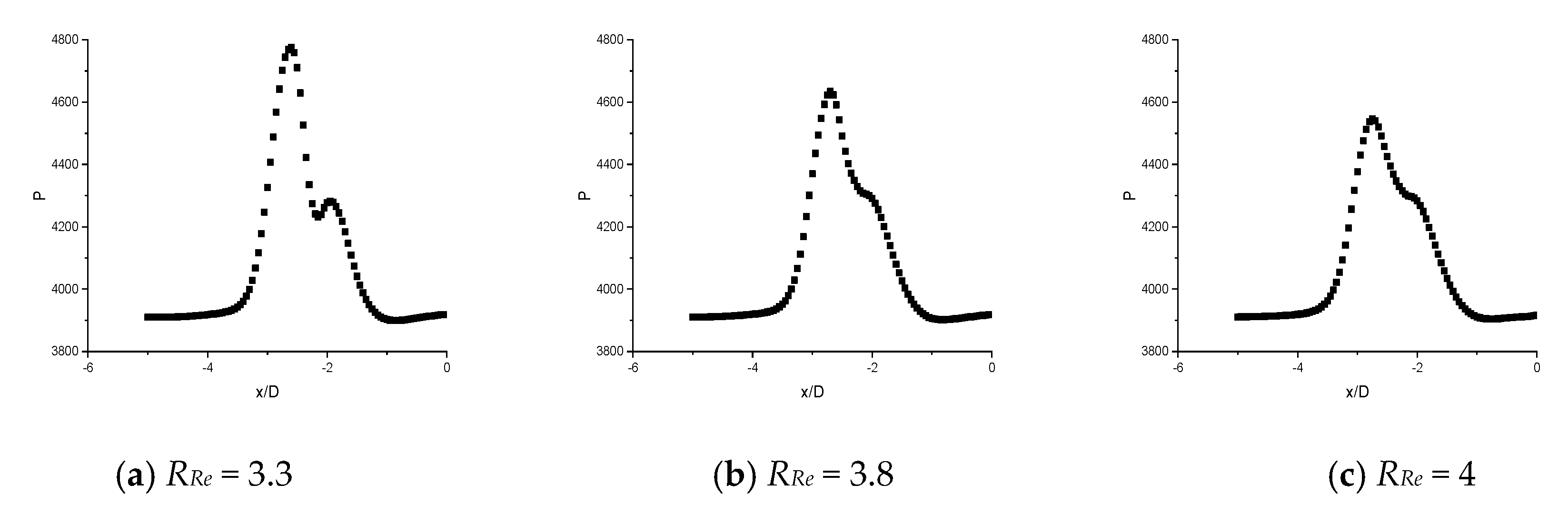
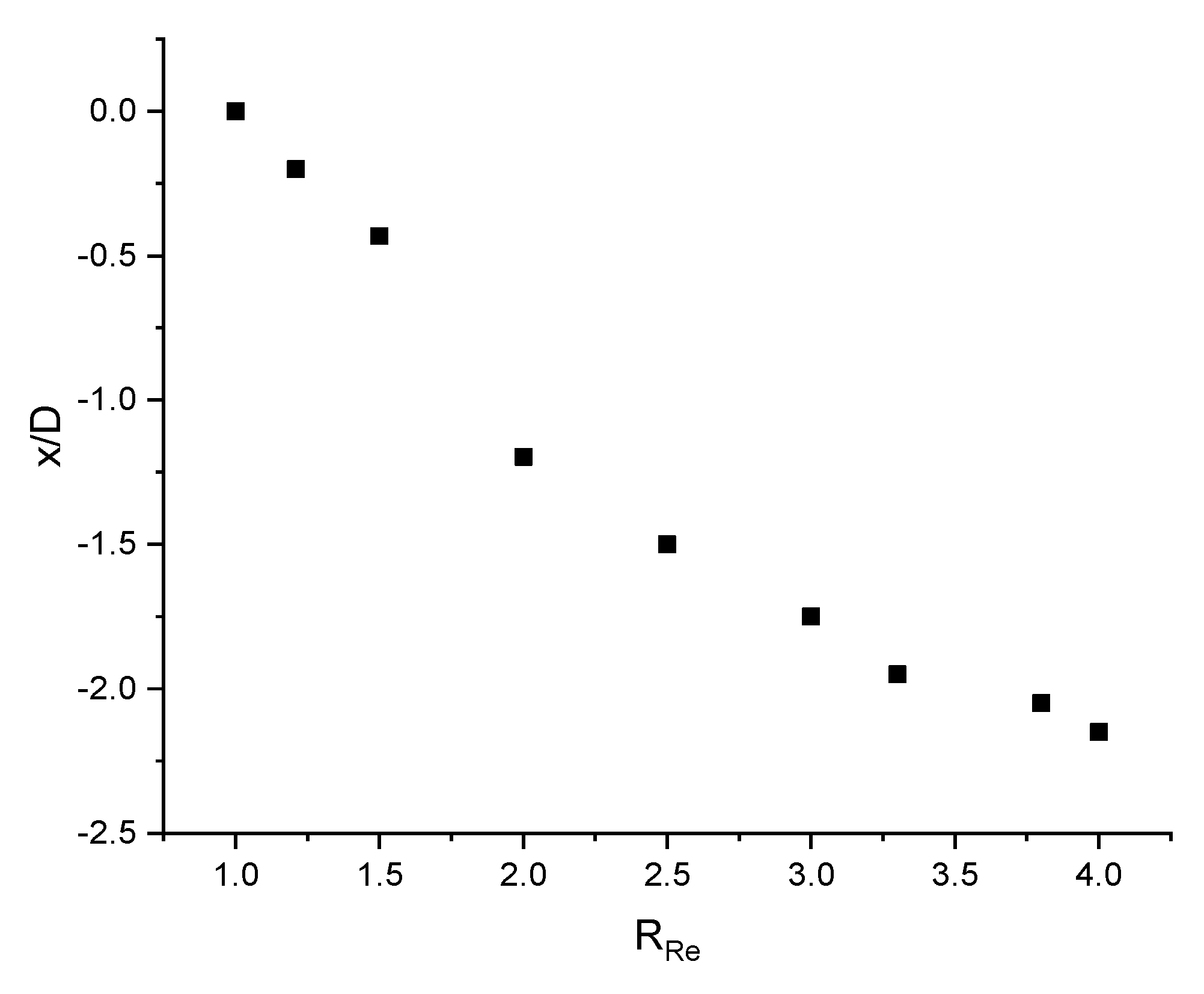
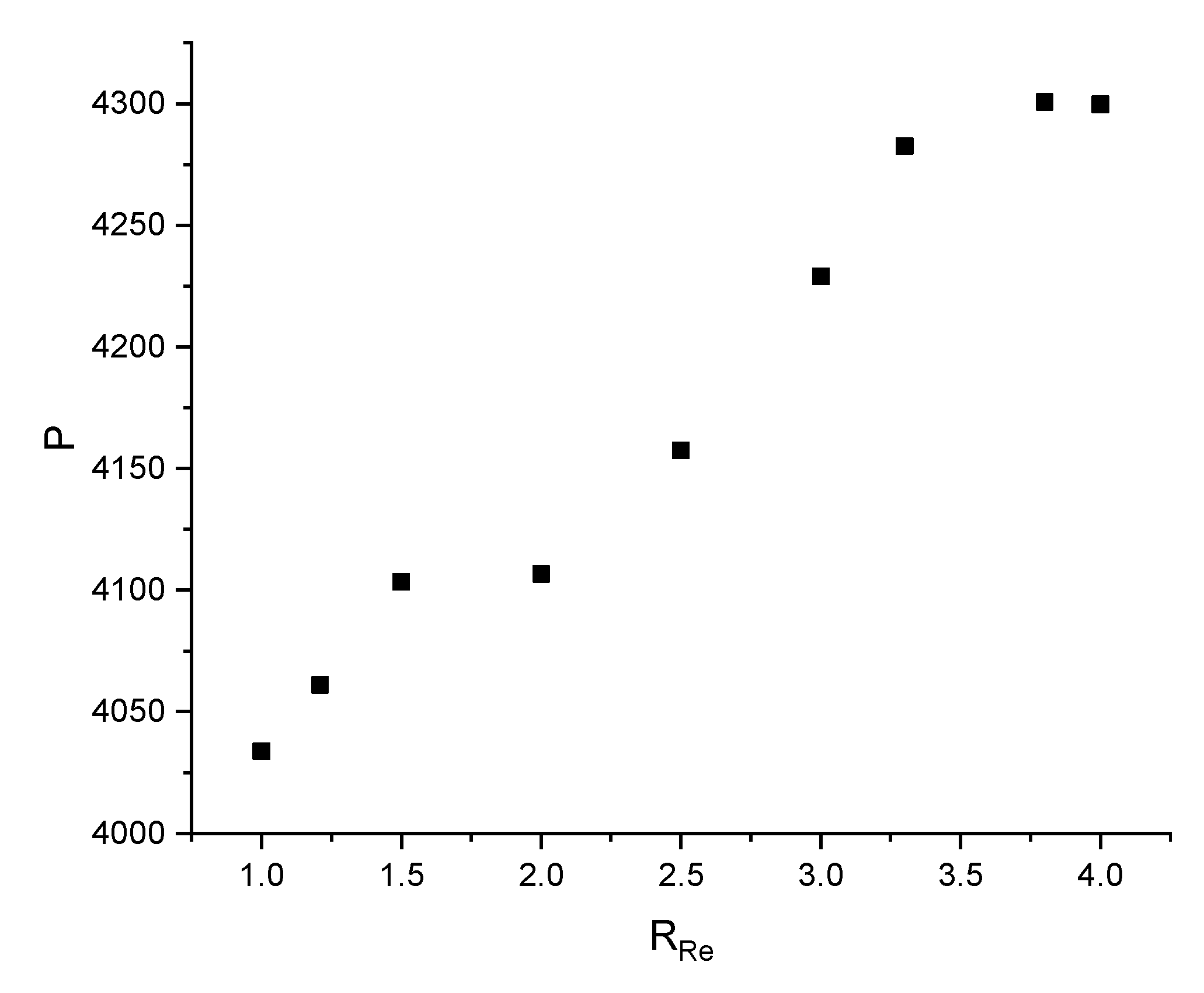
- Pressure at the fountain center is highly sensitive to the inlet Reynolds number of the jets when distance between the jets S, is small. However, the pressure coefficient is much less sensitive to inlet Reynolds number than pressure in Pascal.
- 4
- Straight fountain exhibits different velocity profiles in regions at different radial distances. Fountain flow has larger acceleration near the bottom plane when radial distance x/D > 0.5 compared to when x/D < 0.5.
- 5
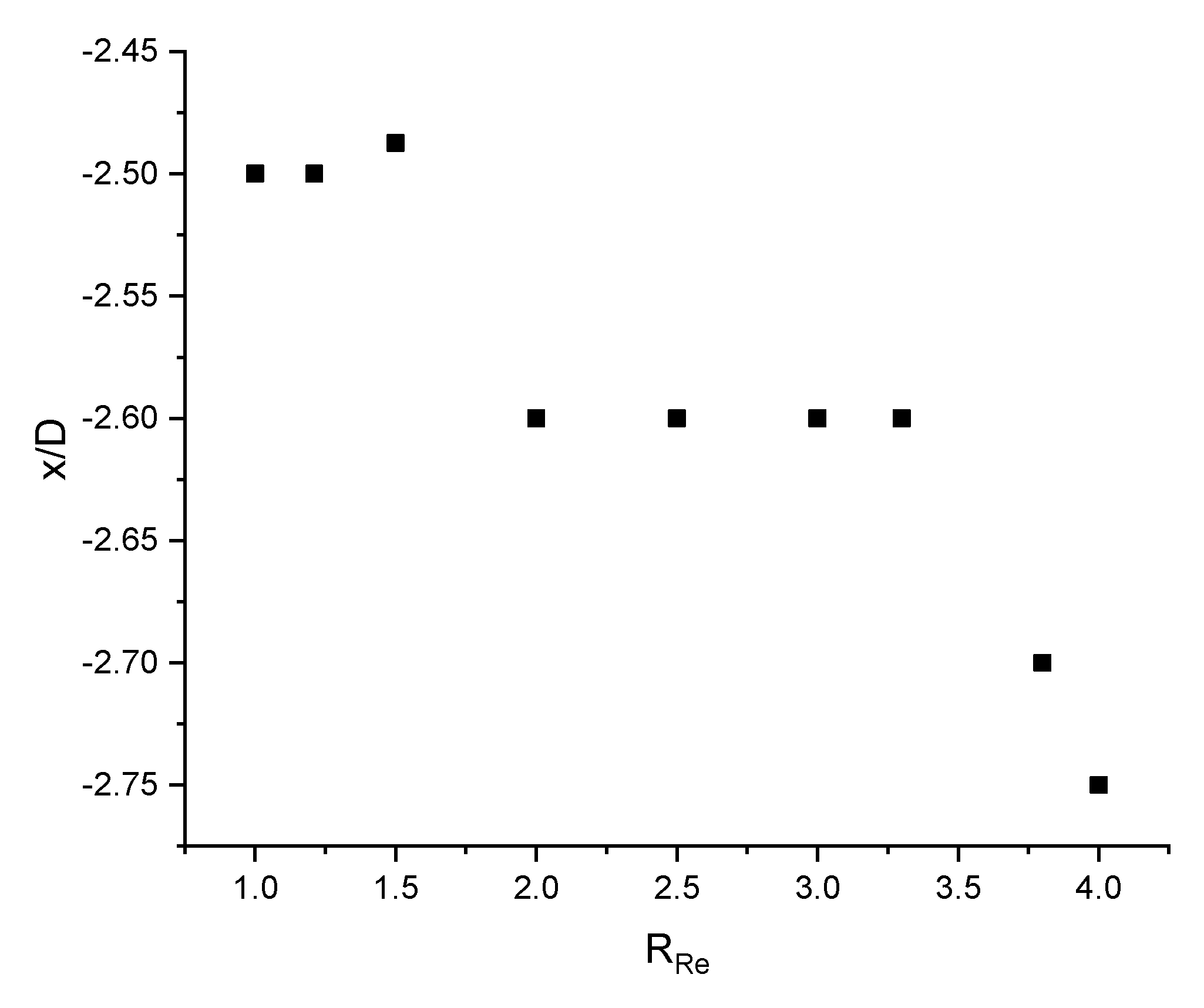
- When inlet Reynolds number of jets are different, the fountain formed by the two jets moves to the side of the jet with smaller inlet Reynolds number and stagnation point of the fountain also moving along the same direction. As the ratio of Reynolds number increases, the fountain reflects back to the jet with larger inlet Reynolds number and the stagnation point of the fountain tends to merge with the stagnation point of the left jet that has smaller inlet Reynolds number. Meanwhile, strong wall jet from the right side has a negative influence on impingement of the left jet.
- 6
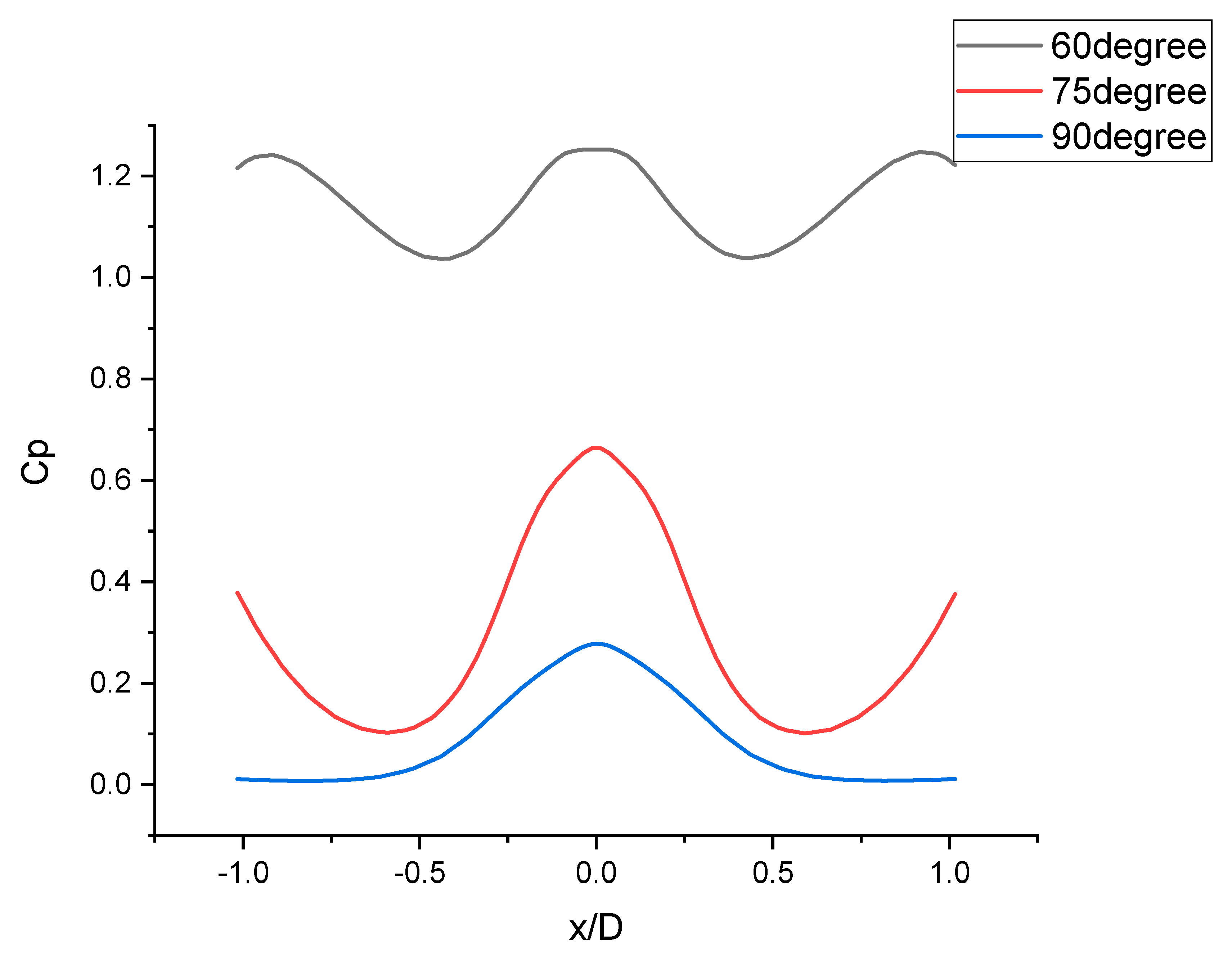
- Change in impinging angle of the jets significantly changes the behavior of the fountain because of the change in strength and location of the wall jets.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Pressure coefficient | |
| D | diameter of water jet |
| H | vertical distance from impingement plane |
| S | Distance between the centerlines of two jets |
| Re | Reynolds number based on the diameter of the pipe |
| dimensionless wall distance of first grid layer | |
| P | static pressure |
| reference pressure | |
| density of water | |
| Vinlet | velocity at jet inlet |
References
- Weigand, B.; Spring, S. Multiple jet impingement—A review. Heat Transf. Res. 2011, 42, 101–142. [Google Scholar] [CrossRef]
- Dewan, A.; Dutta, R.; Srinivasan, B. Recent trends in computation of turbulent jet impingement heat transfer. Heat Transf. Eng. 2012, 33, 447–460. [Google Scholar] [CrossRef]
- Ostheimer, D.; Yang, Z. A CFD Study of Twin Impinging Jets in a Cross-Flow. Open Numer. Methods J. 2012, 4, 24–34. [Google Scholar] [CrossRef] [Green Version]
- Saripalli, K.R. Visualization of Multi-Jet Impingement Flow. AIAA J. 1983, 21, 483–484. [Google Scholar] [CrossRef]
- Ozmen, Y. Confined impinging twin air jets at high reynolds numbers. Exp. Therm. Fluid Sci. 2011, 35, 355–363. [Google Scholar] [CrossRef]
- Barata, J.M.; Durao, D.F.G.; Heitor, M.V.; McGuirk, J. Impingement of single and twin turbulent jets through a crossflow. AIAA J. 1991, 29, 595–602. [Google Scholar] [CrossRef]
- Greco, C.S.; Ianiro, A.; Astarita, T.; Cardone, G. On the near field of single and twin circular synthetic air jets. Int. J. Heat Fluid Flow 2013, 44, 41–52. [Google Scholar] [CrossRef]
- Abdel–Fattah, A. Numerical and experimental study of turbulent impinging twin-jet flow. Exp. Therm. Fluid Sci. 2007, 31, 1061–1072. [Google Scholar] [CrossRef]
- Wang, C.; Wang, X.; Shi, W.; Lu, W.; Tan, S.K.; Zhou, L. Experimental investigation on impingement of a submerged circular water jet at varying impinging angles and Reynolds numbers. Exp. Therm. Fluid Sci. 2017, 89, 189–198. [Google Scholar] [CrossRef]
- Taghinia, J.; Rahman, M.M.; Siikonen, T. Numerical investigation of twin–Jet impingement with hybrid–type turbulence modeling. Appl. Therm. Eng. 2014, 73, 648–657. [Google Scholar] [CrossRef]
- Attalla, M.; Maghrabie, H.M.; Specht, E. Effect of inclination angle of a pair of air jets on heat transfer into the flat surface. Exp. Therm. Fluid Sci. 2017, 85, 85–94. [Google Scholar] [CrossRef]
- Sharif, M.A.R. Heat transfer from an isothermally heated flat surface due to twin oblique slot-jet impingement. Procedia Eng. 2013, 56, 544–550. [Google Scholar] [CrossRef] [Green Version]
- Faris, A.M.; Zulkifli, R.; Harun, Z.; Abdullah, S.; Wan Ghopa, W.A. Experimental and numerical simulation of the heat transfer enhancement on the twin impingement jet mechanism. Energies 2018, 11, 927. [Google Scholar] [CrossRef] [Green Version]
- Shih, T.-H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ϵ eddy viscosity model for high Reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Han, X.; Wray, T.J.; Agarwal, R.K. Application of a new DES model based on Wray-Agarwal turbulence model for simulation of wall-bounded flows with separation. In Proceedings of the 47th AIAA Fluid Dynamics Conference, Denver, CO, USA, 5–9 June 2017; AAIA: Reston, VA, USA, 2017; p. AIAA2017-3966. [Google Scholar]
- Turbulence Modeling Resource. Available online: https://www.turbmodels.larc.nasa.gov/wray_agarwal.html (accessed on 22 September 2019).
- Wray Agarwal Models. Available online: https://www.github.com/xuhanwustl/WrayAgarwalModels (accessed on 14 August 2019).











© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Agarwal, R.K. Numerical Simulation of Fountain Formation due to Normal and Inclined Twin-Jet Impingement on Ground. Fluids 2020, 5, 132. https://doi.org/10.3390/fluids5030132
Zhang X, Agarwal RK. Numerical Simulation of Fountain Formation due to Normal and Inclined Twin-Jet Impingement on Ground. Fluids. 2020; 5(3):132. https://doi.org/10.3390/fluids5030132
Chicago/Turabian StyleZhang, Xiang, and Ramesh K. Agarwal. 2020. "Numerical Simulation of Fountain Formation due to Normal and Inclined Twin-Jet Impingement on Ground" Fluids 5, no. 3: 132. https://doi.org/10.3390/fluids5030132





