NARMAX Identification Based Closed-Loop Control of Flow Separation over NACA 0015 Airfoil
Abstract
:1. Introduction
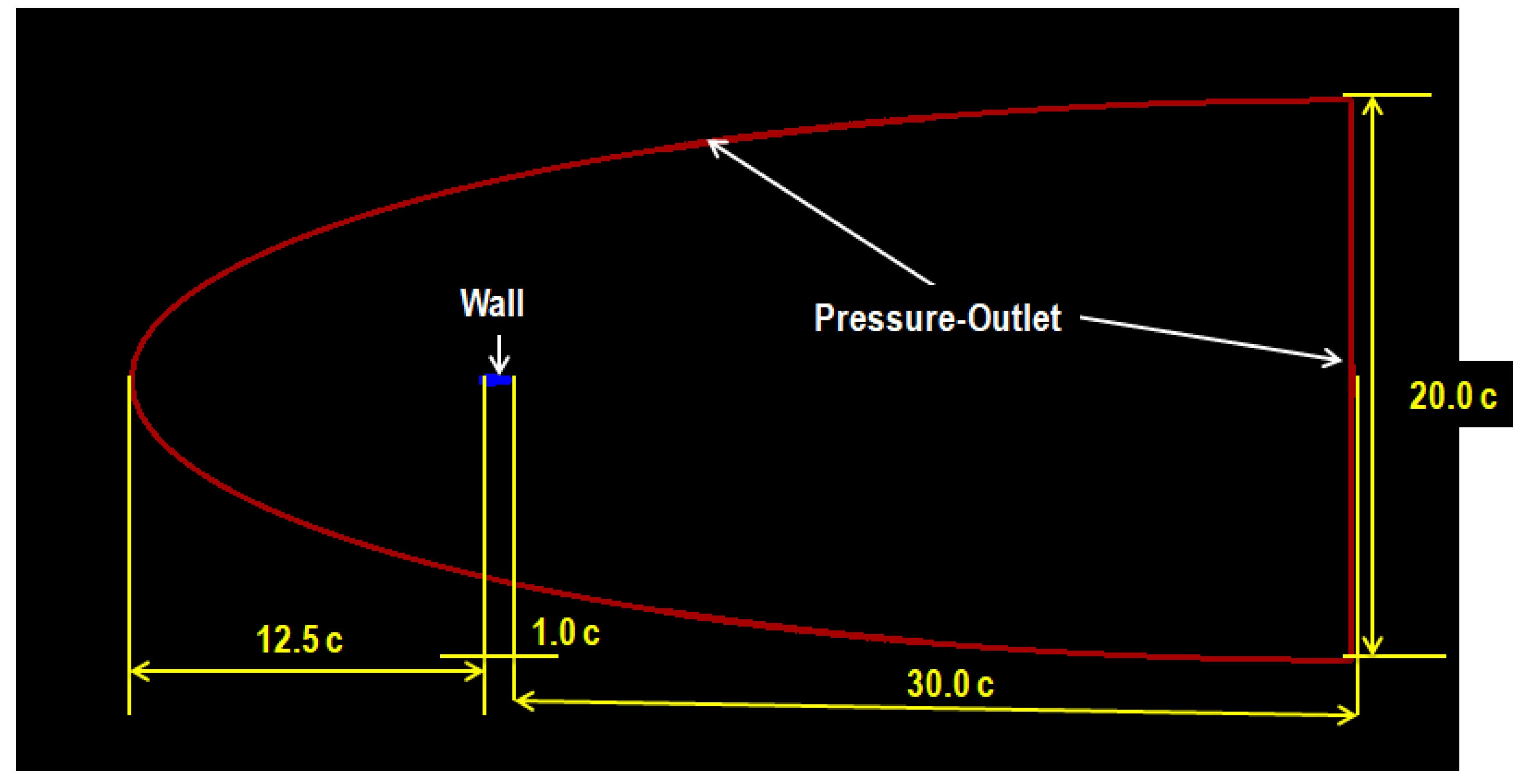
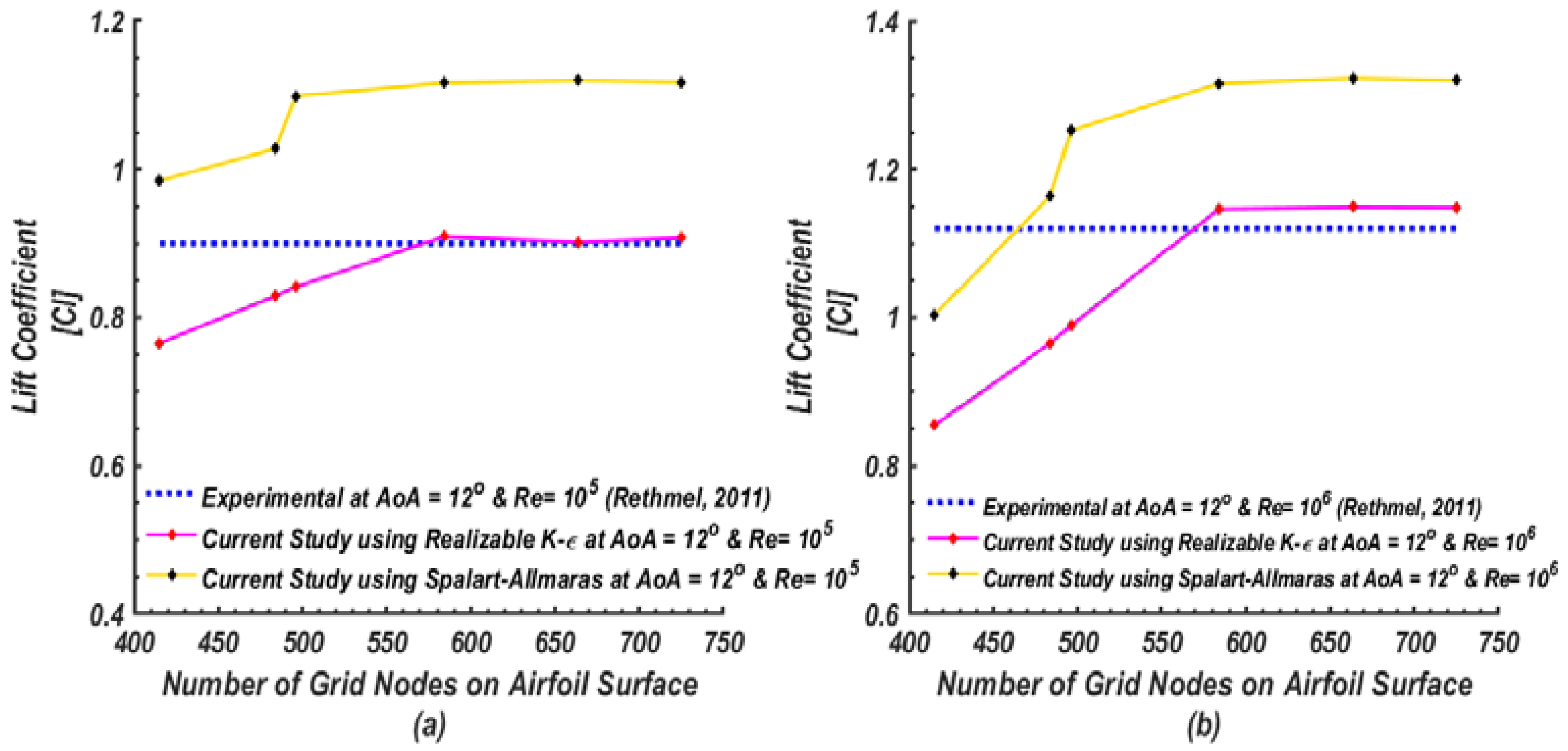
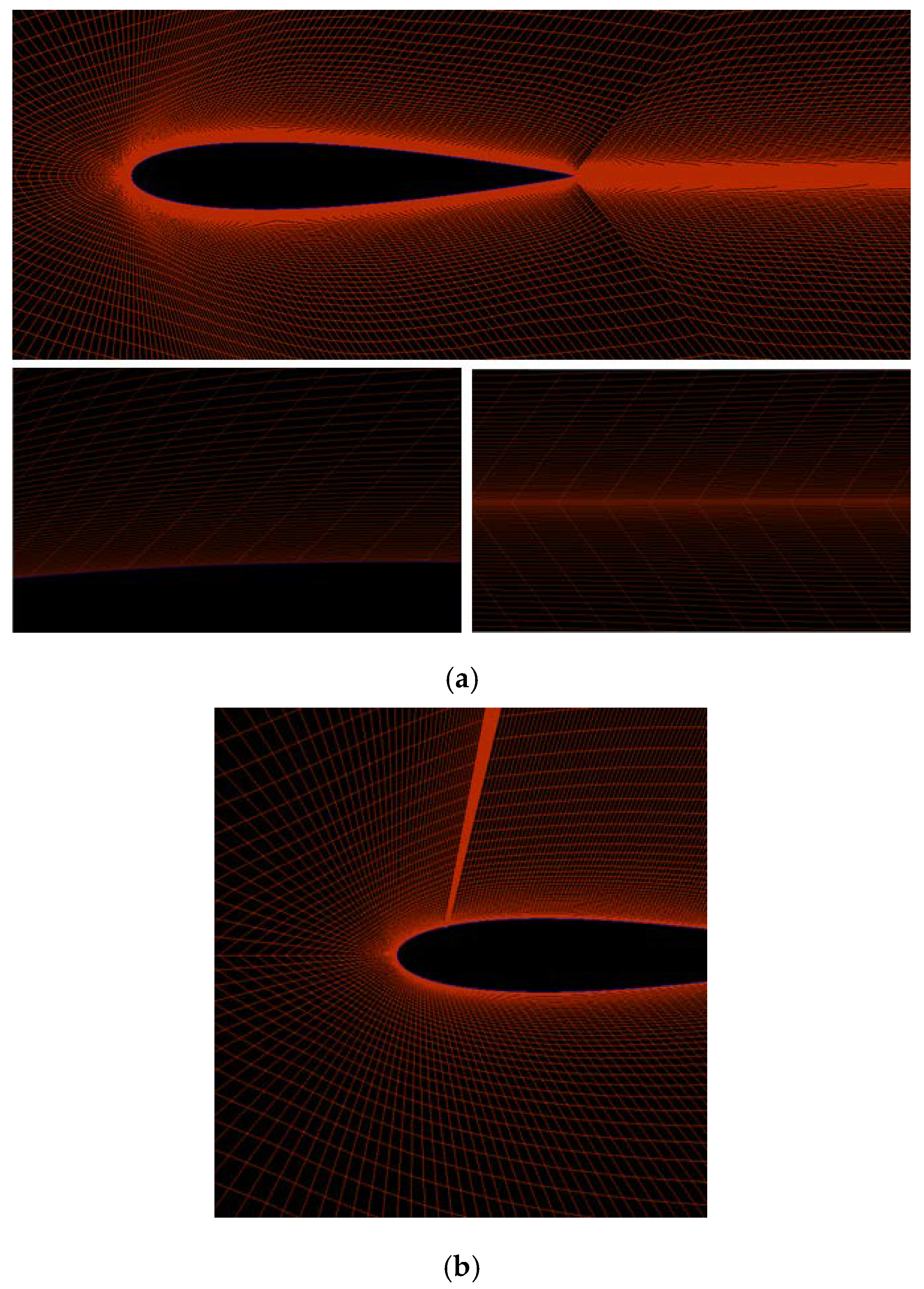
2. Numerical Simulation of Flow over the NACA 0015 Airfoil
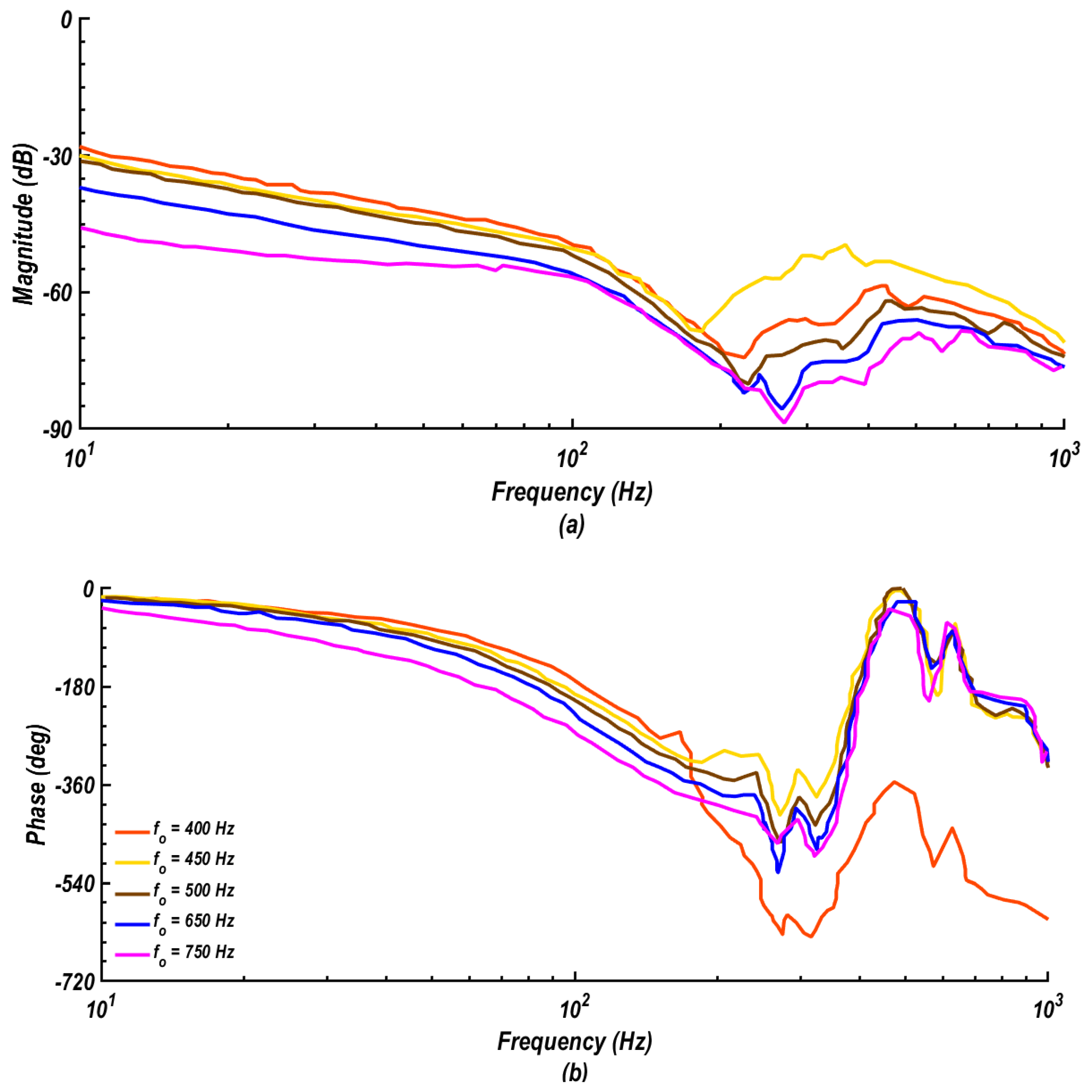
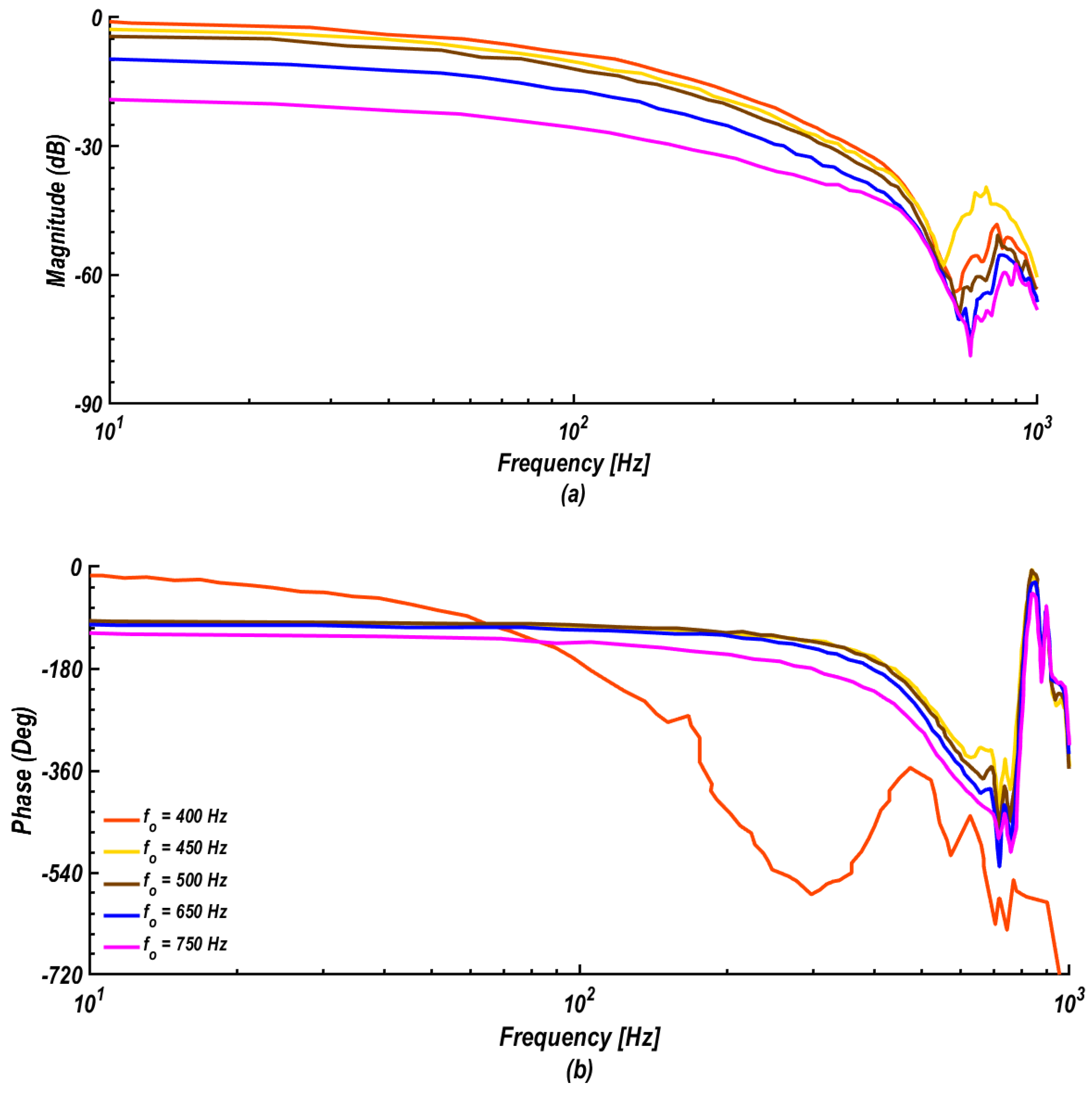
3. NARMAX Identification of Flow over an Airfoil
4. Flow Control Problem
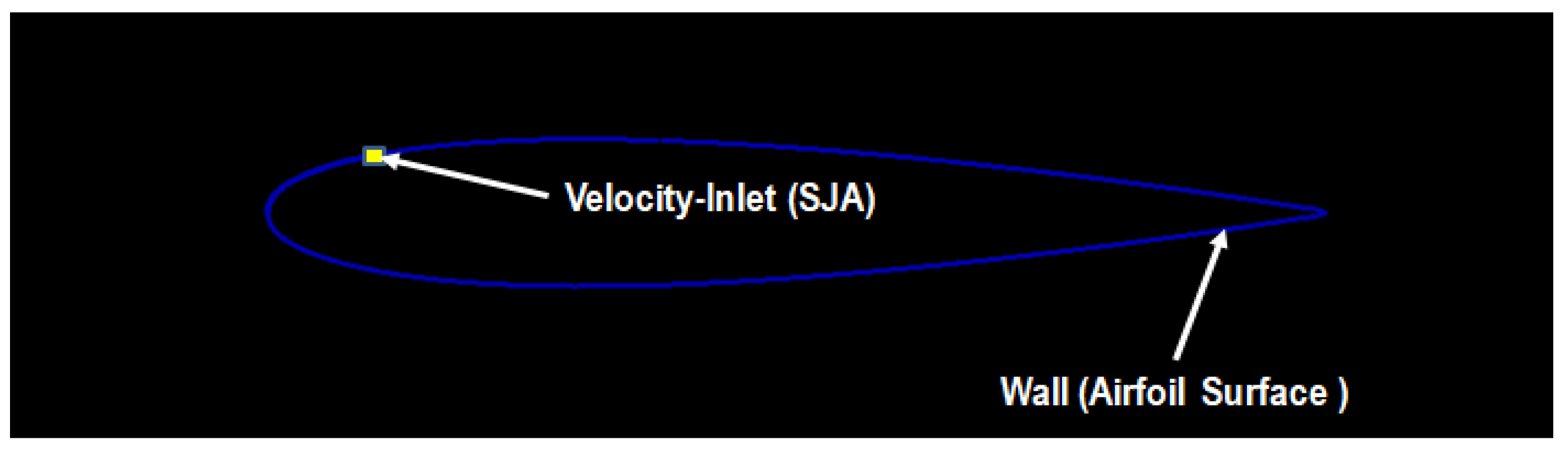
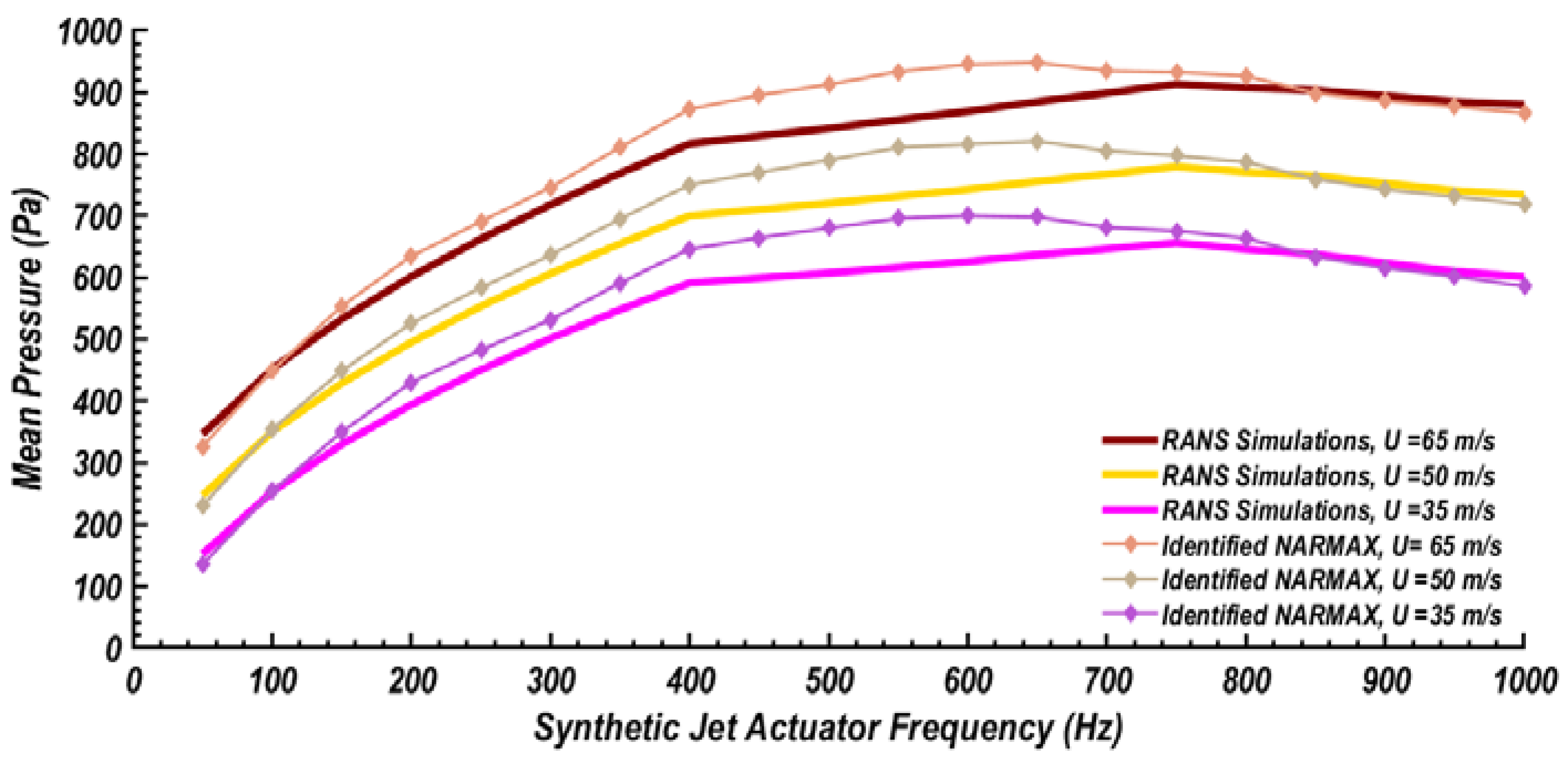
5. Modeling of Synthetic Jet Actuators
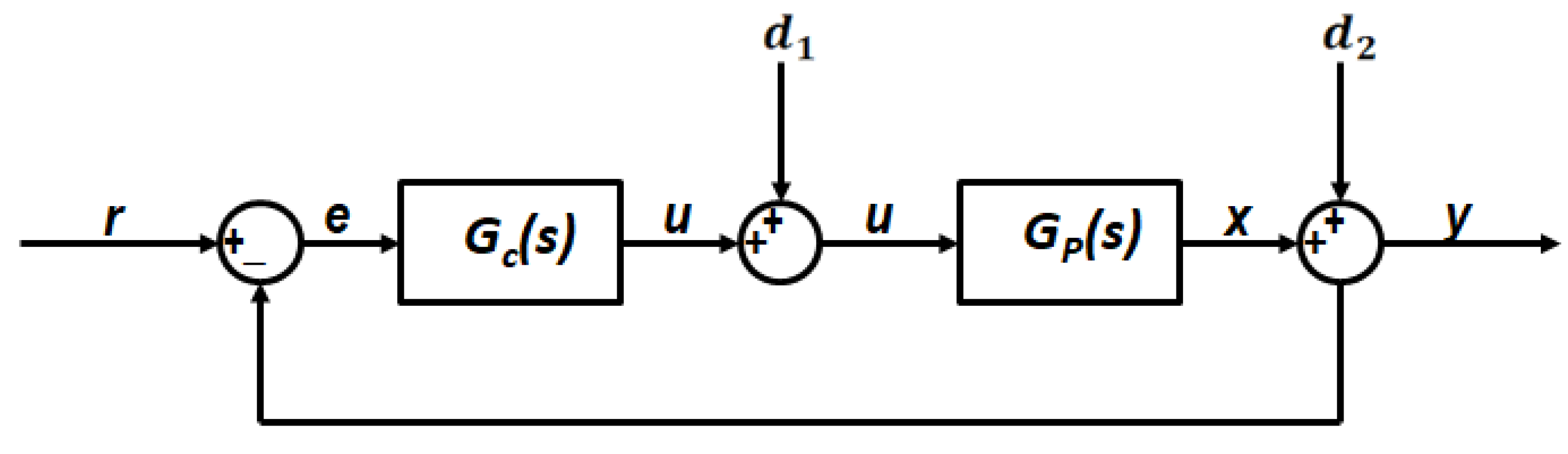
6. Feedback Controller Design and Performance
6.1. Open-Loop Control
6.2. Closed Loop Control
6.3. Closed-Loop Control Results
7. Conclusions
- ▪
- The k-ε model was found to be an acceptable turbulence model for predicting the airflow around an airfoil at different angles of attack.
- ▪
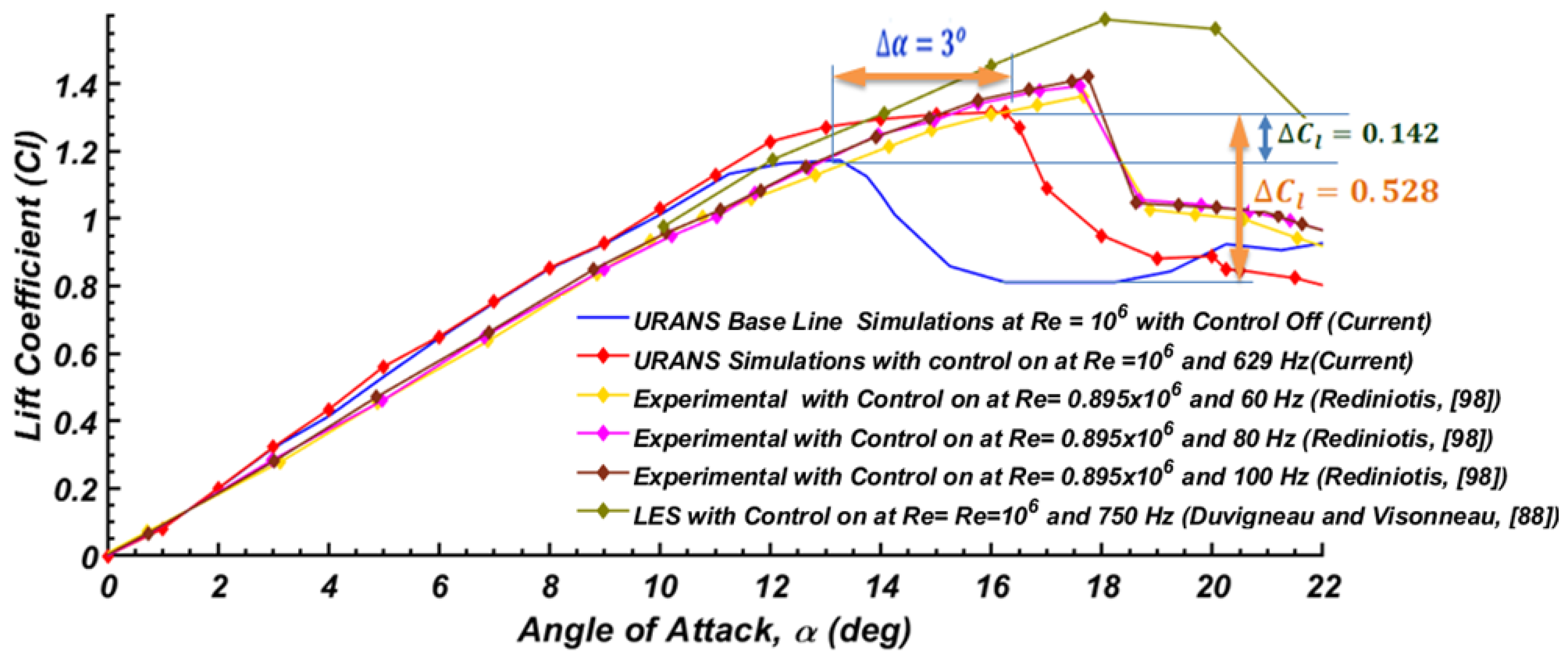
- An increase in the angle of attack led to the increase of the lift coefficient until the maximum of 1.15 at α = 13° is reached. The lift coefficient then sharply dropped for further increase in the angle of attack. Before stall, The slope of the lift versus incidence angle,, was approximately a constant at about before the stall. After the stall incident angle, decreased significantly, leading to a lift coefficient of 0.79 at α = 17°.
- ▪
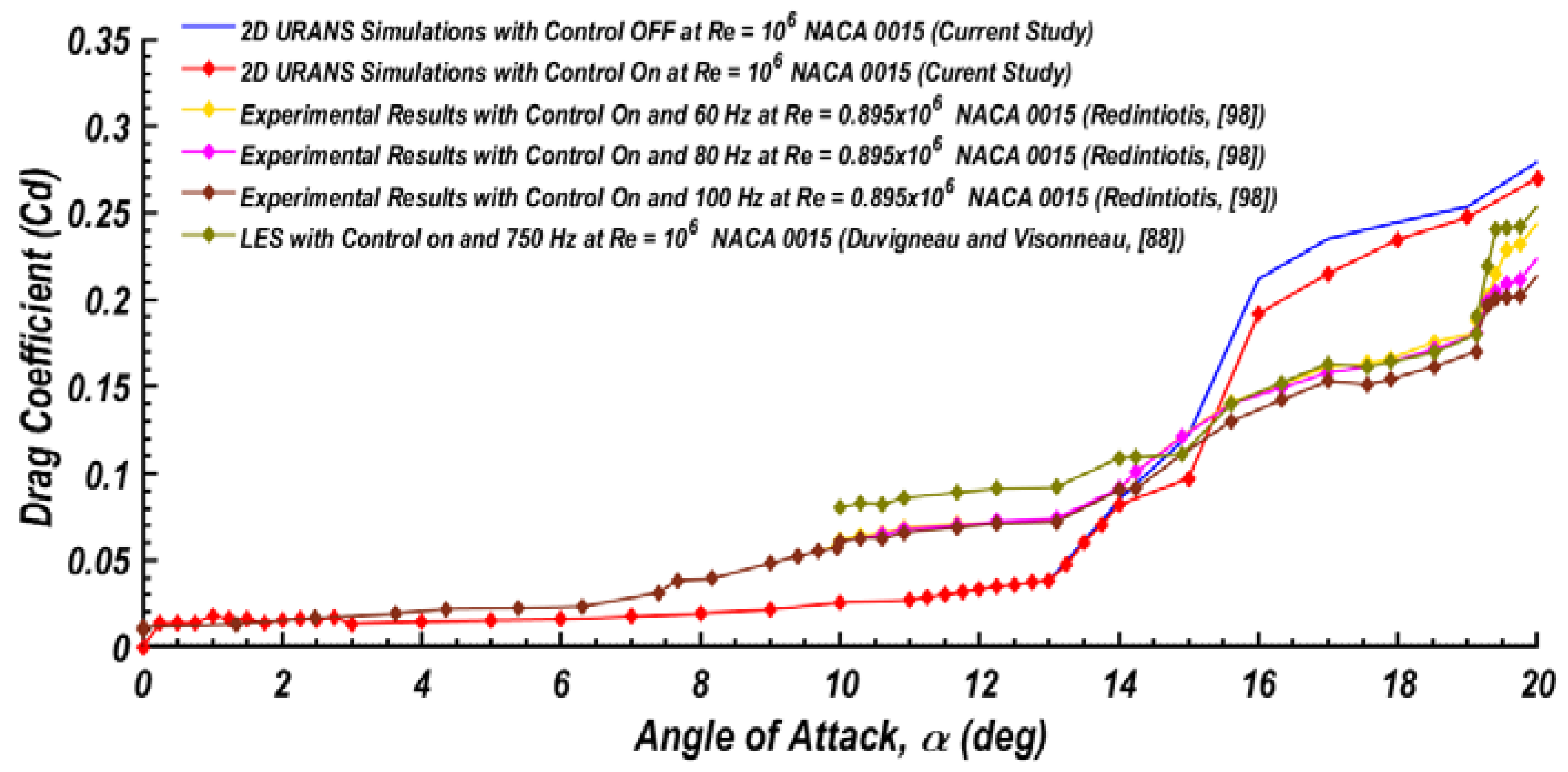
- At zero angles of attack, the drag coefficient was small but increased gradually with to 0.038 at the stall condition. The slope of the drag variation with the angle of attack, , was approximately constant at about 0.003. After the stall condition, the drag increased sharply with the increase of the incident angle of attack to attain a value of 0.28 at = 20°. The slope of the drag against the angle of attack, , increases to 0.04 after the stall condition.
- ▪
- The simulation results showed that synthetic jets are a suitable means to suppress flow separation.
- ▪
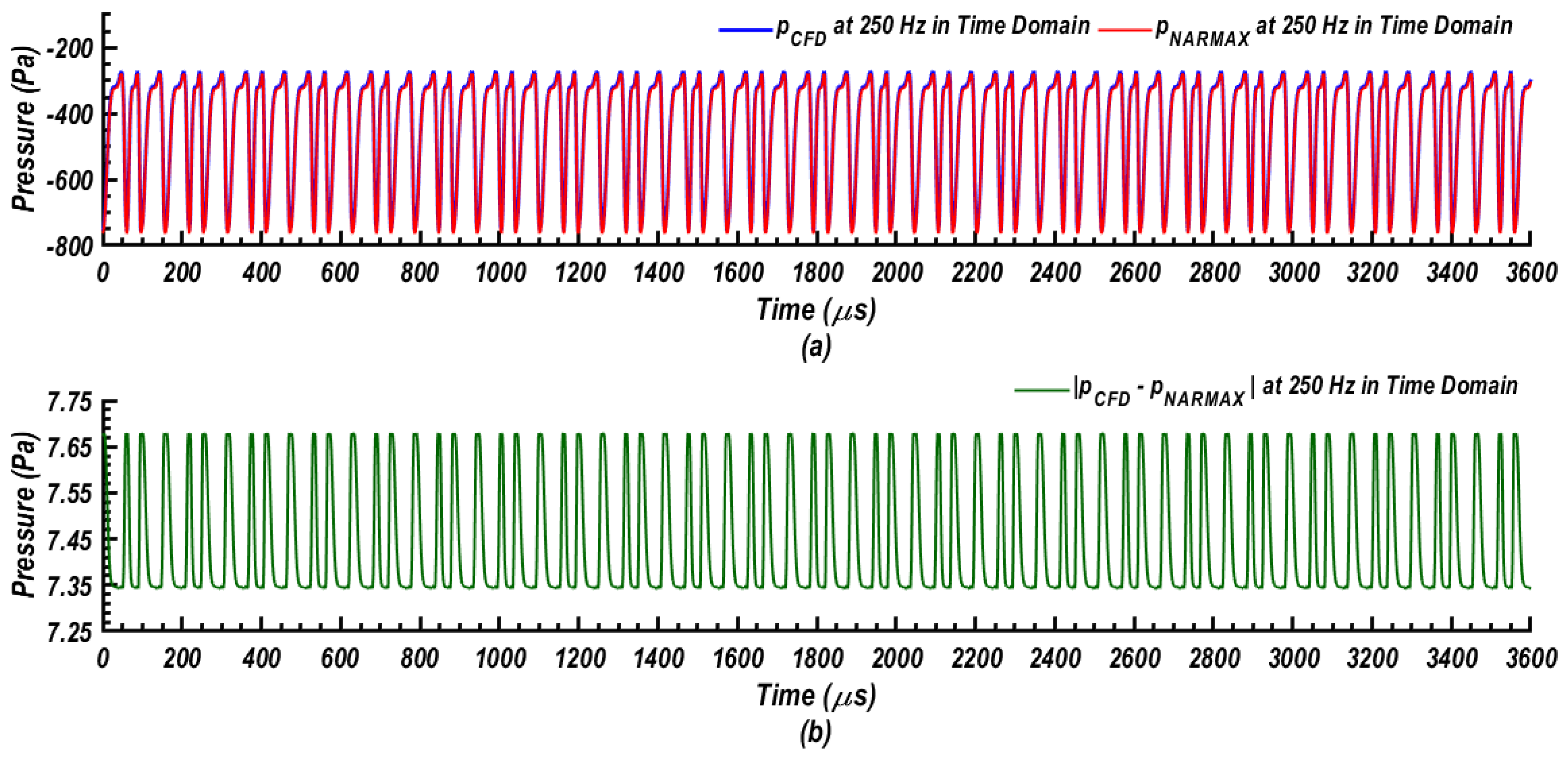
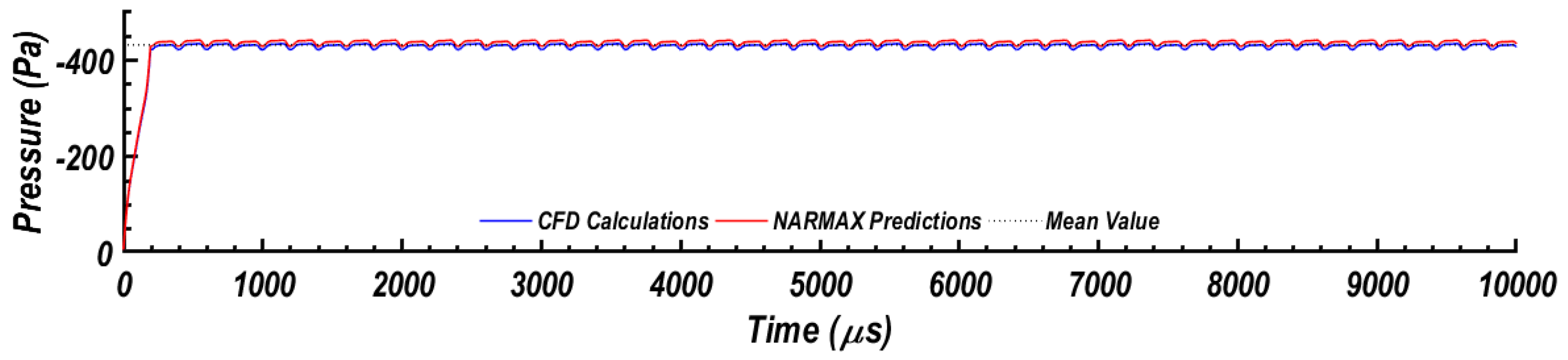
- At an attack angle of 16° and the flow Reynolds number of 106, the NARMAX identification found as a powerful tool for modeling the mean static pressure signal. Identified static pressure matches well with the URANS simulation results. The associated differences were found to be within 9%.
- ▪
- The Low-pass filtering approach utilized in the controller design facilitated treat the system as a quasi-linear in the frequency domain. The sinusoidal input describing function applied in the frequency domain analysis assisted in applying the linear control theories.
- ▪
- A standard proportional-integral (PI) algorithm for the single-input single-output system was designed based on a reference signal that was determined during the open-loop performance of the plant at the conditions corresponding to a fully re-attached flow.
- ▪
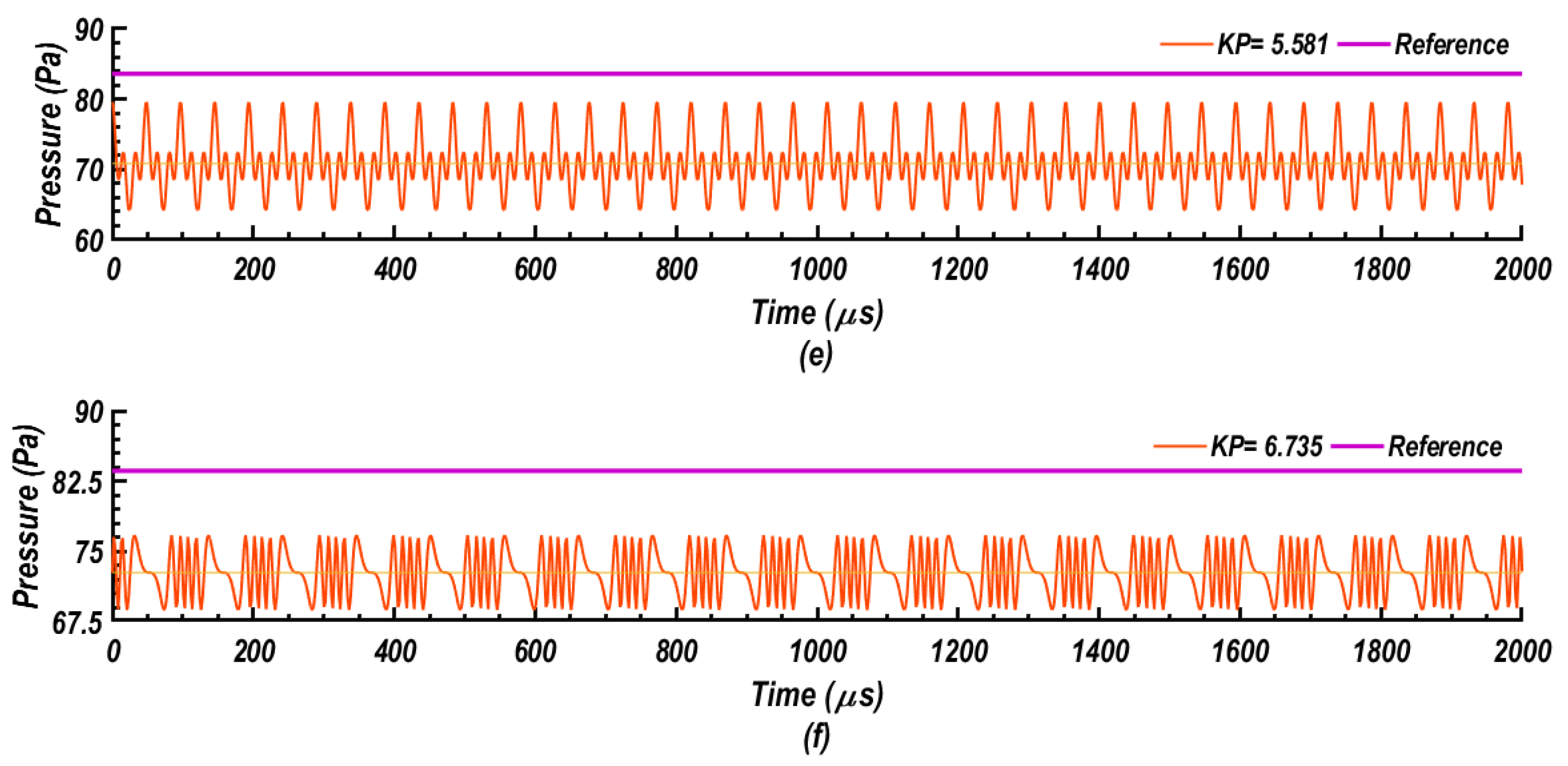
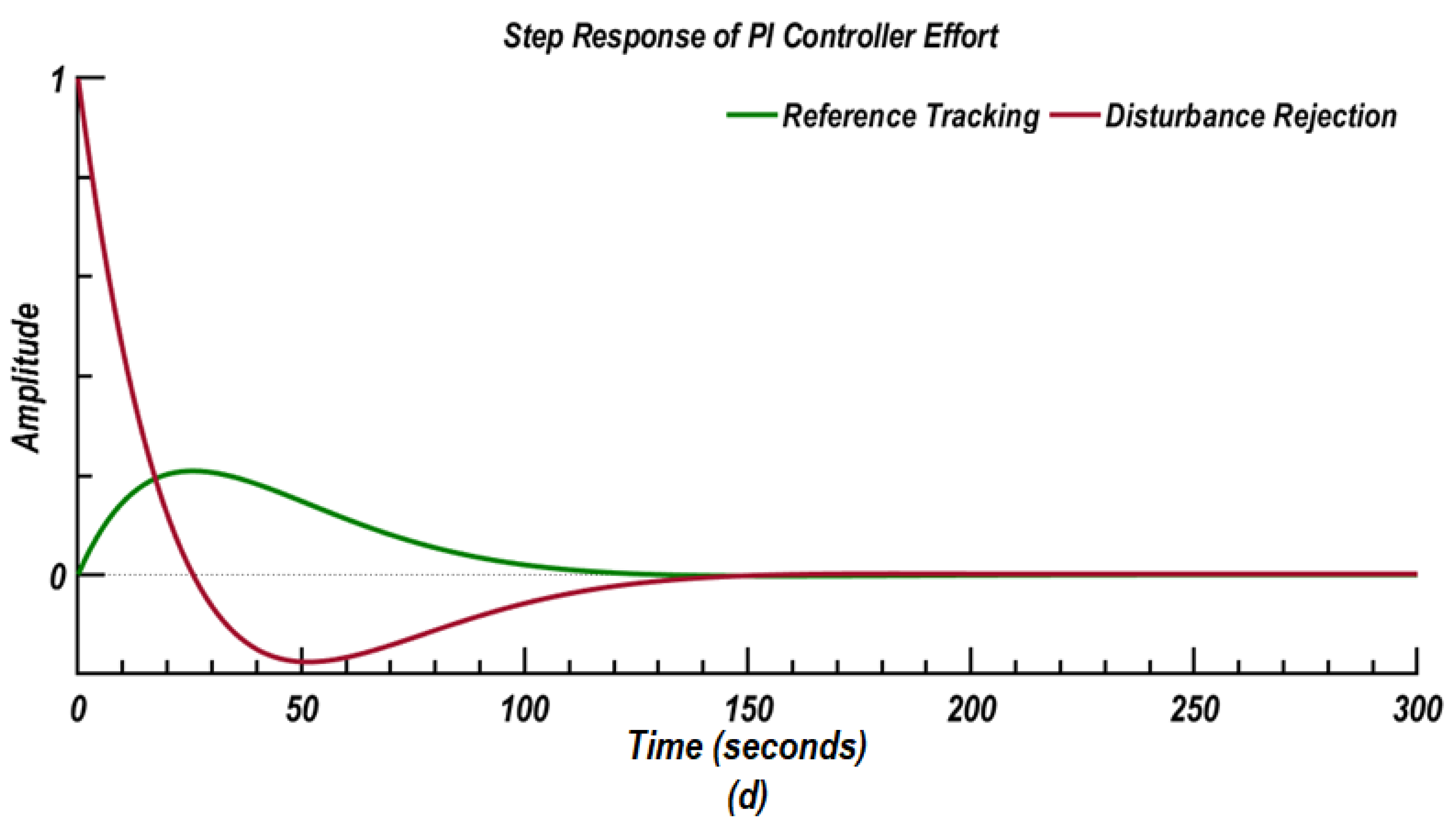
- When inspected for different values of proportional gain (KP) and integral gain (KI), the proposed closed-loop controller with KP = 3.27 and KI = 0.083 is found to be efficient for both reference tracking and disturbance rejection for open-loop and closed-loop modes.
- ▪
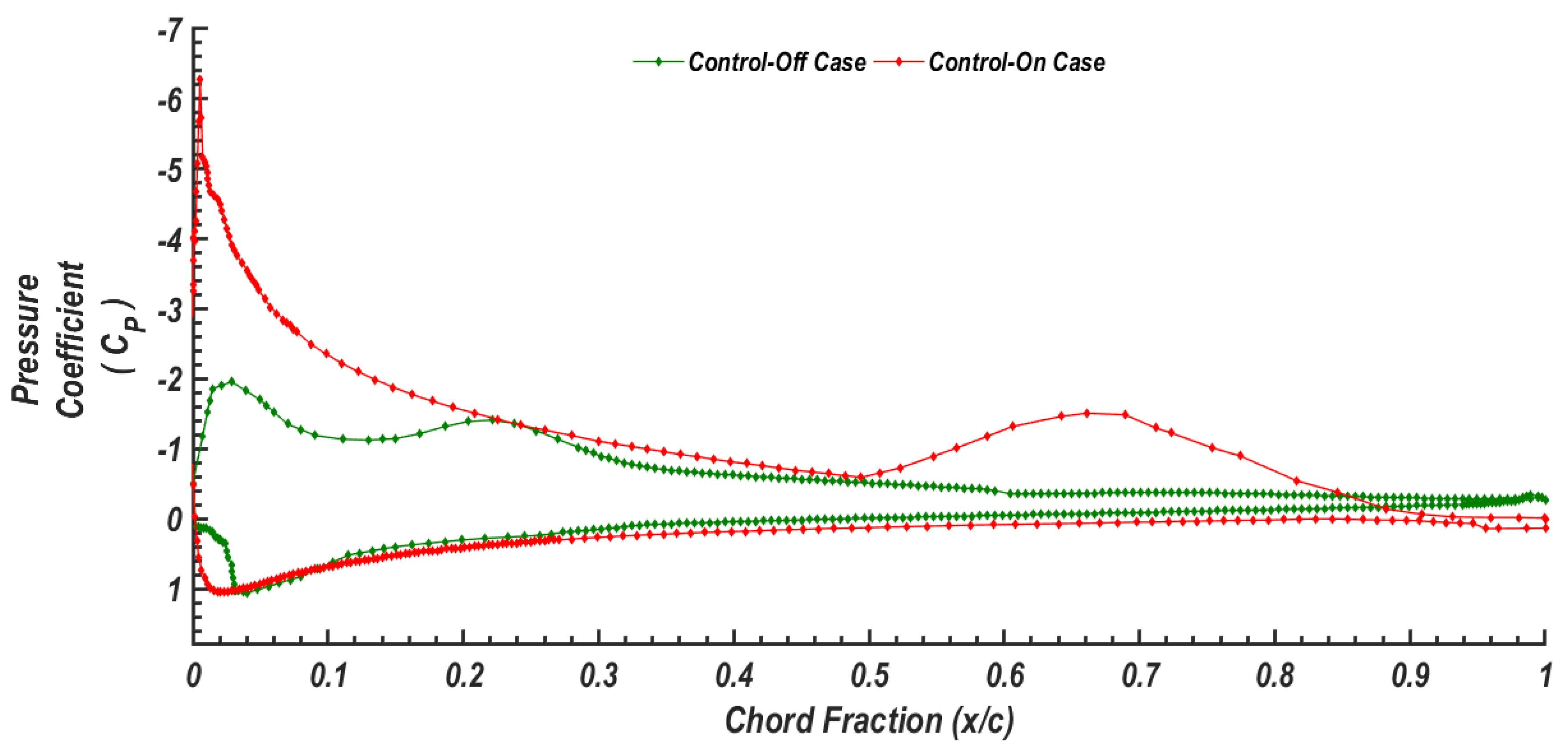
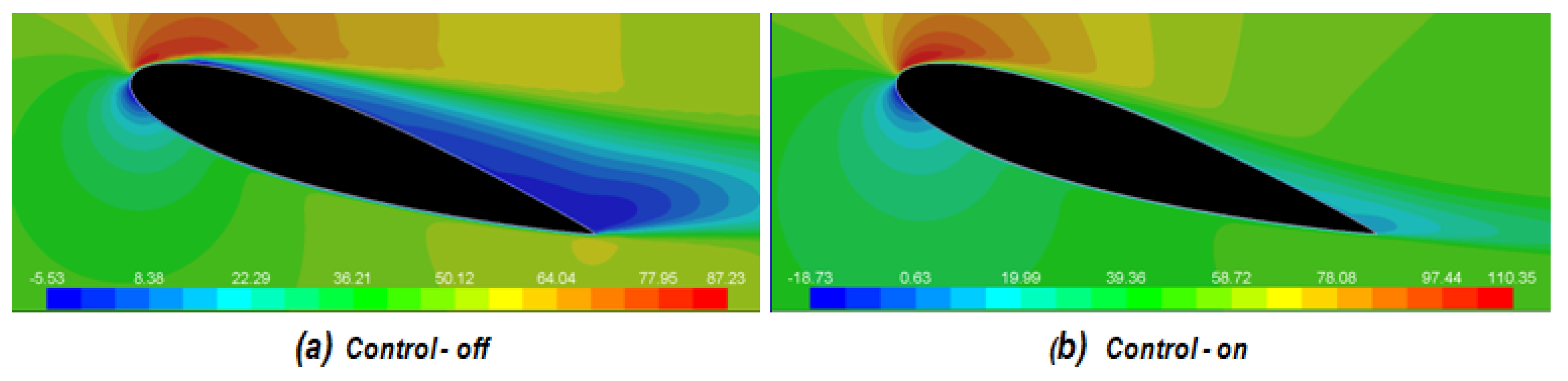
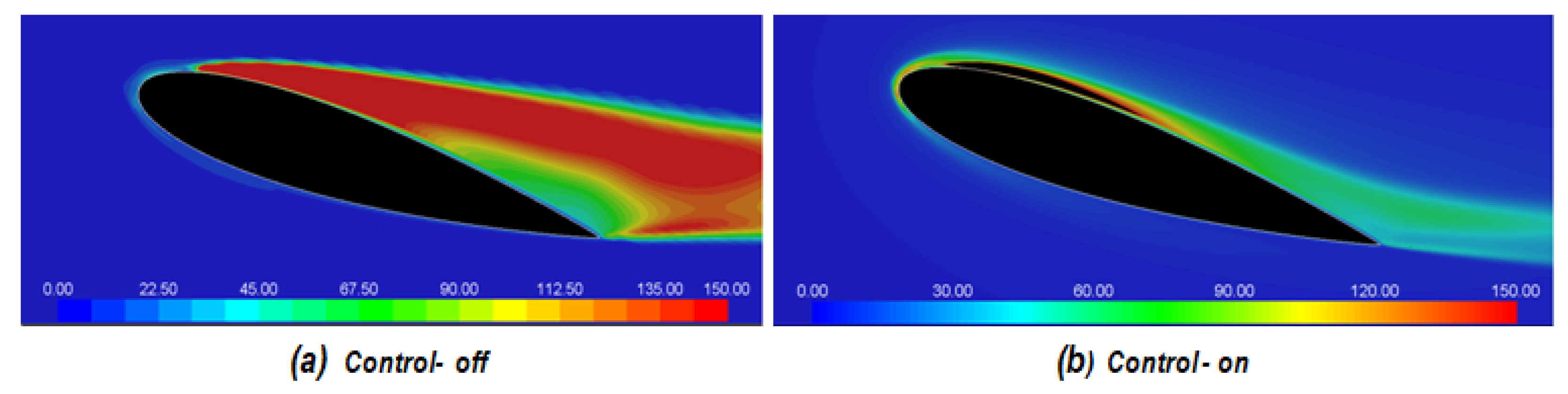
- Flow features around the NACA 0015 airfoil were significantly improved for the control-on state. This is clearly seen by comparing contours of static pressure, x-velocity, and turbulence kinetic energy around the airfoil at AoA = 16° for the control-off state with those of control-on state. For the control-on case, the flow separation regions over the airfoil upper surface were found to reduce significantly. The turbulence kinetic energy was also much reduced by the activation of the synthetic jet actuators. At AoA = 16°, the lift coefficient increased by about 67% and the stall angle of attack increase by 3°.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Control Terminology
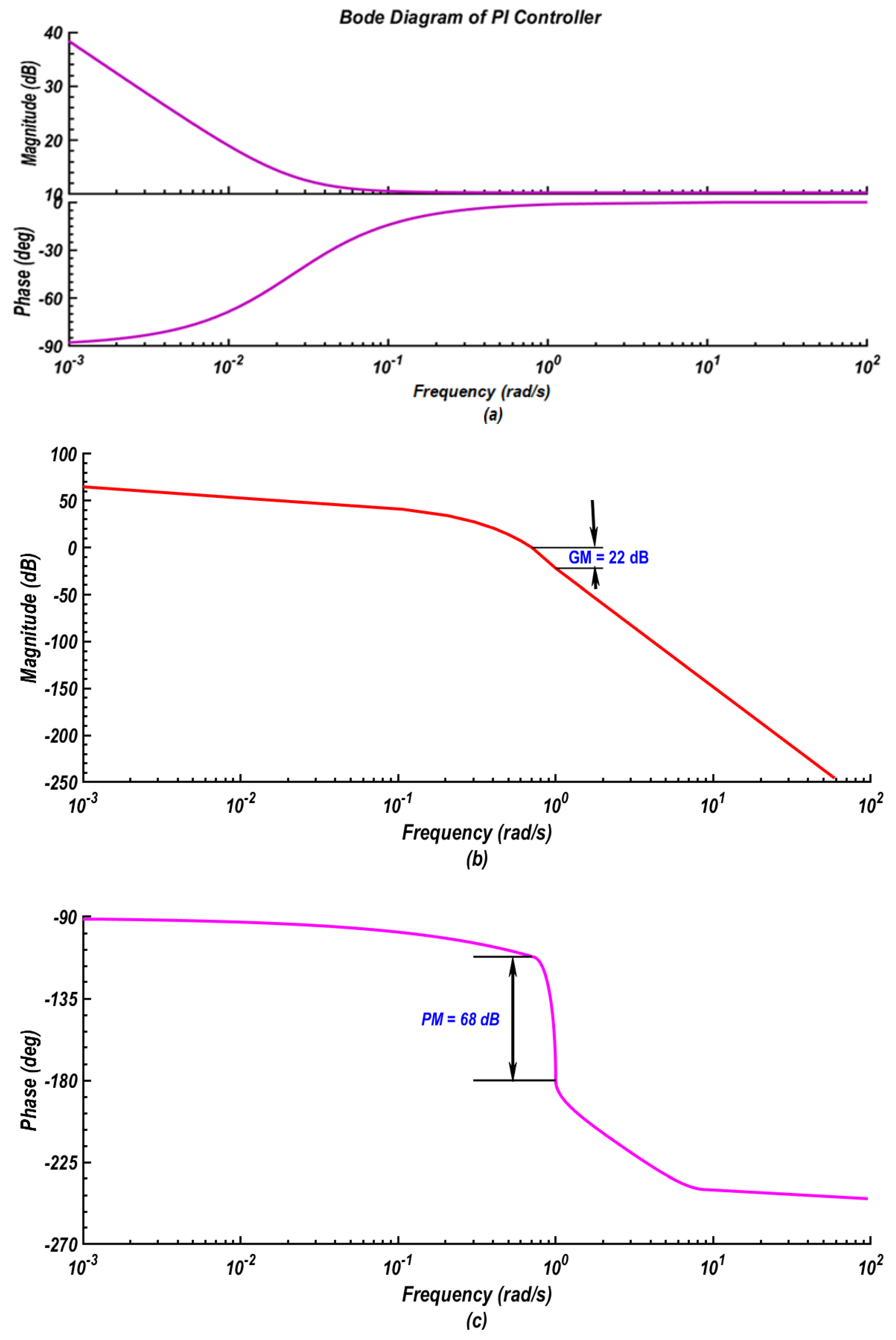
Appendix A.2. Single Degree of Freedom PI Controller (1-DOF PI) Analysis
- ▪
- Open-loop transfer function which defined by
- ▪
- Closed-loop system reference tracking (from r to y), which is called the complementary sensitivity function:
- ▪
- Closed-loop system noise sensitivity function used for controller action (effort) calculations due to limitations caused by practical constraints, such as controller saturation (from r to y),
- ▪
- Closed-loop system response to a load disturbance (for a step disturbance at the plant input,) (from to y), which is called the load disturbance sensitivity functionand
- ▪
- Closed-loop system response to a step disturbance at plant output, .which is called the sensitivity function (from to y)
References
- Gad-El-Hak, M. Flow Control: The Future. J. Aircr. 2001, 38, 402–418. [Google Scholar] [CrossRef]
- Simpson, R.L. Turbulent Boundary-Layer Separation. Annu. Rev. Fluid Mech. 1998, 21, 205–232. [Google Scholar] [CrossRef]
- Benard, N.; Cattafesta, L.N.; Moreau, E.; Griffin, J.; Bonnet, J.-P. On the benefits of hysteresis effects for closed-loop separation control using plasma actuation. Phys. Fluids 2011, 23, 083601. [Google Scholar] [CrossRef]
- Mabe, J.H.; Calkins, F.T.; Wesley, B.; Woszidlo, R.; Taubert, L.; Wygnanski, I. Single Dielectric Barrier Discharge Plasma Actuators for Improved Airfoil Performance. J. Aircr. 2009, 46, 847–855. [Google Scholar] [CrossRef]
- Huebsch, W.W.; Gall, P.D.; Hamburg, S.; Rothmayer, A.P. Dynamic Roughness as a Means of Leading-Edge Separation Flow Control. J. Aircr. 2012, 49, 108–115. [Google Scholar] [CrossRef]
- Schrauf, G. Application of Laminar Flow Technology on Transport Aircraft. In Proceedings of the CEAS Drag Reduction Conference, Potsdam, Germany, 3–5 June 2000; pp. 19–21. Available online: https://ntrs.nasa.gov/search.jsp?R=19780019127-2020-01-26T01:38:49+00:00Z (accessed on 17 May 2019).
- Joslin, R.D.; Miller, D.N. (Eds.) Fundamentals and Applications of Modern Flow Control; American Institute of Aeronautics and Astronautics (AIAA): Reston, VA, USA, 2009; Volume 231, pp. 1–20. [Google Scholar] [CrossRef]
- Cattafesta, L.; Song, Q.; Williams, D.R.; Rowley, C.W.; Alvi, F.S. Active control of flow-induced cavity oscillations. Prog. Aerosp. Sci. 2008, 44, 479–502. [Google Scholar] [CrossRef]
- Williams, D.R.; MacMynowski, D. Brief History of Flow Control Fundamentals and Applications of Modern Flow Control; AIAA: Reston, VA, USA, 2008; Chapter 1; pp. 1–20. [Google Scholar] [CrossRef]
- Bechert, D.W.; Bruse, M.; Hage, W.; Van Der Hoeven, J.T.; Hoppe, G. Experiments on drag-reducing surfaces and their optimization with an adjustable geometry. J. Fluid Mech. 1997, 338, 59–87. [Google Scholar] [CrossRef]
- Fisher, D.; Cobleigh, B.; Banks, D.; Hall, R.; Wahls, R. Reynolds number effects at high angles of attack. In Proceedings of the 20th AIAA Advanced Measurement and Ground Testing Technology Conference, Albuquerque, NM, USA, 15–18 June 1998. [Google Scholar] [CrossRef] [Green Version]
- Kaplanski, F.; Kartushinsky, A.; Hussainov, M.; Rudi, U.; Konhen, G.; Rüger, M. Some Experimental and Numerical Investigations of Flow near the Riblet Surfaces. In Proceedings of the 9th Workshop on Two-phase Flow Predictions, Merseburg, Germany, 13–16 April 1999; pp. 226–231. Available online: https://wwwresearchgate.net/publication/278242403 (accessed on 12 August 2019).
- Kaplanski, F.; Hussainov, M.; Kartushinsky, A.; Rudi, Ü. Flow near the Hemispherical Depressions. J. Mech. Behav. Mater. 2000, 11, 407–417. [Google Scholar] [CrossRef]
- Hussainov, M.; Kartushinsky, A.; Rudi, Ü.; Shcheglov, I.; Kohnen, G.; Sommerfeld, M. Experimental investigation of turbulence modulation by solid particles in a grid-generated vertical flow. Int. J. Heat Fluid Flow 2000, 21, 365–373. [Google Scholar] [CrossRef]
- Hussainov, M.; Kartushinsky, A.; Rudi, U.; Shcheglov, I.; Tisler, S. Experimental Study of the Effect of Velocity Slip and Mass Loading on the Modification of Grid-Generated Turbulence in Gas-Solid Particles Flows. Proc. Estonian Acad. Sci. Eng. 2005, 11, 169–180. [Google Scholar]
- Noack, B.; Morzyński, M.; Tadmor, G. Reduced Order Modeling for Flow Control; Springer Wien New York: Udine, Italy, 2011; Available online: https://www.springerprofessional.de/en/reduced-order-modelling-for-flow-control/4427676 (accessed on 8 February 2019).
- Bushnell, D.M. Turbulence Sensitivity and Control in Wall Flows. In Theoretical Approaches to Turbulence; Springer: New York, NY, USA, 1985. [Google Scholar] [CrossRef]
- Lumley, J.; Blossey, P. Control of Turbulence. Annu. Rev. Fluid Mech. 1998, 30, 311–327. [Google Scholar] [CrossRef]
- Cattafesta, L.; Sheplack, M. Actuators and Sensors. In Fundamentals and Applications of Modern Flow Control; AIAA: Reston, VA, USA, 2008; Chapter 6; pp. 149–176. [Google Scholar] [CrossRef]
- Mathew, J.; Song, Q.; Sankar, B.; Sheplak, M.; Cattafesta, L.N., III. Optimized Design of Piezoelectric Flap Actuators for Active Flow Control. AIAA J. 2006, 44, 2919–2928. [Google Scholar] [CrossRef]
- Wong, C.; Kontis, K. Flow Control by Spanwise Blowing on a NACA 0012. J. Aircr. 2007, 44, 337–340. [Google Scholar] [CrossRef]
- Eldredge, R.; Bons, J. Active Control of a Separating Boundary Layer with Steady Vortex Generating Jets–Detailed Flow Measurements. In Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 5–8 January 2004. [Google Scholar] [CrossRef]
- Shan, H.; Jiang, L.; Liu, C.; Love, M.; Maines, B. Numerical study of passive and active flow separation control over a NACA0012 airfoil. Comput. Fluids 2008, 37, 975–992. [Google Scholar] [CrossRef]
- Seifert, A.; Greenblatt, D.; Wygnanski, I.J. Active separation control: An overview of Reynolds and Mach numbers effects. Aerosp. Sci. Technol. 2004, 8, 569–582. [Google Scholar] [CrossRef]
- Amitay, M.; Glezer, A. Controlled transients of flow reattachment over stalled airfoils. Int. J. Heat Fluid Flow 2002, 23, 690–699. [Google Scholar] [CrossRef]
- Seifert, A.; Darabi, A.; Wyganski, I. Delay of airfoil stall by periodic excitation. J. Aircr. 1996, 33, 691–698. [Google Scholar] [CrossRef]
- Billings, S.A.; Leontaritis, I.J. Parameter Estimation Techniques for Non-linear Systems. In Proceedings of the 6th IFAC Symposium on System Identification and Parameter Estimation, Washington, DC, USA, 7–11 June 1982; pp. 505–510. [Google Scholar] [CrossRef]
- Nishizawa, A.; Takagi, S.; Abe, H.; Kikushima, Y.; Maeda, R.; Yoshida, H. Toward Smart Control of Separation around Wing-part 1. In Proceedings of the 5th Symposium of Smart Control of Turbulence, Tokyo, Japan, 2–5 March 2005. [Google Scholar] [CrossRef]
- Nishizawa, A.; Takagi, S.; Abe, H.; Segawa, T.; Yoshida, H. Smart Control of Separation around a Wing–Control System. In Proceedings of the 6th Symposium of Smart Control of Turbulence, Tokyo, Japan, 6–9 March 2005; pp. 1–8. Available online: https://www.nmri.go.jp/oldpages/turbulence/PDF/symposium/FY2003/Nishizawa.pdf (accessed on 15 January 2020).
- Abe, H.; Segawa, T.; Kikushima, Y.; Pang, J.; Yoshida, H.; Nishizawa, A.; Takagi, S. Smart Control of Separation around a Wing—Control Device. In Proceedings of the 6th Symposium, Smart Control of Turbulence, Tokyo, Japan, 2–5 March 2005; Available online: https://www.nmri.go.Jp/oldpages2/turbulence/PDF/symposium/FY2004/Abe.pdf (accessed on 15 January 2020).
- Segawa, T.; Yoshida, H.; Nishizawa, A.; Murakami, K.; Mizunuma, H. Sensors and Actuators for Smart Control of Separation. In Proceedings of the Theoretical and Applied Mechanics, Tokyo Japan, 12–17 March 2003; Volume 52, pp. 117–125. Available online: https://www.jstage.jst.go.jp/article/nctam/52/0/52_0_117/_article/-char/ja (accessed on 2 January 2020).
- Tian, Y.; Cattafesta, L.; Mittal, R. Adaptive Control of Separated Flow. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006; pp. 1401–1411. [Google Scholar] [CrossRef] [Green Version]
- Tian, Y.; Song, Q.; Cattafesta, L. Adaptive Feedback Control of Flow Separation. In Proceedings of the 3rd AIAA Flow Control Conference, San Francisco, CA, USA, 5–8 June 2006. [Google Scholar] [CrossRef] [Green Version]
- Song, Q.; Tian, Y.; Cattafesta, L. MIMO Feedback Control of Flow Separation. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007. [Google Scholar] [CrossRef]
- Pinier, J.; Ausseur, J.M.; Glauser, M.N.; Higuchi, H. Proportional Closed-Loop Feedback Control of Flow Separation. AIAA J. 2007, 45, 181–190. [Google Scholar] [CrossRef]
- Ausseur, J.; Pinier, J.; Glauser, M. Estimation Techniques in a Turbulent Flow Field. In Proceedings of the 37th AIAA Fluid Dynamics Conference and Exhibit, Miami, FL, USA, 25–28 June 2007; Available online: https://www.researchgate.net/publication/259676298 (accessed on 19 December 2019).
- Becker, R.; King, R.; Petz, R.; Nitsche, W. Adaptive Closed-Loop Separation Control on a High-Lift Configuration Using Extremum Seeking. AIAA J. 2007, 45, 1382–1392. [Google Scholar] [CrossRef]
- Allan, B.; Juang, J.; Raney, D.; Seifert, A.; Pack, L.; Brown, D. Closed-Loop Separation Control Using Oscillatory Flow Excitation; NACA/CR, Technical Report; NACA Langley Research Center: Hampton, VA, USA, 2000; pp. 1–24. Available online: https://www.researchgate.net/publication/24301862 (accessed on 2 January 2020).
- Becker, R.; Garwon, M.; Gutknecht, C.; Bärwolff, G.; King, R. Robust control of separated shear flows in simulation and experiment. J. Process. Control. 2005, 15, 691–700. [Google Scholar] [CrossRef]
- Henning, L.; King, R. Multivariable Closed-Loop Control of the Reattachment Length Downstream of a Backward-Facing Step. In Proceedings of the 16th International IFAC World Congress, Praha, Czech Republic, 4–8 July 2005. [Google Scholar] [CrossRef]
- Becker, R.; King, R. Comparison of a robust and a flatness based control for a separated shear flow. In Proceedings of the 16th International IFAC World Congress, Praha, Czech Republic, 4–8 July 2005. [Google Scholar] [CrossRef]
- Duvigneau, R.; Visonneau, M. Optimization of a synthetic jet actuator for aerodynamic stall control. Comput. Fluids 2006, 35, 624–638. [Google Scholar] [CrossRef] [Green Version]
- Bourgois, P.R. Closed-Loop Proportional Controller for Flow Separation on ONERA Airfoil; CNRS UMR 7128; ONERA Publications: Toulouse, France, 2009; pp. 1–34. Available online: https://www.imft.fr/IMG/pdf/liste_des_publications_2005_2009_imft.pdf (accessed on 2 March 2019).
- Cattafesta, L.; Tian, Y.; Mittal, R. Adaptive Control of Post-Stall Separated Flow Application to Heavy Vehicles. In The Aerodynamics of Heavy Vehicles II: Trucks, Buses, and Trains, Lecture Notes in Applied and Computational Mechanics Fracture Mechanics; Springer: Berlin/Heidelberg, Germany, 2009; Volume 41, pp. 151–160. Available online: https://www.researchgate.net/publication/227108242 (accessed on 2 March 2019).
- Cho, Y.C.; Fledderjohn, M.; Holzel, M.; Jayaraman, B.; Santillo, M.; Bernstein, D.S.; Shyy, W. Adaptive Flow Control of Low Reynolds Number Aerodynamics Using a Dielectric Barrier Discharge Actuator. In Proceedings of the 47th AIAA Aerospace Sciences Meeting Including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. [Google Scholar] [CrossRef] [Green Version]
- Taira, K.; Rowley, C.W.; Colonius, T. Feedback Control of High-Lift State for a Low-Aspect-Ratio Wing. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010. [Google Scholar] [CrossRef] [Green Version]
- Benard, N.; Moreau, E.; Griffin, J.; Iii, L.N.C. Slope seeking for autonomous lift improvement by plasma surface discharge. Exp. Fluids 2009, 48, 791–808. [Google Scholar] [CrossRef]
- Luchtenburg, D.M.; Aleksić, K.; Schlegel, M.; Noack, B.R.; King, R.; Tadmor, G.; Günther, B.; Thiele, F. Turbulence Control Based on Reduced-Order Models and Nonlinear Control Design. In Active Flow Control II; King, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 341–356. [Google Scholar] [CrossRef]
- Colonius, T.; Williams, D.R. Control of vortex shedding on two-and three-dimensional aerofoils. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2011, 369, 1525–1539. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tuck, A.; Soria, J. Separation control on a NACA 0015 airfoil using a 2D micro ZNMF jet. Aircr. Eng. Aerosp. Technol. 2008, 80, 175–180. [Google Scholar] [CrossRef]
- Amitay, M.; Glezer, A. Role of Actuation Frequency in Controlled Flow Reattachment over a Stalled Airfoil. AIAA J. 2002, 40, 209–216. [Google Scholar] [CrossRef]
- He, Y.; Cary, A.; Peters, D. Parametric and dynamic modeling for synthetic jet control of a post-stall airfoil. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001. [Google Scholar] [CrossRef]
- Amitay, M.; Kibens, V.; Parekh, D.; Glezer, A. The dynamics of flow reattachment over a thick airfoil controlled by synthetic jet actuators. In Proceedings of the 37th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 11–14 January 1999. [Google Scholar] [CrossRef]
- Crook, A.; Sadri, A.; Wood, N. The development and implementation of synthetic jets for the control of separated flow. In Proceedings of the 17th Applied Aerodynamics Conference, Norfolk, VA, USA, 28 June–1 July 1999. [Google Scholar] [CrossRef]
- Seifert, A.; Pack, L. Oscillatory excitation of unsteady compressible flows over airfoils at flight Reynolds numbers. In Proceedings of the 37th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 11–14 January 1999. [Google Scholar] [CrossRef] [Green Version]
- Amitay, M.; Smith, D.; Kibens, V.; Parekh, D.; Glezer, A. Aerodynamic Flow Control of Bluff Bodies Using Synthetic Jet Actuators. In Proceedings of the IUTAM Symposium on Mechanics of Passive and Active Control, Gottingen, Germany, 7–11 September 1998; Available online: https://link.springer.com/chapter/10.1007/978-94-011-4199444 (accessed on 19 December 2019).
- Smith, D.; Amitay, M.; Kibens, V.; Parekh, D.; Glezer, A. Modification of lifting body aerodynamics using synthetic jet actuators. In Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 12–15 January 1998. [Google Scholar] [CrossRef]
- Amitay, M.; Pitt, D.; Glezer, A. Separation Control in Duct Flows. J. Aircr. 2002, 39, 616–620. [Google Scholar] [CrossRef]
- Parekh, D.; Williams, S.; Amitay, M.; Glezer, A.; Washburn, T.; Gregory, I.; Scott, R. Synthetic Jet Aerodynamic Control on a Full Scale UAV. In Proceedings of the 33rd AIAA Fluid Dynamics Conference and Exhibit, Orlando, FL, USA, 23–26 June 2003. [Google Scholar] [CrossRef]
- Ciuryla, M.; Liu, Y.; Farnsworth, J.; Kwan, C.; Amitay, M. Flight Control Using Synthetic Jets on a Cessna 182 Model. J. Aircr. 2007, 44, 642–653. [Google Scholar] [CrossRef]
- Smith, B.L.; Glezer, A. Jet vectoring using synthetic jets. J. Fluid Mech. 2002, 458, 1–34. [Google Scholar] [CrossRef]
- Maldonado, V.; Farnsworth, J.; Gressick, W.; Amitay, M. Active control of flow separation and structural vibrations of wind turbine blades. Wind. Energy 2010, 13, 221–237. [Google Scholar] [CrossRef]
- Chatlynne, E.; Rumigny, N.; Amitay, M.; Glezer, A. Virtual aero-shaping of a Clark-Y airfoil using synthetic jet actuators. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001. [Google Scholar] [CrossRef]
- Amitay, M.; Horvath, M.; Michaux, M.; Glezer, A. Virtual aerodynamic shape modification at low angles of attack using synthetic jet actuators. In Proceedings of the 15th AIAA Computational Fluid Dynamics Conference, Anaheim, CA, USA, 11–14 June 2001. [Google Scholar] [CrossRef]
- Farnsworth, J.A.N.; Vaccaro, J.C.; Amitay, M. Active Flow Control at Low Angles of Attack: Stingray Unmanned Aerial Vehicle. AIAA J. 2008, 46, 2530–2544. [Google Scholar] [CrossRef]
- Timor, I.; Ben-Hamou, E.; Guy, Y.; Seifert, A. Maneuvering Aspects and 3D Effects of Active Airfoil Flow Control. Flow Turbul. Combust. 2007, 78, 429–443. [Google Scholar] [CrossRef]
- Darabi, A.; Wygnanski, I. Active Management of Naturally Separated Flow over a Solid Surface. Part 1: The forced reattachment process. J. Fluid Mech. 2004, 510, 105–129. [Google Scholar] [CrossRef]
- Darabi, A.; Wygnanski, I. Active Management of Naturally Separated Flow over a Solid Surface. Part 2: The Separation Process. J. Fluid Mech. 2004, 510, 131–144. [Google Scholar] [CrossRef]
- Amitay, M.; Glezer, A. Flow transients induced on a 2D airfoil by pulse-modulated actuation. Exp. Fluids 2005, 40, 329–331. [Google Scholar] [CrossRef]
- Mathis, R.; Lebedev, A.; Collin, E.; Delville, J.; Bonnet, J.-P. Experimental study of transient forced turbulent separation and reattachment on a bevelled trailing edge. Exp. Fluids 2008, 46, 131–146. [Google Scholar] [CrossRef]
- Jones, D.A.; Clarke, D.B. Simulation of Flow Past a Sphere Using the Fluent Code; Maritime Platforms Division: Fishermans Bend, Australia, 2008; pp. 1–35. Available online: https://pdfs.Semanticscholar.org/34cf/df61323f0c871e3c97e7cbce1e1f7dbef00e.pdf (accessed on 2 March 2019).
- Slotnick, J.; Khodadoust, A.; Alonso, J.; Darmofal, D.; Gropp, W.; Lurie, E.; Mavriplis, D. CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences; NASA Langley Research Center: Hampton, VA, USA, 2014; pp. 1–58. Available online: https://ntrs.nasa.gov/search.jsp?R=20140003093 (accessed on 2 March 2019).
- Choi, H.; Moin, P.; Kim, J. Active turbulence control for drag reduction in wall-bounded flows. J. Fluid Mech. 1994, 262, 75. [Google Scholar] [CrossRef]
- Kim, J. Control of turbulent boundary layers. Phys. Fluids 2003, 15, 1093–1105. [Google Scholar] [CrossRef]
- Banaszuk, A.; Naraynan, S.; Zhang, Y. Adaptive Control of Flow Separation in a Planar Diffuser. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 6–9 January 2003. [Google Scholar] [CrossRef]
- Chen, S.; Billings, S.A. Representation of Non-linear Systems: The NARMAX Model. Int. J. Control 1989, 49, 1013–1032. Available online: http://eprints.soton.ac.uk/id/eprint/251145 (accessed on 27 December 2019).
- Billings, S.A. Nonlinear System Identification, NARMAX Methods in the Time, Frequency, and Spatio-Temporal Domains; John Wiley & Sons: Hoboken, NJ, USA, 2013; ISBN 978-1-119-94359-4. Available online: https://www.wiley.com/en-us/exportProduct/pdf/9781119943594 (accessed on 4 January 2019).
- Liu, Y.P. Identification of Nonlinear Systems: The NARMAX Polynomial Model Approach. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 1988. Available online: https://sheffield.libguides.com/guideacse/communicating (accessed on 4 January 2019).
- Leontaritis, I.J.; Billings, S.A. Input-output parametric models for non-linear systems Part II: Stochastic non-linear systems. Int. J. Control 1985, 41, 329–344. [Google Scholar] [CrossRef]
- Thomson, M.; Schooling, S.; Soufian, M. The practical application of a nonlinear identification methodology. Control. Eng. Pr. 1996, 4, 295–306. [Google Scholar] [CrossRef]
- Swain, A.; Billings, S.; Stansby, P.; Baker, M. Accurate prediction of non-linear wave forces: Part I (fixed cylinder). Mech. Syst. Signal Process. 1998, 12, 449–485. [Google Scholar] [CrossRef]
- Billings, S.; Stansby, P.; Swain, A.; Baker, M. Accurate Prediction of Non-Linear Wave Forces: Part II (Responding Cylinder). Mech. Syst. Signal Process. 1998, 12, 487–498. [Google Scholar] [CrossRef]
- Kukreja, S.L.; Brenner, M.J. Nonlinear System Identification of Aero-elastic Systems: A Structure-detection Approach. In Identification and Control; Part II; Springer: London, UK, 2007; pp. 117–145. [Google Scholar] [CrossRef]
- Ching, S.; Eun, Y.; Kabamba, P.T.; Meerkov, S.M. Quasilinear Control Theory: An Overview. In Proceedings of the 18th IFAC World Congress, Milano, Italy, 28 August–2 September 2011. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.M.; Lu, X.Y.; Denney, A.G.; Fan, M.; Wu, J.Z. Post-stall Lift Enhancement on an Airfoil by Local Unsteady Control Part I, Lift, Drag and Pressure Characteristics. In Proceedings of the 4th Shear Flow Control Conference, Snowmass Village, CO, USA, 29 June–2 July 1997; Available online: http://staff.ustc.edu.cn/~xlu/download/JFM_1998.pdf (accessed on 27 December 2019).
- Abbott Ira, H.; Von Doenhoff, A.E. Theory of Wing Sections: Including a Summary of Airfoil Data (Dover Books on Aeronautical Engineering); Courier Corporation: North Chelmsford, MA, USA, March 1959; pp. 324–390. ISBN 978-0486605869. Available online: https://aeroknowledge77.files.wordpress.com/2011/09/589-86488-theory-of-wing-sections-including-a-summary-of-airfoil-data.pdf (accessed on 1 February 2020).
- Dolle, T.J.A. Flap Performance Improvement by Surface Excitation. Master’s Thesis, Aerospace Engineering at Delft University of Technology, Mekelweg, The Netherlands, 2009; pp. 1–144. Available online: http://resolver.tudelft.nl/uuid:985ea160-f12c-472f-9670-fd8ad333ee64 (accessed on 27 December 2019).
- Duvigneau, R.; Visonneau, M. Simulation and optimization of stall control for an airfoil with a synthetic jet. Aerosp. Sci. Technol. 2006, 10, 279–287. [Google Scholar] [CrossRef] [Green Version]
- Anderson, W.; Bonhaus, D.L. An implicit upwind algorithm for computing turbulent flows on unstructured grids. Comput. Fluids 1994, 23, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Bakker, A. Solution Methods Applied Computational Fluid Dynamics. In Lectures of Fluent Instructor; Lecture 5Fluent Inc.: New York, NY, USA, 2002; pp. 1–45. Available online: http://www.bakker.org/dartmouth06/engs150/05-solv.pdf (accessed on 7 January 2020).
- Obeid, S.; Jha, R.; Ahmadi, G. RANS Simulations of Aerodynamic Performance of NACA 0015 Flapped Airfoil. Fluids 2017, 2, 2. [Google Scholar] [CrossRef] [Green Version]
- Rethmel, C.C. Airfoil Leading Edge Flow Separation Control Using Nano-second Pulse DBD Plasma Actuators. Master’s Thesis, The Ohio State University, Columbus, OH, USA, May 2011; pp. 1–80. Available online: http://rave.ohiolink.edu/etdc/view?acc_num=osu1306348260 (accessed on 27 December 2019).
- You, D.; Moin, P. Active control of flow separation over an airfoil using synthetic jets. J. Fluids Struct. 2008, 24, 1349–1357. [Google Scholar] [CrossRef]
- Joseph, D.D.; Liao, T.Y. Potential flows of viscous and viscoelastic fluids. J. Fluid Mech. 1994, 265, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Schroeder, E.J. Low Reynolds Number Flow Validation Using Computational Fluid Dynamics with Application to Micro Air Vehicles. Master’s Thesis, University of Maryland, College Park, MD, USA, 2005; pp. 20–23. Available online: https://drum.lib.umd.edu/handle/1903/3349 (accessed on 2 March 2019).
- Manni, L.; Nishino, T.; Delafin, P.-L. Numerical study of airfoil stall cells using a very wide computational domain. Comput. Fluids 2016, 140, 260–269. [Google Scholar] [CrossRef] [Green Version]
- Sharma, D.M. Experimental Investigations of Dynamic Stall for an Oscillating Airfoil. Ph.D. Thesis, Aeronautical Engineering, Indian Institute of Technology Kanpur, Kanpur, India, 2010; pp. 90–102. [Google Scholar] [CrossRef]
- Rediniotis, O.K. Synthetic Jet Actuation—Modeling, Actuator Development and Application to Separation Control; Texas Engineering Experiment College Station, Texas A&M University: College Station, TX, USA, 2004. Available online: https://apps.dticmil/dtic/tr/fulltext/u2/a424008.pdf (accessed on 4 February 2020).
- Billings, S.A.; Leontaritis, I.J. Identification of Non-Linear System Using Parameter Estimation. In Proceedings of the 6th IFAC Symposium on Identification and System Parameter Estimation, Washington, DC, USA, 7–11 June 1982; Volumes 15, pp. 505–510. Available online: https://www.sciencedirect.com/journal/ifac-proceedings-volumes/vol/15/issue/4 (accessed on 10 October 2019).
- Leontaritis, I.J.; Billings, S.A. Input-output parametric models for non-linear systems Part I: Deterministic non-linear systems. Int. J. Control 1985, 41, 303–328. [Google Scholar] [CrossRef]
- Chiras, N.; Evans, C.; Rees, D. Nonlinear gas turbine computer modelling using NARMAX structures. In Proceedings of the 17th IEEE Instrumentation and Measurement Technology Conference, Baltimore, MD, USA, 1–4 May 2000; pp. 1278–1284. [Google Scholar] [CrossRef]
- Billings, S.A.; Chen, S. Extended model set, global data and threshold model identification of severely non-linear systems. Int. J. Control 1989, 50, 1897–1923. [Google Scholar] [CrossRef]
- Aguirre, L.A.; Billings, S.A. Improved structure selection for nonlinear models based on term clustering. Int. J. Control 1995, 62, 569–587. [Google Scholar] [CrossRef]
- Billings, S.A.; Aguirre, L.A. Effects of the Sampling Time on the Dynamics and Identification of Nonlinear Models. Int. J. Bifurc. Chaos 1995, 5, 1541–1556. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models. J. Hydraul. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Mittal, R.; Kotapati, R.B. Resonant Mode Interaction in a Canonical Separated Flow. In Proceedings of the Sixth IUTAM Symposium on Laminar-Turbulent Transitions, Bangalore, India, 11–15 June 2006; Volume 78, pp. 341–348. [Google Scholar] [CrossRef]
- Ho, C.; Huerre, P. Perturbed Free Shear Layers. Annu. Rev. Fluid Mech. 1984, 16, 365–422. [Google Scholar] [CrossRef]
- Wu, J.-Z.; Lu, X.-Y.; Denny, A.G.; Fan, M.; Wu, J.-M. Post-stall flow control on an airfoil by local unsteady forcing. J. Fluid Mech. 1998, 371, 21–58. [Google Scholar] [CrossRef] [Green Version]
- Kim, K. Feedback Control of FlowFlow Separation Using Synthetic Jets. Ph.D. Thesis, Texas A&M University, Bizzell St, TX, USA, December 2005; pp. 1–187. Available online: https//etd-tamu-2005C-MEEN-Kim.pdf (accessed on 27 December 2019).
- Lavoie, P. Control of Separated Flows. Available online: http://arrow.utias.utoronto.ca/crsa/sssa/2016/lavoie.phil-UTIAS-separation.control-2016sssa.pdf (accessed on 14 February 2020).
- Maldonado, V.; Farnsworth, J.; Gressick, W.; Amitay, M. Active Enhancement of Wind Turbine Blades Performance. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008. [Google Scholar] [CrossRef]
- Benard, N.; Moreau, E. Capabilities of the dielectric barrier discharge plasma actuator for multi-frequency excitations. J. Phys. D Appl. Phys. 2010, 43, 145201. [Google Scholar] [CrossRef] [Green Version]
- Glezer, A.; Amitay, M. Syntheticjets. Annu. Rev. Fluid Mech. 2002, 34, 503–529. [Google Scholar] [CrossRef]
- Tang, H.; Zhong, S.; Jabbal, M.; Garcillan, L.; Guo, F.; Wood, N.; Warsop, C. Towards the Design of Synthetic-jet Actuators for Full-scale Flight Conditions. Flow Turbul. Combust. 2007, 78, 309–329. [Google Scholar] [CrossRef]
- Sharma, R.N. Some Insights into Synthetic Jet Actuation from Analytical Modelling. In Proceedings of the 16th Australasian Flu. Mechanics Conference, Gold Coast, Australia, 2–7 December 2007; pp. 1242–1248. Available online: https://people.eng.unimelb.edu.au/imarusic/proceedings/16/Sharma2.pdf (accessed on 11 August 2019).
- Kugelstadt, T. Active Filter Design Techniques. In Fundamentals of Low-Pass Filters Book; Texas Instruments: Dallas, TX, USA, March 2002; Chapter 16; pp. 1–66. Available online: https://www2.seas.gwu.edu/~ece121/Spring-11/filterdesign.pdf (accessed on 2 March 2019).
- Taylor, J.H.; Strobel, K.L. Applications of a Nonlinear Controller Design Approach based on Quasilinear System Models. In Proceedings of the 1984 American Control Conference, San Diego, CA, USA, 7–10 June 1984; pp. 817–824. [Google Scholar] [CrossRef]
- Taylor, J.H. Sinusoidal-Input Describing Function (SIDF). Available online: https://ocw.mit.edu/courses/aeronautics-and-astronautics/16-30-estimation-and-control-of-aerospace-systems-spring-2004/readings/gelb_ch2_ocr.pdf (accessed on 19 December 2019).
- Schwartz, C.; Gran, R. Describing function analysis using MATLAB and Simulink. IEEE Control. Syst. 2001, 21, 19–26. [Google Scholar] [CrossRef]
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control; Prentice-Hall: Englewood Cliffs, NJ, USA, 1991; pp. 191–433. ISBN 0-13-040890-5. Available online: http://www.ioe.nchu.edu.tw/Pic/CourseItem/4497APPLIED%20NONLINEAR%20CONTROLslotine_Part1.pdf (accessed on 27 December 2019).
- Kim, K.; Kerr, M.; Beskok, A.; Jayasuriya, S. Frequency-domain based feedback control of flow separation using synthetic jets. In Proceedings of the American Control Conference, Minneapolis, MN, USA, 14–16 June 2006. [Google Scholar] [CrossRef]
- Vukic, Z.; Kuljaca, O. Lectures on PID Controllers; University of Texas: Arlington, TX, USA, 2002; pp. 5–41. Available online: http://www.uta.edu/utari/acs/jyotirmay/EE4343/Labs_Projects/pidcontrollers.pdf (accessed on 27 December 2019).
- Taylor, J.H. A General Limit Cycle Analysis Method for Multivariable Systems. In New Approaches to Nonlinear Problems in Dynamics; Holmes, P.J., Ed.; SIAM (Society of Industrial and Applied Mathematics): Philadelphia, PA, USA, 1980; ISBN 978-0898711677. Available online: https://trove.nla.gov.au/version/11860584 (accessed on 2 July 2019).
- Taylor, J.H. Describing Functions. In Electrical Engineering Encyclopedia; John Wiley & Sons, Inc.: New York, NY, USA, 1999. [Google Scholar] [CrossRef]
- Kotapati, R.B.; Mittal, R.; Marxen, O.; Ham, F.; You, D.; Cattafesta, L.N. Nonlinear dynamics and synthetic-jet-based control of a canonical separated flow. J. Fluid Mech. 2010, 654, 65–97. [Google Scholar] [CrossRef] [Green Version]
- Glass, J.W.; Franchek, M.A. Frequency-based nonlinear controller design for regulating systems subjected to time-domain constraints. Int. J. Robust Nonlinear Control 2000, 10, 39–57. [Google Scholar] [CrossRef]
- John, A. Understanding Bode Plots; Motion Engineering Inc. Notes: Santa Barbara, CA, USA, 2019; pp. 1–99. Available online: http://support.Motioneng.com/utilities/bode/bode_16.html (accessed on 2 January 2020).
- Shahzad, U. Design and Analysis of a Control System Using Root Locus and Frequency Response Methods. ITEE J. 2017, 6, 14–19. Available online: https://www.researchgate.net/publication/319653031 (accessed on 12 January 2020).
- Patino, D.; Riedinger, P.; Iung, C. Practical Optimal State Feedback Control Law for Continuous-Time Switched Affine Systems with Cyclic Steady State. Int. J. Control 2010, 82, 1251–1276. [Google Scholar] [CrossRef]
- Berk, Z. Elements of Process Control. In Food Process Engineering Technology; Science Dirt Elvester Book; Springer: New York, NY, USA, 2009; Chapter 5; pp. 129–151. Available online: https://www.sciencedirect.com/book/9780123736604/food-process-engineering-and-technology (accessed on 8 February 2020).
- Horowitz, I.M. Synthesis of Feedback Systems, 1st ed.; Elsevier: Amsterdam, The Netherlands, 1963; ISBN 9781 4 83267708. Available online: https://www.elsevier.com/books/synthesis-of-feedback-systems/horowitz/978-1-4832-3282-9 (accessed on 19 January 2020).
- Vandoren, V. Designing a Feedback Control Loop Starts with Understanding its Objective as well as the Process’s Behavior. Control Engineering Magazine. 7 March 2011, pp. 1–13. Available online: https://www.controleng.com/articles/disturbance-rejection-vs-setpoint-tracking-controllers (accessed on 23 December 2019).
- Åström, K.J. Control System Design. In Lecture Notes for ME 155A on Department of Mechanical Environmental Engineering; University of California: Santa Barbara, CA, USA, 2002; Available online: http://clux.x-pec.com/files/fronter/ENE103%20-%20Reguleringsteknikk/fagstoffsuplement%20Reg%20tek%20engelsk%20.pdf (accessed on 19 December 2019).
- MATLAB. Control System Tool Box, User’s Guide; The Math Works, Inc.: Natick, MA, USA, 2019; pp. 1–1815. Available online: https://www.mathworks.com/help/pdf_doc/control/index.html?s.cid=doc.ftr (accessed on 3 June 2019).
- Seborg, D.E.; Edgar, T.F.; Mellichamp, D.A.; Doyle, F.I., III. Process Dynamics and Control, 4th ed.; Johns Wiley & Sons: Hoboken, NJ, USA, 2017; Available online: https://www.wiley.com/en-us/Process.Dynamics.and.Control.4th.Edition-p-9781119285915 (accessed on 7 January 2020).
















© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Obeid, S.; Ahmadi, G.; Jha, R. NARMAX Identification Based Closed-Loop Control of Flow Separation over NACA 0015 Airfoil. Fluids 2020, 5, 100. https://doi.org/10.3390/fluids5030100
Obeid S, Ahmadi G, Jha R. NARMAX Identification Based Closed-Loop Control of Flow Separation over NACA 0015 Airfoil. Fluids. 2020; 5(3):100. https://doi.org/10.3390/fluids5030100
Chicago/Turabian StyleObeid, Sohaib, Goodarz Ahmadi, and Ratneshwar Jha. 2020. "NARMAX Identification Based Closed-Loop Control of Flow Separation over NACA 0015 Airfoil" Fluids 5, no. 3: 100. https://doi.org/10.3390/fluids5030100





