Investigation of High Lift Force Generation of Dragonfly Wing by a Novel Advanced Mode in Hover
Abstract
:1. Introduction
2. Mathematical and Numerical Formulation
3. Geometry and Kinematics of Dragonfly Wing
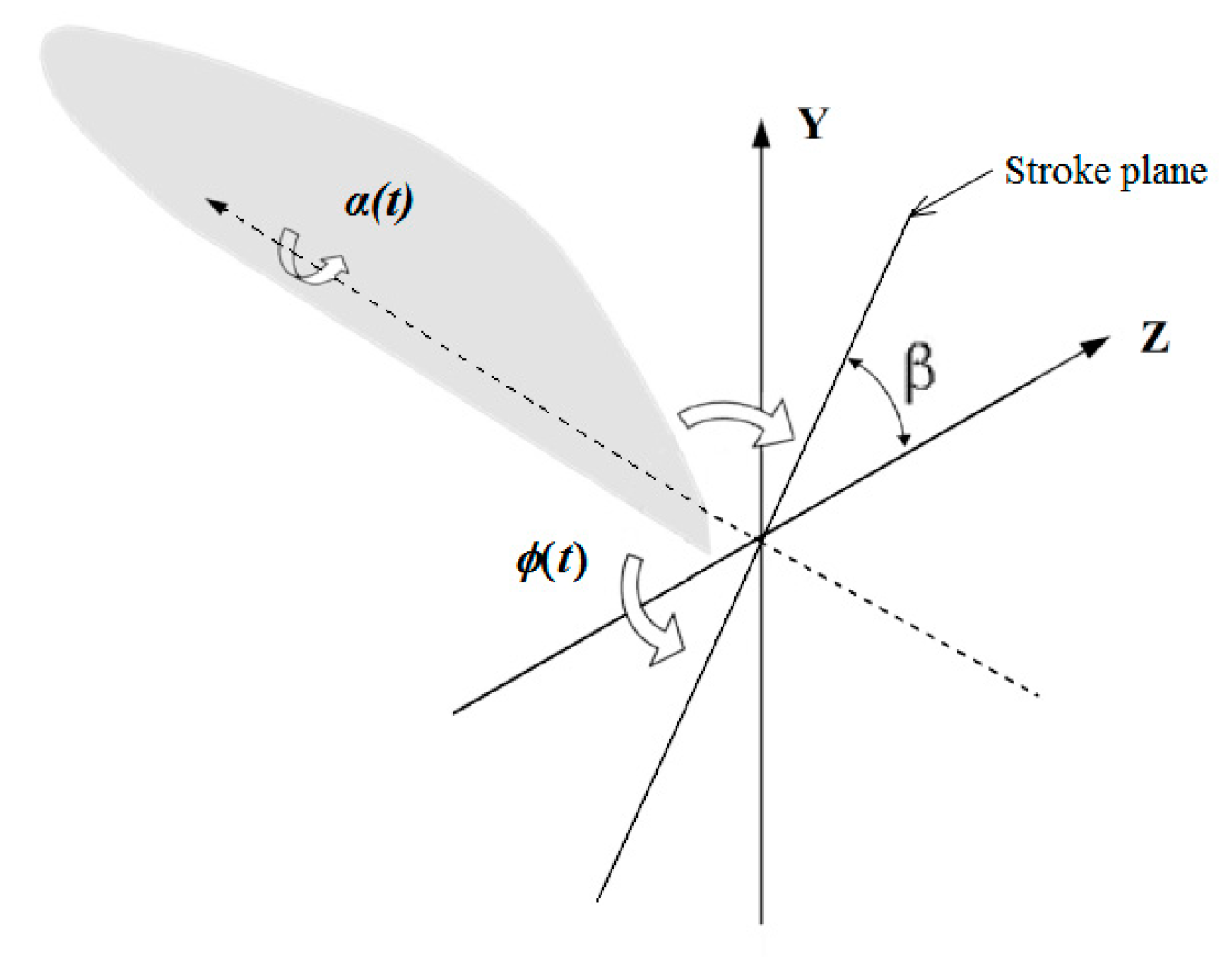
3.1. Geometry of Dragonfly Wing
3.2. The Traditional Kinematics of Hovering Motion
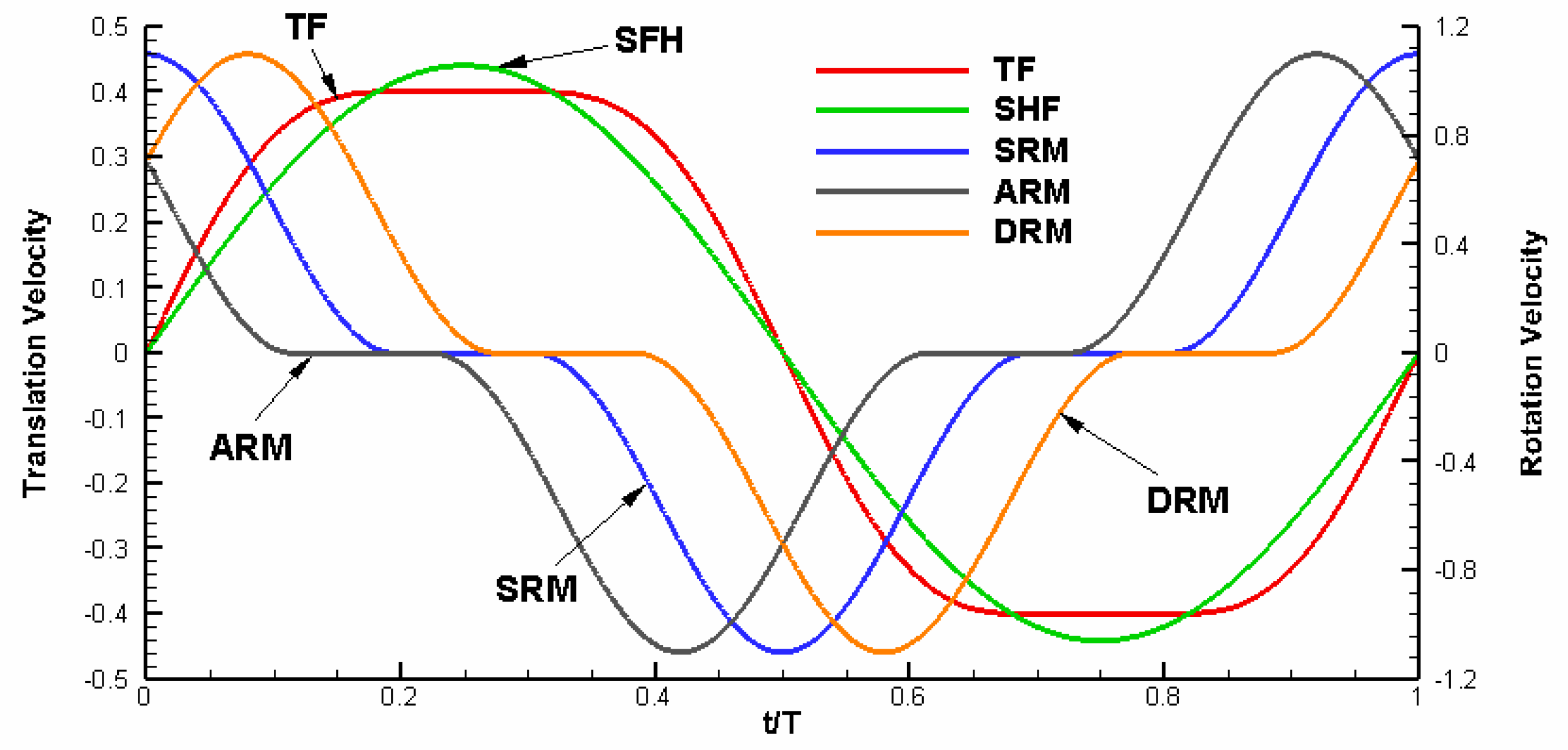
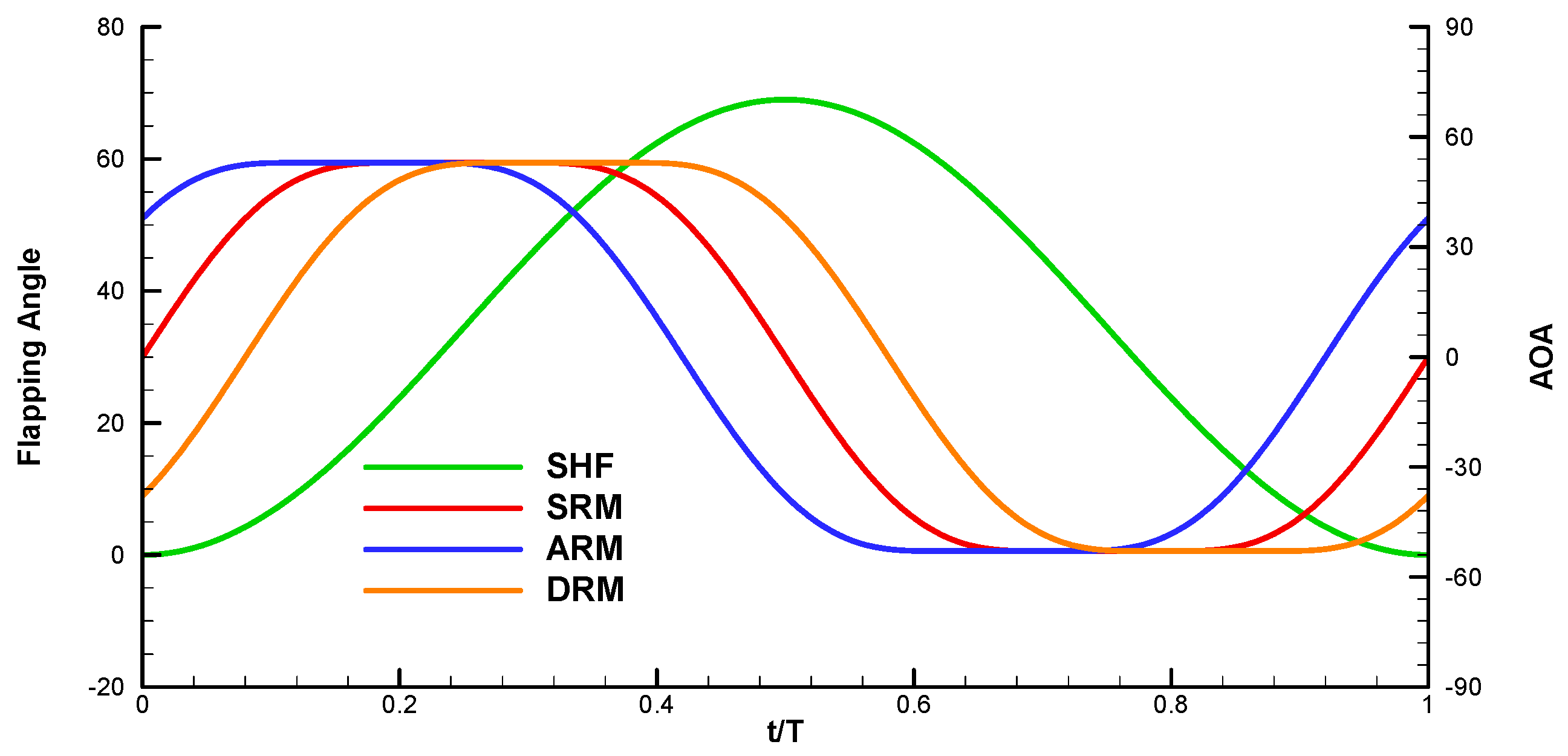
3.3. The New Kinematics of Flapping Motion
3.4. Model Setup
4. Results and Discussions
4.1. Mesh Convergence Test
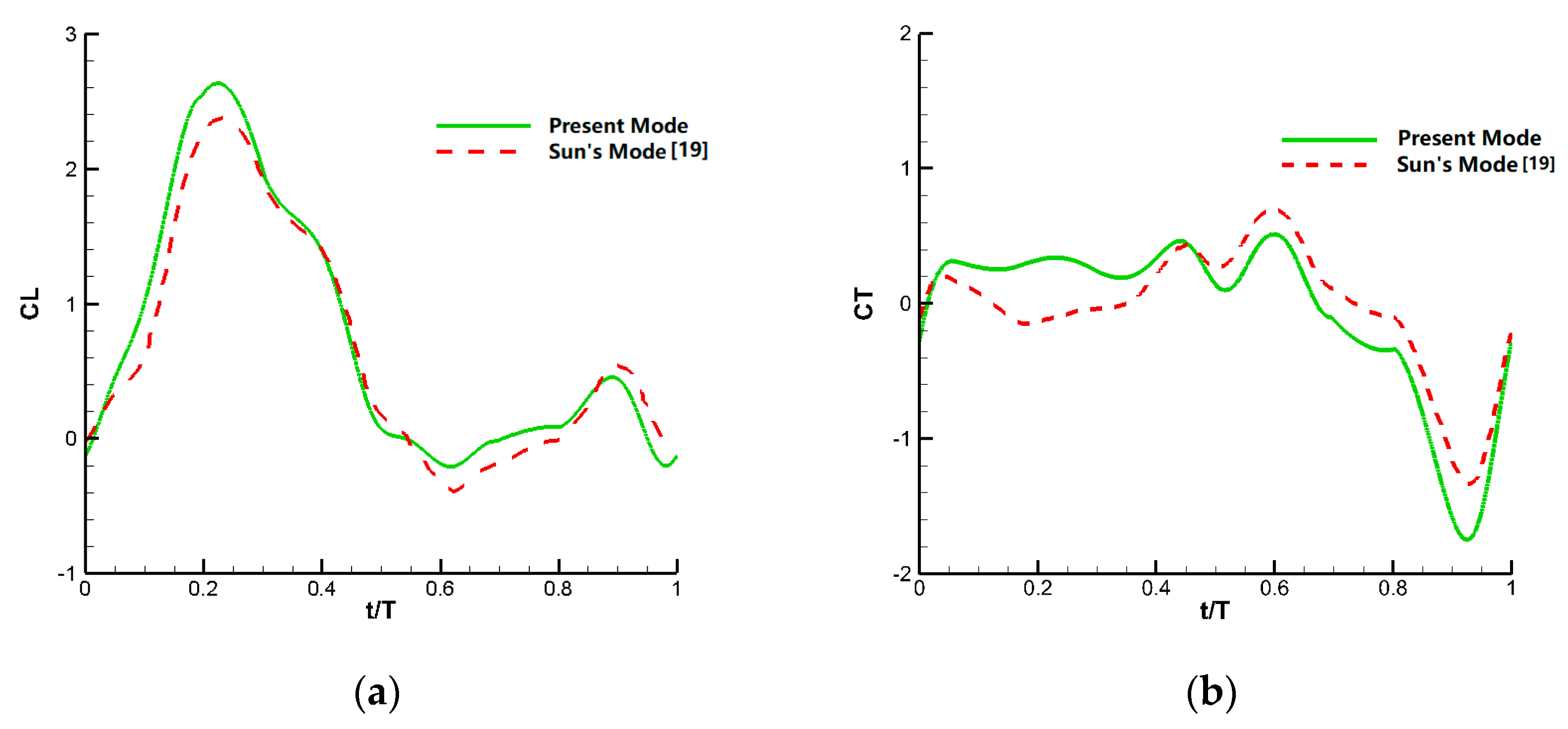
4.2. Aerodynamic Performance of Symmetrical Model and Validation of Results
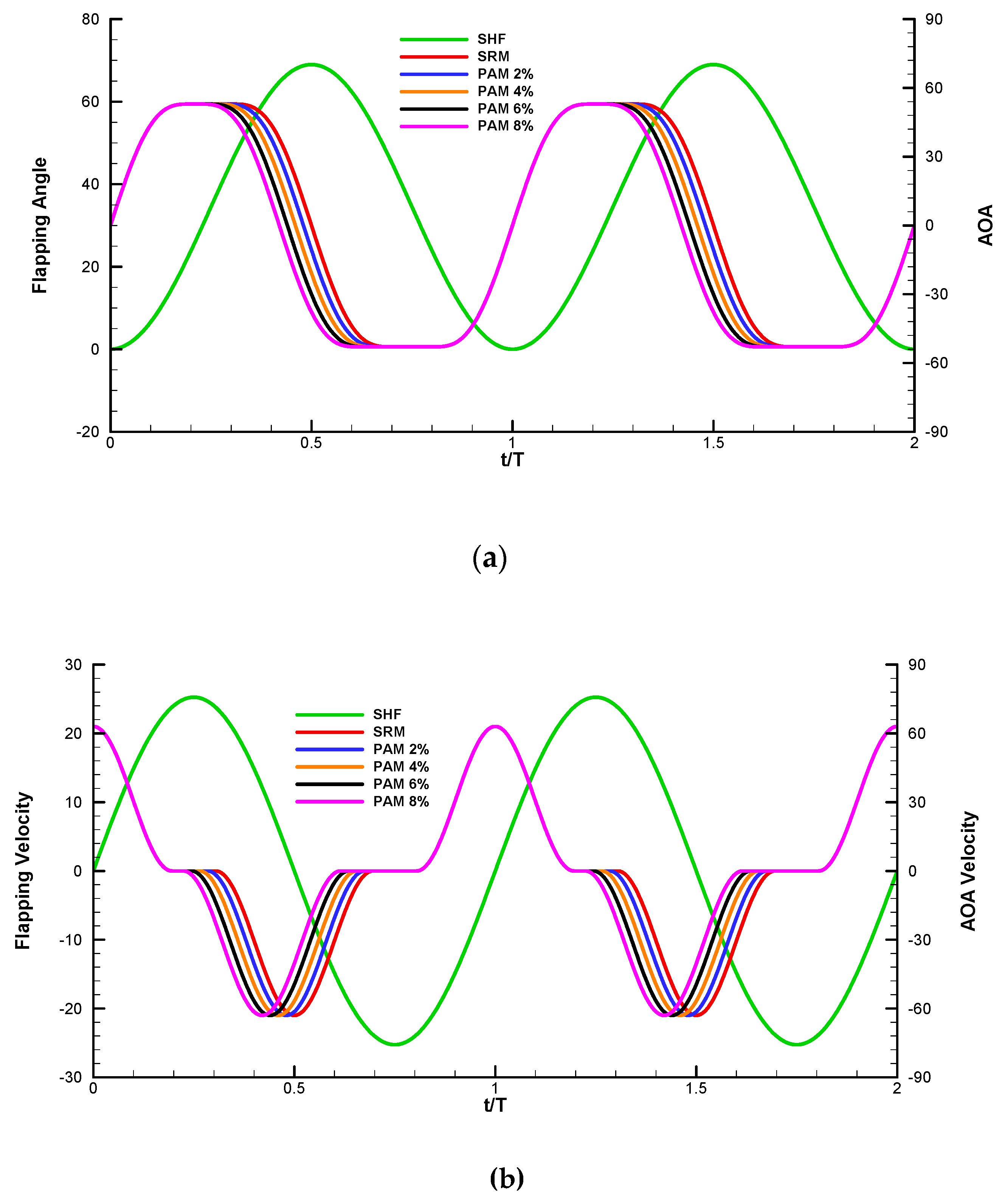
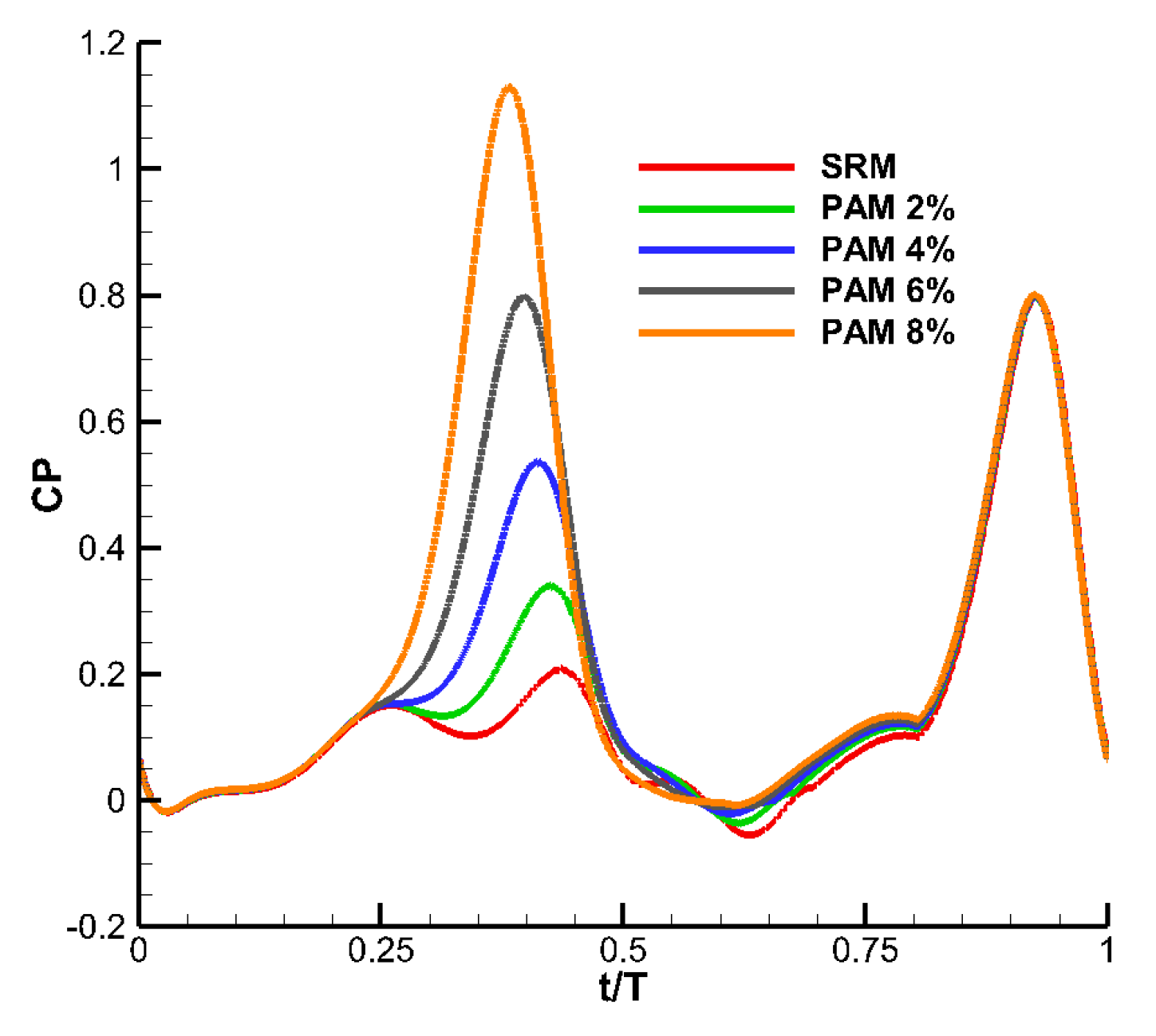
4.3. Aerodynamic Performance of PAM
4.3.1. The Shift Time Effects of PAM and PDM
4.3.2. The Comparisons of PAM and ARM Modes
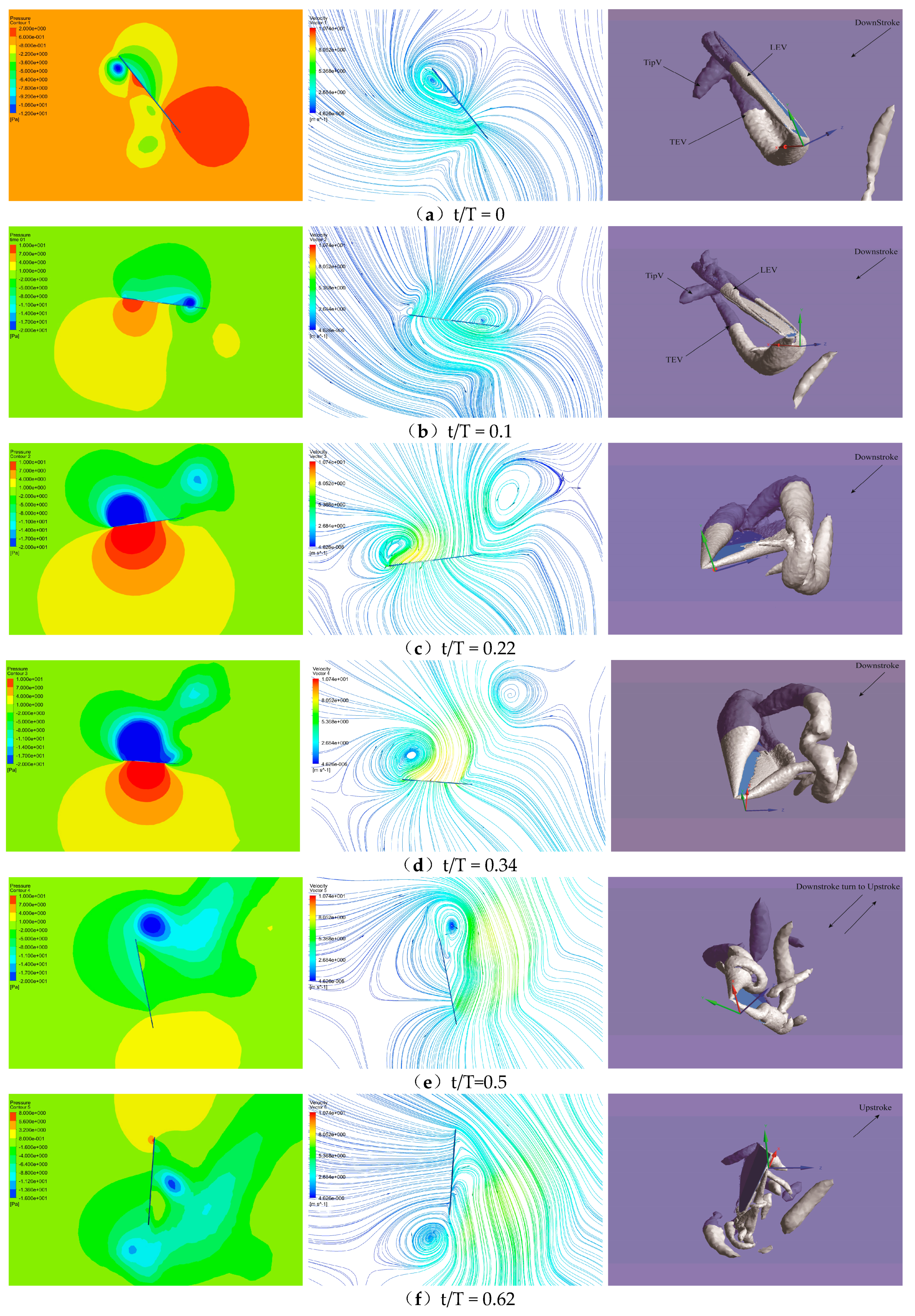
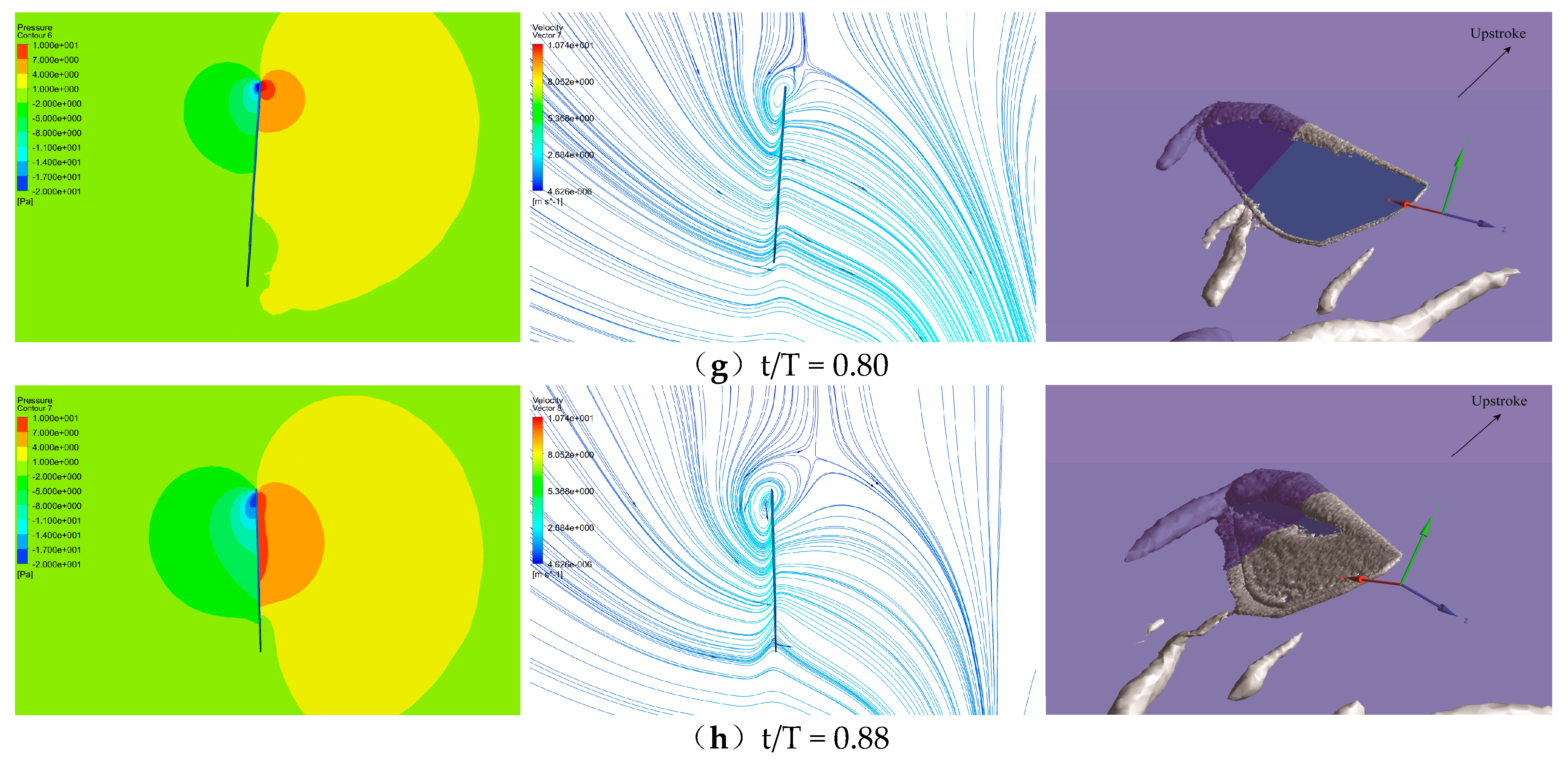
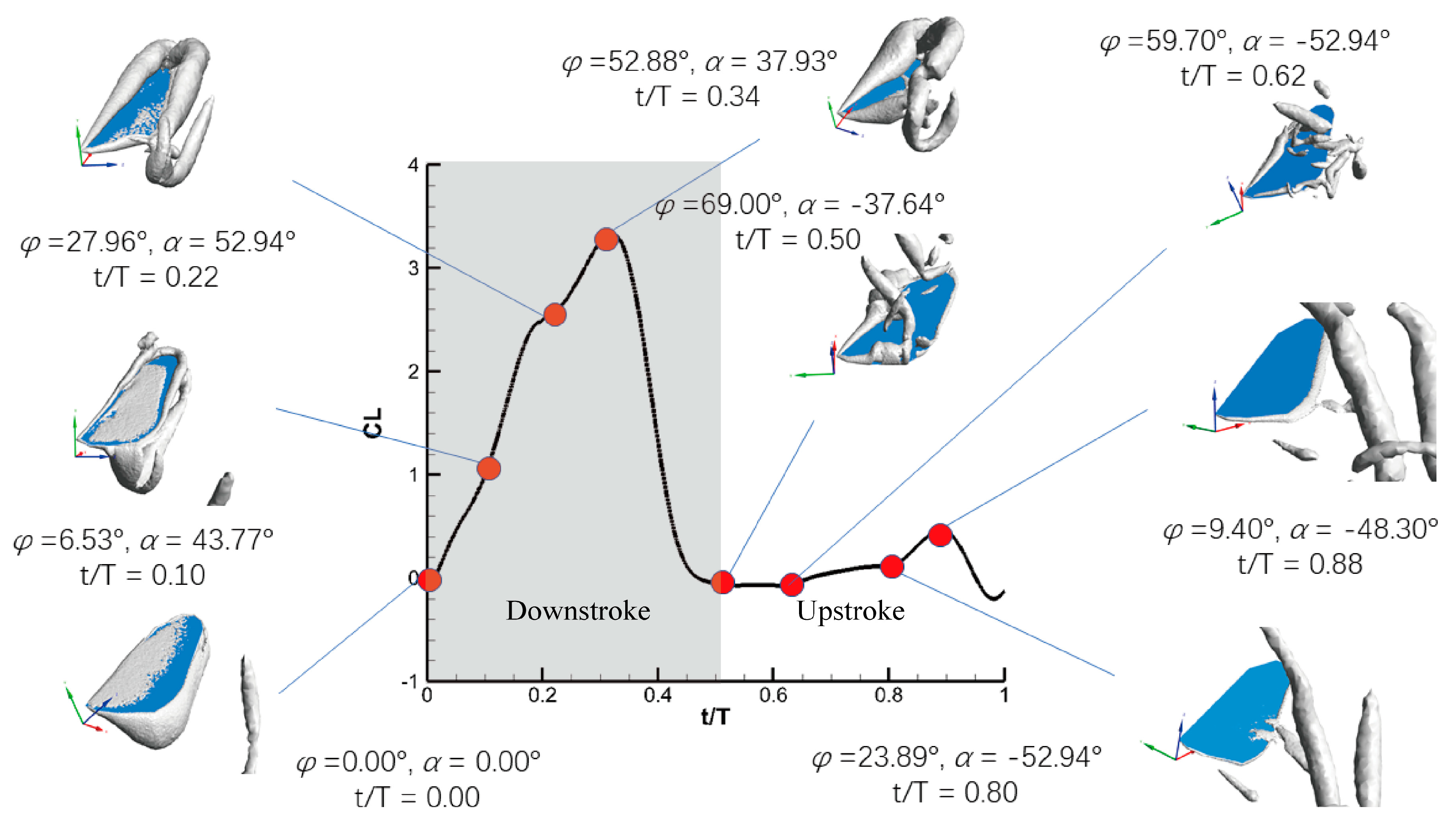
4.4. Vortex Analyses in Lift Force Generation by PAM
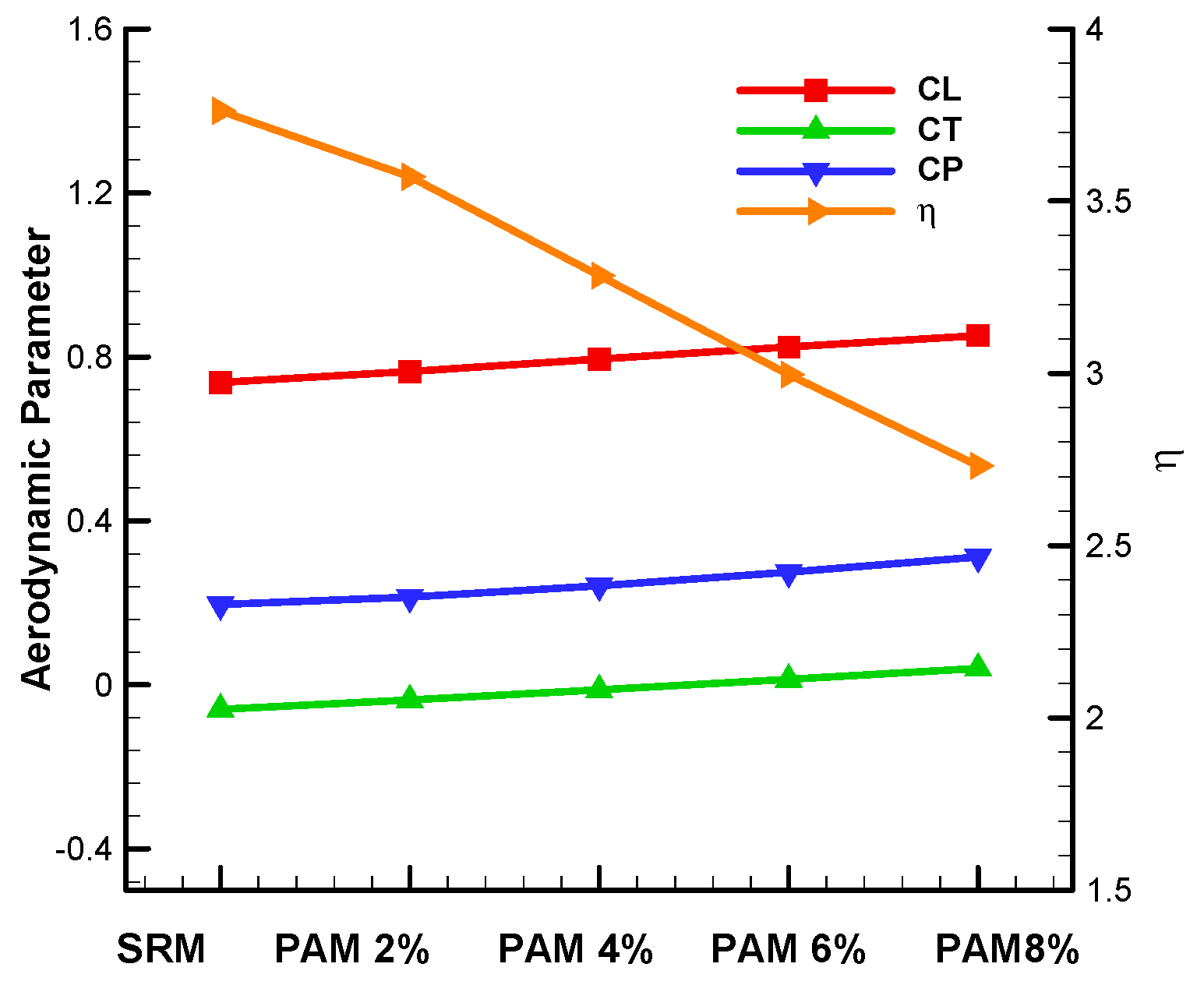
4.5. Energy Consumption Analyses Using PAM
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| symbol | meaning | unit |
| c | average chord length | cm |
| C | preconditioning matrix | - |
| CL | lift force coefficient | - |
| CT | thrust coefficient | - |
| Fc | convective flux | - |
| Fv | viscous flux | - |
| K | unit matrix with first element equal to zero | - |
| R | wing length | cm |
| Re | Reynolds number | - |
| t | time | s |
| t0 | ratio of shifted start time to time period | s |
| trd | divided point from translate to rotate in downstroke | s |
| tud | divided point from translate to rotate in upstroke | s |
| duration of wing flip | s | |
| T | flapping period | s |
| X,Y,Z | rectangular coordinate system | - |
| α | angle of attack | 0 |
| αd | midstroke geometric angle of attack of downstroke | 0 |
| αu | midstroke geometric angle of attack of upstroke | 0 |
| α0 | phase angle of flapping motion | 0 |
| αs | angle of attack in symmetrical rotation mode | 0 |
| β | artificial compressibility coefficient | - |
| β | inclined angle | 0 |
| wing efficiency parameter | - | |
| μ | dynamic viscosity | kg/m/s |
| ρ | air density | kg/m3 |
| φ | flapping angle | 0 |
| φ0 | amplitude of flapping angle | 0 |
References
- Dickinson, M.H.; Gotz, K.G. Unsteady aerodynamic performance of model wings at low Reynolds numbers. J. Exp. Biol. 1993, 174, 45–64. [Google Scholar]
- Dickinson, M.H.; Lehman, F.O.; Sane, S.P. Wing rotation and the aerodynamic basis of insect flight. Science 1999, 284, 1954–1960. [Google Scholar] [CrossRef] [PubMed]
- Ellington, C.P. The aerodynamics of hovering insect flight. VI. Lift and power requirements. Philos. Trans. R. Soc. London B 1984, 305, 145–181. [Google Scholar]
- Sun, M.; Du, G. Lift and power requirements of hovering insect flight. Acta Mech. Sinica 2003, 19, 24–31. [Google Scholar]
- Sun, M. High-lift generation and power requirements of insect flight. Fluid Dyn. Res. 2005, 37, 21. [Google Scholar] [CrossRef]
- Whitney, J.P.; Wood, R.J. Conceptual design of flapping-wing micro air vehicles. Bioinspir. Biomim 2012, 7, 036001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, C.; Rossi, C. A review of compliant transmission mechanisms for bio-inspired flapping-wing micro air vehicles. Bioinspir. Biomim 2017, 12, 025005. [Google Scholar] [CrossRef] [PubMed]
- Weis-Fogh, T. Energetics of hovering flight in hummingbirds and in Drosophila. J. Exp. Biol 1972, 56, 79–104. [Google Scholar]
- Shyy, W.; Trizila, P.; Kang, C.K.; Aono, H. Can tip vortices enhance lift of a flapping wing? AIAA J. 2009, 47, 289–293. [Google Scholar] [CrossRef] [Green Version]
- Trizila, P.; Kang, C.; Visbal, M.; Shyy, W. Unsteady Fluid Physics and Surrogate Modeling of Low Reynolds Number, Flapping Airfoils. In Proceedings of the 38th Fluid Dynamics Conference and Exhibit, Seattle, WA, USA, 23–26 June 2008. [Google Scholar]
- Du, G.; Sun, M. Effects of wing deformation on aerodynamic forces in hovering hoverflies. J. Exp. Biol. 2010, 213, 2273–2283. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Su, X.H.; Zhen, Y.; Cao, Y.W.; Zhao, Y. 2017. Numerical investigations on aerodynamic forces of deformable foils in hovering motions. Phys. Fluids 2017, 29, 041902. [Google Scholar] [CrossRef]
- Walker, S.M.; Thomas, A.L.R.; Taylor, G.K. Deformable wing kinematics in free-flying hoverflies. J. R. Soc. Interface 2009. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, Y.; Tai, C.H. Higher-order characteristics-based method for incompressible flow computation on unstructured grids. AIAA J 2001, 39, 1280–1287. [Google Scholar] [CrossRef]
- Tai, C.H.; Zhao, Y. Parallel unsteady incompressible viscous flow simulation using an unstructured multigrid method. J. Comput. Phys. 2003, 192, 277–311. [Google Scholar] [CrossRef]
- Su, X.H.; Zhao, Y.; Huang, X.H. On the characteristics-based ACM for incompressible flows. J. Comput. Phys. 2007, 227, 1–11. [Google Scholar] [CrossRef]
- Su, X.H.; Cao, Y.W.; Zhao, Y. An unstructured mesh arbitrary Lagrangian-Eulerian unsteady incompressible flow solver and its application to insect flight aerodynamics. Phys. Fluid 2016, 28, 061901. [Google Scholar] [CrossRef]
- Norberg, R.A. Hovering flight of the dragonfly Aeschna juncea L., kinematics and aerodynamics. In Swimming and Flying in Nature; Wu, T.Y.-T., Brokaw, C.J., Brennen, C., Eds.; Springer: Boston, MA, USA, 1975; pp. 763–781. [Google Scholar]
- Sun, M.; Lan, S.L. A computational study of the aerodynamic forces and power requirements of dragonfly (Aeschna juncea) hovering. J. Exp. Biol 2004, 207, 1887–1901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Masoud, H.; Alexeev, A. Resonance of flexible flapping wings at low Reynolds number. Phys. Rev. E 2010, 81, 056304. [Google Scholar] [CrossRef] [PubMed] [Green Version]


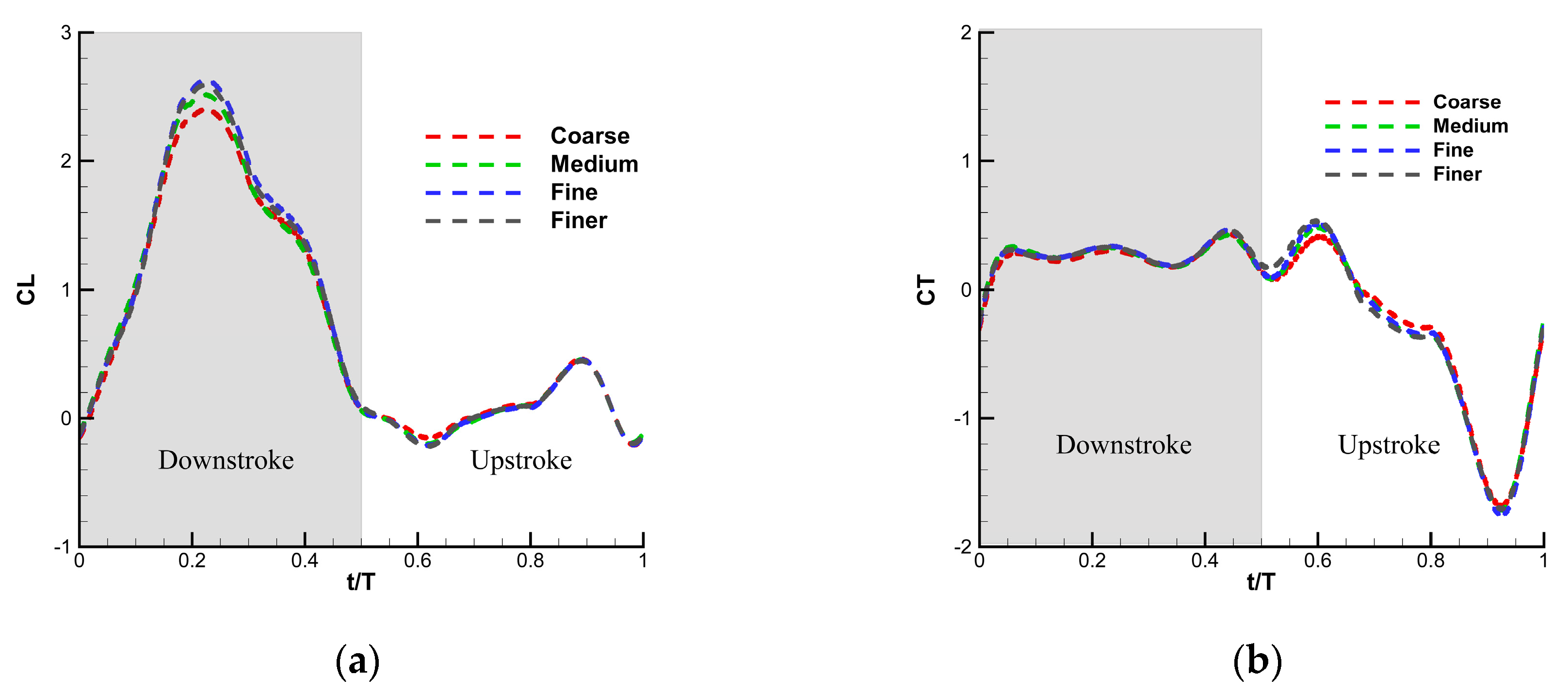


| Mesh Model | Wing Surface Mesh | Total Mesh | Node Point |
|---|---|---|---|
| Coarse | 1024 | 35,566 | 6566 |
| Medium | 1024 | 68,497 | 12,058 |
| Fine | 2786 | 113,614 | 19,995 |
| Finer | 6084 | 233,150 | 40,746 |
| Model | η | |||
|---|---|---|---|---|
| Symmetry | 0.7374 | −0.0593 | 0.196 | 3.7622 |
| 2% | 0.7642 | −0.0368 | 0.214 | 3.5710 |
| 4% | 0.7946 | −0.0124 | 0.242 | 3.2835 |
| 6% | 0.8240 | 0.0134 | 0.275 | 2.9964 |
| 8% | 0.8522 | 0.0401 | 0.312 | 2.7314 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, X.; Zhang, K.; Zheng, J.; Zhao, Y.; Han, R.; Zhang, J. Investigation of High Lift Force Generation of Dragonfly Wing by a Novel Advanced Mode in Hover. Fluids 2020, 5, 59. https://doi.org/10.3390/fluids5020059
Su X, Zhang K, Zheng J, Zhao Y, Han R, Zhang J. Investigation of High Lift Force Generation of Dragonfly Wing by a Novel Advanced Mode in Hover. Fluids. 2020; 5(2):59. https://doi.org/10.3390/fluids5020059
Chicago/Turabian StyleSu, Xiaohui, Kaixuan Zhang, Juan Zheng, Yong Zhao, Ruiqi Han, and Jiantao Zhang. 2020. "Investigation of High Lift Force Generation of Dragonfly Wing by a Novel Advanced Mode in Hover" Fluids 5, no. 2: 59. https://doi.org/10.3390/fluids5020059
APA StyleSu, X., Zhang, K., Zheng, J., Zhao, Y., Han, R., & Zhang, J. (2020). Investigation of High Lift Force Generation of Dragonfly Wing by a Novel Advanced Mode in Hover. Fluids, 5(2), 59. https://doi.org/10.3390/fluids5020059






